Нод 45 и 56: НОД и НОК для 45 и 56 (с решением)

Наибольший общий делитель 5 класс

#5 класс #Математика #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование

Наибольший общий делитель

Верно ли высказывание ? Число 1 – простое. Наименьшее двузначное простое число – это 11. Составное число имеет один делитель. Простое число имеет ровно два делителя. Наибольшее двузначное составное число – это 99. Делителем числа называется число, которое делится на данное без остатка.

Проверьте, правильно ли выполнено разложение на простые множители: 285 2850 10 5 95 3 19 19 1 2·5 2850=2 ·3 ·52 ·19 2850=2 ·3 ·5·5 ·19

Найдите делители каждого из чисел 24 и 60. Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Найдите общие делители чисел 24 и 60.

Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. Найдите общие делители чисел 24 и 60.

Какой из них наименьший? Какой из них наибольший? Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Какой из них наименьший? Какой из них наибольший? Делители 24: 1, 2, 3, 4, 6, 8, 12, 24. Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Чему равен наименьший общий делитель данных чисел?

Как найти наибольший общий делитель данных чисел?

12 24 2 2 6 2 3 3 1 60 30 15 5 1 2 2 3 5 1. Разложить числа на простые множители. Как найти наибольший общий делитель данных чисел?

12 24 2 2 6 2 3 3 1 60 30 15 5 1 2 2 3 5 2.

Взять простые множители, входящие в каждое разложение, и перемножить. НОД( 24, 60)=2 ·2 · 3 = 12 Как найти наибольший общий делитель данных чисел?

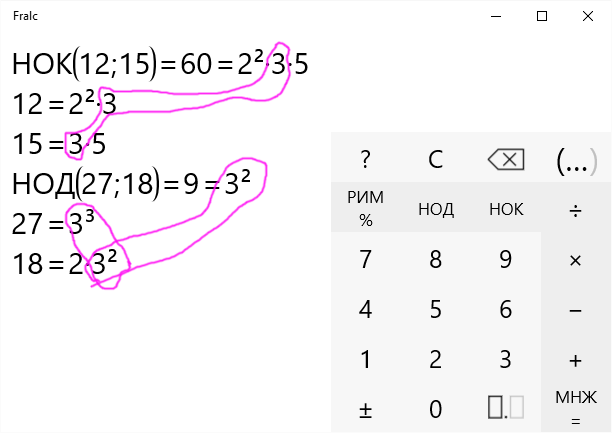
Для того, чтобы найти наибольший общий делитель нескольких чисел, нужно: 1.Разложить числа на простые множители. 2. Взять простые множители, входящие в каждое разложение, и перемножить.

28 56 2 2 14 2 7 7 1 45 15 5 1 3 3 5 1. Разложить числа на простые множители. Найти наибольший общий делитель чисел 56 и 45.

28 56 2 2 14 2 7 7 1 45 15 5 1 3 3 5 2. Среди простых множителей чисел общих нет, значит наименьший и наибольший общий делитель чисел 56 и 45 равен 1. НОД( 56, 45)= 1 Найти наибольший общий делитель чисел 56 и 45

2. Элементы теории чисел Основные определения и понятия темы

Отношение делимости на множестве целых чисел, наибольший общий делитель целых чисел, наименьшее общее кратное целых чисел, простые и составные числа, взаимно простые числа, числовые функции τ(n), σ(n), φ(n), каноническое разложение натурального числа, систематические числа, сравнимость чисел a и b по модулю m.

Основные теоремы и утверждения темы

Теорема о делении с остатком, теорема о нахождении наибольшего общего делителя с помощью алгоритма Евклида, теорема о нахождении НОД и НОК целых чисел с помощью разложения этих чисел на простые множители, теорема о вычислении наименьшего общего кратного, теорема о линейном представлении наибольшего общего делителя целых чисел, теорема о свойствах простых чисел, основная теорема арифметики, теоремы о вычислении числовых функций, критерий сравнимости двух чисел по модулю, свойства сравнений.

Рекомендуемая литература

1. Алгебра и теория чисел. Под ред. Н.Я. Виленкина. Часть 3. М: Просвещение, 1974, — 200 с.

2. А.А. Бухштаб. Теория чисел. М: Просвещение, 1966, — 384 с.

3. В.У. Грибанов, П. И. Титов. Сборник упражнений по теории чиcел. М: Просвещение, 1964, — 144 с.

4. А.А. Кочева. Задачник-практикум по алгебре и теории чисел. Часть 3. М: Просвещение, 1984, — 41 с.

Задание 2.1. Даны целые числа a и b. Найти:

а) наибольший общий делитель a и

b;

b) линейное представление наибольшего общего делителя a и b;

с) наименьшее общее кратное a и b.

1. a=2576, b=154.

2. a=1073, b=3683.

3. a=2585, b=7975.

4. a=4598, b=1474.

5. a=9163, b=2737.

6. a=529, b=1817.

7. a=2346, b=646.

8. a=2223, b=1767.

9. a=1232, b=1672.

10. a=9639, b=2737.

11. a=1541, b=1817.

12. a=476, b=1258.

13. a=1491, b=2247.

14. a=2227, b=9911.

15. a=1541, b=529.

16. a=731, b=663.

17. a=629, b=1445.

18. a=3653, b=3107.

19. a=6919, b=1443.

20. a=1786, b=705.

Задание 2.2. Найти натуральные числа a и b, если:

Задание 2. 3. Для натурального числа n найти:

1. число τ(n) всех натуральных делителей;

2. сумму σ(n) всех натуральных делителей;

3. количество φ(n) натуральных чисел, меньших n и взаимно простых с n.

1. n=1542.

2. n=1440.

3. n=1575.

4. n=1404.

5. n=1224.

6. n=20825.

7. n=22869.

8. n=4320.

9. n=2925.

10. n=7875.

11. n=9016.

12. n=19600.

13. n=15092.

14. n=11424.

15. n=1500.

16. n=1890.

17. n=18144.

18. n=5040.

19. n=2310.

20. n=3963.

Задание 2.4.

1. Найти наименьшее натуральное число, имеющее 12 натуральных делителей.

2. Найти натуральное число, которое делится на два простых числа, если число его натуральных делителей равно 6, а их сумма – 28.

3. Найти количество натуральных чисел, меньших числа 1476 и имеющих с ним наибольшим общим делителем число 41.

4. Найти количество натуральных чисел, меньших числа 300 и имеющих с ним наибольшим общим делителем число 20.

5. Некоторое натуральное число имеет два простых делителя. Его квадрат имеет 15 делителей. Сколько делителей имеет куб этого числа?

6. Найти натуральное число, если оно делится на 3 и на 4 и имеет 14 делителей.

7. Найти количество натуральных чисел, меньших числа 1665 и имеющих с ним наибольшим общим делителем число 37.

8. Найти наименьшее натуральное число, имеющее 10 натуральных делителей.

9. Найти наименьшее натуральное число, имеющее 8 натуральных делителей.

10. Найти натуральное число a=p⋅q, p,q∈ℕ, если p≠q, p—q=2 и φ(a)=120.

11. Найти натуральное число a=3^α⋅5^β⋅7^γ, если φ(a)=3600.

12. Найти количество натуральных чисел, не превосходящих числа 1680 и имеющих с ним наибольшим общим делителем число 24.

13. Найти наименьшее натуральное число, имеющее 15 натуральных делителей.

14. Найти натуральное число a=2^α⋅3^β⋅5^γ⋅7^λ, если φ(a)=40.

15. Найти количество натуральных чисел, меньших 120 и не взаимно простых с числом 30.

16. Найти натуральное число a=2^α⋅3^β⋅5^γ, если φ(a)=320.

17. Найти натуральное число a=p²⋅q², p,q∈ℕ, p≠q, если φ(a)=11424.

18. Некоторое натуральное число имеет два простых делителя, его квадрат – 81 натуральный делитель. Сколько делителей имеет куб этого числа?

19. Найти натуральное число вида a=2^α⋅3^β⋅5^γ, если половина его имеет на 30 делителей меньше, треть – на 35 и пятая часть – на 42 делителя меньше, чем само число.

20. Найти все четырехзначные натуральные числа, имеющие 15 натуральных делителей.

Задание 2.5. Разложить на простые множители число n!, если

1. n=45.

2. n=35.

3. n=40.

4. n=33.

5. n=25.

6. n=30.

7. n=28.

8. n=34.

9. n=55.

10. n=38.

11. n=22.

12. n=36.

13. n=47.

14. n=43.

15. n=37.

16. n=27.

17. n=39.

18. n=41.

19. n=56.

20. n=49.

Задание 2.6. Записать число N в g—ичной системе счисления. Сделать проверку.

1. N=2042, g=2.

2. N=2786, g=3.

3. N=17527, g=8.

4. N=3625, g=3.

5. N=25387, g=6.

6. N=25625, g=8.

7. N=63254, g=5.

8. N=4726, g=2.

9. N=34586, g=4.

10. N=27186, g=5.

11. N=18536, g=7.

12. N=24125, g=9.

13. N=25117, g=4.

14. N=31254, g=3.

15. N=42578, g=6.

16. N=14320, g=9.

17. N=22243, g=5.

18. N=23777, g=4.

19. N=47264, g=7.

20. N=24055, g=6.

Задание 2.7. Вычислить, не переводя в десятичную систему счисления:

1. 3215₍₇₎⋅24₍₇₎ – 11461₍₇₎ : 25₍₇₎+1532₍₇₎.

2. 1141043₍₅₎ : 23₍₅₎+4303₍₅₎⋅34₍₅₎.

3. 50624₍₇₎⋅23₍₇₎ – 150335₍₇₎ : 23₍₇₎.

4. 76₍₈₎⋅64₍₈₎ – 20671₍₈₎ : 131₍₈₎.

5. 351₍₆₎⋅14₍₆₎ – 1153₍₆₎ : 31₍₆₎ – 150₍₆₎.

6. 23213₍₅₎ : 32₍₅₎+113₍₅₎⋅31₍₅₎.

7. 1531315₍₇₎ : 23₍₇₎+343₍₇₎⋅125₍₇₎.

8. 471222₍₈₎ : 27₍₈₎+23₍₈₎⋅563₍₈₎.

9. 425₍₆₎⋅54₍₆₎ – 1520₍₆₎ : 12₍₆₎.

10. 232011₍₅₎ : 104₍₅₎+1234₍₅₎⋅322₍₅₎.

11. 6325₍₇₎⋅56₍₇₎ – 150356₍₇₎ : 13₍₇₎.

12. (215₍₈₎+532₍₈₎)⋅16₍₈₎ – 10302₍₈₎ : 32₍₈₎.

13. 425₍₆₎⋅54₍₆₎ – 10021₍₆₎ : 25₍₆₎.

14. (23054₍₇₎+4326₍₇₎) – 25651₍₇₎ : 56₍₇₎.

15. 3433₍₅₎ : 32₍₅₎+1234₍₅₎⋅34₍₅₎.

16. 104₍₅₎⋅32₍₅₎ – 314012₍₅₎ : 34₍₅₎.

17. 41202₍₆₎ : 54₍₆₎+531₍₆₎⋅43₍₆₎.

18. 113₍₅₎⋅32₍₅₎+21022₍₅₎ : 34₍₅₎.

19. 425₍₆₎⋅54₍₆₎– 145244₍₆₎ : 245₍₆₎.

20. (11031₍₈₎ – 527₍₈₎) : 32₍₈₎+215₍₈₎⋅16₍₈₎.

Задание 2.8. Найти остаток от деления:

1. a=284²⁴⁵ на 90.

2. a=253⁴⁶⁷ на 24.

3. a=538⁴⁶⁷ на 32.

4. a=583⁴⁹² на 27.

5. a=782³²⁷ на 31.

6. a=589⁴⁵⁷ на 41.

7. a=109³⁴⁵ на 14.

8. a=293²⁷⁵ на 48.

9. a=22²³⁴² на 14.

10. a=439²⁹¹ на 60.

11. a=246³⁵¹ на 39.

12. a=345²⁷⁵ на 42.

13. a=34³⁷⁴¹ на 26.

14. a=162⁵⁷⁸ на 24.

15. a=383¹⁷⁵ на 45.

16. a=178²⁷⁴¹ на 22.

17. a=208²⁰⁸ на 23.

18. a=10²⁷³² на 22.

19. a=243¹³² на 34.

20. a=12²⁷⁵¹ на 10.

Наибольший общий делитель чисел 45 и 56 (НОД 45, 56)

Вы ищете НОД чисел 45 и 56? Так как вы находитесь на этой странице, я так думаю! В этом кратком руководстве мы расскажем, как вычислить наибольший общий делитель для любых чисел, которые вам нужно проверить. Давайте прыгать!

Хотите быстро узнать или показать учащимся, как найти НГК двух или более чисел? Включи это очень быстрое и веселое видео прямо сейчас!

Во-первых, если вы торопитесь, вот ответ на вопрос «каков GCF 45 и 56?» :

GCF 45 и 56 = 1

Что такое наибольший общий делитель?

Проще говоря, GCF набора целых чисел — это наибольшее положительное целое число (т. е. целое число, а не десятичное), которое без остатка делится на все числа набора. Он также широко известен как:

• Наибольший общий знаменатель (GCD)
• Наивысший общий множитель (HCF)
• Наибольший общий делитель (НОД)

Существует несколько различных способов расчета GCF набора чисел в зависимости от того, сколько чисел у вас есть и насколько они велики.

Для меньших чисел вы можете просто посмотреть на множители или кратные для каждого числа и найти их наибольшее общее кратное.

Для 45 и 56 эти коэффициенты выглядят так:

• Коэффициенты для 45: 1 , 3, 5, 9, 15 и 45
• Коэффициенты для 56: 1 , 2, 8, 4 , 14, 28 и 56

Как вы видите, перечисляя делители каждого числа, 1 — это наибольшее число, на которое делятся 45 и 56.

Прайм Факторс

По мере того, как числа становятся больше, или если вы хотите сравнить несколько чисел одновременно, чтобы найти GCF, вы можете увидеть, что перечисление всех факторов стало бы слишком большим. Чтобы исправить это, вы можете использовать простые множители.

Перечислите все простые множители для каждого числа:

• Простые множители для 45: 3, 3 и 5
• Простые множители для 56: 2, 2, 2 и 7

Теперь, когда у нас есть список простых множителей, нам нужно найти любые, которые являются общими для каждого числа.

Поскольку нет общих простых множителей между приведенными выше числами, это означает, что наибольший общий множитель равен 1:

GCF = 1

Найдите GCF с помощью алгоритма Евклида

Окончательный метод вычисления GCF чисел 45 и 56 следующий: использовать алгоритм Евклида. Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами НОД.

Если вы хотите узнать больше об алгоритме и, возможно, попробовать его самостоятельно, загляните на страницу Википедии.

Надеюсь, сегодня вы немного изучили математику и поняли, как вычислять НОД чисел. Возьмите карандаш и бумагу и попробуйте сами. (или просто используйте наш калькулятор GCD — мы никому не скажем!)

Процитируйте, дайте ссылку или ссылку на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедитесь, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• Наибольший общий делитель чисел 45 и 56

• «Наибольший общий делитель чисел 45 и 56». VisualFractions.com . По состоянию на 19 февраля 2023 г. http://visualfractions.com/calculator/greatest-common-factor/gcf-of-45-and-56/.

• «Наибольший общий делитель чисел 45 и 56». VisualFractions.com , http://visualfractions.com/calculator/greatest-common-factor/gcf-of-45-and-56/. Доступ 19Февраль 2023 г.

• Наибольший общий делитель чисел 45 и 56. VisualFractions.com. Получено с http://visualfractions.com/calculator/greatest-common-factor/gcf-of-45-and-56/.

Millers Falls Block и специальные рубанки №№ 45–67

• Модели с 07 по 37
• Модели с 68 по 206B
• Модели от 296 до 9775

• Блочные и специальные самолеты домашние
• Самолеты домой
• Дом Миллер Фолс

Большая часть представленной ниже информации получена в результате изучения каталогов Millers Falls. Пожалуйста, имейте в виду, что коллекция, используемая в качестве ресурса, не является исчерпывающей, и копия каталога MF может быть поразительно неточной. Имейте в виду, что перечисленные эквиваленты Стэнли можно назвать «близкими совпадениями» и что некоторые детали самолетов не обязательно идентичны.

Регулируемая блок-плоскость

Оснащен колпачком с эксцентриковым замком и винтовой регулировкой глубины. Железо легировано при двадцати градусах. Корпус покрыт черной эмалью. В более ранних версиях используется ручка из палисандра, а тропическая твердая древесина появляется позже. Уменьшенная версия нет. 75.

1. 1929 — крышка эксцентрика окрашена в красный цвет.
2. к 1936 г. — крышка кулачкового замка окрашена в черный цвет. Номер модели и название производителя выбиты на левой щеке.
3. к 1949 г. — ручка крепится к корпусу видимым снаружи винтом.

Иллюстрация из каталога 1938 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 45	№ 203	5 1/2 дюйма	1 3/8 дюйма	1929	1964

Регулируемая плоскость с малым углом наклона

Оснащена регулируемым горлом, крышкой с эксцентриковым замком и винтовой регулировкой глубины. Железо залегает при двенадцати градусах. Корпус покрыт черной эмалью. Хотя на каталожной иллюстрации изображена черная эмаль, колпачок никелирован. Идентичен раннему нету. 56 за исключением покрытия на крышке.

1. 1929 — название производителя выбито на станине перед ручкой регулировки.
2. к 1936 году — имя производителя выбито на левой щеке, а не брошено в постель. Номер модели выбит на левой щеке.

Millers Falls использовал ту же иллюстрацию для низкоугольных номеров. 46 и 56. Это сделал и автор. Иллюстрация из каталога 1938 года.

№ 46

№ 60

6 дюймов

1 3/8 дюйма

1929

1942

Регулируемая плоскость с малым углом наклона

Оснащена регулируемой горловиной и винтовой регулировкой глубины. Железо залегает при двенадцати градусах. Оснащен никелированной крышкой рычага шарнирного соединения. Корпус покрыт черной эмалью.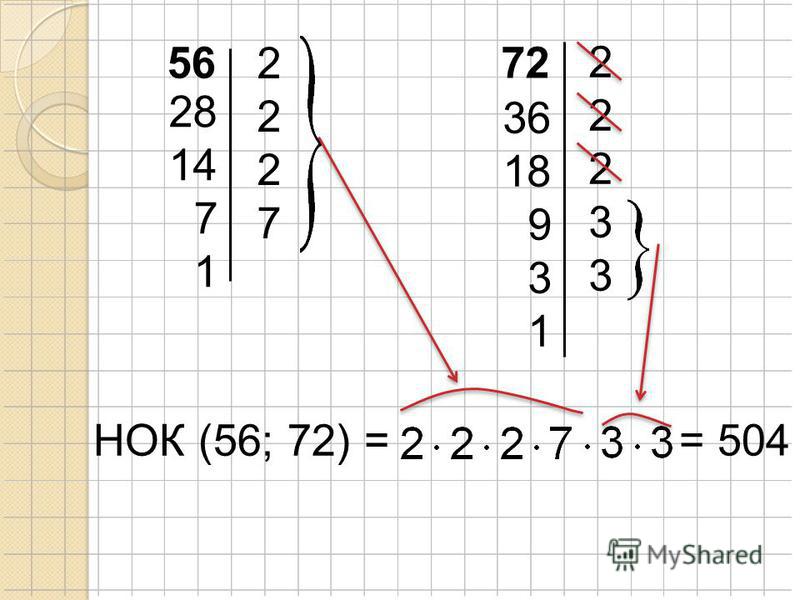

Крышки шарнирных рычагов, которые могут разблокироваться при небрежном обращении, поколения плотников называли «разрушителями костяшек». Идентичен нету. 57, за исключением крышки шарнирного соединения.

1. 1929 — название производителя выбито на станине перед ручкой регулировки. Товарный знак проштампован в нижней передней части крышки рычага.
2. к 1936 г. — торговая марка исчезает с крышки рычага. Имя производителя выбито на левой щеке, а не брошено в постель. Номер модели выбит на левой щеке.

Иллюстрация из каталога 1938 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 47	№ 65	7 дюймов	1 5/8 дюйма	1929	к июню 1948 г.

Регулируемая блок-плоскость

Оснащен винтовым зажимом и рычажной регулировкой глубины. Боковые стороны не фрезерованы. Железо легировано при двадцати градусах. Корпус покрыт черной эмалью. Аналогичен № 5, но с регулятором глубины.

1. 1929— крышка окрашена в красный цвет. Название производителя и номер модели выгравированы на пуговице кровати.
2. к 1936 г. — крышка окрашена в черный цвет.
3. к 1956 году — имя производителя и номер модели больше не бросаются в глаза.

Иллюстрация из каталога 1938 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 55	№ 103	5 1/2 дюйма	1 3/8 дюйма	1929	1960

Регулируемая плоскость с малым углом наклона

Оснащен регулируемым горлом, крышкой с эксцентриковым замком и винтовой регулировкой глубины. Железо залегает при двенадцати градусах. Корпус покрыт черной эмалью.

1. 1929 — крышка эксцентрика окрашена в красный цвет. Название производителя выбито на станине перед ручкой регулировки.
2. на 1936—крышка эксцентрика окрашена в черный цвет. Имя производителя выбито на левой щеке, а не брошено в постель. Номер модели выбит на левой щеке.
3. к 1976 г. — ручка регулировки глубины изготовлена ​​из пластика.

Millers Falls использовал ту же иллюстрацию для низкоугольных номеров. 56 и 57. Это сделал и автор. Иллюстрация из каталога 1938 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 56	№ 60 1/2	6 дюймов	1 3/8 дюйма	1929	1976

Регулируемая плоскость блока

Оснащена регулируемой горловиной, колпачком с эксцентриковым замком, рычагом поперечной регулировки, стойкой и регулировкой глубины колеса. Железо легировано при двадцати градусах.

Самолет выпущен в различном количестве цветовых сочетаний. Были замечены черные и темно-синие корпуса, а также черные, серые, красные и темно-синие крышки эксцентрикового замка. Клейкая этикетка идентифицирует название компании.

Иллюстрация из каталога 1979 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 56	№ 9 1/2	6 дюймов	1 5/8 дюйма	1976	после 1984 г.

Регулируемая плоскость с малым углом наклона

Оснащен регулируемым горлом, крышкой с эксцентриковым замком и винтовой регулировкой глубины. Железо залегает при двенадцати градусах. Корпус покрыт черной эмалью.

1. 1929 — крышка эксцентрика окрашена в красный цвет. Название производителя выбито на станине перед ручкой регулировки.
2. к 1936 г. — крышка кулачкового замка окрашена в черный цвет. На левой щеке выбито название производителя. а не бросать в постель. Номер модели выбит на левой щеке.

Millers Falls использовал ту же иллюстрацию для низкоугольных номеров. 56 и 57. Это сделал и автор.

Иллюстрация из каталога 1938 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 57	№ 65 1/2	7 дюймов	1 5/8 дюйма	1929	1964

Скребок

Оснащен регулируемым держателем резака. Корпус покрыт черной эмалью. Более раннее производство с двойной ручкой из кокоболо — лиственные породы появятся позже. № 65 идентичен № 65. 64, но с нижней частью из палисандра.

Компания Millers Falls использовала одну иллюстрацию для изображения обоих самолетов. Автор тоже так сделал. Иллюстрация из каталога 1938 года.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 64	№ 12	6 1/4 дюйма	2 7/8 дюйма	1929	1942
№ 65	№ 12 1/2	6 1/4 дюйма	2 7/8 дюйма	1929	1942

Регулируемая плоскость с малым углом наклона

Оснащена никелированной крышкой с эксцентриковым замком и винтовой регулировкой глубины. Железо залегает при двенадцати градусах. Корпус покрыт черной эмалью. В более ранних версиях используется ручка из палисандра, а тропическая твердая древесина появляется позже. Был повторно представлен, ок. 1956, как нет. 1455.

1. 1929 — никелированная крышка эксцентрикового замка. Название производителя и номер модели брошены на кровать в задней части самолета.
2. к 1936 г. — крышка кулачкового замка окрашена в черный цвет. Название производителя и номер модели выбиты на левой щеке, а не на кровати.
3. ок. 1941 г. — крышка кулачкового замка окрашена в черный цвет.

Каталоги постоянно изображали самолет с окрашенной крышкой эксцентрикового замка, хотя это было неточным на протяжении большей части существования самолета. Иллюстрация из 1938 каталог.

Модель	Эквивалент Стэнли.	Длина	Резак	Дата начала	Дата окончания
№ 66	№ 61	6 дюймов	1 3/8 дюйма	1929	к 1944 году

Фреза с открытой горловиной

Включает насадку для закрытия горловины для использования на узких поверхностях.