Объединение множеств
Объединением множеств А и В называют множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А и В. Объединение множеств А и В обозначается символом , т.е. .
Определение объединения множеств можно записать как
1.6
Объединение множеств иногда называют суммой множеств и обозначают А+В. Однако свойства объединения множеств несколько отличаются от свойств суммы при обычном арифметическом понимании. Поэтому термином сумма пользоваться не рекомендуется.
Примеры.
Пусть А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда
={1,2,4,5,7,8,12,16,17, 21,30}.
 Тогда
={a,b,c,d,e,f,g}.
Тогда
={a,b,c,d,e,f,g}.
Е сли множества А и В представить в виде точек, ограниченных окружностями А и В соответственно, то объединение множеств представляет собой закрашенную область, ограниченную обоими кругами, как это показано на рис. 1.1.
Понятие объединения множеств можно распространить и на большее число множеств. Пусть М={X1, X2,…. Xn} – совокупность n множеств X1, X2, … Xn, называемую системой множеств. Объединение этих множеств представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств системы М.
1.7
Для объединения множеств справедливы коммутативный и ассоциативный законы:
;
1.
. 1.9
Вполне очевидно, что . 1.10
Пересечением множеств А и В называют множество, состоящее только их тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. Пересечение множеств обозначается символом , т.е. . Определение пересечения может быть записано как
1.11
Пересечение множеств иногда называют произведением множеств, что некорректно.
Примеры.
Если А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}, то ={5,12,21}.
Если A={a,b,c,d}; B={a,d,e,f,g}, то ={a,d}.
Если А – множество
левого круга, В – множество правого
круга, то пересечение множеств
представляет
собой закрашенную область, являющуюся
общей частью обоих кругов, как это
показано на рис. 1.2.
1.2.
Множества А и В называются непересекающимися, если они не имеют общих элементов, т.е. =.
Пример. Пусть А={3,4,5}, B={2,6,7}. Тогда =.
Множества А и В находятся в общем положении, если выполняются три условия:
Существует элемент множества А, не принадлежавший множеству В;
Существует элемент множества В, не принадлежавший множеству А;
Существует элемент, принадлежащий как множеству А, так и множеству В.
Пересечение распространяется и на большее количество множеств. Пусть имеем систему множеств М={X1, X2,…. Xn}. Множество
1.12
представляет собой множество, элементы которого принадлежат каждому из множеств системы М.
Пересечение множеств обладает свойством коммутативности
1. 13
13
и ассоциативности
1.14
Пересечение и объединение множеств 9 класс онлайн-подготовка на Ростелеком Лицей
Повторение знаний о множестве
Пересечение и объединение множеств – операции над множествами.
Пример на применение объединения и пересечения множеств
Пример: В классе 19 учеников: 10 девочек, 9 мальчиков.
10 девочек – это множество .
9 мальчиков – это множество .
Класс из 19 учеников – это множество С, которое объединяет два множества.
Пусть в классе 5 отличников – это множество D.
Из них 2 мальчика – это множество E.
Из какие элементов состоит множество Е?
Мальчики входят в множества В, так как 2 мальчика – отличники, они входят в множество D.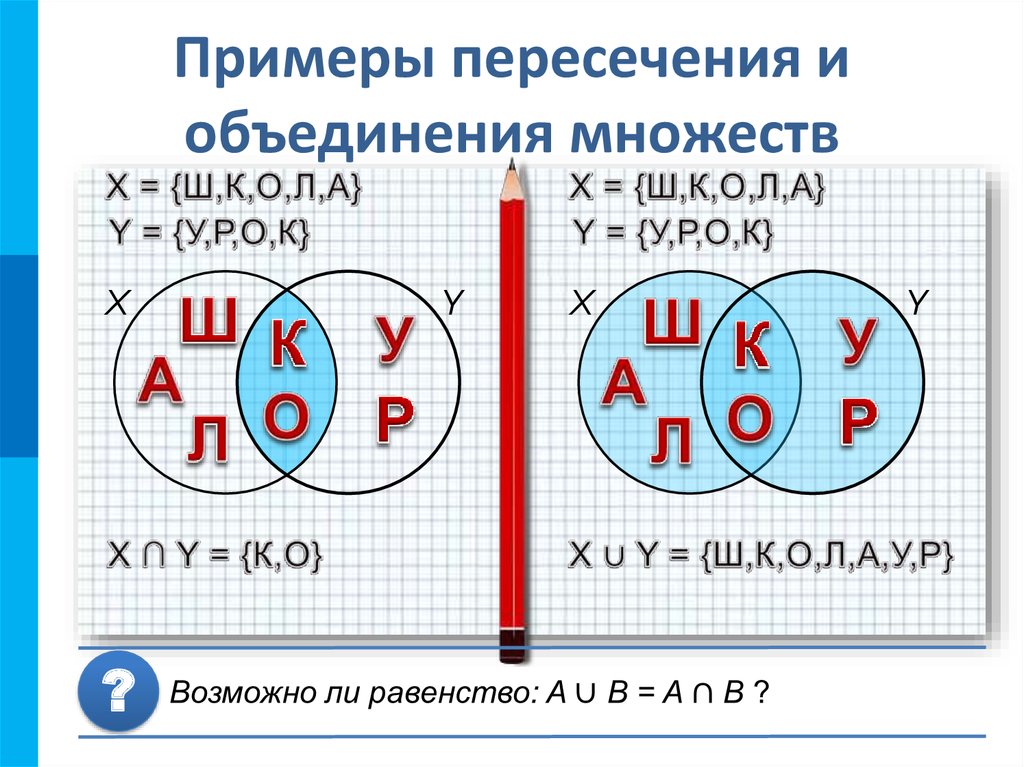
Рис. 1. Пересечение двух множеств
Множество Е есть пересечение двух множеств В и D(рис. 1).
Определение понятия объединение множеств
Определение: объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или В (рис. 3).
Рис. 2. Множества
Рис. 3. Объединение множеств
– знак объединения.
Множество состоит из всех элементов , которые входят или в множество , или в множество . Это можно записать следующим образом:
Пример № 1 на применение определения объединение множеств
Дано множество = и .
Найти объединение множеств .
Решение:
Пример № 2 на объединение бесконечных множеств
Дано множество и .
Найти объединение множеств .
Решение:
Имеем совокупность неравенств:
Пример № 3. Решение квадратного неравенства
Решить квадратное неравенство .
Решение:
Рассмотрим функцию .
Найдём корни функции .
По теореме Виета: .
Имеем объединение двух множеств .
Схематически изобразим график функции:
при или .
Ответ:.
Определение понятия пересечение множеств
Пересечение множеств
Пересечением множеств Aи B называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество А, и в множество В.
– знак пересечения
Рис. 4а. Пересечение множеств
– пересечение множеств на рис. 4а
Рис. 4б. Пересечения множеств нет
На рис. 4б множества не пересекаются, их пересечение – пустое множество
4б множества не пересекаются, их пересечение – пустое множество
Пример № 4 на применение определения пересечения множеств
Даны множества и . Найти пересечение множеств .
Решение
По определению пересечения, решением будут те элементы, которые одновременно входят в оба множества:
– пересечение множеств.
Сравним с объединением:
C= – объединение множеств.
Пример № 5 на пересечение бесконечных множеств
Найти пересечение бесконечных множеств
Решение
Нужно найти такие х, которые принадлежат пересечению :
Нужно решить систему неравенств. На оси изображаем множества и находим их пересечение
Ответ:
.
Сравним с объединением множеств:
Пример № 6. Решение системы неравенств
Решить систему неравенств
Решение:
Рассмотрим ось х:
Ответ:
Пересечением множеств будет:
Итог
Мы рассмотрели объединение и пересечение множеств; решили типовые задачи.
Список литературы
- В.А. Ильин, В.А. Садовничий, Бл.Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. – 3-е изд., перераб. и доп. – М.: Проспект, 2006. – Т. 1. – С. 66. – 672 с.
- А.Г. Мордкович, П.В. Семёнов. Алгебра. 9 класс. В 2-х частях. Часть 1. Учебник. (ФГОС) 16-е издание, исправленное. – М.: Мнемозина, 2013.
- А.Г. Мордкович, П.В. Семёнов. Алгебра. 9 класс. В 2-х частях. Часть 1. Задачник. 16-е издание, исправленное. – М.: Мнемозина, 2013.
- А.Г. Мордкович, П.В. Семёнов. Алгебра. 9 класс. Методическое пособие для учителя. – М.: Мнемозина, 2013.
- А.Г. Мордкович, Н.П. Николаев. Алгебра. 9 класс. В 2-х частях. Часть 1 – учебник. (ФГОС) Учебник для классов с углублённым изучением математики. – М.: Мнемозина, 2014.
- А.Г. Мордкович. Преподавание алгебры. Методическое пособие для учителя. 8–9 класс. – М.: Мнемозина, 2014.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Raal100.
 narod.ru (Источник).
narod.ru (Источник). - Men-c.com (Источник).
- Википедия (Источник).
Домашнее задание
- Даны множества А = {3,5, 0, 11, 12, 19}, В = {2,4, 8, 12, 18,0}. Найдите множества AU В.
- Пусть A – это множество натуральных чисел, делящихся на 2, а В – множество натуральных чисел, делящихся на 4. Какой вывод можно сделать относительно данных множеств?
- Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом – 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
Объединение множеств — формула, значение, примеры
Объединение множеств — одна из операций над множествами, используемая в теории множеств. Помимо объединения множеств, другими операциями над множествами являются разность и пересечение. Все операции над множествами представлены с помощью уникального оператора. Объединение множеств аналогично арифметическому сложению. Объединение двух заданных множеств — это множество, содержащее все элементы, присутствующие в обоих множествах. Символом объединения множеств является «∪». Для любых двух множеств A и B объединение A ∪ B (читается как A union B) перечисляет все элементы множества A, а также множества B. Таким образом, для два заданных набора, Set A = {1,2,3,4,5} и Set B = {3,4,6,8}, A ∪ B = {1,2,3,4,5,6,8 }
Объединение множеств аналогично арифметическому сложению. Объединение двух заданных множеств — это множество, содержащее все элементы, присутствующие в обоих множествах. Символом объединения множеств является «∪». Для любых двух множеств A и B объединение A ∪ B (читается как A union B) перечисляет все элементы множества A, а также множества B. Таким образом, для два заданных набора, Set A = {1,2,3,4,5} и Set B = {3,4,6,8}, A ∪ B = {1,2,3,4,5,6,8 }
В этой статье вы узнаете об объединении множеств, его определении, свойствах с решенными примерами.
| 1. | Что такое Союз наборов? |
| 2. | Диаграмма Венна объединения наборов |
| 3. | Свойства объединения наборов |
| 4. | Объединение наборов Примеры |
| 5. | Часто задаваемые вопросы по Union of Sets |
Что такое объединение наборов?
Объединение любых двух или более наборов приводит к совершенно новому набору, содержащему комбинацию элементов, присутствующих в обоих этих двух или более заданных наборах.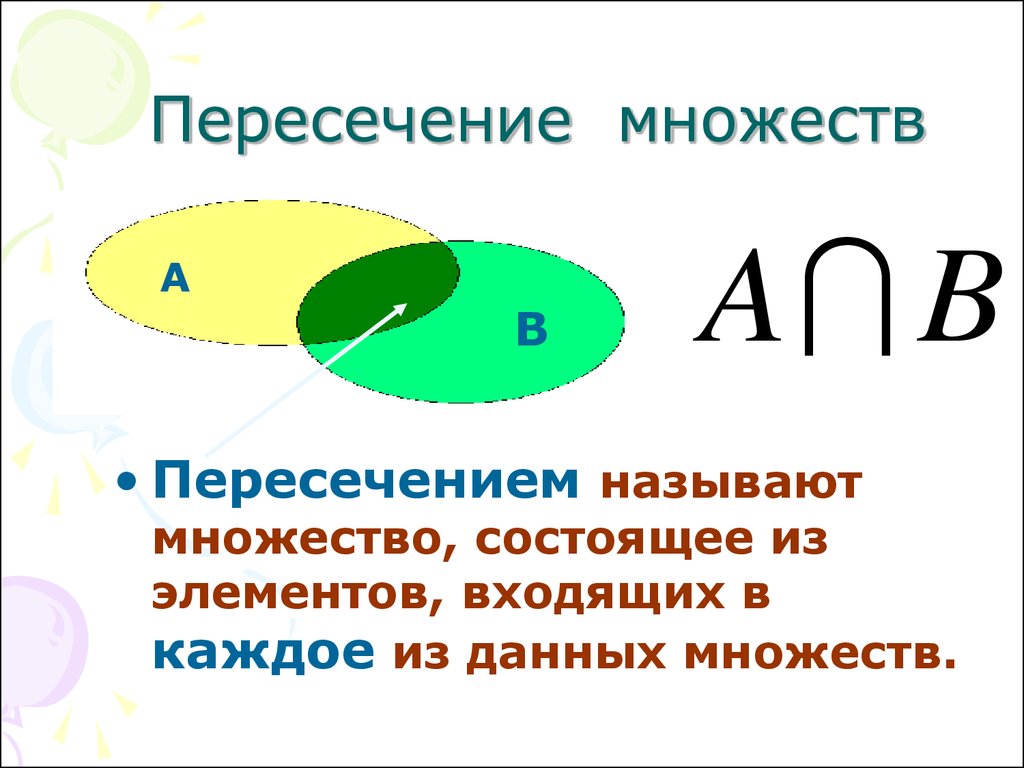
A ∪ B = {x: x ∈ A или x ∈ B}. Здесь x — это элемент, присутствующий в обоих множествах, A и B.
Нахождение объединения множеств
Давайте рассмотрим следующий пример, чтобы понять процесс нахождения объединения множеств. У нас есть два множества A и B, поскольку A = {a, b, j, k} и B = {h, t, k, c}. Нам нужно найти элементы, присутствующие в объединении A и B.
Согласно определению объединения двух множеств результирующее множество будет включать элементы, присутствующие в A, в B или в обоих множествах. Таким образом, элементами обоих множеств являются a, b, c, j, k, h, t, но так как элемент k присутствует в обоих множествах, то он будет рассмотрен только один раз, так как является общим для обоих заданных множеств. Следовательно, в объединении множеств A и B присутствуют элементы a, b, c, j, k, h, t
Следовательно, в объединении множеств A и B присутствуют элементы a, b, c, j, k, h, t
Обозначение объединения множеств
Мы используем уникальное математическое обозначение для представления каждой операции с множествами. Математическое обозначение, которое используется для представления объединения двух множеств, — «∪». Этот оператор называется инфиксной записью и окружен операндами.
Рассмотрим два множества P и Q, где P = {2,5,7,8} и Q = {1,4,5,7,9}. П ∪ Q = {1,2,4,5,7,8,9}.
Диаграмма Венна объединения наборов
Диаграммы Венна относятся к диаграммам, которые используются для представления или объяснения взаимосвязи между заданными операциями множества. Любая операция множества может быть представлена с помощью диаграммы Венна. Диаграммы Венна представляют каждый набор с помощью кругов. Давайте посмотрим, как использовать диаграмму Венна для представления объединения двух множеств. Для этого нам сначала понадобится универсальное множество, подмножествами которого являются два заданных множества P и Q.
На приведенной выше диаграмме Венна область синего цвета показывает объединение множеств P и Q. Это также означает, что объединение между этими множествами включает все элементы, присутствующие в P или Q или в обоих множествах. Хотя здесь использовалась операция объединения двух множеств, диаграмма Венна часто используется для представления объединения нескольких множеств при условии, что множества конечны.
Свойства объединения наборов
В этом разделе вы узнаете о некоторых важных свойствах объединения множеств. Эти свойства необходимо учитывать при объединении множеств.
| Свойства Союза | Обозначение |
|---|---|
| Коммутативная собственность | А ∪ В = В ∪ А |
| Ассоциативная собственность | (А ∪ В) ∪ С = А ∪ (В ∪ С) |
| Идемпотентное свойство | А ∪ А = А |
| Собственность Ⲫ/ Закон о личности | А ∪ Ⲫ = А |
| Собственность универсального набора | А ∪ U = U |
Свойство коммутативности
Согласно свойству коммутативности объединения порядок операционных наборов не влияет на результирующий набор. Это означает, что если изменить положение операндов, решение останется прежним и не изменится. В математических терминах мы можем сказать, что: A ∪ B = B ∪ A
Это означает, что если изменить положение операндов, решение останется прежним и не изменится. В математических терминах мы можем сказать, что: A ∪ B = B ∪ A
Рассмотрим два множества P и Q:
P = {a, m, h, k, j}, Q = {2, 3, 4, 6}
Чтобы доказать коммутативность этих множеств, сначала нужно решить левую часть уравнения, которое имеет вид:
P ∪ Q = {a, m, h, k, j} U {2, 3, 4, 6} = {a, m, h, k, j, 2, 3, 4, 6}
Теперь решим правую часть уравнения:
Q ∪ P = {2, 3, 4, 6} U {a, m, h, k, j} = { a, m, h, k, j, 2, 3, 4, 6}
Теперь мы можем заключить, что свойство коммутативности выполняется для объединения заданных множеств.
Ассоциативное свойство
В соответствии с ассоциативным свойством объединения, когда наборы группируются с помощью круглых скобок, результат не изменяется. Это означает, что когда положение скобок изменяется в любом выражении множеств, включающем объединение, это не повлияет на результирующее множество. В математических терминах
В математических терминах
(A ∪ B) ∪ C = A ∪ (B ∪ C) , где A, B и C — любые конечные множества.
Докажем, что ассоциативность объединения выполняется для следующих множеств:
A = {2, 3, 4}, B = {2, 5, 6}, C = {1, 6, 9}
Решим левую часть приведенного выше уравнения:
(A ∪ B) = {2, 3, 4} U {2, 5, 6} = {2, 3, 4, 5, 6}
(A ∪ B) ∪ C = {2, 3, 4, 5, 6} U {1, 6, 9} = {1, 2, 3, 4, 5, 6, 9}
Теперь решим правую часть уравнения:
(B ∪ C) = {2, 5, 6 } ∪ {1, 6, 9} = {1, 2, 5, 6, 9}
A ∪ (B ∪ C) = {2, 3, 4} ∪ {1, 2, 5, 6, 9} = {1, 2, 3, 4, 5, 6, 9}
Из левой и правой частей уравнений можно заключить, что для заданных множеств A, B и C верно ассоциативное свойство объединения.
Свойство идемпотента
Свойство идемпотента утверждает, что объединение любого набора с одним и тем же набором приведет к самому набору. Математически это можно представить как A ∪ A = A .
Докажем это для A = {2,4,6,8,10}
Таким образом, A ∪ A = {2,4,6,8,10} ∪ {2,4,6,8,10} = {2,4,6,8,10} = A
Свойство Ⲫ/ Закона об идентичности
Согласно свойству нулевого набора, объединение любого набора с нулевым набором или пустым набором приведет к поставил себе. Математически мы можем записать это как А ∪ Ⲫ = А .
Математически мы можем записать это как А ∪ Ⲫ = А .
Докажем это для A = {p,q,r}
Таким образом, A∪∅ = {p,q,r} ∪ {} = {p,q,r}
Свойство универсального множества
As согласно свойству универсального набора, объединение универсального набора с любым набором приводит к универсальному набору. Математически это можно представить как A ∪ U = U .
Докажем это для A = {a,e} и U = {a,b,c,d,e,f,g,h}
, тогда A∪U = {a,e} ∪ {a,b ,c,d,e,f,g,h} = {a,b,c,d,e,f,g,h} = U
Статьи по теме Объединение множеств
Ознакомьтесь со следующими страницами, посвященными объединению множеств
- Конечные и бесконечные множества
- Наборы Формула
Важные замечания по объединению множеств
Вот список нескольких важных моментов, связанных с объединением множеств.
- Объединение любых двух наборов приводит к совершенно новому набору, содержащему элементы, присутствующие в обоих исходных наборах.

- Результирующий набор содержит все элементы, присутствующие в первом наборе, втором наборе или элементы, которые есть в обоих наборах.
- В результате объединения двух непересекающихся множеств получается множество, включающее элементы обоих множеств.
- В соответствии с коммутативным свойством объединения порядок операционных множеств не влияет на результирующее множество.
- Чтобы определить кардинальное число объединения множеств, используйте формулу: n(A ∪ B) = n(A) + n(B) — n(A ∩ B)
Часто задаваемые вопросы по Union of Sets
Что такое объединение множеств в математике?
В математике объединение любых двух множеств представляет собой совершенно новое множество, содержащее элементы, присутствующие в обоих исходных множествах. Результирующий набор представляет собой комбинацию всех элементов, присутствующих в первом наборе, втором наборе или элементов, которые есть в обоих наборах. Например, объединение множеств A = {0,1,2,3,4} и B = {13} можно представить как A ∪ B = {0,1,2,3,4,13}.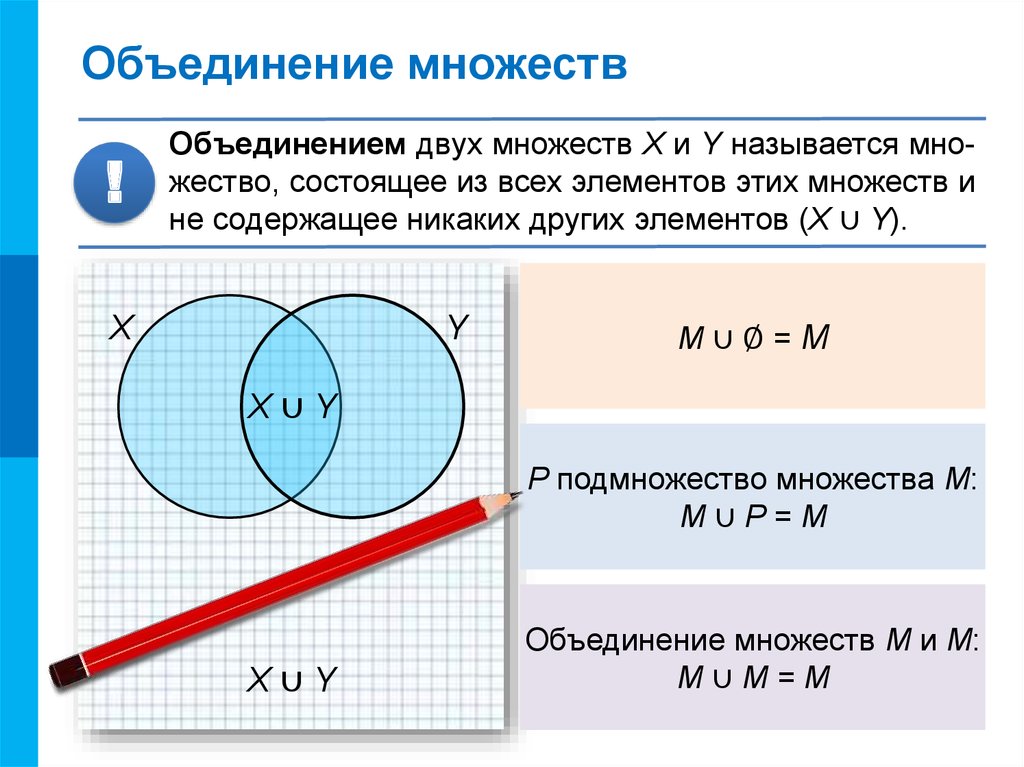
В чем разница между пересечением и объединением множеств?
Объединение любых двух наборов приводит к созданию совершенно нового набора, содержащего элементы, присутствующие в первом наборе, втором наборе или элементы, присутствующие в обоих наборах. Принимая во внимание, что пересечение множеств будет содержать элементы, общие для обоих множеств. Рассмотрим два множества A = {1,2} и B = {2,3}. Здесь объединение A и B будет A ∪ B = {1,2,3}, тогда как пересечение A и B будет A ∩ B = {2}.
Что такое символ объединения наборов?
Математическое обозначение, которое используется для представления объединения наборов, — ‘∪’. Этот оператор называется инфиксной записью и окружен операндами.
Что такое коммутативное свойство объединения множеств?
Согласно коммутативному свойству объединения, порядок операционных наборов не влияет на результирующий набор. При изменении положения операндов решение останется прежним, оно не изменится. В математических терминах мы можем сказать, что: A ∪ B = B ∪ A.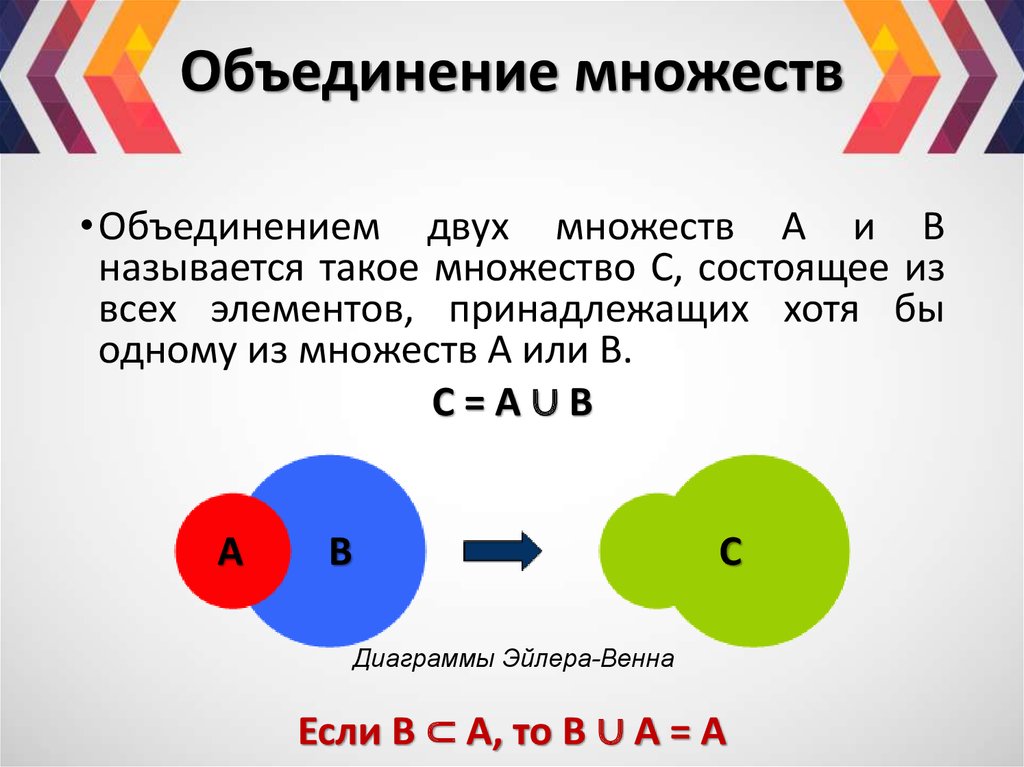
Что такое ассоциативное свойство объединения множеств?
В соответствии с ассоциативным свойством объединения, когда наборы группируются с помощью круглых скобок, результирующий набор не изменяется при изменении положения скобок в любом выражении множеств, включающем объединение. Говоря математическим языком, (A ∪ B) ∪ C = A ∪ (B ∪ C), где A, B и C — любые конечные множества.
Что такое Идемпотентное свойство объединения множеств?
Свойство идемпотента указывает, что объединение любого набора с тем же самым набором приведет к самому набору. Математически это можно показать как A ∪ A = A.
Какое свойство Ⲫ в объединении множеств?
Согласно свойству нулевого набора, объединение любого набора с нулевым набором или пустым набором приведет к самому набору. Математически это можно записать как A ∪ Ⲫ = A.
Что такое объединение множеств a и b?
Объединение двух множеств A и B определяется как множество всех элементов, присутствующих в множестве A и множестве B, или обоих элементах в A и B вместе взятых.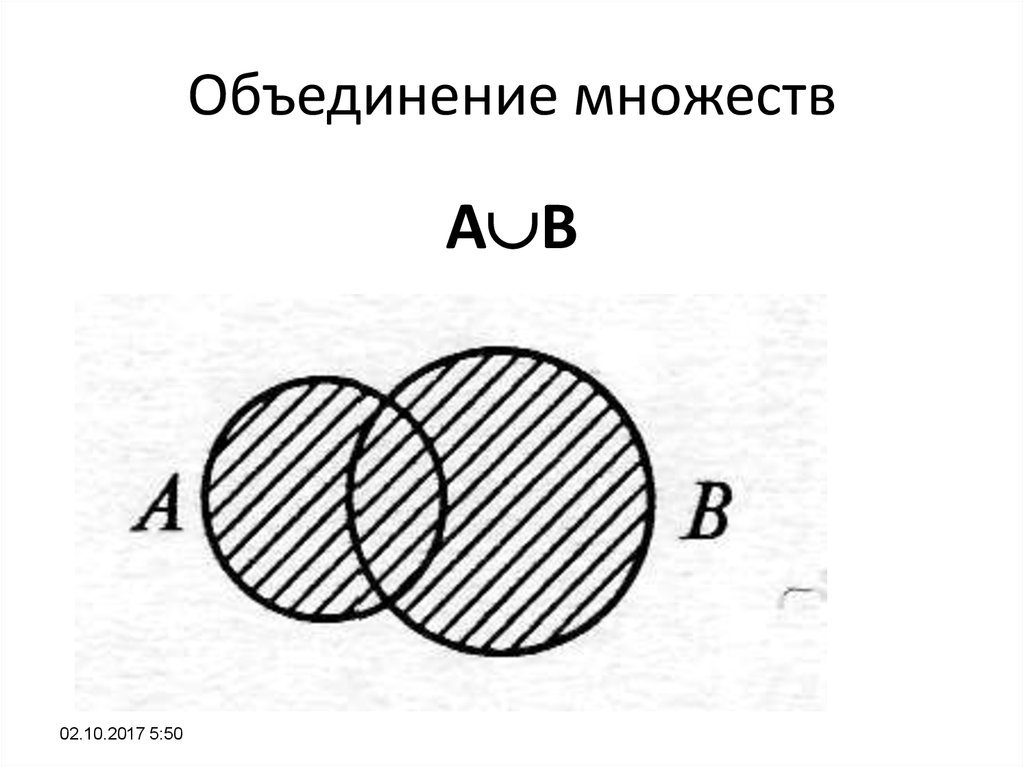 Объединение множеств a и обозначается как «a ∪ b».
Объединение множеств a и обозначается как «a ∪ b».
Что такое процесс поиска союза?
Объединение двух множеств можно рассматривать как наименьшее множество, состоящее из элементов обоих множеств. Чтобы найти объединение двух множеств, выполните шаги, указанные ниже:
- Шаг 1: Рассмотрим два или более заданных множества.
- Шаг 2: Выберите элементы из двух или более заданных наборов и подготовьте результирующий набор, в котором ни один элемент не повторяется.
- Шаг 3: Представьте объединение множеств с помощью символа ‘∪’.
Например, объединение X = {11,12,13,14,15,16,17,18,19,20} и Y = {13,17,21} = X∪Y = {11,12 ,13,14,15,16,17,18,19,20,21}.
Какова мощность объединения множеств A и B?
Для конечных множеств A и B количество элементов подсчитывается с использованием однозначного соответствия, но дубликаты не учитываются. Например, если объединение множеств = {3, 2, 1, 2, 3}, то оно имеет мощность 3.
Операции над множествами | Союз | Пересечение | Дополнение | Разница | Взаимоисключающие | Перегородки | Закон де Моргана | Распределительный закон
← предыдущая
следующая →
Объединение двух множеств представляет собой множество, содержащее все элементы, которые находятся в $A$ или в
$B$ (возможно, оба).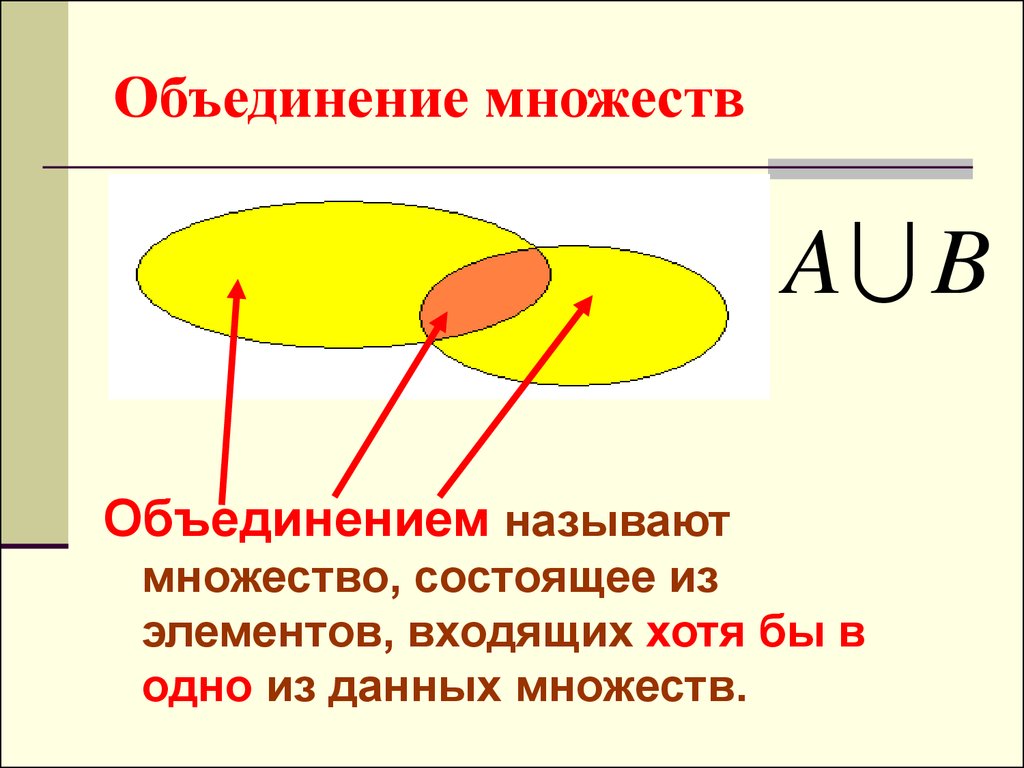 {n} A_i.$$
Например, если $A_1=\{a,b,c\}, A_2=\{c,h\}, A_3=\{a,d\}$, то $\bigcup_{i} A_i=A_1 \cup А_2
\cup A_3=\{a,b,c,h,d\}$. Аналогичным образом мы можем определить объединение бесконечного числа множеств
$A_1 \чашка A_2 \чашка A_3 \чашка\cdots$.
{n} A_i.$$
Например, если $A_1=\{a,b,c\}, A_2=\{c,h\}, A_3=\{a,d\}$, то $\bigcup_{i} A_i=A_1 \cup А_2
\cup A_3=\{a,b,c,h,d\}$. Аналогичным образом мы можем определить объединение бесконечного числа множеств
$A_1 \чашка A_2 \чашка A_3 \чашка\cdots$.
Пересечение двух множеств $A$ и $B$, обозначаемое $A \cap B$, состоит из всех элементов которые оба находятся в $A$ $\underline{\textrm{and}}$ $B$. Например, $\{1,2\}\cap\{2,3\}=\{2\}$. На рис. 1.5 пересечение множеств $A$ и $B$ показано заштрихованной областью с помощью диаграммы Венна.
Рис.1.5 — Заштрихованная область показывает множество $B \cap A$.В более общем случае для множеств $A_1,A_2,A_3,\cdots$ их пересечение $\bigcap_i A_i$ определяется как набор, состоящий из элементов, которые есть во всех $A_i$. На рис. 1.6 показано пересечение трех множеств. 9с$.
Рис.1.8 — Заштрихованная область показывает множество $A-B$. Два множества $A$ и $B$ являются взаимоисключающими или непересекающимися , если они не имеют общих
элементы; т. е. их пересечение есть пустое множество $A \cap B=\emptyset$. В общем, несколько наборов
называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов.
На рис. 1.9 показаны три непересекающихся множества.
е. их пересечение есть пустое множество $A \cap B=\emptyset$. В общем, несколько наборов
называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов.
На рис. 1.9 показаны три непересекающихся множества.
Если земная поверхность является нашим эталонным пространством, мы можем захотеть разделить его на разные континенты. Точно так же страна может быть разделена на разные провинции. В общем, набор непустых наборы $A_1, A_2,\cdots$ — это разбивает множества $A$, если они не пересекаются и их объединение равно $A$. На рис. 1.10 множества $A_1, A_2, A_3$ и $A_4$ образуют разбиение универсального множества $S$.
Рис.1.10 — Набор множеств $A_1, A_2, A_3$ и $A_4$ является разбиением $S$.Вот несколько правил, которые часто бывают полезны при работе с множествами. Вскоре мы увидим примеры их использования.
Теорема : Закон Де Моргана
Для любых множеств $A_1$, $A_2$, $\cdots$, $A_n$ имеем
9с$.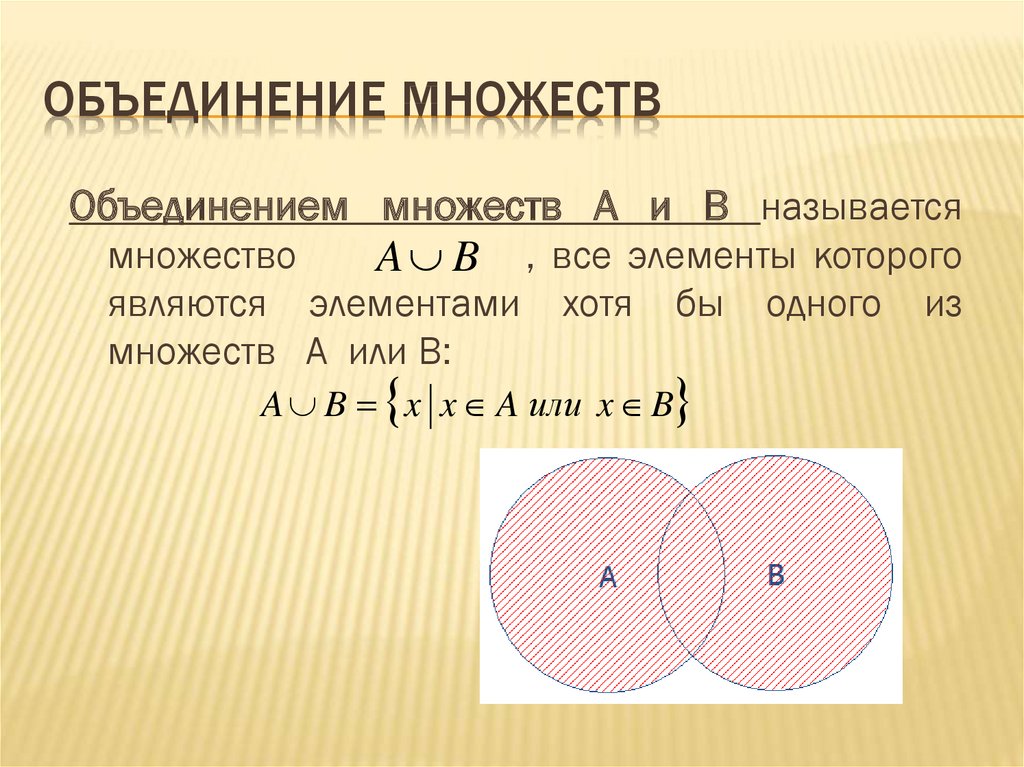
Теорема : Закон распределения
Для любых множеств $A$, $B$ и $C$ имеем
- $A \cap (B \cup C)=(A \cap B) \cup (A\cap C)$;
- $A \чашка (B \крышка C)=(A \чашка B) \крышка (A\чашка C)$.
Пример
Если универсальный набор задан как $S=\{1,2,3,4,5,6\}$ и $A=\{1,2\}$, $B=\{2, 4,5\}, C=\{1,5,6\} $ — три множества, найдите следующие множества:
- $A\чашка B$
- $A\cap B$ 9c=\{3,4,5,6\} \cap \{1,3,6\}=\{3,6\}.$$
- У нас есть $$A \cap (B \cup C)=\{1,2\} \cap \{1,2,4,5,6\}=\{1,2\},$$, что равно такой же как $$(A \cap B) \cup (A\cap C)=\{2\} \cup \{1\}=\{1,2\}.$$
Декартово произведение двух множеств $A$ и $B$, записанное как $A\times B$, представляет собой множество, содержащее упорядоченных пары из $A$ и $B$. То есть, если $C=A \times B$, то каждый элемент $C$ имеет вид $(x,y)$, где
$x \in A$ и $y \in B$:
$$A \times B = \{(x,y) | x \in A \textrm{ и } y \in B \}.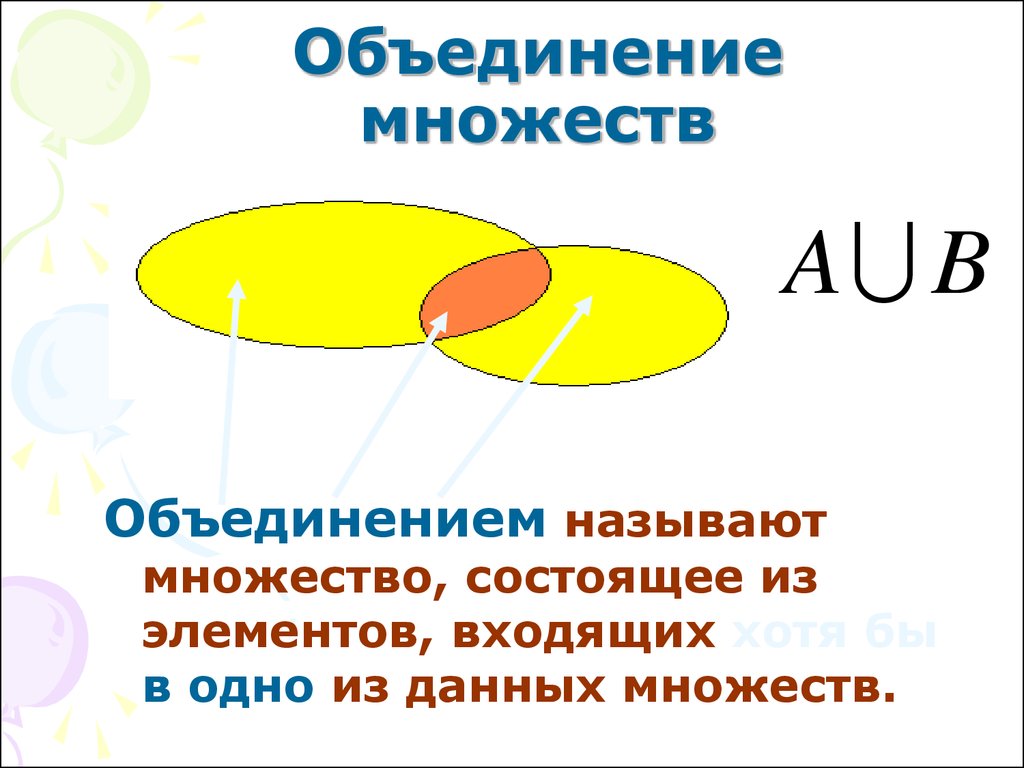 $$
Например, если $A=\{1,2,3\}$ и $B=\{H,T\}$, то
$$A \times B=\{(1,H),(1,T),(2,H),(2,T),(3,H),(3,T)\}.$$
Обратите внимание, что здесь пары упорядочены, например, $(1,H)\neq (H,1)$. Таким образом, $A \times B$ равно не то же, что $B \times A$.
$$
Например, если $A=\{1,2,3\}$ и $B=\{H,T\}$, то
$$A \times B=\{(1,H),(1,T),(2,H),(2,T),(3,H),(3,T)\}.$$
Обратите внимание, что здесь пары упорядочены, например, $(1,H)\neq (H,1)$. Таким образом, $A \times B$ равно не то же, что $B \times A$.
Если у вас есть два конечных множества $A$ и $B$, где $A$ состоит из $M$ элементов, а $B$ состоит из $N$ элементов, то $A \times B$
имеет $M \times N$ элементов. Это правило называется принципом умножения и очень полезно при подсчете
количества элементов в наборах. Количество элементов в множестве обозначается $|A|$, поэтому здесь мы пишем $|A|=M,
|B|=N$ и $|A \times B|=MN$. В приведенном выше примере $|A|=3, |B|=2$, поэтому $|A \times B|=3 \times 2 = 6$.
Аналогично можно определить декартово произведение $n$ множеств $A_1, A_2, \cdots, A_n$ как
$$A_1 \times A_2 \times A_3 \times \cdots \times A_n = \{(x_1, x_2, \cdots, x_n) | x_1 \in A_1 \textrm{ и }
x_2 \in A_2 \textrm{ и }\cdots x_n \in A_n \}.$$
Принцип умножения утверждает, что для конечных множеств $A_1, A_2, \cdots, A_n$, если $$|A_1|=M_1, |A_2|=M_2,
\cdots, |A_n|=M_n,$$ затем $$\mid A_1 \times A_2 \times A_3 \times \cdots \times A_n \mid=M_1 \times M_2
\times M_3 \times \cdots \times M_n.

 Тогда
={a,b,c,d,e,f,g}.
Тогда
={a,b,c,d,e,f,g}.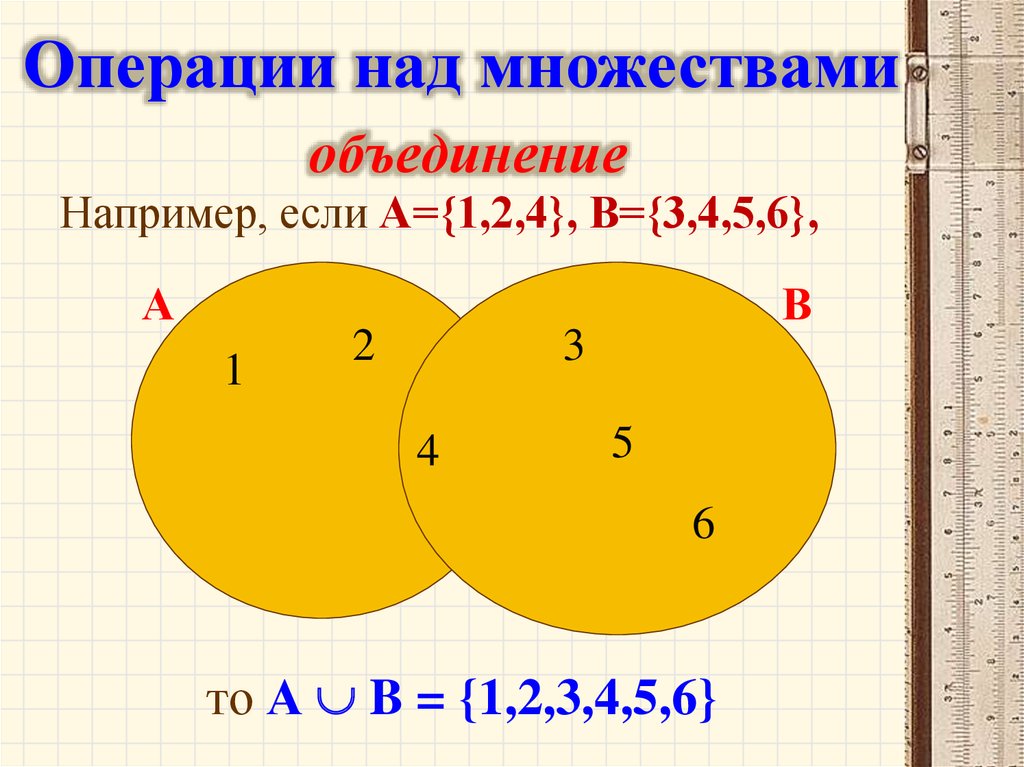 narod.ru (Источник).
narod.ru (Источник). 