Объем фигуры онлайн: Объем фигур | Онлайн калькулятор

Содержание

Найти объем фигур — калькуляторы объемов

Справочник
Онлайн-калькуляторы
Тесты с ответами

С помощью нашего сайта легко понять, как посчитать объем геометрических фигур. Вы находите в разделе нужную фигуру, вводите условие и видите пошаговое решение. Все это моментально в режиме онлайн и совершенно бесплатно.

Чтобы справиться с заданием, используйте сервис Zaochnik и получите:

Нужную формулу. Вам не придется вспоминать или искать формулу, чтобы найти ответ. Она уже заложена в программе.
Автоматические переводы внутри программы. Перед вычислениями не надо приводить данные к одной единице измерения. Вводите условия задания, а сервис выполнит все преобразования.
Точный ответ. Автоматические расчеты исключают вероятность ошибки.

Объем пирамиды
Объем куба
Объем цилиндра (Радиус основания и высота)
Объем цилиндра (Площадь основания и высота)

Объем конуса (Радиус основания и высота)
Объем конуса (Площадь основания и высота)
Объем шара
Объем параллелепипеда

Объем прямоугольного параллелепипеда

Как найти объем тела, изучается в школьной программе, поэтому разделом чаще всего пользуются школьники.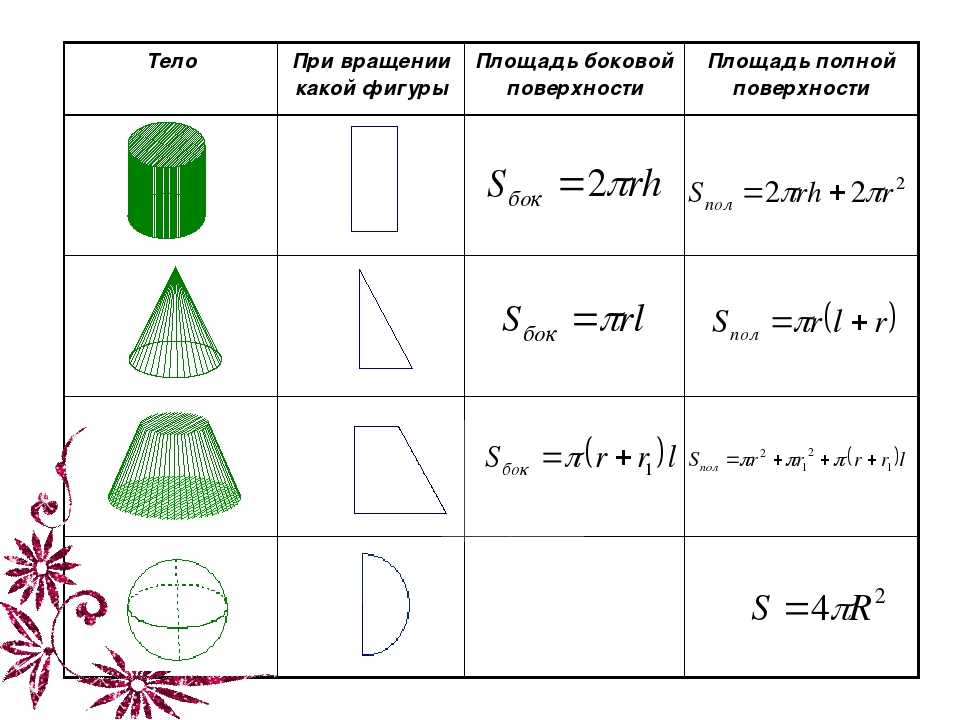 Чем сервис полезен ученику:

Самопроверка. Чтобы подтвердить уверенность в правильности решения, достаточно ввести данные из условия задачи и свериться с собственными вычислениями.
Изучение темы. Не всегда учащийся знает, каким способом решать задачу и какую формулу использовать. Благодаря открытому подробному решению можно заполнить пробелы в знаниях без привлечения репетиторов.

Отработка материала. Запросы на расчет не ограничены в количестве. Во время тренировки визуально запоминаются формулы и алгоритм вычисления.

Программа также полезна родителям учащихся для контроля домашних заданий, преподавателям для проверки работ и планирования уроков. Студенты также могут использовать раздел для ускорения расчетов в составных задачах.

Если у вас нестандартное задание и расчет объема онлайн-калькулятором не принес результата, напишите консультанту. Он предложит вам услуги преподавателя, который по выгодной цене доступно объяснит тему и поможет с расчетом.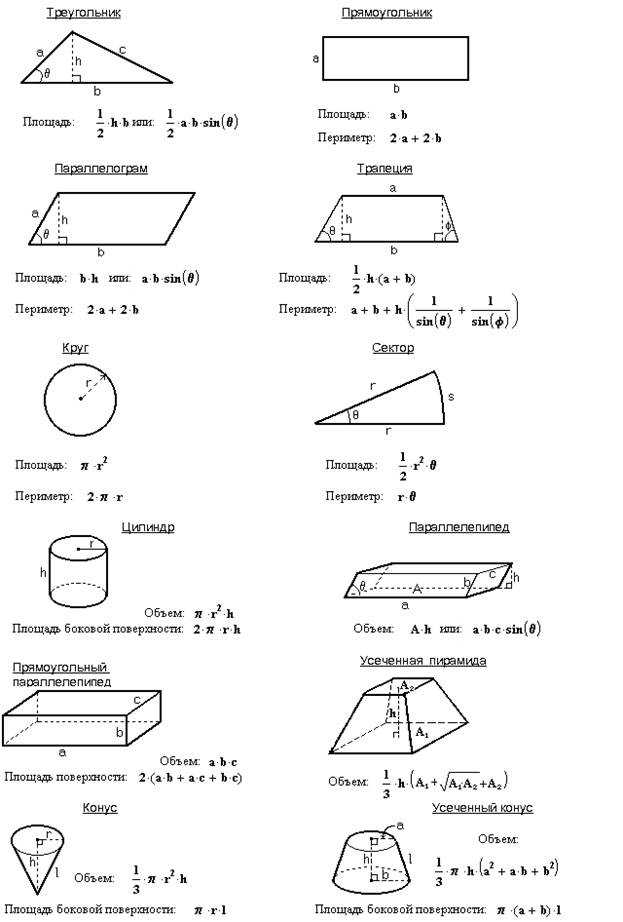

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

Процент
Решение матриц

Точка, прямая, плоскость
Конвертеры
Объем фигур
Калькуляторы площади фигур
Решение уравнений
Операции над векторами

Периметр фигур

Популярные калькуляторы

Решение систем линейных уравнений методом Гаусса
Угол между векторами
Каноническое уравнение прямой проходящей через две точки
Решение систем линейных уравнений методом Крамера

Длина вектора. Модуль вектора
Площадь треугольника (по 3 сторонам)

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Онлайн-калькулятор расчета объема цилиндра: через диаметр, радиус

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы для расчета объема цилиндра через площадь основания/радиус/диаметр и высоту.

Расчет объема
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислен объем фигуры с учетом указанных данных.

Через площадь основания и высоту

Формула расчета

Через радиус основания и высоту

Формула расчета

Через диаметр основания и высоту

Формула расчета

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Вычислить объем куба онлайн

Если вам нужно c Вычислить объем куба Наш онлайн-инструмент позволяет найти объем этой правильной геометрической фигуры, просто введя длину одной из ее сторон.

Когда вы нажмете кнопку расчета, вы получите желаемый результат.

Разделы статьи

Формула для вычисления объема куба
Как вычислить площадь куба, не зная длины ребра

Формула для вычисления объема куба

Куб – правильная геометрическая фигура. , который состоит из шести граней квадратной формы. Это означает, что все ребра имеют одинаковые размеры.

Это значительно упрощает вычисления, потому что, если вы хотите вычислить площадь квадрата, мы должны возвести длину стороны в квадрат, а чтобы узнать объем, нам нужно возвести в куб значение ребра Это представлено в следующем математическом выражении. формула:

объем куба = a ³

Представим, что у нас есть куб со стороной 3 сантиметра, в этом случае объем фигуры будет:

объем = 3 х 3 х 3 х 3 = 27 см ³

Важно помнить, что так как мы работаем с объемами, то единица также поднимается на в кубе.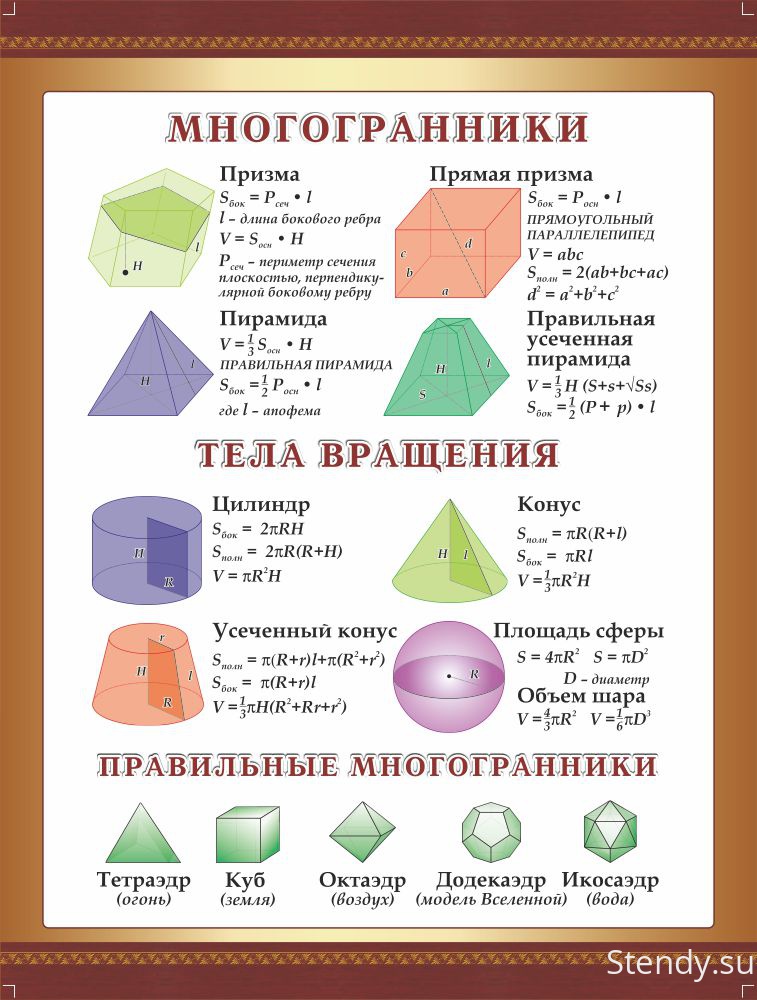 В предыдущем примере мы начинаем с сантиметров и заканчиваем кубическими сантиметрами.

Если вы хотите рассчитать объем прямоугольного куба, то рекомендуем вам научиться вычислять объем прямоугольного куба. объем призмы практически одинаков, но с учетом разных измерений каждой стороны.

Как вычислить площадь куба, не зная длины ребра

Возможно, в математическом упражнении для вычислить объем куба не дайте нам длины ребра, но дайте нам, сколько составляет поверхность одной из его граней.

В этом случае мы знаем, что поверхность квадрата равна квадрату основания (b ² ). Следовательно, зная площадь поверхности , мы можем узнать, какой длины одна из сторон равна 9.0004 фигуры и оттуда найдите ее объем.

Чтобы сделать это, первое, что мы должны сделать, это вычислить длину стороны грани куба от его поверхности. Просто

делаем квадратный корень из значения площади поверхности и результатом будет длина ребра.
Наконец, мы кубируем полученное значение, как мы видели в предыдущем пункте, и все. Мы нашли объем этой правильной фигуры по поверхности одной из ее граней.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Вычислить объем цилиндра
Вычислить объем конуса
Вычислить объем куба
Вычислить объем сферы
Вычисление объема прямоугольной призмы
Додекаэдр
Икосаэдр
Тетраэдр
Объем пирамиды
Калькулятор объема — Примеры, Калькулятор объема онлайн
Калькулятор объема помогает найти объем для заданной формы, такой как сфера, куб, цилиндр, конус, прямоугольный параллелепипед, треугольная призма или треугольная пирамида.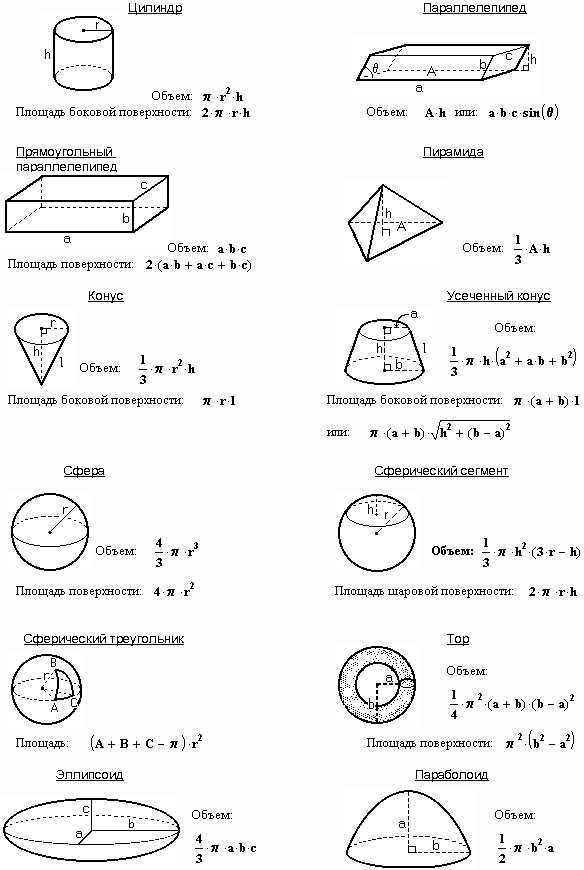 Объем можно определить как общее пространство, заключенное в трехмерную замкнутую форму. Единицей объема в системе СИ является кубический метр.
Что такое калькулятор объема?
Калькулятор объема — это онлайн-инструмент, используемый для расчета объема трехмерной фигуры. Предположим, у нас есть бутылка, вмещающая до краев 50 см ³ воды. Тогда объем бутылки будет 50см ³ . Чтобы использовать калькулятор объема , выберите форму из раскрывающегося меню и введите значения в поле ввода.
Калькулятор объема
Как пользоваться калькулятором объема?
Чтобы найти объем с помощью онлайн-калькулятора объема, выполните следующие действия:
Шаг 1: Перейдите к онлайн-калькулятору объема Cuemath.
Шаг 2: Выберите форму из раскрывающегося списка и введите значения в поле ввода калькулятора объема.
Шаг 3: Нажмите кнопку « Рассчитать », чтобы найти объем.
Шаг 4: Нажмите кнопку « Сброс », чтобы очистить поля и ввести новые значения.
Как работает калькулятор объема?
В зависимости от формы существует несколько различных формул для расчета объема. Площадь основания, умноженная на высоту, дает объем большинства фигур.
1. Объем прямоугольного параллелепипеда: Прямоугольный параллелепипед представляет собой трехмерную фигуру, состоящую из 6 четырехугольных граней. Формула для расчета объема прямоугольного параллелепипеда:
Объем прямоугольного параллелепипеда = площадь основания × высота = l × b × h.
Площадь основания прямоугольного параллелепипеда представляет собой прямоугольник размером l × b.
Где «l» — длина основания, «b» — ширина основания, а «h» — высота прямоугольного параллелепипеда.
2. Объем куба: Куб можно рассматривать как частный случай кубоида, у которого все стороны равны. Формула для расчета объема куба:
Объем куба = а ³ .
Базовая площадь представляет собой квадрат, равный ² .
Где «а» — сторона куба.
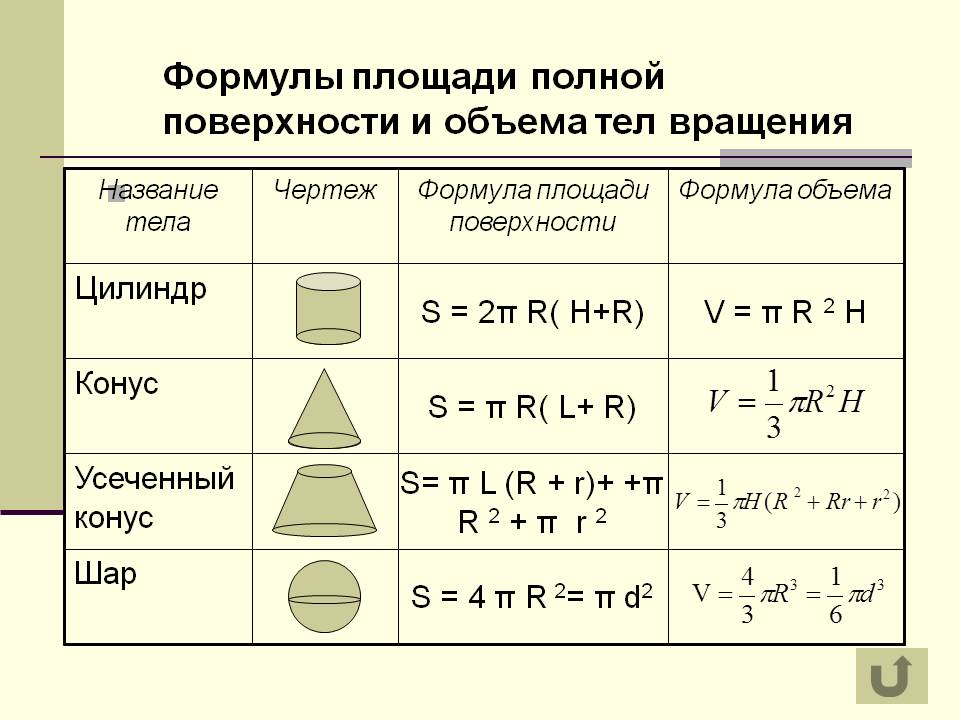
3. Объем цилиндра: Цилиндр имеет два параллельных круглых основания и соединен криволинейной поверхностью, образуя трубчатую структуру. Формула для расчета объема цилиндра:
Объем цилиндра = πr ² ч.
Площадь основания цилиндра представляет собой круг, равный πr ² .
Где r — радиус, h — высота, а π(Pi) — математическая константа с приблизительным значением 3,14 или 22/7.
4. Объем конуса: Конус имеет круглое основание с треугольными гранями, которые сходятся на вершине. Формула для расчета объема конуса:
Объем конуса = (1/3)πr ² час.
Площадь основания конуса – это круг, который равен πr ² .
Где «r» — радиус, а «h» — высота конуса.
5. Объем сферы: Сфера представляет собой геометрическую фигуру, напоминающую шар. Формула для расчета объема сферы:
Объем сферы = 4/3 × π × r ³ .
Где ‘r’ — радиус сферы.
6. Объем треугольной призмы: Треугольная призма имеет два треугольных основания с тремя гранями, соединяющими стороны. Формула для расчета объема треугольной призмы:
Объем треугольной призмы = площадь основания × высота призмы = 1/2 × (b × h) × l.
Где «b» — длина основания, «h» — высота, а «l» — расстояние между основаниями или высота треугольника призмы.
7. Объем треугольной пирамиды: Треугольная пирамида имеет треугольное основание и треугольные грани, которые сходятся на вершине. Формула для расчета объема треугольной пирамиды:
Объем треугольной пирамиды = 1/3 × Площадь основания треугольника × Высота пирамиды.
Примечание. Площадь основания треугольника равна 1/2 × ширины основания треугольника × высоты основания треугольника.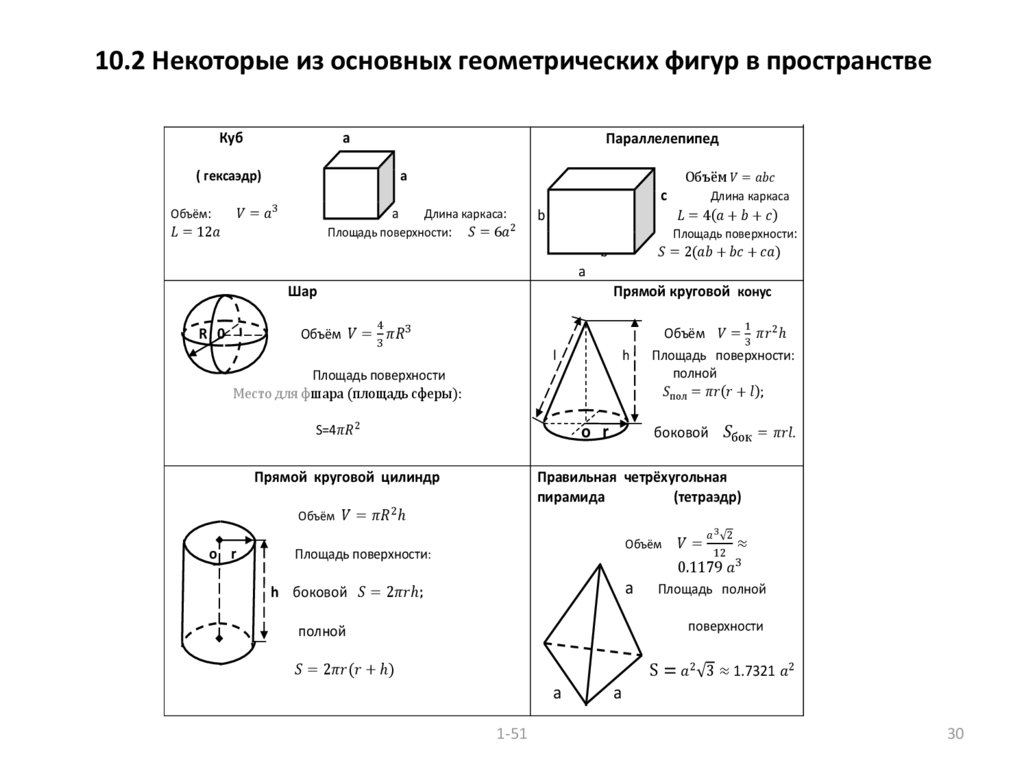
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе объема
Пример 1:
Найдите объем куба, если длина стороны равна 9 единицам, и проверьте его с помощью калькулятора объема.
Решение:
Формула для нахождения объема куба = a ³ кубических единиц
= (9) ³ кубических единиц.
= 9×9×9 кубических единиц.
=729 кубических единиц.
Пример 2:
Найдите объем конуса, высота которого равна 3 единицам, а радиус = 7 единицам.
Решение:
Зная высоту и радиус, мы можем использовать формулу для вычисления объема конуса.
Объем = (1/3)πr²h
=(1/3)π × 7² × 3
= 153,86 кубических единиц
Точно так же вы можете попробовать вычислить объем с помощью онлайн-калькулятора объема для следующих :
Найдите объем прямоугольного параллелепипеда, если длина его основания равна 5 единицам, ширина основания равна 6 единицам, а высота прямоугольного треугольника равна 7 единицам.
No related posts.