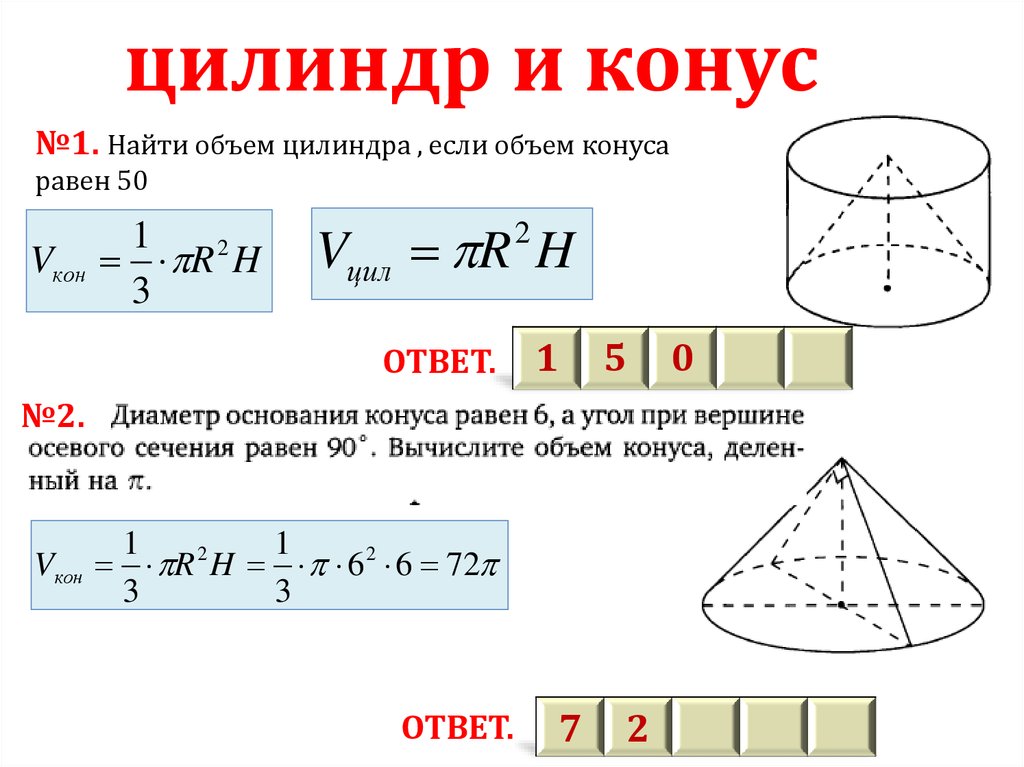
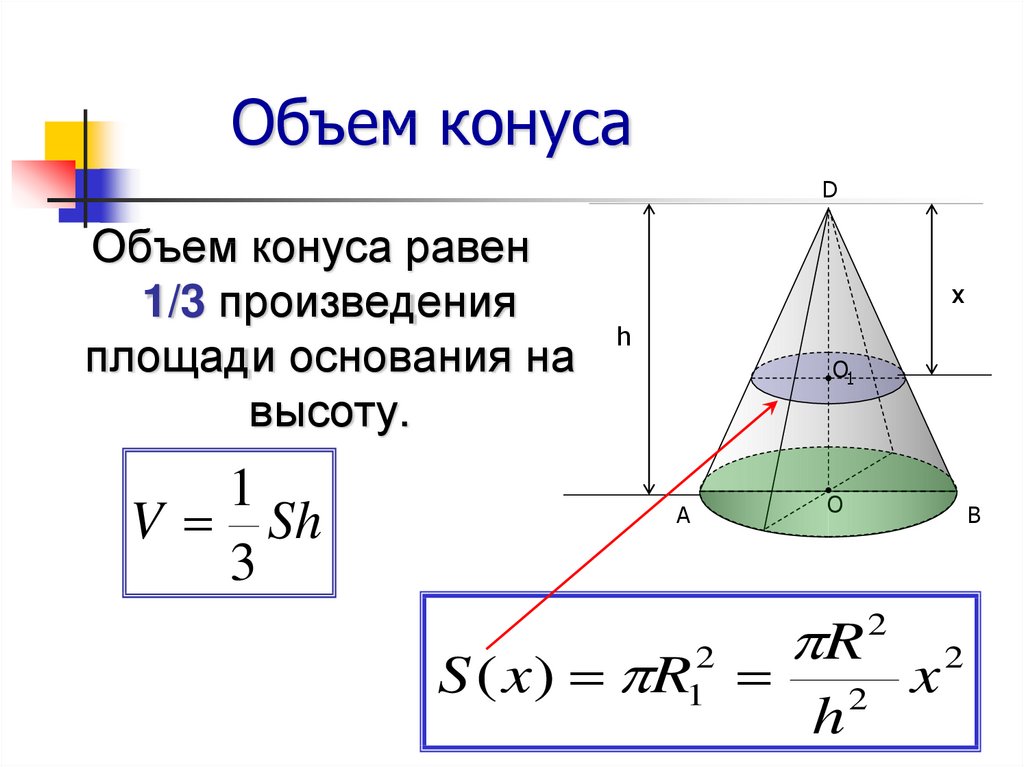
Объем конуса: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Введите 1 величину
Сторона A
Диагональ фигуры (D)
Диагональ грани (d)
Введите 1 величину
Радиус (r)
Диаметр (d)
Введите 3 величины
Сторона A
Сторона B
Сторона C
Диагональ фигуры (d)
Введите 2 величины (радиус и диаметр основания приняты за одну величину)
Высота (h)
Образующая конуса (s)
Радиус (r)
Диаметр (d)
Введите H и 1 величину
Высота (h)
Радиус (r)
Диаметр (d)
Введите 3 величины
Количество сторон (n)
Высота (h)
Сторона a
Количество сторон (n)
Введите 2 величины
Сторона основания (a)
Высота (h)
Длина бокового ребра (s)
Угол (α)
Между стороной и плоскостью основания
{$ main.
Результат расчёта
- Объём: {$ result.v|number:4 $}
- Площать: {$ result.s|number:4 $}
- Площать: {$ result.s $}
Конус — это геометрическое тело вращения, образованное путем вращения прямоугольного треугольника вокруг одного из катетов. Также коническая фигура — это тело в евклидовом пространстве, которое создается путем объединения лучиков, выходящих из вершины и входящих в круг, лежащий в основании. Если в основании конуса лежит не круг, а многоугольник, то фигура превращается в пирамиду.
Геометрия конуса
По-гречески «konos» означает сосновую шишку, и эта фигура знакома людям с давних времен. Известно, что геометрию конусов изучали еще Архимед и Демокрит, которые при помощи решения задачи о пересекающихся цилиндрах вывели формулы для определения объемов пирамидальных и конических фигур.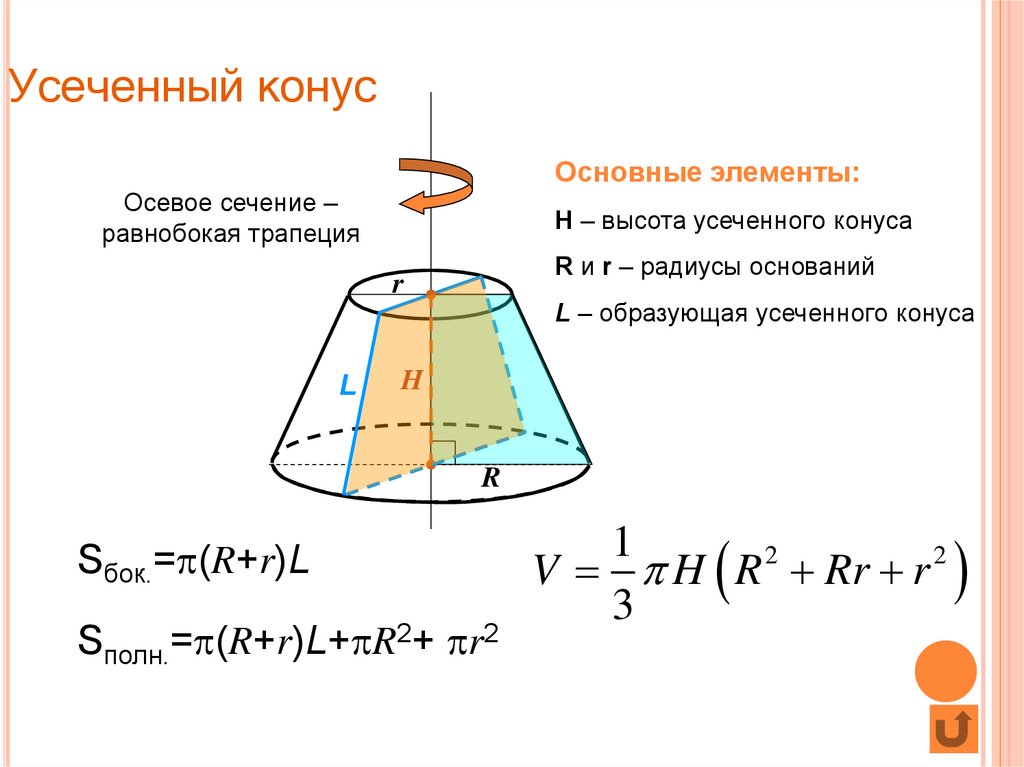
Геометрически конус представляет собой тело, состоящее из круга, который лежит в основании, и точки, не принадлежащей плоскости круга. Данная точка является вершиной, из которой выходит бесконечное количество лучей, направленных в окружность основания. Эти лучи образуют боковую поверхность, а каждый луч называется образующей конической фигуры.
Другая интерпретация конуса представляет фигуру в виде тела вращения. Такое тело образуется путем вращения прямоугольного треугольника вокруг одного из катетов. В этом случае гипотенуза треугольника считается образующей конуса, противолежащий катет — высотой, а прилежащий — радиусом основания. Такой конус называется прямым, так как высота, опущенная из вершины, перпендикулярна площади основания.
Конус широко применяется в реальной жизни: его можно встретить в быту, производстве или науке. К примеру, форму конуса имеют рожки для мороженого, пожарные ведра, громкоговорители, абажуры для ламп, воронки, шатры, дорожные знаки. Конусообразные вещи широко распространены в природе: вулканы, горы, кроны хвойных деревьев или шляпки грибов имеют форму прямого конуса.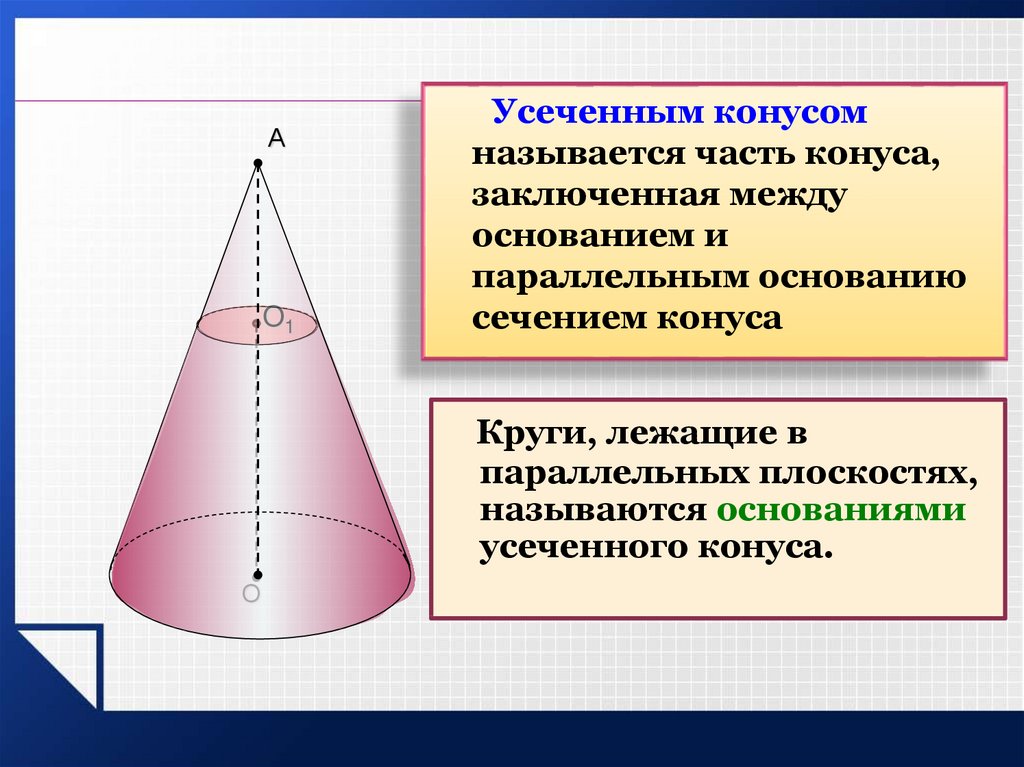 Именно поэтому вам может понадобиться узнать площадь поверхности или объем конической фигуры не только при решении школьных задач, но и в реальной практике.
Именно поэтому вам может понадобиться узнать площадь поверхности или объем конической фигуры не только при решении школьных задач, но и в реальной практике.
Объем конуса
Объем конической фигуры — это свойство тела вращения, которое показывает, сколько единичных кубов может уместиться внутри конуса. Объем конической фигуры, как и пирамиды, которая является частным случаем конуса, определяется как:
V = 1/3 × So × h = (pi × R 2 × h) / 3,
где R — радиус основания, а h — высота тела вращения.
При помощи удобного онлайн-инструмента вы можете рассчитать объем конуса, зная всего 2 его параметра:
- радиус и высоту;
- радиус и образующую.
Высота и образующая конуса связаны теоремой Пифагора, поэтому эти параметры взаимозаменяемы. Кроме того, в некоторых случаях удобнее замерить диаметр, а не радиус, поэтому калькулятор позволяет оперировать удобными для измерения или указанными в задании параметрами. Рассмотрим примеры.
Примеры
Быт
Допустим, вам надо набрать 50 л воды для дачных целей, но нормального ведра в виде усеченной конусной фигуры у вас нет. В вашем распоряжении есть только пожарное ведро в виде конуса. Неясно, какой объем воды влезет в такое ведерко, поэтому чтобы не бегать лишний раз, лучше заранее определить объем конуса. Пусть высота пожарного ведра составляет h = 50 см, а его радиус r = 15 см. Тогда объем такого конуса составит:
В вашем распоряжении есть только пожарное ведро в виде конуса. Неясно, какой объем воды влезет в такое ведерко, поэтому чтобы не бегать лишний раз, лучше заранее определить объем конуса. Пусть высота пожарного ведра составляет h = 50 см, а его радиус r = 15 см. Тогда объем такого конуса составит:
V = 11 780
Таким образом, объем пожарного ведра равен 11 780 кубическим сантиметрам или 11,78 л. Зная объем емкости, вы можете прикинуть, что с ярким пожарным конусом вам придется 4 раза бегать до водоема и обратно.
Производство
Допустим, вы производите мороженое и хотите сделать сливочный факел в вафельном рожке. Вам необходимо прикинуть, сколько мороженого требуется для заполнения одного рожка, который выполнен в виде прямого конуса. Пусть рожок имеет диаметр, равный d = 7 см, а образующая вафельного конуса равна s = 15 см. Введите параметры в форму онлайн-калькулятора и получите результат в виде:
V = 187,11
Это означает, что объем рожка составляет 187,1 кубический сантиметр или 187 миллилитров, следовательно, именно столько мороженого понадобится для заполнения одного вафельного конуса. Это минимальный объем вещества, необходимого для наполнения рожка до краев.
Это минимальный объем вещества, необходимого для наполнения рожка до краев.
Заключение
Конические фигуры широко встречаются в реальной жизни, поэтому вам может понадобиться вычислить объем тела вращения не только в школьных задачах, но и в быту, на производстве или в научных изысканиях. Наш онлайн-калькулятор пригодится для тех пользователей, которым важны простота интерфейса программы и понятная форма результата.
Объём конуса. Калькулятор объёма конуса онлайн
- Главная
- Справочник
- Геометрия
- Формулы объема
- Формула объема конуса
- Связанные определения для конуса
- Объем прямого углового конуса
- Первый способ вычисления объема конуса
- Второй способ вычисления объема конуса
- Калькулятор объема конуса
- Объем усеченного конуса
- Первый способ вычисления объема усеченного конуса
- Второй способ вычисления объема усеченного конуса
- Калькулятор объема усечённого конуса
Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называют также конусом вращения.
Связанные определения для конуса
Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Коническая поверхность. Образующая поверхность конуса является конической поверхностью.
Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Угол раствора конуса. Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым.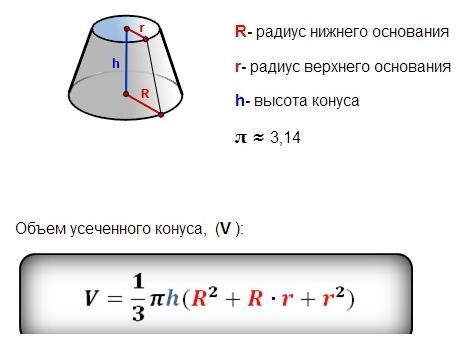 При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (наклонный) конус. Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус. Круговой конус — конус, основание которого является кругом.
Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Объем прямого углового конуса
Конус — это геометрическое тело, которое образовано вращением прямоугольного треугольника около одного из его катетов.
где:
V — объем конуса
H — высота конуса
π — число пи (3.1415)
r — радиус конуса
Калькулятор объема конуса
Объем усеченного конуса
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
Первый способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
\[ \LARGE V = \frac{1}{3} \left( H\cdot S_2 + h \cdot s_1 \right) \]
где:
V — объем конуса
h — расстояния от плоскости верхнего основания до вершины
H — расстояния от плоскости нижнего основания до вершины
S1 — площадь верхнего (ближнего к вершине) основания
S2 — площадь нижнего основания
Второй способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
\[ \LARGE V = \frac{1}{3} \pi h \left( R^2 + R \cdot r + r^2 \right) \]
где:
V — объем конуса
h — высота конуса
R — радиус нижнего основания
r — радиус верхнего основания
Калькулятор объема усечённого конуса
В вашем браузере отключен Javascript.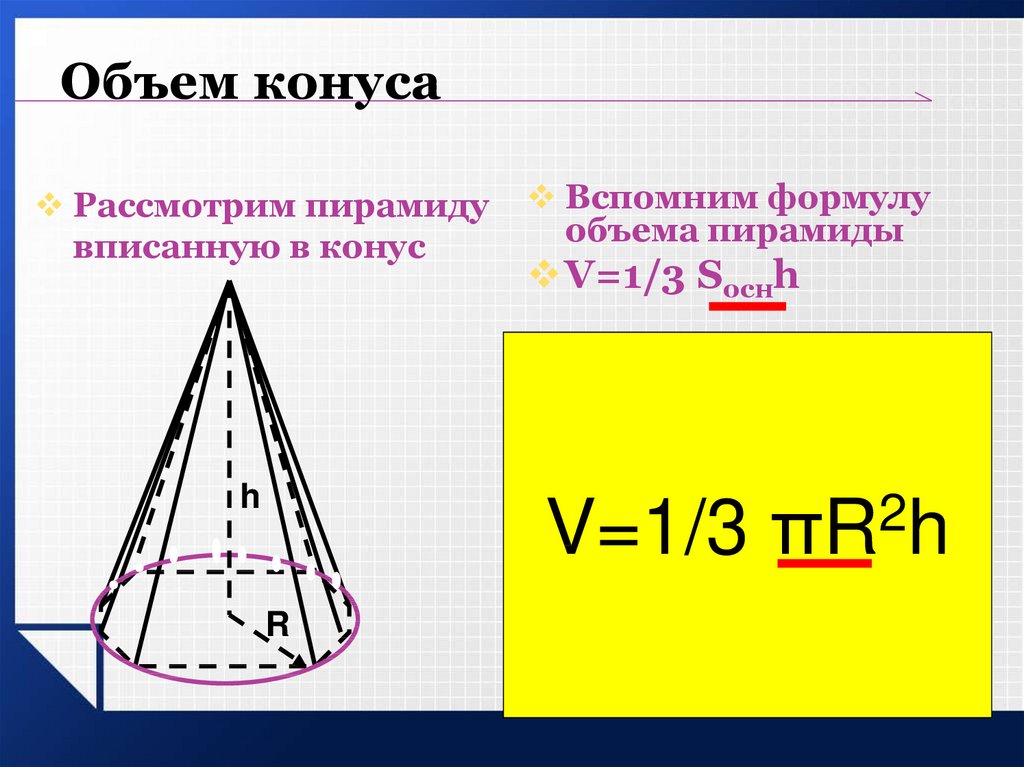 2 H_1=\dfrac{1}{8}V_1=\dfrac{64}{8}=8 \)
2 H_1=\dfrac{1}{8}V_1=\dfrac{64}{8}=8 \)Уровень5 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Объем конуса через площадь основания и высоту — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Объем конуса равен трети произведения основания и высоты. Результат можно получить из самостоятельных расчетов. Ускорить вычисления можно воспользовавшись онлайн-калькулятором на нашем сайте. Для этого введите данные – сервис выполнит необходимые преобразования и вычисления. Вам сразу будут доступны действия и ответ.
Существуют и другие способы решения задачи.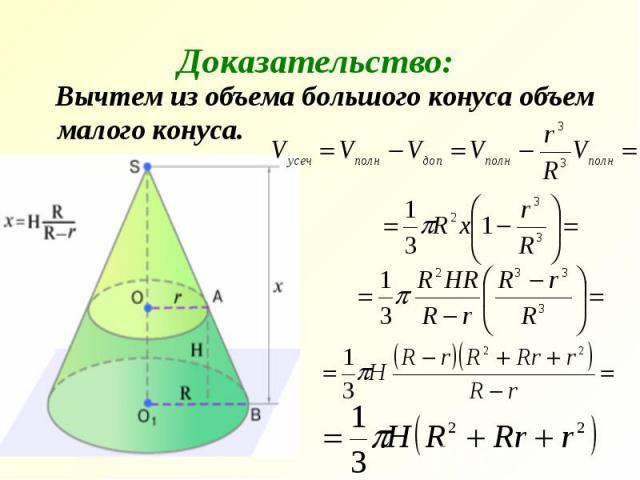 Если вводных параметров в вашем задании не хватает, поищите нужный калькулятор в разделе на сайте.
Если вводных параметров в вашем задании не хватает, поищите нужный калькулятор в разделе на сайте.
- Введите площадь основания конуса и высоту.
- Установите единицы измерения для данных и искомых величин. Отправьте задание на расчет кнопкой «Найти».
- Получите решение и ответ.
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Объем пирамиды
- Объем куба
- Объем цилиндра (Радиус основания и высота)
- Объем цилиндра (Площадь основания и высота)
- Объем конуса (Радиус основания и высота)
- Объем шара
- Объем параллелепипеда
- Объем прямоугольного параллелепипеда
В программу заложена формула объема конуса, которая рассчитывается по площади основания и высоте:
Для отправления данных на расчет не требуется регистрироваться на сайте и оплачивать услугу.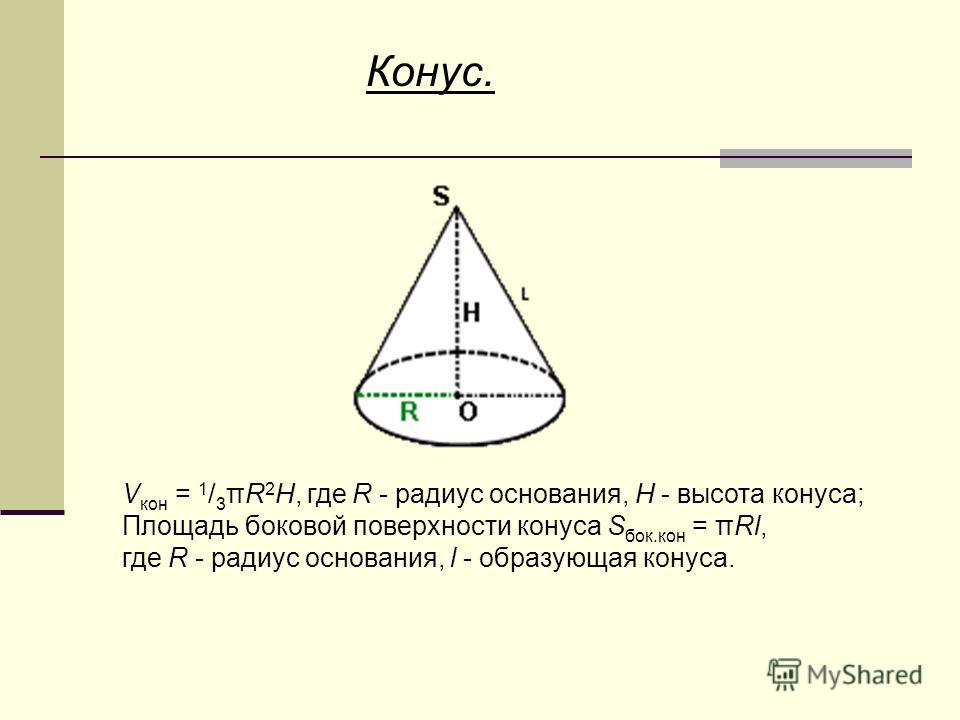 Количество запросов на вычисление не ограничивается.
Количество запросов на вычисление не ограничивается.
Кому полезна программа:
- Школьникам. Новая тема легче усваивается с готовым чертежом и возможностью самопроверки. Сверяясь с готовым решением можно найти и исправить ошибку, запомнить алгоритм подсчетов, применять их в других заданиях.
- Студентам. Быстрый ответ поможет сдать экзамен или зачет, а подробное решение – подсмотреть нужную формулу.
- Преподавателям. Большое количество заданий, выполненных учениками, теперь можно проверять с помощью сервиса. Также сокращается время на планирование уроков.
Еще расчетами пользуются родители для проверки подготовки детей. В строительной отрасли быстрые подсчеты без погрешностей незаменимы, когда под рукой нет специализированного программного обеспечения.
Если тема все равно непонятна, в короткий срок необходима онлайн-помощь или решить задачи, напишите консультанту. Он найдет преподавателя для объяснения материала, подберет куратора для дистанционного сопровождения по доступной цене.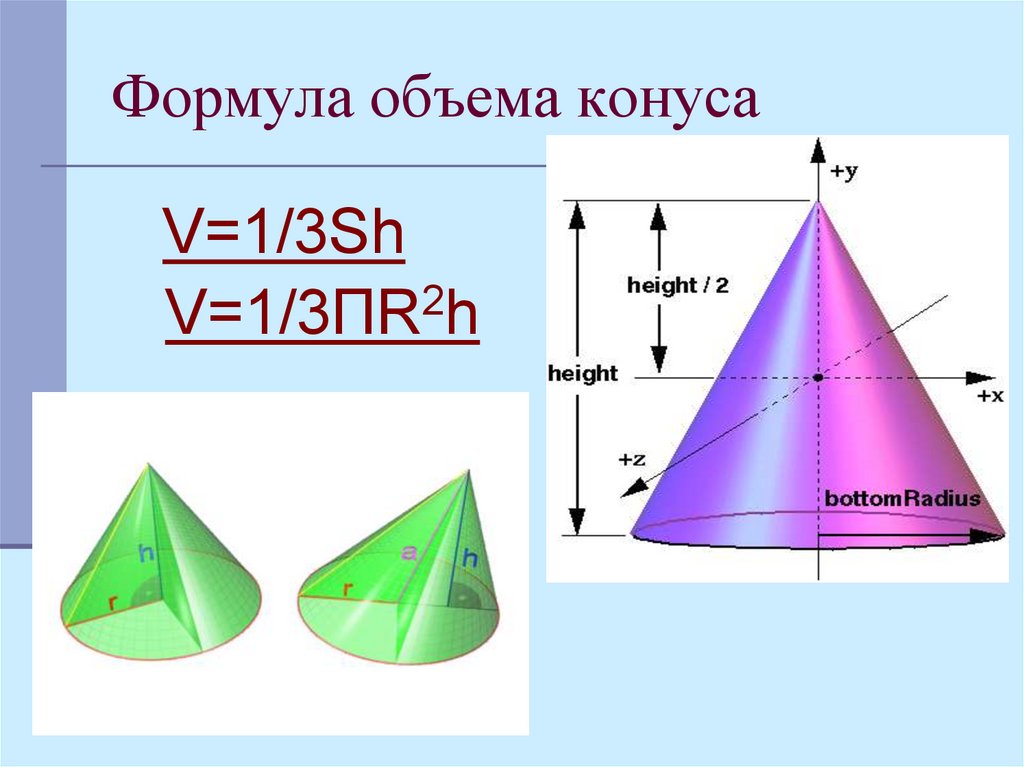
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
Калькулятор Объема Конуса | Формула И Результаты
Математические Калькуляторы
Этот калькулятор вычисляет объем конуса и может быть использован для решения школьных задач.
Калькулятор квадратных метров
Выберите форму:
кубПрямоугольная призма (коробка)ЦилиндрСфераКонусПирамидаТреугольная призмаКапсулаполушарие
Длина стороны
inftydmmcmm
Результат
Оглавление
| ◦Что такое конус? |
| ◦Что такое объем? |
| ◦Объем усеченного конуса (объем усеченного конуса) |
| ◦Объем косого конуса |
| ◦Вручную рассчитать объем конуса. |
| ◦Соотношение между объемом конуса и цилиндра |
| ◦Каков объем типичного рожка мороженого? |
| ◦Таблица преобразования и единиц объема |
Что такое конус?
Конус твердый с круглым основанием и одной вершиной.
Конус с многоугольным основанием известен как пирамида.
[Перейдите по этой ссылке для получения дополнительной информации. ] (https://en.wikipedia. 3).
3).
Объем усеченного конуса (объем усеченного конуса)
Усеченный конус — это конус, вершина которого срезана, а высота срезана перпендикулярно. Вычисление объема усеченного конуса можно выполнить путем вычитания меньшего объема конуса (среза) из большего базового объема. Или вы можете использовать формулу:
объем = (1/3) * π * глубина * (ᵣ² + r * R + R²)
R: радиус основания конуса
r: радиус верхней поверхности
Объем косого конуса
Косой конус — это конус, вершина которого не выше центра его основания. Она наклонена в одну сторону, похожа на косую цилиндрическую. Формула объема конуса для наклонного конуса будет такой же, как и для правильного.
Вручную рассчитать объем конуса.
Вот шаги, которые вам нужно выполнить, чтобы определить объем конусов:
Найдите основание конуса. Найдите его, если не знаете радиус основания конуса.
Найдите высоту.
Будет применена формула выпуклого объема. Используйте объем = (1/3) * a * h, если вы знаете свою базовую площадь или объем = (1/3) * π * ᵣ² * h.
Соотношение между объемом конуса и цилиндра
Конус и цилиндр должны иметь одинаковую высоту и радиус в основании. Объем конуса будет равен одной трети объема цилиндра. Это означает, что вам потребуется три конуса, чтобы заполнить этот цилиндр. Это же соотношение применимо к объему пирамиды или призмы, учитывая, что они оба имеют одинаковую высоту и площадь основания.
Каков объем типичного рожка мороженого?
Хотя размер вафли с мороженым может сильно различаться, есть некоторые размеры, которые можно считать обычными:
| Radius | Height | Volume |
| 1 in | 6 in | 6.3 cu in |
| 3 cm | 11 cm | 34.6 cm³ |
| 2.5 cm | 11.5 cm | 30.1 cm³ |
| 1 7/8 in | 4 5/8 in | 9.1 cu in |
| 1 3/16 in | 6 in | 7. 5 cu in 5 cu in |
Таблица преобразования и единиц объема
Вот самые популярные единицы объема:
Метрические единицы объема
Стандарт США, Великобритания
Автор статьи
Parmis Kazemi
Пармис — создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Калькулятор Объема Конуса русский
Опубликовано: Thu Mar 10 2022
В категории Математические калькуляторы
Добавьте Калькулятор Объема Конуса на свой сайт
Калькулятор Объема Конуса на других языках
آلة حاسبة حجم المخروطCalculateur De Volume De CôneKegelvolumenrechnerコーンボリューム計算機शंकु मात्रा कैलकुलेटरKoni Hacmi HesaplayıcıKalkulator Volume KerucutCalculator De Volum ConicКалькулятар Аб’ёму КонусаKalkulačka Objemu Kužeľa
Как добавить Калькулятор Объема Конуса на мой сайт?
Вы можете легко добавить Калькулятор Объема Конуса на свой веб-сайт с помощью нашего кода. Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!
Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!
Как добавить виджет Калькулятор Объема Конуса на сайт WordPress?
Добавить Калькулятор Объема Конуса на ваш сайт Wordpres быстро и легко! Найдите страницу, на которую вы хотите добавить калькулятор, перейдите в режим редактирования, нажмите «Текст» и вставьте туда код.
Как добавить HTML-виджет на страницу WordPress с помощью нового редактора кодаКак добавить HTML-виджет на страницу WordPress с помощью старого редактора кода
Другие математические калькуляторы
Калькулятор Векторного Произведения
Калькулятор Треугольников 30 60 90
Калькулятор Ожидаемой Стоимости
Математический Онлайн Калькулятор
Калькулятор Стандартного Отклонения
Калькулятор Процентов
Калькулятор Дробей
Конвертер Фунтов В Чашки: Мука, Сахар, Молоко..
Калькулятор Окружности
Калькулятор Формулы Двойного Угла
Вычисление Корня
Калькулятор Площади Треугольника
Калькулятор Котерминального Угла
Калькулятор Скалярного Произведения
Калькулятор Средней Точки
Конвертер Значащих Цифр (калькулятор Sig Figs)
Калькулятор Длины Дуги Для Круга
Калькулятор Балльной Оценки
Калькулятор Процентного Увеличения
Калькулятор Процентной Разницы
Калькулятор Линейной Интерполяции
Калькулятор QR-разложения
Калькулятор Транспонирования Матрицы
Калькулятор Гипотенузы Треугольника
Калькулятор Тригонометрии
Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника)
45 45 90 Калькулятор Треугольника (калькулятор Прямоугольного Треугольника)
Калькулятор Умножения Матриц
Калькулятор Среднего
Генератор Случайных Чисел
Калькулятор Погрешности
Калькулятор Угла Между Двумя Векторами
LCM Calculator — Калькулятор Наименьшего Общего Кратного
Калькулятор Площади В Квадратных Футах
Калькулятор Экспоненты (калькулятор Мощности)
Калькулятор Математического Остатка
Правило Трех Калькуляторов — Прямая Пропорция
Калькулятор Квадратичных Формул
Калькулятор Суммы
Калькулятор Периметра
Калькулятор Z-счета (значение Z)
Калькулятор Фибоначчи
Калькулятор Объема Капсулы
Калькулятор Объема Пирамиды
Калькулятор Объема Треугольной Призмы
Калькулятор Объема Прямоугольника
Калькулятор Объема Куба
Калькулятор Объема Цилиндра
Калькулятор Масштабного Коэффициента Расширения
Калькулятор Индекса Разнообразия Шеннона
Калькулятор Теоремы Байеса
Калькулятор Антилогарифмов
Eˣ Калькулятор
Калькулятор Простых Чисел
Калькулятор Экспоненциального Роста
Калькулятор Размера Выборки
Калькулятор Обратного Логарифма (логарифма)
Калькулятор Распределения Пуассона
Мультипликативный Обратный Калькулятор
Калькулятор Процента Оценок
Калькулятор Отношения
Калькулятор Эмпирических Правил
Калькулятор P-значения
Калькулятор Объема Шара
Калькулятор Чистой Приведенной Стоимости
Калькуляторы онлайн | Сосуды и аппараты | Трубопроводы
- Подробности
Расчет на прочность | Расчет исполнительной толщины стенки |
эллиптического днища | эллиптического днища |
цилиндрической обечайки | цилиндрической обечайки |
определение допускаемых напряжений | |
плюсовой и минусовой допуск по толщине стенки для трубы | |
предельные отклонения по наружному диаметру | |
Расчет характеристик сечений | |
кольцевого сечения (трубы) | перевод градусов в радианы и радиан в градусы |
круглого сечения | |
прямоугольного сечения | |
полого прямоугольного сечения | |
Калькуляторы дробей | Калькуляторы процентов |
сложение, вычитание, умножение, деление дробей | выделение, прибавление, вычитание процентов |
сокращение дробей | |
Формулы | Калькуляторы интерполяций |
формулы тригонометрические | интерполяция квадртичная |
таблица производных | интерполяция линейная |
экстраполяция линейная | |
уравнение прямой | |
КАЛЬКУЛЯТОР ФУНКЦИЙ | |
функции тригонометрические | |
функции обратные тригонометрические | |
функции логорифмов | |
Калькуляторы расчета площади поверхности тел | Калькуляторы расчета площади плоских фигур |
площадь поверхности конуса | площадь квадрата |
площадь поверхности куба | площадь кольца |
площадь поверхности параллелепипеда | площадь сектора кольца |
площадь поверхности правильной пирамиды | площадь круга |
площадь поверхности правильной усеченной пирамиды | площадь сегмента круга |
площадь поверхности сферы | площадь сектора круга |
площадь поверхности усеченного конуса | площадь параллелограмма |
площадь поверхности цилиндра | площадь правильного шестиуголльника |
площадь поверхности шарового сегмента | площадь прямоугольника |
площадь поверхности шарового сектора | площадь ромба |
площадь поверхности шарового слоя | площадь трапеции |
площадь треугольника | |
площадь четырехугольника | |
площадь эллипса | |
Объем тел | Периметр фигур |
| объем конуса | периметр квадрата |
| объем куба | периметр круга или длина окружности |
| объем параллелепипеда | периметр параллелограмма |
| объем пирамиды | периметр прямоугольника |
| объем правильной пирамиды | периметр ромба |
| объем тетраэдра | периметр трапеции |
| объем усеченного конуса | периметр треугольника |
| объем усеченной пирамиды | |
| объем цилиндра | |
| объем шара | |
| объем шарового сегмента | |
| объем шарового сектора | |
| объем шарового слоя |
ФорумСпециалистыО нас
Ссылка для цитирования в списке литературы: CAE-CUBE: [Электронный ресурс]. | premierdevelopment.ru, все права защищены, 2015 - 2021 e-mail: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. |
Расчет объема конуса онлайн. Как найти объем конуса
Геометрия наука непростая, но полезная. Все мы в школе проходили вычисление объемов трехмерных тел, но не все хорошо помнят формулы этих вычислений. Эта статья поможет вам освежить в памяти знания о том, как найти объем конуса. Данная трехмерная фигура образована круговым вращением прямоугольного треугольника. Вычислить его объем можно разными способами, в зависимости от того, какими исходными данными вы владеете.
Инструкция:
- В большинстве случаев для вычисления используется радиус окружности основания и высота. Формула объема конуса в таком случае имеет вид: V= πRh , где π=3.
 2.
2. - Но, как найти объем конуса, если ни длина боковой стороны, ни радиус основания неизвестны? В таком случае вам необходимо знать градус угла при вершине конуса и его высоту. Владея этими данными, вы можете вычислить радиус основания. Не забываем о том, что конус – фигура, образованная вращением прямоугольного треугольника вокруг одного из его катетов. Если угол при вершине разделить надвое, вы получите градус одного из двух острых углов этого треугольника. Используя определения тригонометрических функций, мы можем выяснить длину стороны противоположной этому углу, то есть, в нашем случае, радиуса основания. Он, в этом случае будет равен l*sin(α) , где l – длина от вершины конуса до основания, высота, соответственно, будет равна l*cos(α) , используя эти значения, выводим следующую формулу радиуса основания R= h/cos(α)*sin(α) или, равнозначно, R = h*tg(α) .
1. Расчет объема куба
a — сторона куба
Формула объема куба, (V ):
2.
 Найти по формуле, объем прямоугольного параллелепипеда
Найти по формуле, объем прямоугольного параллелепипедаa , b , c — стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V ):
3. Формула для вычисления объема шара, сферы
R — радиус шара
По формуле, если дан радиус, можно найти объема шара, (V ):
4. Как вычислить объем цилиндра?
h — высота цилиндра
r — радиус основания
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V ):
5. Как найти объем конуса?
R — радиус основания
H — высота конуса
Формула объема конуса, если известны радиус и высота (V ):
7. Формула объема усеченного конуса
r — радиус верхнего основания
R — радиус нижнего основания
h — высота конуса
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8.
 Объем правильного тетраэдра
Объем правильного тетраэдраПравильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а — ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V ):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V ):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V ):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V ):
Все формулы объемов геометрических тел
Геометрия, Алгебра, Физика
Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.1415)
R — радиус шара
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
Формулы объема
Формулы объема и онлайн программы для вычисления объема
Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.
Объем фигуры — это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Параллелепипед .
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Цилиндр .
Объем цилиндра равен произведению площади основания на высоту.
Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
Пирамида .
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.
Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники.
Усеченная пирамида .
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S 1 (abcde), нижнего основания усеченной пирамиды S 2 (ABCDE) и средней пропорциональной между ними.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .
Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Усеченный конус получится, если в конусе провести сечение, параллельное основанию.
V = 1/3 πh (R 2 + Rr + r 2)
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Призма .
Объем призмы равен произведению площади основания призмы, на высоту.
Сектор шара .
Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.
Сегмент шара — это часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом
Формула объема
Формула объема куба, шара, пирамиды, параллелограмма, цилиндра, тетраэдра, конуса, призмы и объемы других геометрических фигур.
В курсе стереометрии один из главных вопросов — как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
В жизни тоже часто приходится сталкиваться с подобными задачами. Например, чтобы рассчитать объем воды, которая помещается в ведро или бочку.
Например, чтобы рассчитать объем воды, которая помещается в ведро или бочку.
Свойства, справедливые для объема каждого тела
- Это значение — всегда положительное число.
- Если тело удается разделить на части так, чтобы не было пересечений, то общий объем оказывается равным сумме объемов частей.
- У равных тел одинаковые объемы.
- Если меньшее тело полностью помещается в большем, то объем первого меньше, чем второго.
Общие обозначения для всех тел
В каждом из них есть ребра и основания, в них строятся высоты. Поэтому такие элементы для них одинаково обозначены. Именно так они записаны в формулах. Как рассчитать объем каждого из тел — узнаем дальше и применим на практике новые умения.
В некоторых формулах имеются другие величины. Об их обозначении будет сказано при появлении такой необходимости.
Призма, параллелепипед (прямой и наклонный) и куб
Эти тела объединены, потому что внешне очень похожи, и формулы того, как рассчитать объем, идентичны:
V = S * h.
Различаться будет только S . В случае с параллелепипедом она рассчитывается, как для прямоугольника или квадрата. В призме основанием может оказаться треугольник, параллелограмм, произвольный четырехугольник или другой многоугольник.
Для куба формула существенно упрощается, потому что все его измерения равны:
V = а 3 .
Пирамида, тетраэдр, усеченная пирамида
Для первого из указанных тел существует такая формула, чтобы вычислить объем:
V = 1/3 * S * н.
Тетраэдр является частным случаем треугольной пирамиды. В нем все ребра равны. Поэтому снова получается упрощенная формула:
V = (а 3 * √2) / 12, или V = 1/ 3 S h
Усеченной пирамида становится тогда, когда у нее срезана верхняя часть. Поэтому ее объем равен разности двух пирамид: той, которая была бы целой, и удаленной верхушки. Если есть возможность узнать оба основания такой пирамиды (S 1 — большее и S 2 — меньшее), то удобно пользоваться такой формулой для расчета объема:
Цилиндр, конус и усеченный конус
V =π * r 2 * h.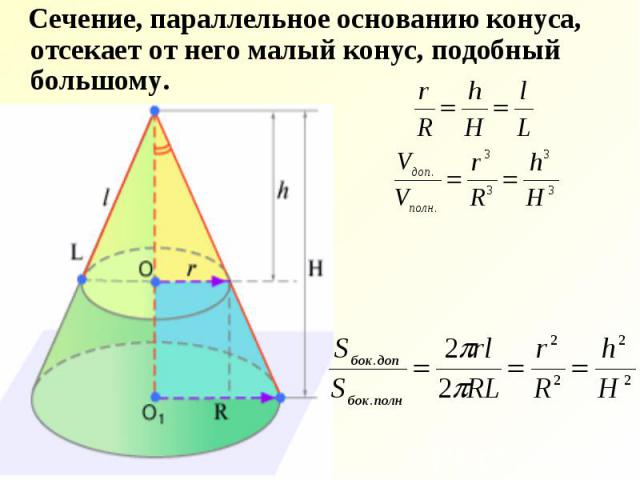
Несколько сложнее обстоит дело с конусом. Для него существует формула:
V = 1/3 π * r 2 * h. Она очень похожа на ту, что указана для цилиндра, только значение уменьшено в три раза.
Так же, как с усеченной пирамидой, дело обстоит непросто с конусом, который имеет два основания. Формула для вычисления объема усеченного конуса выглядит так:
V = 1/3 π * h * (r 1 2 + r 1 r 2 + r 2 2). Здесь r 1 — радиус нижнего основания, r 2 — верхнего (меньшего).
Шар, шаровые сегменты и сектор
Это самые сложные для запоминания формулы. Для объема шара она выглядит так:
V = 4/3 π *r 3 .
В задачах часто есть вопрос о том, как рассчитать объем шарового сегмента — части сферы, которая как бы срезана параллельно диаметру. В этом случае на выручку придет такая формула:
V = π h 2 * (r — h/3). В ней за h взята высота сегмента, то есть та часть, которая идет по радиусу шара.
Сектор делится на две части: конус и шаровой сегмент. Поэтому его объем определяется как сумма этих тел. Формула после преобразований выглядит так:
Поэтому его объем определяется как сумма этих тел. Формула после преобразований выглядит так:
V = 2/3 πr 2 * h. Здесь h также высота сегмента.
Примеры задач
Про объемы цилиндра, шара и конуса
Условие: диаметр цилиндра (1 тело) равен его высоте, диаметру шара (2 тело) и высоте конуса (3 тело), проверить пропорциональность объемов V 1: V 2: V 3 = 3:2:1
Решение. Сначала потребуется записать три формулы для объемов. Потом учесть, что радиус — это половина диаметра. То есть высота будет равна двум радиусам: h = 2r. Произведя простую замену получается, что формулы для объемов будут иметь такой вид:
V 1 = 2 π r 3 , V 3 = 2/3 π r 3 . Формула для объема шара не изменяется, потому что в ней не фигурирует высота.
Теперь осталось записать отношения объемов и произвести сокращение 2π и r 3 . Получается, что V 1: V 2: V 3 = 1: 2/3: 1/3. Эти числа легко привести к записи 3: 2: 1.
Про объем шара
Условие: имеется два арбуза радиусами 15 и 20 см, как их выгоднее съесть: первый вчетвером или второй ввосьмером?
Решение. Чтобы ответить на этот вопрос, потребуется найти отношение объемов частей, которые достанутся от каждого арбуза. Принимая во внимание, что они — шары, нужно записать две формулы для объемов. Потом учесть, что от первого каждому достанется только четвертая часть, а от второго — восьмая.
Чтобы ответить на этот вопрос, потребуется найти отношение объемов частей, которые достанутся от каждого арбуза. Принимая во внимание, что они — шары, нужно записать две формулы для объемов. Потом учесть, что от первого каждому достанется только четвертая часть, а от второго — восьмая.
Осталось записать отношение объемов частей. Оно будет выглядеть так:
(V 1: 4) / (V 2: 8) = (1/3 π r 1 3) / (1/6 π r 2 3). После преобразования остается только дробь: (2 r 1 3) / r 2 3 . После подстановки значений и вычисления получается дробь 6750/8000. Из нее ясно, что часть от первого арбуза будет меньше, чем от второго.
Ответ. Выгоднее съесть восьмую часть от арбуза с радиусом 20 см.
Про объемы пирамиды и куба
Условие: имеется пирамида из глины с прямоугольным основанием 8Х9 см и высотой 9 см, из этого же куска глины сделали куб, чему равно его ребро?
Решение. Если обозначить стороны прямоугольника буквами в и с, то площадь основания пирамиды вычисляется, как их произведение. Тогда формула для ее объема:
Тогда формула для ее объема:
Формула для объема куба написана в статье выше. Эти два значения равны: V 1 = V 2 . Осталось приравнять правые части формул и сделать необходимые вычисления. Получается, что ребро куба будет равно 6 см.
Про объем параллелепипеда
Условие: требуется сделать ящик вместимостью 0,96 м 3 , известны его ширина и длина — 1,2 и 0,8 метра, какой должна быть его высота?
Решение. Поскольку основание параллелепипеда — прямоугольник, его площадь определяется как произведение длины (а) на ширину (в). Поэтому формула для объема выглядит так:
Из нее легко определить высоту, разделив объем на площадь. Получится, что высота должна быть равна 1 м.
Ответ. Высота ящика равна одному метру.
Как рассчитать объем различных геометрических тел?
В курсе стереометрии одна из главных задач — как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
Шар, объем которого равен 8π, вписан в куб. Найдите объем куба.
Решение
Пусть a — это сторона куба. Тогда объем куба равен V = a 3 .
Так как шар вписан в куб, то радиус шара равен половине ребра куба, т.е R = a/2 (см. рис.).
Объем шара равен V ш = (4/3)πR 3 и равен 8π, поэтому
(4/3)πR 3 = 8π,
А объем куба равен V = a 3 = (2R) 3 = 8R 3 = 8*6 = 48.
Задание B9 (Типовые варианты 2015)
Объем конуса равен 32. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение
Рассмотрим задачи:
72353. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Сразу отметим, что исходный и отсечённый конус подобны и если рассматривать отсечённый конус относительно исходного, то можно сказать так: меньший конус подобен большему с коэффициентом равным одной второй или 0,5.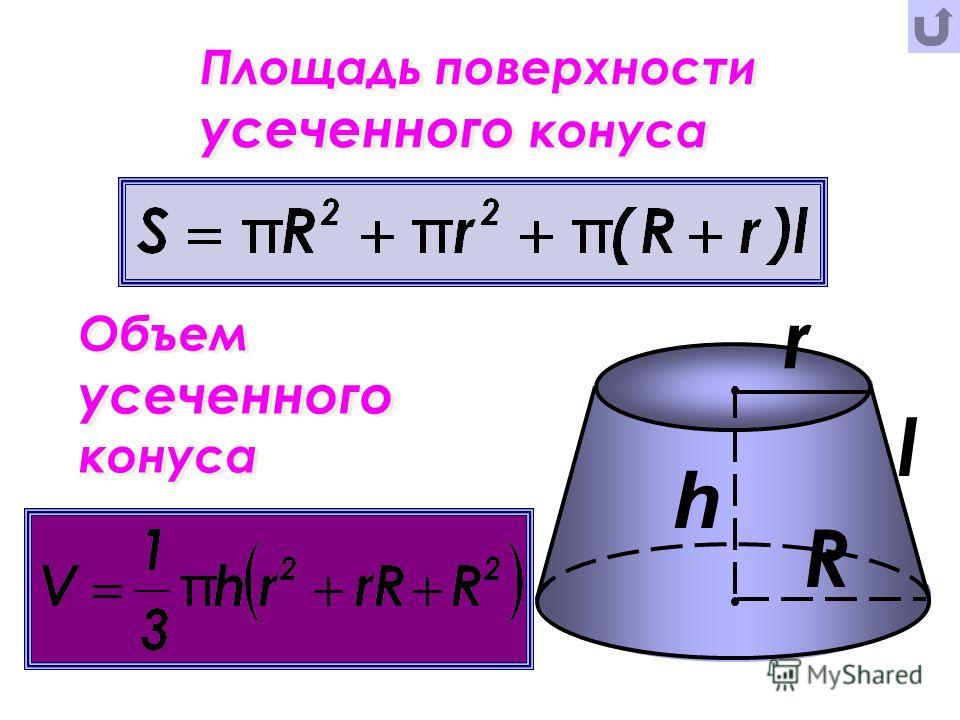 Можем записать:
Можем записать:
Можно было записать:
Можно было рассудить так!
Рассмотрим исходный конус относительно отсечённого. Можно сказать – больший конус подобен отсечённому с коэффициентом равным двум, запишем:
Теперь посмотрите решение без использования свойств подобия.
Объём конуса равен одной трети произведения площади его основания и высоты:
Рассмотрим боковую проекцию (вид сбоку) с указанным сечением:
Пусть радиус большего конуса равен R, высота равна Н. Сечение (основание меньшего конуса) проходит через середину высоты, значит его высота будет равна Н/2. А радиус основания равен R/2, это следует из подобия треугольников.
Запишем объём исходного конуса:
Объём отсечённого конуса будет равен:
Столь подробные решения представлены для того, чтобы вы видели как можно выстроить рассуждения. Действуйте любым способом – главное, чтобы вы понимали суть решения. Пусть путь, который вы выбрали будет не рационален, важен результат (верный результат).
Ответ: 1,25
318145. В сосуде, имеющем форму конуса, уровень жидкости достигает половину высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Данная задача схожа с предыдущей. Хоть речь здесь и идёт о жидкости, принцип решения один и тот же.
Имеем два конуса – это сам сосуд и «малый» конус (наполненный жидкостью), они являются подобными. Известно, что объёмы подобных тел соотносятся следующим образом:
Исходный конус (сосуд) подобен конусу наполненному жидкостью с коэффициентом равным 2, так как сказано, что уровень жидкости достигает половину высоты. Можно записать подробнее:
Вычисляем:
Таким образом, долить нужно:
Другие задачи с жидкостями.
74257. Найдите объем V конуса, образующая которого равна 44 и наклонена к плоскости основания под углом 30 0 . В ответе укажите V/Пи.
Объем конуса:
Высоту конуса найдем по свойству прямоугольного треугольника.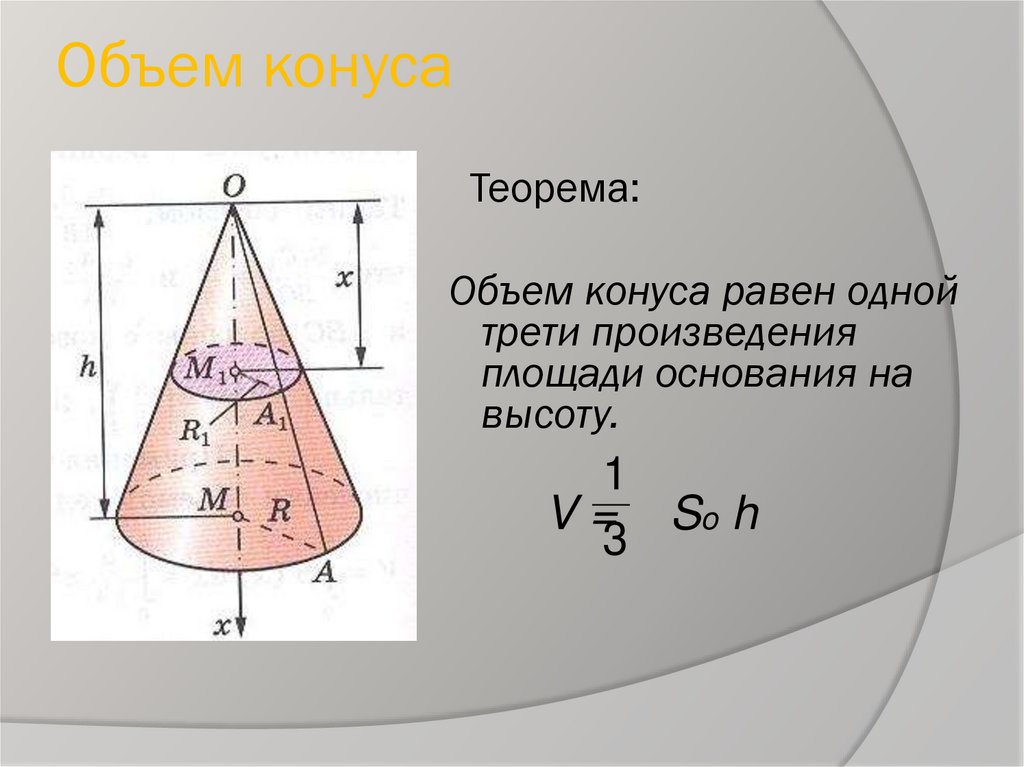
Катет лежащий против угла 30° равен половине гипотенузы. Гипотенуза, в данном случае, является образующей конуса. Следовательно высота конуса равна 22.
Квадрат радиуса основания найдем по теореме Пифагора:
*Нам нужен квадрат радиуса, а не сам радиус.
Геометрия как наука сформировалась в Древнем Египте и достигла высокого уровня развития. Известный философ Платон основал Академию, где пристальное внимание уделялось систематизации имеющихся знаний. Конус как одна из геометрических фигур впервые упоминается в известном трактате Евклида «Начала». Евклид был знаком с трудами Платона. Сейчас мало кто знает, что слово «конус» в переводе с греческого языка обозначает «сосновая шишка». Греческий математик Евклид, живший в Александрии, по праву считается основоположником геометрической алгебры. Древние греки не только стали преемниками знаний египтян, но и значительно расширили теорию.
История определения конуса
Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.
Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.
В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.
Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах. Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.
Основные определения
Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.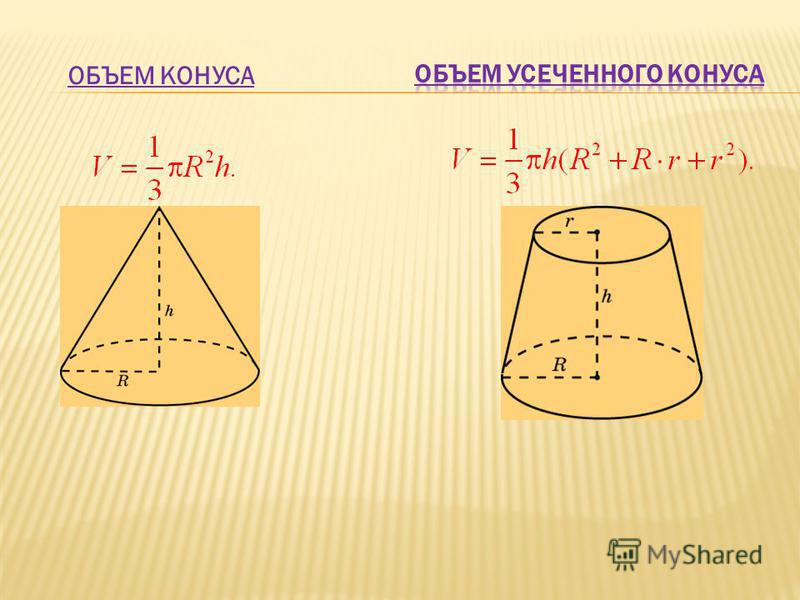
Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.
Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Формула расчета объема конуса
Для расчета объема конуса используется следующая формула:
где S является площадью основания конуса. Так как основание — круг, его площадь рассчитывается так:
Отсюда следует:
где V — объем конуса;
n — число, равное 3,14;
R — радиус основания, соответствующий отрезку AO на рисунке 1;
H — высота, равная отрезку OS.
Усеченный конус, объем
Имеется прямой круговой конус. Если плоскостью, перпендикулярной высоте, отсечь верхнюю часть, то получится усеченный конус. Два его основания имеют форму круга с радиусами R 1 и R 2 .
Если прямой конус образуется вращением прямоугольного треугольника, то усеченный конус — вращением прямоугольной трапеции вокруг прямой стороны.
Объем усеченного конуса рассчитывается по следующей формуле:
V=n*(R 1 2 +R 2 2 +R 1 *R 2)*H/3.
Конус и его сечение плоскостью
Перу древнегреческого математика Аполлония Пергского принадлежит теоретический труд «Конические сечения». Благодаря его работам в геометрии появились определения кривых: параболы, эллипса, гиперболы. Рассмотрим, причем здесь конус.
Возьмем прямой круговой конус. Если плоскость пересекает его перпендикулярно оси, то в разрезе образуется круг. Когда секущая пересекает конус под углом к оси, то в разрезе получается эллипс.
Секущая плоскость, перпендикулярная основанию и параллельная оси конуса, образует на поверхности гиперболу. Плоскость, разрезающая конус под углом к основанию и параллельная касательной к конусу, создает на поверхности кривую, которую назвали параболой.
Плоскость, разрезающая конус под углом к основанию и параллельная касательной к конусу, создает на поверхности кривую, которую назвали параболой.
Решение задачи
Даже простая задача о том, как изготовить ведро определенного объема, требует знаний. Например, необходимо рассчитать размеры ведра, чтобы оно имело объем 10 литров.
V=10 л=10 дм 3 ;
Развертка конуса имеет вид, схематически приведенный на рисунке 3.
L — образующая конуса.
Чтобы узнать площадь поверхности ведра, которая вычисляется по следующей формуле:
S=n*(R 1 +R 2)*L,
необходимо вычислить образующую. Ее находим из величины объема V=n*(R 1 2 +R 2 2 +R 1 *R 2)*H/3.
Отсюда H=3V/n*(R 1 2 +R 2 2 +R 1 *R 2).
Усеченный конус образуется вращением прямоугольной трапеции, в которой боковая сторона является образующей конуса.
L 2 =(R 2- R 1) 2 +H 2 .
Теперь у нас имеются все данные, чтобы построить чертеж ведра.
Почему пожарные ведра имеют форму конуса?
Кто задумывался, почему пожарные ведра имеют, казалось бы, странную коническую форму? А это не просто так. Оказывается, коническое ведро при тушении пожара имеет много преимуществ перед обычным, имеющим форму усеченного конуса.
Оказывается, коническое ведро при тушении пожара имеет много преимуществ перед обычным, имеющим форму усеченного конуса.
Во-первых, как оказывается, пожарное ведро быстрее наполняется водой и при переноске она не расплескивается. Конус, объем которого больше обычного ведра, за один раз позволяет перенести больше воды.
Во-вторых, воду из него можно выплеснуть на большее расстояние, чем из обычного ведра.
В-третьих, если коническое ведро сорвется с рук и упадет в огонь, то вся вода выливается на очаг возгорания.
Все перечисленные факторы позволяют сэкономить время — главный фактор при тушении пожара.
Практическое применение
У школьников часто возникает вопрос о том, зачем учить, как рассчитывать объем разных геометрических тел, в том числе конуса.
А инженеры-конструкторы постоянно сталкиваются с необходимостью рассчитать объем конических частей деталей механизмов. Это наконечники сверл, части токарных и фрезерных станков. Форма конуса позволят сверлам легко входить в материал, не требуя первоначальной наметки специальным инструментом.
Объем конуса имеет куча песка или земли, высыпанная на землю. При необходимости, проведя несложные измерения, можно рассчитать ее объем. У некоторых вызовет затруднение вопрос о том, как узнать радиус и высоту кучи песка. Вооружившись рулеткой, измеряем окружность холмика C. По формуле R=C/2n узнаем радиус. Перекинув веревку (рулетку) через вершину, находим длину образующей. А вычислить высоту по теореме Пифагора и объем не составит труда. Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.
Некоторые здания имеют форму усеченного конуса. Например, Останкинская телебашня приближается к форме конуса. Ее можно представить состоящей из двух конусов, поставленных друг на друга. Купола старинных замков и соборов представляют собой конус, объем которого древние зодчие рассчитывали с удивительной точностью.
Если внимательно присмотреться к окружающим предметам, то многие из них являются конусами:
- воронки-лейки для наливания жидкостей;
- рупор-громкоговоритель;
- парковочные конусы;
- абажур для торшера;
- привычная новогодняя елочка;
- духовые музыкальные инструменты.

Как видно из приведенных примеров, умение рассчитать объем конуса, площадь его поверхности необходимо в профессиональной и повседневной жизни. Надеемся, что статья придет вам на помощь.
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Калькулятор объема конуса | Бесплатный онлайн-калькулятор объема конуса с шагами
Онлайн-калькулятор объема конуса
Как пользоваться калькулятором объема конуса?
Выполните следующие действия, чтобы использовать калькулятор объема конуса:
- Введите две известные величины (т. е. радиус, объем и высоту) в соответствующее поле ввода, и будет рассчитана неизвестная мера.

- Выберите соответствующую единицу измерения для входов и выходов.
- Вы также можете выбрать желаемое значение «пи» из раскрывающегося списка. Значения могут быть 3,14, \(\pi\) или \(\frac{22}{7}\).
- Теперь нажмите «Решить», чтобы получить результат.
- Нажмите кнопку «Показать шаги», чтобы узнать пошаговое решение для поиска недостающей меры.
- Нажмите кнопку, чтобы ввести новые данные и начать заново.
- Нажмите кнопку «Пример», чтобы поиграть с различными случайными входными значениями.
- При нажатии на кнопку «Исследовать» можно увидеть, как изменяется объем конуса при изменении радиуса и высоты конуса. Вы также можете вращать конус с помощью ползунка наклона.
- На странице «Исследовать» нажмите кнопку «Рассчитать», если хотите вернуться к калькулятору.
Каков объем конуса?
Объем конуса — это площадь, занимаемая конусом. Если мы используем коническую чашку в качестве примера, вода, которая наполняет чашку до краев, приблизительно равна объему конической чашки.
Формулы, используемые в «Калькуляторе объема конуса»
Если известны радиус \(r\) и высота \(h\) конуса, объем конуса \(V\) рассчитывается как : 92+\frac{1}{3}\pi r\)
= \(\frac{\pi r\ (r+1)}{3}\)
Разница между их объемами может записывается как \(\frac{\pi r\ (r+1)}{3}\).
Калькулятор объема решенного конуса Примеры
Пример 1 :
Найдите объем конуса высотой 9 футов и диаметром основания 12 футов. (Возьмите \(\pi\) как 3.14)
Решение :
Диаметр основания равен 12 футам. Следовательно, радиус основания будет \(\frac{12}{2}=6\) футов. 92\times9\)
= \(339,12\) кубических футов
Объем конуса равен 339,12 кубических футов.
Пример 2:
Найдите высоту конуса, если его объем 22 кубических дюйма, а диаметр 2 дюйма. (Возьмите \(\pi\) как \(\frac{22}{7}\))
Решение :
Диаметр равен 2 дюймам.
Следовательно, радиус будет равен \(\frac{2}{2}=1\) дюйму.
92}\)
= 21 дюйм
Пример 3 : Вычислите радиус конуса, высота которого 30 дюймов, а объем 3140 кубических дюймов. (Возьмем \(\pi\) как 3.14)
Решение :
Радиус конуса, \(r=\sqrt{\frac{3V}{\pi h}}\)
\( r=\sqrt{\frac{3\\times\ 3140}{\pi\ \times\ 30}}\)
\(r=10\) дюймов
Следовательно, радиус конуса составляет 10 дюймов.
Часто задаваемые вопросы
Основание конуса какой формы?
Форма основания конуса — круг.
Как найти объем конуса, используя площадь основания?
Формула объема конуса: (1/3)πr 2 ч. Конус – это тело с круглым основанием. Следовательно, площадь основания (BA) — это площадь круга, равная πr 2 . Таким образом, объем конуса можно записать как: (1/3)×BA×h
Какие объекты вокруг вас имеют коническую форму?
Примеры предметов конической формы: праздничная шляпа, кончик карандаша, рожок мороженого и т. д.
д.
Ознакомьтесь с другими нашими курсами
| Геометрия | Формы | Контакты и конфиденциальность | Геометрические калькуляторы | Немецкий: Geometriechner, Formen |
| 1DЛиния, дуга окружности, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Круглые формы: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron Archimedean Solids: Catalan Solids: Johnson Solid: 0, дискенов. Круглые формы: | Anzeige Расчеты на прямом круговом конусе. Формулы: pi: Радиус, высота и длина имеют одну и ту же единицу измерения (например, метр), поверхности имеют эту единицу в квадрате (например, квадратный метр), объем имеет эту единицу в степени три (например, кубический метр). У A/V есть этот блок -1 . Поделиться: © Jumk. Anzeige |
Объем усеченного конуса Калькулятор
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо.ⓘ Высота [h] | 902 of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |||||||||||||||||||
✖radius 1 является радиальной линией от фокусировки до точки кривой 1 -й радиус. | 85895899589999999999999 495894 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 444 | А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% |
✖radius 2 является радиальной линией от фокусировки к кривой 2 -й радиусе. | А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% |
✖Объем — это объем пространства, которое занимает вещество или объект или которое заключено в контейнере. | Акр-футАкр-фут (исследование США)Акр-дюймБаррель (нефть)Бочка (Великобритания)Баррель (США)Баня (библейская)Досковая футКабина (библейская)СантилитрЦент кубический футКор (библейская)КордКубический ангстремКубический сантиметрКубический дециметрКубический футКубический дюймКубический километрКубический ярдКубический метрКубический миллиметрКубический миля Метрическая система)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДекастерДекастрДесертная ложка (Великобритания)Десертная ложка (США)Драм КапляОбъем ЗемлиФемтолитрУнция жидкости (Великобритания)Унция жидкости (США)Галлон (Великобритания)Галлон (США)ГигалитрГилл (Великобритания)Гилл (США)ГектолитрГин (Библейский)ХогсхедГомер (Библейский)Сто кубических футовКилолитрЛог (Библейский)МегалитрМикролитрМиллилитрМинимум (Великобритания)Минимум (Великобритания)Минимум (США)НанолитрПеталитрПиколитрПинта (Великобритания)Пинта (США)Кварта (Великобритания)Кварта (США)СтереСтоловая ложка (Метрика)Столовая ложка (Великобритания)Столовая ложка (США) Таза (испанский)Чайная ложка (Метрическая)Чайная ложка (Великобритания)Чайная ложка (США)ТералитрТон РегистрТон | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Объем усеченного конуса Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Высота: 12 метров —> 12 метров, преобразование не требуется
Радиус 1: 12 метров —> 12 метров, преобразование не требуется
Радиус 2: 13 м —> 13 м Преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения
5893,62781813445 Кубический метр —> Преобразование не требуется 5
3
< 10+ калькуляторов объемов 92))Что такое усеченный конус?
Усеченный конус представляет собой коническую форму, вершина которой срезана под углом. Иногда вам может понадобиться разработать эти усеченные конусы в качестве элементов воздуховода. Разработка усеченного конуса может быть трудной, но если вы понимаете концепцию «линии истинной длины», эта разработка будет для вас легкой.
Иногда вам может понадобиться разработать эти усеченные конусы в качестве элементов воздуховода. Разработка усеченного конуса может быть трудной, но если вы понимаете концепцию «линии истинной длины», эта разработка будет для вас легкой.
Как рассчитать объем усеченного конуса? 92) где r — радиус верхнего основания, R — радиус нижнего основания, h — высота усеченного конуса. Объем обозначается символом
V T . Как рассчитать объем усеченного конуса с помощью этого онлайн калькулятора? Чтобы использовать этот онлайн-калькулятор для объема усеченного конуса, введите высоту (h) , радиус 1 (r 1 ) и радиус 2 (r 2 ) и нажмите кнопку расчета. Вот как можно объяснить вычисление объема усеченного конуса с заданными входными значениями -> 92)) . Чтобы рассчитать объем усеченного конуса, вам нужно высота (h) , радиус 1 (r 1 ) и радиус 2 (r 2 ) .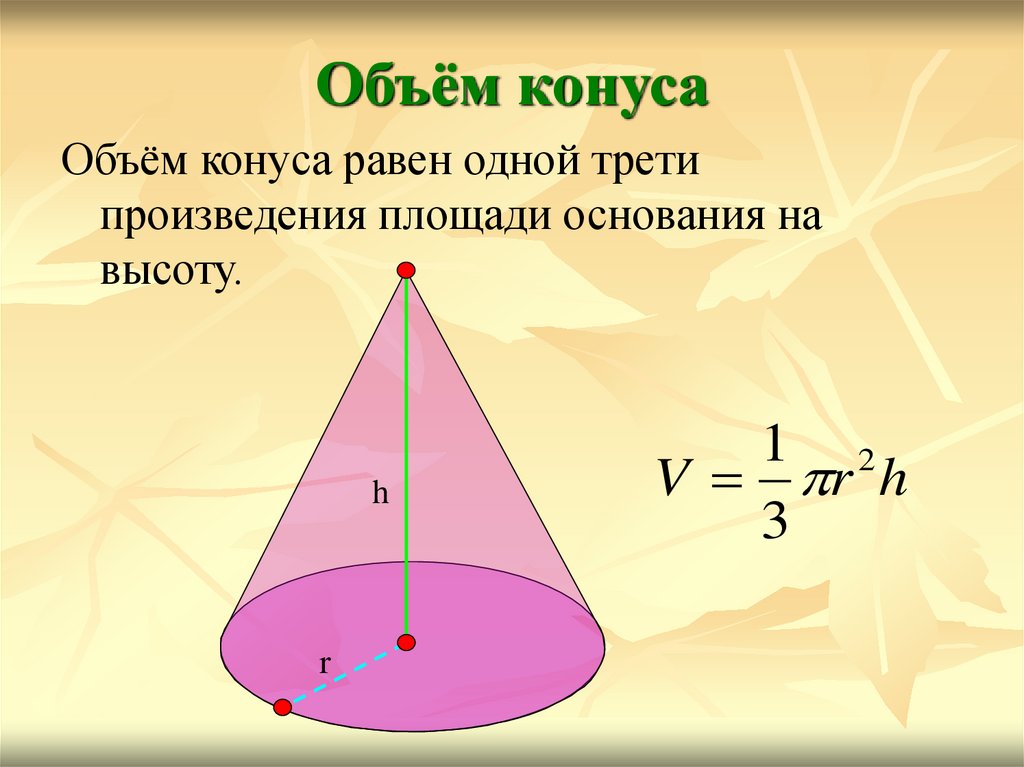 С помощью нашего инструмента вам нужно ввести соответствующие значения высоты, радиуса 1 и радиуса 2 и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
С помощью нашего инструмента вам нужно ввести соответствующие значения высоты, радиуса 1 и радиуса 2 и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов расчета объема?
В этой формуле Объем использует Высоту, Радиус 1 и Радиус 2. Мы можем использовать 13 других способов, чтобы вычислить то же самое, которые следующие: — 93)/(6*кв.(2))
Поделиться
Скопировано!
Калькулятор объема конуса
Создано Davide Borchia
Последнее обновление: 11 июля 2022 г.
Содержание:- Что такое конус?
- Как рассчитать объем конуса: по какой формуле находится объем конуса?
- Как рассчитать объем усеченного конуса?
- Почему важны конусы?
- Как найти объем конуса: несколько примеров
- Как найти объем конуса по наклонной высоте?
Рассчитайте объем любого конуса, от дорожных конусов до мороженого, от воронок до крыш замков, с помощью нашего калькулятора! Следуйте за нами в быстром путешествии по этим круглым телам.
Здесь вы узнаете:
- Что такое конус;
- Но самое главное, что такое усеченный конус ;
- Как найти объем конуса;
- Как рассчитать объем усеченного конуса;
- Как рассчитать объем конуса по его наклонной высоте;
- Несколько примеров; и
- Пара слов о ракетах.
Изучение конусов будет таким же гладким, как и они, но как насчет более «острых» форм? Перейдите к нашему калькулятору объема пирамиды, чтобы узнать ответ!
Что такое конус?
Конус представляет собой тело вращения , трехмерная форма, полученная путем полного вращения многоугольника вокруг главной оси. Другими главными телами вращения являются:
- Сфера;
- Цилиндр; и
- Усеченный конус.
Конус строится вращением прямоугольного треугольника вокруг одного из его катетов на 360°360\градус360°. Кроме того, вы можете повернуть равнобедренный треугольник на 180°180\градус180°.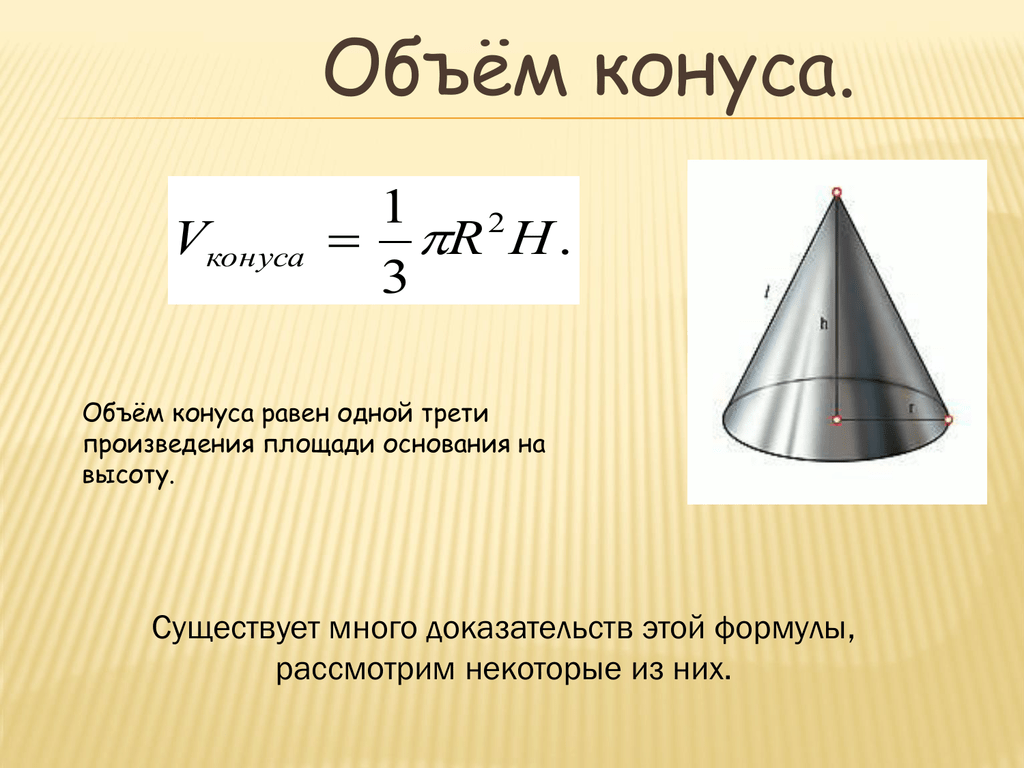 В результате получается круговое основание , соединенное с вершиной (или вершина ) на наклонную высоту конуса.
В результате получается круговое основание , соединенное с вершиной (или вершина ) на наклонную высоту конуса.
🙋 Конусы — единственные элементарные тела с одной вершиной!
Если «разрезать» конус горизонтальной плоскостью. Вы получаете две формы: меньший конус и тело с двумя параллельными круглыми основаниями : одно меньше другого (тривиальный случай, когда основания одинаковы, — это цилиндр). Мы называем усеченный конус с параллельными основаниями усеченным конусом .
Поскольку конус является результатом вращения треугольника, усеченная часть является результатом вращения трапеции (прямой или равнобедренной). 92\cdot \pi\cdot hV=31⋅r2⋅π⋅h
Где:
- rrr — радиус основания конуса;
- hhh — высота конуса; и
- π\piπ здесь, потому что мы что-то повернули!
Как рассчитать объем усеченного конуса?
Если вы хотите узнать, как рассчитать объем усеченного конуса, вы попали по адресу! Есть два способа рассчитать объем усеченного конуса:
- Вы можете вычесть объем меньшего конуса (с радиусом основания rrr) из объема большего конуса (с радиусом основания RRR), используя формулу: 92\right)V=31⋅π⋅h⋅(r2+r⋅R+R2)
Результат тот же!
Почему важны конусы?
Конусы повсюду.
 От мороженого до дорожного движения, от геометрии до расширения струи частиц, поскольку они обладают вращательной симметрией, которая не отдает предпочтение какому-либо конкретному направлению, они обычно встречаются как в природе, так и в искусственных объектах.
От мороженого до дорожного движения, от геометрии до расширения струи частиц, поскольку они обладают вращательной симметрией, которая не отдает предпочтение какому-либо конкретному направлению, они обычно встречаются как в природе, так и в искусственных объектах.Усеченные конусы, напротив, обнаружить немного сложнее. Впрочем, примеры найти не так уж и сложно. Горшки для цветов обычно имеют такую форму (вы можете воспользоваться нашим калькулятором, чтобы точно узнать, сколько земли вам нужно!). Но мы можем найти их и в колесах поездов (хотя разница действительно небольшая), и… в ракетах.
Сегменты, соединяющие различные ступени ракеты «Сатурн-5», которая первой отправила людей на Луну с орбиты Земли, были спроектированы с учетом формы усеченного конуса!
На ракете Сатурн-5 видны усеченные формы.Как найти объем рожка: несколько примеров
Сколько мороженого поместится в рожке? Размеры:
- Высота: h=15 смh=15\text{ см}h=15 см;
- Радиус: r=2,5 см r=2,5\text{ см}r=2,5 см 93V=31⋅2,52⋅π⋅15=98,17 см3
Почти 100 мл100\ \text{мл}100 мл, как раз то, что нужно для мороженого!
Теперь посчитаем объем усеченного конуса.
 Найдены размеры отрезка, соединяющего вторую и третью ступени ракеты «Сатурн-5»:
Найдены размеры отрезка, соединяющего вторую и третью ступени ракеты «Сатурн-5»:- Меньший радиус 3,30 м3,30\ \text{м}3,30 м;
- Больший радиус 5,03 м5,03\ \text{м}5,03 м;
- Высота 5,90м5,90\ \text{м}5,90м.
Введите эти величины в нижнюю часть нашего калькулятора или примените формулу: 92}h=s2−r2
Где sss — наклонная высота.
Давиде Борчиа
Вычислить объем усеченного конуса и площадь его поверхности
и отношение поверхности к объему усеченного прямого кругового конуса
Определение усеченного прямого кругового конуса: Усеченный прямой круговой конус конус (усеченный конус) — геометрическая фигура, которая получается из прямого круглого конуса путем срезания вершины конуса перпендикулярно его высоте Н . малый h высота усеченного конуса.
Основание радиуса, R:Верхний радиус, r:высота, h:дюйм:дюйм-фут-сантиметр-метрсм.
 другие единицы
другие единицы
точность:0123456789Отношение поверхности к объему | Преобразуйте 564,44 дюйм³ в вес для: соединений | еда | gravelsshow all units
The volume of the
truncated cone
= 564.44centimeter³ 9 249.51 foot³ 0.33 inch³ 564.44 meter³ 0.01 The surface to volume ratio of this truncated cone
= 0.69 Surface area to объемное отношение также известно как отношение поверхности к объему и обозначается как sa÷vol, где sa — площадь поверхности, а vol — объем.показать все блоки
α
degree 79.  7
7 radian 1.39 Unit
allThe area of the surface
of the truncated coneA base
= 78,54A Верхняя9 total
= 387.81centimeter² 506.71 182.41 1 812.85 2 501.97 foot² 0.55 0.2 1.95 2.69 дюйм² 78,54 28,27 280,99 387,81 387,81 387,81 .0285 0.05 0.02 0.  18
180.25 Unit
allHeight
H
= 27.5Apothem
l
= 11.18centimeter 69,85 28,4 Foot 2,29 0,93 777777777777777777777777777777777777777777777777777777777777777777777777777777777789н.0118 meter 0.7 0.28 Unit
allThe radii and height
of the truncated coneR base
= 5r top
= 3height
h
= 11centimeter 12.7 7.62 27.  94
94foot 0.42 0.25 0.92 inch 5 3 11 meter 0.13 0.08 0.28 Блок
ВсеДиаметры
Усеченный конусD Основание
= 10D TOP
=D TOP
= 6D TOP
= 6D .0863 centimeter 25.4 15.24 foot 0.83 0.5 inch 10 6 meter 0.25 0.15 - Ссылка (ID: N/A)
- 1.
 И.Н. Бронштейн, К.А. Семендяев, Герхард Мусиол, Хайнер Мюлиг. Справочник по математике 6-е изд. Спрингер. Берлин, Гейдельберг, Нью-Йорк. 2015. Последнее посещение: 29Август 2020 г. (платная ссылка amazon.com).
И.Н. Бронштейн, К.А. Семендяев, Герхард Мусиол, Хайнер Мюлиг. Справочник по математике 6-е изд. Спрингер. Берлин, Гейдельберг, Нью-Йорк. 2015. Последнее посещение: 29Август 2020 г. (платная ссылка amazon.com).
Пищевые продукты, питательные вещества и калории
ВСЯ ПЛАПЕШКА, UPC: 0411
976
содержат 417 калорий на 100 грамм (≈7,53 унции) Список этих продуктов, начиная с самого высокого содержания свободного холина и самого низкого содержания свободного холинаГравий, вещества и масла
Субстрат, флюорит весит 1 005 кг/м³ (62,7401 фунт/фут³) с удельным весом 1,005 относительно чистой воды. Подсчитайте, сколько этого гравия требуется для достижения определенной глубины в цилиндрическом, четвертьцилиндрическом или прямоугольном аквариуме или пруду [вес к объему | объем к весу | цена ]
Оксихлорид селена [SeOCl 2 или Cl 2 OSe] весит 2 420 кг/м³ (151,07566 фунт/фут³) [вес к объему | объем к весу | цена | моль к объему и весу | масса и молярная концентрация | плотность ]
Преобразование объема в вес, веса в объем и стоимости для Хладагент R-422A, жидкий (R422A) с температурой в диапазоне от -40°C (-40°F) до 60°C (140°F )
Веса и измерения
Астрономическая единица в час в квадрате является единицей измерения ускорения
Поглощенная доза радиации — это мера радиации в виде энергии на единицу массы, поглощенной конкретным объектом, например тканью человека.

переводная таблица фунтов/дюйм² в унции т/мм², конвертер единиц фунт/дюйм² в унции т/мм² или перевод всех единиц измерения поверхностной плотности.
Калькуляторы
Расчет объема, площади и отношения поверхности к объему тора
Калькулятор объема конуса — Calculator Hub
by CalcHub Team
Определение объема конуса никогда не было проще благодаря этому онлайн-калькулятору объема конуса. Чтобы рассчитать объем конуса, просто введите высоту и радиус конической формы.
Конусы представляют собой трехмерные объекты с кругом на одном конце и точкой на другом. Треугольное твердое тело образовано глубиной конуса.
На приведенном выше стандартном рисунке конуса «r» представляет радиус конуса, а «h» представляет высоту конуса.
Калькулятор объема конуса Используйте
- Для расчета объема предметов конической формы используйте этот калькулятор объема конуса.
- В приведенном выше калькуляторе введите высоту и радиус конуса в соответствующие поля.
- Калькулятор покажет объем конуса на основе введенной информации.
Для расчета объема конуса можно использовать простую формулу. Используя приведенную ниже формулу, мы можем рассчитать объем конуса, используя радиус (r) и высоту (h) конуса.
Как вычислить объем конусаНа уроке геометрии все научились вычислять объем конуса. Однако не все вспоминают об этом после окончания средней школы. Если вы знаете радиус и высоту объекта конической формы, вычислить объем несложно. Вы можете легко рассчитать объем конуса, используя приведенную выше формулу. Ниже мы решили несколько пошаговых примеров, чтобы помочь вам рассчитать объем конуса.

Пример
1. Шляпа на день рождения имеет радиус 10 дюймов и высоту 18 дюймов. Рассчитайте объем шапки на день рождения, которая имеет коническую форму.
Решение:
Радиус шляпы (r) = 10 дюймов
Высота шляпы на день рождения (h) = 18 дюймовИспользуя формулу объема конуса,
Объем = (1/3) x π r² h
Объем = (1/3) x 3,141592654 x 10 2 x 18
Объем = 1884,95559 куб. дюймовОбъем праздничной шляпы 1884,95559 кубических дюймов .
Пример
2. Высота конуса мороженого 12 дюймов, а диаметр его основания 4 дюйма. Определите, сколько мороженого он может вместить.
Решение:
Высота конуса мороженого = 12 дюймов
Диаметр конуса = 4 дюймаРадиус конуса необходим для использования формулы объема конуса, но вместо этого указывается диаметр конуса мороженого. . Во-первых, мы должны определить радиус конуса.

Радиус круга всегда равен половине его диаметра. В результате радиус конуса равен
Радиус = (1/2) x диаметр
Радиус = (1/2) x 4
Радиус = 2 дюймаИспользуя формулу объема конуса,
Объем = ( 1/3) x π r² h
Объем = (1/3) x 3,141592654 x 2 2 x 12
Объем = 50,2655 куб. дюймовРожок для мороженого может вместить 50,2655 кубических дюймов мороженого.
Как рассчитать объем усеченного конусаУсеченные конусы внешне похожи на основные конусы. Единственное отличие состоит в том, что у него нет заостренной стороны, а вместо этого он имеет круглую сторону, которая меньше нижнего круга. Проще говоря, усеченный конус можно создать, разрезав заостренную верхнюю сторону конуса. Иллюстрация ниже поможет вам понять, что такое усеченный конус.
Размеры усеченного конуса очень похожи на размеры обычного конуса. Разница лишь в том, что у нормального конуса один радиус, а у усеченного конуса — два, один меньше, а другой больше.


 URL: https://premierdevelopment.ru/ (дата обращения
)
URL: https://premierdevelopment.ru/ (дата обращения
) 2.
2. 
 Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник  Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр
Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр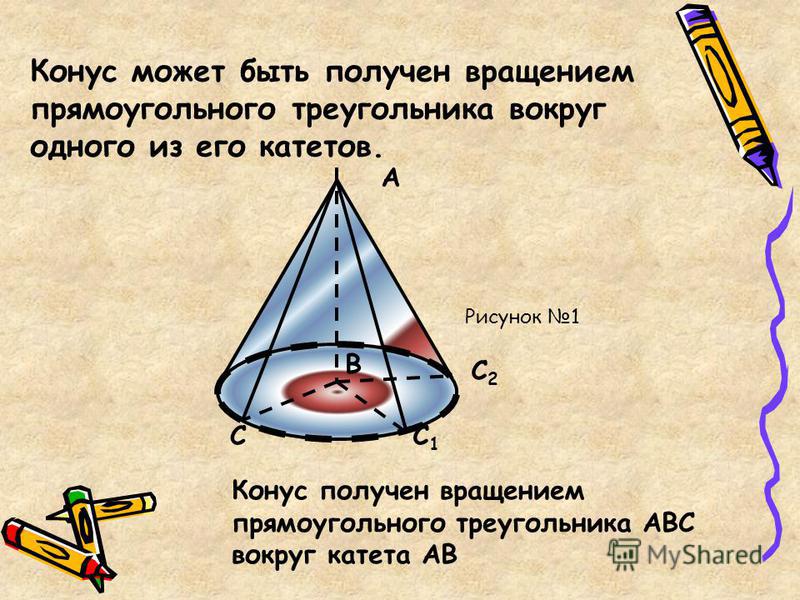 Наклонная высота — это расстояние между вершиной и краем основания, боковая поверхность — это поверхность без основания. Угол раскрытия — это угол при вершине, угол основания — это угол между наклонной линией и основанием. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать единицы измерения угла. Для расчета общих конусов см. общую пирамиду.
Наклонная высота — это расстояние между вершиной и краем основания, боковая поверхность — это поверхность без основания. Угол раскрытия — это угол при вершине, угол основания — это угол между наклонной линией и основанием. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать единицы измерения угла. Для расчета общих конусов см. общую пирамиду. de Веб-проекты | Онлайн калькуляторы
de Веб-проекты | Онлайн калькуляторы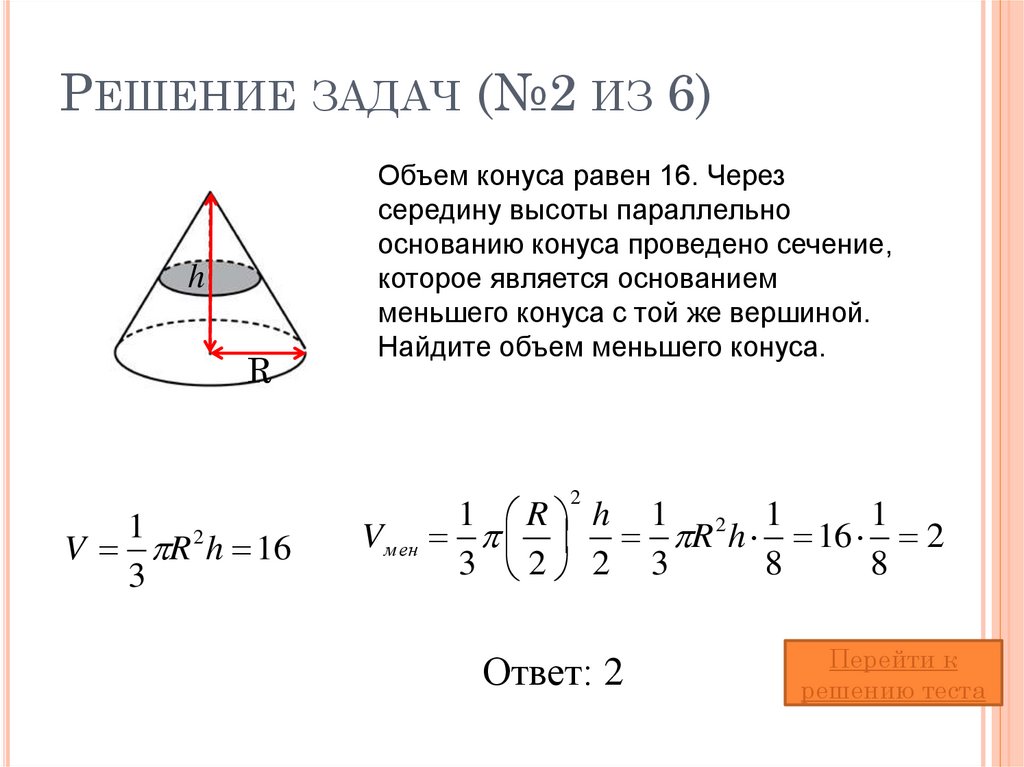 Радиус 1 [R 1 00]
Радиус 1 [R 1 00]
 ⓘ Объем усеченного конуса [V T ]
ⓘ Объем усеченного конуса [V T ]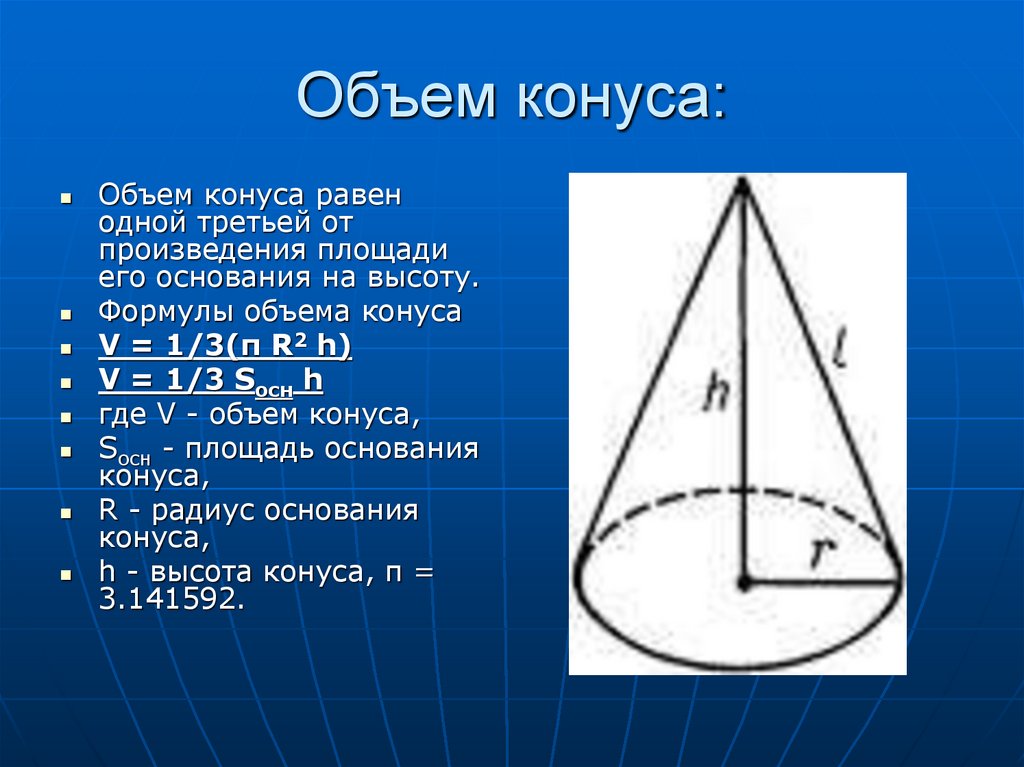 От мороженого до дорожного движения, от геометрии до расширения струи частиц, поскольку они обладают вращательной симметрией, которая не отдает предпочтение какому-либо конкретному направлению, они обычно встречаются как в природе, так и в искусственных объектах.
От мороженого до дорожного движения, от геометрии до расширения струи частиц, поскольку они обладают вращательной симметрией, которая не отдает предпочтение какому-либо конкретному направлению, они обычно встречаются как в природе, так и в искусственных объектах.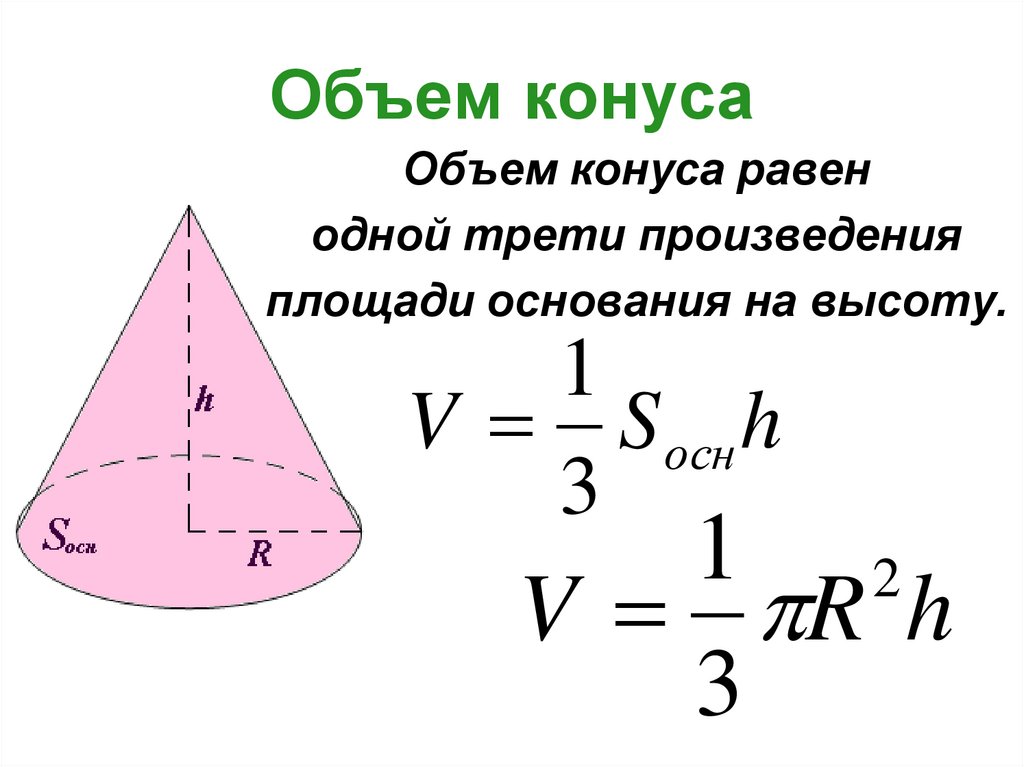 Найдены размеры отрезка, соединяющего вторую и третью ступени ракеты «Сатурн-5»:
Найдены размеры отрезка, соединяющего вторую и третью ступени ракеты «Сатурн-5»: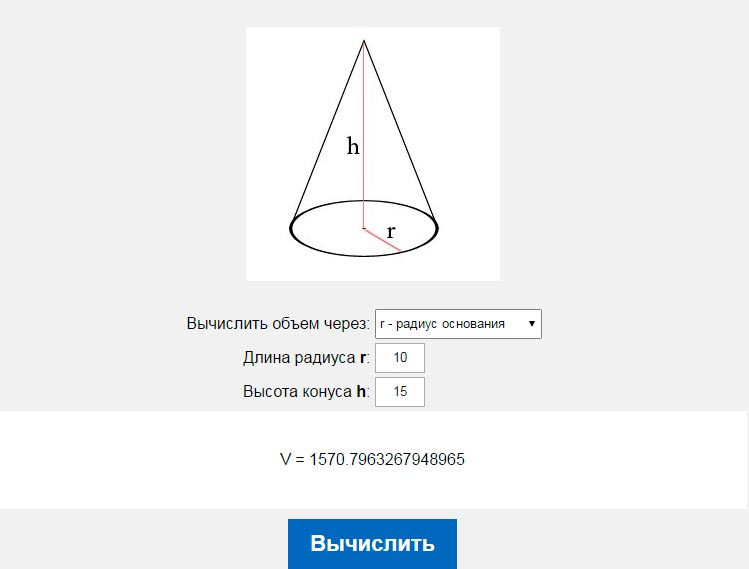 другие единицы
другие единицы  7
7 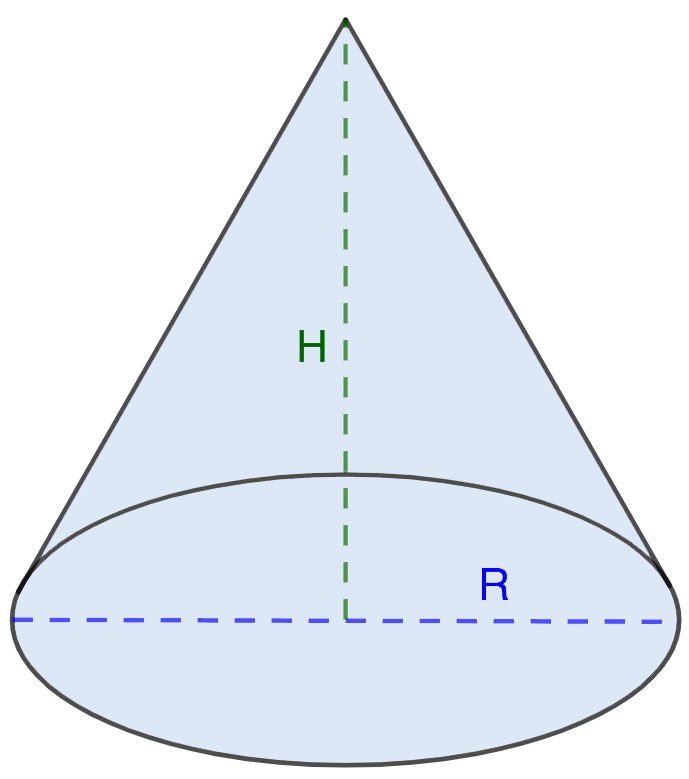 18
18 94
94 И.Н. Бронштейн, К.А. Семендяев, Герхард Мусиол, Хайнер Мюлиг. Справочник по математике 6-е изд. Спрингер. Берлин, Гейдельберг, Нью-Йорк. 2015. Последнее посещение: 29Август 2020 г. (платная ссылка amazon.com).
И.Н. Бронштейн, К.А. Семендяев, Герхард Мусиол, Хайнер Мюлиг. Справочник по математике 6-е изд. Спрингер. Берлин, Гейдельберг, Нью-Йорк. 2015. Последнее посещение: 29Август 2020 г. (платная ссылка amazon.com).