Как вычислить объем куба — Wiki How To Русский
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),ia(!0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Возведение в куб ребра куба
Вычисление объема по площади поверхности
Вычисление объема по диагонали
Дополнительные статьи
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
Шаги
1
Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
- Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
2
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза. Если s — длина ребра куба, то s * s *s = s3 и, таким образом, вы вычислите объем куба.
- Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть, другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и равна высоте, то этот процесс можно заменить возведением ребра куба в третью степень.

- В нашем примере объем куба равен 5 * 5 *5 = 53 = 125.
- Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть, другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и равна высоте, то этот процесс можно заменить возведением ребра куба в третью степень.
3
К ответу припишите единицы измерения объема (если вы этого не сделаете, ваша оценка может быть снижена). Так как объем — это количественная характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические единицы (кубические сантиметры, кубические метры и так далее).
- В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах (или в см3). Итак, объем куба равен 125 см3.
- Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих кубических единицах. Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125
Реклама
1
В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых можно найти ребро куба и его объем.
 Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.
Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.- Площадь поверхности куба равна 6s2, где s — длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так как у куба 6 равных граней).
- Рассмотрим пример. Площадь поверхности куба равна 50 см2. Найдите объем куба.
2
Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь одной грани куба).
В свою очередь площадь одной грани куба равна s2, где s — длина ребра куба.- В нашем примере: 50/6 = 8,33 см2 (не забывайте, что площадь измеряется в квадратных единицах — см2, м2 и так далее).
3
Так как площадь одной грани куба равна s2, то извлеките квадратный корень из значения площади одной грани и получите длину ребра куба.

- В нашем примере, √8,33 = 2,89 см.
4
Возведите в куб полученное значение, чтобы найти объем куба (как описано в предыдущем разделе).
- В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см
Реклама
- В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см
1
Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив диагональ на √2.
- Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см3.
- Запомните: d2 = 2s2, где d — диагональ грани куба, s — ребро куба. Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае ребер), то есть d2 = s2 + s2 = 2s2.

2
Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3. Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный D2 = 3s2 (где D — диагональ куба, s — ребро куба).
- Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет — это ребро, а второй катет — это диагональ грани куба, равная 2s2), то есть D2 = s2 + 2s2 = 3s2.
- Рассмотрим пример. Диагональ куба равна 10 м. Найдем объем куба:
- D2 = 3s2
- 102 = 3s2
- 100 = 3s2
- 33,33 = s2
- 5,77 м = s
- Объем куба равен 5,773 = 192,45 м3
Реклама
Об этой статье
На других языках
Как вычислить объем куба — Wiki How Русский
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
Эту страницу просматривали 589 857 раз.
Реклама
По какой формуле вычисляется объем куба? – Обзоры Вики
Расчет объема
Формула для определения объема умножает длину на ширину и высоту. Хорошая новость для куба заключается в том, что измерение каждого из этих измерений точно такое же. Следовательно, длину любой стороны можно умножить в три раза. Это приводит к формуле: Объем = сторона * сторона * сторона.
Отсюда, по какой формуле рассчитать объем? В то время как основная формула площади прямоугольной формы – длина × ширина, основная формула объема – длина × ширина × высота.
Каков объем куба и прямоугольного параллелепипеда? Формулы куба и прямоугольного параллелепипеда
| Cubo,en | Кубоид |
|---|---|
| Объем куба = (Сторона) 3 | Объем от прямоугольный параллелепипед = (длина × ширина × высота) |
| Диагональ куба = √3l | Диагональ кубоида = √ (l 2 + b 2 +h 2 ) |
| Периметр куба = 12 сторон | Периметр кубоида = 4 (длина + ширина + высота) |
Дополнительно Как найти объем прямоугольного параллелепипеда? Объем прямоугольного параллелепипеда находится по формуле умножение длины на ширину на высоту.
Каков объем 3 кубов? Поскольку все 6 граней куба имеют одинаковый размер, мы знаем, что каждое ребро куба равно √9 = 3 дюймам. Следовательно, объем куба равен 3 дм х 3 дм х 3 дм = 27 кубических дюймов.
Как найти объем прямоугольного параллелепипеда в м3?
Кубоид будет иметь длину, ширину и высоту. Объем прямоугольного параллелепипеда = (длина × ширина × высота) кубических единиц.
Что такое формула куба? Объем прямоугольного параллелепипеда (v) = ш × б × ч
где l — длина, b — основание, h — высота прямоугольного параллелепипеда.
Каков объем прямоугольного параллелепипеда в см3? Найден объем прямоугольного параллелепипеда умножив длину х ширину х высоту. Единицы в кубе, например, см3‘. Объем этого прямоугольного параллелепипеда находится путем умножения длины на ширину и высоту в любом порядке. 4см х 3см х 3см = 36см3.
Каков объем куба 5x5x5?
3Давайте посмотрим здесь на проверку формулы куб плюс b куб. Чтобы доказать или проверить, что3 + b3 = (а + Ь) (а2 — ab + b2) здесь нужно доказать левый = правый. Давайте начнем со следующих шагов.
Является ли куб прямоугольным параллелепипедом?
Куб — это частный случай квадратного прямоугольного параллелепипеда, у которого все шесть граней — квадраты.
…
| Прямоугольный кубоид | |
|---|---|
| Тип | Призма Плезиоэдр |
| Лики | 6 прямоугольника |
| Ребра | 12 |
| вершины | 8 |
Сколько кубиков в параллелепипеде? Таким образом, общее количество кубиков в прямоугольной призме = 2 × 24 = 48 кубика. Теперь дано, что объем 1 куба = 1 кубометру. Таким образом, объем 48 кубов = 1(48) = 48 кубических метров. Итак, это требуемый объем прямоугольного параллелепипеда.
Сколько кубиков в параллелепипеде?
Разница между кубом и кубоидом
| Cubo,en | Кубоид |
|---|---|
| В кубе все шесть лиц квадраты | У прямоугольного параллелепипеда все шесть граней прямоугольники. |
| Куб, состоящий из 12 диагоналей с одинаковой площадью поверхности | Всего у кубоида 12 диагоналей, из которых 3 диагонали различны по мере. |
Как найти недостающую длину куба?
Каков объем 4см? Например, если длина 4 см, ширина 6 см, высота 7. 3.
3.
Как считать кубики в стопке?
Сколько кубиков на рисунке ниже?
Правильный вариант: C
Существуют 20 кубика.
Каков объем 6 кубов? Количество единичных кубов 6, объем 6 куб см. 2.
Как найти объем прямоугольного куба?
Чтобы найти объем прямоугольной призмы, умножьте его 3 измерения: длина x ширина x высота. Объем выражается в кубических единицах.
Какова длина куба с объемом 8?
Если объем куба равен 8, то длина стороны 2. Если длину каждой стороны удвоить, длина стороны будет равна 4, что даст объем 64.
Как найти объем куба
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Твердая геометрия » Кубики » Как найти объем куба
Меры коробки. Сколько игральных костей может поместиться в эту коробку, если игральные кости представляют собой кубы со сторонами определенной длины ?
Сколько игральных костей может поместиться в эту коробку, если игральные кости представляют собой кубы со сторонами определенной длины ?
Возможные ответы:
Dice
Dice
Dice
Dice
Dice
Правильный ответ:
Dice
Объяснение:
Так как игральные кости находятся на каждой из сторон, их длина будет измеряться, если стоять лицом к лицу. Это означает, что игральные кости поместятся вдоль края прямоугольника, который измеряет .
игральные кости также поместятся на краю коробки, измеряемой , но не поместятся, так как добавление дополнительного кубика увеличит длину игральных костей, стоящих лицом к лицу, до . Для заполнения пробела нет полукубиков, поэтому с этой стороны есть небольшое пустое место.
игральные кости подходят по той стороне, которая измеряет .
Рассматривая «кости» как единицу измерения вместо и учитывая только объем, в который поместятся кости, в итоге получается прямоугольная форма, измеряющая игральные кости игральные кости кости. Объем этой фигуры — это количество игральных костей, которые поместятся в этой области (и, следовательно, в коробке). Найдите объем, перемножив все длины сторон фигуры вместе:
dice dice.
Сообщить об ошибке
Каков объем куба со стороной 7?
Возможные ответы:
Правильный ответ:
Объяснение:
При поиске объема куба мы ищем количество пространства, ограниченного кубом.
Чтобы найти это, мы должны знать формулу объема куба, которая равна
. Используя эту формулу, мы подставляем длину стороны за, чтобы получить
Куб длину стороны, чтобы получить ответ
Ответ .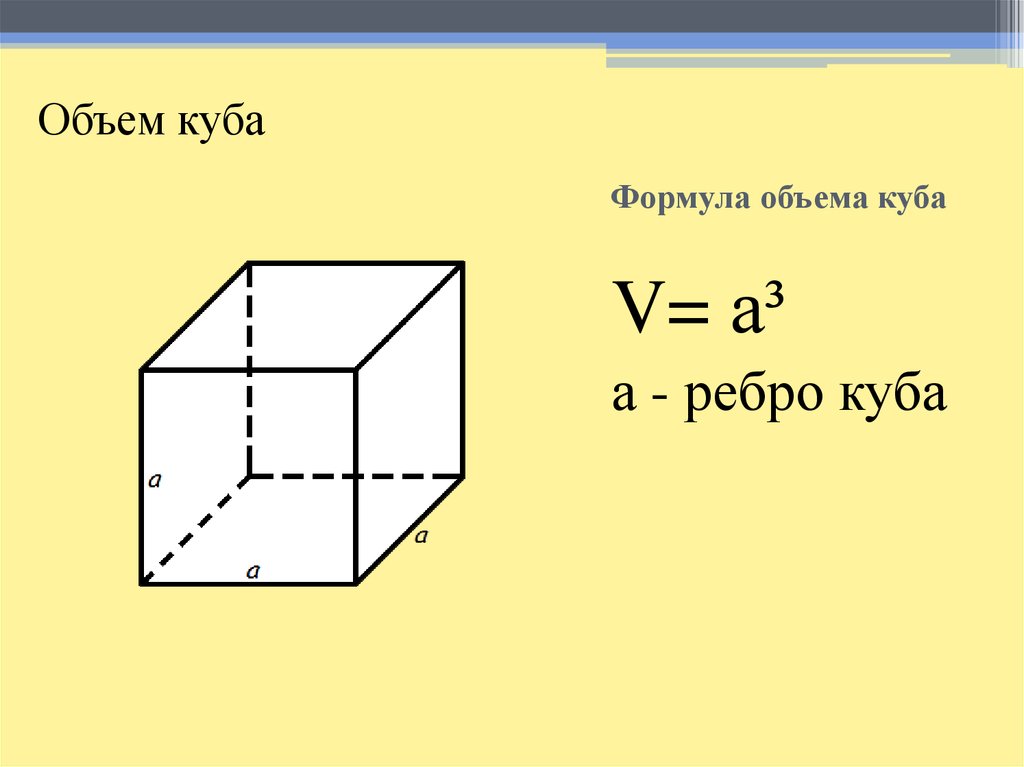
Сообщить об ошибке
Если объем куба равен 3375, какова длина каждой стороны?
Возможные ответы:
Правильный ответ:
Объяснение:
. Мы подставляем объем в уравнение, что дает
Затем мы извлекаем кубический корень из обеих сторон, что дает нам
Теперь мы знаем
Ответ .
Сообщить об ошибке
Какова сумма количества вершин, ребер и граней куба?
Возможные ответы:
18
26
Ни один из ответов не является правильным
24
20
Правильный ответ:
26
Пояснение:
Вершины = три плоскости, сходящиеся в одной точке = 8
Ребра = две плоскости, сходящиеся в линию = 12
Грани = одна плоскость как поверхность твердого тела = 6
Вершины + Ребра + Грани = 8 + 12 + 6 = 26
Сообщить об ошибке
Каков объем в сантиметрах прямоугольной призмы с длина, ширина и высота?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, нам нужно убедиться, что измерения даны в единых единицах.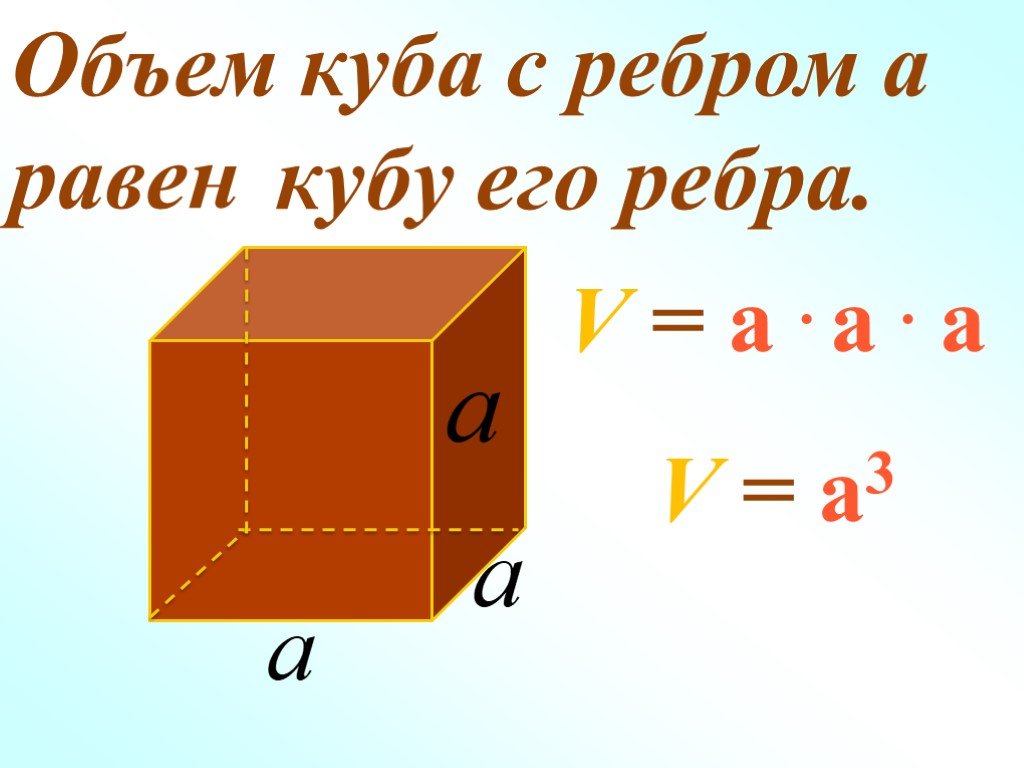 В этом случае мы будем использовать сантиметры; поэтому нам необходимо преобразовать другие единицы измерения, метры и миллиметры, в сантиметры с помощью анализа размеров.
В этом случае мы будем использовать сантиметры; поэтому нам необходимо преобразовать другие единицы измерения, метры и миллиметры, в сантиметры с помощью анализа размеров.
Найдите ширину.
Найдите высоту.
Теперь найдите объем по формуле .
Если вы рассчитали , значит, вы не конвертировали в соответствующие единицы.
Сообщить об ошибке
Каков объем куба с диагональю одной из граней ?
Возможные ответы:
Недостаточно информации для решения
Правильный ответ:
Объяснение:
Для решения этой задачи необходимо знать несколько фактов. Заметьте, что диагональ квадратной грани куба делит четырехугольник на два прямоугольных равнобедренных треугольника; следовательно, длина стороны квадрата до его диагонали равна катету равнобедренного прямоугольного треугольника до его гипотенузы: .
Изменить решение для .
Теперь определите объем.
Сообщить об ошибке
Здание имеет форму идеального куба со стороной . Каков объем здания в кубометрах?
Возможные ответы:
Недостаточно информации, чтобы решить Объяснение:
Чтобы решить этот вопрос, нам нужно преобразовать мили в метры с помощью анализа размеров, а затем найти объем здания.
Теперь найдем объем.
Сообщить об ошибке
Эта фигура представляет собой куб с одной гранью площадью 16 в 2 .
Каков объем куба (в 3 )?
Возможные ответы:
Правильный ответ:
Пояснение:
Объем куба равен одной стороне куба.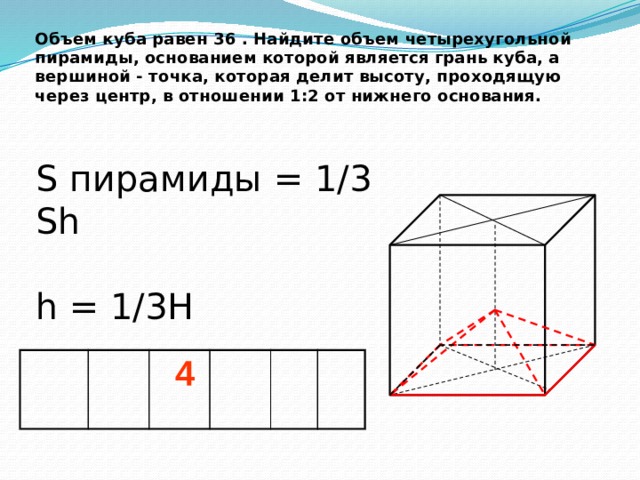 Поскольку мы знаем, что одна грань имеет площадь 16 в 2 , мы знаем, что одна сторона должна быть квадратным корнем из 16 или 4. Таким образом, объем равен .
Поскольку мы знаем, что одна грань имеет площадь 16 в 2 , мы знаем, что одна сторона должна быть квадратным корнем из 16 или 4. Таким образом, объем равен .
Сообщить об ошибке
Куб имеет высоту 4 фута. Каков объем куба в футах?
Возможные ответы:
Правильный ответ:
Объяснение:
У нас есть длина только одного ребра, но этого достаточно для нахождения объема. Объем куба равен одному ребру, умноженному на себя трижды:
Сообщить об ошибке
Площадь поверхности куба составляет единиц в квадрате. Каков его объем?
Возможные ответы:
единицы в кубе
единицы в кубе
единицы в кубе
единицы в кубе
Правильный ответ:
единиц в кубе
Объяснение:
Поскольку куб имеет квадратные грани, а площадь поверхности каждой грани определяется путем умножения длины одной стороны квадратной грани на саму себя, уравнение для площади поверхности куба , где – длина одной сторона одной грани (т.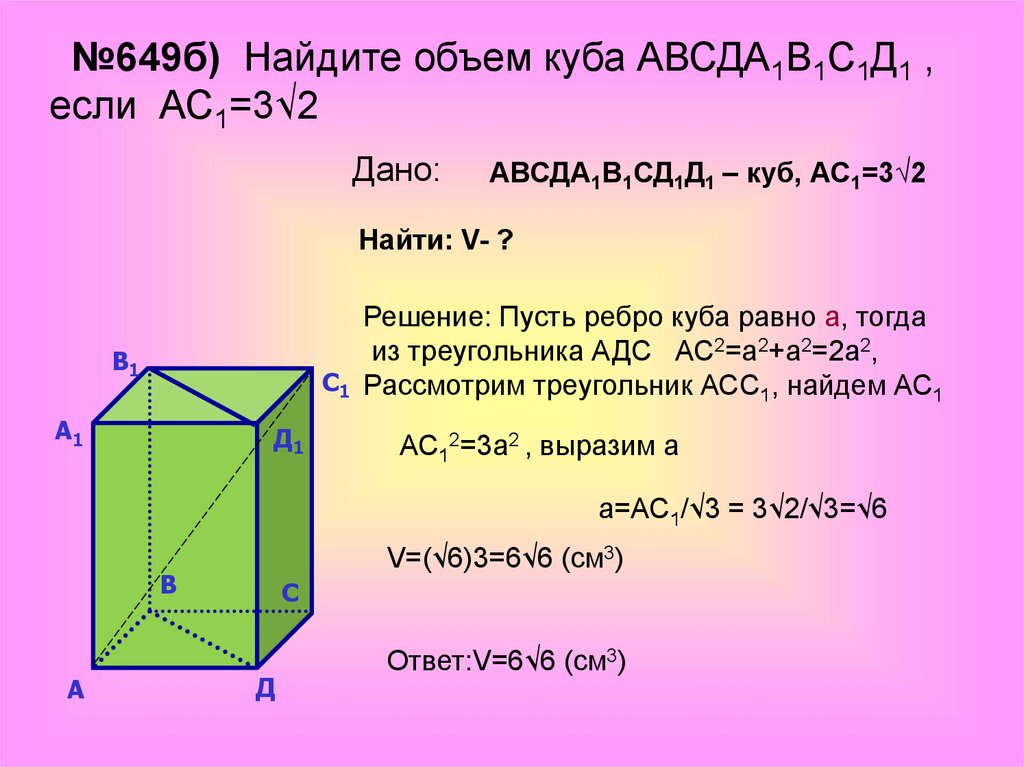 е. одно ребро куба). Найдите длину одной стороны/ребра данного куба, установив заданную площадь поверхности равной :
е. одно ребро куба). Найдите длину одной стороны/ребра данного куба, установив заданную площадь поверхности равной :
единиц
Объем куба равен , где – длина одного из ребер куба. Подстановка решения предыдущего уравнения для в уравнение объема дает объем куба:
единиц в кубе
Сообщить об ошибке
← Предыдущий 1 2 Следующий →
Все права защищены
Школьные математические ресурсы
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Учитесь по концепции
геометрия — Почему объем куба с дробными единицами меньше?
спросил
Изменено 3 года, 2 месяца назад
Просмотрено 1к раз
$\begingroup$
Итак, объем куба равен V = l x w x h .

 Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.
Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.