Объем с помощью двойного интеграла: Вычисление объёмов / Двойной интеграл / 3dstroyproekt.ru

Вычисление ⭐ объемов тел с помощью определенного интеграла: примеры решения задач

Вычисление объема тел с помощью интеграла

Понятие интеграла является довольно обширным и делится на несколько классов: определенный/неопределенный, двойной/тройной/одиночный.

Известно, что определенный интеграл численно равен площади под кривой, уравнение которой находится под интегралом.

Перейдем от задач на плоскости к задачам в пространстве. Пусть дано цилиндрическое тело D. Зададим оси координат так, что бы основание D — σ лежало в плоскости XOY, а поверхность, задаваемая функцией f(x, y) ограничивала тело D сверху.

Определение  1

Цилиндрическим называют тело, ограниченное поверхностями, параллельными друг другу.

Тогда объем тела D можно вычислить по формуле: 

Формула 1

Примечание 

Двойной интеграл — обобщенное понятие интеграла в случае функции двух переменных. Физический смысл двукратного интегрирования — вычисление объема.

Далее рассмотрим случаи нахождения объемов с помощью двойных и тройных интегралов. Советуем составить краткие конспекты алгоритмов расчета.

Вычисление объема с помощью двойного интеграла

Вычисление объема сводится к записи определенного двойного интеграла и последующего его решения.

Сначала приведем несколько свойств двойного интеграла, которые помогут упростить работу по его вычислению:

1. Двойной интеграл по основанию тела равен площади самой поверхности:
2. Константу можно вынести за знак интеграла: 
3. Интеграл суммы функций равен сумме интегралов: 
4. Если основание σ можно разбить на две поверхности так, что они не будут иметь внутренних общих точек, то: 

Рассмотрим алгоритм вычисления объема тела с помощью двойного интеграла:

1. Рекомендуется построить на плоскости XOY область интегрирования. Для этого строят графики функций и штрихуют заданную область. Этот пункт уместен, когда заданные поверхности и кривые достаточно просто представить графически.
2. Определить порядок обхода, расставить пределы интегрирования.
3. Вычислить внутренний интеграл.
4. Вычислить внешний интеграл.

Для некоторых поверхностей, например, сферических, удобнее записывать и решать двойные интегралы в полярной системе координат.

Тогда, если область интегрирования σ в полярных координатах задана неравенствами: ,  являются непрерывными на отрезке  объем вычисляется по формуле:

Формула 2

Во втором интеграле появился дополнительный множитель — якобиан. В данном случае якобиан равен r.

Определение 2

Якобиан — понятие в математическом анализе, неравенство нулю которого определяет возможность преобразований старых координат в новые в малой окрестности точки.

Вычисление объема тел с помощью тройного интеграла

В том случае, когда тело ограничено сверху и снизу двумя плоскими поверхностями, используют двойной интеграл. Но в случае, когда тело ограничено некоторыми поверхностями, использование двойного интеграла неприемлемо.

Чтобы вычислить объем тела, ограниченного некоторыми не плоскими поверхностями, используют тройной интеграл:

Формула 3

Свойства тройных интегралов аналогичны свойствам двойного. Последовательность действий при двукратном и троекратном интегрировании также аналогична.

Тройное интегрирование возможно выполнять в цилиндрических координатах (аналог полярной системы координат в пространстве): 

Формула 4

и в сферических: 

Формула 5

Примеры решения задач с ответами

Пример 1

Найти объем тела, ограниченного поверхностями 

Решение.

Сначала построим основание заданного тела. Поверхность ограничена параболой  и прямой y = 2

Выберем порядок обхода: 

Запишем двойной интеграл и вычислим его:

Ответ:.

Пример 2

Вычислить объем единичной полусферы.

Решение.

Уравнение сферы имеет вид: . Уравнение полусферы, расположенной в положительной части оси 

Чтобы найти объем, переведем уравнение в полярную систему координат:  .

Выберем порядок обхода:  . Запишем двойной интеграл: 

Сделаем подстановку: 

Тогда: 

Ответ: 

Пример 3

Дана сфера радиусом 2R. Вычислить объем сферы, используя интегралы.

Решение.

Для решения не понадобится чертеж, так как фигура является достаточно простой. Объем найдем с помощью тройного интеграла в сферической системе координат.

Ответ: 

Дифференциальное и интегральное исчисления для втузов, т.2

Дифференциальное и интегральное исчисления для втузов, т.2

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985. — 560 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Второй том включает разделы: дифференциальные уравнения, кратные и криволинейные интегралы, интегралы по поверхности, ряды, уравнения математической физики, операционное исчисление, элементы теории вероятностей и математической статистики, матрицы. Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА XIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. Постановка задачи. Уравнение движения тела при сопротивлении среды, пропорциональном скорости. Уравнение цепной линии § 2. Определения § 3. Дифференциальные уравнения первого порядка (общие понятия) § 4. Уравнения с разделенными и разделяющимися переменными. Задача о распаде радия § 5. Однородные уравнения первого порядка § 6. Уравнения, приводящиеся к однородным § 7. Линейные уравнения первого порядка § 8. Уравнение Бернулли § 9. Уравнение в полных дифференциалах § 10. Интегрирующий множитель § 11. Огибающая семейства кривых § 12. Особые решения дифференциального уравнения первого порядка § 13. Уравнение Клеро § 14. Уравнение Лагранжа § 15. Ортогональные и изогональные траектории § 16. 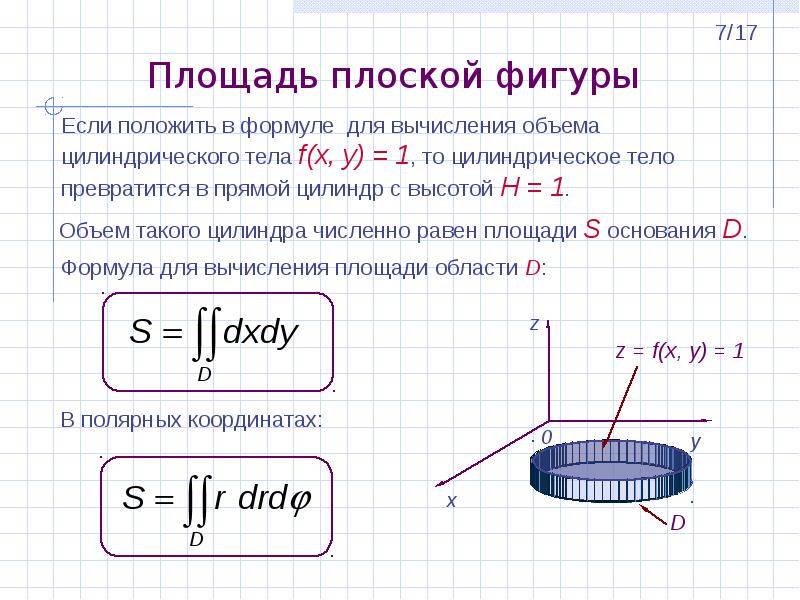(n) = f(x) § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14. Момент инерции и координаты центра масс тела § 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13. Степенные ряды. Интервал сходимости § 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4. Ряды Фурье для четных и нечетных функций § 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи § 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7. Дифференцирование изображения § 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей § 2. Классическое определение вероятности и непосредственный подсчет вероятностей § 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15. Нормальный закон распределения. Математическое ожидание нормального распределения § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27. Задачи математической статистики. Статистический материал § 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому § 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ

б f(x)dx$ при положительных $f(x)$ можно интерпретировать как площадь под кривая $f(x)$ на интервале $[a,b]$.

Интеграл – это площадь между кривой $f(x)$ и осью $x$.

Таким же образом двойной интеграл $\iint_\dlr f(x,y)\,dA$ положительный $f(x,y)$ можно интерпретировать как объем под поверхностью $z=f(x,y)$ над областью $\dlr$. Представьте, что синий предмет ниже — поверхность $z=f(x,y)$, плавающая над плоскостью $xy$. двойной интеграл $\iint_\dlr f(x,y)\,dA$ можно интерпретировать как объем между поверхностью $z=f(x,y)$ и плоскостью $xy$, т.е. «цилиндр» над областью $\dlr$.

Это также видно из суммы Римана, аппроксимирующей интеграл \начать{выравнивать*} \sum_{i,j} f(x_{ij}, y_{ij}) \Delta x \Delta y \конец{выравнивание*} Каждый член суммы Римана — это объем тонкой коробки с основанием $\Delta x \times \Delta y$ и высоту $f(x_{ij},y_{ij})$.

Следовательно, полная сумма Римана аппроксимирует объем под поверхностью по объему связки этих тонких ящиков. В пределе как $\Delta x, \Delta y \to 0$, получим полный объем под поверхностью над область $\dlr$, т. е. $\iint_\dlr f(x,y)\, dA$. 92 года $. Объем вычисляется по области $D$, определяемой $0 \le x \le 2$ и $0 \le y \le 1$. Следовательно, реальный объем равен двойному интегралу $\iint_D f\,dA$. Объем ящиков равен $$\sum_{i,j} f(x_{i},y_{j})\Delta x \Delta y$$, где $x_i$ — середина $i$-го интервала вдоль по оси $x$, а $y_j$ — середина $j$-го интервала по оси $y$. {\pi/2 } =\фракция{3\пи}{2}. \конец{выравнивание*}

Использование двойного интеграла для нахождения объема объекта — Криста Кинг Математика

Нахождение объема с помощью двойного интеграла

Мы уже знаем, что можем использовать двойные интегралы для нахождения объема под функцией в некоторой области ???R=[a,b]\times[c,d]???.

Используем формулу двойного интеграла

???V=\int\int_Df(x,y)\ dA???

найти том, где ???D??? представляет регион, по которому мы интегрируем, и ???f(x,y)??? это кривая, ниже которой мы хотим найти объем.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Нам нужно превратить двойной интеграл в повторный интеграл, найдя пределы интегрирования для ???x??? и ???y???.

Как с помощью двойного интеграла найти объем твердого тела

Пройти курс

Хотите узнать больше о Calculus 3? У меня есть пошаговый курс для этого.

🙂

Узнать больше

Нахождение объема под поверхностью и над областью, определяемой тремя линиями

Пример

Нахождение объема под функцией над областью ???D???, где ???D??? треугольник, ограниченный линиями ???y=1???, ???x=1??? и ???y=3-x???.

???z=2xy???

Первое, что мы сделаем, это зарисуем область ???D???. Будет легко, если мы найдем точки пересечения трех линий.

Мы найдем пересечение ???y=1??? и ???х=1???.

Сопряжение ???x=1??? с ???y=1???, точка пересечения ???(1,1)???.

Найдем пересечение ???y=1??? и ???y=3-x???.

???3-x=1???

???-x=-2???

???х=2???

Сопряжение ???x=2??? с ???y=1???, точка пересечения ???(2,1)???.

Найдем пересечение ???x=1??? и ???y=3-x???.

???у=3-х???

???y=3-1???

???y=2???

Сопряжение ???x=1??? с ???y=2???, точка пересечения ???(1,2)???.

Если мы нанесем эти точки и нарисуем соединяющие их линии, мы увидим треугольную область ???D???.

Поскольку у нас есть только одно комплексное уравнение, ???y=3-x??? а на ???y??? решено, проинтегрируем по ???y??? во-первых, это означает, что мы будем рассматривать это как интеграл типа I, и поэтому внутренний интеграл будет иметь пределы интегрирования для ???y???.

Нам нужно превратить двойной интеграл в повторный интеграл, найдя пределы интегрирования для x и y.

Если мы разделим треугольную область ???D??? на вертикальные срезы, верхние части этих срезов определяются линией ???y=3-x???, а нижние — ???y=1???. Глядя на эскиз области ???D???, мы видим, что ???x??? определяется на ???[1,2]???. Таким образом, мы получим

???V=\int\int_Df(x,y)\ dA???

94\право]???

???V=16-16+4-\влево(4-2+\frac14\вправо)???

???V=2-\frac14???

???V=\frac74???

Можно сказать, что объем под кривой ???z=2xy??? по региону ???D??? ???7/4???.

Получите доступ к полному курсу Calculus 3

Начать

Изучайте математикуКриста Кинг 30 октября 2020 г.