Объем шара формула через радиус: Вычислить объем шара, если его радиус равен 4 см

основные формулы и пример их использования

Шар это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра.

Вычислить объем шара

Объем шара можно вычислить по формуле:

R – радиус шара

V – объем шара

Найти объем шара радиусом сантиметров.

Для того чтобы вычислить объем шара формула используется следующая:

где – искомый объем шара, – , – радиус.

Таким образом, при радиусе сантиметров объем шара равен:

V

3,14 × 103

= 4186,7

кубических сантиметров.

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара.

Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится

вычислять объем шара . Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары.

С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение.

Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки.

Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений.

В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы.

Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий.

Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Сфера — одно из простейших геометрических тел, в котором все точки ее поверхности находятся на одном и том же расстоянии от центра изображения. Расстояние от центра сферы до любой точки на ее поверхности называется радиусом.

Объем мяча

Диаметр шара называется удвоенным радиусом.

Как найти объем шара вокруг его радиуса

Если мы знаем радиус сферы, мы можем легко вычислить ее величину. Для этого умножьте куб на радиус и четверное число Pi, после чего результат будет разделен на три. Формула для определения объема шара по его радиусу выглядит следующим образом: .
Для тех, кто забыл, мы помним, что число Pi является фиксированным значением и равно 3.14.

Как найти объем сферы на диаметр

Если диаметр сферы известен из условий задачи, ее объем вычисляется по следующей формуле: , то есть.

число Pi следует умножить на диаметр диаметра, то полученный результат делится на 6.

Как определить массу шара

Масса тела — это физическая величина, указывающая степень ее инертности. Масса физического тела зависит от объема занимаемого пространства и плотности материала, из которого он собирается. Объем тела правильной формы (скажем, бить ) нетрудно рассчитать, и если материал, из которого он изготовлен, также известен, навалом это разрешено быть очень примитивным.

инструкции

первый Укажите сумму бить .

Как рассчитать объем шара

Для этого достаточно знать один из ваших параметров — радиус, диаметр, поверхность и т. Д. Скажите, знаете ли вы диаметр бить (d), его объем (V) разрешается определять, как одна шестая часть продукта с диаметром поднимается в кубе с числом Pi: V = π * d? / 6.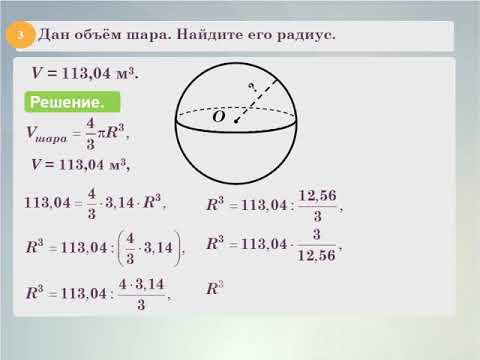 Через радиус бить (r) объем выражается как одна треть произведения числа Pi, который в четыре раза увеличивается с радиусом, помещенным в куб: V = 4 * π * r? / 3.

второй подсчитывать навалом бить (m), умножьте его объем с великолепной плотностью вещества (p): m = p * V.

Если это материал бить не однородный, то мы должны взять среднюю плотность. В этой формуле мы заменяем объем бить через его известные параметры, допускается принимать по известному диаметру бить формула m = p * π * d? / 6 и для главного радиуса m = p * 4 * π * r? / 3.

третий Используйте для расчетов, например, типичный калькулятор программного обеспечения, который входит в базовую операционную систему Windows, любую сильную версию, используемую сегодня.

Самый простой способ начать — нажатием win + r, чтобы открыть типичный диалог для запуска программы, затем введите команду calc и нажмите кнопку OK.

В меню «Калькулятор» разверните раздел «Вид» и выберите строку «Инженер» или «Ученый» (в зависимости от используемой версии ОС) — интерфейс этого режима имеет кнопку для ввода номера номера Pi одним щелчком мыши.

3.

ПРОЕКТИРОВАНИЕ ВОДЫ И САНИТАЦИИ

E-mail: [email protected]

Время работы: Пн-Пт с 9-00 до 18-00 (без обеда)

Вычисление объема сферы через радиус или диаметр

Сфера — это геометрическое тело, представляющее собой совокупность всех точек пространства, расположенных от центра на некотором расстоянии.

Как рассчитать объем шара

Основной математической характеристикой шара является его радиус.

Количество шара — это количественная характеристика этого числа во Вселенной.

Формула расчета объема шара:

V = 4/3 * π * r 3

V = 1/6 * π * d 3

r — радиус сферы;
d — диаметр сферы.

См. Также статью о всех геометрических фигурах (линейный 1D, плоский 2D и 3D 3D).

Эта страница является самым простым веб-калькулятором для расчета объема шара по радиусу или диаметру.

Сферические фигуры окружают нас практически везде, однако, мы настолько к ним привыкли, что не придаем этому внимания. Тем временем, случается так, что нам необходимо узнать объем какой-нибудь из них. Но все ли знают, как найти объем шара ? Углубляться в школьные воспоминания, чтобы восстановить в голове курс геометрии? Не затрудняйте себе задачу. Давайте лучше включим логику, и разберемся с этим вопросом.

Инструкция:

• Начнем с примера, когда формула объема шара нам не понадобится — представим, что у нас есть возможность произвести вычисления практическим путем . Один из наиболее простых способов это сделать — последовать по стопам Архимеда, определив объем не самого шара непосредственно, а вытесненной им воды . Для этого нужно положить его в емкость, подходящую по размерам, предварительно отметив уровень воды. Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
• Если вы уверены в том, из какого именно материала сделана сфера, постарайтесь определить ее плотность — эта информация наверняка найдется на просторах всемирной сети. В этой ситуации от вас потребуется лишь взвесить данную фигуру, после чего воспользоваться простой формулой объема шара, разделив вес предмета на его плотность: V=m/p .
• Может случиться, что предыдущие варианты вам недоступны. Не отчаивайтесь — если есть возможность узнать радиус шара, к нам на помощь придет нужная формула, более сложная, чем предыдущая, но доступная. Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара:
  V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
• Бывает и так, что гораздо легче найти диаметр фигуры , нежели его радиус. Этот вариант даже лучше — можно не производить таких сложных вычислений, формула становится значительно проще. Нам нужно будет лишь умножить диаметр в кубе на число Пи, после чего разделить получившееся число на шесть: V=π*d³/6 . К примеру, вы узнали, что диаметр вашей сферы составляет 25 см., тогда ее объем будет равняться: 3,14*25³/6 = 8177,08333см³ ≈ 0,818м³.

где V – искомый объем шара , π – 3,14 , R – радиус.

Таким образом, при радиусе 10 сантиметров объем шара равен:

V

3,14 × 10 3

= 4186,7

кубических сантиметров.

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара . Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий. Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.

Шар и сфера

Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.

Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.

Объем шара

Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.

Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3

Объем цилиндра вычисляется по формуле:

Vc = pi × R 2 × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R 3 .

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3

Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же

Vsh = 4/3 pi × R 3

Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.

Примеры из жизни

Пушечные ядра

Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде

Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.

Воздушные шары

Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат

Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.

Заключение

Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.

Радиус шара (обозначается как r или R) – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Как и в случае круга, радиус шара является важной величиной, которая необходима для нахождения диаметра шара, длины окружности, площади поверхности и/или объема. Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.

Шаги

Формулы для вычисления радиуса

Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2 . Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.

• Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см . Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).

Вычислите радиус по длине окружности. Используйте формулу: r = C/2π . Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.

• Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см .
• Такая же формула используется при вычислении радиуса и длины окружности круга.

Вычислите радиус по объему шара. Используйте формулу: r = ((V/π)(3/4)) 1/3 . Объем шара вычисляется по формуле V = (4/3)πr 3 . Обособив r на одной стороне уравнения, вы получите формулу ((V/π)(3/4)) 3 = г, то есть для вычисления радиуса объем шара делим на π, результат умножаем на 3/4, а полученный результат возводим в степень 1/3 (или извлекаем кубический корень).

• Например, дан шар с объемом 100 см 3 . Радиус этого шара вычисляется так:
  • ((V/π)(3/4)) 1/3 = r
  • ((100/π)(3/4)) 1/3 = r
  • ((31,83)(3/4)) 1/3 = r
  • (23,87) 1/3 = r
  • 2,88 см = r

Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)) . Площадь поверхности шара вычисляется по формуле А = 4πr 2 . Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π. Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.

• Например, дан шар с площадью поверхности 1200 см 3 . Радиус этого шара вычисляется так:
  • √(A/(4π)) = r
  • √(1200/(4π)) = r
  • √(300/(π)) = r
  • √(95,49) = r
  • 9,77 см = r

Определение основных величин

1. Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности.

   Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.

Нахождение радиуса по расстоянию между двумя точками

1. Найдите координаты (х,у,z) центра шара. Радиус шара равен расстоянию между его центром и любой точкой, лежащей на поверхности шара. Если известны координаты центра шара и любой точки, лежащей на его поверхности, можно найти радиус шара по специальной формуле, вычислив расстояние между двумя точками. Сначала найдите координаты центра шара. Имейте в виду, что так как шар является трехмерной фигурой, то точка будет иметь три координаты (х,у,z), а не две (х,у).

   • Рассмотрим пример. Дан шар с центром с координатами (4,-1,12) . Воспользуйтесь этими координатами, чтобы найти радиус шара.

2. Найдите координаты точки, лежащей на поверхности шара. Теперь нужно найти координаты (х,у,z) любой точки, лежащей на поверхности шара. Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.

   • В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0) . Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.

3. Вычислите радиус по формуле d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2). Узнав координаты центра шара и точки, лежащей на его поверхности, вы можете найти расстояние между ними, которое равно радиусу шара. Расстояние между двумя точками вычисляется по формуле d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2), где d – расстояние между точками, (x 1 ,y 1 ,z 1) – координаты центра шара, (x 2 ,y 2 ,z 2) – координаты точки, лежащей на поверхности шара.

   • В рассматриваемом примере вместо (x 1 ,y 1 ,z 1) подставьте (4,-1,12), а вместо (x 2 ,y 2 ,z 2) подставьте (3,3,0):
     • d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2)
     • d = √((3 — 4) 2 + (3 — -1) 2 + (0 — 12) 2)
     • d = √((-1) 2 + (4) 2 + (-12) 2)
     • d = √(1 + 16 + 144)
     • d = √(161)
     • d = 12,69 . Это искомый радиус шара.

4. Имейте в виду, что в общих случаях r = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2). Все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара. Если в формуле для нахождения расстояния между двумя точками «d» заменить на «r», получится формула для вычисления радиуса шара по известным координатам (x 1 ,y 1 ,z 1) центра шара и координатам (x 2 ,y 2 ,z 2) любой точки, лежащей на поверхности шара.

   • Возведите обе стороны этого уравнения в квадрат, и получите r 2 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2 . Отметьте, что это уравнение соответствует уравнению сферы r 2 = x 2 + y 2 + z 2 с центром с координатами (0,0,0).

• Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
• В этой статье рассказывается о вычислении радиуса шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
• π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.

Объем шара

На этом уроке мы дадим определение шара. Выведем формулу для вычисления объёма шара. А затем с её помощью выведем формулу для вычисления площади сферы.

Прежде чем приступить к рассмотрению данной темы, давайте вспомним, что такое шар.

Определение:

Шар – это совокупность всех точек пространства, находящихся от данной точки на расстоянии, не больше данного. Причём, данная точка называется центром шара, а данное расстояние – радиусом шара.

Радиусом шара называют всякий отрезок, соединяющий центр шара с любой точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.

Отрезок, соединяющий две точки шаровой поверхности и не являющийся диаметром шара, т.е. не проходящий через центр шара, называется хордой шара.

Понятно, что сечение шара плоскостью есть круг.

Сечение шара плоскостью, проходящей через его центр, называется большим кругом шара.

Итак, справедлива следующая теорема: объём шара радиуса  равен .

Докажем теорему. Пусть нам дан шар радиуса  с центром в точке . Выберем ось  так, чтобы начало оси совпадало с центром шара.

Тогда отрезок  это есть радиус шара .

Докажем, что объём шара равен .

На оси  отметим произвольную точку  и рассмотрим сечение шара плоскостью проходящее через эту точку перпендикулярно к оси . Заметим, что такое сечение шара плоскостью является кругом с центром в точке .

Отрезок .

Обозначим радиус этого круга через , а его площадь через , где  – абсцисса точки .

Выразим площадь  через  и радиус шара .

Из прямоугольного треугольника  по теореме Пифагора найдём радиус круга. Тогда имеем .

Площадь круга . Заменим радиус круга  выражением . Тогда получаем, что .

Заметим, что эта формула верна для любого положения точки  на диаметре .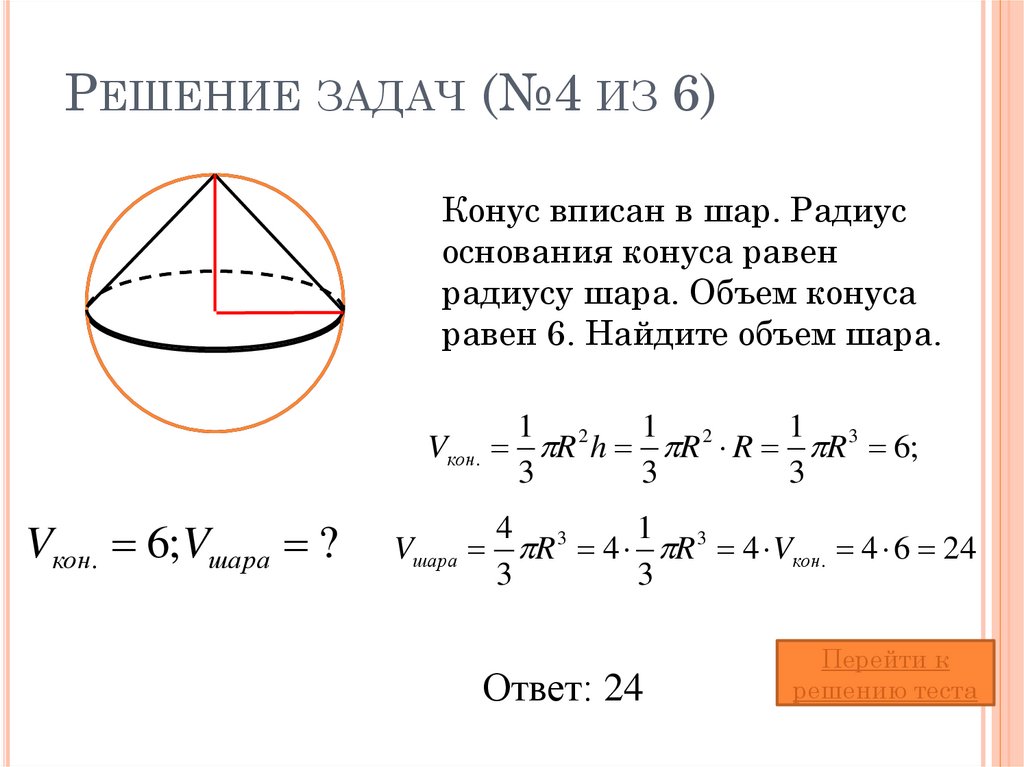 Иначе говоря, верна для всех , удовлетворяющих условию .

Так как мы с вами выразили площадь через , то можем вычислить объём шара с помощью основной формулы объёма тела. Вспомним её: объем тела равен .

Итак, применяя основную формулу для вычисления объёмов тел получаем, что объём шара равен .

Этим мы с вами доказали, что объём шара с радиусом равным  можно вычислить по формуле .

Что и требовалось доказать.

Ранее мы с вами без доказательства привели формулу для вычисления площади сферы. Напомню, что площадь сферы можно вычислить по формуле: .

Теперь давайте выведем эту формулу, пользуясь формулой объёма шара.

Итак, рассмотрим сферу радиуса  с центром в точке О и описанный около неё многогранник, имеющий  граней.

Напомним, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.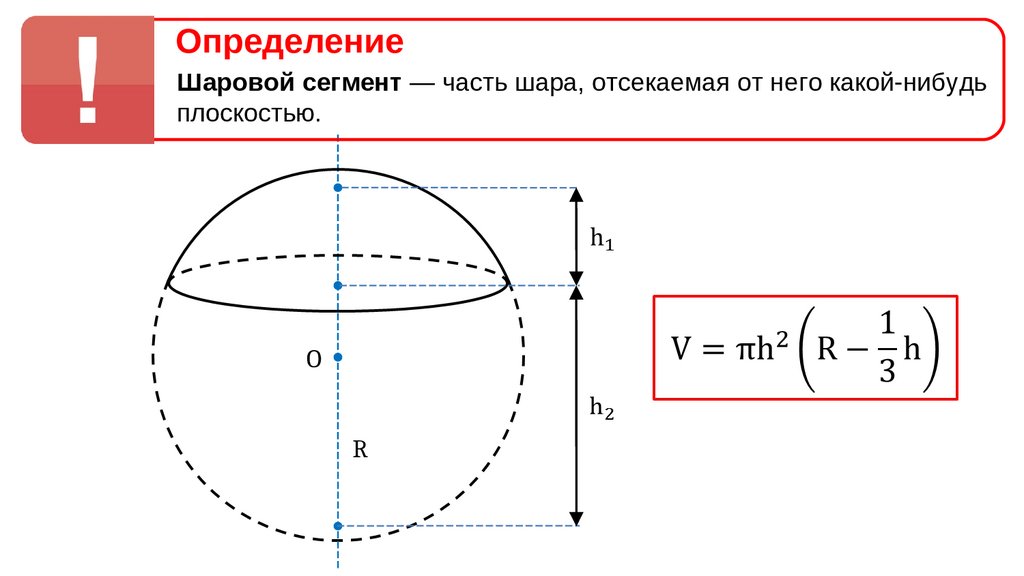

Занумеруем грани в произвольном порядке и обозначим через  – площадь -й грани.

Затем соединим центр О сферы отрезками со всеми вершинами многогранника. При этом получим эн пирамид с общей вершиной О, основаниями которых являются грани многогранника, а высотами – радиусы сферы, проведенные в точки касания граней многогранника со сферой.

Следовательно, объём -й пирамиды равен , а объём всего описанного многогранника равен: . Где  – площадь поверхности многогранника.

Отсюда получаем: .

Теперь будем неограниченно увеличивать  таким образом, чтобы наибольший размер каждой грани описанного многогранника стремился к нулю. При этом объём  описанного многогранника будет стремиться к объёму шара. В самом деле, если наибольший размер каждой грани описанного многогранника не превосходит , то описанный многогранник содержится в шаре радиуса  с центром в точке .

Но ведь с другой стороны, описанный многогранник содержит исходный шар радиуса . Значит, объём .

Так как выражение  при , то и объем  при  ().

Переходя затем к пределу, получаем, что .

По определению площади сферы , следовательно, .  

Что и требовалось доказать.

Задача: объём шара равен равен  см³. Найдите диаметр шара.

Решение: запишем формулу для вычисления объёма шара.

По условию задачи объём шара равен  см³.

Отсюда видим, что радиус шара равен  (см). Напомним, что диаметр шара вдвое больше его радиуса. Тогда диаметр нашего шара равен  (см).

Запишем ответ.

Задача: радиус шара увеличили в  раза. Во сколько раз увеличился объём шара?

Решение: запишем формулу для вычисления объёма шара.

Так как по условию задачи радиус исходного шара увеличили в 2 раза, то радиус данного шара будет равен . Подставляя данный радиус в формулу для вычисления объёма шара  видим, что объём исходного шара увеличился в 8 раз.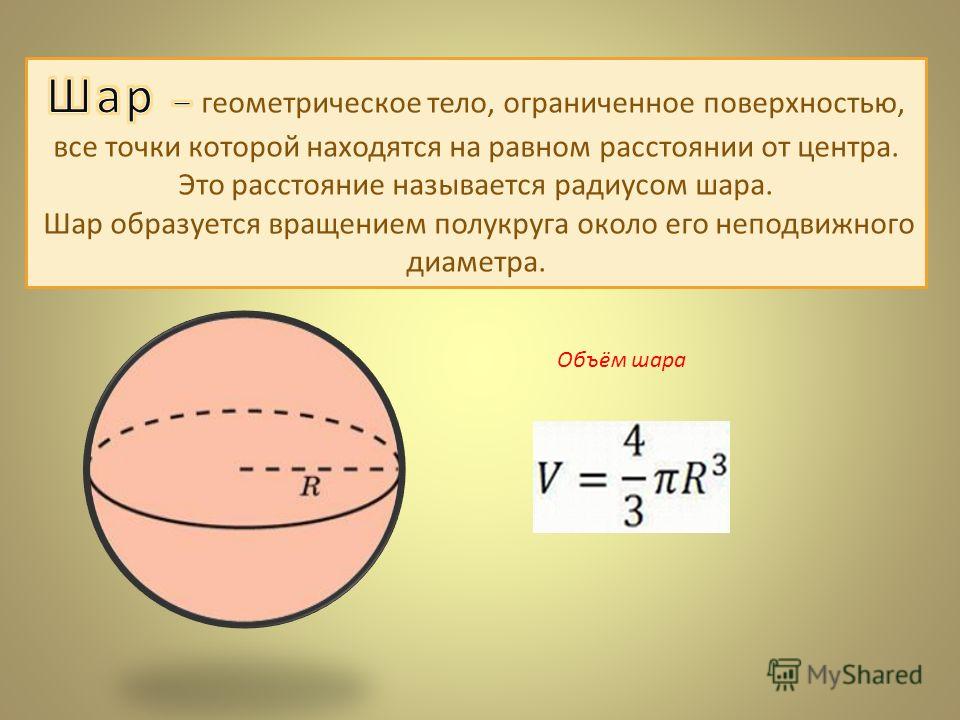 Следовательно, ответ: объём шара увеличился в 8 раз.

Задача: в цилиндр вписан шар. Найдите отношение объёма шара к объёму цилиндра.

Решение: шар, вписанный в цилиндр, касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга, параллельной основаниям цилиндра. Отсюда следует, что , а высота цилиндра равна .

Объём шара вычисляется по формуле , а объём данного цилиндра можно вычислить по формуле , где  – это площадь основания,  - высота цилиндра. Так как высота данного цилиндра равна двум радиусам, а площадь основания равна , то объём цилиндра равен .

Найдём отношение объёма шара к объёму цилиндра. Получаем, что объём шара относится к объёму цилиндра, как .

Эту задачу называют «Задачей Архимеда». Во времена Архимеда формула объёма шара была неизвестна. Поэтому данная задача считалась очень трудной и, решив ее, Архимед испытал большую радость. На могиле Архимеда был поставлен памятник с изображением шара и описанного около него цилиндра.

Итоги:

На этом уроке мы дали определение шара. Вывели формулу для вычисления объёма шара. А затем с её помощью вывели формулу для вычисления площади сферы.

 

Объяснение урока: Объемы сфер

В этом объяснении мы научимся находить объемы сфер и решать задачи, в том числе ситуации из реальной жизни.

Напомним, что в формулах вычисления площади и длины окружности мы встречали специальная математическая константа 𝜋(=3,14159…). Мы произносить эту греческую букву так же, как слово пирог , и важно помнить что оно просто представляет собой число, для которого мы иногда используем более простые приближения 3.14 или 227. Ввиду этого, может быть, и неудивительно, что мы встречаем 𝜋 снова, когда мы переходим к трехмерной задаче вычисления объем шара.

Формула: Объем сферы

Объем 𝑉 сферы радиусом 𝑟 определяется выражением формула 𝑉=43𝜋𝑟.

Поскольку 43 и 𝜋 — это просто числа, это означает, что пока мы знаем радиус сферы, мы всегда можем применить эту формулу, чтобы найти ее объем. Давайте начнем с рассмотрения примера с диаграммой.

Пример 1. Нахождение объема сферы по ее радиусу

Определите объем сферы, дав ответ с точностью до двух знаков после запятой. места.

Ответ

Из диаграммы видно, что сфера имеет радиус 6,3 см. Ссылаясь на формулу 𝑉=43𝜋𝑟, где 𝑉 — объем и 𝑟 — радиус сферы, можно заменить 𝑟=6,3 в правую часть, чтобы получить 𝑉=43×𝜋×(6,3)=1047,394….

Следовательно, объем сферы, округленный до двух знаков после запятой, равен 1‎ ‎047,39. Поскольку радиус был указан в сантиметрах, это объем в кубических сантиметрах; в объем сферы 1‎ ‎047.39см ³ до двух знаков после запятой места.

Обратите внимание, что, поскольку 𝜋 — бесконечное десятичное число, мы обычно имеем чтобы округлить ответ, показанный на нашем калькуляторе. По этой причине некоторые вопросы требуют ответы должны быть даны с точки зрения 𝜋. А также быть более аккуратным, чтобы выразить, эти ответы имеют то преимущество, что они точны.

Пример 2. Вычисление объема сферы в единицах Пи

Сфера имеет диаметр 18 см. Работайте над объемом сферы, давая свой ответ с точки зрения 𝜋.

Ответ

Здесь нам дан диаметр сферы, 18 см, что в два раза больше радиус. Теперь вспомним формулу 𝑉=43𝜋𝑟, где 𝑉 — объем сферы, а 𝑟 — радиус. Чтобы применить эту формулу для расчета объема, нам сначала нужно вычислить радиус, поэтому мы уменьшите диаметр вдвое, чтобы получить 𝑟=18÷2=9. Затем, заменив 𝑟 в формуле имеем 𝑉=43×𝜋×9.

Обратите внимание, что поскольку радиус 9, кратно знаменателю, 3, мы можем разложить 9 как 9×9 и переупорядочить выражение на правая часть до 43×9×𝜋×9.

Затем это упрощается до 4×3×𝜋×9=4×3×𝜋×81=4×3×81×𝜋=972𝜋. 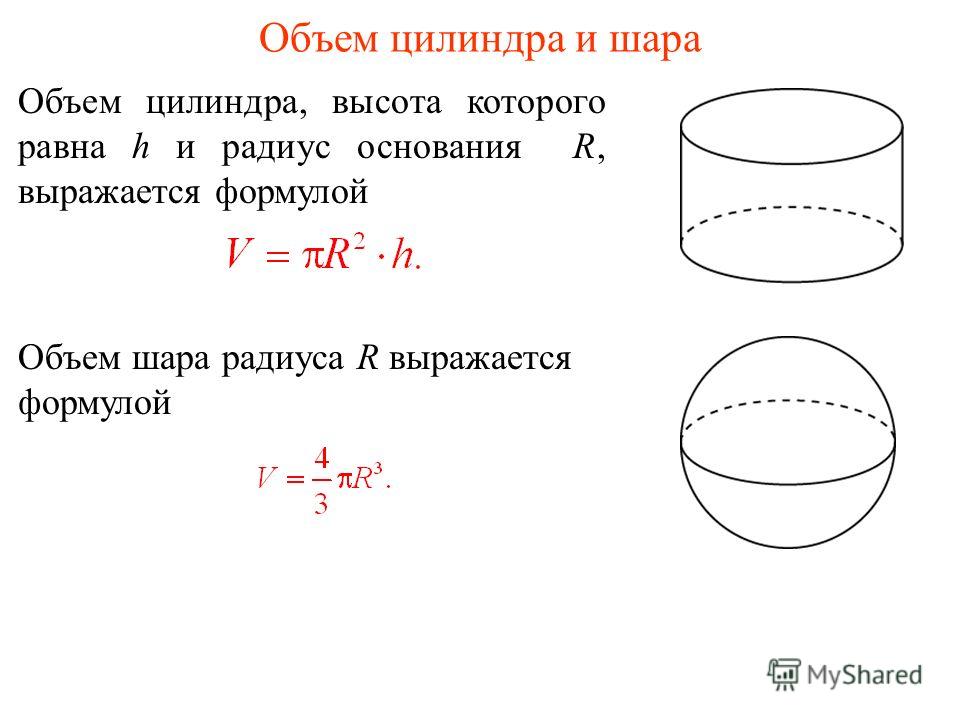

Нет необходимы дальнейшие вычисления, потому что этот ответ кратен 𝜋. Поскольку диаметр дан в сантиметрах, объем шара должен быть 972 см ³ .

Формула объема сферы содержит только две переменные, 𝑉 и 𝑟. Это означает, что если нам дан объем шара, то мы можем всегда работайте в обратном направлении, чтобы найти его радиус. После того, как мы определили радиус, при необходимости мы можем удвойте это значение, чтобы получить диаметр. В следующем примере показано, как изменить формулу для решения этого типа проблемы.

Пример 3. Нахождение диаметра сферы по ее объему

Найдите диаметр сферы, объем которой равен 113,04 см ³ . (Брать 𝜋=3,14).

Ответ

Сначала вспомним формулу для вычисления объема 𝑉 сферы из радиус 𝑟: 𝑉=43𝜋𝑟.

Объем 𝑉=113,04 вместе с приближением 3,14 для 𝜋. Подставляя оба этих значения в формулу, получаем 113,04=43×3,14×𝑟, что упрощается до 113,04=31475×𝑟. 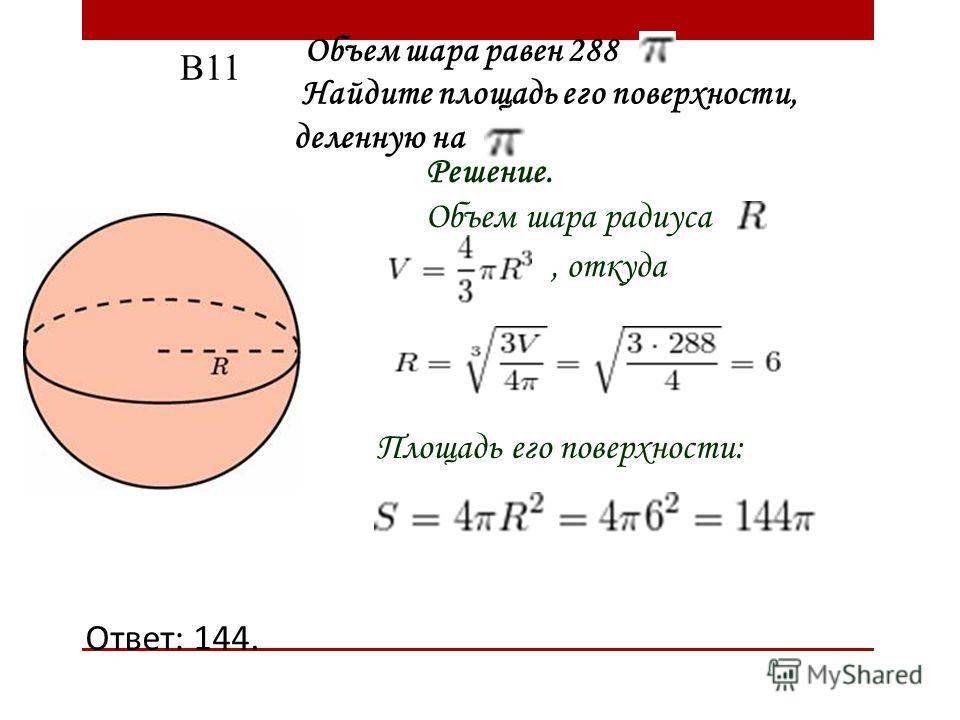

Умножение обеих сторон на 75 дает нам 8478=314×𝑟,, а деление на 314 дает нам 27=𝑟.

Чтобы найти 𝑟, нам нужно взять кубические корни из обеих частей: √27=√𝑟, так 3=𝑟, что совпадает с 𝑟=3.

Единицей объема является кубический сантиметр, поэтому радиус выражается в сантиметрах. Удвоение стоимости радиуса, находим, что диаметр сферы равен 6 см.

Обратите внимание, что в приведенном выше примере мы подставили значение для 𝑉, объем сферы, в формулу 𝑉=43𝜋𝑟, а затем переставить чтобы найти значение радиуса, 𝑟. Альтернативный подход заключается в перестановке формула, чтобы сделать 𝑟 предметом, а затем заменить 𝑉 напрямую. Здесь мы обрисовываем в общих чертах, как получить эту формулу для радиуса в с точки зрения объема.

Начиная с исходной формулы 𝑉=43𝜋𝑟 и переписывая правую часть, чтобы включить знаки умножения, мы имеем 𝑉=43×𝜋×𝑟.

Умножив обе части на 3, мы получим 3𝑉=4×𝜋×𝑟, и разделив на 4𝜋, получим 3𝑉4𝜋=𝑟. 

Наконец, возьмем кубические корни с обеих сторон: что является нашей формулой для радиуса. Если бы мы подставили 𝑉=113,04 в этой формулы вместе с приближением 3.14 для 𝜋, то мы получили бы 𝑟=3, то же значение радиуса, что и в предыдущем пример.

Формула: Радиус сферы при заданном ее объеме

Радиус 𝑟 сферы объемом 𝑉 определяется выражением формула 𝑟=3𝑉4𝜋.

При разрезании сферы плоскостью, проходящей через ее центр, пересечение сфера и плоскость называется большим кругом . Другой способ думать об этом состоит в том, что большой круг сферы — это круг, который делит сферу ровно пополам, образуя два полушария. Это означает, что радиус большого круга будет также радиусом сферы (а также каждого полушария).

Мы можем использовать информацию о больших кругах для расчета объема соответствующего сферы или полушария. (Обратите внимание, что, поскольку объем полушария ровно вдвое меньше объема соответствующей сферы, мы можем настроить выражение 43𝜋𝑟 для объем сферы радиусом 𝑟 до 23𝜋𝑟 для объема полушария радиуса 𝑟. )

Пример 4: Расчет объема полушария

Рассчитайте объем полушария, давая ответ с точностью до двух десятичных знаков места.

Ответ

Диаграмма включает большой круг с радиусом 8,3 м. А теперь вспомните формулу 𝑉=43𝜋𝑟, где 𝑉 — объем сфера, а 𝑟 — ее радиус. Так как радиус большого круга также радиус соответствующей сферы, затем подставив 𝑟=8,3 в формулы, мы имеем, что объем этой сферы 𝑉=43×𝜋×(8,3)=2395,095….

Чтобы вычислить объем вышеприведенного полушария, мы делим этот ответ на 2, что дает 1197,547…. Радиус большого круга был указан в метрах, поэтому полушарие должно иметь объем. 1‎ ‎197,55 м ³ округлить до двух знаков после запятой места.

Описанный выше метод легко адаптировать для нахождения других частей сферы. За Например, если нас попросят найти объем трети сферы радиуса 𝑟, мы можно принять выражение 43𝜋𝑟 для объема сферы радиус 𝑟 и умножьте его на 13.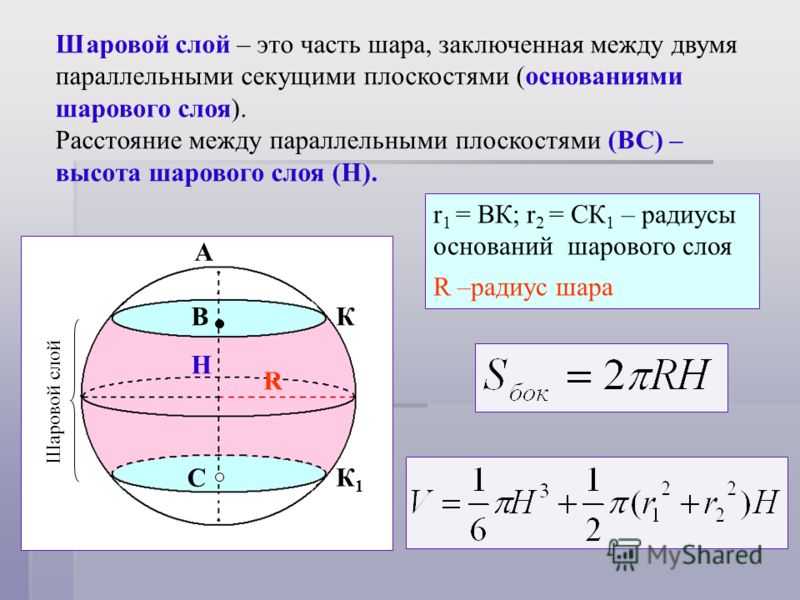 Это говорит нам, что объем трети сферы радиуса 𝑟 равен 13×43𝜋𝑟=49𝜋𝑟.

Наконец, мы иногда встречаем вопросы с реальным контекстом, которые даются как слово задачи, без схем. В таких случаях важно внимательно прочитать вопрос и выяснить именно то, что нас просят найти. Сделав это, мы должны быть в состоянии применить формулу, возможно, более одного раза, чтобы получить наш ответ.

Пример 5. Решение текстовой задачи с объемами сфер

Металлическая сфера радиусом 14,1 см была расплавлена ​​и разделена на 4 равные части. сферы. Найдите радиус одной из меньших сфер, давая ответ на вопрос ближайший сантиметр.

Ответ

Наш первый шаг — определить общий объем металла в исходной сфере. Отзывать что объем 𝑉 сферы радиуса 𝑟 определяется выражением формула 𝑉=43𝜋𝑟. Применяя эту формулу с 𝑟=14,1, получаем 43×𝜋×(14,1)=11742,104….

Разделив этот общий объем на 4, мы вычисляем объем каждой меньшей сферы как 2935.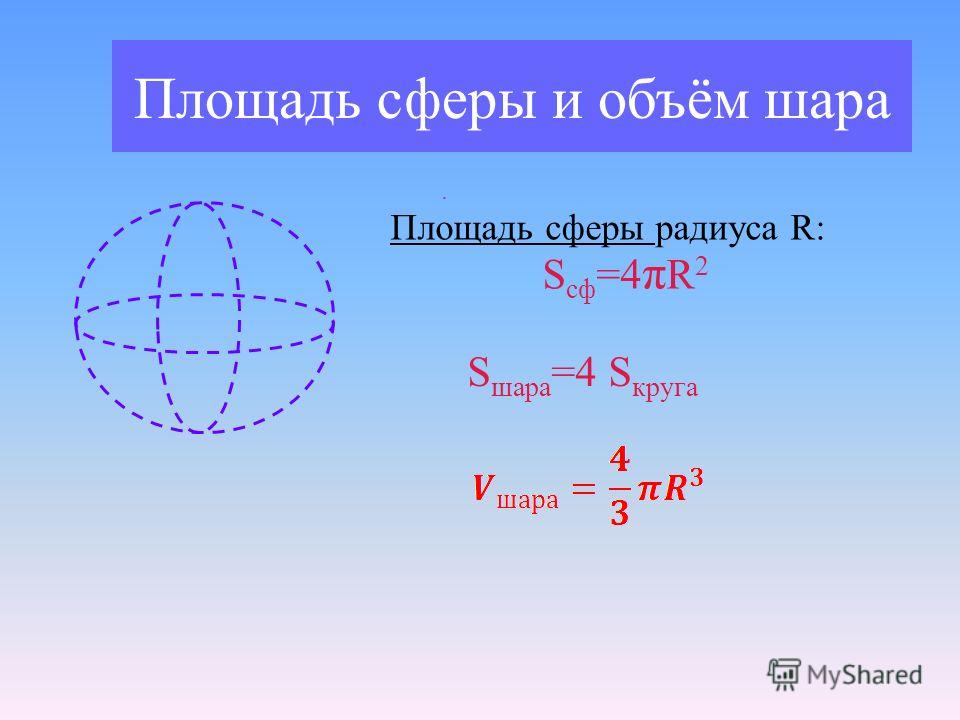 526… см ³ .

Затем мы применяем формулу к одной из меньших сфер, используя объем для работы соответствующий радиус: 2935,526…=43×𝜋×𝑟.

Умножая обе части на 3, получаем 8806,578…=4×𝜋×𝑟, и деление на 4𝜋 дает 700,805…=𝑟.

Наконец, мы берем кубические корни с обеих сторон, чтобы получить 𝑟=8,882…, что дает ответ 9 при округлении до ближайшего сантиметра. Следовательно, длина радиус одной из меньших сфер равен 9 см.

Давайте закончим повторением некоторых ключевых понятий из объяснения.

Ключевые точки

• Объем 𝑉 сферы радиуса 𝑟 определяется формулой формула 𝑉=43𝜋𝑟.
• Поскольку формула содержит только две переменные, 𝑉 и 𝑟, если нам дан объем сферы, мы всегда можем вернуться к найдите его радиус (или диаметр).
• Большой круг сферы — это круг, который делит сферу ровно пополам, образуя два полушария. Большой круг и соответствующая ему сфера имеют один и тот же центр и радиус.
• Формулу можно использовать для нахождения объема полушария или других частей сфере, в том числе в реальных вопросах, представленных в виде текстовых задач.

Объем сферы — математика GCSE

Введение

Каков объем шара?

Как рассчитать объем сферы

Объем рабочего листа сферы

Расчет радиуса по объему

Как рассчитать радиус сферы, зная объем

Распространенные заблуждения

Практика объем вопросов сферы

Объем сферы GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Еженедельные онлайн-уроки повторения математики GCSE теперь доступны

Узнать больше

Введение

Каков объем шара?

Как рассчитать объем сферы

Объем рабочего листа сферы

Расчет радиуса по объему

Как рассчитать радиус сферы, зная объем

Распространенные заблуждения

Практика Объем шара вопросы

Объем сферы GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем об объеме сферы, в том числе о том, как рассчитать объем сферы по ее радиусу и как найти объем полусферы.

Также есть рабочие листы тома сферы, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли. 93 \\text{до 1 дп} \end{выровнено}

Каков объем шара?

Как рассчитать объем шара

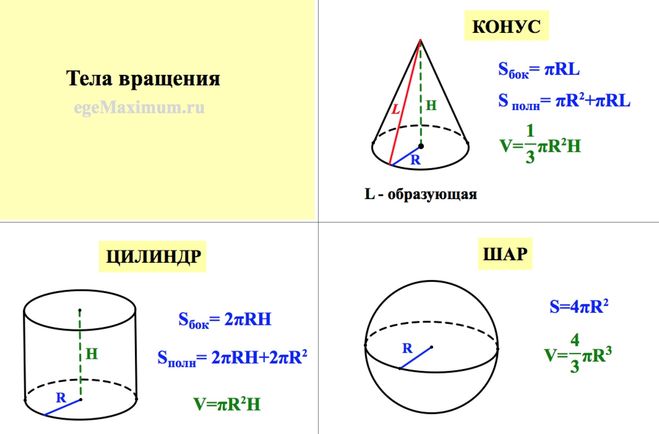
Чтобы рассчитать объем шара:

1. Запишите формулу объема шара.
2. Подставьте указанные значения в формулу.
3. Завершите расчет.
4. Напишите ответ, включая единицы измерения.

Объясните, как вычислить объем сферы

Объем и площадь поверхности рабочего листа сферы

Получите бесплатный объем и площадь поверхности рабочего листа сферы из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Объем и площадь поверхности рабочего листа сферы

Получите бесплатный объем и площадь поверхности рабочего листа сферы из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы. 93) сделать r (радиус) предметом формулы.

Теперь у нас есть формула для определения радиуса сферы при заданном объеме:

r=\sqrt[3]{\frac{3V}{4\pi}} .

Как рассчитать радиус сферы по объему

Чтобы рассчитать радиус сферы по объему:

1. Запишите формулу радиуса сферы в единицах объема .
2. 93 . Вычислите радиус сферы с точностью до 2 знаков после запятой.

   Запишите формулу радиуса сферы в пересчете на объем.

   r=\sqrt[3]{\frac{3V}{4\pi}}

   Подставьте данные значения в формулу.

   Нам дан объем, поэтому мы можем подставить его в формулу для расчета радиуса:

   
   r=\sqrt[3]{\frac{3\times{3000}}{4\pi}} .

   Завершите расчет.

   \ начало {выровнено} r&=\sqrt[3]{\frac{9000}{4\pi}} \\\\ &=\sqrt[3]{716.1972439…} \\\\ &=8,947002289… \end{aligned}

   Напишите ответ, включая единицы измерения. 3 . Запишите ответ с точностью до сантиметра.

   Запишите формулу радиуса сферы в пересчете на объем.

   Здесь нам нужно использовать

   
   r=\sqrt[3]{\frac{3V}{4\pi}} .

   Подставьте указанные значения в формулу.

   Подставив значение объема, мы получим

   
   r=\sqrt[3]{\frac{3\times{8460}}{4\pi}} .

   Завершите расчет.

   \begin{align} r&=\sqrt[3]{\frac{25380}{4\pi}} \\\\ &=\sqrt[3]{2019.676228…} \\\\ &=12.64039323… \end{aligned}

   Напишите ответ, включая единицы измерения.

   Здесь нас просят дать ответ с точностью до сантиметра.

   
   r=12,64039323…=12,64 \; м=1264 \; см

   
   Радиус сферы 1264\; см .

   Распространенные заблуждения

   • Использование правильной формулы

   Существует несколько формул, которые можно использовать, поэтому нам нужно сопоставить правильную формулу с правильным контекстом.

   No related posts.