Калькулятор для расчета объема шара
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
через основание и высоту через две стороны и угол по трем сторонам (формула Герона) через радиус вписанной окружности через радиус описанной окружностиТреугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
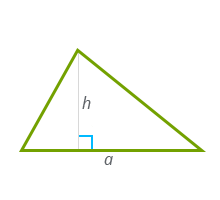
1) через основание и высоту
 a – основание треугольника,
a – основание треугольника,h – высота треугольника.
2) через две стороны и угол
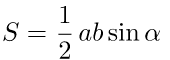 a, b – стороны треугольника,
a, b – стороны треугольника,α – угол между сторонами.
3) По трем сторонам. Формула Герона.
 a, b, с – стороны треугольника,
a, b, с – стороны треугольника,4) Через радиус вписанной окружности.
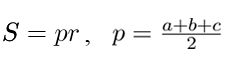 a, b, с – стороны треугольника,
a, b, с – стороны треугольника,p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
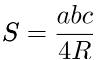 a, b, с – стороны треугольника,
a, b, с – стороны треугольника,R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
Объем шара — онлайн калькулятор через диаметр и радиус

Скачать, сохранить результат
Выберите способ сохранения
Информация
В геометрии на сегодняшний день сложились определенные базовые формулы, аксиомы и теории, которые являются неотъемлемой частью нашей жизни. Формула объема шара является одной из таких формул. Особенно в такой сфере деятельности, как строительство, часто возникает необходимость расчета необходимого объема материалов для того или иного объекта. Чтобы не задаваться вопросом «Как найти объем шара?» был создан калькулятор, позволяющий найти необходимые Вам значения через встроенные в него формулы. Например, Вы выбираете формулу нахождения объема шара, и Вам необходимо найти объем шара через диаметр, калькулятор предоставляет Вам информацию о том, какие данные следует ввести, чтобы была применима формула объема шара через диаметр.Введя необходимые данные, Вы получите точно рассчитанный объем шара. Также может быть применима формула нахождения шара через радиус, которая посчитает нужный Вам показатель автоматически после введения базовых показателей.
Наш калькулятор применяет следующие вычисления объема шара:
- Способ вычисления по формуле объема шара через радиус:
- Способ вычисления по формуле объема шара через диаметр:
- Способ вычисления объема шара через длину окружности:
Существует множество преимуществ, которые даст Вам наш онлайн калькулятор:
- экономия времени, благодаря автоматизации подсчета;
- гарантия точности рассчитанного показателя;
- комфортное применение интерфейса калькулятора и много другое.
Таким образом, используя наш калькулятор, Вы сможете избежать необходимости самостоятельного расчета формул и всех значений, сэкономив время и силы. При этом наш калькулятор исключает возможность возникновения ошибок в расчетах и Вы получите максимально точный и правильный ответ.
поделиться и оценить
Смотрите также:
Добавить комментарий
Калькулятор онлайн — Вычисление объема шара
Этот математический калькулятор онлайн поможет вам вычислить объём шара. Программа для вычисления объёма шара не просто даёт ответ задачи, она приводит подробное решение с пояснениями
, т.е. отображает процесс получения результата.Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac{5}{7} \)
Калькулятор объема шара онлайн
Формула объема шара V = 4/3 × π × R³
Для расчета нам понадобиться только радиус шара – R.
Вставьте в поле величину радиуса и получите результат.
Похожие калькуляторы:
Раздел: Калькуляторы объемаОбъем шара: онлайн калькулятор, формулы, примеры решений
Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.
Шар и сфера
Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.
Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.
Объем шара
Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.
Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:
0,5 Vsh = Vc − Vk
Объем конуса вычисляется по простой формуле:
Vk = 1/3 × So × h,
но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:
Vk = 1/3 × pi × R × R2 = 1/3 pi × R3
Объем цилиндра вычисляется по формуле:
Vc = pi × R2 × h,
но считая, что высота цилиндра равна его радиусу, мы получаем:
Vc = pi × R3.
Используя эти формулы, Архимед получил:
0,5 Vsh = pi × R3 — 1/3 pi × R3 или Vsh = 4/3 pi × R3
Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же
Vsh = 4/3 pi × R3
Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.
Примеры из жизни
Пушечные ядра
Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде
V = 463,24
Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.
Воздушные шары
Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат
V = 4188,7
Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.
Заключение
Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.
Калькулятор объёма и площади поверхности шара. Формулы
Главная / Математические калькуляторы / Объём и площадь поверхности шараШар — геометрическая фигура, состоящая из точек, находящихся от центра на равном или меньшем расстоянии, чем заданное. Ниже приведены формулы расчета объёма (V) и площади поверхности (S) шара через радиус (R), диаметр (D) или длину окружности (L). Для расчета можно воспользоваться онлайн-калькулятором
Формулы расчета объема шара:
- через радиус:
- через диаметр:
- через длину окружности:
Формулы расчета площади поверхности шара:
- через радиус:
- через диаметр:
- через длину окружности:
V — объём
S — площадь поверхности
R — радиус
D — диаметр
L — длина окружности
Онлайн-калькулятор шара
через радиусчерез диаметр
через длину окружности
Радиус
Округление
Округление до целого числа
Округление до 1 знака после запятой
Округление до 2 знаков после запятой
Округление до 3 знаков после запятой
Округление до 4 знаков после запятой
Делить на разряды (для больших чисел)
Рассчитать
Исходный радиус: 70,00 ед.
Объём шара: 1 436 755,04 ед.3
Площадь поверхности шара: 61 575,22 ед.2
Другие калькуляторы
Калькулятор объёма и площади поверхности куба
Калькулятор объёма и площади поверхности цилиндра
Решение примеров дробей со скобками
Площадь земельного участка
Расчёт площади окраски трубы
Онлайн калькулятор: Сегмент шара
 Сегмент шара
Сегмент шара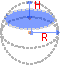 Сферический сегмент
Сферический сегментШаровым сегментом называется часть шара, отсеченная от него плоскостью.
Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема

Сегмент шара
Точность вычисленияЗнаков после запятой: 5
Площадь боковой поверхности
Площадь основания
Площадь поверхности
save Сохранить extension Виджет
 Слой шара
Слой шара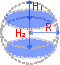 Сферический слой
Сферический слойШаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
Формулы:
— площадь боковой поверхности
— объем

Шаровой слой
Точность вычисленияЗнаков после запятой: 5
Площадь боковой поверхности
Площадь поверхности
save Сохранить extension Виджет
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
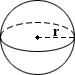 |
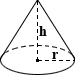
Калькулятор объема конуса
 |
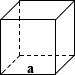
Калькулятор объема куба
 |
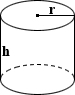
Калькулятор объема цилиндра
 |
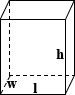
Калькулятор объема прямоугольного резервуара
 |
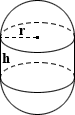
Калькулятор объема капсулы
 |
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
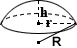 |
Калькулятор объема конической ствола
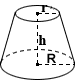 |
Калькулятор объема эллипсоида
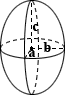 |
Калькулятор объема квадратной пирамиды
 |
Калькулятор объема трубки
 |
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единицей измерения объема в системе СИ является кубический метр, или м 3 . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных фигур можно рассчитать с помощью интегрального исчисления, если существует формула для границы фигуры.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром, d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом для борьбы с ее заклятым врагом Хильдой на воздушных шарах в ближайшие выходные. Необходимый объем уксуса можно рассчитать с помощью приведенного ниже уравнения:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован так же, как круг, набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другую основу).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полуосей, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее конус.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб — частный случай многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что ему нужно привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в общепринятом использовании термин «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником утилизации отходов, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который каждая может вместить, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно строит замок из песка в своем доме и в качестве дополнительного бонуса экономит электроэнергию на ночном освещении, поскольку его замок из песка светится ярко-зеленым в темноте.
Прямоугольный бак
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + з) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу с радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, которая отделена от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферическая крышка называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментируется двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Для двух значений предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
где r — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Коническая Frustum
Усеченный конус — это часть твердого тела, которая остается, когда конус рассекается двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, что мороженое остается упакованным внутри рожка, а поверхность мороженого находится на уровне и параллельно плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна ее рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Беа осталась коническая усеченная пирамида, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 из 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки линии, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его пучок имеет длину оси 1.5 дюймов, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1,5 × 2 × 5 = 62,832 дюйм 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямых линий. Есть много возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат.Другое отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания. Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
.Калькулятор объема
Квадратная пирамида
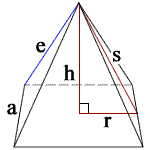
h = высота
s = наклонная высота
a = длина стороны
e = длина боковой кромки
г = а / 2
В = объем
L = площадь боковой поверхности
B = площадь базовой поверхности
S = общая площадь поверхности
Рассчитывайте больше с
Калькулятор пирамид
Использование калькулятора
Онлайн-калькулятор для расчета объема геометрических тел, включая капсулу, конус, усеченную вершину, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу и сферический колпачок.
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Единицы измерения указывают на порядок результатов, например футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете a и h в мм, ваши вычисления приведут к V в мм 3 .
Ниже приведены стандартные формулы объема.
Формулы объема:
.Объем капсулы
- Объем = πr 2 ((4/3) r + a)
- Площадь поверхности = 2πr (2r + a)
Объем и площадь кругового конуса
- Объем = (1/3) πr 2 ч
- Площадь боковой поверхности = πrs = πr√ (r 2 + h 2 )
- Площадь базовой поверхности = πr 2
- Общая площадь
= L + B = πrs + πr 2 = πr (s + r) = πr (r + √ (r 2 + h 2 ))Объем круглого цилиндра
- Объем = πr 2 ч
- Площадь верхней поверхности = πr 2
- Площадь нижней поверхности = πr 2
- Общая площадь
= L + T + B = 2πrh + 2 (πr 2 ) = 2πr (h + r)Объем конической усадки
- Объем = (1/3) πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Площадь боковой поверхности
= π (r 1 + r 2 ) s = π (r 1 + r 2 ) √ ((r 1 — r 2 ) 2 + h 2 )- Площадь верхней поверхности = πr 1 2
- Площадь базовой поверхности = πr 2 2
- Общая площадь
= π (r 1 2 + r 2 2 + (r 1 * r 2 ) * s)
= π [r 1 2 + r 2 2 + (r 1 * r 2 ) * √ ((r 1 — r 2 ) 2 + h 2 )]Объем куба
- Объем = a 3
- Площадь поверхности = 6a 2
Объем полушария
- Объем = (2/3) πr 3
- Площадь изогнутой поверхности = 2πr 2
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Объем пирамиды
- Объем = (1/3) 2 ч
- Площадь боковой поверхности = a√ (a 2 + 4h 2 )
- Площадь базовой поверхности = 2
- Общая площадь
= L + B = a 2 + a√ (a 2 + 4h 2 ))
= a (a + √ (a 2 + 4h 2 ))Объем прямоугольной призмы
- Объем =
л / ч- Площадь поверхности = 2 (lw + lh + wh)
Объем сферы
- Объем = (4/3) πr 3
- Площадь поверхности = 4πr 2
Сферическая крышка объем
- Объем = (1/3) πh 2 (3R — h)
- Площадь поверхности = 2πRh
Объем треугольной призмы
\ [V = \ dfrac {1} {4} h \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
Калькулятор сфер
Форма сферы
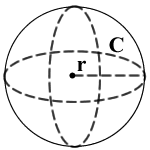
r = радиус
В = объем
A = площадь поверхности
C = окружность
π = пи = 3,1415926535898
√ = квадратный корень
Использование калькулятора
Этот онлайн-калькулятор рассчитает 3 неизвестных значения сферы для любой 1 известной переменной, включая радиус r, площадь поверхности A, объем V и длину окружности C.Он также даст ответы для объема, площади поверхности и окружности с точки зрения PI π. Сфера — это набор точек в трехмерном пространстве, которые расположены на равном расстоянии r (радиус) от данной точки (центральной точки).
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Единицы измерения указывают порядок результатов, например футы, футы 2 или футы 3 .Например, если вы начинаете с мм и знаете r в мм, ваши вычисления приведут к A в мм 2 , V в мм 3 и C в мм.
Формулы сферы для радиуса r:
- Объем шара:
- Окружность сферы:
- Площадь поверхности шара:
Объем сферы
\ [V = \ frac {4} {3} \ pi r ^ 3 \]
\ [V \ около 4.{1/3} \]
\ [r = \ sqrt {\ frac {A} {4 \ pi}} \]
\ [r \ приблизительно 0,2821 \ sqrt {A} \]
\ [r = \ frac {C} {2 \ pi} \]
\ [r \ приблизительно 0,1592C \]
Окружность сферы
\ [C = 2 \ pi r \]
\ [C \ около 6.{1/3} \]
\ [C = \ sqrt {\ pi A} \]
\ [C \ приблизительно 1.77245 \ sqrt {A} \]
Расчет сфер:
Используйте следующие дополнительные формулы наряду с формулами выше.
- Зная радиус сферы, вычислите объем, площадь поверхности и длину окружности.
Дано r найти V, A, C - Зная объем сферы, вычислите радиус, площадь поверхности и длину окружности.
Для данного V найти r, A, C - Зная площадь поверхности сферы, вычислите радиус, объем и длину окружности.
Дано A найти r, V, C - Зная длину окружности сферы, рассчитайте радиус, объем и площадь поверхности.
Для данного C найти r, V, A
Калькулятор объема — Калькуляторы для нескольких фигур
Вычислите объем любой из приведенных ниже форм, введя свои измерения в любых единицах, и получите результаты в британских или метрических единицах измерения.
Выберите форму:Калькулятор объема прямоугольной призмы
Калькулятор объема цилиндра
Калькулятор объема пирамиды
Калькулятор объема капсулы
Как определить объем обычного объекта или геометрической формы
Объем — это мера трехмерного пространства, которое занимает геометрическая форма или объект, и измеряется в кубических единицах, таких как кубические дюймы или галлоны.Используйте приведенные ниже формулы, чтобы найти объем множества различных геометрических фигур.
Одним из важных соображений при измерении является выполнение всех измерений с использованием одной и той же единицы измерения. Если ваши измерения представлены в разных единицах, преобразуйте каждое измерение в те единицы, в которых вы хотите получить результаты.
Используйте наши калькуляторы для преобразования единиц длины, чтобы преобразовать ваши измерения в единые единицы измерения. Вы также можете использовать наш калькулятор преобразования единиц объема, чтобы преобразовать результат в другую единицу измерения.
Воспользуйтесь нашим калькулятором площади поверхности, чтобы узнать площадь этих геометрических фигур.








Как найти объем необычного объекта
Приведенные выше формулы можно использовать для вычисления обычных объектов, имеющих определенную формулу, но многие объекты нерегулярны или не имеют очевидной формулы. Вытеснение воды — это метод, используемый для определения объема неправильного объекта. Техника вытеснения воды включает наполнение контейнера водой и измерение количества воды, вытесненной путем погружения объекта неправильной формы в воду в контейнере.
Например, наполните емкость водой и рассчитайте объем воды по формулам выше.
Погрузите нестандартный предмет в воду и убедитесь, что уровень воды в емкости поднялся.
Измерьте количество воды, как раньше, и рассчитайте объем воды с погруженным объектом.
Вычтите начальный результат на результат после того, как объект неправильной формы был помещен в воду, чтобы найти объем объекта.
Общие измерения объема
| Кубический дюйм | Кубический фут | Кубический ярд | Кубический сантиметр | Кубический метр | |
|---|---|---|---|---|---|
| 1 Кубический дюйм = | 1 из 3 | 0.000579 фут 3 | 0,000021434 ярд 3 | 16,3871 см 3 | 0,000016387 м 3 |
| 1 Кубический фут = | 1728 дюймов 3 | 1 фут 3 | 0,037037 ярд 3 | 28 317 см 3 | 0,028317 м 3 |
| 1 Кубический ярд = | 46 656 дюйм 3 | 27,0000 49 футов 3 | 1 ярд 3 | 764,555 см 3 | 0.764555 м 3 |
| 1 Кубический сантиметр = | 0,06 1024 дюйма 3 | 0,000035315 футов 3 | 0,000001308 ярд 3 | 1 см 3 | 0,0000010 м 3 |
| 1 Кубический метр = | 61 024 дюйма 3 | 35,314 725 футов 3 | 1.30795 ярд 3 | 1000000 см 3 | 1 м 3 |
