Объёмные геометрические фигуры и их названия. Геометрические фигуры. Играем в геометрическое лото
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны.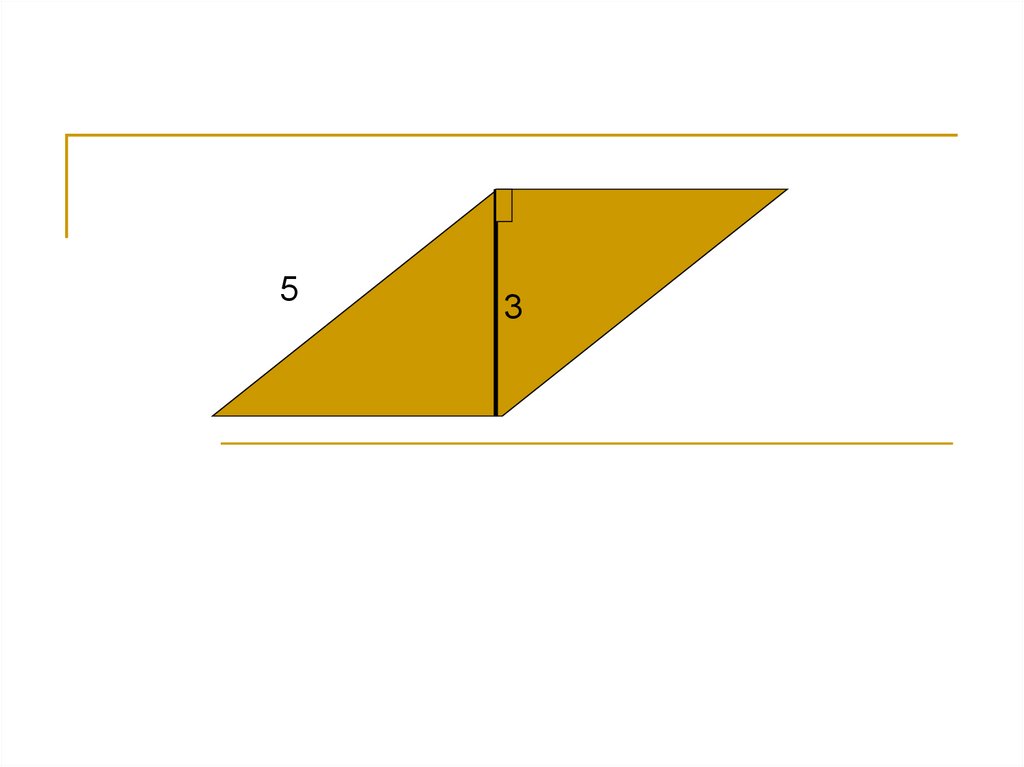 При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки.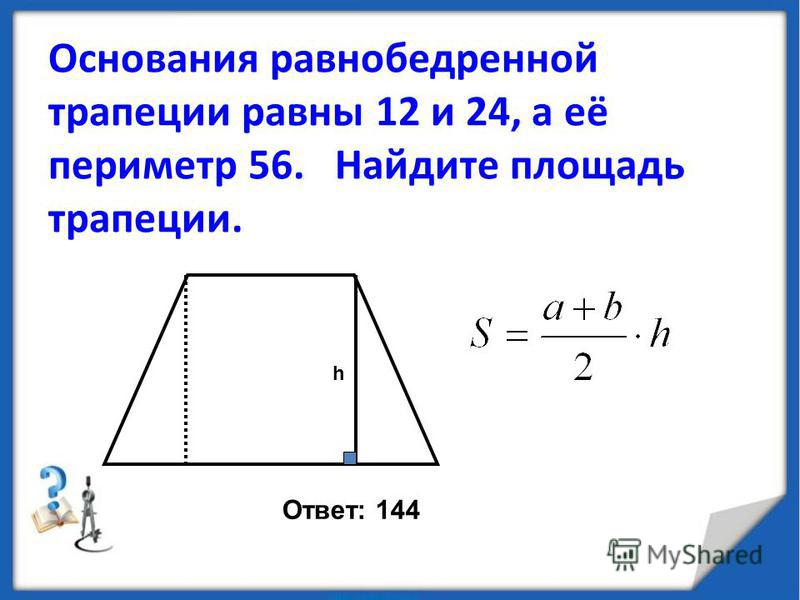 А последние, в свою очередь, принято считать сторонами.
А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.

- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Чукур Людмила Васильевна
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур
«ГЕОМЕТРИЧЕСКАЯ ФИГУРА .
ОСОБЕННОСТИ ВОСПРИЯТИЯ ДЕТЬМИ
Подготовила : ст. воспитатель Чукур Л . В.
1. Понятие «геометрическая фигура » . Особенности развития представлений о форме предметов у детей дошкольного возраста
Одним из свойств окружающих предметов является их форма . Форма предметов получила обобщенное отражение в геометрических фигурах .
Фигура — латинское слово , означает «образ» , «вид» , «начертание» ; это часть плоскости, ограниченная замкнутой линией, или часть пространства, ограниченная замкнутой поверхностью.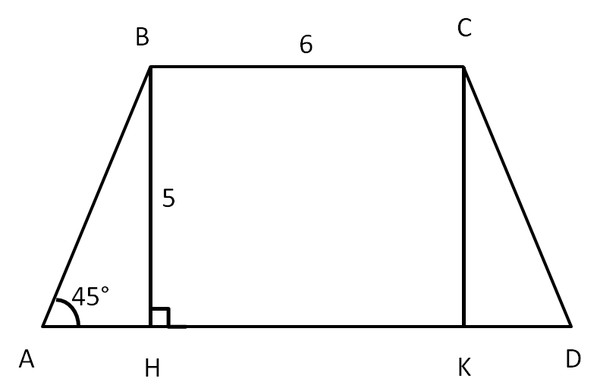 Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — «форма » , также означающее «наружный вид» , «внешнее очертание предмета » .
Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — «форма » , также означающее «наружный вид» , «внешнее очертание предмета » .
Наблюдая за предметами окружающего мира , люди заметили, что есть некоторое общее свойство, позволяющее объединить предметы в одну группу . Это свойство было названо геометрической фигурой . Геометрическая фигура – это эталон для определения формы предмета , всякое непустое множество точек; обобщенное абстрактное понятие.
Само определение понятия геометрической фигуры дали древние греки
Упоминание о первых геометрических фигурах встречается и у древних египтян и древних шумеров.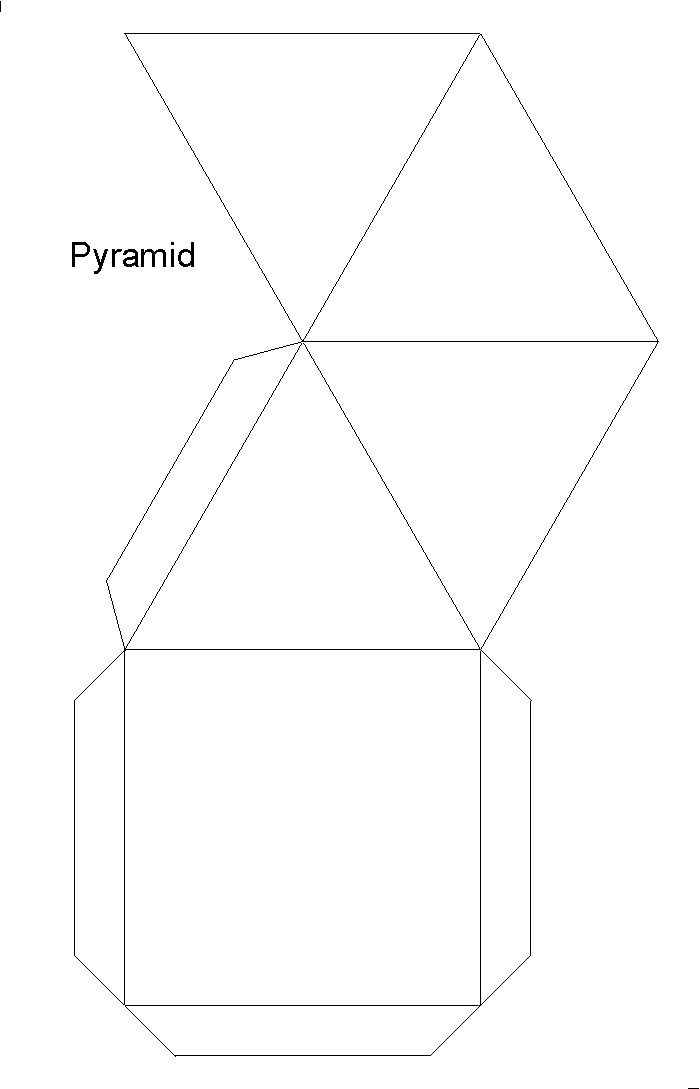 Учеными-археологами был найден папирусный свиток с геометрическими задачами , в которых упоминались геометрические фигуры . И каждая из них называлась каким-то определенным словом .
Учеными-археологами был найден папирусный свиток с геометрическими задачами , в которых упоминались геометрические фигуры . И каждая из них называлась каким-то определенным словом .
Таким образом, представление о геометрии и изучаемых этой наукой фигурах имели люди с давних времен, но название, «геометрическая фигура » и названия всем геометрическим фигурам дали древнегреческие ученые.
В наше время знакомство с геометрическими фигурами начинается с раннего детства и продолжается на всём пути обучения. Дошкольники, познавая окружающий мир, сталкиваются с разнообразием форм предметов , учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур .
Форма – это внешнее очертание предмета . Множество форм бесконечно .
Представления о форме предметов возникают у детей достаточно рано. В исследованиях Л. А. Венгера выясняется, возможно ли различение формы предметов детьми , у которых еще не сформировался акт хватания . В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
Детям предъявлялись два объемных тела одинакового стального цвета и размера (призма и шар, одно из них подвешивалась над манежем, чтобы угасить ориентировочную реакцию; затем снова подвешивалась пара
Л. А. Венгер заметил также, что что на геометрической фигуре с изменением пространственной ориентации возникает такое же зрительное сосредоточение, как и на новой геометрической фигуре .
Исследования М. Денисовой и Н. Фигурина показали , что грудной ребенок по форме на ощупь определяет бутылочку , соску, материнскую грудь. Зрительно дети начинают различать форму предметов с 5 месяцев . При этом индикатором различения являются движения рук, корпуса по направлению к экспериментальному объекту и схватывание его (при пищевом подкреплении) .
В других исследованиях выявлено, что, если предметы отличаются цветом , то ребенок 3-х лет выделяет их форму только в том случае , если предмет знаком ребенку из практического опыта (опыт манипуляций, действий) .
Это доказывает и тот факт, что ребенок одинаково узнает прямые и перевернутые изображения (может рассматривать и понимать знакомые картинки, держа книжку «вверх ногами» , предметы , окрашенные в несвойственные цвета (черное яблоко, но квадрат, повернутый на угол, т. е. в виде ромба, не узнает, так как исчезает непосредственное сходство формы предмета , которого нет в опыте.
2. Особенности восприятия детьми дошкольного возраста формы предметов и геометрических фигур
Одним из ведущих познавательных процессов детей дошкольного возраста является восприятие . Восприятие помогает отличить один предмет от другого , выделить какие-то предметы или явления из других похожих на него.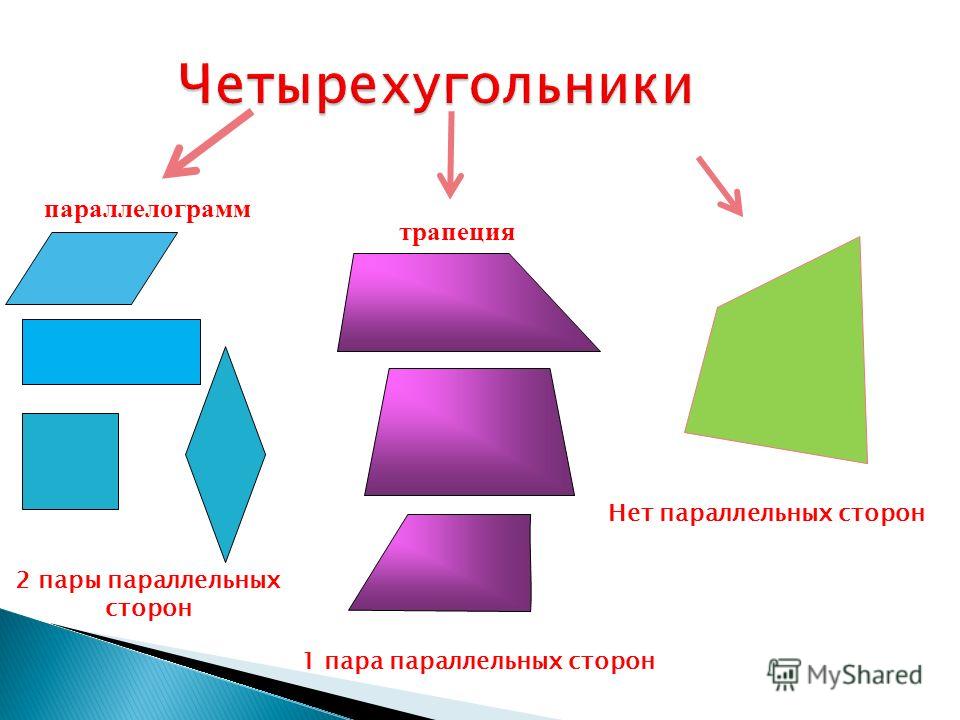
Первичное овладение формой предмета Форма предмета , как таковая, не предмета предшествовать практическим действиям. Действия детей с предметами на разных этапах различны.
Исследования психолога С. Н. Шабалина показывают, что геометрическая фигура воспринимается дошкольниками своеобразно. Если взрослый воспринимает ведро или стакан как предметы , имеющие цилиндрическую форму , то в его восприятие включается знание геометрических форм . У дошкольника происходит обратное явление.
В 3-4 года дети опредмечивают геометрические фигуры , так как они в их опыте представлена нераздельно с предметами , не абстрагированы. Геометрическая фигура воспринимается детьми как картинка , как некоторый предмет : квадрат — это платочек, кармашек; треугольник — крыша, круг — колесо, мячик, два круга рядом — очки, несколько кругов рядом — бусы и т. п.
В 4 года опредмечивание геометрической фигуры возникает только при столкновении ребенка с незнакомой фигурой : цилиндр — это ведро, стаканчик.
В 4-5 лет ребенок начинает сравнивать геометрическую фигуру с предметом : про квадрат говорит «это как платочек» .
В результате организованного обучения дети начинают выделять в окружающих предметах знакомую геометрическую фигуру , сравнивать предмет с фигурой (стаканчик как цилиндр, крыша как треугольник, учится давать правильное название геометрической фигуры и формы предмета , в их речи появляются слова «квадрат» , «круг» , «квадратный» , «круглый» и т. п.
Проблему знакомства детей с геометрическими фигурами и их свойствами следует рассматривать в двух аспектах :
В плане сенсорного восприятия форм геометрических фигур
В смысле познания особенностей их структуры , свойств, основных свя-зей и закономерностей в их построении, т. е. собственно геометри-ческого материала .
Контур предмета это общее начало , которое является исходным как для зрительного, так и для осязательного восприятия . Однако вопрос о роли контура в восприятии формы и формировании целостного образа требует еще дальнейшей разработки.
Однако вопрос о роли контура в восприятии формы и формировании целостного образа требует еще дальнейшей разработки.
Первичное овладение формой предмета осуществляется в действиях с ним. Форма предмета , как таковая, не воспринимается отдельно от предмета , она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета появляются в конце второго года жизни и начинают предшествовать
практическим действиям.Действия детей с предметами на разных этапах различны. Малыши стремятся, прежде всего, захватить предмет руками и начать манипулировать им. Дети 2,5 лет, прежде чем действовать, довольно подробно зрительно и осязательно — двигательно знакомятся с предметами . Значение практических действий остается главным. Отсюда следует вывод о необходимости руководить развитием перцептивных действий двухлетних детей. В зависимости от педагогического руководства характер перцептивных действий детей постепенно достигает познавательного уровня. Ребенка начинают интересовать различные признаки предмета , в том числе и форма . Однако он еще долго не может выделить и обобщить тот или иной признак, в том числе и форму разных предметов .
Ребенка начинают интересовать различные признаки предмета , в том числе и форма . Однако он еще долго не может выделить и обобщить тот или иной признак, в том числе и форму разных предметов .
Сенсорное восприятие формы предмета должно быть направлено не только на то, чтобы
Экспериментальные данные Л. А. Венгера показали, что возможностью различать геометрические фигуры обладают дети 3-4 месяцев. Сосредоточение взгляда на новой фигуре — свидетельство этому.
Уже на втором году жизни дети свободно выбирают фигуру по образцу из таких пар : квадрат и полукруг, прямоугольник и треугольник. Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры осуществляют дети пятого и шестого года жизни.
Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры осуществляют дети пятого и шестого года жизни.
Под обучающим воздействием взрослых восприятие геометрических фигур постепенно перестраивается. Геометрические фигуры начинают восприниматься детьми как эталоны , с помощью которых познание структуры предмета , его формы и размера осуществляется не только в процессе восприятия той или иной формы зрением , но и путем активного осязания, ощупывания ее под контролем зрения и обозначения словом.
Совместная работа всех анализаторов способствует более точному восприятию формы предметов . Чтобы лучше познать предмет , дети стремятся коснуться его рукой, взять в руки, повернуть; причем рассматривание и ощупывание различны в зависимости от формы и конструкции познаваемого объекта. Поэтому основную роль в восприятии предмета и определении его формы имеет обследование , осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов ; чаще всего они ограничиваются беглым зрительным восприятием и поэтому не различают близкие по сходству фигуры (овал и круг, прямоугольник и квадрат, разные треугольники) .
Поэтому основную роль в восприятии предмета и определении его формы имеет обследование , осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов ; чаще всего они ограничиваются беглым зрительным восприятием и поэтому не различают близкие по сходству фигуры (овал и круг, прямоугольник и квадрат, разные треугольники) .
В перцептивной деятельности детей осязательно-двигательные и зрительные приемы постепенно становятся основным способом рас-познавания формы . Обследование фигур не только обеспечивает целостное их восприятие , но и позволяет ощутить их особенности (характер, направления линий и их сочетания, образующиеся углы и вершины, ребенок учится чувственно выделять в любой фигуре образ в целом и его части. Это дает возможность в дальнейшем сосредоточить внимание ребенка на осмысленном анализе фигуры , сознательно выделяя в ней структурные элементы (стороны, углы, вершины) . Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры , дети находят уже общность между ними («У куба есть квадраты» , «У бруса — прямоугольники, у цилиндра — круги» и т. д.).
Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры , дети находят уже общность между ними («У куба есть квадраты» , «У бруса — прямоугольники, у цилиндра — круги» и т. д.).
Сравнение фигуры с формой того или иного предмета помогает детям понять, что с геометрическими фигурами можно сравнивать разные предметы или их части . Так, постепенно геометрическая фигура становится эталоном определения формы предметов .
3. Особенности обследования и этапы обучения обследованию детьми дошкольного возраста формы предметов и геометрических фигур
Известно, что в основе познания всегда лежит сенсорное обследование, опосредованное мышлением и речью. В исследованиях Л. Венгера с детьми 2-3 лет индикатором зрительного различения формы предметов служили предметные действия ребенка .
По исследованиям С. Якобсон, В. Зинченко, А. Рузской дети 2-4 лет лучше узнавали предметы по форме , когда предлагалось сначала ощупать предмет , а потом найти такой же. Более низкие результаты наблюдались тогда, когда предмет воспринимался зрительно .
Исследования Т. Гиневской раскрывают особенности движений рук при обследовании предметов по форме . Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания .
В 3-4 года – движения исполнительные (катают, стучат, возят) . Движения немногочисленны, внутри фигуры , иногда (однократно) по осевой линии, много ошибочных ответов, смешение разных фигур . В 4-5 лет – движения установочные (зажимают в руке) . Количество движений увеличивается в два раза; судя по траектории, ориентированы на размер и площадь; крупные, размашистые, обнаруживаются группы близко расположенных фиксаций, относящихся к наиболее характерным признакам фигуры ; дают более высокие результаты. В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость) . Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период , наблюдается смешение близких фигур . В 6-7 лет – движения по контуру, пересечение поля фигуры , причем движения сосредотачиваются на наиболее информативных признаках , наблюдаются отличные результаты не только при узнавании, но и при воспроизведении .
В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость) . Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период , наблюдается смешение близких фигур . В 6-7 лет – движения по контуру, пересечение поля фигуры , причем движения сосредотачиваются на наиболее информативных признаках , наблюдаются отличные результаты не только при узнавании, но и при воспроизведении .
Таким образом, для того, чтобы ребенок выделил существенные признаки геометрических фигур , необходимо их зрительное и двигательное обследование. Движения рук организовывают движения глаз и этому детей необходимо научить.
Этапы обучения обследованию
Задача первого этапа обучения детей 3-4 лет — это сенсорное восприятие формы предметов и геометрических фигур .
Второй этап обучения детей 5-6 лет должен быть посвящен формированию системных знаний о геометрических фигурах и развитию у них начальных приемов и способов «геометрического мышления » .
«Геометрическое мышление » вполне возможно развить еще в дошкольном возрасте. В развитии «геометрических знаний » у детей прослеживается несколько различных уровней.
Первый уровень характеризуется тем, что фигура воспринимается детьми как целое , ребенок еще не умеет выделять в ней отдельные элементы, не замечает сходства и различия между фигурами , каждую из них воспринимает обособленно .
На втором уровне ребенок уже выделяет элементы в фигуре и устанавливает отношения как между ними, так и между отдельными фигурами , однако еще не осознает общности между фигурами .
На третьем уровне ребенок в состоянии устанавливать связи между свойствами и структурой фигур , связи между самими свойствами. Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах у детей развивалось и элементарное геометрическое мышление .
Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах у детей развивалось и элементарное геометрическое мышление .
Познание геометрических фигур , их свойств и отношений расширяет кругозор детей, позволяет им более точно и разносторонне воспринимать форму окружающих предметов , что положительно отражается на их продуктивной деятельности (например, рисовании, лепке) .
Большое значение в развитии геометрического мышления и про-странственных представлений имеют действия по преобразованию фигур (из двух треугольников составить квадрат или из пяти палочек сложить два треугольника).
Все эти разновидности упражнений развивают пространственные представления и начала геометрического мышления детей , формируют у них умения наблюдать, анализировать, обобщать, выделять главное, существенное и одновременно с этим воспитывают такие качества личности, как целенаправленность, настойчивость.
Итак, в дошкольном возрасте происходит овладение перцептивной и интеллектуальной систематизацией форм геометрических фигур . Перцептивная деятельность в познании фигур опережает развитие интеллектуальной систематизации.
Библиографический список
1. Белошистая А. В. Знакомство с геометрическими понятиями / А . Белошистая // Дошкольное воспитание . — 2008. — № 9. — с. 41- 51
2. Венгер Л. А. Воспитание сенсорной культуры ребенка / Л. А. Венгер Э. Г. Пилюгина, Н. Б. Венгер. — М. : Просвещение, 1988.- 144с.
3. Воспитание и обучение детей пятого года жизни : книга для воспитателя детского сада / (А. Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.) ; под ред. В. В. Холмовской. — М. : Просвещение, 1986. — 144 с.
Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.) ; под ред. В. В. Холмовской. — М. : Просвещение, 1986. — 144 с.
4. Габова М. А. Знакомство детей с геометрическими фигурами / М . А. Габова // Дошкольное воспитание . — 2002. — № 9. — с. 2- 17.
5. Дидактические игры и упражнения по сенсорному воспитанию дошкольников : (пособие для воспитателя детского сада / под ред. Л. А. Венгера). — М. : Просвещение, 1978. — 203 с.
6. Кербс Е. В. Математические досуги / Е. В. Кербс // Ребёнок в детском саду. — 2008. — № 3. — с. 21- 23.
7.Математика в детском саду : (пособие для воспитателя дет . сада / составитель Г. М. Лямина). — М. : Просвещение, 1977. — С. 224 — 228.
8. Метлина Л. С.Математика в детском саду : (пособие для воспитателя дет . сада) / Л. С. Метлина. — М. : Просвещение, 1994. — 256 с.
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей.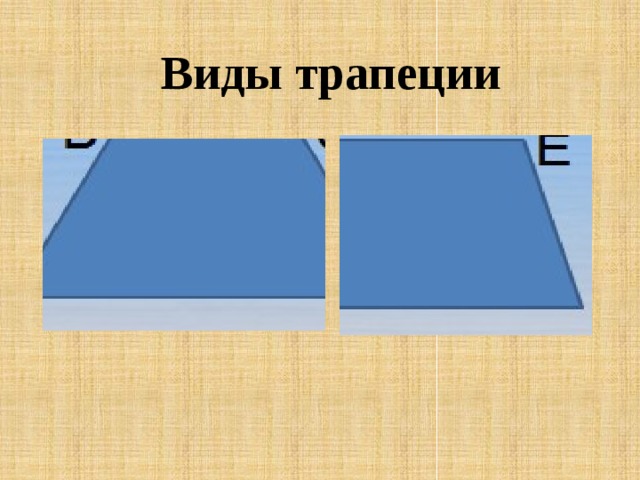 Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев.
 Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.
Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)
Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину.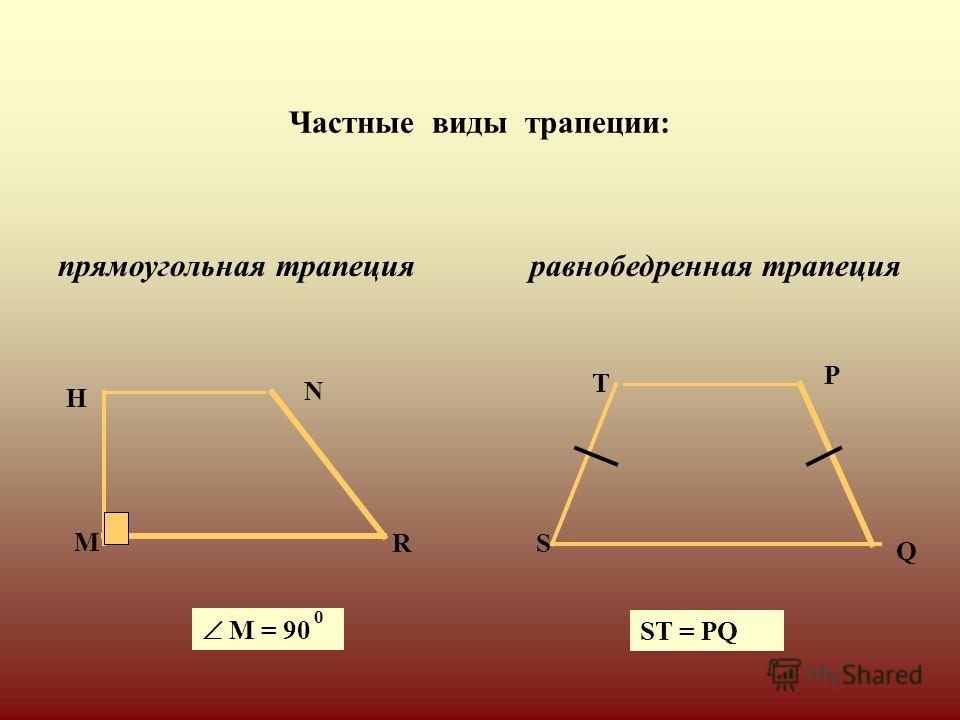 Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.
Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.
В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.
Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.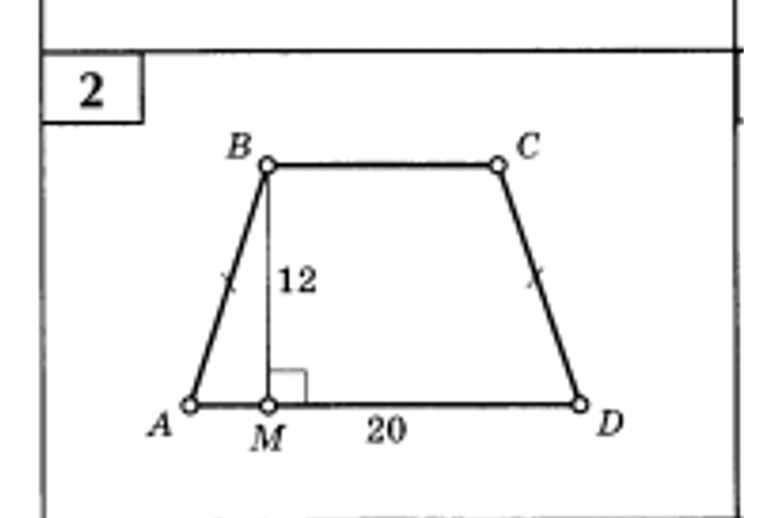
Ромб
Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.
Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.
Приемы запоминания
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
- Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.
- Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор – очень много интересных сочетаний можно выложить, комбинируя разные фигурки.
- Купите линейку с отверстиями в форме круга, квадрата, треугольника и других – для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки – интереснейшее занятие.
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.
Геометрические объемные тела
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
- Они ортогональны друг другу, то есть перпендикулярны.
- Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.

- Любая из осей координат — это результат векторного произведения двух других.
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
- Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
- Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
- Наличие определенного объема, который фигура занимает в пространстве.

- Наличие у каждой объемной фигуры площади поверхности.
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Фигура куб: описание
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.
Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.
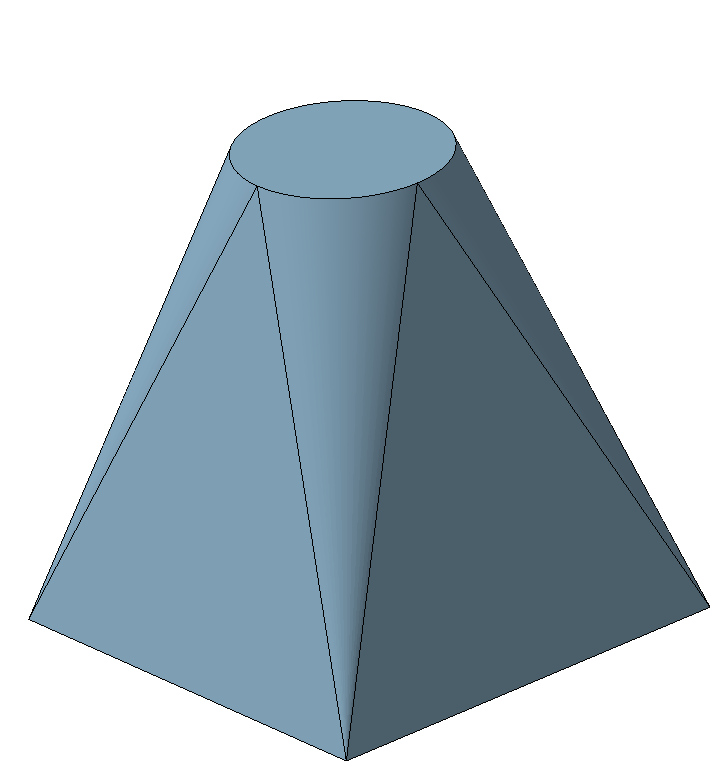
Фигура пирамида
Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.
Фигура тетраэдр: описание
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a — длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH 4 , в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Фигура призма
Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Призма — это полиэдр, поэтому для нее верна Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.
Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi — число пи (3,14), r — радиус сферы (шара).
Как найти среднюю линию трапеции. Как находить среднюю линию трапеции
Автор Historian Просмотров 48 Опубликовано
Первая страна, сделавшая это сложное открытие, Россия, стала лидером мирового сообщества и будет недосягаема для других стран еще многие века.
Содержание
- Ср линия трапеции равна – Все формулы средней линии трапеции
- Средняя линия трапеции | Треугольники
- чему равна, свойства, доказательство теоремы
- Свойства средней линии трапеции
- Доказательство теоремы о средней линии трапеции
- Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Через площадь и высоту
- Примеры задач
- Свойство и формулы
- Примеры заданий
- Трапеция — коротко о главном
- Что такое трапеция?
- Свойства трапеции
- Свойства равнобедренной трапеции:
- Формулы трапеции:
- Как называется объемная трапеция?
- Мировая экономика
- Справочники
- Востребованные технологии
- Поиск технологий
- О чём данный сайт?
- О Второй индустриализации
Ср линия трапеции равна – Все формулы средней линии трапеции
Стол имеет форму с четырьмя сторонами, обе из которых параллельны, а две другие не очень. Параллельные стороны называются верхним и нижним основаниями. Два других называются сторонами. Средняя линия трапеции соединяет средние стороны и параллельна основанию. Длина средней линии равна половине суммы оснований.
Параллельные стороны называются верхним и нижним основаниями. Два других называются сторонами. Средняя линия трапеции соединяет средние стороны и параллельна основанию. Длина средней линии равна половине суммы оснований.
1. трапециевидный мужчина со средней линией через основание
B — верхнее основание
A — нижнее основание
M — средняя линия
B — верхнее основание
A — нижнее основание
H — высота трапеции
Средняя линия
Тип трапециевидной средней линии, (m):.
3. вид трапециевидной средней линии с диагоналями, высотами и углами между диагоналями
a, b — угол между диагоналями
d1 , d2 — Трапециевидная косоугольность
H — высота трапеции
Средняя линия
Тип трапециевидной средней линии, (m):.
4. тип трапециевидной средней линии через площадь и высоту
S-трапециевидная область
H — высота трапеции
Средняя линия
Тип трапециевидной средней линии, (м):.
Тип области любого стола
Тип баланса изошелла
Тип трапеции
Средняя линия трапеции | Треугольники
Что такое трапециевидная средняя линия? Какие свойства доступны?
Средняя линия трапеции — это часть трапеции, соединяющая средства.
Mn — средняя линия трапеции ABCD.
Свойства средней линии трапеции
(1) Средняя линия трапеции параллельна основанию.
2) Средняя линия трапеции равна половине суммы оснований.
Основание трапеции равно 4:7, а средняя линия равна 55 см. Найдите основание трапеции.
ad bc, mn — средняя линия трапеции.
Пусть k — коэффициент пропорциональности.
По свойствам трапециевидной средней линии имеем
BC = 4∙10 = 40 см, AD = 7°C = 70 см.
Средняя линия трапеции составляет 15 см, а одно из оснований на 6 см больше другого. Найдите основания трапеции.
ad bc, mn — средняя линия трапеции.
Мн = 15 см, ad на 6 см больше, чем bc.
Пусть bc = x см и ad = (x+6) см.
Так как средняя линия трапеции равна сумме половин оснований
Составим уравнение и решим его: bc = x см, ad = (x+6 см).
Следовательно, bc = 12 см и ad = 12+6 = 18 см.
чему равна, свойства, доказательство теоремы
Средняя линия трапеции, и в частности ее свойства, очень часто используются в геометрии для решения задач и доказательства некоторых теорем.
Стол — это четырехугольник, у которого только две стороны параллельны друг другу. Параллельная сторона называется основанием (на рисунке 1 AD и BC), а две другие стороны называются (в форме AB и CD).
Средняя линия стола — это отрезок, соединяющий средства его сторон (рис. 1 -кл).
Свойства средней линии трапеции
Доказательство теоремы о средней линии трапеции
Средняя линия трапеции равна половине суммы ее оснований, что доказывает, что она параллельна этим основаниям.
Таблица ABCD задана медианой KL. Доказательство этих свойств требует построения прямой, проходящей через точки B и L. На рисунке 2 показана линия BQ. Также продолжите рекламную базу линии BQ.
Рассмотрим возникающие треугольники LBC и LQD.
- По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
- ∠ BLC = ∠ QLD, так как эти углы вертикальные.
- ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD .
Из этих трех уравнений треугольники, рассмотренные ранее, имеют вид
LBC и LQD равны одной стороне и двум прилежащим углам (см. рисунок 3). Поэтому lbc =∠LQD, bc = dq и, самое главное, bl = lq => kl — средняя линия бункера ABCD и средняя линия треугольника ABQ. В зависимости от состояния средней линии треугольника ABQ, мы получаем
- KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
- KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC .
Для закрепления сказанного рекомендуем посмотреть видеоурок на эту тему.
Если вам понравилась эта статья, расскажите о ней своим друзьям:.
Возможно, вам это будет интересно:.
Диагонали, образованные сторонами, треугольников и документов равны, т.е. имеют равные площади.
Как вычислить, основные формулы
Через основания
Здесь Ǿ(a \) — нижнее основание, Ǿ(b \) — верхнее основание и Ǿ(m \) — центральная линия.
Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до ликвидации). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Через основание, высоту и углы при нижнем основании
Где, ɑ (a \) — нижнее основание, ɑ (b \) — верхнее основание, ɑ (m \) — средняя линия, ɑ (h \) — высота, ɑ (ɑ alpha, ɑ beta \) — угол нижнего основания.
Через диагонали, высоту и угол между диагоналями
Где \(a \) — нижнее основание, \(b \) — верхнее основание, \(m \) — средняя линия, \(h \) — высота, \(ˉ alpha, ˉ beta \) — диагональ, угол между \(d_1 \) и \(d_2 \) является диагональю трапеции.
Через площадь и высоту
Здесь ˉ (h \) — высота трапеции, ˉ (m \) — средняя линия и ˉ (s \) — площадь.
Примеры задач
Найдите площадь трапеции, если большое основание равно 18, наименьшее основание равно 6, а боковые стороны равны 7.
\Угол \ (угол 섹 abc) и угол 섹 bah являются одним типом 섹 (섹 правая стрелка 섹 угол abc + 섹 угол bah \).
Основания трапеции равны 4 и 10. Какова наибольшая часть отрезка, делящего среднюю линию трапеции?
Трапеция ABCD также является сексагоном треугольников ABC и ACD, проходящим через одну из боковых сторон и параллельным основанию. Таким образом, из треугольника ACD x = 5.
ABCD — таблица, BC = 2, AD = 3, PQ — средняя линия, BD и AC — диагонали. Найти Мн.
Участок MN лежит на средней линии трапеции. Докажите, что PM и NQ являются средними треугольников ABC и BCD, а M и N — средними AC и BD соответственно. Найдите из треугольника abc длину pm = 1, а из треугольника bcd длину nq = 1, поэтому mn = 2,5-1-1 = 0,5.
Параллельные стороны трапеции называются основаниями. Два других — это боковые стороны. Если стороны равны, таблица называется изошаром.
Свойство и формулы
Средняя линия равна половине суммы двух оснований. Это определение является теоремой и доказательством, и чтобы сформулировать его, необходимо обратить внимание на статус центральной линии треугольника.
Доказательство теоремы простое. Для этого нарисуйте на столешнице среднюю линию, спускающуюся от вершины формы и пересекающую обширное нижнее основание. Эта линия делит четырехугольник на два треугольника. Среднее основание также принадлежит треугольнику и выполняет ту же функцию. В нижней половине он образован двумя секциями, равными трапециевидному основанию.
Свойство таких отрезков заключается в том, что они параллельны основанию в четырехугольнике. Учитывая эти данные, их можно использовать как указание при решении различных задач на определение этого понятия.
Для тех, кто найдет, написано: m = (a + b) / (a + b)
m = (a + b) / 2, где a и b — символы основания базы.
Угловая тригонометрия применяется к уравнению.
Сумма половин оснований трапеции вычисляется через диагонали, углы пересечения и высоты. Вот почему ее нашли:.
Углы A и B находятся внизу, а линия h — высота, вписанная в этот отрезок.
Вид трапециевидной средней линии через площадь и высоту записывается следующим образом.
Кроме того, такой участок делит диаграмму на две части, одна из которых — поверхность. Это представлено в следующей форме
S 1 /S 2 =3a+b/a+3b, где основания a
Все эти типы используются для решения проблем и доказательства определенных утверждений.
Примеры заданий
Средняя величина трапеции составляет 15 дм, причем одно основание на 6 дм длиннее другого. Определите длины параллельных сторон трапеции.
Чтобы найти правую часть, предположим, что одна сторона равна x дм, а другая — (x + 6)дм. Учитывая свойства средней точки на этой диаграмме, m = a + b/2.
Поскольку m = 2x + 6/2 = 15, имеем x =12 dm.
В результате получается a = 12 дм и b = 18 дм.
Следующая проблема возникает, когда нужно найти ребра, которые параллельны. Если соотношение 4:7, то средняя линия равна 55 дм.
Поэтому, если k — коэффициент пропорциональности, то дно ассоциируется как 4 k:7k. Получено уравнение (4k + 7k) / 2 = 55. Видно, что k = 10. Это означает, что необходимые участки составляют 40 дм и 70 дм соответственно.
Поэтому средние линии треугольника и трапеции обладают одинаковыми свойствами. Темы очень похожи. Поэтому средняя линия трапеции равна половине суммы двух оснований.
Дана таблица ABCD. Диагональ AC, пересекающая среднюю линию, образует точку K, а диагональ BD — точку L. Докажите, что отрезок KL равен половине разности оснований.
Трапеция — коротко о главном
Что такое трапеция:.
Трапеция — это четырехугольник с двумя параллельными сторонами (называемыми основаниями) и двумя непараллельными сторонами (боковыми сторонами).
\ displaystyle \ угол 3+ \ угол 4 = 180)
Трапециевидная средняя линия:.
Средняя линия трапеции (Ј displaystyle MN \) — это часть, соединяющая середины сторон: Ј displaystyle AM = MB, Ј displaystyle \ \ CN = ND \).
Средняя линия параллельна основанию: 텞(텞 displaystyle MN \ параллель BC \ параллель AD \).
Длина средней линии трапеции равна половине суммы длин оснований: \(⌘ displaystyle MN = \ frac \).
Диагонали трапеции:.
Диагонали каждой трапеции пересекаются в точке O.
Треугольники, образованные основанием и диагональными отрезками (⌘ (⌘ displaystyle BOC \) и ⌘ (⌘ displaystyle AOD \)), подобны по двум углам, причем подобие равно отношению оснований. \(⌘ displaystyle k = \ frac \)).
Треугольники, образованные сторонами и диагоналями трапеции, равны по площади: 섹 (섹 displaystyle _> = _> \)).
> \).
Если стол может быть зарегистрирован в круге…
Если трапецию можно вписать в окружность, то это равносторонний треугольник.
Площадь трапеции
Площадь трапеции равна половине суммы оснований высот: ߡ (ߡ displaystyle _> = \ frac \ cdot h \).
Примечание: учебники ЕГЭ по математике охватывают все темы по планетометрии и стереометрии (и алгебре).
Что такое трапеция?
Трапеция — это прямоугольник с двумя параллельными сторонами и двумя непараллельными сторонами.
Параллельные стороны называются основаниями, а непараллельные — боковыми сторонами.
Трапеция (как и треугольник) может быть равнобедренным треугольником.
Если стороны равностороннего треугольника равны, он называется равнобедренным.
В связи с этим возникает вопрос: может ли трапеция иметь равные основания?
Нет, это не так. \\\\ circ \).
\\\\ circ \).
А точно такие же 섹 (섹 displaystyle \ ange 3 \) и 섹 (섹 displaystyle \ angle 4 \) являются одним углом внутри одной параллели 섹 (섹 displaystyle ad \) и 섹 (섹 displaystyle bc \), но вторичной теперь 섹 (섹 displaystyle bc \). displaystyle cd \).
Как видите, основную роль играет то, что она должна быть параллельна основанию. Давайте проанализируем еще несколько свойств трапеции.
Как и у каждого четырехугольника, у стола есть диагонали. Их два — см. рисунок:.
Обратите внимание, что высота, проходящая через диагональное пересечение, лежит на оси симметрии, а высота, проходящая через равнобедренный стол, делит стол на два равных прямоугольных стола. Это означает, что базы разделены по середине этой высоты.
Свойства равнобедренной трапеции:
1. прямая, проходящая через среднюю точку основания, перпендикулярна основанию, поэтому симметрия изо-оболочки.
2. высота, приходящаяся на одну вершину большего основания трапеции изошеллы, делит ее на две части.
3. углы каждого основания изошара равны.
4. сумма противоположных углов изошильды равна 180°.
5. длины диагоналей равных трапеций равны.
6. циклы могут быть описаны вокруг таблицы изошелл.
7. если диагональ перпендикулярна таблице изошелей, то ее высота равна половине суммы оснований.
Формулы трапеции:
Пусть a — наибольшее основание трапеции, b — наименьшее основание трапеции, c — левая сторона трапеции, d — правая сторона трапеции, a и b — нижние углы основания трапеции, d1 и г2 — это диагонали трапеции, m — средняя линия трапеции, h — высота трапеции, c и d — углы между диагоналями трапеции, s — площадь трапеции, p — периметр трапеции.
Введите определение сторон трапеции:.
Через центральную линию и одно из оснований трапеции.
Через высоту и угол к нижнему основанию трапеции: p — высота и угол трапеции.
Через стороны и углы нижнего основания: через
Через высоту и угол к нижнему основанию трапеции: p — высота и угол трапеции.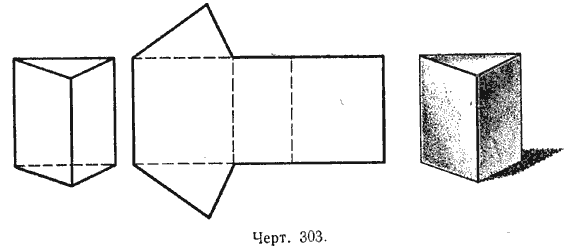
Тип, определяющий центральную линию трапеции:.
Через длину основания трапеции: через длину основания трапеции.
Через площадь и высоту трапеции: через высоту трапеции
Тип, определяющий высоту трапеции: через
Через боковые и смежные углы и через углы, прилегающие к нижнему основанию трапеции: через углы, прилегающие к нижнему основанию трапеции
Через диагонали трапеции и углы между ними: через
Через диагонали трапеции и угол между ними и средней линией трапеции: через диагонали трапеции
Через площадь и длину основания трапеции:.
Через площадь и длину трапециевидной средней линии:.
Тип определения периметра трапеции:.
Через площадь и длину трапеции: тип определения площади трапеции: тип определения площади трапеции
Через основание и высоту трапеции: через основание и высоту трапеции
Через среднюю линию и высоту трапеции: через высоту трапеции
Через диагонали трапеции и углы между ними:.
Через каждую сторону трапеции:.
Через таблицу типа Geron:.
Как называется объемная трапеция?
Если стол представлен объемом, то такая форма похожа на граненую пирамиду.
В обычной усеченной пирамиде грани представляют собой таблицы с равными сторонами.
Примечание: © фотографии https: //www.pexels.com, https: //pixabay.com
Мировая экономика
Справочники
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 946)
- Экономика Второй индустриализации России (103 201)
- Этилен (этен), получение, свойства, химические реакции (29 512)
- Программа искусственного интеллекта ЭЛИС (29 470)
- Метан, получение, свойства, химические реакции (26 572)
- Крахмал, свойства, получение и применение (26 037)
- Природный газ, свойства, химический состав, добыча и применение (25 164)
- Целлюлоза, свойства, получение и применение (24 311)
- Пропилен (пропен), получение, свойства, химические реакции (23 557)
- Прямоугольный треугольник, свойства, признаки и формулы (23 269)
Поиск технологий
О чём данный сайт?
Сайт посвящен научным разработкам автора в области экономики и научным идеям по осуществлению второй индустриализации России.
Включает:- Экономика второй индустриализации в России — Теории, методологии и инструменты инновационного развития — Реализация второй индустриализации в России — Организационные механизмы второй индустриализации в России — Справочник по инновационным технологиям.
Продукты и технологии не продаются. Производители и изобретатели! Вы должны связаться с ними напрямую!
Мы ведем переговоры с отечественными производителями и изобретателями инновационных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Применение второй российской индустриализации базируется на качественно новых научных основаниях (теориях, методологиях и инструментах), разработанных авторами.
Конечным результатом второй индустриализации России является рост благосостояния всех членов общества — среднего человека, предприятия и государства.
Вторая индустриализация России — это совокупность научных, технологических и других инновационных идей, планов и разработок, широко применимых к практике хозяйственной деятельности в краткосрочной перспективе (3-5 лет), ведущих к развитию качественно нового прогрессивного общества.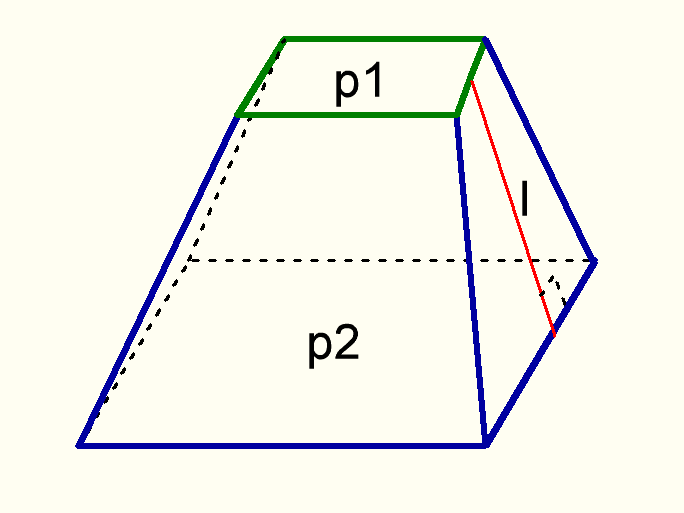 в ближайшие 50-75 лет.
в ближайшие 50-75 лет.
Первая страна, сделавшая это сложное открытие, Россия, стала лидером мирового сообщества и будет недосягаема для других стран еще многие века.
Пирамида. Формулы и свойства
Навигация по странице: Определение пирамиды Элементы пирамиды Объём и площадь поверхности пирамиды Свойства пирамиды Связь пирамиды со сферой, конусом и цилиндром Виды пирамид
Определение.
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
| Рис.1 |
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение.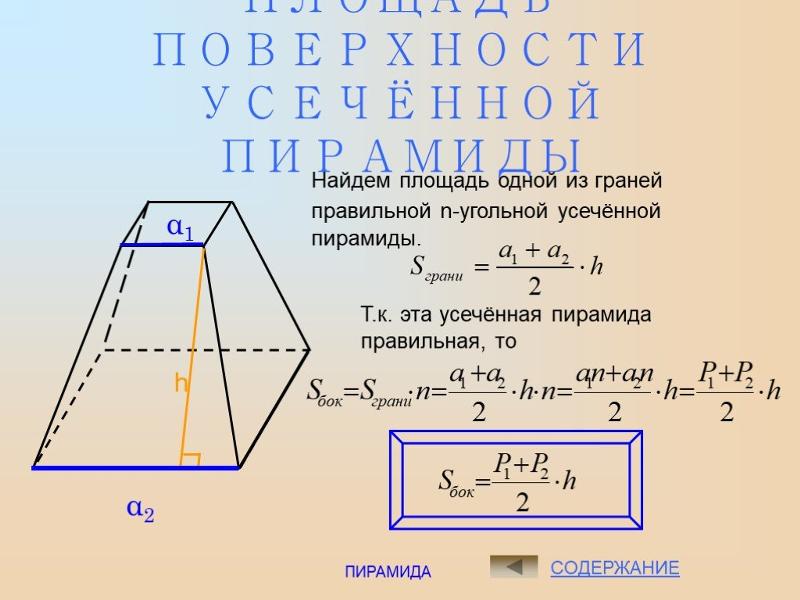 Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
| V = | 1 | SоснH |
| 3 |
Определение. Боковая поверхность пирамиды — это совокупная площадь всех боковых граней пирамиды.
Определение. Полная поверхность пирамиды — это совокупность площадей боковой поверхности и площади основания пирамиды.
Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
| Sb = | 1 | ph |
| 2 |
Для определения площади основания пирамиды смотрите формулы площади плоских фигур
Для определения площади основания правильной пирамиды смотрите формулы площади правильных многоугольников
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.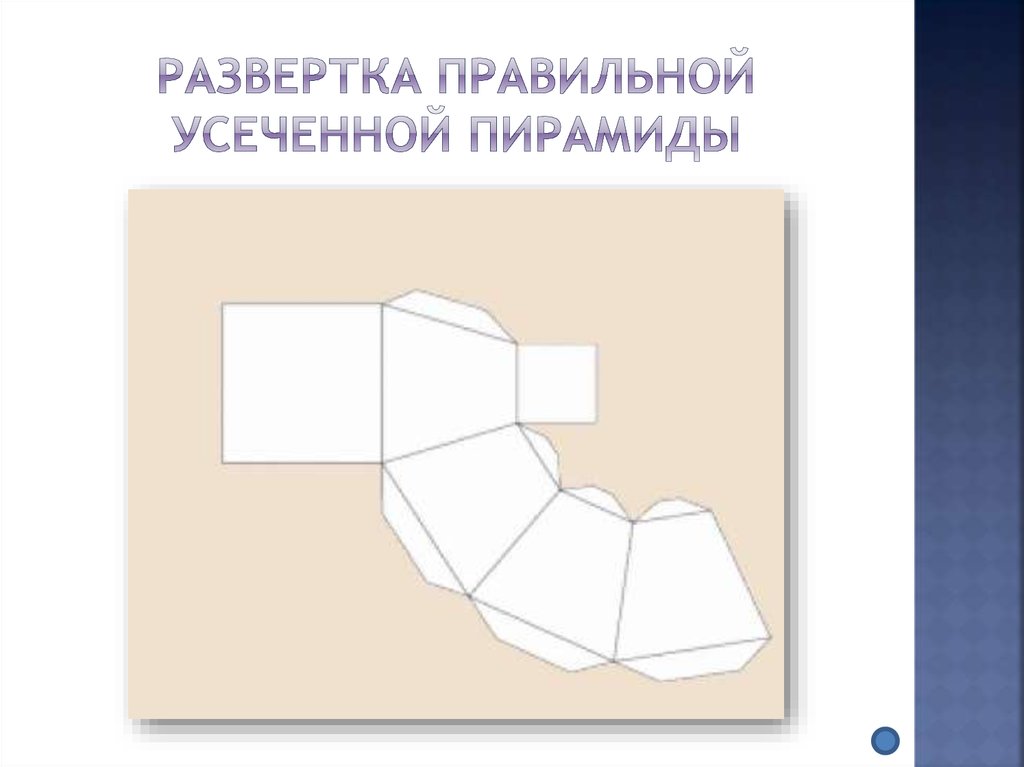
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
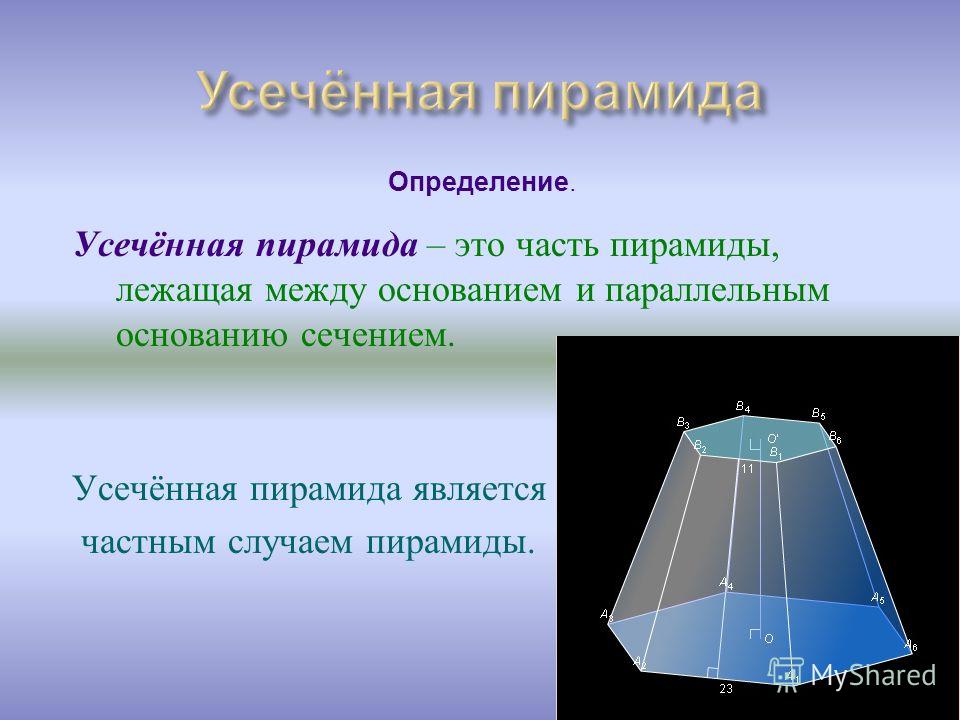
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.
Все таблицы и формулы
Криволинейная трапеция — Энциклопедия по экономике
Кривая у = /(ж) и прямые ж = а, х = b и у = 0 ограничивают некоторую область плоскости, называемую областью под кривой у = /(ж) от а до 6, или криволинейной трапецией. [c.223]Если требуется вычислить площадь S криволинейной трапеции, то можно, например, покрыть плоскость сетью мелких квадратов и сосчитать число квадратов, лежащих внутри нашей области (рис.
 12.1). Это не дает еще всей площади, поскольку некоторые из квадратов лежат частично внутри, а частично вне рассматриваемой области. Но если сделать сеть достаточно густой, то можно вычислить S с любой степенью точности.
[c.223]
12.1). Это не дает еще всей площади, поскольку некоторые из квадратов лежат частично внутри, а частично вне рассматриваемой области. Но если сделать сеть достаточно густой, то можно вычислить S с любой степенью точности.
[c.223]Можно вычислить площадь криволинейной трапеции и с помощью тонких прямоугольников. Лейбниц считал, что криволинейная трапеция составлена из бесконечно тонких прямоугольников (рис. 12.2). Каждый такой прямоугольник поднимается над точкой ж интервала [а, ] он имеет высоту /(ж) и бесконечно [c.223]
| Рис. 12.2. Вычисление площади криволинейной трапеции |
Если а определенный интеграл равен алгебраической сумме площадей соответствующих криволинейных трапеций (рис.
 12.3) [c.228]
12.3) [c.228]Искомую площадь можно рассматривать как разность двух криволинейных трапеций, ограниченных данными линиями. Поэтому [c.247]
Объем тела вращения. Пусть на отрезке [а, Ь] задана непрерывная неотрицательная функция у — /(ж). Необходимо найти объем Vx тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями у = /(ж), у = О, ж = а, х = Ъ (рис. 12.1). [c.249]
Она выражает объем тела, полученного от вращения криволинейной трапеции вокруг оси Оу. [c.252]
Задача 2. Вычислить объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной линия- [c.253]
На практике часто встречаются интегралы, которые не выражаются через элементарные функции или выражаются очень сложно. Нередко подынтегральная функция задается таблицей или графиком. В этих случаях интегралы находят численными методами. Основа численных методов построения формул приближенного вычисления интегралов состоит в замене частичных криволинейных трапеций, образующихся при разбиении отрезка интегрирования, на более простые фигуры. В формуле прямоугольников — это прямоугольники в формуле трапеций — трапеции в формуле парабол — параболы. Рассмотрим эти методы более подробно.
[c.254]
В формуле прямоугольников — это прямоугольники в формуле трапеций — трапеции в формуле парабол — параболы. Рассмотрим эти методы более подробно.
[c.254]
Формула прямоугольников. Пусть на отрезке [а, 6] задана функция у = f(x]. Требуется вычислить площадь криволинейной трапеции S1, ограниченной кривой у = f(x] и прямыми х = а, х = Ъ и у = 0 (рис. 12.1). [c.254]
В основе этого метода лежит замена частичных криволинейных трапеций, ограниченных сверху функцией /(ж), на криволинейную трапецию, ограниченную сверху параболой вида [c.259]
Искомый несобственный интеграл расходится. Геометрически это означает, что соответствующая криволинейная трапеция ( бесконечный шпиль ) имеет бесконечную площадь (рис. 12.17). А [c.266]
Геометрически это означает, что соответствующая криволинейная трапеция ( бесконечный шпиль ) имеет площадь равную двум (рис. 12.17). По сравнению с предыдущим примером площадь оказалась конечной. Это является следствием того, что [c.
 268]
268]Если определенный интеграл от неотрицательной непрерывной функции выражает площадь криволинейной трапеции, то двойной интеграл от неотрицательной непрерывной функции равен объему тела, построенного на области D плоскости хОу как на основании и ограниченного сверху поверхностью z = /(ж, у). Этот объемный аналог криволинейной трапеции называют цилиндроидом. [c.300]
Филлипса 25 Криволинейная трапеция 223 Критерий Сильвестра 312 [c.458]
С геометрической точки зрения нахождение квантиля уа заключается в таком выборе значения Y = ya, при котором площадь заштрихованной криволинейной трапеции была бы равна а. [c.29]
| Рис. 7.1. Пример криволинейной трапеции |
Решение. Искомый объем (ела вращения равен разности объемов, образованных вращением криволинейных трапеции с верхними границами, соответственно, у = Лх ч у -л.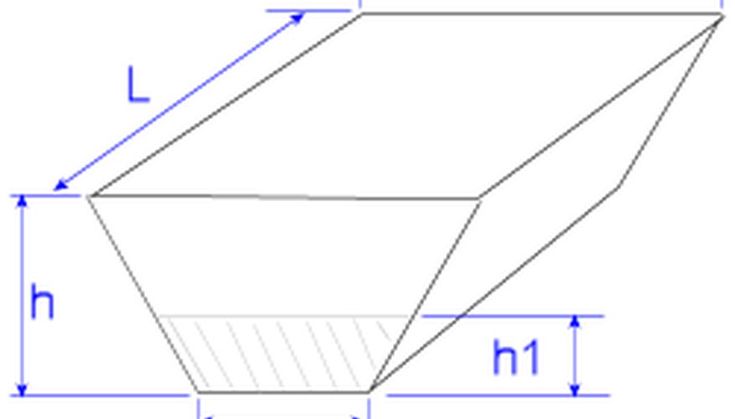 Пределы интегрирования оп-
[c.143]
Пределы интегрирования оп-
[c.143]
Вероятность р = р(3/7 интервал времени между двумя соседними заказами больше 3-х и меньше 5-ти дней, равна по значению площади заштрихованной на рис. 7.5 криволинейной трапеции, которая вычисляется по формуле [c.118]
Площадь криволинейной трапеции, ограниченной кривой у = 1(к), осью Ох, прямыми х = а, х = Ь, находят по формуле [c.158]
Рассмотрим распределение Паретто (рис. 2.4.9). Площадь криволинейной трапеции, образованной приращением функции Л F(t0) и частью кривой, приближенно равна значению L0(t0)AF(tg), тогда коэффициент Джини [c.102]
Ученые XVIII века находили объем тела вращения следующим образом. Они считали, что криволинейная трапеция состоит из бесконечно малых прямоугольников со сторонами dx и /(ж) [c.249]
Если фигура ограничена сверху и снизу неотрицательными функциями /(.г) и g (х) соотвествешю, непрерывными на отрезке [а, Ь], то пло-щаль 5 криволинейной фигуры равна разности площадей криволинейных трапеции, ограниченных сверху графикам и /(j ) и g(x) [c. 141]
141]
Плоские и объемные геометрические фигуры :: SYL.ru
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно.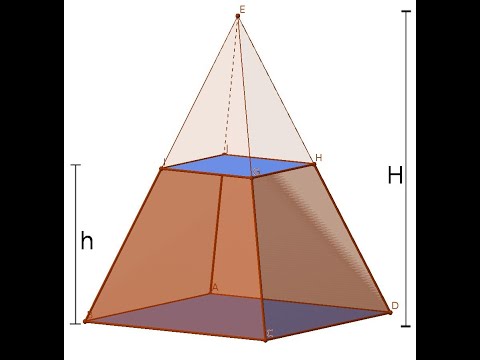 Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
К этой категории стоит отнести геометрические фигуры разнообразных форм, ломаная линия контуров которых замыкается.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
К этой категории причисляют следующие конструкции:
- куб;
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
- тор.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.

- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Ее величество трапеция
Научно – исследовательская работа
«Ее величество Трапеция»
Автор: Соснина Анастасия
Студентка 1 курса
Руководитель: Богаева Н.В.
преподаватель математики
КГУ «Глубоковский технический колледж»
2021 г
Содержание:
- Введение
Стихотворение «Трапеция» (проблемно-поисковая ситуация)
- Основной блок
- Математическая сказочка
- Элементы и виды трапеции
- Свойства трапеции
- Стихотворение «Все (или не все?) о трапеции»
- Исследовательский блок: теория
Методы «борьбы» с трапециями
- Исследовательский блок: практика
«Задача одна-решения разные!»
- Образцы карточек с разноуровневыми заданиями
- Заключение
ТРАПЕЦИЯ, ТРАПЕЦИЯ
Фигура есть такая,
Мне грустно потому,
Что я её не знаю.
Ты где живёшь, трапеция,
В Америке, в Китае?
Может, за трапецией
Поехать надо в Грецию?
А мама говорит: — Не надо,
Трапеция с тобою рядом.
Развею я твою тоску,
Ты подожди минутку.
И на гладильную доску
Укладывает юбку,
Вот тебе ТРАПЕЦИЯ,
Не стоит ехать в Грецию.
Паспорт.
Цель исследования:
Изучив теоретический материал учебника и дополнительных источников выявить методы решения задач по теме «Трапеция» и различные способы нахождения площади трапеции.
Задачи исследования:
1)Изучить соответствующую литературу.
2)Провести исследование по выявлению методов решения задач с помощью дополнительных построений.
3)Провести исследование возможности решения задачи на нахождение площади трапеции несколькими способами.
4)Выявить примеры проявления трапеции в окружающем мире.
Актуальность:
Вопрос о нахождении площадей плоских фигур всегда актуален, так как находится в центре внимания деятельности человека. Знания и умения находить площадь трапеции имеют огромное значение для решения задач, в том числе и заданий единого национального тестирования. Данное исследование, которое выходит за рамки нашей школьной программы, поможет найти новые подходы к решению геометрических задач. Поэтому именно эта тема нас заинтересовала, появился интерес узнать то, что находится за страницами учебника.
Практическая значимость:
Данная тема очень актуальна. В школьных учебниках по этой теме есть задания с применением знаний о нахождении площадей плоских фигур. Математические олимпиады и конкурсы содержат задачи, в которых необходимы навыки решения заданий нестандартным способом. Но особенно значим этот проект при подготовке к ВОУД и ЕНТ, так как в тестах содержатся задачи на нахождение площадей плоских фигур. Созданный проект по этой теме позволяет учащимся самостоятельно поработать и получить необходимые знания. Данную работу можно использовать:
Созданный проект по этой теме позволяет учащимся самостоятельно поработать и получить необходимые знания. Данную работу можно использовать:
- На уроках
- На дополнительных занятиях
- В кружковой работе
- При проведении предметных недель
- На научно-исследовательской конференции в школе
- На консультациях, индивидуальных и дополнительных занятий при подготовке к ВОУД и ЕНТ.
Гипотеза:
Существуют ли методы решения задач помощью дополнительных построений и различные способы нахождения площади трапеции.
Объект исследования: трапеция
Предмет исследования: площадь трапеции.
Исследовательский метод определяется как самостоятельное решение проблемы с применением рассуждения, доказательства и анализ фактов.
В своей работе мы поместили стихи об этой геометрической фигуре.
Ход исследования:
1. Изучить теоретический материал учебника и дополнительных источников информации и найти новые способы нахождения площади трапеции.
Изучить теоретический материал учебника и дополнительных источников информации и найти новые способы нахождения площади трапеции.
2. Оформить документ в виде папки.
3. Создать презентацию.
4. Сделать сообщение учащимся 8 класса на уроке и на школьной НПК.
5. Разработать серию карточек с задачами на готовых чертежах.
6. Провести проверочную работу по карточкам с учащимися 8 класса.
7. Оформить результаты, сделать соответствующие выводы.
В ходе работы нам предстояло подтвердить или опровергнуть суждение о том, что существуют другие способы нахождения площади трапеции
Содержание:
- Введение
Стихотворение «Трапеция» (проблемно-поисковая ситуация)
- Основной блок
- Математическая сказочка
- Элементы и виды трапеции
- Свойства трапеции
- Стихотворение «Все (или не все?) о трапеции»
- Исследовательский блок: теория
Методы «борьбы» с трапециями
- Исследовательский блок: практика
«Задача одна-решения разные!»
- Образцы карточек с разноуровневыми заданиями
- Заключение
Введение
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, он использовал свои геометрические знания, полученные из наблюдений и опытов. Почти все великие учёные древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон,
Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, он использовал свои геометрические знания, полученные из наблюдений и опытов. Почти все великие учёные древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон,
проводивший беседы со своими учениками, одним из девизов своей школы провозгласил: «Не знающие геометрии не допускаются!»
Среди множества различных геометрических фигур на плоскости выделяется большое семейство четырёхугольников. В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Каждый понимает смысл слов: площадь комнаты, площадь садового участка. Подумайте и самостоятельно ответьте на вопрос: что такое “площадь”? И вы увидите, что не так-то это просто. Даже математики смогли создать соответствующую математическую теорию сравнительно недавно. Правда, это никому не мешало успешно использовать понятие площади и в науке, и на практике с незапамятных времен. Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычисление их площадей. Лишь в последствие было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника, трапеции и других многоугольников. Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников. На уроке геометрии мы доказывали теорему о нахождении площади трапеции.
Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычисление их площадей. Лишь в последствие было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника, трапеции и других многоугольников. Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников. На уроке геометрии мы доказывали теорему о нахождении площади трапеции.
ТРАПЕЦИЯ, ТРАПЕЦИЯ
Фигура есть такая,
Мне грустно потому,
Что я её не знаю.
Ты где живёшь, трапеция,
В Америке, в Китае?
Может, за трапецией
Поехать надо в Грецию?
А мама говорит: — Не надо,
Трапеция с тобою рядом.
Развею я твою тоску,
Ты подожди минутку.
И на гладильную доску
Укладывает юбку,
Вот тебе ТРАПЕЦИЯ,
Не стоит ехать в Грецию.
Трапеция.
Математическая сказочка.
Жил-был когда-то давно в Древней сказочной стране маленький трапезный столик по имени Трапезио. Он очень любил гулять в одиночестве. Но случилась однажды беда: налетел ураган и понес Трапезио неизвестно куда. Долго ли, коротко ли странствовал бедный столик, только как-то теплым весенним днем опустил его все-таки ураган на землю. Да только страна оказалась совсем необычной – Страна Геометрия. Почувствовал столик, что появились у него какие-то новые элементы, изменились старые, да только увидеть себя ему ну никак не удавалось. Шел Трапезио по этой далекой стране, брел куда-то, и, наконец увидел озеро, наклонился, а там… Смотрела на него необыкновенная геометрическая фигура. Так и появилась на свет Трапеция.
Так и появилась на свет Трапеция.
- Трапе́ция(от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Элементы и виды трапеций.
Параллельные стороны называются основаниями трапеции.
Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Расстояние между основаниями называется высотой трапеции.
Трапеция, у которой боковые стороны равны, называется равнобедренной (или равнобокой), название равнобедренная используется чаще.
Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
(Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
В равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
У равнобедренной трапеции углы при любом основании равны.
У равнобедренной трапеции диагонали равны.
Если трапеция равнобедренная, то около неё можно описать окружность.
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.
Если у равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Всё (или не всё?) о трапеции
Все, что имеем мы на свете
Геометрия разметит,
На фигуры, на прямые
И на точки веховые.
Землю, дом, сады, скамейки,
Все измерит по линейке.
Геометрия сначала,
Только землю измеряла,
А потом в ней, как поэмы,
Появились теоремы,
О фигурах, об углах,
Об отрезках и лучах.
В клуб такой многоугольный,
Видно по протекции,
Королевою вступает
Важная Трапеция,
Основательная дама-
Есть два Основания.
Параллельные друг другу,
Обрати внимание.
Две другие стороны,
Даже могут быть равны,
О Равнобокой мы узнали,
Равны ее Диагонали,
Равны углы при основании,
Но мы продолжили дознанье,
А супротивные углы,
Что в градусах измерены
180 в сумме дать должны
И в этом мы уверены.
Еще узнали у нее,
Такое вот поветрие,
Чрез середины оснований
Проходит Ось симметрии.
Бока поделим пополам,
Перпендикулярами,
С осью в точку их сведем,
Не тратя даром время мы,
И Центр окружности готов,
Описывай без лишних слов.
Подруги есть две у трапеции нашей,
О них мы, конечно,
Немного расскажем.
Одна из трапеций-
На нашу похожа,
Есть два основанья,
Но как-то построже.
С одной стороны
Она точно такая,
С другой же, прямая,
Ну, очень прямая.
Но наша трапеция
Очень довольна,
Подругой своею
Прямоугольной.
Вторая подруга-
Приносит волнение
Криволинейность ее поведения,
И вся в интегралах,
Ее не понять,
Пока мы не можем ее описать.
А площадь трапеции
Как же узнать?
Берешь основанья,
Их вместе слагаешь,
Дели пополам,
Перемножь с высотой
И делай, что хочешь,
Ты с площадью той!
Исследование: теория
Очень часто в задачах по планиметрии встречается такая замечательная геометрическая фигура, как трапеция. С трапециями связано много интересных утверждений, каждое из которых в той или иной ситуации помогает найти аккуратные не громоздкие решения задач.
С трапециями связано много интересных утверждений, каждое из которых в той или иной ситуации помогает найти аккуратные не громоздкие решения задач.
При решении задач с трапецией часто используются различные дополнительные построения. Мы попытались эти построения упорядочить (классифицировать), т.е. сделали попытку выяснить, какое именно дополнительное построение поможет решить задачу.
Исследование: практика
Результаты исследования: Методы «борьбы с трапециями»
Метод 1. Продолжить боковыестороны трапеции до взаимногопересечения.
Метод 2. Провести через вершину верхнего основания (например С) прямую, параллельную боковой стороне (СF || АВ)
Метод 3.Провести через вершину верхнего основания трапеции (например С) прямую, параллельную диагонали ВD(СF || ВD)
Метод 4.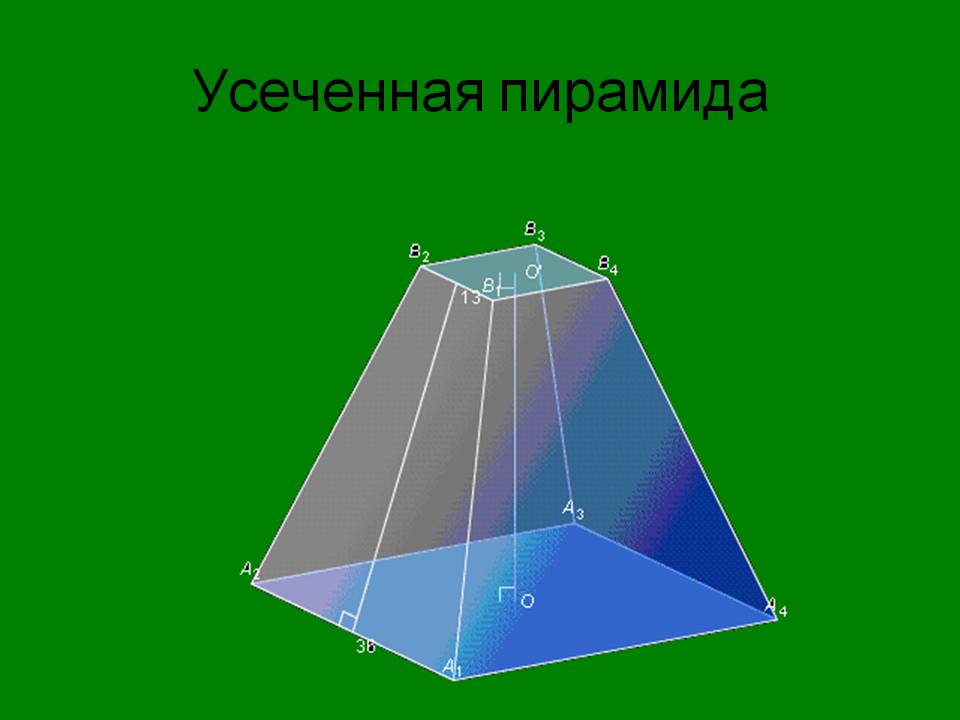 Провести высоту в равнобедренной или прямоугольной трапециях.
Провести высоту в равнобедренной или прямоугольной трапециях.
Трапеции, приятнейшей из дам,
В любви признался Параллелограмм.
А та, на общий угол намекая,
«А площадь, — говорит, — у вас какая?»
Исследование: практика
«Задача одна – решения разные»
Вот трапеция дана,
Площадь нам ее нужна!
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ:
Дана трапеция ABCD. Найти её площадь.
Первый способ:
Решение.
- Провели высоты ВН и СК , ВН = СК, HK = BC. Тогда наша трапеция разбивается на три части: треугольник АВН, прямоугольник НВСK и треугольник CKD.
- Таким образом, SABCD = SABH + SHBCK + SCKD
- SABCD = AH ∙ BH2+ BH∙HK+ CK ∙ KD2 = BH ∙12AH+HK+ 12KD=
=BH ∙ AH+2HK+KD2=BH ∙ AH+HK+BC+KD2=BH ∙ BC+AD2 .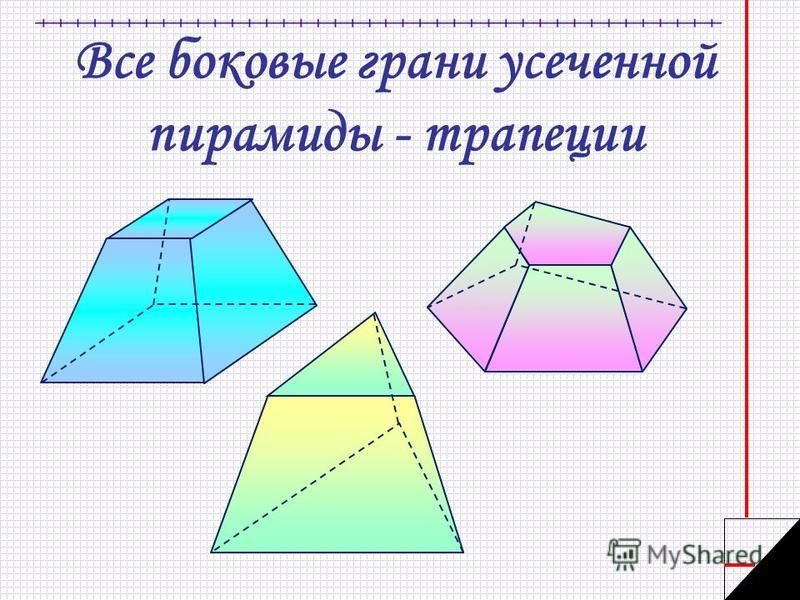
Второй способ:
Решение.
- Провели высоты АН и DК , AН = DК, AD = HK. Тогда наша трапеция разбивается на три части: треугольник АHВ, прямоугольник AНKD и треугольник CKD.
2. Таким образом, SABCD = SAHKD – SAHВ — S DKC
3. SABCD = AH∙AD- AH ∙HB2— DK ∙CK2 = AH ∙AD- 12HB- 12CK=
=AH ∙ 2AD—HB—CK2=AH ∙ AD+HK-HB-CK2=AH ∙ BC+AD2 .
Третий способ:
Решение.
- Провели СК‖АВ, высоту ВН. Тогда наша трапеция разбивается на две части: параллелограмм АВСК (по определению, так как АВ‖СК по построению, АК‖ ВС по условию) и ΔКСD.
 Причём, высоты параллелограмма и треугольника равны.
Причём, высоты параллелограмма и треугольника равны.
2. Таким образом, SABCD = SABCK + S KCD
3. SABCD = AK∙BH+ KD ∙ BH2 = BH ∙AK+ 12KD=
=BH ∙ 2AK+KD2=BH ∙ AK+AK+KD2=BH ∙ BC+AD2 .
Четвёртый способ:
Решение.
- Через середину стороны CD (точка К) провели прямую, пересекающую сторону AD в точке L.
- Рассмотрим треугольники BCK и LDC: CK = DK (по построению), ∟ВCК = ∟LDK (как соответственные при параллельных прямых), ∟CKB = ∟DKL (как вертикальные), Δ BCK = ΔLDК (по стороне и двум прилежащим к ней углам), следовательно, BC = LD и SBCK = SLDК.

- SABCD = SABL = 12AL∙BH= AD+DL2 ∙ BH= AD+BC2 ∙ BH
Пятый способ:
Решение.
- Через середины сторон AB и CD (точки M и K ) провели перпендикуляры NH и PT к основаниям трапеции.
- Рассмотрим Δ AMH и ΔBMN: ∟H = ∟N = 900 , AM = MB (по условию), ∟AMH = ∟BMN (как вертикальные), значит, ΔAMH = ΔBMN (по гипотенузе и острому углу), следовательно, AH = BN и SAMH = SBMN
- Рассмотрим Δ CPK и ΔDTK: ∟T = ∟P = 900 , CK = KD (по условию), ∟CKP = ∟DKT (как вертикальные), значит, ΔCPK = ΔDTK (по гипотенузе и острому углу), следовательно, CP = DT и S CPK = S DTK
- SABCD = SHNPT = NH ∙ NP
Шестой способ:
Решение.
- Провели диагональ BD. Тогда наша трапеция разбивается на две части: два треугольника ΔABD и ΔBCD.

- SABCD = SABD + S BCD = AD ∙BH2+ BC ∙BH2 =BH ∙ AD+BC2.
Седьмой способ:
Решение.
- В трапеции даны диагонали AC = d1, BD = d2, ∟COD = α .
- ∟AOB = ∟COD (как вертикальные), ∟BOC = ∟AOD = 1800 – α , и sin1800— α = sinα .
- SABCD = SABO + SBOC + SCOD + SAOD = 12AO ∙BO ∙ sinα +
+ 12CO ∙BO ∙ sinα + 12DO ∙CO ∙ sinα + 12AO ∙DO ∙ sinα =
= 12sinα AO ∙BO+BO ∙CO+CO ∙ DO+AO ∙ DO =
= 12sinα ∙ BO ∙ AO+CO+ DO ∙ CO+AO =
= 12sinα AC ∙ BO+DO = 12 sinα ∙AC ∙BD=
= 12 d1d2sinα .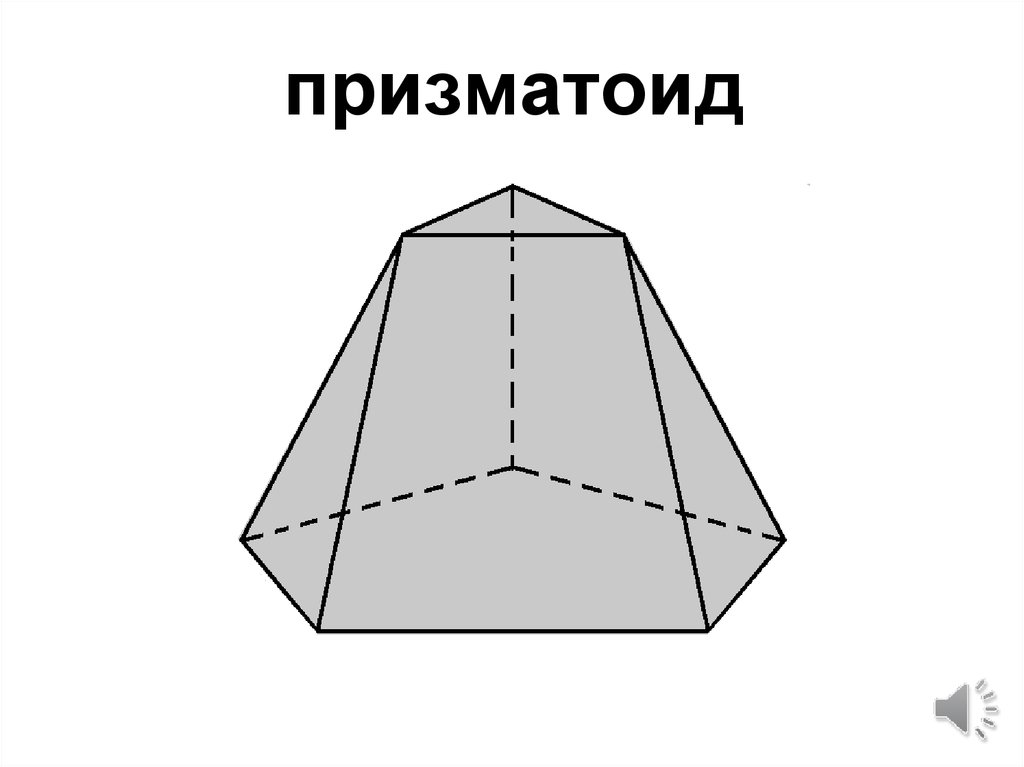
Восьмой способ:
Решение.
- В трапеции ABCD MN – средняя линия, т. е. AM = MB и CN = ND, MN = AD+BC2 .
- Так как SABCD = AB+BC2 ∙BH=MN ∙BH .
Девятый способ:
Решение.
- Через середину стороны CD трапеции ABCD провели перпендикуляр KM к стороне AB, т. е. CK = KD, KM = q, AB = d.
- PN ‖ AB.
- ΔCPK = ΔDNK по стороне и двум прилежащим к ней углам (∟CKP = =∟DKN (как вертикальные, CK = DK (по условию), ∟PCK = ∟NDK (как накрест лежащие при параллельных прямых), значит, SCPK = SDNK
- SABCD = SABCKN + SCPK = SABPN = dq.
Трапеция в окружающем мире и жизни человека.
Трапеция и архитектура
Своды в виде трапеции встречаются в самых древних архитектурных сооружениях.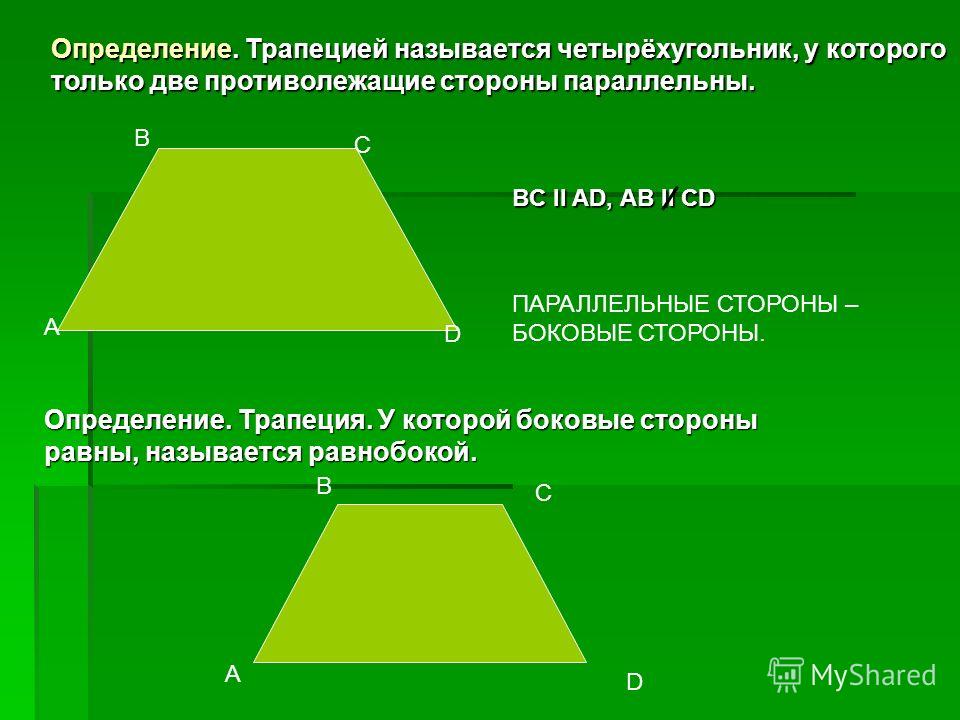 Простые и логические линии Арки Трапеция придают помещению торжественность и возвышенность, подчёркивая архитектонику всего сооружения. Интерьер может быть любым—от строго классического до современного. Трапеция — символ архитектуры инков. Трапеция — типичная архитектурная особенность Священной Долины. Тот факт, что подобные формы можно увидеть в других областях Перу, севернее Куско, возможно объясняется распространением влияния инков, или просто подражанием местными строителями архитектурным формам Священной Долины. Интересно отметить то, что в районе Тиауанако, который в общем-то, считается источником инкской культуры, трапециевидные формы не встречаются.
Простые и логические линии Арки Трапеция придают помещению торжественность и возвышенность, подчёркивая архитектонику всего сооружения. Интерьер может быть любым—от строго классического до современного. Трапеция — символ архитектуры инков. Трапеция — типичная архитектурная особенность Священной Долины. Тот факт, что подобные формы можно увидеть в других областях Перу, севернее Куско, возможно объясняется распространением влияния инков, или просто подражанием местными строителями архитектурным формам Священной Долины. Интересно отметить то, что в районе Тиауанако, который в общем-то, считается источником инкской культуры, трапециевидные формы не встречаются.
Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление.
Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках.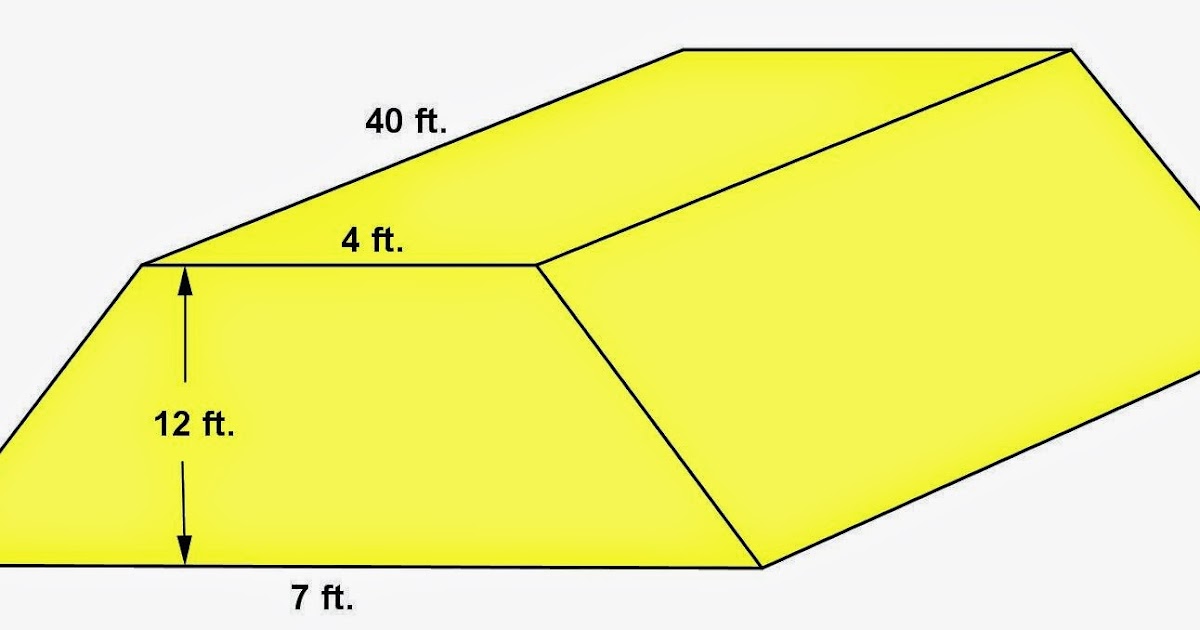 Ниши могли иметь разнообразные функции, существует предположения, что в них размещались идолы или какие-либо другие культовые предеты. В жилых домах они могли выполнять роль хозяйственных шкафов для утвари и различных вещей.
Ниши могли иметь разнообразные функции, существует предположения, что в них размещались идолы или какие-либо другие культовые предеты. В жилых домах они могли выполнять роль хозяйственных шкафов для утвари и различных вещей.
Трапеция и природа
В верховьях ледника Октябрьский высится пик Трапеция (6050 м). На него советские альпинисты поднялись в 1935 году.Гора Трапеция (абхазское название Хатхуа).
Ещё в 1880-е гг. известный русский ученый, директор Московской терапевтической клиники проф. А. А. Остроумов, пленившись красотой этого места, приобрёл на склоне горы участок земли, где построил дачу и заложил большой сад. В 1901 г. рядом со старой, деревянной, новая, каменная дача, где в этом же году гостил А. П. Чехов. У подножия горы на средства Остроумова в 1902 г. была построена Сухумская городская больница на 35 коек, которая функционирует до сих пор. Любопытно, что в советское время эта же больница была рассчитана на одновременное лечение 300 больных.
Гора Альпамайо (Алпамайо, Alpamayo) расположена на горной цепи Кордильера Бланка, Анды, Перу.Высота Альпамайо достигает 5947 метров от уровня моря. Название происходит от деревушки расположенной неподалеку. Гора Альпамайо считается самой красивой горой в мире.
На Большом Кавказе известно одно такое карстово-тектоническое озеро — Самурское; площадь его 65 тыс. м2, максимальная глубина 7 м. Оно расположено на северном склоне Пастбищного хребта в бассейне реки Пшеха (левый приток реки Белой) в 6 км севернее станицы Самурской Апшеронского района Краснодарского края. Согласно легенде, на месте озера стоял когда-то черкесский аул. Во время землетрясения он провалился и на его месте образовалось озеро. Оно имеет вид неправильной трапеции, берега его изрезаны и обрывисты. Здесь много уютных бухточек и скалистых мысов. В зеленоватой, слегка мутной воде в тихую погоду отражается темная стена дубово-букового леса, окружающего озеро плотным кольцом.
Трапеция и космос
В созвездии Ориона, возле Пояса Ориона, находится туманная область, которая называется Большой Туманностью Ориона, или М42. В этой туманности имеется яркое звёздное скопление под именем Трапеции Ориона. Там происходит процесс образования новых звёздных систем в гигантских комплексах газа и пыли, так называемых проплидах. Если внимательно посмотреть на рисунок, то можно увидеть, что газ и пыль, окружающие некоторые слабые звёзды, образуют структуры, вытянутые по направлению от ярких звёзд. Рисунок представляет собой фото монтаж (в условном цвете) изображений, полученных космическим телескопом имени Хаббла.
В этой туманности имеется яркое звёздное скопление под именем Трапеции Ориона. Там происходит процесс образования новых звёздных систем в гигантских комплексах газа и пыли, так называемых проплидах. Если внимательно посмотреть на рисунок, то можно увидеть, что газ и пыль, окружающие некоторые слабые звёзды, образуют структуры, вытянутые по направлению от ярких звёзд. Рисунок представляет собой фото монтаж (в условном цвете) изображений, полученных космическим телескопом имени Хаббла.
Взгляните на прилагаемый фрагмент звездной карты. На нем изображены звезды, образующие Трапецию Ориона: A, B, C и D. Звездная величина самой яркой из них – звезды С – 5.4m. Звезда D — вторая по яркости – имеет блеск 6.3m. Блеск звезды А составляет примерно 6.8m. Дело в том, что в 1975 году астрономы выяснили, что это затменно-переменная звезда с периодом 65.432 дней. И это не единственная переменная звезда в Трапеции Ориона: звезда В также является затменно-переменной звездой, но с периодом 6,471 день. Теперь обратите внимание на звезды одиннадцатой звездной величины: E и F. Угловое расстояние между ними и соседними яркими звездами (А и С соответственно) составляет порядка 4 угловых секунд. Это неплохой способ проверить возможности своего телескопа. Дело в том, что в небольшие телескопы (диаметр объектива 70-80 мм) эти две слабые звездочки видны лишь в очень темные и прозрачные ночи. Если апертура вашего телескопа порядка 200 мм и более, то эти звезды будут легким объектом для наблюдений
Теперь обратите внимание на звезды одиннадцатой звездной величины: E и F. Угловое расстояние между ними и соседними яркими звездами (А и С соответственно) составляет порядка 4 угловых секунд. Это неплохой способ проверить возможности своего телескопа. Дело в том, что в небольшие телескопы (диаметр объектива 70-80 мм) эти две слабые звездочки видны лишь в очень темные и прозрачные ночи. Если апертура вашего телескопа порядка 200 мм и более, то эти звезды будут легким объектом для наблюдений
Трапеция и мода
По-прежнему модной остается трапециевидная стилистика, которая заявила о себе еще в далеком прошлом. Трапеция и стиль A-лайн невероятно популярны у молодых женщин, которые уже устали от бесформенных курток, но еще не готовы перейти на классические приталенные пальто. Воротник этих пальто может варьироваться от широкого до плоского воротника стойкой, хотя встречаются и стильные модели пальто-трапеции без воротника.
Трапеция больше на крышу похожа.
Юбку рисуют трапецией тоже.
Взять треугольник и верх удалить —
Трапецию можно и так получить.
Прежде всего, модные сумки условно можно разделить на два вида: декоративные (порой с элементами эпатажа и китча, c бантами и стразами) и повседневные простые и незатейливые). Практически в любой модной коллекции можно найти сумки-трапеции и сумки-корзинки (полукруглые, объемные сумочки с двумя короткими ручками, такие были популярны в 70-х годах).
Идеальное платье для вас: платье-трапеция. Чтобы придать формам стройность, нет ничего лучше платья с юбкой-трапецией. Такая юбка от таки расходится и принимает форму трапеции, плавно облегая фигуру и расширяясь книзу. Расхождение между сторонами трапеции не должно быть слишком большим, иначе вы будете похожи не на звонкий колокольчик, а на царь-колокол. Юбки-трапеции особенно удачно сочетаются с верхом без бретелек или глубоким V-образным декольте, что придает платью откровенную оригинальность.
Это интересно!
При составлении персонального гороскопа конфигурация «Трапеция» предполагает однонаправленный путь и большое упорство. Обычно это сопровождается сомнениями и борьбой. Человек имеет защиту и в то же время постоянно испытывает посягательство на свою стабильность: однако многие бури просто проносятся над головой. Обладатель гороскопа «Трапеция» часто делает удачную карьеру.
Обычно это сопровождается сомнениями и борьбой. Человек имеет защиту и в то же время постоянно испытывает посягательство на свою стабильность: однако многие бури просто проносятся над головой. Обладатель гороскопа «Трапеция» часто делает удачную карьеру.
Вывод:
Существует много способов нахождения площади трапеции. При решении задач используется тот метод, который удобен.
Трапеция присутствует в окружающем мире и жизни человека.
В ходе работы я узнала много нового, расширила и углубила свои знания по этой теме. Научилась составлять карточки с задачами. Выступив с презентацией на своем курсе мы провели проверочную работу по этим карточкам и мои однокурсники показали такие результаты:
«5» — 1, «4» — 8, «3» — 6, «2» — 0. При 100% успеваемости качество знаний составляет 60%.
Выдвинутая нами гипотеза нашла свое подтверждение.
Трапециевидная призма — формулы, свойства, определение, примеры
Трапециевидная призма представляет собой трехмерную фигуру, состоящую из двух трапеций, соединенных четырьмя прямоугольниками. Призмы состоят из многоугольников, образующих их основания. Одним из наиболее узнаваемых примеров трапециевидной призмы является кирпич, особенно круглый кирпич для костра. Трапециевидная призма происходит от формы трапеции. Давайте узнаем больше о его определении, свойствах, формулах и решим несколько примеров.
Призмы состоят из многоугольников, образующих их основания. Одним из наиболее узнаваемых примеров трапециевидной призмы является кирпич, особенно круглый кирпич для костра. Трапециевидная призма происходит от формы трапеции. Давайте узнаем больше о его определении, свойствах, формулах и решим несколько примеров.
| 1. | Определение трапециевидной призмы |
| 2. | Свойства трапециевидной призмы |
| 3. | Трапециевидная призматическая сетка |
| 4. | Объем трапециевидной призмы |
| 5. | Площадь поверхности трапециевидной призмы |
| 6. | Часто задаваемые вопросы о трапециевидной призме |
Определение трапециевидной призмы
Трапециевидная призма – это трехмерная фигура с трапециевидным поперечным сечением в одном направлении и прямоугольным поперечным сечением в другом направлении, что означает, что призма состоит из двух конгруэнтных трапеций, соединенных друг с другом четырьмя прямоугольниками. Эти конгруэнтные трапеции находятся на вершине и дне призмы, которые называются основаниями. Четыре прямоугольника называются боковыми гранями призмы-трапеции. Трапециевидная призма имеет шесть граней, восемь вершин и 12 ребер. Чтобы построить трапециевидную призму, нам нужно сначала нарисовать трапецию, которая имеет две параллельные стороны и высоту, то есть расстояние между сторонами. На изображении ниже показано, как выглядит трапециевидная призма. H указывает высоту трапеции, S указывает площадь поверхности, L указывает боковую площадь, а B 1 и B 2 обозначают длину основания.
Эти конгруэнтные трапеции находятся на вершине и дне призмы, которые называются основаниями. Четыре прямоугольника называются боковыми гранями призмы-трапеции. Трапециевидная призма имеет шесть граней, восемь вершин и 12 ребер. Чтобы построить трапециевидную призму, нам нужно сначала нарисовать трапецию, которая имеет две параллельные стороны и высоту, то есть расстояние между сторонами. На изображении ниже показано, как выглядит трапециевидная призма. H указывает высоту трапеции, S указывает площадь поверхности, L указывает боковую площадь, а B 1 и B 2 обозначают длину основания.
Свойства трапециевидной призмы
Свойства трапециевидной призмы очень похожи на свойства трапеции, они перечислены ниже:
- Трапециевидная призма состоит из двух трапеций, соединенных четырьмя прямоугольниками
- Трапециевидная призма состоит из восьми вершин
- Трапециевидная призма состоит из шести граней
- Трапециевидная призма состоит из 12 ребер
- Трапециевидная призма представляет собой многоугольник, состоящий из трапеций
Трапециевидная призматическая сетка
Сеть трапециевидной призмы состоит из шести граней, восьми вершин и 12 ребер. Когда трапециевидная призма открывается плоско, мы можем видеть четыре прямоугольных объекта, которые помогают соединить два трапециевидных объекта вместе, чтобы сформировать трапециевидную призму. На изображении ниже показана сплющенная версия трапециевидной призмы.
Когда трапециевидная призма открывается плоско, мы можем видеть четыре прямоугольных объекта, которые помогают соединить два трапециевидных объекта вместе, чтобы сформировать трапециевидную призму. На изображении ниже показана сплющенная версия трапециевидной призмы.
Объем трапециевидной призмы
Чтобы найти объем трапециевидной призмы, нам нужно умножить площадь основания на высоту. Площадь рассчитывается как площадь поверхности одной из трапеций по расстоянию между двумя трапециями. Следовательно, чтобы найти объем трапециевидной призмы, нужно сначала найти площадь одной трапеции. Следовательно, чтобы найти объем трапециевидной призмы, мы можем использовать следующие формулы:
9где – высота трапеции, l – высота призмы, a и b – длины вершины и низа трапециевидной призмыПлощадь поверхности трапециевидной призмы
Площадь поверхности трапециевидной призмы рассчитывается путем умножения площади поверхности одной из призм на два, а затем прибавления суммы периметров к высоте трапециевидной призмы. Формула для расчета трапециевидной призмы:
Формула для расчета трапециевидной призмы:
Площадь поверхности трапециевидной призмы = h (b + d) + l (a + b + c + d) квадратных единиц
, где h — высота, b и d — длины основания, a + b + c + d — периметр, l — площадь боковой поверхности. Чтобы лучше понять это, вы можете проверить страницу о том, как найти площадь поверхности трапециевидной призмы.
Связанные темы
Ниже перечислены некоторые интересные темы, связанные с трапециевидной призмой.
- Прямоугольная призма
- Площадь трапеции
- Площадь поверхности прямоугольной призмы
- Пятиугольная призма
Пример 1: Сэнди устанавливает палатку в форме трапециевидной призмы с размерами высотой 4 единицы, длиной трапеции 4 и 8 единицами и длиной призмы 10 единицами. Сколько кубических футов пространства в ее палатке?
Решение: Чтобы найти место в ее палатке, нам нужно найти объем палатки.
 Дано h = 4, a = 8, b = 4 и I = 10
Дано h = 4, a = 8, b = 4 и I = 10Объем трапециевидной призмы = A × I кубических единиц
Нам нужно найти площадь трапеции. формула:
Площадь (A) = ½ × h × (a + b)
A = ½ × 4 × (8 + 4)
A = 2 × 12
A = 24 квадратных фута
Давайте найти объем сейчас.
Объем трапециевидной призмы = A × I
V = 24 × 10
V = 240 кубических футов
Следовательно, количество кубических футов пространства в палатке Сэнди составляет 240 кубических футов.
Пример 2: Найдите площадь поверхности данной трапециевидной призмы с высотой 3 единицы, длинами оснований 4,5 единицы и 6 единицами, боковой длиной 5 и сторонами призмы 2,5 единицы.
Решение: Добавим в формулу все значения, которые у нас есть из данного изображения.
Площадь поверхности трапециевидной призмы = h (b + d) + l (a + b + c + d)
A = 3 (4,5 + 6) + 5 (4,5 + 2,5 + 6 + 2,5)
A = 3 × 10,5 + 5 × 15,5
A = 31,5 + 77,5
A = 109 единиц 2
Следовательно, площадь поверхности данной трапециевидной призмы равна 109 единицам 20
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о трапециевидной призме
Что такое трапециевидная призма?
Трапециевидная призма представляет собой трехмерную фигуру с двумя трапециями в основании, соединенными четырьмя прямоугольниками. Трапециевидная призма получила свое название из-за того, что состоит из трапеций. Трапециевидная призма имеет шесть граней, восемь вершин и 12 ребер. Одним из ярких примеров трапециевидной призмы, которую мы видим в повседневной жизни, является огнеупорный кирпич.
По какой формуле вычисляется объем трапециевидной призмы?
Чтобы найти объем трапециевидной призмы, нам нужно сначала найти площадь одной трапеции. Формула для расчета объема трапециевидной призмы:
Объем трапециевидной призмы = A × I
Площадь (A) = ½ × h × (a + b) или ½ h(b 1 + b 2 )
Где h – высота трапеции, l – высота призмы, a и b – длины вершины и низа трапециевидной призмы
Какая формула используется для расчета площади поверхности трапециевидной призмы?
Формула для расчета площади поверхности трапециевидной призмы:
Площадь поверхности трапециевидной призмы = h (b + d) + l (a + b + c + d)
, где h – высота , b и d — длины основания, a + b + c + d — периметр, l — площадь боковой поверхности.
Что такое развертка трапециевидной призмы?
Сеть трапециевидной призмы состоит в том, что она состоит из двух трапеций и четырех прямоугольников. Когда трапециевидная призма сплющена, мы можем ясно видеть эти два изображения.
Как найти высоту трапециевидной призмы?
Чтобы найти высоту трапециевидной призмы, нам нужно найти площадь одной из трапеций. Так как призма состоит из двух трапеций, для расчета объема нам нужно найти высоту одной из трапеций по следующей формуле: площадь, h — высота, a и b — длины оснований трапеций
Почему трапециевидная призма является трехмерной фигурой?
Трехмерная фигура трапеции называется трапециевидной призмой, поскольку эти фигуры имеют длину, ширину и глубину. Ребра призмы – это места, где встречаются грани, а вершины призмы – это углы, в которых встречаются три или более поверхностей.
Трехмерные фигуры | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) представляют собой твердые фигуры с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
Подробнее о работе с полигонами см. на нашей странице Свойства полигонов.
Многогранники определяются как имеющие:
- Прямые ребра .
- Плоские стороны называются гранями .
- Углов, называемых вершинами .
Многогранники также часто определяются по количеству ребер, граней и вершин, которые они имеют, а также по тому, имеют ли все их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником. Платоновые тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью пятиугольными гранями.
- Икосаэдр с двадцатью равносторонними треугольными гранями.

См. рисунок выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, имеющий два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. стороны призмы параллелограммы — четырехгранные фигуры с двумя парами сторон одинаковой длины.
Антипризмы аналогичны обычным призмам тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с многоугольником в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре основания, т.0091 Правая пирамида или может иметь вершину не по центру, если это Наклонная пирамида .
Кроме того, пирамида может иметь вершину прямо в центре основания, т.0091 Правая пирамида или может иметь вершину не по центру, если это Наклонная пирамида .
Более сложные многогранники
Существует множество других типов многогранников: симметричные и асимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями. Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками. Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Обычные трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
Сфера, имеющая форму шара или шара, представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образуется путем вращения меньшего круга вокруг большего круга. Существуют и более сложные формы торов. |
Площадь поверхности
На нашей странице, посвященной расчету площади, объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.
Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двухмерных фигур для вычисления площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически представляет собой двумерную форму.
Таким образом, вы вычисляете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее. Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба равна площади одной грани (длина x ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно провести только одно измерение — длина и ширина квадрата по определению одинаковы.
Таким образом, одна грань этого куба равна 10 × 10 см = 100 см 2 . Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и умножив результат на общее количество сторон — см. диаграмму основных многогранников выше. .
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см 2 .
Пирамида
Чтобы вычислить площадь поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
Умножьте ответ на 2.
Наконец, сложите площадь основания и сторон вместе, чтобы найти общую площадь поверхности пирамиды.
Для расчета площади поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон). Возможно, вам придется измерить стороны по отдельности.
Возможно, вам придется измерить стороны по отдельности.
Диаграммы сетей
Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о схемах сети см. нашу страницу 3D-формы и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги. Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник. Следовательно, вам нужно найти площадь двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003
Измерьте высоту цилиндра. В данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем суммирования площадей кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
0 Длина наклона
Конус
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.
Однако вычислить относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонной части, можно найти по следующей формуле:
π (пи) × радиус × длина наклона.
В нашем примере расчет равен 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
теннисный мяч:
диаметр = 2,6 дюйма
сфера
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр — расстояние поперек сферы. Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.
Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа, чтобы найти общую поверхность площадь примерного тора.
125,6 × 25,12 = 3155,072 см 2 .
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам нужны» для счета
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Заполнение твердого тела: объем
Для трехмерных фигур вам также может понадобиться знать объем объем у них есть.
Другими словами, если вы наполнили их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Объяснение урока: 3D-фигуры | Nagwa
В этом объяснителе мы узнаем, как называть трехмерные фигуры, включая пирамиды и призмы; описывать трехмерные фигуры по таким свойствам, как количество ребер, граней и вершин; и создавать трехмерные фигуры.
Трехмерные (3D) фигуры расширяются, как следует из названия, в трех измерениях. Наоборот в двумерные (2D) формы, которые можно нарисовать как такое на бумаге, 3D фигуры не могут. Мы можем только нарисовать их, используя перспективу, чтобы предложить иллюзию их трехмерности.
Полезный язык
Трехмерная фигура ограничена своими гранями, ребрами и вершинами.
Лица 2D (плоские) формы, составляющие трехмерную фигуру.
Края являются линиями пересечения двух граней.
Вершины
точки, где заканчиваются 3 или более граней.
Обратите внимание на разные размеры: грань — 2D, ребро — 1D, а вершина — 0D.
Давайте посмотрим на определение двух важных трехмерных фигур: призмы и пирамиды.
Определение: Призма
Призма представляет собой твердое тело с двумя параллельными конгруэнтными гранями, называемыми основаниями. Его крест участок, параллельный основания постоянна по всей своей высоте (также называемой длиной).
Определение: Пирамиды
Пирамиды представляют собой трехмерные геометрические фигуры или твердые объекты, основанием которых является многоугольник (треугольник, квадрат, прямоугольник, пятиугольник и т. д.), а все остальные стороны являются треугольниками, которые пересекаются в вершина или вершина .
Правая пирамида — это пирамида, вершина которой лежит выше центра тяжести основания.
Правильная пирамида — это правильная пирамида, основание которой представляет собой правильный многоугольник: все стороны основания равны
равной длины, и все боковые ребра пирамиды имеют одинаковую длину.
Призмы и пирамиды называются по их основанию: призма с треугольным основанием называется треугольной пирамидой; пирамида, основанием которой является пятиугольник, называется пятиугольной пирамидой. В следующей таблице приведены соответствия между названием основания и прилагательным, используемым для описания призмы или пирамиды.
| Shape of Base | Name of Prism | Name of Pyramid |
|---|---|---|
| Triangle | Triangular prism | Triangular pyramid |
| Square | Cuboid | Square pyramid |
| Rectangle | Куб | Прямоугольная пирамида |
| Параллелограмм | Параллелепипед | Пирамида на основе параллелограмма |
| Trapezoid | Trapezoidal prism | Trapezoidal pyramid |
| Pentagon | Pentagonal prism | Pentagonal pyramid |
| Hexagon | Hexagonal prism | Hexagonal pyramid |
| Heptagon | Heptagonal prism | Heptagonal pyramid |
| Восьмиугольник | Восьмиугольная призма | Восьмиугольная пирамида |
Давайте рассмотрим несколько вопросов, чтобы проверить наше понимание.
Пример 1. Определение вершин трехмерной фигуры
Сколько вершин имеет фигура?
Ответ
Вершины — это точки, в которых заканчиваются 3 или более граней. Находим, что их 5.
Пример 2. Идентификация граней трехмерной фигуры
Сколько граней имеет фигура?
Ответ
Гранями трехмерной фигуры являются ее плоские части. Мы насчитали их 6 здесь.
Пример 3. Определение краев трехмерной фигуры
Сколько ребер у фигуры?
Ответ
Края трехмерной фигуры — это линии пересечения двух граней. Мы насчитали 12 из них.
Пример 4. Идентификация 3D-формы
Для рисунка ниже определите форму основания(ей). Затем классифицируйте фигуру.
Ответ
Эта трехмерная фигура не имеет основания и вершины, но имеет две параллельные конгруэнтные грани, которые являются основаниями. Форма оснований – четырехугольник с двумя параллельными сторонами: это трапеция. 3D
форма, таким образом, является трапециевидной призмой.
Иногда нас просят ответить на вопросы, которые не дают изображения, которое могло бы нам помочь. В этих случаях, часто бывает полезно нарисовать нашу собственную фигуру, чтобы ответить на вопрос. В следующем примере мы увидим один такой вопрос.
Пример 5: Свойства трехмерных фигур
Определите, верно ли это утверждение всегда, иногда или никогда: призма имеет 2 основания и 4 стороны.
Ответ
Рассмотрим несколько призм. Начиная с треугольной призмы, у нас есть два треугольных основания. (один вверху и один внизу). Тогда для каждого ребра треугольного основания у нас есть сторона. Следовательно, у нас есть три стороны, как показано на рисунке.
Это означает, что у треугольной призмы есть 2 основания, но нет 4 сторон, поэтому утверждение неверно для треугольной призмы.
Теперь рассмотрим квадратную призму, также известную как прямоугольный параллелепипед. Он имеет два квадратных или прямоугольных основания,
и для каждого из четырех ребер основания есть сторона. Следовательно, у нас есть два основания и четыре стороны.
Следовательно, у нас есть два основания и четыре стороны.
Следовательно, для прямоугольного параллелепипеда утверждение верно. Поэтому можно сказать, что утверждение «У призмы 2 основания и 4 стороны» иногда верно.
Ключевые точки
- Трехмерная фигура ограничена своими гранями, ребрами и вершинами. Лица 2D
(плоские) формы, составляющие трехмерную фигуру.
Ребра линии пересечения двух граней.
Вершины точки, где заканчиваются 3 или более граней. Обратите внимание на разные измерения: грань двухмерна, ребро одномерно, и вершина нульмерна. - Призма представляет собой твердое тело с двумя параллельными конгруэнтными гранями, называемыми основаниями. Его поперечное сечение параллельно основания постоянна по всей своей высоте (также называемой длиной).
- Пирамиды представляют собой трехмерные геометрические фигуры или твердые объекты, в основе которых лежит многоугольник
(треугольник, квадрат, прямоугольник, пятиугольник и т.
 д.) и все остальные стороны являются треугольниками, которые встречаются в вершине или вершине .
Правая пирамида — это пирамида, вершина которой лежит над центром тяжести основания.
д.) и все остальные стороны являются треугольниками, которые встречаются в вершине или вершине .
Правая пирамида — это пирамида, вершина которой лежит над центром тяжести основания.
Правильная пирамида — это правильная пирамида, основание которой представляет собой правильный многоугольник: все стороны основания равны равной длины, и все боковые ребра пирамиды имеют одинаковую длину.
Формула трапеции — GeeksforGeeks
Измерение — это раздел геометрической математики, который измеряет геометрические величины, такие как общая площадь поверхности, площадь боковой поверхности, периметр, длина, ширина и объем. 2D и 3D — это два разных типа измерений.
Двухмерные фигуры состоят из двух или более прямых линий или замкнутых круговых линий. Эти фигуры не имеют ни высоты, ни глубины. Для этих фигур можно определить такие величины, как площадь и периметр. Они известны как фигурки самолетов.
Например, круг, треугольник, квадрат, прямоугольник. Трехмерные фигуры образованы рядом поверхностей или плоскостей. Они имеют длину, ширину и высоту. Это твердые цифры. Для этих фигур можно определить общую площадь поверхности, площадь боковой поверхности и объем. Пример: конус, цилиндр, куб.
Что такое трапеция?
Четырехугольник с одной парой параллельных сторон и другим набором непараллельных сторон. Параллельные стороны называются основаниями. Две другие непараллельные стороны называются боковыми сторонами. Высота или высота – это кратчайшее расстояние между двумя параллельными сторонами.
Типы трапеций
Существует три типа трапеций. Это
- Равнобедренная трапеция: длины непараллельных сторон равны.
- Прямоугольная трапеция: имеет набор прямых углов.
- Разносторонняя трапеция: стороны не равны.
Свойства трапеции
- Трапеция имеет только одну пару параллельных сторон.

- Сумма всех углов трапеции равна 360 или .
- У равнобедренной трапеции оба угла при основании конгруэнтны, непараллельные стороны конгруэнтны и диагонали конгруэнтны.
- Медиана параллельна обоим основаниям и является средней длиной оснований.
- Сумма смежных углов равна 180 o .
Формулы трапеции
Формула трапеции состоит из площади и периметра. Теперь давайте посмотрим, как выводятся формулы.
Площадь трапеции
Рассмотрим трапецию PQRS, SR и PQ — параллельные стороны, а ST — кратчайшее расстояние между ними, которое является перпендикулярным и обозначается через h. Разобьем трапецию на отрезки. Это дает нам два треугольника PTS и UQR и прямоугольник TURS. Теперь, если мы найдем площади всех трех и просуммируем их, мы получим площадь трапеции.
При записи площадь треугольника, PTS = 1/2 (основание × высота)
Площадь треугольника, PTS = 1/2 (PT × ST)
= 1/2 (xh) …. .(1)
.(1)
При записи площади прямоугольника TURS = длина × ширина
Площадь прямоугольника TURS = bh …..(2)
3 Площадь треугольника UQR = 1/2 (основание × высота)
Площадь треугольника UQR = 1/2 ( yh) …..(3)
Суммируя три площади, т. е. уравнения (1), (2) и ( 3) получаем площадь трапеции.
При суммировании всех трех уравнений
Площадь трапеции = 1/2 (xh) + bh + 1/2 (yh)
Взяв 1/2 (h) общего, мы можем записать уравнение как
Площадь трапеции = (1/ 2) h (x + 2b + y)
Площадь трапеции = (1/2) h ( x + b + b + y)
Из рисунка видно, что суммируя x, b и у дает а. Итак,
Площадь трапеции = (1/2) × h × (a+b)
или
Площадь трапеции = (1/2) × (высота) × (сумма параллельных сторон )
Следовательно, площадь трапеции равна половине произведения высоты на сумму параллельных сторон.
Периметр трапеции
Для нахождения периметра нужно сложить длины всех сторон.
Периметр трапеции = сумма длин параллельных и непараллельных сторон
или
Периметр трапеции = PQ + RS + QR + PS
или
3 Периметр трапеции = a + b + c + d
Следовательно, периметр трапеции равен сумме длин параллельных сторон и сумме длин непараллельных сторон.
Примеры вопросов
Вопрос 1. Найдите площадь трапеции, если основания равны 10 см и 16 см. Кратчайшее расстояние между параллельными сторонами равно 8 см.
Ответ:
Даны длины оснований, a = 10 см и b = 16 см, высота h = 8 см.
Площадь трапеции = (1/2) h (a+b)
= (1/2) 8 (10+16)
= 140 см 2
Вопрос 2: Если площадь длина трапеции равна 240 см 2 , а сумма длин параллельных сторон равна 30 см, найдите высоту трапеции.
Ответ:
Дано, Площадь = 240см 2 ,(a+b) = 30см
Площадь трапеции = (1/2) h (a+b) 90 002/1900 2) ч (30)
h = (240 × 2) / 30
= 16 см
Отсюда высота трапеции 16 см .
Вопрос 3: Найдите периметр трапеции, если длины сторон равны 15 см, 6 см, 12 см и 8 см соответственно.
Ответ:
Дано, a = 15 см, b = 6 см, c = 12 см и d = 8 см.
Периметр трапеции = сумма длин параллельных сторон и сумма длин непараллельных сторон.
= a + b + c + d
= 15+6+12+8
= 41 см
Вопрос 4: Если периметр трапеции равен 48 см, а сумма параллельных сторон равна 26 см, а длина третьей стороны 10 см. Найдите длину четвертой стороны.
Ответ:
Дано, a+b = 26 см, c = 10 см и периметр = 48 см
Периметр трапеции = сумма длин параллельных сторон и сумма длин непараллельных стороны.
Периметр трапеции = a + b + c + d
48 = 26 + 10 + d
d = 48- 26 – 10
= 12 см
Отсюда длина четвертой стороны равна 92 см
0 1 .
Вопрос 5: Если длина одной стороны больше другой на 6 см, а площадь трапеции равна 240 см 2 . Найдите длины параллельных сторон, если кратчайшее расстояние между параллельными сторонами равно 14 см.
Ответ:
Дано, Площадь = 240 см 2 и Высота = 14 см.
Пусть параллельная сторона a = x ,
По заданному условию
b = x + 6
Площадь трапеции = (1/2) h (a+b)
240 = (1 /2) (14) (x + x + 6)
(240×2) / 14 = 2x + 6
2x = 34,28 – 6
2x = 28,28
x = 14,1429 а см
b = x + 6
b = 14,14 + 6
b = 20,14 см
Отсюда 14,14 см и 20,14 см — длины параллельных сторон.
Трехмерная реконструкция чашечки Хельда и ее постсинаптического главного нейрона в медиальном ядре трапециевидного тела
. 2002 г., 15 декабря; 22 (24): 10567-79.
doi: 10.1523/JNEUROSCI.22-24-10567.2002.
Курт Зетцлер 1 , Леандер Ф. Золь, Йоханн Х. Боллманн, Дж. Герард Г. Борст, Майкл Фрочер, Берт Сакманн, Иоахим Х. Р. Любке
принадлежность
- 1 Кафедра клеточной физиологии, Институт медицинских исследований им. Макса Планка, D-69120 Гейдельберг, Германия.
- PMID: 12486149
- PMCID: PMC6758464
- DOI:
10.
 1523/JNEUROSCI.22-24-10567.2002
1523/JNEUROSCI.22-24-10567.2002
Бесплатная статья ЧВК
Курт Сэтцлер и др. Дж. Нейроски. .
Бесплатная статья ЧВК
. 2002 г., 15 декабря; 22 (24): 10567-79.
doi: 10.1523/JNEUROSCI.22-24-10567.2002.
Авторы
Курт Зетцлер 1 , Леандер Ф. Золь, Йоханн Х. Боллманн, Дж. Герард Г. Борст, Майкл Фрочер, Берт Сакманн, Иоахим Х. Р. Любке
принадлежность
- 1 Кафедра клеточной физиологии, Институт медицинских исследований им.
 Макса Планка, D-69120 Гейдельберг, Германия.
Макса Планка, D-69120 Гейдельберг, Германия.
- PMID: 12486149
- PMCID: PMC6758464
- DOI: 10.1523/JNEUROSCI.22-24-10567.2002
Абстрактный
Трехмерная морфология аксосоматических синаптических структур между чашечкой Хельда и главным нейроном в медиальном ядре трапециевидного тела (MNTB) в стволе мозга молодых постнатальных 9-дневных крыс была реконструирована из серийных ультратонких срезов. В зоне аппозиции между чашечкой и главным нейроном выявлены два типа мембранных специализаций: синаптические контакты (СК) с активными зонами (АЗ) и связанные с ними постсинаптические плотности (ППС) составляют примерно 35% (n = 554) специализаций. ; остальные 65% (n = 1010) были точечными прилипаниями (PA). Синаптические контакты составляют примерно 5% площади соприкосновения пресинаптической и постсинаптической мембран. СК имел среднюю площадь 0,100 мкм(2), а ближайшие соседи были разделены в среднем на 0,59 мкм.микрон Примерно половина синаптических везикул чашечки была сгруппирована на расстоянии 200 нм от площади АЗ-мембраны, кластер, состоящий примерно из 60 синаптических везикул (n = 52 SCs). Приблизительно две синаптические везикулы на SC были «анатомически состыкованы». Сопоставляя геометрию синаптической структуры с ее ранее изученными функциональными свойствами, мы обнаруживаем, что при однократном пресинаптическом потенциале действия (ПД) (1) примерно 35% АЗ выделяют квант медиатора, (2) количество ПД и анатомически состыкованных везикул сопоставим с низкими оценками легко высвобождаемого пула (RRP) квантов, и (3) широкое распределение областей PSD [коэффициент вариации (CV) = 0,9], вероятно, способствует большой изменчивости миниатюрных пиков EPSC.
; остальные 65% (n = 1010) были точечными прилипаниями (PA). Синаптические контакты составляют примерно 5% площади соприкосновения пресинаптической и постсинаптической мембран. СК имел среднюю площадь 0,100 мкм(2), а ближайшие соседи были разделены в среднем на 0,59 мкм.микрон Примерно половина синаптических везикул чашечки была сгруппирована на расстоянии 200 нм от площади АЗ-мембраны, кластер, состоящий примерно из 60 синаптических везикул (n = 52 SCs). Приблизительно две синаптические везикулы на SC были «анатомически состыкованы». Сопоставляя геометрию синаптической структуры с ее ранее изученными функциональными свойствами, мы обнаруживаем, что при однократном пресинаптическом потенциале действия (ПД) (1) примерно 35% АЗ выделяют квант медиатора, (2) количество ПД и анатомически состыкованных везикул сопоставим с низкими оценками легко высвобождаемого пула (RRP) квантов, и (3) широкое распределение областей PSD [коэффициент вариации (CV) = 0,9], вероятно, способствует большой изменчивости миниатюрных пиков EPSC. Геометрия реконструированного синапса предполагает, что каждый из сотен SC, вероятно, независимо вносит вклад в размер и фазу роста EPSC во время одного AP.
Геометрия реконструированного синапса предполагает, что каждый из сотен SC, вероятно, независимо вносит вклад в размер и фазу роста EPSC во время одного AP.
Цифры
Рис. 1.
Выпуск передатчика на MNTB…
Рис. 1.
Высвобождение передатчика в синапсах MNTB во время химической фиксации. А, Слева , Афферентно…
Рисунок 1. Высвобождение передатчика в синапсах MNTB во время химической фиксации. A, слева , афферентно вызванные преспайки (пресинаптическая ПД, зарегистрированная в постсинаптической клетке) и ВПСТ в трех разных временных точках во время перфузии ванны экспериментальной камеры с фиксаторами (1% параформальдегид/2,5% глутаральдегид, растворенные в растворе Рингера, рН 7,4) . В низ , показан контроль до фиксации. средних трасс показывают ~20 с после начала фиксации, а верхних трасс — через 2 мин после начала фиксации. A, справа . Те же кривые показаны с более низким временным разрешением, иллюстрируя постсинаптическую реакцию на каинат ( KA ; 1 мм, растворенный в растворе Рингера), который применялся путем выброса давления из ближайшей пипетки. ВПСТ были заблокированы до предспайков или до явного изменения чувствительности к КА (9).0726 средние следы ). B , Химическая фиксация не сопровождалась увеличением спонтанных или отсроченных EPSC. В этом эксперименте фиксаторы наносились путем выброса под давлением из ближайшей пипетки. На нижней кривой перед фиксацией за афферентно вызванными ВПСТ (амплитуда ~1,5 нА при -80 мВ) следовали отсроченные и спонтанные ВПСТ. В средней трассе в начале фиксации как вызванные ВПСТ, так и спонтанные ВПСТ были снижены. В верхней трассе 907–27 в конце фиксации блокировались как вызванные, так и спонтанные ВПСТ.
В низ , показан контроль до фиксации. средних трасс показывают ~20 с после начала фиксации, а верхних трасс — через 2 мин после начала фиксации. A, справа . Те же кривые показаны с более низким временным разрешением, иллюстрируя постсинаптическую реакцию на каинат ( KA ; 1 мм, растворенный в растворе Рингера), который применялся путем выброса давления из ближайшей пипетки. ВПСТ были заблокированы до предспайков или до явного изменения чувствительности к КА (9).0726 средние следы ). B , Химическая фиксация не сопровождалась увеличением спонтанных или отсроченных EPSC. В этом эксперименте фиксаторы наносились путем выброса под давлением из ближайшей пипетки. На нижней кривой перед фиксацией за афферентно вызванными ВПСТ (амплитуда ~1,5 нА при -80 мВ) следовали отсроченные и спонтанные ВПСТ. В средней трассе в начале фиксации как вызванные ВПСТ, так и спонтанные ВПСТ были снижены. В верхней трассе 907–27 в конце фиксации блокировались как вызванные, так и спонтанные ВПСТ. В моделях A и B трассы смещены по вертикали для удобства отображения.
В моделях A и B трассы смещены по вертикали для удобства отображения.
Рис. 2.
Поперечный срез чашечки…
Рис. 2.
Поперечный срез чашечки Гельда и главного нейрона в…
Рис. 2. Поперечный срез чашечки Хельда и главного нейрона в MNTB. A , ЭМ-изображение нервного окончания и тела клетки основного нейрона в MNTB. Изображение получено путем компьютерного монтажа пяти электронных микрофотографий одного ультратонкого среза (изображение получено при увеличении в 3000 раз). Интересующие структуры были очерчены и прозрачно наложены поверх монтажа; пресинаптическая чашечка показана на желтый , постсинаптический главный нейрон синий и ядро коричневый . Масштабная линейка, 5 мкм. B , Область в рамке в A при большем увеличении (изображение с увеличением 20 400×). SC отмечен стрелкой , а соседний PA отмечен стрелкой . Масштабная линейка, 0,3 мкм.
Масштабная линейка, 5 мкм. B , Область в рамке в A при большем увеличении (изображение с увеличением 20 400×). SC отмечен стрелкой , а соседний PA отмечен стрелкой . Масштабная линейка, 0,3 мкм.
Рис. 3.
Последовательный разрез через синаптическую…
Рис. 3.
Серийный разрез через синаптический контакт. A–H , Отдельные серийные секции…
Рис. 3. Последовательный разрез через синаптический контакт. AH , Избранные серийные срезы SC ( стрелка ) между пресинаптической чашечкой и постсинаптическим главным нейроном. Открытая стрелка в D указывает на везикулу, сросшуюся с пресинаптической мембраной. Масштабная линейка: (в H ) A–H , 0,25 мкм.
Рис. 4.
Последовательный раздел через PA.…
Рис. 4.
Последовательный раздел через PA. A–H , Последовательные участки через усилитель мощности…
Рис. 4.Последовательный раздел через PA. A–H , Показаны серийные разрезы усилителя мощности. В A видны два соседних SC для сравнения двух разных типов прилегания мембраны. PA помечен стрелками , а SC помечен стрелками . В отличие от SCs, PA показывает симметричную пресинаптическую и постсинаптическую плотности и не имеет скопления синаптических пузырьков и расширения щели. Вся PA кажется перфорированной, как видно на B-D, G . Масштабная линейка: (в H ) A–H , 0,25 мкм.
Рис. 5.
5.
Шиповидный выпяч…
Рис. 5.
Шиповидное выпячивание в соме главного нейрона. А, В, Два…
Рис. 5.Шиповидное выпячивание сомы главного нейрона. A, B Два последовательных ЭМ-изображения срезов двух типичных шиповидных мембранных выпячиваний сомы постсинаптической клетки (обозначены цифрой 9).0726 с ). Выступ на слева имеет узкую «шейку позвоночника». Обратите внимание на наличие СК, идентифицируемых по плотному скоплению синаптических пузырьков ( черные стрелки, ) и многочисленным ПА. Помечены только СК на шиповидных выпячиваниях. Масштабная линейка, 0,5 мкм.
Рис. 6.
Трехмерная реконструкция контурного…
Рис. 6.
6.
Трехмерная реконструкция контурных сечений. A , Наложение контурных сечений на…
Рис. 6.Трехмерная реконструкция по контурным сечениям. A , Наложение контурных участков для формирования «набора контуров» из серийных ЭМ-изображений позвоночно-подобного выступа. Постсинаптическая мембрана отмечена синим , АЗ красный и PSD-файлы оранжевый . Два SC находятся на расстоянии 0,5 мкм друг от друга. B , Стек контуров, показанный в A , был заполнен тетраэдрами, которые создают треугольную поверхность ( контуры из треугольников , отмеченные серым цветом ). Толщина среза 60 нм.
Рис. 7.
Поверхностные виды трехмерного…
Рис. 7.
7.
Виды поверхности трехмерной реконструкции чашечки Хельда и…
Рис. 7. Виды поверхности трехмерной реконструкции чашечки Хельда и главного нейрона. A , Вид сверху на чашечку и тело клетки главного нейрона MNTB. Чашечка ( слева ) показана желтым цветом , а главный нейрон ().0726 правый ) синий . Нервное окончание образует чашеобразную структуру, покрывающую примерно 40% площади поверхности главного нейрона. Конечная часть претерминального аксона, дающая начало гигантскому терминалу, видна на слева . B , Вид сбоку после поворота реконструкции на 90° вокруг оси x . По краям шляпки можно определить многочисленные пальцеобразные стебельки. C , Поверхностный вид реконструкции, в которой часть поверхностной мембраны была сделана прозрачной, чтобы проиллюстрировать эксцентричное расположение ядра ( коричневый ) рядом с чашечкой. Мембранные специализации можно увидеть в виде небольших пятен в красных (SCs) и пурпурных (PA) соответственно. Постсинаптический аксон ( снизу ) и дендритные отростки ( справа ) полностью не реконструировались.
Мембранные специализации можно увидеть в виде небольших пятен в красных (SCs) и пурпурных (PA) соответственно. Постсинаптический аксон ( снизу ) и дендритные отростки ( справа ) полностью не реконструировались.
Рис. 8.
Распределение мембранных специализаций в…
Рис. 8.
Распределение мембранных специализаций в зоне соприкосновения между чашечкой и…
Рис. 8. Распределение мембранных специализаций в зоне соприкосновения между чашечкой и главным нейроном. A , Вид анфас на синаптическую поверхность чашечки ( желтый ) , показывающий распределение SC , выделенных красным . Б , Реконструкция той же поверхности чашечки , что и на A , с распределением PA , выделенным пурпурным цветом . C , Тот же вид, что и в A и B , показывающий наложение распределений SC и PA. Используется тот же цветовой код, что и в A и B .
C , Тот же вид, что и в A и B , показывающий наложение распределений SC и PA. Используется тот же цветовой код, что и в A и B .
Рис. 9.
Геометрия мембран специализации в…
Рис. 9.
Геометрия специализаций мембран в зонах соприкосновения между чашечкой и…
Рис. 9. Геометрия специализаций мембран в зонах соприкосновения между чашечкой и главным нейроном. A , Гистограмма ( слева ) распределения площадей поверхности СК ( серый ; среднее 0,100 ± 0,086 мкм 2 ) и PA ( черный ; среднее значение 0,046 ± 0,042 мкм 2 ) и соответствующую кумулятивную гистограмму ( справа ). Ширина ячейки, 0,01 мкм 2 . B , Гистограмма распределения расстояний до ближайших соседей между SC, отмеченными серым (среднее, 0,589 ± 0,296 мкм) и PA, отмеченным черным (среднее, 0,374 ± 0,179 мкм). На правой панели показаны соответствующие кумулятивные гистограммы (тот же цветовой код). Ширина ячейки 0,02 мкм. пунктирных линий — это расстояния до ближайших соседей, взятые из смоделированного представления SCs ( пунктирная серая линия ) и PA ( пунктирная черная линия ), которые были случайным образом распределены по области соприкосновения чашечки и главного нейрона.
B , Гистограмма распределения расстояний до ближайших соседей между SC, отмеченными серым (среднее, 0,589 ± 0,296 мкм) и PA, отмеченным черным (среднее, 0,374 ± 0,179 мкм). На правой панели показаны соответствующие кумулятивные гистограммы (тот же цветовой код). Ширина ячейки 0,02 мкм. пунктирных линий — это расстояния до ближайших соседей, взятые из смоделированного представления SCs ( пунктирная серая линия ) и PA ( пунктирная черная линия ), которые были случайным образом распределены по области соприкосновения чашечки и главного нейрона.
Рис. 10.
Количественная оценка кластера синаптических пузырьков…
Рис. 10.
Количественная оценка геометрии кластеров синаптических пузырьков в SCs. A, B , Два разных…
A, B , Два разных…
Количественная оценка геометрии кластеров синаптических пузырьков в SCs. A, B , Два разных СК при большом увеличении с анатомически состыкованными везикулами (отмечены звездочками ). Масштабная линейка, 0,1 мкм. C , Электронная микрофотография другого одиночного SC, показывающая плотное скопление синаптических пузырьков в AZ. Шкала баров: С, D , 0,25 мкм. D . Та же микрофотография, что и в C . Схематическое изображение геометрических измерений показано для подмножества синаптических пузырьков: мембраны AZ ( красная линия ) и кратчайшее расстояние ( зеленые прямые линии ) между мембраной синаптических пузырьков ( зеленые кружки ) и мембраной AZ. Анатомически купированные везикулы отмечены звездочками . Все параметры измерялись в двух измерениях.
Рис. 11.
11.
Трехмерная реконструкция КА…
Рис. 11.
Трехмерная реконструкция СК и связанных с ними скоплений пузырьков. A , Группа…
Рис. 11.Трехмерная реконструкция СК и связанных с ними кластеров пузырьков. A , Скопление синаптических пузырьков вблизи SC. Поверхностная мембрана главного нейрона показана на синий , АЗ в красный и синаптические пузырьки в зеленый . Обратите внимание на большой размер пула синаптических пузырьков в этом СК ( n = 304). B , Два шиповидных выступа, один с двумя НЦ (на справа ). СК расположены напротив друг друга на шейке выступа. Используется тот же цветовой код, что и в A . При этом отдельные скопления синаптических пузырьков на этих двух СК четко не различимы ( n = 358).
Рис. 12.
12.
Геометрия кластеров синаптических пузырьков.…
Рис. 12.
Геометрия кластеров синаптических пузырьков. A , Трехмерный вид одиночного КА…
Рис. 12. Геометрия кластеров синаптических пузырьков. A , Трехмерное изображение одного SC, показывающее распределение расстояний синаптических пузырьков ( зеленый ) из мембраны AZ ( красный ). Расстояния показаны как линий , соединяющих синаптический пузырек и ближайшую точку на АЗ. Для наглядности для отображения был выбран относительно небольшой КА. B , Гистограмма распределения расстояний синаптических пузырьков от пресинаптической мембраны на SC показана в A . Общее количество синаптических пузырьков составило 37. Количество синаптических пузырьков, сгруппированных в пределах 200 нм, составило 28. C , Гистограмма, показывающая количество SC с 0–4, 5–9и др. синаптических пузырьков в пределах 200 нм от АЗ. D , Количество СК с 0, 1, 2 и т. д. анатомически состыкованными везикулами (т. е. без видимого цитоплазматического пространства между синаптическим везикулой и мембраной AZ). Количество SCs без пристыкованных везикул представлено серой колонкой . E , Диаграмма, показывающая количество синаптических пузырьков на SC (среднее значение ± стандартное отклонение), расположенных на заданном расстоянии от мембраны AZ. F , Гистограмма распределения диаметров везикул (в среднем 46 ± 7 нм; n = 7799).
C , Гистограмма, показывающая количество SC с 0–4, 5–9и др. синаптических пузырьков в пределах 200 нм от АЗ. D , Количество СК с 0, 1, 2 и т. д. анатомически состыкованными везикулами (т. е. без видимого цитоплазматического пространства между синаптическим везикулой и мембраной AZ). Количество SCs без пристыкованных везикул представлено серой колонкой . E , Диаграмма, показывающая количество синаптических пузырьков на SC (среднее значение ± стандартное отклонение), расположенных на заданном расстоянии от мембраны AZ. F , Гистограмма распределения диаметров везикул (в среднем 46 ± 7 нм; n = 7799).
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Ультраструктурные основы синаптической передачи между концевыми луковицами Хельда и кустистыми клетками в улитковом ядре крысы.

Никол М.Дж., Уолмсли Б. Никол М.Дж. и соавт. Дж. Физиол. 2002 г., 15 марта; 539 (часть 3): 713-23. doi: 10.1113/jphysiol.2001.012972. Дж. Физиол. 2002. PMID: 11897843 Бесплатная статья ЧВК.
Структурные детерминанты передачи в синапсах крупных мшистых волокон гиппокампа.
Ролленхаген А., Сэтцлер К., Родригес Э.П., Йонас П., Фрочер М., Любке Й.Х. Ролленхаген А. и др. Дж. Нейроски. 2007 26 сентября; 27 (39): 10434-44. doi: 10.1523/JNEUROSCI.1946-07.2007. Дж. Нейроски. 2007. PMID: 17898215 Бесплатная статья ЧВК.
Сопоставление in vivo постсинаптической возбудимости со спонтанными синаптическими входами при формировании чашечки синапса Хелда у крыс.
Sierksma MC, Tedja MS, Borst JG.
 Sierksma MC, et al.
Дж. Физиол. 1 января 2017 г .: 595 (1): 207–231. дои: 10.1113/JP272780. Epub 2016 15 сентября.
Дж. Физиол. 2017.
PMID: 27426483
Бесплатная статья ЧВК.
Sierksma MC, et al.
Дж. Физиол. 1 января 2017 г .: 595 (1): 207–231. дои: 10.1113/JP272780. Epub 2016 15 сентября.
Дж. Физиол. 2017.
PMID: 27426483
Бесплатная статья ЧВК.Оценка квантовых параметров чашечки синапса Хельда.
Сакаба Т., Шнеггенбургер Р., Неер Э. Сакаба Т. и др. Нейроси Рес. 2002 г., декабрь; 44 (4): 343–56. doi: 10.1016/s0168-0102(02)00174-8. Нейроси Рес. 2002. PMID: 12445623 Обзор.
Морфология возбуждающих центральных синапсов: от строения к функции.
Ролленхаген А, Любке Ю.Х. Ролленхаген А. и др. Сотовые Ткани Res. 2006 ноябрь; 326(2):221-37. doi: 10.1007/s00441-006-0288-z. Epub 2006 24 августа. Сотовые Ткани Res. 2006. PMID: 16932936 Обзор.

Посмотреть все похожие статьи
Цитируется
Нейропептиды и низкомолекулярные трансмиттеры аминов: совместная передача сигналов в нервной системе.
Эйден Л.Э., Эрнандес В.С., Цзян С.З., Чжан Л. Эйден Л.Э. и соавт. Cell Mol Life Sci. 2022 23 августа; 79 (9): 492. doi: 10.1007/s00018-022-04451-7. Cell Mol Life Sci. 2022. PMID: 35997826 Обзор.
Повышенное высвобождение Ca 2+ из эндоплазматического ретикулума приводит к нарушению пресинаптической функции при семейной болезни Альцгеймера.
Адеой Т., Шах С.И., Демуро А., Рабсон Д.А., Улла Г. Адеой Т. и соавт. Клетки. 2022 11 июля; 11 (14): 2167. doi: 10.3390/ячейки11142167. Клетки.
 2022.
PMID: 35883609
Бесплатная статья ЧВК.
2022.
PMID: 35883609
Бесплатная статья ЧВК.Множественные роли актина в экзо- и эндоцитозе.
Ву Л.Г., Чан С.И. Ву Л.Г. и соавт. Передние синаптические нейроны. 2022 4 марта; 14:841704. doi: 10.3389/fnsyn.2022.841704. Электронная коллекция 2022. Передние синаптические нейроны. 2022. PMID: 35308832 Бесплатная статья ЧВК. Обзор.
Созревание синапсов и нарушение развития в медиальном ядре трапециевидного тела.
Чокр С.М., Милинкевичуте Г., Крамер К.С. Чокр С.М. и др. Фронт Integr Neurosci. 2022 9 фев; 16:804221. doi: 10.3389/fnint.2022.804221. Электронная коллекция 2022. Фронт Integr Neurosci. 2022. PMID: 35221938 Бесплатная статья ЧВК. Обзор.
Сходство и разнообразие пресинаптических молекул в нервно-мышечных соединениях и центральных синапсах.

Такикава К., Нисимунэ Х. Такикава К. и др. Биомолекулы. 2022 21 января; 12 (2): 179. doi: 10.3390/biom12020179. Биомолекулы. 2022. PMID: 35204679 Бесплатная статья ЧВК. Обзор.
Просмотреть все статьи «Цитируется по»
термины MeSH
вещества
Опишите двумерные фигуры, полученные в результате нарезки трехмерных фигур: CCSS.Math.Content.7.G.A.3
All Common Core: математические ресурсы для 7-го класса
7 диагностических тестов 110 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Common Core: Справка по математике для 7-го класса »
Геометрия »
Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур: CCSS. Math.Content.7.G.A.3
Math.Content.7.G.A.3
Какая двумерная фигура получается, когда предоставленная фигура разрезается по вертикали?
Возможные ответы:
Треугольник
прямоугольник
Трапезионный
квадрат
Правильный ответ:
. Объяснение:
Вертикальный разрез — это разрез вверх и вниз.
Эта фигура представляет собой правильную прямоугольную пирамиду, с основанием в виде прямоугольника и сторонами в форме треугольников; таким образом, при вертикальном разрезе получится треугольник.
Сообщить об ошибке
Что представляет собой двумерная фигура, которая создается при вертикальном разрезании предоставленной формы?
Возможные ответы:
Прямоугольник
Трапециализатор
Треугольник
Правый треугольник
Правильный ответ:
прямоугольник
Объяснение:
Вертикальный разрез — это разрез вверх и вниз.
Эта форма представляет собой прямоугольную призму, основание и стороны которой имеют форму прямоугольников; таким образом, двухмерная форма представляет собой прямоугольник.
Сообщить об ошибке
Что представляет собой двухмерная фигура, которая создается при вертикальном разрезании предоставленной формы?
Возможные ответы:
Трапезиоид
Треугольник
квадрат
Прямоугольник
Правильный ответ:
квадрат
Объяснение:
Вертикальный разрез — это разрез вверх и вниз.
Эта фигура представляет собой куб, основание и стороны которого имеют форму квадратов; таким образом, двухмерная форма представляет собой квадрат.
Сообщить об ошибке
Какая двухмерная форма получается при вертикальном разрезе прямоугольной призмы?
Возможные ответы:
Прямоугольный треугольник
Прямоугольник
Треугольник
Трапеция
Правильный ответ:
3 900 Объяснение:
Вертикальный разрез — это разрез вверх и вниз.
Эта форма представляет собой прямоугольную призму, основание и стороны которой имеют форму прямоугольников; таким образом, двухмерная форма представляет собой прямоугольник.
Сообщить об ошибке
Какая двумерная фигура получается при вертикальном разрезании куба?
Возможные ответы:
Квадрат
Прямоугольный треугольник
Прямоугольник
Треугольник
Правильный ответ:
Квадрат3 Объяснение:
Вертикальный разрез — это разрез вверх и вниз.
Эта фигура представляет собой куб, основание и стороны которого имеют форму квадратов; таким образом, двухмерная форма представляет собой квадрат.
Сообщить об ошибке
Какая двумерная фигура получается при вертикальном разрезе правильной прямоугольной пирамиды?
Возможные ответы:
Прямоугольник
Квадрат
Трапеция
Треугольник
Правильный ответ: 3
3
3 Объяснение:
Вертикальный разрез — это разрез вверх и вниз.
Эта фигура представляет собой правильную прямоугольную пирамиду, с основанием в виде прямоугольника и сторонами в форме треугольников; таким образом, при вертикальном разрезе получится треугольник.
Сообщить об ошибке
Что представляет собой двухмерная фигура, которая создается, когда предоставленная фигура разрезается по горизонтали?
Возможные ответы:
Треугольник
Правый треугольник
Прямоугольник
Правильный ответ:
прямоугольник
. Объяснение:
Горизонтальный разрез — это боковой разрез.
Эта форма представляет собой прямоугольную призму, основание и стороны которой имеют форму прямоугольников; таким образом, двухмерная форма представляет собой прямоугольник.
Сообщить об ошибке
Что представляет собой двумерная фигура, которая создается при горизонтальном разрезании предоставленной формы?
Возможные ответы:
квадрат
Треугольник
Трапезиоид
прямоугольник
Правильный ответ:
квадрат
Объяснение:
Горизонтальный разрез — это боковой разрез.
Эта фигура представляет собой куб, основание и стороны которого имеют форму квадратов; таким образом, двухмерная форма представляет собой квадрат.
Сообщить об ошибке
Что представляет собой двумерная фигура, которая создается при горизонтальном разрезании предоставленной формы?
Возможные ответы:
Треугольник
Правый треугольник
Прямоугольник
ТРАПЕЗОИДНАЯ
Правильный ответ:
прямая ярмарка
Правильный ответ:
Объяснение:
Горизонтальный разрез — это боковой разрез.
Эта фигура представляет собой правильную прямоугольную пирамиду, с основанием в виде прямоугольника и сторонами в форме треугольников; таким образом, горизонтальный разрез даст прямоугольник.


 Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.

 \ displaystyle \ угол 3+ \ угол 4 = 180)
\ displaystyle \ угол 3+ \ угол 4 = 180)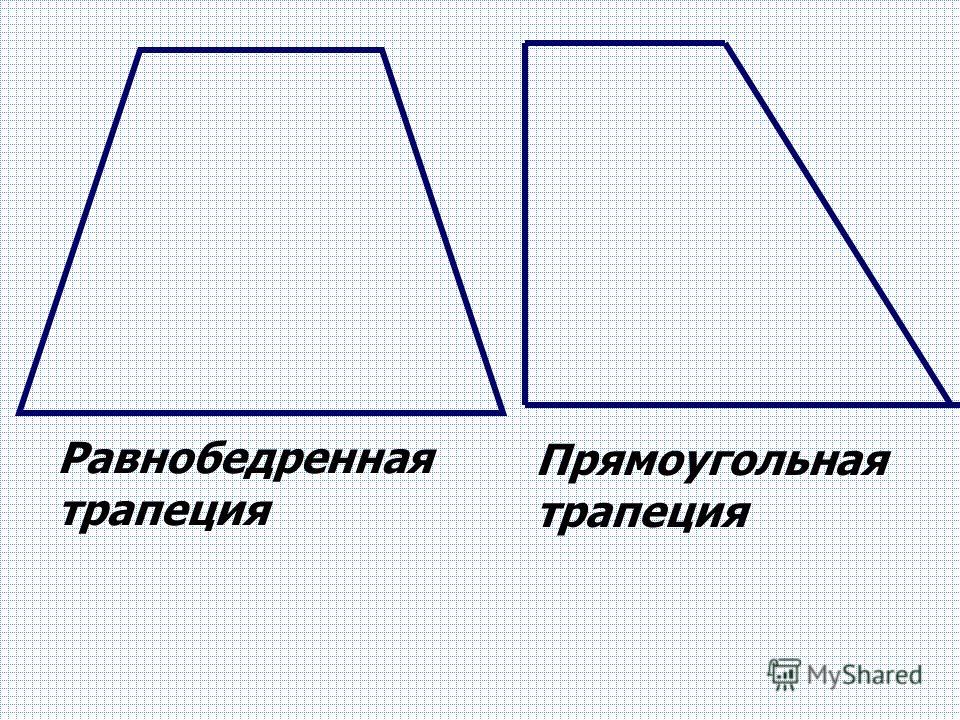 > \).
> \).
 Причём, высоты параллелограмма и треугольника равны.
Причём, высоты параллелограмма и треугольника равны.