Образуют ли базис векторы онлайн: Онлайн калькулятор. Проверить образуют ли вектора базис

Координаты вектора в базисе

Доказать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
Пусть в R³ относительно канонического базисы даны четыре вектора f₁ = (1,2,3), f₂ = (2,3,7), f₃=(1,3,1), x = (2,3,4). Докажите, что векторы f₁, f₂, f₃ можно принять за новый базис. Найдите координаты η₁, η₂, η₃ вектора х относительно этого базиса.

Решение:
Записываем матрицу перехода А:

и находим ее определитель
 <>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁, f₂, f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R³

.
Находим обратную матрицу А^-1.
Транспонированная матрица:

Алгебраические дополнения:
                    
                   
                   
                   
                    
                   
                   
                  
                   
Обратная матрица А^-1

Находим координаты вектора х относительно нового базиса.

Перейти к онлайн решению своей задачи

Пример №1. Даны векторы a{1;2;1}, b{2;-2;1}, c{1;-2;0} и d {0;3;1}. Установить, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:

α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т. е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c:
d = 1/2a + 1/2b — 3/2c

Пример №2. Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Решение. Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис.
Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор нельзя разложить по данному базису. Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор можно разложить по данному базису. Т.е. существуют такие числа α,β,γ что имеет место равенство:

Запишем данное равенство в координатной форме:
(-3;5;4)=α(5;1;2) + β(3;4;-1) + γ(-4;2;1)
Используя свойства векторов, получим следующее равенство:
(-3;5;4) = (5α;α;2α) + (3β;4β;-β) + (-4γ;2γ;γ)
(-3;5;4) = (5α+3β-4γ;α+4β+2γ;2α-β+γ)
По свойству равенства векторов имеем:
Решая полученную систему уравнений методом Гаусса (методом последовательного исключения неизвестных из уравнений системы), выберем в качестве ведущего уравнения второе уравнение системы:

Выразим из первого уравнения полученной системы α и подставим полученное выражение во второе и третье уравнения системы:


Разделим второе уравнение системы на -1 ,а третье уравнение системы на -3 и выразим из полученного равенства γ :

Подставим полученное выражение для γ в третье уравнение системы: Тогда:

В итоге получим разложение вектора в базисе :

Ответ:

Пример №3. Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»

1, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

A =	4 3 5 6 7 1 9 1 8

B =	-1 3 -2 -4 1 2 3 -4 5

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A^-1. Умножим слева обе части уравнения на A^-1: A^-1·A·X = A^-1·B, тогда получим E·X = A^-1·B, или X = A^-1·B.
Найдем обратную матрицу A^-1.

A-1 = -1/182

55 -19 -32 -39 -13 26 -57 23 10

Матрицу Х ищем по формуле:

X = A-1·B = -1/182

55 -19 -32 -39 -13 26 -57 23 10

*

-1 3 -2 -4 1 2 3 -4 5

=

75/182 -146/91 19/13 -13/14 12/7 -1 5/182 13/91 -12/13

Ответ:
x’₁ = ⁷⁵/₁₈₂x₁ -1⁴⁶/₉₁x₂ + 1⁹/₁₃
x’₂ = ^-13/₁₄x₁ + 1²/₇ -x₃
x’₃ = ⁵/₁₈₂x₁ + 1³/₉₁x₂ -1²/₁₃x₃

Пример №4. В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e₁=AB, e₂=AC, e₃=AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN, где M и N – середины ребер AD и DC соответственно;

з) разложение вектора MN по базису (e₁, e₂, e₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Скачать решение

Скачать

Задание 1. Разложить вектор d=(8;-5) по векторам a=(1;-2) и b=(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = αa+βb, где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Следовательно, =+.

Перейти к онлайн решению своей задачи

Пример №2. Разложите вектор v = (36; -6) по базису e1=(-5;3),e2=(-2;-4).
Решение. Даны векторы ε₁(-5;3), ε₂(-2;-4), X(36;-6). Показать, что векторы образуют базис двухмерного пространства и найти координаты вектора X в этом базисе.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:

E =	-5 3 -2 -4

∆ = (-5)*(-4) — (-2)*3 = 26
Определитель матрицы равен ∆ =26
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α₁, α₂, что имеет место равенство:
X = α₁ε₁ + α₂ε₂
Запишем данное равенство в координатной форме:
(36;-6) = α(-5;3) + α(-2;-4)
Используя свойства векторов, получим следующее равенство:
(36;-6) = (-5α₁;3α₁😉 + (-2α₂;-4α₂😉
(36;-6) = (-5α₁ -2α₂;3α₁ -4α₂)
По свойству равенства векторов имеем:
-5α₁ -2α₂ = 36
3α₁ -4α₂ = -6
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:

X = -6ε₁ -3ε₂

Разложить вектор d по векторам a,b,c

Базис системы векторов. Аффинные координаты

• Понятие базиса системы векторов
• Разложение вектора по базису
• Аффинные координаты

Тема базиса системы векторов связана с понятием линейной независимости векторов и линейной комбинации.

Определение 1. Три линейно независимых вектора (система векторов) , и образуют в пространстве базис, если любой вектор может быть представлен в виде некоторой линейной комбинации векторов , и , т.е. если для любого вектора найдутся такие вещественные числа , и , что справедливо равенство

.   (2)

Аналогично определяется базис на некоторой плоскости.

Определение 2.. Два лежащих в плоскости линейно независимых вектора (система векторов) и образуют на этой плоскости базис, если любой лежащий в этой же плоскости вектор может быть представлен в виде некоторой линейной комбинации векторов и , т.е. если для любого лежащего в этой плоскости вектора найдутся такие вещественные числа и , что справедливо равенство

.   (3)

Справедливы следующие утверждения:

1) любая тройка некомпланарных векторов , и образует базис в пространстве,

2) любая пара лежащих в данной плоскости неколлинеарных векторов и образует базис на этой плоскости.

Определение 3. Векторное пространство называется n-мерным, если в нём существует в точности n линейно независимых векторов.

Базисом  n-мерного пространства называется любая система из n независимых векторов этого пространства.

---

Пример 1.  Доказать, что векторы

образуют базис в четырёхмерном пространстве.

Решение. Система векторов образует базис, если: 1) количество векторов равно размерности пространства; 2) эти векторы линейно независимы. Первое требование выполнено, остаётся доказать, что эти векторы линейно независимы. Попытаемся составить из них линейную нулевую комбинацию:

Подставим в это равенство вместо данных векторов их выражения в координатах и преобразуем левую часть:

или

 

Но вектор является нулевым, когда все его проекции равны нулю, т. е.

Таким образом, из данных векторов невозможно составить нулевую линейную комбинацию, у которой хотя бы один коэффициент был отличен от нуля. Поэтому векторы

линейно независимы и, следовательно, образуют базис в четырёхмерном пространстве.

---

Итак, пусть , и — произвольный базис в пространстве, т.е. произвольная тройка некомпланарных векторов. Тогда для любого вектора найдутся такие вещественные числа , и , что будет справедливо равенство

.   (2)

Принято называть равенство (2) разложением вектора по базису , , , а числа , и — координатами вектора относительно базиса , , .

Аналогичным образом определяется разложение вектора по базису на плоскости: базис образуется двумя векторами, а координат разложенного по базису вектора также две.

Теорема 6. При сложении двух векторов и их координаты (относительно любого базиса , , ) складываются:

.

При умножении вектора на любое число все его координаты умножаются на это число:

.

Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными операциями над числами — координатами этих векторов.

---

Пример 2 Разложить вектор

по базису где

Решение. Рассматриваемые векторы принадлежат двумерному пространству: базис в этом пространстве должен состоять из двух векторов. В примере 7 установлено, что векторы

и

линейно независимы и, следовательно, образуют базис. Запишем разложение вектора по этому базису:

Чтобы найти значения и , подставим в это разложение выражения векторов , и через координаты:

Выполнив преобразования в правой части равенства, получим

или

Равенство векторов означает равенство их соответствующих координат, т. е.

откуда

Следовательно, разложение вектора по базису , имеет вид

---

Замечание. В каждом векторном пространстве существует бесконечное множество различных базисов и в различных базисах один и тот же вектор имеет различные разложения (подобно тому, как точка имеет различные координаты в различных системах коорднат).

Аффинные координаты в пространстве определяются заданием базиса , , и некоторой точки O, называемой началом координат.

Аффинными координатами любой точки M называются координаты вектора (относительно базиса , , .)

Так как каждый вектор может быть, и притом единственным способом, разложен по базису , , , то каждой точке пространства M однозначно соответствует тройка аффинных координат , , .

Декартовы прямоугольные координаты являются частным случаем аффинных координат, соответствующим тройке взаимно ортогональных и единичных базисных векторов.

Назад

Листать

Вперёд>>>

Поделиться с друзьями

Начало темы «Векторы»

Векторы: определения и действия над векторами

Сложение векторов: длина суммы векторов и теорема косинусов

Скалярное произведение векторов

Линейная зависимость векторов. Линейные комбинации векторов

Продолжение темы «Векторы»

Векторное и смешанное произведение векторов

Базис векторного пространства

Пусть V будет подпространством R ⁿ для некоторого n . Коллекция B = { V ₁ , V ₂ ,…, V _R } векторов из V , как говорят, составляет для V V . если B линейно независим и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для В . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор из V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.

Пример 1 : Коллекция { i, j } является базисом для R ² , поскольку он охватывает R ² , а векторы i и j линейно независимы (поскольку ни один из них не кратен другому). Это называется стандартной базой для R ² . Аналогично набор { i, j, k } называется стандартным базисом для R ³ и вообще

является стандартной основой для Р ^п .

Пример 2 : Набор { i, i+j , 2 j } не является основой для R ² . Хотя он охватывает R ² , он не является линейно независимым. Никакая коллекция из 3 и более векторов из R ² не может быть независимой.

Пример 3 : Набор { i+j, j+k } не является основой для R ³ . Хотя он линейно независим, он не охватывает все Р ³ . Например, не существует линейной комбинации i + j и j + k , равной i + j + k .

Пример 4 : Набор { i + j, i − j } является основой для R ² . Во-первых, оно линейно независимо, поскольку ни i + j , ни i − j не кратны другим. Во-вторых, он охватывает все R ² , потому что каждый вектор в R ² может быть выражено как линейная комбинация i + j и i − j . В частности, если A I + B J — любой вектор в R ² , тогда, если K ₁ = ½ ( A + B ) и K K K K K K K K K K K K K K K K K K K K K K K и K K K K K K K K K K K и _. = ½( а — б ).

Пространство может иметь много разных оснований. Например, как { i, j }, так и { i + j, i − j } являются основаниями для Р ² . Фактически, любой набор , содержащий ровно два линейно независимых вектора из R ² , является основой для R ² . Точно так же любой набор, содержащий ровно три линейно независимых вектора из R ³ , является основой для R ³ и так далее. Хотя ни одно нетривиальное подпространство R ⁿ не имеет уникальной базы, есть нечто такое, что должно быть общим для всех баз данного пространства.

Пусть V будет подпространством R ⁿ для некоторого n . Если V имеет базис, содержащий ровно r векторов, то каждый базис для V содержит ровно r векторов. То есть выбор базисных векторов для данного пространства не уникален, но число базисных векторов является уникальным. Этот факт позволяет четко определить следующее понятие: число векторов в базисе векторного пространства V ⊆ R ⁿ называется размером из V , обозначается тусклый V .

Пример 5 : Поскольку стандартный базис для R ² , { i, j } содержит ровно 2 вектора, каждый базис для R ² содержит ровно 2 90 вектора, поэтому ² = 2. Аналогично, поскольку { i, j, k } является основой для R ³ , который содержит ровно 3 вектора, каждую основу для R ³ содержит ровно 3 вектора, так что DIM R ³ = 3. В целом, DIM R ^N = N для каждого натурального числа n .

Пример 6 : В R ³ векторы i и k охватывают подпространство размерности 2. Это плоскость x−z , как показано на рисунке .

Рисунок 1

Пример 7: Одноэлементный набор { i + j = (1, 1)} является базой для одномерного подпространства V of R ² , состоящего из строки y = х . См. рис.

Рисунок 2

Пример 8 : Тривиальное подпространство, { 0 }, в R ⁿ , как говорят, имеет размерность 0. Таким образом, чтобы соответствовать определению размерности, основание для { 0 } должна быть коллекцией, не содержащей элементов; это пустой набор, ø.

Подпространства R ¹ , R ² и R ³ , некоторые из которых были проиллюстрированы в предыдущих примерах, можно резюмировать следующим образом:

  

Пример 9 : Найдите размерность подпространства V из R ⁴ , натянутого на векторы

 

The collection { v ₁ , v ₂ , v ₃ , v ₄ } is not a basis for V —and dim V is not 4— потому что { v ₁ , v ₂ , v ₃ , v ₄ } не является линейно независимым; см. расчет, предшествующий приведенному выше примеру. Отбрасывание v ₃ и v ₄ из этой коллекции не уменьшает пролет { V ₁ , V ₂ , V ₃ , V ₄ }, но res wreult ₁ , v ₂ }, линейно независима. Таким образом, { v ₁ , v ₂ } является основой для V , поэтому dim V = 2,

Пример 10 : Найдите размер промежутка векторов

 

Так как эти векторы находятся в R ⁵ , их диапазон, S , является подпространством R ⁵ . Однако это не трехмерное подпространство R ⁵ , поскольку три вектора w ₁ , w ₂ и w 3 _{не являются линейно независимыми1. Фактически, поскольку w 3 = 3w 1 + 2w 2 , вектор w 3 можно исключить из коллекции без уменьшения диапазона. Поскольку векторы w 1 и w 2 независимы — ни один из них не является скалярным кратным другого, набор { w 1 , w 1 , w 2 служит базисом1 для 2 } S , поэтому его размерность равна 2.}

Наиболее важным атрибутом базиса является возможность записать каждый вектор в пространстве в виде уникальный способ с точки зрения базисных векторов. Чтобы понять, почему это так, пусть B = { v ₁ , v ₂ , …, v _r } пространство будет базисом a 9 . Поскольку базис должен охватывать V , каждый вектор v в V может быть записан по крайней мере одним способом как линейная комбинация векторов в B . То есть существует скаляров k ₁ , k ₂ , …, k _r такие, что

Чтобы показать, что никакой другой выбор скалярных множителей не может дать v , предположим, что

также является линейной комбинацией базисных векторов, равной v .

Вычитание (*) из (**) дает

 

Это выражение представляет собой линейную комбинацию базисных векторов, которая дает нулевой вектор. Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю:

 

Следовательно, K ′ ₁ = K ₁ , K ′ ₂ = K ₂ ,… и K _R = K _R , так что PRESTATE *) действительно уникален. Когда v записывается в виде линейной комбинации (*) базисных векторов v ₁ , v ₂ , …, v _r , скалярно определенный коэффициент0082 k ₁ , k ₂ , …, k _r называются компонентами из v относительно основы B . Вектор ряда ( K ₁ , K ₂ ,…, K _R ) называется Vector из V относительно B и Denoted Vected V . ) _Б . Иногда удобно записать вектор компонентов в виде столбец вектор; В этом случае вектор компонентов ( K ₁ , K ₂ ,…, K _R ) ^T обозначен [ V ] ₂₉₃₃ .

Пример 11 : Рассмотрим набор C = { i, i + j , 2 j } векторов в R ² . Заметим, что вектор v = 3 i + 4 j можно записать как линейную комбинацию векторов в С следующим образом:

   

и

Тот факт, что существует более одного способа выразить вектор v в R ² в виде линейной комбинации векторов в C , еще раз указывает на то, что C не может быть основой для R ² . Если бы C были базисом, то вектор v можно было бы записать как линейную комбинацию векторов из C в одной девятке.0082 и только один способ .

Пример 12 : Рассмотрим базис B = { i + j , 2 i − j } числа R ² . Определить компоненты вектора v = 2 i − 7 j относительно B .

Компоненты v относительно B представляют собой скалярные коэффициенты k ₁ и k ₂ которые удовлетворяют уравнению

 

Это уравнение эквивалентно системе

 

Решение этой системы: k ₁ = −4 и k ₂ = 3, поэтому

 

Example 13 : Relative to the standard basis { i, j, k } = { ê ₁ , ê ₂ , ê ₃ } for R ³ , компонентный вектор любого вектора v в R ³ равен самому v : ( v ) _B = v . Тот же результат справедлив для стандартного базиса { х ₁ , х ₂ ,…, х _n } для каждого R

Ортонормированные базисы . Если В = { v ₁ , v ₂ , …, v _n } является основой для векторного пространства V , тогда каждый вектор v может быть записан как линейная комбинация V базисных векторов одним и только одним способом:

 

Нахождение компонент v относительно базиса B — скалярные коэффициенты0083 в приведенном выше представлении — обычно включает решение системы уравнений. Однако, если базисные векторы ортонормированы , то есть взаимно ортогональные единичные векторы, то вычисление компонентов особенно легко. Вот почему.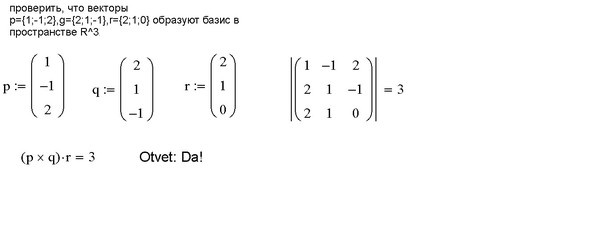 Предположим, что B = {vˆ ₁ ,vˆ ₂ ,…,vˆ _n } является ортонормированным базисом. Начиная с приведенного выше уравнения, где vˆ ₁ , vˆ ₂ ,…, vˆ _n вместо v ₁ , v ₂ , …, v _n , чтобы подчеркнуть, что базисные векторы теперь считаются единичными векторами — возьмите скалярное произведение обеих сторон с vˆ 5 ^{1 :} 0

 

В силу линейности скалярного произведения левая часть становится равной

.

 

Теперь, в силу ортогональности базисных векторов, vˆ _i · vˆ ₁ = 0 для i = 2 через n . Кроме того, поскольку vˆ — единичный вектор, vˆ ₁ · vˆ ₁ = ‖vˆ ₁ ‖1 ² = 1 ² = 1. Следовательно, приведенное выше уравнение упрощается до утверждения

в целом, если B = { Vˆ ₁ , Vˆ ₂ ,…, Vˆ _N } — ортонормальная основа для вектора V , тогда — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — , а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем — 9008, а затем и ортонормальная основа для пространства вектора . k _i , любого вектора v относительно B находятся по простой формуле

 

Пример 14 : Рассмотрим векторы

из Р ³ . Эти векторы взаимно ортогональны, как вы можете легко проверить, проверив, что V ₁ · V ₂ = V ₁ · V ₃ = V . V. . . . . . V. v ₃ = 0. Нормализуем эти векторы, тем самым получив ортонормированный базис для R ³ и затем найти компоненты вектора v = (1, 2, 3) относительно этого базиса.

Ненулевой вектор нормализуется — преобразуется в единичный вектор — путем деления его на длину. Следовательно,

 

с B = { Vˆ ₁ , Vˆ ₂ , Vˆ ₃ } — это ортонормальная основание, что на R ³ , это является представленным на основе R ³ , что является представленным примером. 0047 v относительно B можно найти, просто взяв следующие скалярные произведения:

Следовательно, ( v ) _B = (5/3, 11/(3√2),3/√2), что означает, что единственное представление v в виде линейной комбинации базиса векторы читаются как v = 5/3 vˆ ₁ + 11/(3√2) vˆ ₂ + 3/√2 vˆ 3 900, как вы можете проверить.

Пример 15 : Докажите, что набор взаимно ортогональных ненулевых векторов линейно независим.

Доказательство . Let { V ₁ , V ₂ ,…, V _R } быть набором нелевых векторов от некоторых R ^N , что является MIT -MALEGURILY, OR MIT IROGIR110, что является MIT -MIGELER, OR MIT -MAROG110. что нет v _i = 0 и v _i · v _j = 0 для i ≠ j . Пусть

   

— линейная комбинация векторов в этом наборе, дающая нулевой вектор. Цель состоит в том, чтобы показать, что k ₁ = k ₂ = … = k _r = 0. Для этого возьмем скалярное произведение обеих частей уравнения с v 1 :

Второе уравнение следует из первого в силу линейности скалярного произведения, третье уравнение следует из второго в силу ортогональности векторов, а итоговое уравнение является следствием того, что ‖ v ₁ ‖ ² ≠ 0 (начиная с v ₁ ≠ 0 ). Теперь легко видеть, что скалярное произведение обеих сторон (*) с v _i дает k _i = 0, устанавливая, что каждые скалярных коэффициента в (*) должны быть нулю, тем самым подтверждая, что векторы v ₁ , v ₂ , …, v _r действительно независимы.

Основание и размер

Цели

1. Понять определение базиса подпространства.
2. Поймите основную теорему.
3. Рецепты: база для столбцового пространства, основа для нулевого пространства, основа для спана.
4. Рисунок: базис подпространства R2 или R3.
5. Теорема : базисная теорема .
6. Основные словарные слова: основа , измерение .

Как мы обсуждали в разделе 2.6, подпространство — это то же самое, что и отрезок, за исключением того, что мы не имеем в виду набор остовных векторов. Существует бесконечно много вариантов остовных множеств для ненулевого подпространства; чтобы избежать избыточности, обычно удобнее всего выбирать остовный набор с минимальным числом векторов в нем. Это идея, лежащая в основе понятия базиса.

Определение

Пусть V — подпространство в Rn. Базис V — это набор векторов {v1,v2,. ..,vm} в V такой, что:

1. V=Span{v1,v2,…,vm} и
2. множество {v1,v2,…,vm} линейно независимо.

Напомним, что набор векторов является линейно независимым тогда и только тогда, когда при удалении любого вектора из набора отрезок уменьшается (теорема 2.5.12). Другими словами, если {v1,v2,…,vm} является базисом подпространства V, то никакое собственное подмножество {v1,v2,…,vm} не будет охватывать V: это минимальное охватный набор. Любое подпространство допускает базис по этой теореме из раздела 2.6.

Ненулевое подпространство имеет бесконечно много различных оснований, но все они содержат одинаковое количество векторов.

Мы оставляем в качестве упражнения доказательство того, что любые два основания имеют одинаковое количество векторов; возможно, вы захотите подождать, пока не изучите теорему об обратимой матрице в разделе 3.5.

Определение

Пусть V — подпространство в Rn. Количество векторов в любом базисе V называется размерностью V и пишется dimV.

Пример (основа R2)

Пример (все базы R2)

Пример (Стандартный базис Rn)

Пример

Из предыдущего примера следует, что любой базис Rn содержит n векторов. Пусть v1,v2,…,vn — векторы в Rn, а A — матрица размера n×n со столбцами v1,v2,…,vn.

1. Утверждение, что {v1,v2,…,vn} охватывает Rn, означает, что A имеет точку поворота в каждой строке : см. эту теорему в разделе 2.3.
2. Сказать, что {v1,v2,…,vn} линейно независима, означает, что A имеет точку поворота в каждой 9-й точке.0082 столбец : см. это важное примечание в Разделе 2.5.

Поскольку матрица A является квадратной, она имеет точку опоры в каждой строке тогда и только тогда, когда она имеет точку опоры в каждом столбце. В разделе 3.5 мы увидим, что два приведенных выше условия эквивалентны обратимости матрицы A.

Пример

Теперь мы покажем, как найти основания для пространства столбцов матрицы и нулевого пространства матрицы. Чтобы найти основу для данного подпространства, обычно лучше всего сначала переписать подпространство как пространство столбца или нулевое пространство: см. это важное примечание в разделе 2.6.

Основа под колонну

Сначала мы покажем, как вычислить базис для пространства столбцов матрицы.

Теорема

Опорные столбцы матрицы A образуют основу для Col(A).

Доказательство

Это переформулировка теоремы из раздела 2.5.

Вышеупомянутая теорема относится к опорным столбцам в исходной матрице, а не к ее уменьшенной ступенчатой ​​форме строк. Действительно, матрица и ее сокращенная эшелонированная форма строк обычно имеют разные пространства столбцов. Например, в матрице A ниже:

A=120-1-2-345240-2FGRREF—→10-8-701430000FGpivotcolumns=basispivotcolumnsinRREF

сводными столбцами являются первые два столбца, поэтому базой для Col(A) является

.

DB1-22C, B2-34CE.

Первые два столбца редуцированной эшелонированной формы строк определенно охватывают другое подпространство, так как

SpanDB100C, B010CE = DBab0CAAAa, binRE = (плоскость xy),

, но Col(A) содержит векторы, последняя координата которых отлична от нуля.

Следствие

Размерность Col(A) — это количество точек опоры A.

Основа пролета

Вычисление основы для диапазона выполняется так же, как вычисление основы для пространства столбца. В самом деле, длина конечного числа векторов v1,v2,…,vm равна пространству столбцов матрицы, а именно матрицы A, столбцами которой являются v1,v2,…,vm:

A=B|||v1v2···vm|||C.

Пример (основа пролета)

Пример (другая основа того же промежутка)

Основа для нулевого пространства

Чтобы вычислить базис нулевого пространства матрицы, нужно найти параметрическую векторную форму решений однородного уравнения Ax=0.

Теорема

Векторы, связанные со свободными переменными в параметрической векторной форме набора решений Ax=0, образуют основу Nul(A).

Доказательство теоремы состоит из двух частей. Первая часть заключается в том, что каждое решение лежит в промежутке заданных векторов. Это происходит автоматически: векторы выбираются точно так, чтобы каждое решение представляло собой линейную комбинацию этих векторов. Вторая часть состоит в том, что векторы линейно независимы. Эта часть обсуждалась в этом примере в Разделе 2.5.

Базис общего подпространства

Как упоминалось в начале этого подраздела, когда задано подпространство, записанное в другой форме, для вычисления базиса обычно лучше всего переписать его как пространство столбца или пустое пространство матрицы.

Пример (базис подпространства)

Напомним, что {v1,v2,…,vn} образует базис для Rn тогда и только тогда, когда матрица A со столбцами v1,v2,…,vn имеет центральную точку в каждой строке и столбце (см. этот пример ). Поскольку A представляет собой матрицу размера n × n, эти два условия эквивалентны: векторы охватывают тогда и только тогда, когда они линейно независимы. Базисная теорема — это абстрактная версия предыдущего утверждения, применимая к любому подпространству.

Основная теорема

Пусть V — подпространство размерности m. Тогда:

• Любые m линейно независимых векторов в V образуют базис для V.
• Любые m векторов, которые охватывают V, образуют основу для V.

Доказательство

Предположим, что B={v1,v2,…,vm} — набор линейно независимых векторов в V. Чтобы показать, что B является базисом для V, мы должны доказать, что V=Span{ v1,v2,…,vm}. Если нет, то существует некоторый вектор vm+1 в V, не содержащийся в Span{v1,v2,…,vm}. По возрастающему критерию размаха в разделе 2.5 множество {v1,v2,…,vm,vm+1} также линейно независимо. Продолжая в том же духе, мы продолжаем выбирать векторы, пока в конце концов не получим линейно независимый остовный набор: скажем, V=Span{v1,v2,…,vm,…,vm+k}. Тогда {v1,v2,…,vm+k} является базисом для V, откуда следует, что dim(V)=m+k>m. Но мы предполагали, что V имеет размерность m, поэтому B уже должна была быть базисом.

Теперь предположим, что B={v1,v2,…,vm} покрывает V. Если B не является линейно независимым, то по этой теореме из раздела 2.5 мы можем удалить некоторое количество векторов из B, не уменьшая его последовательность.

No related posts.