Общий знаменатель 9 и 16: Какой наименьший общий знаменатель чисел 9 и 16?

Что такое общий знаменатель?

Но что такое общий знаменатель простыми словами?

Общий знаменатель — это любое целое число, которое делится без остатка на первый и второй знаменатель.

Пример общего знаменателя :

Для таких маленьких чисел, как 2 и 3 — «нок» будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.

Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.

Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 — 1*3/2*3 = 3/6.

А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.

После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.

Когда мы нашли «общий знаменатель» мы смогли выполнить необходимое действие с дробями.

В каком случае ноз двух дробей будет являться произведением знаменателей?

Когда ноз двух дробей равен произведению знаменателей?

И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.

Скопировать ссылку

Формула общего знаменателя

Первую дробь умножаем на знаменатель второй дроби.

А вторую дробь умножаем на знаменатель первой дроби

Нахождение общего знаменателя с помощью нок.

Для того чтобы найти общий знаменатель, можно воспользоваться правилом «НОК» для двух чисел, которые здесь — знаменатели.

Пример нахождения общего знаменателя методом разложения на множители

Это тоже самое. что и выше приведенный «НОК» — только может называться по другому…смайлы

Этот способ может называться как «нахождение общего знаменателя методом разложения на множители»

Либо «метод нахождения наименьшего общего знаменателя» или просто «НОЗ»

Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.

Надо расположить в первую строчку наибольший знаменатель — это 8 и разложить его на множители:

Ниже раскладываем меньший знаменатель :

Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе… это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :

Итого получаем общий знаменатель = 24.

Пример номер 2 подбора общего знаменателя

Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.

Берем больший знаменатель раскладываем его на множители :

Раскладываем меньший знаменатель :

Виртуально исключаем повторяющиеся множители из второго знаменателя — это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :

Итого получаем общий знаменатель 20, двух чисел 4 и 10.

Скопировать ссылку

Как найти общий знаменатель дробей онлайн

Прежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.

Пусть это будут два знаменателя 20 и 6.

Раскладываем больший знаменатель на множители :

Раскладываем на множители второй знаменатель :

Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.

Умножаем больший знаменатель на 2 :

Итого получаем их общий знаменатель 40.

Переходим к нахождению общего знаменателя онлайн

Вводим первый знаменатель 20.

Нажимаем кнопку «НОК»

Набираем второй знаменатель 8.

Нажимаем равно — «=»

Получаем результат нахождения общего знаменателя онлайн :

Скопировать ссылку

Что такое

Но, что же такое «наименьший общий знаменатель»

Определение, что же такое «наименьший общий знаменатель»

Наименьший общий знаменатель двух знаменателей — это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.

Скопировать ссылку

Формула наименьшего общего кратного

Для нахождения «наименьшего общего знаменателя» двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
Сравниваем две строки и удаляем из второй все цифры, которые повторяются в первой строчке.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.

Разложим больший знаменатель на множители :

Разложим второй знаменатель на множители :

Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.

Умножаем больший знаменатель на 3.

Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.

Скопировать ссылку

Как найти

Раскладываем большее число на множители :

Раскладываем меньшее число на множители :

Исключаем повторяющиеся цифры — это одна 2 и 3, остается 2.

Умножаем большее число на 2.

Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.

Теперь проверим правильность нахождения «нок» на калькуляторе.

Открываем калькулятор.

Набираем первое число – пусть это будет число 12

Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.

После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.

И нам отсеется нажать кнопку равно!

И видим результат нахождения наименьшего общего кратного на калькуляторе…

Скопировать ссылку

Как найти общий знаменатель трех дробей

Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!

Для подтверждения данного тезиса — давайте решим задачку/пример.

Задача/пример найдите общий знаменатель для трех дробей.

У нас даны три дроби и у них у всех три разных знаменателя :

Для такой простой задачи можно в уме посчитать… перебором…, а потом подтвердим наше решение через «НОК».

5 — не подходит — не делится на 3.

10 — не подходит — не делится на 3.

15 — не подходит, не делится на 2.

20 — не подходит, не делится на 3.

25 — не подходит, не делится на 2.

, делится на все без остатка. .. мы нашли общий знаменатель для трех дробей, методом перебора

Найдем общий знаменатель для трех дробей на калькуляторе через НОК.

Набираем первый знаменатель — 2.

Нажимаем кнопку — «НОК».

Набираем второй знаменатель — 3.

Нажимаем равно — «=».

Далее опять нажимаем — «НОК».

Набираем третий знаменатель — 6.

Нажимаем равно — «=».

Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.

Скопировать ссылку

Как найти общий знаменатель дробей с разными знаменателями

Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели — иначе, зачем искать общий знаменатель — ведь знаменатели одинаковые.

Вариант разложения знаменателей на множители.

Вариант нахождения общего знаменателя с помощью НОК и т. д

Теги :
как найти общий знаменатель
как найти наименьший общий знаменатель
как найти общий знаменатель дробей с разными
как найти общий знаменатель у дробей
как найти наименьший общий знаменатель дробей
найдите общий знаменатель дробей
найти общий знаменатель онлайн
найти общий знаменатель чисел
найдите наименьшее общее кратное знаменателей
как быстро найти общий знаменатель
как найти общий знаменатель дробей класс
как найти наибольший общий знаменатель
найти общее кратное знаменателей дробей
найдите наименьший общий знаменатель дробей
найти общий знаменатель дробей онлайн
найдите наименьший общий знаменатель дробей
как найти общий знаменатель при сложении
калькулятор найти общий знаменатель
как найти общий знаменатель двух дробей
как быстро найти общий знаменатель у дроби с большим знаменателем
общий знаменатель дробей это такое простыми словами
общий знаменатель трех дробей онлайн
решение общего знаменателя

Наибольший общий делитель чисел 9 и 16 (НОД 9, 16)

Вы ищете НОД чисел 9 и 16? Так как вы находитесь на этой странице, я так думаю! В этом кратком руководстве мы расскажем, как вычислить наибольший общий делитель для любых чисел, которые вам нужно проверить. Давайте прыгать!

Хотите быстро узнать или показать учащимся, как найти НГК двух или более чисел? Включи это очень быстрое и веселое видео прямо сейчас!

Во-первых, если вы торопитесь, вот ответ на вопрос «каков GCF 9 и 16?» :

GCF 9 и 16 = 1

Что такое наибольший общий делитель?

Проще говоря, GCF набора целых чисел — это наибольшее положительное целое число (т. е. целое число, а не десятичное), которое без остатка делится на все числа набора. Он также широко известен как:

• Наибольший общий знаменатель (GCD)
• Наивысший общий множитель (HCF)
• Наибольший общий делитель (НОД)

Существует несколько различных способов расчета GCF набора чисел в зависимости от того, сколько чисел у вас есть и насколько они велики.

Для меньших чисел вы можете просто посмотреть на множители или кратные для каждого числа и найти их наибольшее общее кратное.

Для 9 и 16 эти коэффициенты выглядят следующим образом:

• Коэффициенты для 9: 1 , 3 и 9
• Коэффициенты для 16: 1 , 2, 4, 8 и 16

Простые множители

По мере того, как числа становятся больше, или если вы хотите сравнить несколько чисел одновременно, чтобы найти GCF, вы можете увидеть, что перечисление всех множителей стало бы слишком большим. Чтобы исправить это, вы можете использовать простые множители.

Перечислите все простые множители для каждого числа:

• Простые множители для 9: 3 и 3
• Простые множители для 16: 2, 2, 2 и 2

Теперь, когда у нас есть список простых факторы, необходимо найти такие, которые являются общими для каждого числа.

Поскольку нет общих простых множителей между приведенными выше числами, это означает, что наибольший общий множитель равен 1:

GCF = 1

Найдите GCF с помощью алгоритма Евклида

Окончательный метод расчета GCF 9и 16 — использовать алгоритм Евклида. Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами НОД.

Если вы хотите узнать больше об алгоритме и, возможно, попробовать его самостоятельно, загляните на страницу Википедии.

Надеюсь, сегодня вы немного изучили математику и поняли, как вычислять НОД чисел. Возьмите карандаш и бумагу и попробуйте сами. (или просто воспользуйтесь нашим калькулятором НОД — мы никому ничего не скажем!)

Процитируйте, дайте ссылку или ссылку на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• Наибольший общий делитель чисел 9 и 16

• «Наибольший общий делитель чисел 9 и 16». VisualFractions.com . По состоянию на 19 апреля 2023 г. http://visualfractions.com/calculator/greatest-common-factor/gcf-of-9-and-16/.

• «Наибольший общий делитель чисел 9 и 16». VisualFractions.com , http://visualfractions. com/calculator/greatest-common-factor/gcf-of-9-and-16/. По состоянию на 19 апреля 2023 г.

• Наибольший общий делитель чисел 9 и 16. VisualFractions.com. Получено с http://visualfractions.com/calculator/greatest-common-factor/gcf-of-9-and-16/.

ЖК-калькулятор. Найти наименьший общий знаменатель

Создано Ханной Памула, доктором философии

Отредактировано Домиником Черниа, доктором философии и Джеком Боуотером

Последнее обновление: 02 февраля 2023 г.

• Какой наименьший общий знаменатель? ЖК по математике
• Как найти наименьший общий знаменатель?
• Способ 1. Список кратных
• Способ 2. Использование простой факторизации
• Способ 3. Использование наибольшего общего делителя (множителя)
• Метод 4. Чертежный стол/сетка/лесенка/торт
• Наименьший общий знаменатель на практике
• Как пользоваться ЖК-калькулятором?
• Реальные применения наименьшего общего знаменателя

Добро пожаловать в ЖК-калькулятор — интуитивно понятный инструмент, который поможет вам найти наименьший общий знаменатель . Все, что вам нужно сделать, это ввести до пяти дробей , и мы рассчитаем LCD и эквивалентные дроби с этим знаменателем. Довольно просто, да? 😉

Однако, если вы хотите сначала узнать , что такое наименьший общий знаменатель или , как найти наименьший общий знаменатель вручную ✍️ — мы здесь для вас тоже. Прокрутите вниз и прочитайте нашу короткую и информативную статью о наименьшем общем знаменателе!

Какой наименьший общий знаменатель? LCD в математике

Наименьший общий знаменатель, также известный как наименьший общий знаменатель, равен наименьшему общему кратному знаменателей данного набора . Пытаетесь отличить LCD от LCM? Сначала проверьте наш калькулятор LCM.

Обычно мы ищем наименьший общий знаменатель, когда хотим выполнить операцию над дробями, например, сложить дроби (и вычесть) или сравнить дроби. Например:

• ЖК-дисплей 1/2 и 1/3 равен 6, потому что LCM(2, 3) = 6;

• Зная ЖКИ, можно найти дроби эквивалентные вашей 1/2 и 1/3 , со знаменателем, равным найденному LCD:

  • 1/2 = 3/6

  • 1/3 = 2/6

• Теперь легко складывать дроби, вычитать их или сравнивать:

  • 3/6 + 2/6 = 5/6
  • 3/6 - 2/6 = 1/6
  • 3/6 > 2/6

Однако, если вы только что загуглили вопрос « Что такое LCD? «, и вы искали определение с наименьшим общим знаменателем, результаты поиска могут вас немного удивить 😮. Аббревиатура LCD также расшифровывается как жидкокристаллический дисплей — тип дисплея, который мы используем в наших компьютерах 💻, экраны телевизоров 📺 , цифровые фотоаппараты 📽️, часы ⌚ и смартфоны 📱. Так что в следующий раз попробуйте « Что такое LCD в математике? » вместо 😉

🙋 Узнайте больше об операциях с дробями с помощью нашего калькулятора умножения дробей и калькулятора сложения дробей!

Как найти наименьший общий знаменатель?

Что ж, самый простой и понятный способ — воспользоваться нашим ЖК-калькулятором. Именно поэтому вы здесь, верно? 😉

Шутки в сторону — мы очень ценим, что вы хотите научиться находить наименьший общий знаменатель . Есть несколько методов, и мы опишем четыре из них здесь. Итак, давайте представим их на относительно простом примере:

Предположим, что у нас есть три дроби: 1/2 , 3/8 и 11/12 . Какова стоимость ЖК? Какие равные дроби имеют одинаковые знаменатели?

Во-первых, нам нужно найти наименьший общий знаменатель наших дробей.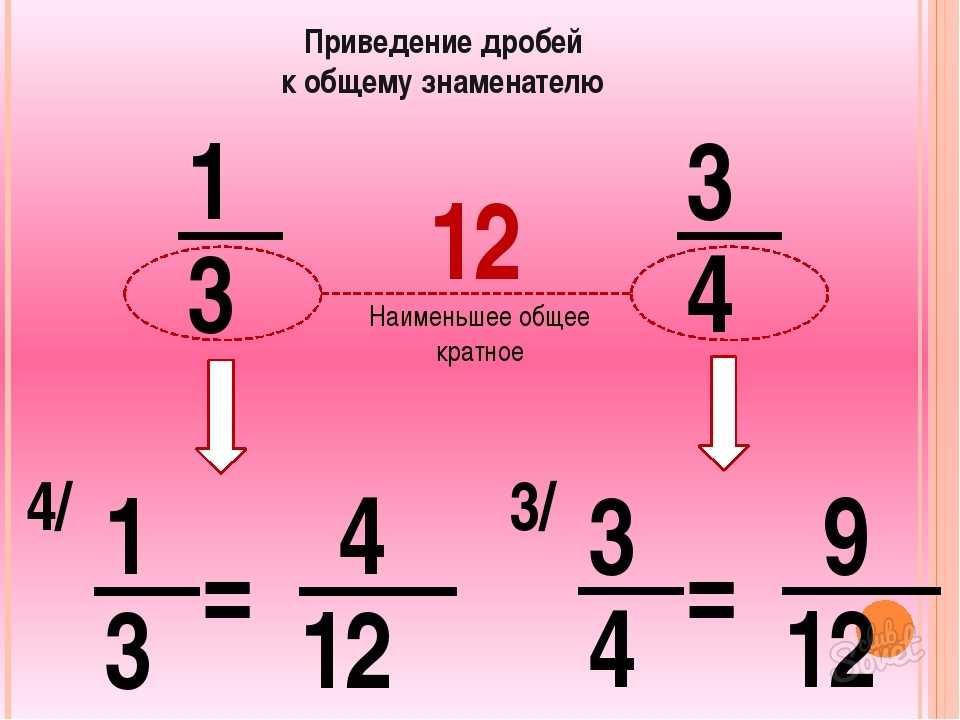 Прочитайте о четырех методах ниже и выберите тот, который вам больше нравится.

Метод 1. Список кратных

Список кратных является методом полного перебора. Это может быть полезно в особых случаях, например, если числа относительно малы. Итак, как найти наименьший общий знаменатель? Составьте список кратных каждому числу, пока не найдете первое общее кратное всех чисел :

• кратные 2:
  2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 , 26, 28..
• Кратность 12:
  12, 24 , 36, 48, 60 …
• Кратность 8:
  8, 16, 24 , 32, 40, 48 …

Обычно это не рекомендуемый метод. Представьте себе перечисление общих знаменателей 2 и 1000 — это не имеет особого смысла, не так ли? 🙂

Способ 2. Использование простой факторизации

Другим методом нахождения наименьшего общего знаменателя является метод разложения на простые множители (подробнее о котором вы можете прочитать в нашем калькуляторе на простые множители 😉):

1. Запишите все числа как произведение их простых множителей :
   • Разложение 2 на простые множители:
     2 = 2¹
   • Разложение числа 12 на простые множители:
     2 * 2 * 3 = 2² * 3¹
   • Разложение числа 8 на простые множители:
     2 * 2 * 2 = 2³
2. Найдите максимальную степень каждого простого числа:
   • 2³ , 3¹
3. Умножьте этих значений вместе:
   • 2³ * 3¹ = 24

Метод 3.

Вы можете рассчитать НОД по значению наибольшего общего делителя (НОД) (как в нашем калькуляторе НОД):

НОД(a,b) = |a * б| / GCF(a,b)

где |a * b| является абсолютным значением a * b .

1. Подставляем первые два числа (2 и 8) в формулу:
   • LCD(2, 8) = |2 * 8| / GCF(2, 8) .
   Мы знаем, что GCF(2, 8) = 2 , поэтому:
   • ЖКД(2, 8) = 16 / 2 = 8
2. Найдите ЖК-дисплей результата предыдущего шага (т. е. 8) и следующего числа в списке, 12:
   • LCD(12, 8) = |12 * 8| / GCF(12, 8)
   Мы вычисляем, что GCF(12, 8) = 4 , поэтому:
   • ЖКД(12, 8) = 96 / 4 = 24

Метод 4. Чертежный стол/сетка/лестница/торт

Последний метод – это метод лестницы. Многим учащимся нравится этот метод, так что попробуйте его, и, возможно, у вас появится новый фаворит:

1. Начните с написания всех ваших чисел рядом друг с другом:

2. Найдите простое число, которое может делиться на не менее двух ваших номеров (без остатка).

Запишите это простое число в левой части:

3. Разделите ваши исходные числа на простые числа и запишите частные под исходными числами. Если ваше число не делится без остатка, просто напишите это число еще раз:
.

4. Повторяйте, пока вся таблица не будет заполнена:

2 2 8 12
2 1 4 6
2 1 2 3
1 1 3

5. Найдите ЖК-дисплей, умножив все значения в оранжевой букве «L» вокруг вашего стола/торта:

   2 * 2 * 2 * 1 * 1 * 3 = 24

Наименьший общий знаменатель на практике

Теперь, когда вы знаете значение LCD, вы можете перейти ко второму шагу — найти дроби, которые эквивалентны вашим основным дробям, но с тем же знаменателем — 24 в нашем случае:

• 1/2 = ?/24 , чтобы получить 24 в знаменателе, умножьте дробь на 12/12 (поскольку 24/2 = 12):
  • 1/2 = 1/2 * 12/12 = 12/24
• 3/8 = ?/24 , умножьте на 3/3 , чтобы получить 24 в качестве нижнего числа:
  • 3/8 = 3/8 * 3/3 = 9/24
• 11/12 = ?/24 , так как 24/12 = 2, умножьте дробь на 2/2 :
  • 11/12 = 11/12 * 2/2 = 22/24

И все! После прочтения вы (надеюсь) поняли, что такое наименьший общий знаменатель, и узнали о четырех методах, которые могут помочь вам найти НОК в математике. И что теперь? Пришло время проверить, как работает ЖК-калькулятор!

Как пользоваться ЖК-калькулятором?

Ознакомьтесь с этим пошаговым руководством, если у вас есть какие-либо сомнения относительно того, как использовать наш инструмент:

1. Выберите тип дроби . Если вам нужны простые дроби, оставьте как есть. Если хотя бы одно из ваших чисел является смешанным числом (или целым числом), выберите вариант «смешанный номер». Что такое смешанные числа? Проверьте наш калькулятор смешанных чисел и узнайте о них больше.
2. Введите дроби . Допустим, мы хотим найти ЖК дроби 1/4 и 14/11 . Для первой дроби введите 1 в качестве числителя и 4 в качестве знаменателя; у второго числитель равен 11, а знаменатель равен 14.
3. Успокойся, расслабься и прочитай результат — ЖК-калькулятор сделал свое дело и нашел наименьший общий знаменатель ! Это 28.

Кроме того, инструмент отображает эквивалентные дроби со значением на ЖК-дисплее в качестве знаменателя:

• 1/4 = 7/28 ; и
• 14/11 = 28/22

4. При желании можно даже выбрать вариант «пошаговое решение» . Из него вы узнаете некоторые подробности о том, как найти LCD по математике!

Реальные приложения с наименьшим общим знаменателем

Теперь, когда вы знаете, что такое наименьший общий знаменатель и как его найти, давайте поговорим о некоторых приложениях для ЖК-дисплеев . Мы почти слышим, как вы стонете «Но где я когда-либо буду использовать его?» Не беспокойтесь — наименьший общий знаменатель полезен во многих жизненных ситуациях. Вы можете использовать его в любое время, когда хотите «выровнять» две или более вещи разной длины, например:

• В строительстве🏗️, например, при возведении стены из кирпича или работе с плиткой разной длины;
• В музыке 🎵 — при вычислении наименьшего количества долей для комбинированного ритма; и
• При организации графиков работы 📅 — например, в ситуации, когда у одного сотрудника выходной каждые 6 дней, а у другого каждые 4 дня, можно рассчитать, когда они оба отсутствуют.

  No related posts.