Калькулятор комплексных чисел • Математика • Онлайн-конвертеры единиц измерения
Определения и формулы
Формы представления комплексных чисел
Комплексная плоскость
Представление комплексного числа в полярных координатах
Отношения и операции с комплексными числами
Равенство комплексных чисел
Сопряженное комплексное число
Сложение и вычитание
Умножение
Получение обратного числа и деление
Квадратный корень
Применение комплексных чисел
Определения и формулы
Комплексное число — это число в форме суммы вещественной части и мнимой части a + bi. Символ i или j в электротехнике (инженеры-электрики думают не так, как все остальные!) называется мнимой единицей и определяется равенством i² = –1. Иными словами, i — квадратный корень из минус единицы (√–1).
Вещественная часть представляет собой вещественное число, а мнимая часть — мнимое число, которое является квадратным корнем отрицательного числа. Обычно мнимую часть приводят к форме вещественного числа, умноженного на квадратный корень из минус единицы. Например,
Обычно мнимую часть приводят к форме вещественного числа, умноженного на квадратный корень из минус единицы. Например,
Формы представления комплексных чисел
Комплексная плоскость
В математическом представлении комплексных чисел используются два оператора для обозначения вещественной и мнимой части: Re(z) и Im(z). Как и вещественные числа, которые представляются в виде точек на числовой оси, комплексное число z, представляемое в виде пары вещественных чисел (Re(z), Im(z)), может быть представлено в виде точки в двумерном пространстве, то есть, на плоскости, которая называется комплексной плоскостью. Горизонтальная ось комплексной плоскости соответствует вещественной части комплексного числа, а вертикальная ось соответствует мнимой части. Видно, что числовая ось с вещественными числами — то же самое, что горизонтальная ось комплексной плоскости, так как мнимая часть вещественных чисел нулевая.
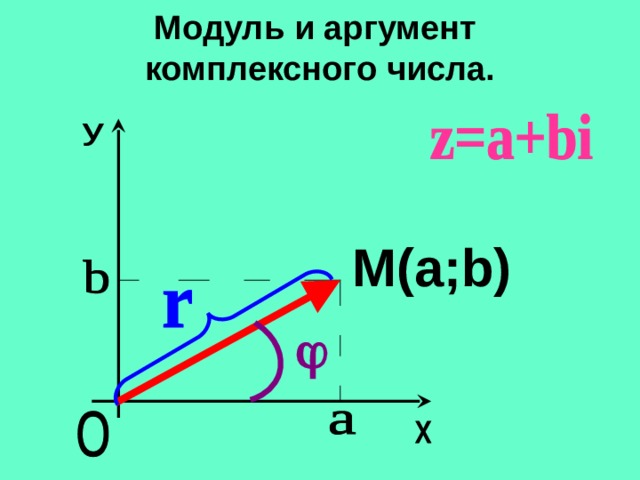
Представление комплексного числа в полярных координатах
Комплексное число z = x + jy = r ∠φ представляется точкой и вектором на комплексной плоскости
Комплексное число z можно также представить в геометрической форме, которая использует другой тип комплексной плоскости, только не в прямоугольных, а в полярных координатах. В этом представлении используются модуль r радиус-вектора от начала координат до комплексной точки z и угол φ между вектором и горизонтальной осью, измеренный в направлении против часовой стрелки. Этот угол называется аргументом.
В этом представлении используются модуль r радиус-вектора от начала координат до комплексной точки z и угол φ между вектором и горизонтальной осью, измеренный в направлении против часовой стрелки. Этот угол называется аргументом.
Модуль (амплитуда) комплексного числа z = x + iy определяется по формуле:
Аргумент (фаза) φ определяется с помощью функции арктангенса с двумя аргументами arctan2(y,x):
Модуль r и аргументφ совместно представляют комплексные числа в тригонометрической форме, так как их сочетание определяет уникальное положение точки, представляющей комплексное число в полярных координатах. Для получения исходных прямоугольных координат пользуются формулой
Формула Эйлера устанавливает связь между тригонометрическими функциями и комплексной экспоненциальной функцией для любого вещественного числа φ:
Формула Эйлера позволяет представить синусоиду в виде комплексной экспоненциальной функции, что удобно использовать во многих областях науки и техники. Геометрическое представление комплексных чисел широко используется в физике, электротехнике и электронике для представления синусоидальных напряжений и токов. В этом представлении вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Геометрическое представление комплексных чисел широко используется в физике, электротехнике и электронике для представления синусоидальных напряжений и токов. В этом представлении вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Комплексные числа, представляющие синусоидальную функцию с амплитудой A, угловой частотой ω и начальной фазой θ, называются фазорами (англ. phasor от phase vector) или комплексными амплитудами. Больше информации о представлении комплексных чисел, фазорах и преобразовании из алгебраической формы в тригонометрическую и обратно вы найдете в нашем Калькуляторе преобразования алгебраической формы комплексного числа в тригонометрическую.
Отношения и операции с комплексными числами
Комплексные числа подчиняются тем же правилам алгебры, что и обычные числа. Мнимая единица i считается константой и если встречается величина i², она заменяется на –1.
Равенство комплексных чисел
Два комплексных числа x + yi и n + mi равны тогда и только тогда, когда x = n и y = m.
Сопряженное комплексное число
Сопряженное комплексное число находят путем изменения знака его мнимой части. Например, такие два числа являются комплексно-сопряженными:
В физике, электротехнике и электронике сопряженные комплексные числа часто обозначаются звездочкой (z*). Пример сопряженных комплексных чисел (щелкните, чтобы посмотреть его в калькуляторе):
Сложение и вычитание
Сумма и разность двух комплексных чисел m + ni и p + qi определяется как
и
То есть, для сложения и вычитания комплексных чисел, нужно отдельно сложить или вычесть их действительные и мнимые части. Примеры (щелкните, чтобы посмотреть в калькуляторе):
Умножение
Два комплексных числа в алгебраической форме умножают путем умножения каждой части одного числа на обе части другого числа с последующим комбинированием результатов в вещественную и мнимую части. При умножении используется определение i² = –1. Например:
Например:
В тригонометрической форме умножение двух комплексных чисел выполнять проще, так как оно сводится к умножению модулей и сложению аргументов, например:
Получение обратного числа и деление
Обратное число к данному ненулевому комплексному числу z = a + bi в алгебраической форме выполняется путем умножения числителя (в данном случае 1) и знаменателя на число, сопряженное числу в знаменателе (в нашем случае — данному комплексному числу) с последующим преобразованием и упрощением:
Деление двух комплексных чисел a + bi и c + di в алгебраической форме выполняется аналогично, с использованием сопряженного комплексного числа в знаменателе:
Как и умножение, деление двух комплексных числе в тригонометрической форме выполнять удобнее, чем в алгебраической. Модуль частного от деления двух чисел определяется путем деления модуля делимого на модуль делителя. Аргумент (угол) частного определяется путем вычитания аргумента делителя из аргумента делимого. Например:
Например:
Квадратный корень
Если мнимая часть комплексного числа отлична от нуля, то квадратные корни этого числа представляют собой пару комплексных чисел с положительным и отрицательным знаками. Положительное число считается главным значением квадратного корня. Этот калькулятор определяет только главное (положительное) значение квадратного корня комплексного числа. Если комплексное число представлено в алгебраической форме, то для вычисления квадратного корня используется следующая формула:
где sgn(y) — функция знака y, определенная следующим образом:
Применение комплексных чисел
Комплексные числа широко используются в науке и технике — в геометрии, теории устойчивости (критерий устойчивости Найквиста — Михайлова, в котором используется построение на комплексной плоскости), в электротехнике и анализе сигналов (периодические сигналы удобно описываются комплексными числами), в квантовой механике, теории относительности и во многих других областях.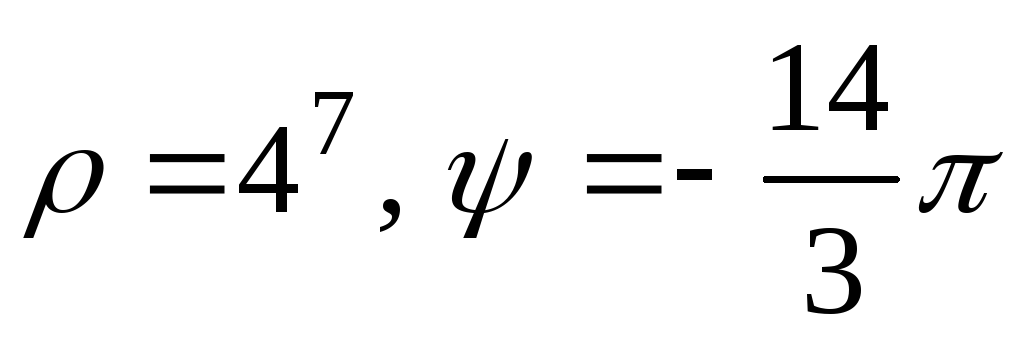 Изобретенные почти 200 лет назад кватернионы, представляющие собой расширение комплексных чисел, используются в компьютерной графике, инерциальной навигации и теории управления.
Изобретенные почти 200 лет назад кватернионы, представляющие собой расширение комплексных чисел, используются в компьютерной графике, инерциальной навигации и теории управления.
Автор статьи: Анатолий Золотков
Комплексные корни и степени чисел онлайн
|
|
|
|||||||||||||||||||||||||||||||||||
Вычислить выражение комплексные числа.
 Комплексные числа и алгебраические действия над ними
Комплексные числа и алгебраические действия над нимиРассмотрим квадратное уравнение .
Определим его корни .
Не существует действительного числа, квадрат которого равен -1. Но если формулой определить оператор
В общем виде комплексное число имеет вид
z = x + iy ,
где x, y – вещественные
числа, – мнимая единица. В ряде прикладных
наук, например, в электротехнике, электронике, теории сигналов мнимая единица
обозначается через j . Вещественные числа x = Re{z} и y = Im{ z} называются вещественной и мнимой частями числа z. Выражение называется алгебраической
формой записи комплексного числа.
Любое действительное число есть частный случай комплексного числа в виде . Мнимое число тоже частный случай комплексного числа .
Определение множества комплексных чисел С
Это выражение читается следующим образом: множество С , состоящее из элементов , таких что x и y принадлежат множеству действительных чисел R и — это мнимая единица. Отметим, что и т.д.
Два комплексных числа и равны, если и только если равны их действительные и мнимые части, т.е. и .
Комплексные числа и функции широко используются в науке и технике, в частности, в механике, анализе и расчете цепей переменного тока, аналоговой электронике, в теории и обработке сигналов, в теории автоматического управления и др. прикладных науках.
- Арифметика комплексных чисел
Сложение двух комплексных чисел состоит в сложении их действительных и мнимых частей, т.е.
Соответственно разность двух комплексных чисел
Комплексное число называется комплексно сопряженным числу z
= x + iy.
Комплексно сопряженные числа z и z * отличаются знаками мнимой части. Очевидно, что
.
Любое равенство между комплексными выражениями остается справедливым, если в этом равенстве всюду i заменить на — i , т.е. перейти к равенству сопряженных чисел. Числа i и – i алгебраически неразличимы, поскольку .
Произведение (умножение) двух комплексных чисел может быть вычислено следующим образом:
Деление двух комплексных чисел:
Пример :
- Комплексная плоскость
Комплексное число графически можно представить в прямоугольной системе координат. Зададим в плоскости прямоугольную систему координат (x, y).
На оси Ox будем располагать действительные части x , она называется действительной (вещественной) осью , на оси Oy –мнимые части y комплексных чисел. Она носит
название мнимой оси . При этом каждому комплексному числу соответствует
определенная точка плоскости, и такая плоскость называется комплексной
плоскостью .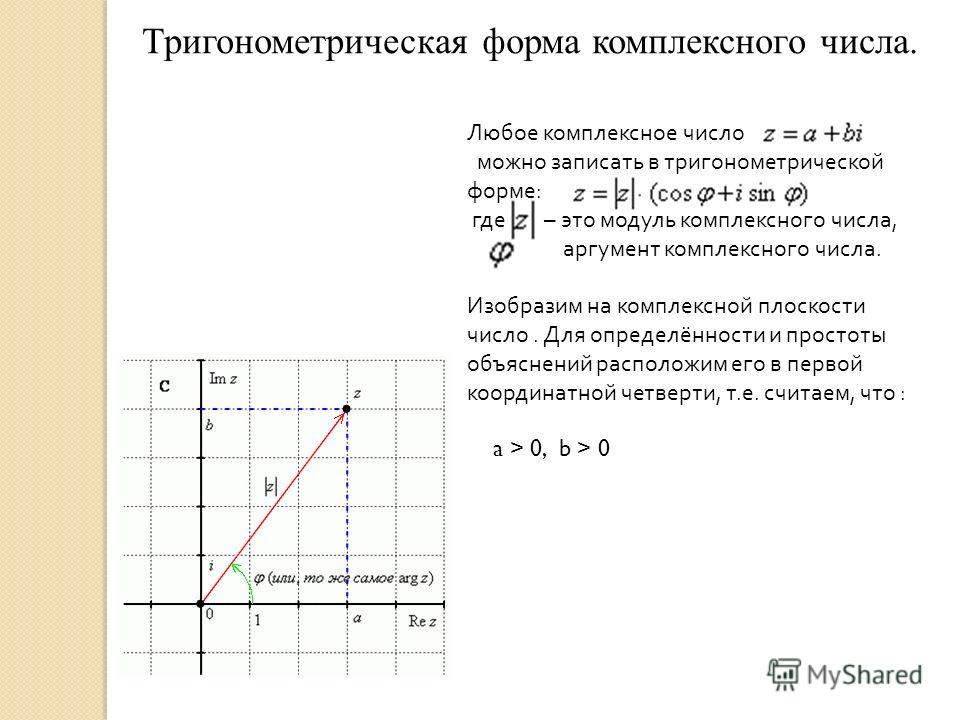 Точке А комплексной плоскости будет соответствовать
вектор ОА .
Точке А комплексной плоскости будет соответствовать
вектор ОА .
Число x называется абсциссой комплексного числа , число y – ординатой .
Пара комплексно сопряженных чисел отображается точками, расположенными симметрично относительно действительной оси.
Если на плоскости задать полярную систему координат , то каждое комплексное число z определяется полярными координатами . При этом модуль числа – это полярный радиус точки, а угол — её полярный угол или аргумент комплексного числа z .
Модуль
комплексного числа всегда неотрицательный. Аргумент комплексного числа не
определяется однозначно. Главное значение аргумента должно удовлетворять
условию . Каждой точке комплексной плоскости
соответствует также общее значение аргумента .
Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент
числа нуль не определен.
Аргумент
числа нуль не определен.
Главное значение аргумента определяют по выражениям:
Очевидно, что
При этом
, .
Представление комплексного числа z в виде
называется тригонометрической формой комплексного числа.
Пример .
- Показательная форма комплексных чисел
Разложение в ряд Маклорена для функций действительного аргумента имеет вид:
Для экспоненциальной функции комплексного аргумента z разложение имеет аналогичный характер
.
Разложение в ряд Маклорена для экспоненциальной функции мнимого аргумента можно представить как
Получившееся тождество называется формулой Эйлера .
Для отрицательного аргумента оно имеет вид
Комбинируя эти выражения, можно определить следующие выражения для синуса и косинуса
.
Пользуясь формулой Эйлера, из тригонометрической формы представления комплексных чисел
можно получить показательную (экспоненциальную,
полярную) форму комплексного числа, т. е. его представление в виде
е. его представление в виде
,
где — полярные координаты точки с прямоугольными координатами (x, y ).
Число, сопряженное комплексному числу , в показательной форме записывается следующим образом .
Для показательной формы легко определить следующие формулы умножения и деления комплексных чисел
Т.е., в показательной форме произведение и деление комплексных чисел выполняется проще, чем в алгебраической форме. При умножении модули сомножителей перемножаются, а аргументы складываются. Это правило распространяется на любое число сомножителей. В частности, при умножении комплексного числа z на i вектор z поворачивается против часовой стрелки на 90
При делении модуль числителя делится на модуль знаменателя, и из аргумента числителя вычитается аргумент знаменателя.
Используя показательную форму комплексных чисел, можно получить выражения для известных тригонометрических тождеств. Например, из тождества
с помощью формулы Эйлера можно записать
Приравнивая действительную и мнимую части в данном выражении, получаем выражения для косинуса и синуса суммы углов
- Степени, корни и логарифмы комплексных чисел
Возведение комплексного числа в натуральную степень n производится по формуле
Пример .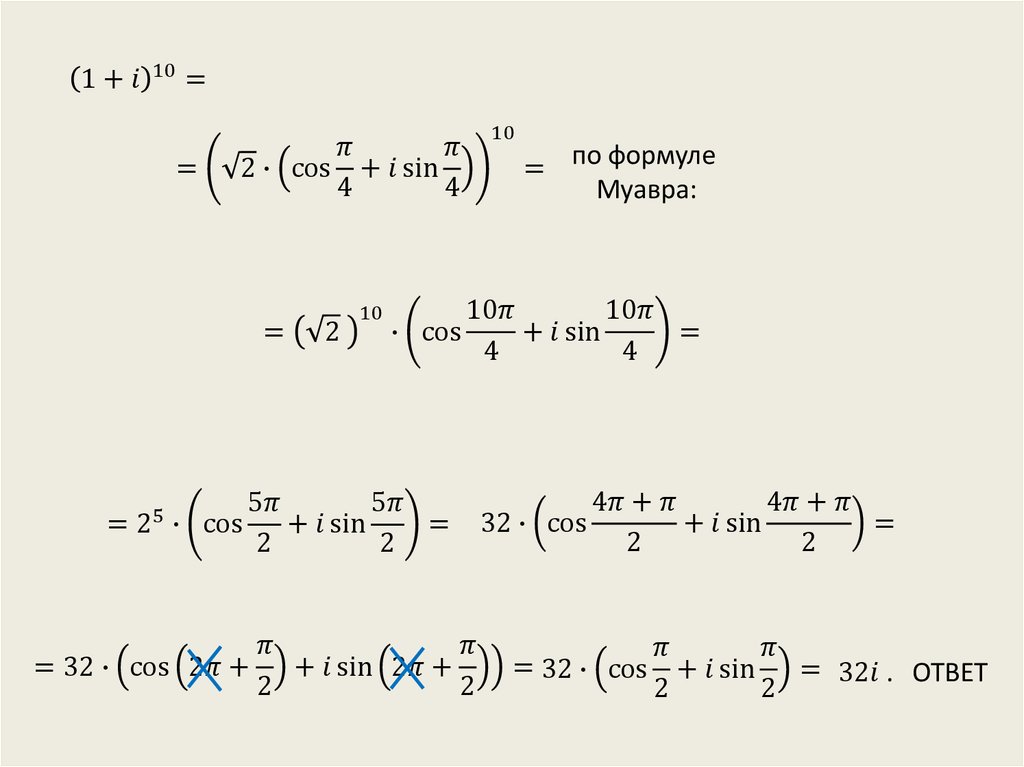 Вычислим .
Вычислим .
Представим число в тригонометрической форме
’
Применяя формулу возведения в степень, получим
Положив в выражении значение r = 1, получим так называемую формулу Муавра , при помощи которой можно определять выражения синусов и косинусов кратных углов.
Корень n –й степени из комплексного числа z имеет n различных значений, определяемых по выражению
Пример . Найдем .
Для этого выразим комплексное число () к тригонометрической форме
.
По формуле вычисления корня из комплексного числа, получаем
Логарифм комплексного числа z – это число w , для которого . Натуральный логарифм комплексного числа имеет бесконечное множество значений и вычисляется по формуле
Состоит
из действительной (косинусоидальной) и мнимой (синусоидальной) части. Такое
напряжение можно представлять как вектор длиной U m , начальной фазой (углом) ,
вращающийся с угловой скоростью ω .
При этом если комплексные функции складываются, то складываются их вещественные и мнимые части. Если комплексная функция умножается на константу или вещественную функцию, то её вещественная и мнимая части умножаются на тот же множитель. Дифференцирование / интегрирование такой комплексной функции сводится к дифференцированию / интегрированию вещественной и мнимой части.
Например, дифференцирование выражения комплексного напряжения
заключается в умножении его на iω — вещественная часть функции f(z), а – мнимая часть функции. Примеры: .
Значение z изображается точкой в комплексной плоскости z, а соответствующее значение w — точкой в комплексной плоскости w . При отображении w = f(z) линии плоскости z переходят в линии плоскости w , фигуры одной плоскости в фигуры другой, но формы линий или фигур могут существенно измениться.
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца.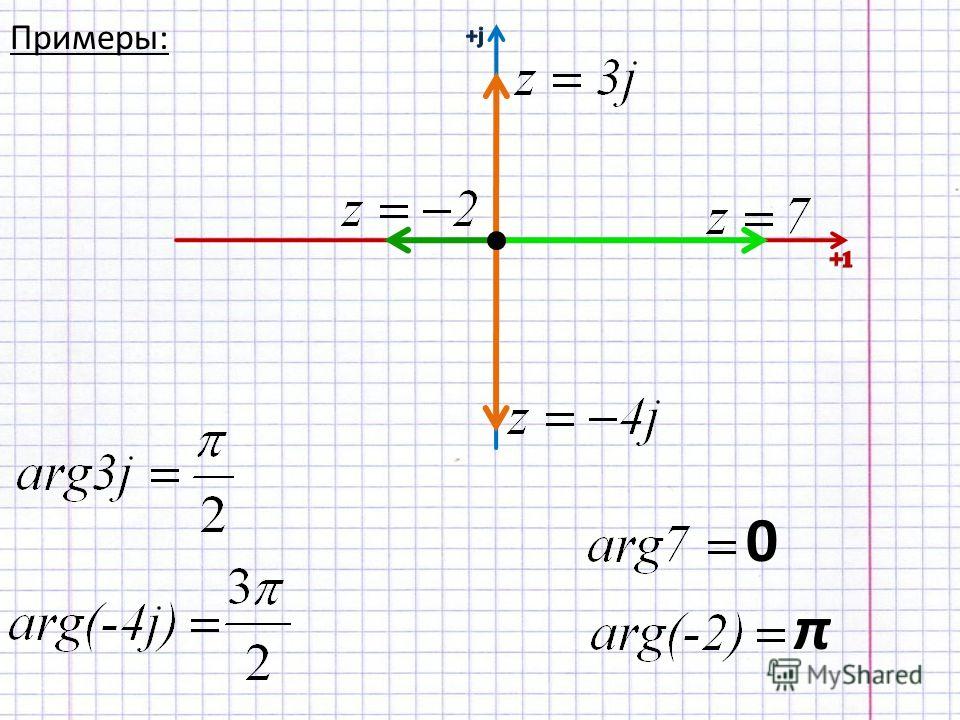 Как правильно сформулировать вопрос в процессе гадания
Как правильно сформулировать вопрос в процессе гадания
«Комплексные числа» — Алгебра, 10 класс
Результаты авторизованых пользователей
| Название теста | Дата | Результат | Пользователь |
|---|---|---|---|
| Информатика / Тест с ответами по информатике “Отношения между множествами” для 6 класса | 09-30-2022 05:41:27 am | 9/20 | Гульсимя Райманова |
| История / Тест с ответами по истории России: “Отечественная война 1812 г.” 9 класс | 09-29-2022 05:02:10 pm | 17/20 | Bepa PaHDa |
| Литература / Тест с ответами: “Олеся” А.И.Куприн | 09-29-2022 04:40:02 pm | 17/20 | Анастасия Баканова |
| Физика / Тест по физике с ответами: “Прямолинейное равномерное движение” 9 класс | 09-29-2022 12:46:31 pm | 15/20 | Ваня Пономарёв |
| География / Тест с ответами: “Геополитика. Понятие и концепция “ | 09-28-2022 08:57:20 pm | 11/20 | Геннадій Ясько |
Все результаты
#1.
 Какое число не является мнимой единицей
Какое число не является мнимой единицейA. 7i
A. 7iB. 2i
B. 2iC. 4
C. 4#2. Чему равна сумма и произведение двух сопряженных чисел
A. действительному числу
A. действительному числуB. мнимому числу с ненулевой действительной частью
B. мнимому числу с ненулевой действительной частьюC. мнимому числу
C. мнимому числу#3. Что является вещественной частью в выражении m + ni
A. i
A. iB. m
B. mC. n
C. n#4. Произведение чисел (1-2i)(3+4i)
A. 3-8i
A. 3-8i B. 11-2i
11-2i
C. 11+2i
C. 11+2i#5. Результатом произведения чисел (3+6i)(3-6i) является число
A. 28
A. 28B. 45
B. 45C. 45i
C. 45i#6. Произведение чисел (3-2i)(2+5i)
A. 11-16i
A. 11-16iB. 16+11i
B. 16+11iC. 6-10i
C. 6-10i#7. Найдите модуль комплексного числа 2+3i
A. 13
A. 13B. √13
B. √13C. √5
C. √5#8. Cуммой чисел (2-9i)+(6-i) является
A. 8+10i
A. 8+10iB. 8-10i
B. 8-10i C. -7+5i
-7+5i
#9. Комплексно-сопряженным для числа 2-8i является
A. -2+8i
A. -2+8iB. 8-2i
B. 8-2iC. 2+8i
C. 2+8i#10. Чему равен i
A. √-1
A. √-1B. √4
B. √4C. √9
C. √9#11. Чему равен модуль комплексного числа z = 5 – 3i
A. √17
A. √17B. √34
B. √34C. √6
C. √6#12. Результатом произведения чисел (5+2i)(5-2i) является число
A. 29i
A. 29iB. 29
B. 29C. 21
C. 21#13. Чему равно частное комплексных чисел 4 + 5i и 3 + 4i
A.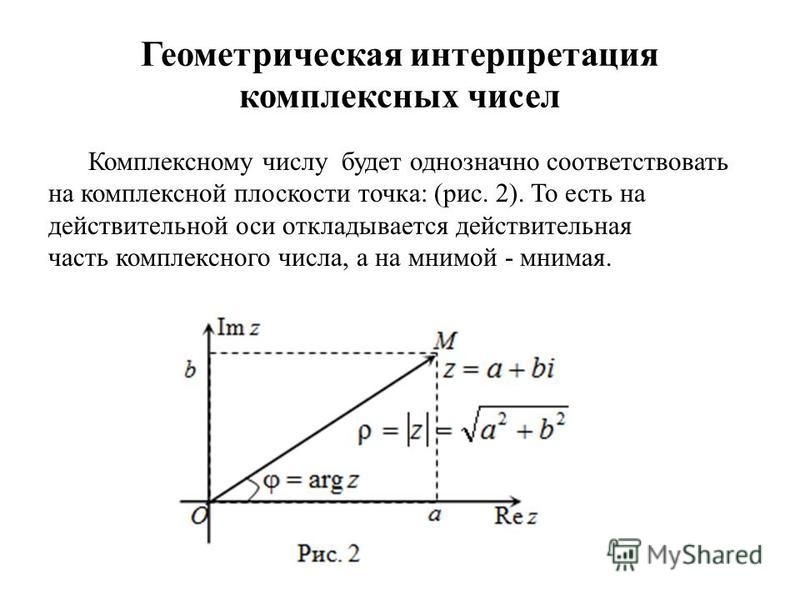 12/27 – 6/19 i
12/27 – 6/19 i
B. 4/31 + 2/53 i
B. 4/31 + 2/53 iC. 32/41 + 1/41 i
C. 32/41 + 1/41 i#14. Про каких условиях два комплексных числа равны
A. x1 > x2, y1 > y2
A. x1 > x2, y1 > y2B. x1 < x2, y1 < y2
B. x1 < x2, y1 < y2C. x1=x2, y1=y2
C. x1=x2, y1=y2#15. Чему равна ReZ комплексного числа Z=-3+5i
A. 5
A. 5B. -3
B. -3C. 3
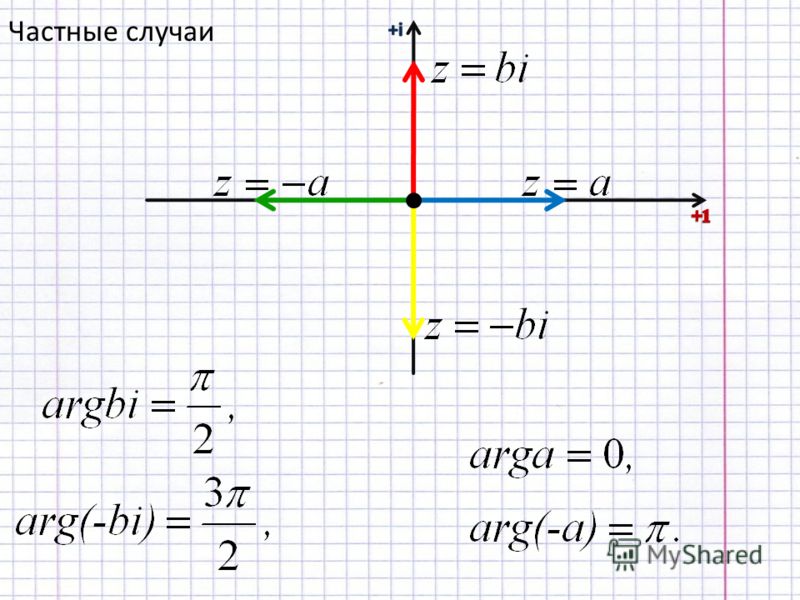
C. 3#16. Что означает символ φ
A. аргумент комплексного числа
A. аргумент комплексного числаB. интеграл
B. интеграл C. мнимую единицу
мнимую единицу
#17. Какой буквой обозначается множество действительных чисел
A. R
A. RB. N
B. NC. Т
C. Т#18. Найдите модуль комплексного числа 7-4i
A. 65
A. 65B. √11
B. √11C. √65
C. √65#19. Кто ввел обозначение i для мнимой единицы
A. Эйлер
A. ЭйлерB. Пифагор
B. ПифагорC. Декарт
C. Декарт#20. На какие комплексные множители можно разложить число 10
A. 3 + 7i и 3 – 7i –
A. 3 + 7i и 3 – 7i –B. 9 + 1i и 9 – 1i –
B. 9 + 1i и 9 – 1i – C. 1 + 3i и 1 – 3i
1 + 3i и 1 – 3i
Показать результаты
Оцените тест после прохождения!
Нажмите на звезду, чтобы оценить!
Средняя оценка 0 / 5. Количество оценок: 0
Оценок пока нет. Поставьте оценку первым.
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
Помощь в написании работы
Вычислить действительную часть комплексного числа
Информация обновлена:
16 декабря 2019
Время на чтение:
9 минут
11
Содержание
- Введите комплексное выражение, которое необходимо вычислить
- Правила ввода комплексных выражений с примерами:
- Видео пример
- Формы
- Изображение
- Как пользоваться калькулятором
- Ввод комплексных чисел
- Поддерживаемые операции и математические функции
- Примеры корректных выражений
- Комплексные числа
- Примеры комплексных чисел
- Основные действия с комплексными числами
- Примеры
- Другие действия над комплексными числами
- Примеры
- Формы представления комплексных чисел
- Пример:
Введите комплексное выражение, которое необходимо вычислить
Выполняет простые операции с комплексными числами. 7 — возведение в степень (5+6j) + 8j — сложение (5+6j) — (7-1j) — вычитание conjugate(1+4j) или conj(1+4j) Сопряженное (комплексно-сопряженное) число для (1 + 4j)
7 — возведение в степень (5+6j) + 8j — сложение (5+6j) — (7-1j) — вычитание conjugate(1+4j) или conj(1+4j) Сопряженное (комплексно-сопряженное) число для (1 + 4j)
Можно использовать следующие функции от x (например, x = 1 + 2.5j):
Правила ввода выражений и функций
Видео пример
© Контрольная работа РУ — калькуляторы онлайн
В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ mathbb $.
Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = sqrt <-1>$, числа $ a,b in mathbb $ вещественные.
Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ mathbb subset mathbb $. $
$
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Видим, что $ a,b in mathbb
$ расположены на соответствующих осях плоскости.Комплексное число $ z = a+ib $ представляется в виде вектора $ overline $.
Аргумент обозначается $ varphi $.
Модуль $ |z| $ равняется длине вектора $ overline $ и находится по формуле $ |z| = sqrt $
Аргумент комплексного числа $ varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.
| Пример 2 |
| Решение |
Помогла статья? Поставьте оценку
0 / 5. 0
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.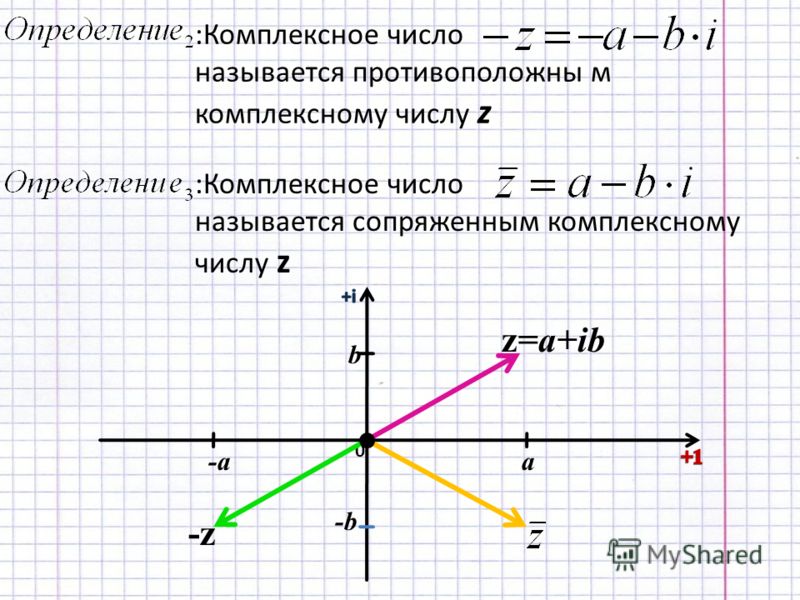 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
калькулятор комплекса номера • Математика • Блок Pengonversi Online
Определения и формулы
Представление комплексных номеров
Кортезианская комплексная плоскость
Полярная комплексная плоскость
Отношения и операции
Эквасия комплексных номеров
Комплексные сопряжения
и добавление и добавление и добавление и добавление и добавление и добавление и добавление и добавление и добавление.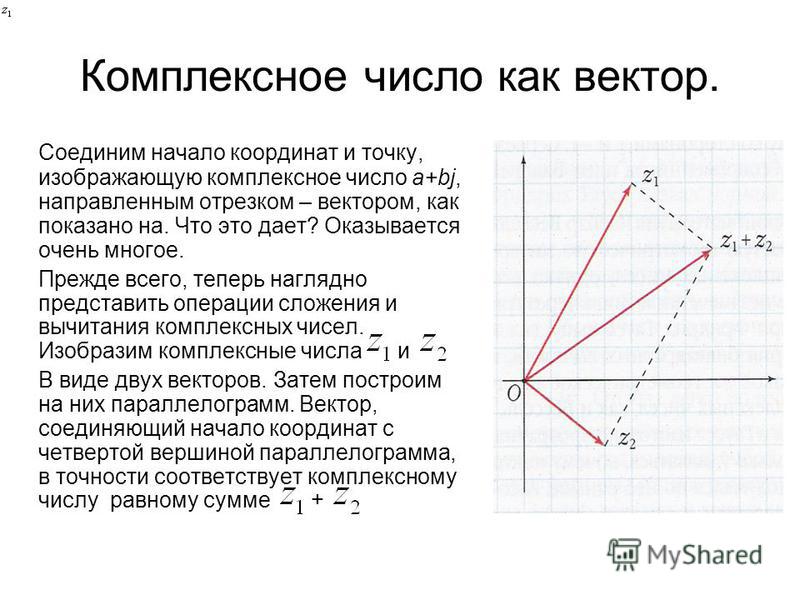 вычитание
вычитание
Умножение
Обратное действие и деление
Извлечение квадратного корня
Приложения
Определения и формулы
Комплексное число — это число в виде суммы действительной части и мнимой части a + bi . Символ i или j в электротехнике (инженеры-электрики мыслят иначе, чем в остальном мире!) называется мнимой единицей и определяется уравнением i ² = –1. Другими словами, i — это квадратный корень из минус единицы (√–1).
Действительная часть — это действительное число, а мнимая часть — это мнимое число, представляющее собой квадратный корень из отрицательного числа. Обычно мнимую часть приводят к действительному числу, умноженному на квадратный корень из минус единицы. Например,
Представление комплексных чисел
Декартова комплексная плоскость
Математическая запись комплексных чисел использует два оператора для разделения комплексного числа на его действительную и мнимую части: Re( z ) и Im( z ). Точно так же, как все действительные числа можно рассматривать как точки на числовой прямой, комплексное число z , которое отождествляется с упорядоченной парой действительных чисел (Re( z ), Im( z )), может быть представлено точкой в двумерном пространстве, называемом комплексной плоскостью. Горизонтальная ось комплексной плоскости соответствует действительной части комплексного числа, а вертикальная ось соответствует мнимой части. Мы можем видеть, что прямая с действительными числами совпадает с действительной (горизонтальной) осью комплексной плоскости, потому что мнимая часть действительных чисел равна нулю.
Точно так же, как все действительные числа можно рассматривать как точки на числовой прямой, комплексное число z , которое отождествляется с упорядоченной парой действительных чисел (Re( z ), Im( z )), может быть представлено точкой в двумерном пространстве, называемом комплексной плоскостью. Горизонтальная ось комплексной плоскости соответствует действительной части комплексного числа, а вертикальная ось соответствует мнимой части. Мы можем видеть, что прямая с действительными числами совпадает с действительной (горизонтальной) осью комплексной плоскости, потому что мнимая часть действительных чисел равна нулю.
Полярная комплексная плоскость
Комплексное число z = x + jy = r ∠φ представлено в виде точки и вектора на комплексной плоскости
Комплексное число z также может быть3 представлена в полярной системе координат, в которой используется другой тип комплексной плоскости в полярной системе координат. Это представление использует величину (модуль) r вектора, начинающегося в начале координат и заканчивающегося в комплексной точке z и угол φ между этим вектором и положительной вещественной осью, измеренный по часовой стрелке. Этот угол называется аргументом.
Это представление использует величину (модуль) r вектора, начинающегося в начале координат и заканчивающегося в комплексной точке z и угол φ между этим вектором и положительной вещественной осью, измеренный по часовой стрелке. Этот угол называется аргументом.
Величина комплексного числа z = x + iy определяется следующим образом:
функция:
Величина r и аргумент φ вместе представляют комплексные числа в полярной форме, поскольку их комбинация определяет уникальное положение точки, представляющей комплексное число, на полярной плоскости. Для получения прямоугольных координат из полярных воспользуемся следующей формулой:
Формула Эйлера устанавливает связь между тригонометрическими функциями и комплексной показательной функцией для любого действительного числа φ :
Формула Эйлера позволяет представить синусоиду как сложную экспоненциальную функцию, удобную во многих областях. В физике и электротехнике полярное представление комплексных чисел широко используется для представления синусоидальных напряжений и токов. В этом представлении термины «амплитуда» и «фаза» используются вместо терминов «модуль» («величина») и «аргумент».
В физике и электротехнике полярное представление комплексных чисел широко используется для представления синусоидальных напряжений и токов. В этом представлении термины «амплитуда» и «фаза» используются вместо терминов «модуль» («величина») и «аргумент».
Комплексное число, представляющее синусоидальную функцию с амплитудой A , угловой частотой ω и начальной фазой θ , называется вектором (от фазового вектора). Дополнительную информацию о визуализации комплексных чисел, векторах и преобразовании полярных чисел в прямоугольные и наоборот вы найдете в нашем калькуляторе векторных преобразований.
Отношения и операции
Комплексные числа подчиняются тем же правилам алгебры, что и обычные числа. Количество i рассматривается как константа, и всякий раз, когда встречается i ², оно заменяется на –1.
Равенство комплексных номеров
Два комплексных номера x + YI и N + миль равны, если и только если x = N и Y = M .
Комплексно-сопряженное число
Комплексно-сопряженное число находится путем изменения знака мнимой части. Например, следующие два числа являются комплексно-сопряженными:
В физике и электротехнике комплексное сопряжение часто обозначается как z *. Сопряженный пример (нажмите для просмотра в калькуляторе):
Сложение и вычитание
Сумма и разность двух комплексных чисел m + ni и p + qi и То есть, чтобы сложить или вычесть два комплексных числа, надо отдельно сложить или вычесть их действительные или мнимые части. Примеры (нажмите для просмотра): Два комплексных числа в прямоугольной форме умножаются путем поочередного умножения каждого члена одного числа на оба члена другого числа и объединения полученных действительных и мнимых членов (называемых j-членами в электротехнике). машиностроение). В полярной форме умножение двух комплексных чисел проще и упрощается до умножения величин и сложения углов, например: Обратное ненулевого комплексного числа z = a + bi в прямоугольной форме получается путем умножения как числителя (в данном случае, 1) комплексным сопряжением знаменателя (в данном случае комплексного числа) и затем объединением слагаемых и упрощением: Деление двух комплексных чисел a + bi и c + di в прямоугольной форме выполняется по тому же принципу с использованием комплексного сопряжения знаменателя: Как и умножение, деление двух чисел в полярной форме проще. Величина частного двух чисел определяется путем деления величины числителя на величину знаменателя. Угол частного определяется путем вычитания угла знаменателя из угла числителя. Если мнимая часть комплексного числа отлична от нуля, то квадратные корни этого числа представляют собой пару комплексных чисел с положительным и отрицательным знаками. Положительное число считается основным значением квадратного корня. Этот калькулятор найдет только главный (положительный) квадратный корень комплексного числа. Для прямоугольного представления комплексного числа используется следующая формула: , где sgn( y ) — знаковая функция числа 9.0029 y определяются как 3 2
, который определяется следующим образом: Умножение
 Определение i ² = –1 также используется в процессе умножения. Например:
Определение i ² = –1 также используется в процессе умножения. Например: Обратное и деление
 Например,
Например, Квадратный корень
Приложения
Комплексные числа широко используются в реальных приложениях, таких как геометрия, теория управления (критерий устойчивости Найквиста, который использует комплексную плоскость), электротехника и сигнализация анализ (периодические сигналы удобно описывать комплексными числами), квантовая механика, теория относительности и многие другие области. Изобретенные почти 200 лет назад кватернионы, расширяющие комплексные числа, используются в компьютерной графике, инерциальной навигации и теории управления. 9{ — 1}} \ влево ( {\ гидроразрыва {4} {3}} \ вправо) \).
9{ — 1}} \ влево ( {\ гидроразрыва {4} {3}} \ вправо) \).
Аналогично, для произвольного комплексного числа \(z = x + yi\) мы можем определить эти два параметра:
- Модуль z . Это расстояние z от начала координат и обозначается \(\left| z \right|\).
- Аргумент z . Это угол между линией, соединяющей z с исходной точкой, и положительным реальным направлением. Обозначается \(\arg \left( z \right)\). 9{ — 1}}1 = \frac{\pi }{4}\]
Таким образом,
\[\begin{align}&\arg \left( {{z_1}} \right) = {\theta _1 } = \frac{\pi} {4}\\&\arg \left( {{z_2}} \right) = — {\theta _2} = — \frac{\pi} {4}\end{align} \]
Мы видели примеры вычисления аргументов для комплексных чисел, лежащих в первом, втором и четвертом квадрантах. Давайте посмотрим, как мы можем вычислить аргумент комплексного числа, лежащего в третьем квадранте.
Пример 4: Найти модуль и аргумент \(z = — 1 — i\sqrt 3 \).
 9{ — 1}}\sqrt 3 = \frac{\pi }{3}\]
9{ — 1}}\sqrt 3 = \frac{\pi }{3}\]Таким образом, угол между OP и положительным направлением Real равен
\[\phi = \pi — \theta = \ pi — \frac{\pi }{3} = \frac{{2\pi }}{3}\]
Теперь, поскольку угол \(\phi \) движется по часовой стрелке, фактический аргумент числа z будет:
\[\arg \left( z \right) = — \phi = — \frac{{2\pi }}{3}\]
Мы также могли вычислить аргумент, вычислив величина угла развертки в направлении против часовой стрелки, как показано ниже:
Таким образом, мы можем записать аргумент как
\[\arg \left( z \right) = \pi + \theta = \pi + \frac{\pi }{3} = \frac{{ 4\pi }}{3}\]
Оба способа записи аргументов верны, так как два аргумента на самом деле соответствуют одному и тому же направлению.
Упрощение комплексных чисел с помощью Python — настоящий Python
Большинство языков программирования общего назначения либо не поддерживают, либо имеют ограниченную поддержку комплексных чисел .
 Типичными вариантами являются изучение какого-либо специализированного инструмента, такого как MATLAB, или поиск сторонней библиотеки. Python — редкое исключение, потому что в него встроены комплексные числа.0003
Типичными вариантами являются изучение какого-либо специализированного инструмента, такого как MATLAB, или поиск сторонней библиотеки. Python — редкое исключение, потому что в него встроены комплексные числа.0003Несмотря на название, комплексные числа не сложные! Они удобны для решения практических задач, с которыми вы познакомитесь в этом руководстве. Вы изучите векторную графику и частотный анализ звука , но комплексные числа также могут помочь в построении фракталов , таких как множество Мандельброта.
В этом руководстве вы узнаете, как:
- Определять комплексные числа с помощью литералов в Python
- Представление комплексных чисел в прямоугольных и полярных координатах
- Использовать комплексные числа в арифметических выражениях
- Воспользуйтесь преимуществами встроенного
модуля cmath - Перевод математических формул непосредственно в код Python
Если вам нужно быстро освежить знания или вкратце ознакомиться с теорией комплексных чисел, вы можете посмотреть серию видеороликов Академии Хана.
 Чтобы загрузить образец кода, используемый в этом руководстве, щелкните ссылку ниже:
Чтобы загрузить образец кода, используемый в этом руководстве, щелкните ссылку ниже:Создание комплексных чисел в Python
Создание и обработка комплексных чисел в Python мало чем отличается от других встроенных типов данных, особенно числовых типов. Это возможно, потому что язык рассматривает их как граждан первого сорта. Это означает, что вы можете выражать математические формулы, включающие комплексные числа, с небольшими накладными расходами.
Python позволяет использовать комплексные числа в арифметических выражениях и вызывать для них функции точно так же, как и для других чисел в Python. Это приводит к элегантному синтаксису, который читается почти как учебник по математике.
Удалить рекламу
Буквенный комплексный номер
Самый быстрый способ определить комплексное число в Python — ввести его литерал непосредственно в исходный код:
>>>
>>> z = 3 + 2j
Хотя это выглядит как алгебраическая формула, выражение справа от знака равенства уже является фиксированным значением, которое не требует дальнейшего вычисления.
. Когда вы проверите его тип, вы убедитесь, что это действительно комплексное число:
Когда вы проверите его тип, вы убедитесь, что это действительно комплексное число:>>>
>>> тип(г) <класс 'сложный'>
Чем это отличается от , складывающего два числа с оператором плюс? Явная поддавка — буква
.j, приклеенная ко второй цифре, что полностью меняет смысл выражения. Если вы удалите букву, вместо этого вы получите знакомый целочисленный результат:>>>
>>> г = 3 + 2 >>> тип(г) <класс 'целое число'>
Кстати, числа с плавающей запятой можно использовать и для создания комплексных чисел:
>>>
>>> z = 3,14 + 2,71j >>> тип(г) <класс 'сложный'>
Литералы комплексных чисел в Python имитируют математическую нотацию комплексного числа, известную также как стандартная форма , алгебраическая форма или иногда каноническая форма .
 В Python вы можете использовать строчные буквы
В Python вы можете использовать строчные буквы jили прописные буквыJв этих литералах.Если вы узнали о комплексных числах на уроках математики, вы, возможно, видели, как они выражаются с помощью
iвместоj. Если вам интересно, почему Python используетjвместоi, вы можете развернуть сворачиваемый раздел ниже, чтобы узнать больше.Традиционная запись комплексных чисел использует букву
iвместоj, поскольку она обозначает мнимую единицу . Если у вас есть математический опыт, вы можете почувствовать небольшой дискомфорт в связи с соглашением Python. Однако есть несколько причин, которые могут оправдать спорный выбор Python:- Инженеры уже приняли это соглашение, чтобы избежать коллизии имен с электрическим током, который обозначается буквой
i. - В вычислительной технике буква
iчасто используется для индексации переменной в циклах.
- Букву
iможно легко перепутать сlили1в исходном коде.
Этот вопрос был поднят в системе отслеживания ошибок Python более десяти лет назад, и сам создатель Python, Гвидо ван Россум, закрыл проблему следующим комментарием:
Это не будет исправлено. Во-первых, буква «i» или заглавная «I» слишком похожи на цифры. То, как числа анализируются синтаксическим анализатором языка (в исходном коде) или встроенными функциями (int, float, complex), не должно быть локализуемым или настраиваемым каким-либо образом; это требует огромных разочарований в будущем. Если вы хотите анализировать комплексные числа, используя «i» вместо «j», у вас уже есть множество доступных решений. (Источник)
Вот и все. Если вы не хотите начать использовать MATLAB, вам придется смириться с использованием
jдля обозначения ваших комплексных чисел.Алгебраическая форма комплексного числа следует стандартным правилам алгебры, что удобно при выполнении арифметических операций.
 Например, у сложения есть коммутативное свойство, которое позволяет поменять местами две части литерала комплексного числа без изменения его значения:
Например, у сложения есть коммутативное свойство, которое позволяет поменять местами две части литерала комплексного числа без изменения его значения:>>>
>>> 3 + 2j == 2j + 3 Истинный
Точно так же вы можете заменить вычитание сложением в литерале комплексного числа, потому что знак минус — это просто сокращенное обозначение эквивалентной формы:
>>>
>>> 3 - 2j == 3 + (-2j) Истинный
Должен ли литерал комплексного числа в Python всегда содержать два числа? Можно ли больше? Они заказаны? Чтобы ответить на эти вопросы, давайте проведем несколько экспериментов. Неудивительно, что если вы укажете только одно число без буквы
j, вы получите обычное целое число или число с плавающей запятой:>>>
>>> z = 3,14 >>> тип(г) <класс 'плавающий'>
С другой стороны, добавление буквы
jк числовому литералу немедленно превратит его в комплексное число:>>>
>>> z = 3,14j >>> тип(г) <класс 'сложный'>
Строго говоря, с математической точки зрения вы только что создали чистое мнимое число , но Python не может представить его как отдельный тип данных.
 Следовательно, без другой части это просто комплексное число.
Следовательно, без другой части это просто комплексное число.А как насчет обратного? Чтобы создать комплексное число без мнимой части, вы можете воспользоваться нулем и добавить или вычесть его следующим образом:
>>>
>>> z = 3,14 + 0j >>> тип(г) <класс 'сложный'>
На самом деле всегда присутствуют обе части комплексного номера. Если вы не видите единицу, это означает, что она имеет нулевое значение. Давайте проверим, что происходит, когда вы пытаетесь вставить в сумму больше терминов, чем раньше:
>>>
>>> 2 + 3j + 4 + 5j (6+8к)
На этот раз ваше выражение больше не является литералом, потому что Python преобразовал его в комплексное число, состоящее только из двух частей. Помните, что основные правила алгебры распространяются на комплексные числа, поэтому, если вы сгруппируете похожие термины и примените покомпонентное сложение, вы получите
6 + 8j.
Обратите внимание, как Python по умолчанию отображает комплексные числа. Их текстовое представление содержит заключающую пару круглых скобок строчную букву 9.0499 j и без пробелов. Кроме того, мнимая часть стоит на втором месте.
Комплексные числа, которые также являются чисто мнимыми числами, появляются без скобок и показывают только свою мнимую часть:
>>>
>>> 3 + 0j (3+0j) >>> 0 + 3j 3j
Это помогает отличить мнимые числа от большинства сложных чисел, состоящих из действительных и мнимых частей.
Удалить рекламу
complex()Заводская функцияPython имеет встроенную функцию
complex(), которую вы можете использовать в качестве альтернативы литералу комплексного числа:>>>
>>> z = комплекс (3, 2)
В этом виде он напоминает кортеж или упорядоченную пару обычных чисел.
 Аналогия не такая уж надуманная. Комплексные числа имеют геометрическую интерпретацию в декартовой системе координат , которую вы вскоре изучите. Вы можете думать о комплексных числах как о двумерных.
Аналогия не такая уж надуманная. Комплексные числа имеют геометрическую интерпретацию в декартовой системе координат , которую вы вскоре изучите. Вы можете думать о комплексных числах как о двумерных.Забавный факт: В математике комплексные числа традиционно обозначаются буквами
z, так как это следующая буква в алфавите послеxиy, которые обычно обозначают координаты.Функция фабрики комплексных чисел принимает два числовых параметра. Первый представляет реальную часть , а второй представляет мнимую часть , обозначенную буквой
jв литерале, который вы видели ранее:>>>
>>> комплекс(3, 2) == 3 + 2j Истинный
Оба параметра являются необязательными, их значения по умолчанию равны нулю, что упрощает определение комплексных чисел без мнимой части или одновременно с действительной и мнимой частями:
>>>
>>> комплекс(3) == 3 + 0j Истинный >>> комплекс() == 0 + 0j Истинный
Версия с одним аргументом может быть полезна при приведении типов .
 Например, вы можете передать нечисловое значение, например строковый литерал, чтобы получить соответствующий
Например, вы можете передать нечисловое значение, например строковый литерал, чтобы получить соответствующий комплексобъект. Обратите внимание, что строка не может содержать пробелов:>>>
>>> сложный("3+2j") (3+2к) >>> сложный("3 + 2j") Traceback (последний последний вызов): Файл "", строка 1, в ValueError: аргумент complex() является неверно сформированной строкой Позже вы узнаете, как сделать ваши классы совместимыми с этим механизмом приведения типов. Интересно, что когда вы передаете комплексное число в
complex(), вы получите обратно тот же экземпляр:>>>
>>> z = комплекс (3, 2) >>> z является комплексным (z) Истинный
Это согласуется с тем, как работают другие типы чисел в Python, потому что все они являются неизменяемыми . Чтобы сделать отличную копию комплексного числа, вы должны снова вызвать функцию с обоими аргументами или объявить другую переменную с литералом комплексного числа:
>>>
>>> z = комплекс (3, 2) >>> z является комплексным (3, 2) ЛОЖЬ
Когда вы предоставляете функции два аргумента, они всегда должны быть числами, например,
int,floatилиcomplex. В противном случае вы получите ошибку времени выполнения. С технической точки зрения,
В противном случае вы получите ошибку времени выполнения. С технической точки зрения, boolявляется подклассомint, так что он тоже будет работать:>>>
>>> complex(False, True) # Логические значения, такие же, как и комплексные (0, 1) 1j >>> комплекс(3, 2) # Целые числа (3+2к) >>> complex(3.14, 2.71) # Числа с плавающей запятой (3,14+2,71к) >>> комплекс("3", "2") # Строки Traceback (последний последний вызов): Файл "", строка 1, в TypeError: complex() не может принимать второй аргумент, если первый является строкой Все становится еще более странным, когда вы предоставляете
.complex()фабричной функции комплексные числа в качестве аргументов. Однако, если вы укажете только первый аргумент, он будет вести себя как прокси, как и раньше:>>>
>>> комплекс(комплекс(3, 2)) (3+2к)
Однако, когда присутствуют два аргумента и хотя бы один из них является комплексным числом, вы получите результаты, которые на первый взгляд может быть трудно объяснить:
>>>
>>> сложный(1, сложный(3, 2)) (-1+3j) >>> комплекс(комплекс(3, 2), 1) (3+3к) >>> комплекс(комплекс(3, 2), комплекс(3, 2)) (1+5к)
Чтобы получить ответы, давайте заглянем в строку документации фабричной функции или в онлайн-документацию, которые объясняют, что происходит под капотом, когда вы вызываете
.complex(real, imag):
Вернуть комплексное число со значением real + imag *1j или преобразовать строку или число в комплексное число. (Источник)
В этом пояснении
realиimagявляются именами аргументов функции. Второй аргумент умножается на воображаемую единицуj, и результат добавляется к первому аргументу. Не волнуйтесь, если это все еще не имеет никакого смысла. Вы можете вернуться к этой части, когда прочитаете об арифметике комплексных чисел. Правила, о которых вы узнаете, сделают это простым.Когда вы хотите использовать комплекс
()заводская функция над литералом? Это зависит от обстоятельств, но вызов функции может быть более удобным, например, когда вы имеете дело с динамически генерируемыми данными.Удалить рекламу
Знакомство с комплексными числами Python
В математике комплексные числа — это надмножество действительных чисел, а это означает, что каждое действительное число также является комплексным числом, мнимая часть которого равна нулю.
. Python моделирует эту взаимосвязь с помощью концепции, называемой числовой башней 9.0277, описанный в PEP 3141:
Python моделирует эту взаимосвязь с помощью концепции, называемой числовой башней 9.0277, описанный в PEP 3141:>>>
>>> номера импорта >>> issubclass(числа.Вещественные, числа.Комплексные) Истинный
Встроенный модуль
номеровопределяет иерархию числовых типов через абстрактных класса , которые можно использовать для проверки типов и классификации чисел. Например, чтобы определить, принадлежит ли значение определенному набору чисел, вы можете вызвать для негоisinstance():>>>
>>> isinstance(3.14, numbers.Complex) Истинный >>> isinstance(3.14, числа.Интеграл) ЛОЖЬ
Значение с плавающей запятой
3.14— это действительное число, которое также является комплексным числом, но не целым числом. Обратите внимание, что вы не можете использовать встроенные типы напрямую в таком тесте:>>>
>>> isinstance(3.
 14, комплекс)
ЛОЖЬ
14, комплекс)
ЛОЖЬ
Отличие
Иерархия типов для чисел в Pythonсложных номеровот. Комплекссостоит в том, что они относятся к отдельным ветвям в дереве иерархии числовых типов, а последний является абстрактным базовым классом без какой-либо реализации:Абстрактные базовые классы, которые на приведенной выше диаграмме обозначены красным цветом, могут обходить обычный механизм проверки наследования путем регистрации несвязанных классов в качестве их виртуальных подклассов. Вот почему значение с плавающей запятой в этом примере кажется экземпляром
чисел. Комплекс, но некомплекс.Доступ к реальным и мнимым частям
Чтобы получить действительную и мнимую части комплексного числа в Python, вы можете обратиться к соответствующим
.realи.imagатрибуты:>>>
>>> z = 3 + 2j >>> г.реал 3.0 >>> z.imag 2.0
Оба свойства доступны только для чтения , поскольку комплексные числа неизменяемы, поэтому попытка присвоить новое значение любому из них не удастся:
>>>
>>> z.
 real = 3,14
Traceback (последний последний вызов):
Файл "
real = 3,14
Traceback (последний последний вызов):
Файл "", строка 1, в AttributeError: атрибут только для чтения Поскольку каждое число в Python является более конкретным типом комплексного числа, атрибуты и методы, определенные в числах
.. Комплекстакже доступен во всех числовых типах, включаяintиfloat:>>>
>>> х = 42 >>> х.реал 42 >>> x.imag 0
Мнимая часть таких чисел всегда равна нулю.
Вычисление сопряженного комплексного числа
Комплексные числа Python имеют только три общедоступных члена. Кроме
.realи.imag, они предоставляют метод.conjugate(), который меняет знак мнимой части:>>>
>>> z = 3 + 2j >>> z.conjugate() (3-2к)
Для чисел, у которых мнимая часть равна нулю, это не будет иметь никакого эффекта:
>>>
>>> х = 3,14 >>> x.
 conjugate()
3.14
conjugate()
3.14
Эта операция обратна самой себе, поэтому, выполнив ее дважды, вы получите исходное число, с которого начали:
>>>
>>> z.conjugate().conjugate() == z Истинный
Хотя комплексное сопряжение может показаться малоценным, оно обладает несколькими полезными арифметическими свойствами, которые, среди прочего, могут помочь вычислить деление двух комплексных чисел с помощью ручки и бумаги.
Удалить рекламу
Арифметика комплексных чисел
Поскольку комплекс
cmath, который является частью стандартной библиотеки. Вы познакомитесь с ним в более поздней части этого руководства.
На данный момент запоминание одного правила позволит вам применить свои знания арифметики начальной школы для вычисления основных операций с комплексными числами. Правило, которое следует запомнить, — это определение воображаемой единицы , которое удовлетворяет следующему уравнению:
Это выглядит неправильно, когда вы думаете о
jкак о реальном числе, но не паникуйте. Если вы проигнорируете это на мгновение и замените каждое вхождениеj2на-1, как если бы это была константа, тогда вы будете установлены. Давайте посмотрим, как это работает.Дополнение
Сумма двух или более комплексных чисел эквивалентна сложению их действительных и мнимых частей покомпонентно:
>>>
>>> z1 = 2 + 3j >>> z2 = 4 + 5j >>> z1 + z2 (6+8к)
Ранее вы узнали, что алгебраические выражения, состоящие из действительных и мнимых чисел, подчиняются стандартным правилам алгебры.
 Когда вы запишете это алгебраически, вы сможете применить распределительное свойство и упростить формулу, выделив и сгруппировав общие термины:
Когда вы запишете это алгебраически, вы сможете применить распределительное свойство и упростить формулу, выделив и сгруппировав общие термины:Python автоматически продвигает операнды к комплексному типу данных
>>>
>>> z = 2 + 3j >>> z + 7 # Добавляем сложное к целому (9+3j)
Это похоже на неявное преобразование
intвfloat, с которым вы, возможно, более знакомы.Вычитание
Вычитание комплексных чисел аналогично их сложению, а значит, вы также можете применять его поэлементно:
>>>
>>> z1 = 2 + 3j >>> z2 = 4 + 5j >>> z1 - z2 (-2-2j)
Однако, в отличие от суммы, порядок операндов имеет значение и приводит к другим результатам, как и в случае с действительными числами:
>>>
>>> z1 + z2 == z2 + z1 Истинный >>> z1 - z2 == z2 - z1 ЛОЖЬ
Вы также можете использовать унарный минус (-) , чтобы сделать отрицательное комплексное число:
>>>
>>> z = 3 + 2j >>> -з (-3-2j)
Инвертирует как действительную, так и мнимую части комплексного числа.

Удалить рекламу
Умножение
Произведение двух и более комплексных чисел становится интереснее:
>>>
>>> z1 = 2 + 3j >>> z2 = 4 + 5j >>> z1 * z2 (-7+22j)
Как, черт возьми, вы получили отрицательное число из одних только положительных? Чтобы ответить на этот вопрос, придется вспомнить определение мнимой единицы и переписать выражение через действительную и мнимую части:
Ключевое наблюдение, которое необходимо сделать, состоит в том, что
jумножить наjдаетj2, который можно заменить на-1. Это инвертирует знак одного из слагаемых, в то время как остальные правила остаются точно такими же, как и раньше.Подразделение
Деление комплексных чисел может показаться пугающим при первом знакомстве:
>>>
>>> z1 = 2 + 3j >>> z2 = 4 + 5j >>> z1 / z2 (0,5609756097560976+0,0487804878048781j)
Хотите верьте, хотите нет, но вы можете получить тот же результат, используя только ручку и бумагу! (Хорошо, калькулятор может избавить вас от некоторых головных болей в будущем.
 ) Когда оба числа выражены в их стандартных формах, хитрость состоит в том, чтобы умножить числитель и знаменатель на сопряженное число последнего:
) Когда оба числа выражены в их стандартных формах, хитрость состоит в том, чтобы умножить числитель и знаменатель на сопряженное число последнего:Знаменатель становится квадратом модуля делителя. Позже вы узнаете больше о модуле комплексных чисел. Когда вы продолжите выводить формулу, вот что вы получите:
Обратите внимание, что комплексные числа не поддерживают деление на этаж, также известное как целочисленное деление:
>>>
>>> z1 // z2 Traceback (последний последний вызов): Файл "
", строка 1, в TypeError: не может взять пол комплексного числа. >>> z1 // 3.14 Traceback (последний последний вызов): Файл " ", строка 1, в TypeError: не может взять пол комплексного числа. Раньше это работало в Python 2.x, но позже было удалено, чтобы избежать двусмысленности.
Возведение в степень
Вы можете возводить комплексные числа в степень, используя двоичный оператор возведения в степень (
**) или встроенныйpow(), но не тот, который определен в модулеmath, который поддерживает только числа с плавающей запятой. значения:
значения:>>>
>>> z = 3 + 2j >>> г**2 (5+12к) >>> pow(z, 2) (5+12к) >>> импортировать математику >>> math.pow(z, 2) Traceback (последний последний вызов): Файл "
", строка 1, в TypeError: невозможно преобразовать комплекс в число с плавающей запятой И основание , и показатель степени могут относиться к любым числовым типам, включая целые числа, числа с плавающей запятой, мнимые или комплексные:
>>>
>>> 2**з (1,4676557979464138+7,864221995j) >>> г**2 (5+12к) >>> г**0,5 (1,8173540210239707+0,5502505227003375j) >>> г**3j (-0,130414867086-0,11115341486478239j) >>> з**з (-5,4097387939-13,410442370412747j)
Ручное возведение комплексных чисел в степень становится очень трудным, когда они представлены в стандартной форме. Намного удобнее переписать число в тригонометрическая форма и рассчитайте мощность, используя базовую тригонометрию.
 Если вам интересна математика, ознакомьтесь с формулой Де Муавра, которая позволяет вам это сделать.
Если вам интересна математика, ознакомьтесь с формулой Де Муавра, которая позволяет вам это сделать.Удалить рекламу
Использование комплексных чисел Python в качестве двумерных векторов
Вы можете визуализировать комплексные числа как точек или векторов на евклидовой плоскости в декартовой или прямоугольной системе координат:
Ось X на комплексной плоскости, также известная как Плоскость Гаусса или Диаграмма Аргана представляет действительную часть комплексного числа, а ось Y представляет его мнимую часть.
Этот факт приводит к одной из самых крутых особенностей сложного типа данных
Получение координат
Бермудский треугольник — легендарный регион, известный своими паранормальными явлениями, который охватывает южную оконечность Флориды, Пуэрто-Рико и крошечный остров Бермудские острова.
. Его вершины примерно обозначены тремя крупными городами, географические координаты которых следующие:
Его вершины примерно обозначены тремя крупными городами, географические координаты которых следующие:- Майами: 25° 45’ 42,054” северной широты, 80° 11’ 30,438” з.д.
- Сан-Хуан: 18° 27’ 58,8” северной широты, 66° 6’ 20,598” з.д.
- Гамильтон: 32° 17’ 41,64” северной широты, 64° 46’ 58,908 дюймов Ш
После преобразования этих координат в десятичные градусы вы получите два числа с плавающей запятой для каждого города. Вы можете использовать комплексный тип данных
miami_fl = сложный (-80.1, 25.761681) san_juan = сложный (-66.105721, 18.466333) Гамильтон = сложный (-64,78303, 32,2949)
Отрицательные значения долготы представляют западное полушарие, а положительные значения широты представляют северное полушарие.

Имейте в виду, что это сферические координаты . Чтобы правильно спроецировать их на плоскую плоскость, вам нужно учитывать кривизну Земли. Одной из первых картографических проекций, используемых в картографии, была проекция Меркатора, которая помогала морякам ориентироваться на своих кораблях. Но давайте проигнорируем все это и предположим, что значения уже выражены в прямоугольной системе координат.
Когда вы нанесете числа на комплексную плоскость, вы получите грубое изображение Бермудского треугольника:
В сопутствующих материалах вы найдете интерактивную записную книжку Jupyter, в которой строится Бермудский треугольник с использованием библиотеки Matplotlib. Чтобы загрузить исходный код и материалы для этого руководства, щелкните ссылку ниже:
Если вам не нравится вызывать фабричную функцию
complex(), вы можете создать псевдоним типа с более подходящим именем или использовать литеральную форму комплексного числа, чтобы сэкономить несколько нажатий клавиш:CityCoordinates = сложный miami_fl = Координаты города (-80.
 1, 25.761681)
miami_fl = -80,1 + 25,761681j
1, 25.761681)
miami_fl = -80,1 + 25,761681j
Если вам нужно упаковать больше атрибутов города, вы можете использовать именованный кортеж или класс данных или создать собственный класс.
Расчет величины
Величина , также известная как модуль или радиус комплексного числа, является длиной вектора, изображающего его на комплексной плоскости:
Вы можете вычислить его по теореме Пифагора, взяв квадратный корень из суммы квадрата действительной части и квадрата мнимой части:
Вы могли бы подумать, что Python позволит вам вычислить длину такого вектора с помощью встроенной
len(), но это не так. Чтобы получить величину комплексного числа, вы должны вызвать другую глобальную функцию с именемabs(), которая обычно используется для вычисления абсолютного значения числа:>>>
>>> len(3 + 2j) Traceback (последний последний вызов): Файл "
", строка 1, в TypeError: объект типа «сложный» не имеет len() >>> абс (3 + 2j) 3.  605551275463989
605551275463989
Эта функция удаляет знак у целых чисел, которые вы передаете, но для комплексных чисел возвращает величину или длину вектора:
>>>
>>> абс(-42) 42 >>> z = 3 + 2j >>> абс(г) 3,605551275463989 >>> из математического импорта sqrt >>> sqrt(z.real**2 + z.imag**2) 3,605551275463989
Возможно, вы помните из предыдущего раздела, что комплексное число, умноженное на сопряженное, дает квадрат его величины.
Удалить рекламу
Нахождение расстояния между двумя точками
Найдем геометрический центр Бермудского треугольника и расстояния до него от трех городов, образующих его границы. Во-первых, вам нужно просуммировать все координаты и разделить результат на их количество, чтобы получить среднее значение:
геометрический_центр = сумма ([Майами_фл, Сан_Хуан, Гамильтон]) / 3
Это даст вам точку, расположенную в Атлантическом океане, где-то внутри треугольника:
Теперь вы можете создавать векторы, привязанные к городам и направленные к геометрическому центру треугольника.
 Векторы создаются путем вычитания исходной точки из целевой:
Векторы создаются путем вычитания исходной точки из целевой:v1 = геометрический_центр - miami_fl v2 = геометрический_центр - сан_цзюань v3 = геометрический_центр - Гамильтон
Поскольку вы вычитаете комплексные числа, каждый вектор также является комплексным числом, состоящим из двух частей. Чтобы получить расстояния, рассчитайте величину каждого вектора:
>>>
>>> абс(v1) 9,83488994681275 >>> абс (v2) 8.226809506084367 >>> абс (v3) 8.784732429678444
Эти длины векторов не отражают значимых расстояний, но являются хорошим приближением для такого игрушечного примера. Чтобы представить точные результаты в материальных единицах, вам придется сначала преобразовать координаты из сферических в прямоугольные или вместо этого рассчитать расстояние, используя метод большого круга.
Перемещение, отражение, масштабирование и вращение
Возможно, вас беспокоит, что треугольник находится во втором квадранте декартовой системы координат.
 Давайте переместим его так, чтобы его геометрический центр совпал с началом координат. Все три вершины будут , переведенные на на длину вектора, указанного геометрическим центром, но в противоположном направлении:
Давайте переместим его так, чтобы его геометрический центр совпал с началом координат. Все три вершины будут , переведенные на на длину вектора, указанного геометрическим центром, но в противоположном направлении:треугольник = miami_fl, san_juan, hamilton смещение = -geometric_center centered_triangle = [вершина + смещение вершины в треугольнике]
Обратите внимание, что вы складываете два комплексных числа вместе, что выполняет их поэлементное сложение. Это аффинное преобразование, поскольку оно не меняет форму треугольника или относительное расположение его вершин:
Зеркальное отражение треугольника вокруг действительной или мнимой оси требует инвертирования соответствующей компоненты в его вершинах. Например, чтобы отразить по горизонтали, вам придется использовать отрицательную часть действительной части, которая соответствует горизонтальному направлению. Чтобы перевернуть его по вертикали, вы возьмете минус мнимой части:
.
flipped_horizontally = [complex(-v.real, v.imag) для v в centered_triangle] flipped_vertically = [complex(v.real, -v.imag) для v в centered_triangle]
Последнее, по сути, то же самое, что и вычисление сопряжения комплексных чисел, поэтому вы можете вызвать
.conjugate()для каждой вершины напрямую, чтобы сделать всю тяжелую работу за вас:flipped_vertically = [v.conjugate() для v в centered_triangle]
Естественно, ничто не мешает вам применить симметрию в любом направлении или в обоих направлениях одновременно. В таком случае вы можете использовать унарный оператор минус перед комплексным числом, чтобы поменять местами его действительную и мнимую части:
flipped_in_both_directions = [-v для v в центрированном_треугольнике]
Поэкспериментируйте с различными комбинациями флипов, используя интерактивный блокнот Jupyter, доступный в загружаемых материалах. Вот как будет выглядеть треугольник, если его перевернуть по обеим осям:
Масштабирование аналогично перемещению, но вместо добавления смещения вы будете умножать каждую вершину на постоянный коэффициент, который должен быть реальным числом :
scaled_triangle = [1,5*вершина для вершины в centered_triangle]
В результате оба компонента каждого комплексного числа умножаются на одинаковую величину.
 Это должно растянуть ваш Бермудский треугольник, чтобы он выглядел больше на графике:
Это должно растянуть ваш Бермудский треугольник, чтобы он выглядел больше на графике:Умножение вершин треугольника на другое комплексное число, с другой стороны, приводит к вращению вокруг начала системы координат. Это сильно отличается от того, как вы обычно умножаете векторы друг на друга. Например, скалярное произведение двух векторов даст скаляр, а их векторное произведение возвращает новый вектор в трехмерном пространстве, который перпендикулярен поверхности, которую они определяют.
Примечание: Произведение двух комплексных чисел не представляет векторное умножение. Вместо этого он определяется как матричное умножение в двумерном векторном пространстве с 1 и
jв качестве стандартной основы. Multiplying ( x 1 + y 1j) by ( x 2 + y 2j) corresponds to the following matrix multiplication:This is the матрица поворота слева, что делает математику просто отличной.

Когда вы умножаете вершины на воображаемую единицу, треугольник повернется на 90° против часовой стрелки. Если вы продолжите повторять это, то в конце концов вернетесь к тому, с чего начали:
.Как найти конкретное комплексное число, которое будет поворачивать другое комплексное число на любой желаемый угол при умножении обоих? Во-первых, взгляните на следующую таблицу, в которой суммированы последовательные вращения на 90°:
поворот на 90° Общий угол Формула Экспонента Значение 0 0° из й01 1 90° × и2 180° × -1 3 270° × - 4 360° × 1 5 450° z × и6 540° z × -1 7 630° z × - 8 720° z × j×j×j1 Когда вы выражаете многократное умножение на
jчерез положительные целые показатели степени, возникает закономерность. Обратите внимание, как возведение воображаемой единицы в последующие степени заставляет ее многократно повторять одни и те же значения. Вы можете экстраполировать это на дробные показатели и ожидать, что они будут соответствовать промежуточным углам.
Обратите внимание, как возведение воображаемой единицы в последующие степени заставляет ее многократно повторять одни и те же значения. Вы можете экстраполировать это на дробные показатели и ожидать, что они будут соответствовать промежуточным углам.Например, показатель степени в середине первого поворота равен 0,5 и представляет собой угол 45°:
Итак, если вы знаете, что степень единицы представляет собой прямой угол, а все, что между ними, масштабируется пропорционально, то вы можете вывести эту общую формулу для произвольных поворотов:
def rotate(z: комплекс, градусы: число с плавающей запятой) -> комплекс: вернуть z * 1j**(градусы/90)Обратите внимание, что вращение становится более естественным, когда вы выражаете свои комплексные числа в полярных координатах, которые уже описывают угол. Затем вы можете воспользоваться экспоненциальная форма , чтобы сделать вычисления более простыми:
Существует два способа поворота числа с использованием полярных координат:
import math, cmath def rotate1(z: комплекс, градусы: число с плавающей запятой) -> комплекс: радиус, угол = cmath. polar(z)
вернуть cmath.rect (радиус, угол + math.radians (градусы))
def rotate2(z: комплекс, градусы: число с плавающей запятой) -> комплекс:
вернуть z * cmath.rect(1, math.radians(степени))
polar(z)
вернуть cmath.rect (радиус, угол + math.radians (градусы))
def rotate2(z: комплекс, градусы: число с плавающей запятой) -> комплекс:
вернуть z * cmath.rect(1, math.radians(степени))
Вы можете суммировать углы или умножать комплексное число на единичный вектор.
Подробнее о них вы узнаете в следующем разделе.
Удалить рекламу
Изучение математического модуля для комплексных чисел:
cmathВы уже видели, что некоторые встроенные функции, такие как
abs()иpow(), принимают комплексные числа, а другие нет. Например, вы не можетеround()комплексное число, потому что такая операция не имеет смысла:>>>
>>> круглый(3 + 2j) Traceback (последний последний вызов): Файл "
", строка 1, в TypeError: сложный тип не определяет метод __round__ Многие расширенные математические функции, такие как тригонометрические , гиперболические или логарифмические функции доступны в стандартной библиотеке.
 К сожалению, даже если вы знаете все о модуле Python
К сожалению, даже если вы знаете все о модуле Python math, это не поможет, потому что ни одна из его функций не поддерживает комплексные числа. Вам нужно будет объединить его с модулемcmath, который определяет соответствующие функции для комплексных чисел.Модуль
cmathпереопределяет все константы с плавающей запятой сmath, чтобы они были у вас под рукой без необходимости импортировать оба модуля:>>>
>>> импортировать математику, cmath >>> для имени в "e", "pi", "tau", "nan", "inf": ... print(name, getattr(math, name) == getattr(cmath, name)) ... д Правда Пи Истинно тау Правда нан Ложь инф True
Обратите внимание, что
nan— это специальное значение, которое никогда не равно ничему другому, включая себя самого! Вот почему вы видите одиночноеFalseв выводе выше. В дополнение к этому,cmathпредоставляет два комплексных аналога для NaN (не числа) и бесконечности, причем оба имеют нулевые действительные части:>>>
>>> из cmath import nanj, infj >>> nanj.
 real, nanj.imag
(0,0, нан)
>>> infj.real, infj.imag
(0.0, инф)
real, nanj.imag
(0,0, нан)
>>> infj.real, infj.imag
(0.0, инф)
В модуле
cmathпримерно вдвое меньше функций, чем в стандартном модулеmath. Большинство из них имитируют исходное поведение, но некоторые из них уникальны для комплексных чисел. Они позволят вам выполнить преобразование между двумя системами координат, которые вы изучите в этом разделе.Преобразование между прямоугольными и полярными координатами
Геометрически комплексное число можно рассматривать двояко. С одной стороны, это точка, чьи горизонтальные и вертикальные расстояния от начала координат однозначно определяют ее местоположение. Они известны как прямоугольные координаты , состоящие из реальной и мнимой частей.
С другой стороны, эту же точку можно описать в полярных координатах , что также позволит найти ее однозначно с двумя расстояниями:
- Радиальное расстояние — это длина радиуса, измеренная от начала координат.

- Угловое расстояние — это угол, измеренный между горизонтальной осью и радиусом.
Радиус , также известный как модуль , соответствует модулю комплексного числа или длине вектора. Угол обычно называют фазой или аргументом комплексного числа. При работе с тригонометрическими функциями полезно выражать угол в радианах, а не в градусах.
Вот изображение комплексного числа в обеих системах координат:
Следовательно, точка (3, 2) в декартовой системе координат имеет радиус примерно 3,6 и угол примерно 33,7°, или примерно π на 5,4 радиана.
Преобразование между двумя системами координат стало возможным благодаря паре функций, скрытых в модуле
cmath. В частности, чтобы получить полярные координаты комплексного числа, вы должны передать его вcmath.polar():>>>
>>> импорт cmath >>> cmath.
 polar(3 + 2j)
(3,605551275463989, 0,5880026035475675)
polar(3 + 2j)
(3,605551275463989, 0,5880026035475675)
Он вернет кортеж, где первый элемент — это радиус, а второй — угол в радианах. Обратите внимание, что радиус имеет то же значение, что и величина, которую вы можете рассчитать, вызвав
abs()для вашего комплексного числа. И наоборот, если вас интересует только угол комплексного числа, вы можете вызватьcmath.phase():>>>
>>> z = 3 + 2j >>> abs(z) # Величина также является радиальным расстоянием 3,605551275463989 >>> импортировать cmath >>> cmath.phase(3 + 2j) 0,5880026035475675 >>> cmath.polar(z) == (abs(z), cmath.phase(z)) Истинный
Угол можно получить с помощью базовой тригонометрии, поскольку действительная часть, мнимая часть и величина вместе образуют прямоугольный треугольник:
Вы можете использовать обратные тригонометрические функции, такие как арксинус , либо из
mathлибоcmath, но последнее даст комплексные значения с мнимой частью равной нулю:>>>
>>> z = 3 + 2j >>> импортировать математику >>> math.
 acos(z.real / abs(z))
0,5880026035475675
>>> math.asin(z.imag / abs(z))
0,5880026035475676
>>> math.atan(z.imag / z.real) # Предпочитает math.atan2(z.imag, z.real)
0,5880026035475675
>>> импортировать cmath
>>> cmath.acos(z.real / abs(z))
(0,5880026035475675-0j)
acos(z.real / abs(z))
0,5880026035475675
>>> math.asin(z.imag / abs(z))
0,5880026035475676
>>> math.atan(z.imag / z.real) # Предпочитает math.atan2(z.imag, z.real)
0,5880026035475675
>>> импортировать cmath
>>> cmath.acos(z.real / abs(z))
(0,5880026035475675-0j)
Однако при использовании функции арктангенс следует соблюдать осторожность, что побудило многие языки программирования разработать альтернативную реализацию под названием
atan2(). Вычисление отношения между мнимой и действительной частями иногда может привести к сингулярности из-за, например, деления на ноль. Более того, при этом теряются отдельные знаки двух значений, что делает невозможным определение угла с уверенностью:>>>
>>> импортировать математику >>> мат.атан(1 / 0) Traceback (последний последний вызов): Файл "
", строка 1, в ZeroDivisionError: деление на ноль >>> math.atan2(1, 0) 1.5707963267948966 >>> math.  atan(1 / 1) == math.atan(-1 / -1)
Истинный
>>> math.atan2(1, 1) == math.atan2(-1, -1)
ЛОЖЬ
atan(1 / 1) == math.atan(-1 / -1)
Истинный
>>> math.atan2(1, 1) == math.atan2(-1, -1)
ЛОЖЬ
Обратите внимание, как
atan()не может распознать две разные точки, расположенные в противоположных квадрантах системы координат. С другой стороны,atan2()ожидает два аргумента вместо одного, чтобы сохранить отдельные знаки перед делением одного на другой, а также избежать других проблем.Чтобы получить градусы вместо радианов, вы можете снова сделать необходимое преобразование, используя модуль
math:>>>
>>> импорт математики >>> math.degrees(0.5880026035475675) # Радианы в градусы 33.6525979785 >>> math.radians(180) # Градусы в радианы 3.1415589793
Обратный процесс, то есть преобразование полярных координат в прямоугольные, зависит от другой функции. Однако вы не можете просто передать тот же кортеж, который вы получили от
cmath.polar(), посколькуcmath.ожидает два отдельных аргумента: rect()
rect() >>>
>>> cmath.rect(cmath.polar(3 + 2j)) Traceback (последний последний вызов): Файл "
", строка 1, в TypeError: rect ожидал 2 аргумента, получил 1 Перед выполнением задания рекомендуется сначала распаковать кортеж и дать этим элементам более описательные имена. Теперь вы можете правильно вызвать
cmath.rect():>>>
>>> радиус, угол = cmath.polar(3 + 2j) >>> cmath.rect(радиус, угол) (3+1,9999999999999996j)
Во время вычислений Python может столкнуться с ошибками округления. За кулисами он вызывает тригонометрические функции для получения действительной и мнимой частей:
>>>
>>> импорт математики >>> радиус*(math.cos(угол) + math.sin(угол)*1j) (3+1,9999999999999996j) >>> импортировать cmath >>> радиус*(cmath.cos(угол) + cmath.sin(угол)*1j) (3+1,9999999999999996j)
Опять же, в этом случае не имеет значения, используете ли вы
mathилиcmath, так как результаты будут идентичными.
Удалить рекламу
Различное представление комплексных чисел
Независимо от системы координат, одно и то же комплексное число можно выразить в нескольких математически эквивалентных формах:
- Алгебраический (стандартный)
- Геометрический
- Тригонометрический
- Экспоненциальный
Этот список не является исчерпывающим, так как существует больше представлений, таких как матричное представление комплексных чисел.
Наличие выбора позволяет выбрать наиболее удобный для решения поставленной задачи. Например, вам понадобится экспоненциальная форма для вычисления дискретного преобразования Фурье в следующем разделе. Использование этой формы также подходит для умножения и деления комплексных чисел.
Вот краткое изложение отдельных форм комплексных чисел и их координат:
Форма Прямоугольный Полярный Алгебраический z = x + y y- Геометрический z = ( x , y ) z = ( r , φ) Тригонометрический г = | z |(cos( x /| z |) + jsin( y /| z |))z = r (cos(φ) + jsin(φ))Экспоненциальный г = | z |e atan2(y/x)jz = r (e jφ )Алгебраическая форма является родной для Python, когда вы указываете комплексные числа, используя их литералы.
 Вы также можете рассматривать их как точки на евклидовой плоскости в декартовой или полярной системе координат. Хотя в Python нет отдельных представлений для тригонометрической или экспоненциальной формы, вы можете проверить, соблюдаются ли математические принципы.
Вы также можете рассматривать их как точки на евклидовой плоскости в декартовой или полярной системе координат. Хотя в Python нет отдельных представлений для тригонометрической или экспоненциальной формы, вы можете проверить, соблюдаются ли математические принципы.Например, подстановка формулы Эйлера в тригонометрическую форму превратит ее в экспоненциальную. Вы можете либо вызвать
exp() модуля, либо возвести константуcmatheв степень, чтобы получить тот же результат:>>>
>>> импорт cmath >>> алгебраический = 3 + 2j >>> геометрический = сложный (3, 2) >>> радиус, угол = cmath.polar(алгебраический) >>> тригонометрический = радиус * (cmath.cos(угол) + 1j*cmath.sin(угол)) >>> экспонента = радиус * cmath.exp(1j*угол) >>> для числа в алгебраическом, геометрическом, тригонометрическом, экспоненциальном: ... печать (формат (число, "g")) ... 3+2j 3+2j 3+2j 3+2j
Все формы действительно представляют собой разные способы кодирования одного и того же числа.
 Однако вы не можете сравнивать их напрямую из-за ошибок округления, которые могут возникать при этом. Используйте
Однако вы не можете сравнивать их напрямую из-за ошибок округления, которые могут возникать при этом. Используйте cmath.isclose()для безопасного сравнения илиformat()числа в виде строк соответственно. В следующем разделе вы узнаете, как форматировать такие строки.Объяснение того, почему различные формы комплексного числа эквивалентны, требует исчисления и выходит далеко за рамки этого руководства. Однако, если вы интересуетесь математикой, то вы обнаружите, что связи между различными областями математики, проявляемые комплексными числами, весьма увлекательны.
Анализ комплексного числа в Python
Вы уже многое узнали о комплексных числах Python и видели предварительные примеры. Однако, прежде чем двигаться дальше, стоит затронуть некоторые заключительные темы. В этом разделе вы узнаете, как сравнивать комплексные числа, форматировать содержащие их строки и многое другое.
Проверка равенства комплексных чисел
Математически два комплексных числа равны, если они имеют одинаковые значения независимо от принятой системы координат.
 Однако преобразование между полярными и прямоугольными координатами обычно приводит к ошибкам округления в Python, поэтому вам нужно следить за незначительными различиями при их сравнении.
Однако преобразование между полярными и прямоугольными координатами обычно приводит к ошибкам округления в Python, поэтому вам нужно следить за незначительными различиями при их сравнении.Например, если вы рассматриваете точку на единичной окружности с радиусом, равным единице, и наклоненной под углом 60°, тогда тригонометрия работает хорошо, что упрощает преобразование с ручкой и бумагой:
>>>
>>> импортировать математику, cmath >>> z1 = cmath.rect(1, math.radians(60)) >>> z2 = комплекс (0,5, math.sqrt (3)/2) >>> z1 == z2 ЛОЖЬ >>> z1.реал, z2.реал (0,5000000000000001, 0,5) >>> z1.imag, z2.imag (0,8660254037844386, 0,8660254037844386)
Даже если вы знаете, что
z1иz2— это одна и та же точка, Python не может это определить из-за ошибок округления. К счастью, в документе PEP 485 определены функции для приблизительного равенства, которые доступны в модуляхmathиcmath:>>>
>>> math.
 isclose(z1.real, z2.real)
Истинный
>>> cmath.isclose(z1, z2)
Истинный
isclose(z1.real, z2.real)
Истинный
>>> cmath.isclose(z1, z2)
Истинный
Всегда используйте их при сравнении комплексных чисел! Если допуск по умолчанию недостаточно хорош для ваших расчетов, вы можете изменить его, указав дополнительные аргументы.
Заказ комплексных номеров
Если вы знакомы с кортежами, то знаете, что Python может их сортировать:
>>>
>>> планеты = [ ... (6, "сатурн"), ... (4, "марс"), ... (1, "ртуть"), ... (5, "юпитер"), ... (8, "нептун"), ... (3, «земля»), ... (7, "уран"), ... (2, "венера"), ... ] >>> из pprint импортировать pprint >>> pprint(отсортировано(планеты)) [(1, 'ртуть'), (2, «венера»), (3, «земля»), (4, «марс»), (5, «юпитер»), (6, «сатурн»), (7, «уран»), (8, «Нептун»)]
По умолчанию отдельные кортежи сравниваются слева направо:
>>>
>>> (6, "сатурн") < (4, "марс") ЛОЖЬ >>> (3, "земля") < (3, "луна") Истинный
В первом случае число
6больше, чем4, поэтому имена планет вообще не учитываются. Однако они могут помочь разрешить ничью. Однако это не относится к комплексным числам, поскольку они не определяют естественное отношение порядка. Например, вы получите ошибку, если попытаетесь сравнить два комплексных числа: 9.0003
Однако они могут помочь разрешить ничью. Однако это не относится к комплексным числам, поскольку они не определяют естественное отношение порядка. Например, вы получите ошибку, если попытаетесь сравнить два комплексных числа: 9.0003>>>
>>> (3 + 2j) < (2 + 3j) Traceback (последний последний вызов): Файл "
", строка 1, в TypeError: «<» не поддерживается между экземплярами «complex» и «complex» Должно ли мнимое измерение иметь больший вес, чем реальное? Следует ли сравнивать их величины? Это зависит от вас, и ответы будут разными. Так как вы не можете напрямую сравнивать комплексные числа, вам нужно указать Python, как их сортировать, указав пользовательский ключевая функция , например,
abs():>>>
>>> города = { ... комплекс(-64.78303, 32.2949): "Гамильтон", ... комплекс(-66.105721, 18.466333): "Сан-Хуан", ... комплекс(-80.1, 25. 761681): "Майами"
... }
>>> для города в сортировке (города, ключ = абс, реверс = истина):
... print(abs(город), города[город])
...
84.22818453809096 Майами
72,386473473 Гамильтон
68.63651945864338 Сан-Хуан
761681): "Майами"
... }
>>> для города в сортировке (города, ключ = абс, реверс = истина):
... print(abs(город), города[город])
...
84.22818453809096 Майами
72,386473473 Гамильтон
68.63651945864338 Сан-Хуан
Это отсортирует комплексные числа по их величине в порядке убывания.
Форматирование комплексных чисел в виде строк
Для комплексных чисел нет специальных кодов формата, но вы можете форматировать их действительную и мнимую части отдельно, используя стандартные коды для чисел с плавающей запятой. Ниже вы найдете несколько техник, демонстрирующих это. Некоторые из них фактически применят ваш спецификатор формата как к реальной, так и к мнимой частям за один раз.
Примечание. Форматирование строки позволяет игнорировать ошибку представления с плавающей запятой и делать вид, что ее не существует:
>>>
>>> импорт cmath >>> z = abs(3 + 2j) * cmath.exp(1j*cmath.phase(3 + 2j)) >>> ул(г) '(3+1.
 9999999999999996j)'
>>> формат(г, "г")
'3+2j'
9999999999999996j)'
>>> формат(г, "г")
'3+2j'
Буква
"g"в спецификаторе формата означает общий формат , который округляет ваше число до требуемой точности. Точность по умолчанию — шесть значащих цифр.Возьмем в качестве примера следующее комплексное число и отформатируем его с двумя десятичными знаками в обеих частях:
>>>
>>> z = pow(3 + 2j, 0,5) >>> напечатать (г) (1,8173540210239707+0,5502505227003375j)
Быстрый способ сделать это — либо вызвать
format()с числовым спецификатором формата, либо создать соответствующим образом отформатированную f-строку:>>>
>>> формат(z, ".2f") '1,82+0,55j' >>> f"{z:.2f}" '1,82+0,55j'Если вы хотите больше контроля, например, добавить дополнительный отступ вокруг оператора «плюс», тогда лучшим выбором будет f-строка:
>>>
>>> f"{z. real:.2f} + {z.imag:.2f}j"
«1,82 + 0,55j»
real:.2f} + {z.imag:.2f}j"
«1,82 + 0,55j»
Вы также можете вызвать
.format()для строкового объекта и передать ему позиционные или ключевые аргументы :>>>
>>> "{0:.2f} + {0:.2f}j".format(z.real, z.imag) '1,82 + 1,82j' >>> "{re:.2f} + {im:.2f}j".format(re=z.real, im=z.imag) «1,82 + 0,55j»Позиционные аргументы предоставляют последовательность значений, а аргументы ключевого слова позволяют ссылаться на них по имени. Точно так же вы можете использовать строковый оператор по модулю (
%) либо с кортежем, либо со словарем:>>>
>>> "%.2f + %.2fj" % (z.real, z.imag) «1,82 + 0,55j» >>> "%(re).2f + %(im).2fj" % {"re": z.real, "im": z.imag} «1,82 + 0,55j»Однако здесь используется другой синтаксис заполнителей, и он несколько устарел.
Создание собственного сложного типа данных
Модель данных Python определяет набор специальных методов, которые можно реализовать, чтобы сделать ваши классы совместимыми с определенными встроенными типами.
 Допустим, вы работали с точками и векторами и хотели получить угол между двумя точками.0274 связанных векторов . Вы можете вычислить их скалярное произведение и провести некоторую тригонометрию. Кроме того, вы можете воспользоваться комплексными числами.
Допустим, вы работали с точками и векторами и хотели получить угол между двумя точками.0274 связанных векторов . Вы можете вычислить их скалярное произведение и провести некоторую тригонометрию. Кроме того, вы можете воспользоваться комплексными числами.Давайте сначала определим ваши классы:
от ввода import NamedTuple класс Point (NamedTuple): х: плавающий у: плавать вектор класса (NamedTuple): точка отсчета конец: ТочкаPointимеет координатыxиy, аVectorсоединяет две точки. Возможно, вы помнитеcmath.phase(), который вычисляет угловое расстояние комплексного числа. Теперь, если вы относитесь к своим векторам как к комплексным числам и знаете их фазы, вы можете вычесть их, чтобы получить желаемый угол.Чтобы Python распознавал экземпляры векторов как комплексные числа, вы должны указать
.__complex__()в теле класса:класс Vector (NamedTuple): точка отсчета конец: Точка защита __complex__(я): реальный = self. end.x - self.start.x
изображение = self.end.y - self.start.y
возвратный комплекс (реальный, имаг)
end.x - self.start.x
изображение = self.end.y - self.start.y
возвратный комплекс (реальный, имаг)
Внутренний код всегда должен возвращать экземпляр типа данных
complex, поэтому он обычно создает новое комплексное число из вашего объекта. Здесь вы вычитаете начальную и конечную точки, чтобы получить горизонтальное и вертикальное смещения, которые служат реальной и мнимой частями. Метод будет выполняться через делегирование , когда вы вызываете глобальныйкомплекс ()для экземпляра вектора:>>>
>>> вектор = вектор (точка (-2, -1), точка (1, 1)) >>> комплекс(вектор) (3+2к)
В некоторых случаях вам не нужно делать такое литье самостоятельно. Давайте рассмотрим пример на практике:
>>>
>>> v1 = вектор (точка (-2, -1), точка (1, 1)) >>> v2 = вектор (точка (10, -4), точка (8, -1)) >>> импортировать математику, cmath >>> math.
 степени(cmath.phase(v2) - cmath.phase(v1))
90,0
степени(cmath.phase(v2) - cmath.phase(v1))
90,0
У вас есть два вектора, идентифицированные четырьмя различными точками. Затем вы передаете их непосредственно в
cmath.phase(), который выполняет преобразование в комплексное число и возвращает фазу. Разность фаз — это угол между двумя векторами.Разве это не прекрасно? Вы уберегли себя от ввода большого количества подверженного ошибкам кода, комбинируя комплексные числа и немного магии Python.
Вычисление дискретного преобразования Фурье с комплексными числами
Хотя для вычисления коэффициентов синуса и косинуса частот периодической функции с помощью преобразования Фурье можно использовать действительные числа, обычно удобнее иметь дело только с одним комплексным коэффициентом на частоту. Дискретное преобразование Фурье в сложном домене задается следующей формулой:
Для каждого бина частоты k измеряется корреляция сигнала и конкретной синусоидальной волны, выраженная комплексным числом в экспоненциальной форме.
 (Спасибо, Леонард Эйлер!) Угловую частоту волны можно рассчитать, умножив угол скругления, равный 2π радианам, на k по количеству дискретных отсчетов:
(Спасибо, Леонард Эйлер!) Угловую частоту волны можно рассчитать, умножив угол скругления, равный 2π радианам, на k по количеству дискретных отсчетов:Кодирование этого на Python выглядит довольно аккуратно, если вы воспользуетесь преимуществом
комплекстип данных:из cmath import pi, exp def дискретное_преобразование Фурье (х, к): омега = 2 * пи * k / (N := len(x)) вернуть сумму (x [n] * exp (-1j * omega * n) для n в диапазоне (N))Эта функция представляет собой буквальную транскрипцию приведенных выше формул. Теперь вы можете запустить частотный анализ звука, который вы загружаете из аудиофайла с помощью модуля Python
waveили который вы синтезируете с нуля. Один из блокнотов Jupyter Notebook, сопровождающих это руководство, позволяет вам играть с синтезом и анализом звука в интерактивном режиме.Чтобы построить частотный спектр с помощью Matplotlib, вы должны знать частоту дискретизации, которая определяет ваше разрешение частотного бина , а также предел Найквиста:
импортировать matplotlib.
 pyplot как plt
определение plot_frequency_spectrum (
образцы,
выборки_в_секунду,
минимальная_частота=0,
макс_частота = нет,
):
num_bins = длина (образцы) // 2
nyquist_frequency = Samples_per_second // 2
величины = []
для k в диапазоне (num_bins):
величины.append (abs (discrete_fourier_transform (выборки, k)))
# Нормализация величин
величины = [m / max(величины) для m в величинах]
# Вычислить бины по частоте
bin_разрешение = выборки_в_секунду / длина (выборки)
Frequency_bins = [k * bin_resolution для k в диапазоне (num_bins)]
plt.xlim (минимальная_частота, максимальная_частота или частота Найквиста)
plt.bar (частота_бинов, величины, ширина = бин_разрешение)
pyplot как plt
определение plot_frequency_spectrum (
образцы,
выборки_в_секунду,
минимальная_частота=0,
макс_частота = нет,
):
num_bins = длина (образцы) // 2
nyquist_frequency = Samples_per_second // 2
величины = []
для k в диапазоне (num_bins):
величины.append (abs (discrete_fourier_transform (выборки, k)))
# Нормализация величин
величины = [m / max(величины) для m в величинах]
# Вычислить бины по частоте
bin_разрешение = выборки_в_секунду / длина (выборки)
Frequency_bins = [k * bin_resolution для k в диапазоне (num_bins)]
plt.xlim (минимальная_частота, максимальная_частота или частота Найквиста)
plt.bar (частота_бинов, величины, ширина = бин_разрешение)
Количество бинов по частоте в спектре равно половине отсчетов, а частота Найквиста ограничивает самую высокую частоту, которую вы можете измерить. Преобразование возвращает комплексное число, величина которого соответствует амплитуде синусоиды на заданной частоте, тогда как ее угол равен фазе .

Примечание: Чтобы получить правильные значения амплитуды, необходимо удвоить число и разделить полученную амплитуду на число выборок. С другой стороны, если вас интересует только гистограмма частоты, вы можете нормализовать величины по их сумме или максимальной частоте.
Вот образец частотного графика звуковой волны, состоящей из трех тонов — 440 Гц, 1,5 кГц и 5 кГц — с одинаковыми амплитудами:
График частотного спектраОбратите внимание, что это был чисто академический пример, поскольку вычисление дискретного преобразования Фурье с вложенными итерациями имеет временную сложность O ( n 2 ), что делает его непригодным для использования на практике. Для реальных приложений вы хотите использовать алгоритм быстрого преобразования Фурье (FFT) , который лучше всего реализован в библиотеке C, такой как FFT в SciPy.
Заключение
Простота использования комплексных чисел в Python делает их удивительно интересным и практичным инструментом.
 Вы видели двумерные вектора реализованные практически бесплатно, и благодаря им вы смогли анализировать звуковые частоты . Комплексные числа позволяют элегантно выразить 90 274 математических формул 90 277 в коде без большого количества стандартного синтаксиса, стоящего на пути.
Вы видели двумерные вектора реализованные практически бесплатно, и благодаря им вы смогли анализировать звуковые частоты . Комплексные числа позволяют элегантно выразить 90 274 математических формул 90 277 в коде без большого количества стандартного синтаксиса, стоящего на пути.Из этого руководства вы узнали, как:
- Определить комплексные числа с литералами в Python
- Представление комплексных чисел в прямоугольных и полярных координатах
- Использовать комплексные числа в арифметических выражениях
- Воспользуйтесь преимуществами встроенного
модуля cmath - Перевод математических формул непосредственно в код Python
Каков ваш опыт работы с комплексными числами Python? Вы когда-нибудь боялись их? Как вы думаете, какие еще интересные задачи они позволят вам решить?
Вы можете щелкнуть ссылку ниже, чтобы получить полный исходный код для этого руководства:
линейная алгебра - Как выяснить аргумент комплексного числа?
Спросил
Изменено 9 лет, 9 месяцев назад
Просмотрено 77 тысяч раз
$\begingroup$
У меня есть абсолютное значение комплексного числа ,
$$ r = |z| = \sqrt{х^2 + у^2}$$
, когда $z = x + iy$ — комплексное число.

Как вычислить аргумент $z$?
Спасибо.
- линейная алгебра
- тригонометрия
- комплексные числа
$\endgroup$
2
$\begingroup$
Вам следует знать, что любое комплексное число можно представить в виде точки на декартовой ($x$-$y$) плоскости. Другими словами, комплексное число $z=a+b\text i$ связано с некоторой точкой (скажем, $A$), имеющей координаты $(a,b)$ на декартовой плоскости. Возможно, вы слышали это как Диаграмма Аргана .
Пусть $\tan \theta$ будет отношением направлений вектора $\vec{OA}$ (Предположим, что линия, соединяющая начало координат , $O$ и точку $A$, является вектором)
Тогда $$\tan\theta =\frac ba \имплицитно \theta= \arctan \Большой (\фракция ба\Большой )$$
Однако мы пока не можем утверждать, что $\theta$ является $\operatorname {Arg}(z)$.
 Есть небольшая деталь, которую нам нужно иметь в виду (спасибо пользователю за указание на это!). Нам нужно следить за квадрантом, в котором лежит наше комплексное число, и работать соответственно.
Есть небольшая деталь, которую нам нужно иметь в виду (спасибо пользователю за указание на это!). Нам нужно следить за квадрантом, в котором лежит наше комплексное число, и работать соответственно.
Пример Допустим, есть 2 комплексных числа $z=a+b\text i$ и $w=-a-b\text i$. Тогда $$\operatorname{Arg}(w)=\arctan\Big( \frac {-b}{-a} \Big )= \arctan\Big( \frac {b}{a} \Big )= \ имя_оператора{Arg}(z)$$ что просто нелепо. Это предполагает, что $w$, лежащий в третьем квадранте на диаграмме Аргана, имеет тот же аргумент, что и комплексное число ($z$), которое находится в первом квадранте. Чтобы исправить эту проблему, нам придется выдвинуть несколько простых условий. Как мы только что видели, один из них может выглядеть примерно так: $\text{ if } a,b<0 \text{ then } \operatorname{Arg}(z)=\theta -\pi$Вот список условий для вычисления аргумента (это уже упоминалось в одном из ответов выше, и я просто повторно размещаю его здесь). Как только вы интуитивно почувствуете это, это должно прийти к вам естественным образом.

$\varphi = \arg(z) = \begin{случаи} \тета & \mbox{если} х > 0 \\ \theta + \pi & \mbox{если } x < 0 \mbox{ и } y \ge 0\\ \theta - \pi & \mbox{если } x < 0 \mbox{ и } y < 0\\ \frac{\pi}{2} & \mbox{если } x = 0 \mbox{ и } y > 0\\ -\frac{\pi}{2} & \mbox{если } x = 0 \mbox{ и } y < 0\\ \mbox{неопределенный} & \mbox{если } x = 0 \mbox{ и } y = 0. \end{case}$В качестве альтернативы вы можете использовать тот факт, что $|z| \sin \theta= b$ (или $|z| \cos \theta= a$), а затем найти $\theta$. Однако вам, возможно, все же придется внести последние поправки (как мы делали ранее), чтобы получить правильный ответ. Так что это не короче из двух методов.
$\endgroup$
6
$\begingroup$
Обратите внимание, что "ответ" $arctan(y/x)$ просто неверен. Чтобы увидеть это, посмотрите на пример $-1-i$: $\arctan(-1/-1) = 45°$, но правильно будет $225°$.
 И это не только проблема с определением диапазона аргумента.
И это не только проблема с определением диапазона аргумента.Правильный ответ дает Википедия:
$\varphi = \arg(z) = \begin{случаи} \arctan(\frac{y}{x}) & \mbox{if } x > 0 \\ \arctan(\frac{y}{x}) + \pi & \mbox{если } x < 0 \mbox{ и } y \ge 0\\ \arctan(\frac{y}{x}) - \pi & \mbox{если } x < 0 \mbox{ и } y < 0\\ \frac{\pi}{2} & \mbox{если } x = 0 \mbox{ и } y > 0\\ -\frac{\pi}{2} & \mbox{если } x = 0 \mbox{ и } y < 0\\ \mbox{неопределенный} & \mbox{если } x = 0 \mbox{ и } y = 0. \end{case}$ 9{-1}(\frac{b}{a})$, если вам удобнее использовать tagent.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Комплексные числа
Существуют две основные формы комплексных чисел
- Декартова
- Полярная
Комплексные числа в декартовой форме
Комплексное число состоит из действительной и мнимой частей и может быть выражено в декартовой форме форма как
Z = a + j b (1)
, где
Z = комплексное число
2 a 90 часть0002 j b = мнимая часть (обычно используется i вместо j)
Комплексное число может быть представлено на диаграмме декартовых осей с действительной и мнимой осью, также называемой диаграммой Аргана :
Пример - комплексные числа на картезианской форме
Комплексные номера
Z A = 3 + J 2 (2A)
Z B = -3 + J 3 (2B) Z B = -3 + J 3 (2B) 0258
Z C = -2 - J 2 (2C)
может быть представлен на диаграмме Арганд:
Добавление и выявление комплексных чисел
.
 отдельно действительные части и мнимые части числа.
отдельно действительные части и мнимые части числа.Пример — сложение двух комплексных чисел
Z A = 3 + j 2
Z B = -3 + j 3
Z (A+B) = (3 + (-3)) + (j 2 + j 3)
= j 9
9004 Комплекс числа в полярной форме
Комплексное число в полярной форме может быть выражено как
Z = r (cosθ + j sinθ) (3)
, где
модуль модуля (или модуля) Z - и пишется как "mod Z" или |Z |θ = аргумент (или амплитуда) Z - и записывается как "arg Z"
r можно определить по теореме Пифагора 2 ) 1/2 (4)
θ can be determined by trigonometry
θ = tan -1 (b / a) (5)
(3) can также выражаться как
Z = r e j θ (6)
Как видно из (1), (3) и (6) - комплексное число можно записать тремя различными способами.

Пример. Комплексное число в полярной форме
Комплексное число
Z a = 3 + j 2
может быть выражено в полярной форме путем вычисления модуля и аргумента.
"Модуль" можно рассчитать по формуле. (4) :
r = (3 2 + 2 2 ) 1/2
= 3,606
(5) :
θ = TAN -1 (2/3)
= 33,69 O
Комплексное число на Polar Form (3):
Комплексное число на полярной форме (3):
.
. = 3,606 (cos(33,69) + j sin(33,69))
Или альтернативно (6)
Z a = 3.606 e j 33.69
Adding or Subtraction of Complex Numbers
Adding Complex Numbers
Z a = a + j b
Z b = C + J D
Z A + Z B = (A + J B) + (C + J D)
= j + ch + ch + ch + ch + ch + ch + c + c + c + c + c + c + c + c + c + c + c + c + ch + ch + ch + j + j + j + j + j + j +.
 г) (6)
г) (6)
or alternative
Z a = r a (cosθ a + j sin θ a )
Z b = r b (cosθ b + j sin θ b )
Z a + Z b = r a (cosθ a + j sin θ a ) + r b (cosθ b + j sin θ b )
= ( r a cosθ a + r b cosθ b ) + j ( r a sin θ a + r b sin θ b ) (6b)
or alternatively
Z a = r a e jθa
Z b = r b e jθb
Z a + Z b = r a e jθa + r b e jθb
= ( r a cosθ a + r b cosθ b ) + j ( r a sin θ a + r b sin θ b ) (6c)
Example - Adding Complex NumbersZ a = 3 + j 2
Z B = 5 - J 4
Z A + Z B = (3 + + J 2) 975) (3 + + Дж.

= (3 + 5) + j (2 + (-4))
= 8 - J 2
. Пример - Adding Adge Adpt Adpt Adding Adding Adding Adged
4. Z
a = 3 (cos 35 + j sin 35)
Z b = 2 (cos 15 + j sin 15)
Z a + Z б = ( 3 cos 35+ 2 cos 15) + j (3 sin 35 + 2 sin 15 )
= 4,388
= 4,388 - 29203
= 4,388 - 29028
.
 8
8 Z a = a + j b
Z b = c + j d
Z a - Z b = (a + j b ) - (C + J D)
= (A - C) + J (B - D) (7)
Пример - Вычищенные номера
Z A A A A A A A A A A A A A A A A A A A A A A A A A A A 0. (cos 35 + j sin 35)
Z B = 2 (COS 15 + J SIN 15)
Z A - 7 Z A - 7.1240 A - Z A - Z A - Z A . ) - 2 (cos 15 + j sin 15)
= ( 3 cos 35 - 2 cos 15 ) + j ( 3 sin 35 - 2 sin 15 )
= 0.
 52 + j 1.2
52 + j 1.2 Multiplication of Complex Numbers
Z a = a + j b
Z b = c + j d
Z a Z b = (a + j b) (c + j d)
= a c + a (j d) + (j b) c + (j b) (j d) 9 02 =
9003 9020 + j a d + j b c + j 2 b d (8)
Since j 2 = -1 - (8) can be transformed to
Z a Z b = (a + j b ) (C + J D)
= (A C - B D) + J (A D + B C) (8B)
Пример - Умножение комплексных номеров
7 - Умножение комплексных номеров
7 - Умножение комплексных номеров
7 . 3 + j 2
3 + j 2 Z b = 5 - j 4
Z a Z b = (3 + j 2) (5 - j 4)
= (3 5 - 2 (-4)) + j(3 (-4) + 2 5)
= 23 - j 2
Комплексное сопряжение
Комплексное сопряжение числа (а + jb) — это (a — jb) .
Multiplying a complex number with its complex conjugate results in a real number like
Z a = a + jb
Z a * = a - jb
Z A Z A * = (A + JB) (JB) (A + JB)
(JB) 88888888888888888 гг.0927 2 - j a b + j a b - j 2 b 2= a 2 - (- b 2 )
= a 2 + b 2 (9)
Example - Multiplying a Complex Number with its Conjugate
Z a = 3 + j 2
Z a * = 3 - j 2
Z a Z a * = (3 + j 2 ) (3 - j 2)
= 3 2 + 2 2
= 1 3
Division of Complex Numbers
Разделение комплексных чисел может быть сделано с помощью конъюгата конфессий:
Z A = A + JB
Z B = Z B = Z B = Z B = Z B = Z B = Z B .


 Произвольное число
Произвольное число

 5i
5i Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн
 Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:
Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:
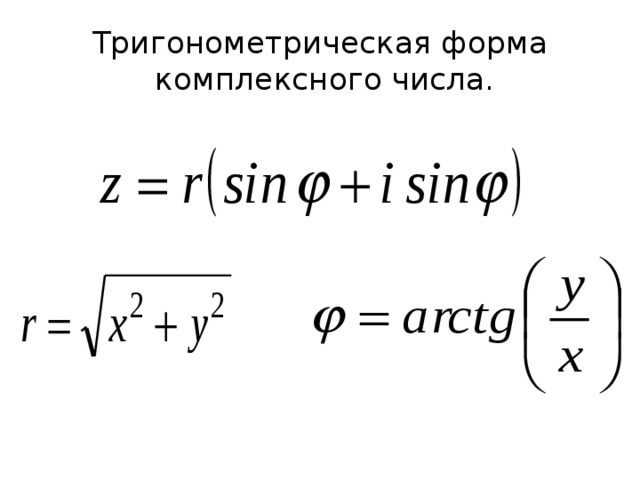
 9{ — 1}}\sqrt 3 = \frac{\pi }{3}\]
9{ — 1}}\sqrt 3 = \frac{\pi }{3}\] Типичными вариантами являются изучение какого-либо специализированного инструмента, такого как MATLAB, или поиск сторонней библиотеки. Python — редкое исключение, потому что в него встроены комплексные числа.0003
Типичными вариантами являются изучение какого-либо специализированного инструмента, такого как MATLAB, или поиск сторонней библиотеки. Python — редкое исключение, потому что в него встроены комплексные числа.0003 Чтобы загрузить образец кода, используемый в этом руководстве, щелкните ссылку ниже:
Чтобы загрузить образец кода, используемый в этом руководстве, щелкните ссылку ниже: Когда вы проверите его тип, вы убедитесь, что это действительно комплексное число:
Когда вы проверите его тип, вы убедитесь, что это действительно комплексное число: В Python вы можете использовать строчные буквы
В Python вы можете использовать строчные буквы 
 Например, у сложения есть коммутативное свойство, которое позволяет поменять местами две части литерала комплексного числа без изменения его значения:
Например, у сложения есть коммутативное свойство, которое позволяет поменять местами две части литерала комплексного числа без изменения его значения: Следовательно, без другой части это просто комплексное число.
Следовательно, без другой части это просто комплексное число.
 Аналогия не такая уж надуманная. Комплексные числа имеют геометрическую интерпретацию в декартовой системе координат , которую вы вскоре изучите. Вы можете думать о комплексных числах как о двумерных.
Аналогия не такая уж надуманная. Комплексные числа имеют геометрическую интерпретацию в декартовой системе координат , которую вы вскоре изучите. Вы можете думать о комплексных числах как о двумерных. Например, вы можете передать нечисловое значение, например строковый литерал, чтобы получить соответствующий
Например, вы можете передать нечисловое значение, например строковый литерал, чтобы получить соответствующий  В противном случае вы получите ошибку времени выполнения. С технической точки зрения,
В противном случае вы получите ошибку времени выполнения. С технической точки зрения, 
 Python моделирует эту взаимосвязь с помощью концепции, называемой числовой башней 9.0277, описанный в PEP 3141:
Python моделирует эту взаимосвязь с помощью концепции, называемой числовой башней 9.0277, описанный в PEP 3141: 14, комплекс)
ЛОЖЬ
14, комплекс)
ЛОЖЬ
 real = 3,14
Traceback (последний последний вызов):
Файл "
real = 3,14
Traceback (последний последний вызов):
Файл " conjugate()
3.14
conjugate()
3.14

 Когда вы запишете это алгебраически, вы сможете применить распределительное свойство и упростить формулу, выделив и сгруппировав общие термины:
Когда вы запишете это алгебраически, вы сможете применить распределительное свойство и упростить формулу, выделив и сгруппировав общие термины:
 ) Когда оба числа выражены в их стандартных формах, хитрость состоит в том, чтобы умножить числитель и знаменатель на сопряженное число последнего:
) Когда оба числа выражены в их стандартных формах, хитрость состоит в том, чтобы умножить числитель и знаменатель на сопряженное число последнего: значения:
значения: Если вам интересна математика, ознакомьтесь с формулой Де Муавра, которая позволяет вам это сделать.
Если вам интересна математика, ознакомьтесь с формулой Де Муавра, которая позволяет вам это сделать. Его вершины примерно обозначены тремя крупными городами, географические координаты которых следующие:
Его вершины примерно обозначены тремя крупными городами, географические координаты которых следующие: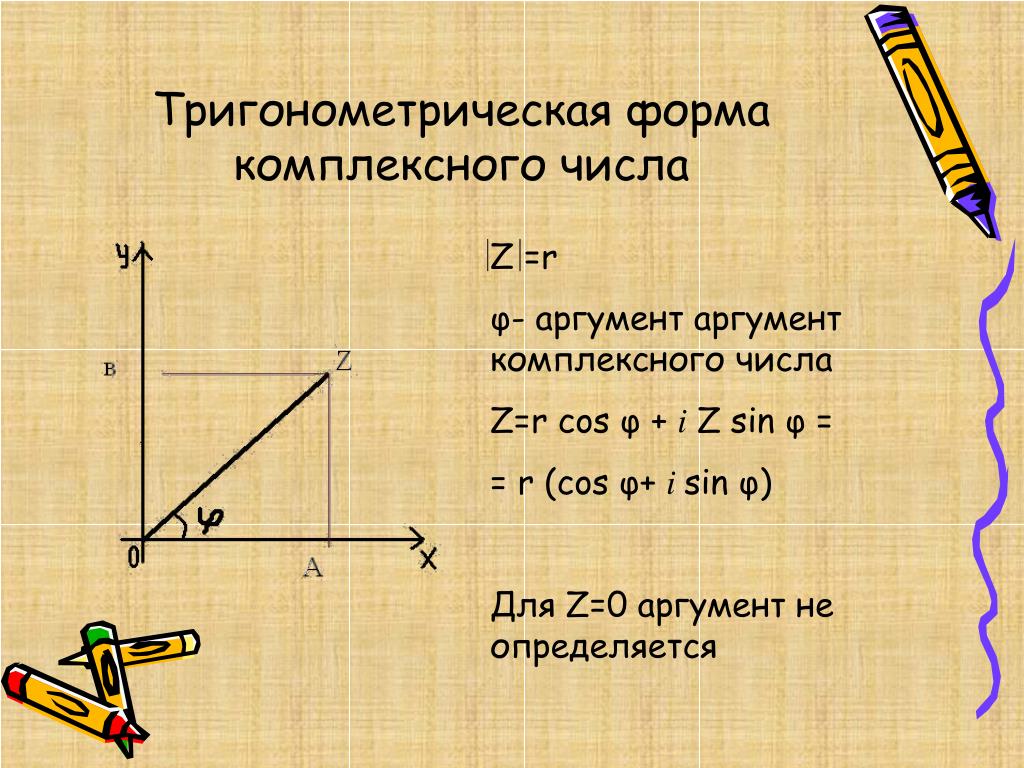
 1, 25.761681)
miami_fl = -80,1 + 25,761681j
1, 25.761681)
miami_fl = -80,1 + 25,761681j
 605551275463989
605551275463989
 Векторы создаются путем вычитания исходной точки из целевой:
Векторы создаются путем вычитания исходной точки из целевой: Давайте переместим его так, чтобы его геометрический центр совпал с началом координат. Все три вершины будут , переведенные на на длину вектора, указанного геометрическим центром, но в противоположном направлении:
Давайте переместим его так, чтобы его геометрический центр совпал с началом координат. Все три вершины будут , переведенные на на длину вектора, указанного геометрическим центром, но в противоположном направлении:
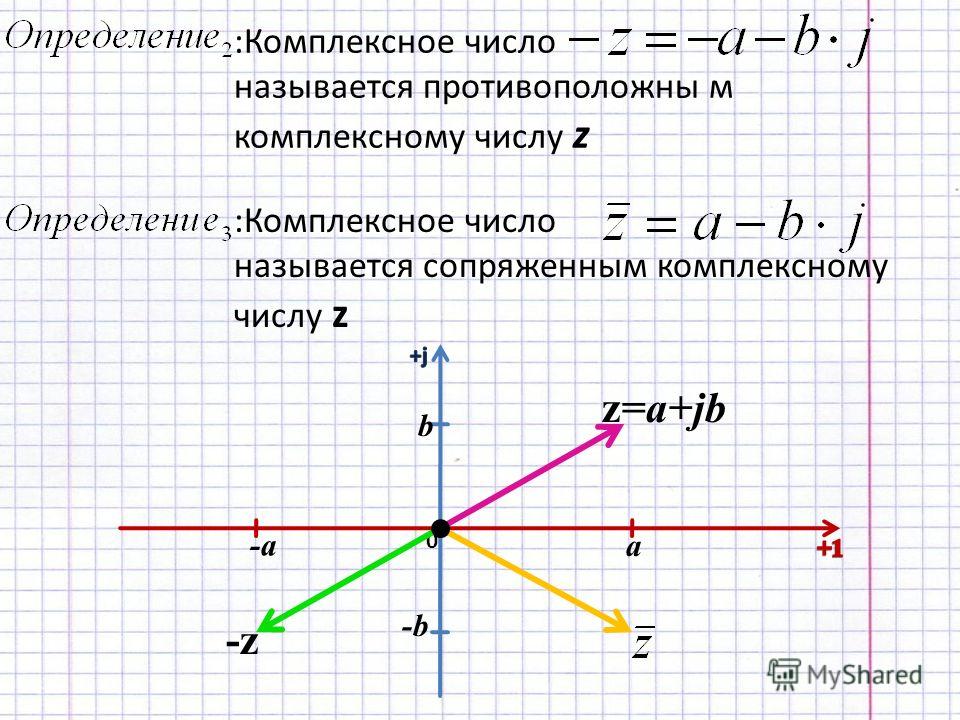 Это должно растянуть ваш Бермудский треугольник, чтобы он выглядел больше на графике:
Это должно растянуть ваш Бермудский треугольник, чтобы он выглядел больше на графике:
 Обратите внимание, как возведение воображаемой единицы в последующие степени заставляет ее многократно повторять одни и те же значения. Вы можете экстраполировать это на дробные показатели и ожидать, что они будут соответствовать промежуточным углам.
Обратите внимание, как возведение воображаемой единицы в последующие степени заставляет ее многократно повторять одни и те же значения. Вы можете экстраполировать это на дробные показатели и ожидать, что они будут соответствовать промежуточным углам. polar(z)
вернуть cmath.rect (радиус, угол + math.radians (градусы))
def rotate2(z: комплекс, градусы: число с плавающей запятой) -> комплекс:
вернуть z * cmath.rect(1, math.radians(степени))
polar(z)
вернуть cmath.rect (радиус, угол + math.radians (градусы))
def rotate2(z: комплекс, градусы: число с плавающей запятой) -> комплекс:
вернуть z * cmath.rect(1, math.radians(степени))
 К сожалению, даже если вы знаете все о модуле Python
К сожалению, даже если вы знаете все о модуле Python  real, nanj.imag
(0,0, нан)
>>> infj.real, infj.imag
(0.0, инф)
real, nanj.imag
(0,0, нан)
>>> infj.real, infj.imag
(0.0, инф)

 polar(3 + 2j)
(3,605551275463989, 0,5880026035475675)
polar(3 + 2j)
(3,605551275463989, 0,5880026035475675)
 acos(z.real / abs(z))
0,5880026035475675
>>> math.asin(z.imag / abs(z))
0,5880026035475676
>>> math.atan(z.imag / z.real) # Предпочитает math.atan2(z.imag, z.real)
0,5880026035475675
>>> импортировать cmath
>>> cmath.acos(z.real / abs(z))
(0,5880026035475675-0j)
acos(z.real / abs(z))
0,5880026035475675
>>> math.asin(z.imag / abs(z))
0,5880026035475676
>>> math.atan(z.imag / z.real) # Предпочитает math.atan2(z.imag, z.real)
0,5880026035475675
>>> импортировать cmath
>>> cmath.acos(z.real / abs(z))
(0,5880026035475675-0j)
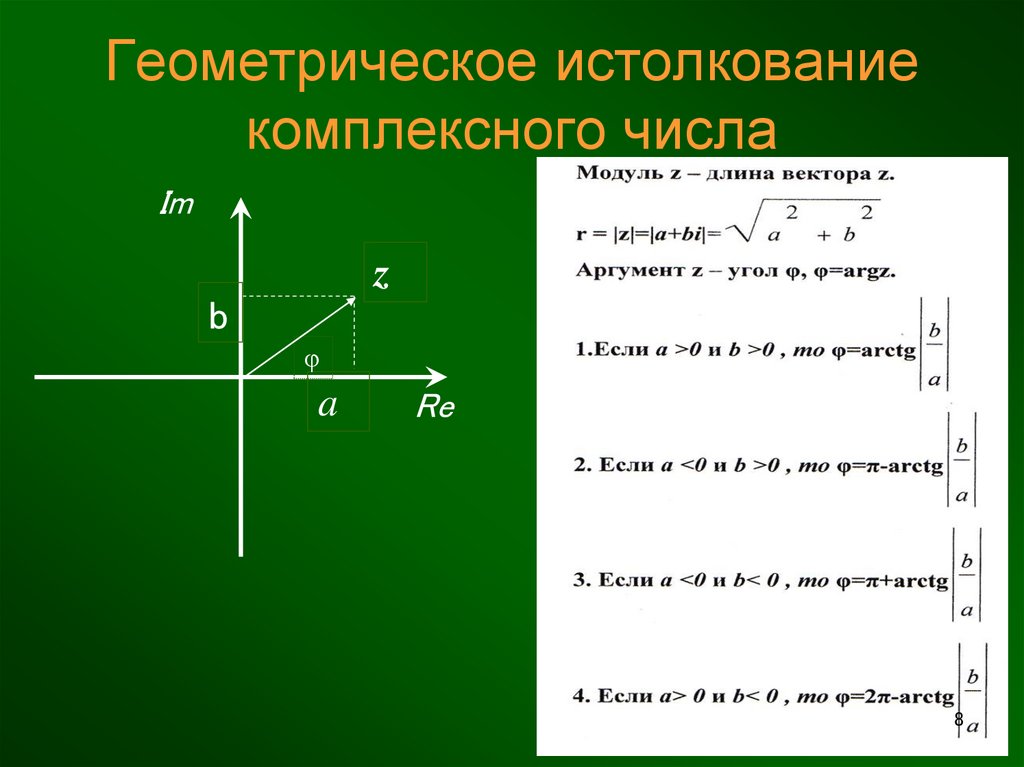 atan(1 / 1) == math.atan(-1 / -1)
Истинный
>>> math.atan2(1, 1) == math.atan2(-1, -1)
ЛОЖЬ
atan(1 / 1) == math.atan(-1 / -1)
Истинный
>>> math.atan2(1, 1) == math.atan2(-1, -1)
ЛОЖЬ
 rect()
rect() 
 Вы также можете рассматривать их как точки на евклидовой плоскости в декартовой или полярной системе координат. Хотя в Python нет отдельных представлений для тригонометрической или экспоненциальной формы, вы можете проверить, соблюдаются ли математические принципы.
Вы также можете рассматривать их как точки на евклидовой плоскости в декартовой или полярной системе координат. Хотя в Python нет отдельных представлений для тригонометрической или экспоненциальной формы, вы можете проверить, соблюдаются ли математические принципы. Однако вы не можете сравнивать их напрямую из-за ошибок округления, которые могут возникать при этом. Используйте
Однако вы не можете сравнивать их напрямую из-за ошибок округления, которые могут возникать при этом. Используйте  Однако преобразование между полярными и прямоугольными координатами обычно приводит к ошибкам округления в Python, поэтому вам нужно следить за незначительными различиями при их сравнении.
Однако преобразование между полярными и прямоугольными координатами обычно приводит к ошибкам округления в Python, поэтому вам нужно следить за незначительными различиями при их сравнении. isclose(z1.real, z2.real)
Истинный
>>> cmath.isclose(z1, z2)
Истинный
isclose(z1.real, z2.real)
Истинный
>>> cmath.isclose(z1, z2)
Истинный
 Однако они могут помочь разрешить ничью. Однако это не относится к комплексным числам, поскольку они не определяют естественное отношение порядка. Например, вы получите ошибку, если попытаетесь сравнить два комплексных числа: 9.0003
Однако они могут помочь разрешить ничью. Однако это не относится к комплексным числам, поскольку они не определяют естественное отношение порядка. Например, вы получите ошибку, если попытаетесь сравнить два комплексных числа: 9.0003 761681): "Майами"
... }
>>> для города в сортировке (города, ключ = абс, реверс = истина):
... print(abs(город), города[город])
...
84.22818453809096 Майами
72,386473473 Гамильтон
68.63651945864338 Сан-Хуан
761681): "Майами"
... }
>>> для города в сортировке (города, ключ = абс, реверс = истина):
... print(abs(город), города[город])
...
84.22818453809096 Майами
72,386473473 Гамильтон
68.63651945864338 Сан-Хуан
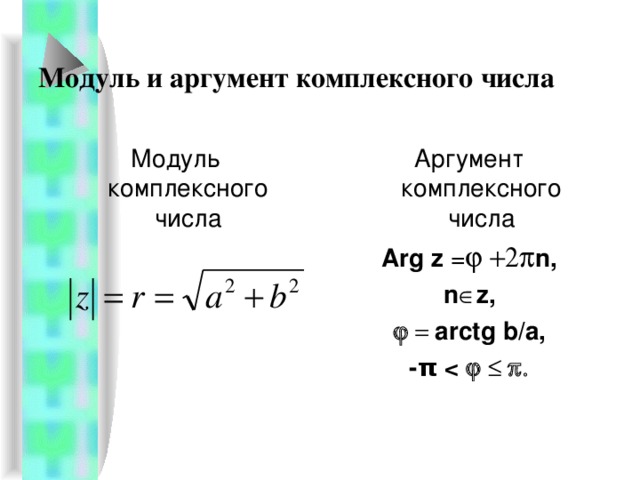 9999999999999996j)'
>>> формат(г, "г")
'3+2j'
9999999999999996j)'
>>> формат(г, "г")
'3+2j'
 real:.2f} + {z.imag:.2f}j"
«1,82 + 0,55j»
real:.2f} + {z.imag:.2f}j"
«1,82 + 0,55j»
 Допустим, вы работали с точками и векторами и хотели получить угол между двумя точками.0274 связанных векторов . Вы можете вычислить их скалярное произведение и провести некоторую тригонометрию. Кроме того, вы можете воспользоваться комплексными числами.
Допустим, вы работали с точками и векторами и хотели получить угол между двумя точками.0274 связанных векторов . Вы можете вычислить их скалярное произведение и провести некоторую тригонометрию. Кроме того, вы можете воспользоваться комплексными числами. end.x - self.start.x
изображение = self.end.y - self.start.y
возвратный комплекс (реальный, имаг)
end.x - self.start.x
изображение = self.end.y - self.start.y
возвратный комплекс (реальный, имаг)
 степени(cmath.phase(v2) - cmath.phase(v1))
90,0
степени(cmath.phase(v2) - cmath.phase(v1))
90,0
 (Спасибо, Леонард Эйлер!) Угловую частоту волны можно рассчитать, умножив угол скругления, равный 2π радианам, на k по количеству дискретных отсчетов:
(Спасибо, Леонард Эйлер!) Угловую частоту волны можно рассчитать, умножив угол скругления, равный 2π радианам, на k по количеству дискретных отсчетов: pyplot как plt
определение plot_frequency_spectrum (
образцы,
выборки_в_секунду,
минимальная_частота=0,
макс_частота = нет,
):
num_bins = длина (образцы) // 2
nyquist_frequency = Samples_per_second // 2
величины = []
для k в диапазоне (num_bins):
величины.append (abs (discrete_fourier_transform (выборки, k)))
# Нормализация величин
величины = [m / max(величины) для m в величинах]
# Вычислить бины по частоте
bin_разрешение = выборки_в_секунду / длина (выборки)
Frequency_bins = [k * bin_resolution для k в диапазоне (num_bins)]
plt.xlim (минимальная_частота, максимальная_частота или частота Найквиста)
plt.bar (частота_бинов, величины, ширина = бин_разрешение)
pyplot как plt
определение plot_frequency_spectrum (
образцы,
выборки_в_секунду,
минимальная_частота=0,
макс_частота = нет,
):
num_bins = длина (образцы) // 2
nyquist_frequency = Samples_per_second // 2
величины = []
для k в диапазоне (num_bins):
величины.append (abs (discrete_fourier_transform (выборки, k)))
# Нормализация величин
величины = [m / max(величины) для m в величинах]
# Вычислить бины по частоте
bin_разрешение = выборки_в_секунду / длина (выборки)
Frequency_bins = [k * bin_resolution для k в диапазоне (num_bins)]
plt.xlim (минимальная_частота, максимальная_частота или частота Найквиста)
plt.bar (частота_бинов, величины, ширина = бин_разрешение)

 Вы видели двумерные вектора реализованные практически бесплатно, и благодаря им вы смогли анализировать звуковые частоты . Комплексные числа позволяют элегантно выразить 90 274 математических формул 90 277 в коде без большого количества стандартного синтаксиса, стоящего на пути.
Вы видели двумерные вектора реализованные практически бесплатно, и благодаря им вы смогли анализировать звуковые частоты . Комплексные числа позволяют элегантно выразить 90 274 математических формул 90 277 в коде без большого количества стандартного синтаксиса, стоящего на пути.
 Есть небольшая деталь, которую нам нужно иметь в виду (спасибо пользователю за указание на это!). Нам нужно следить за квадрантом, в котором лежит наше комплексное число, и работать соответственно.
Есть небольшая деталь, которую нам нужно иметь в виду (спасибо пользователю за указание на это!). Нам нужно следить за квадрантом, в котором лежит наше комплексное число, и работать соответственно. 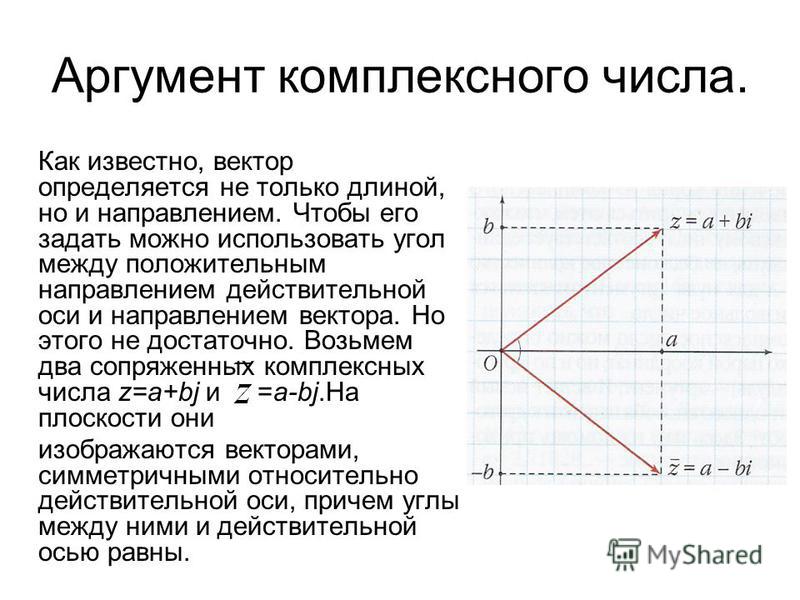
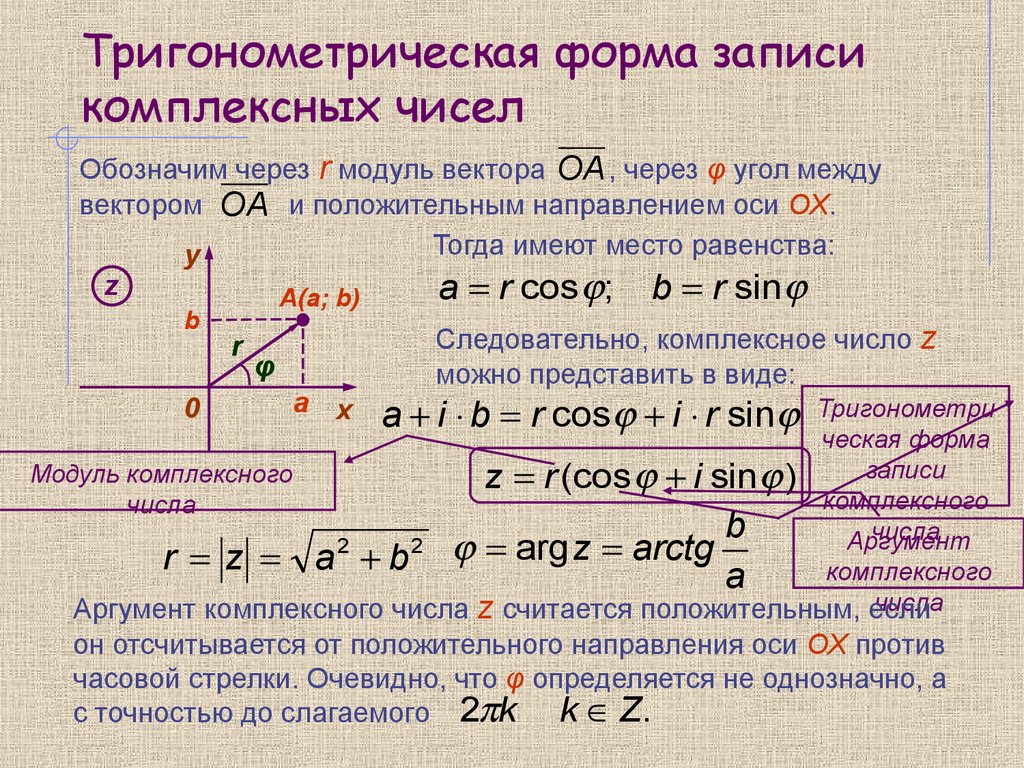 И это не только проблема с определением диапазона аргумента.
И это не только проблема с определением диапазона аргумента.
 отдельно действительные части и мнимые части числа.
отдельно действительные части и мнимые части числа.
 г) (6)
г) (6) 
 8
8  52 + j 1.2
52 + j 1.2  3 + j 2
3 + j 2 