+ онлайн-решатель с бесплатными шагами
Калькулятор неравенств – это онлайн-инструмент для оценки неравенств . Его можно использовать для решения квадратного неравенства и линейного неравенства с одной неизвестной переменной .
Каждый раз расчеты выполняются пошагово и выдаются точные результаты.
Что такое калькулятор неравенств?
Калькулятор неравенств – это онлайн-инструмент, который определяет абсолютное значение, рациональное, полиномиальное, квадратичное и линейное неравенства.
Неравенства — это математические формулы, которые используются для проведения неравных сравнений. Однако, если оба выражения равны, используется выражение равенства.
Многочисленные математические задачи на сравнение чисел с использованием различных неравенств, в том числе меньше ($<$), больше ($>$), меньше или равно ($\leq$), больше или равно ($\ geq$) и не равно ($\neq$).
Неравенства меньше и больше – единственные из них, которые считаются строгими неравенствами.
Как пользоваться калькулятором неравенств?
Вы можете использовать Калькулятор неравенства , следуя подробному решению, изложенному ниже. Калькулятор неравенств рассчитает значение неизвестной переменной для заданного выражения.
Шаг 1
Введите данные и введите количество решек и направлений в указанные поля на макете Калькулятора.
Шаг 2
Нажмите кнопку «Отправить» , чтобы найти значение неизвестного для заданного выражения, а также будет отображено полное пошаговое решение для Расчет неравенств .
Как работает калькулятор неравенств?
Калькулятор неравенств работает по тем же принципам, что и решение задач на основе уравнений, но поскольку присутствует знак сравнения, требуются следующие дополнительные рекомендации:
- Направление неравенства изменяется путем умножения обеих сторон на одно и то же строго отрицательное действительное число:
если a$<$b и c$<$0, то a x c $>$ b x c
- Направление неравенства сохраняется не изменится, если обе части умножить на одно и то же строго положительное целое число.

если a$<$b и c$>$0, то a x c $<$ b x c
- 0056
Если a $<$ b и c $<$ 0, то a . в > б. c
- Деление на одно и то же строго положительное действительное число с каждой стороны неравенства не меняет направления неравенства:
Если a $<$ b и c $>$ 0, то a . с < б . c
- Вещественное число, добавленное к каждой стороне неравенства, будь то положительное или отрицательное, не влияет на направление неравенства.
если a$<$b и c $\in R $, то a+c$<$b+c
- Вещественное число, одинаковое с обеих сторон неравенства, будь то положительное или отрицательное, не влияет на направление неравенства.
, если a$<$b и c $\in R $, то a-c$<$b-c
- Направление неравенства не зависит от возведения в квадрат каждой из его положительных сторон:
, если 0$<$a$<$ b then $ a_2 if a$<$b$<$0 then $ a_2>b_2$ если a$<$b, то $ \frac{1}{a}> \frac{1}{b}$ It также возможно объединить несколько неравенств: если a$<$b и c$<$d, то a+c$<$b+ d если 0$<$a$<$b и 0$<$c$<$d, то a x c$<$b x d 92 $ всегда больше x, когда x отрицательно, вторая часть решения должна быть точной. Вот несколько примеров, чтобы лучше понять работу Калькулятора неравенств . Решить 4x+3 $<$ 23? Учитывая, что \[ 4x+3 < 23 \] Вычтите «-3» с обеих сторон. \[ 4x+3 -3 < 23 – 3 \] \[ 4x < 20 \] Разделить ‘4’ на обе части \[ \frac{4x}{4} < \frac{20}{4} \] x $<$ 5 Решить для c \[ 3(x + c) – 4y \geq 2x – 5c \] Здесь ‘c’ рассматривается как переменная, а ‘x’ как константа. \[ 3(x + c) – 4y \geq 2x – 5c \] \[ 3x + 3c – 4y \geq 2x – 5c \] \[ 3x – 2x – 4y \geq -5c -3c \] \[ х – 4y \geq -8c \] \[ 8c \leq 4y – x \] \[ c \leq (4y – x)/ 8 \] Решить данное неравенство \[ -2 < 6 – \frac{ 2x}{3} < 4 \] Сначала умножим каждую часть неравенства на 3. Поскольку умножается положительное число, неравенство не меняется: -6 $< $ 6 – 2x $<$ 12 Теперь после умножения вычтите число 6 с каждой стороны неравенства: -12 $<$ -2x $<$ 6 После этого разделите каждую сторону на 2: -6 $<$ -x $<$ 3 Наконец, умножьте каждую сторону на − 1. Поскольку мы умножаем обе стороны на отрицательное число , неравенства меняют направление, а это означает, что символ «меньше» превратился в символ «больше», как показано ниже: 6 $>$ x $>$ — 3 И это решение Хотя, для порядка, поменяем местами числа (и убедимся, что неравенства указывают правильно) 92} — 3x — 10 > 0\quad \стрелка вправо \quad \left( {x — 5} \right)\left( {x + 2} \right) > 0\] Итак, как только мы перенесем все на левую сторону и разложим, мы увидим, что левая часть будет равна нулю при \(x = 5\) и \(x = — 2\).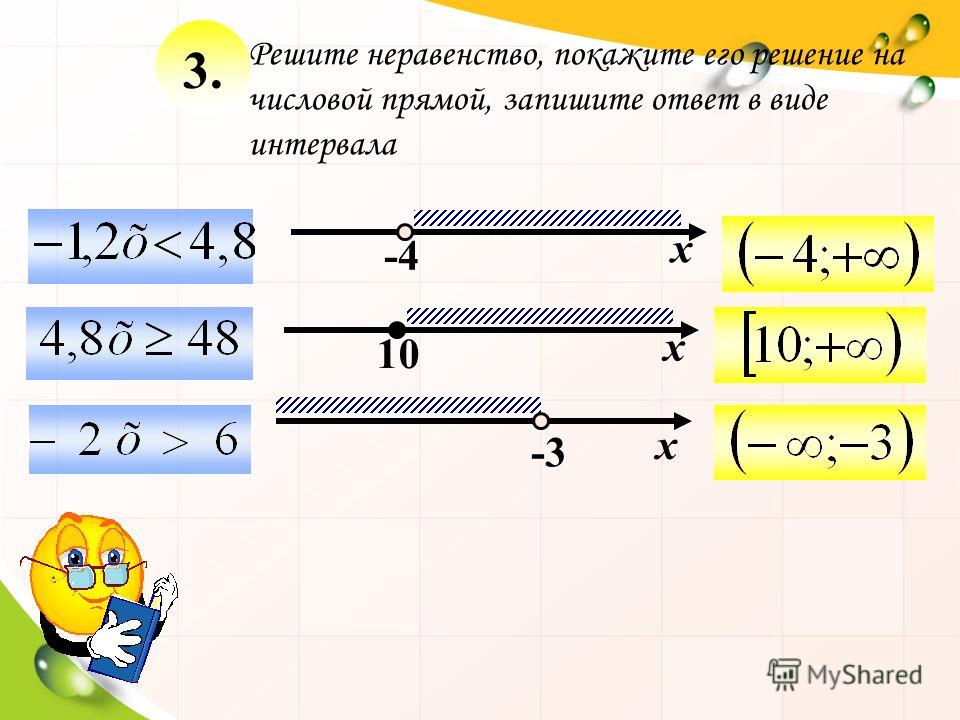
Принцип решения неравенства
Решенные примеры
Пример 1
Решение
Пример 2
Решение

Пример 3
Решение

Чтобы найти решение этого неравенства, нужно вспомнить, что многочлены — это хорошие гладкие функции, не имеющие разрывов. Это означает, что если мы движемся по числовой прямой (в любом направлении), если значение многочлена меняет знак (скажем, с положительного на отрицательный), то оно ДОЛЖНО перейти через ноль!
Итак, это означает, что эти два числа (\(x = 5\) и \(x = — 2\)) являются ЕДИНСТВЕННЫМИ местами, где многочлен может менять знак. Затем числовая линия делится на три области. В каждом регионе, если неравенство выполняется для одной точки из этого региона, то оно выполняется для ВСЕХ точек в этом регионе. Если это не так ( т.е. в одной точке области было положительно, а в другой отрицательно), то где-то в этой области тоже должно быть ноль, но этого не может быть, так как мы уже определили все места, где многочлен может быть равен нулю! Точно так же, если неравенство не выполняется для какой-то точки в этом регионе, оно не выполняется для ЛЮБОЙ точки в этом регионе.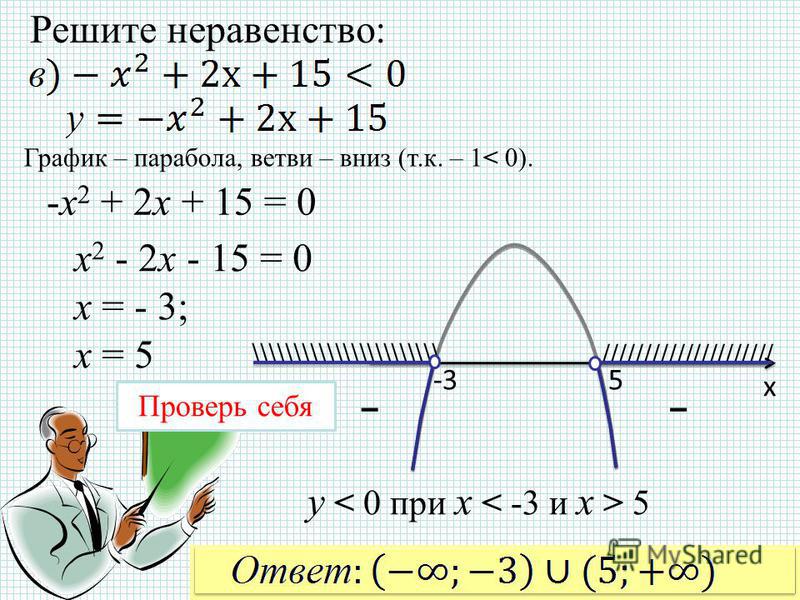
Это означает, что все, что нам нужно сделать, это выбрать контрольную точку из каждого региона (с которой легко работать, , т.е. небольших целых чисел, если возможно) и подставить ее в неравенство. Если контрольная точка удовлетворяет неравенству, то удовлетворяет каждая точка в этой области, а если контрольная точка не удовлетворяет неравенству, то ни одна точка в этой области не удовлетворяет.
Последнее замечание по этому поводу. У меня есть три версии приведенного выше неравенства. Вы можете подставить контрольную точку в любой из них, но обычно проще всего подставить контрольные точки в факторизованную форму неравенства. Итак, если вы доверяете своим факторинговым возможностям, используйте именно его. Однако, если вы допустили ошибку при факторинге, вы можете получить неверное решение, если будете использовать для тестирования факторизованную форму. Это компромисс. С факторинговой формой во многих случаях работать проще, но если вы допустили ошибку при факторинге, вы можете получить неверное решение.

