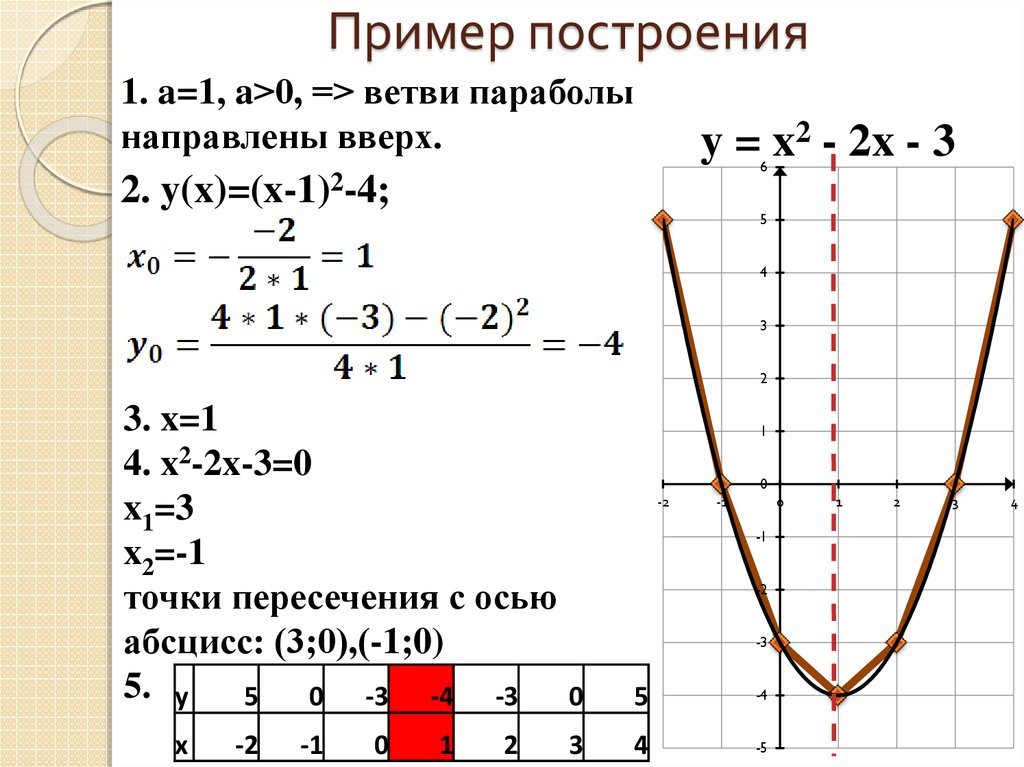
Как только вы введете правильное квадратичное выражение, вы можете нажать на кнопку «Вычислить», и на экране появится окно график функции будет сгенерирован, показывая этапы вычисления вершина параболы и Ось симметрии а также .
Квадратичные функции занимают главенствующее место в базовой алгебре, поскольку они часто используются в контексте решения задачи
квадратные уравнения
и прикладные проблемы.
Как построить график квадратичной формы?
Построить график квадратичной функции просто, в том смысле, что вы знаете, что ВСЕ квадратичные функции будут иметь форму параболы. Но все же парабол бесконечно много. Нам нужно знать немного больше, чтобы определить точную параболу, которая представляет данную квадратичную функцию.
Шаги для нахождения графика квадратичной функции
- Шаг 1: Четко определите заданную квадратичную функцию и при необходимости упростите ее
-
Шаг 2: После упрощения определите функцию в виде f(x) = ax² + bx + c.
Обратите внимание, что a не может быть нулем
- Шаг 3: Если a > 0, вы знаете, что график будет параболой, раскрывающейся вверх, тогда как если a
- Шаг 4: Ось симметрии находится в точке x* = -b/(2a), что указывает на «центр» параболы
- Шаг 5: Обратите внимание, что x* = -b/(2a) — координата x вершины параболы, а y* = f(x*) = a(x*)² + b(x*) + c — координата y вершины
Обратите внимание, что a не может быть нулем
Этого должно быть достаточно, чтобы иметь четкое представление о соответствующем квадратичном графике. Дальнейшим шагом будет построение некоторых точек на графике, выбирая различные точки на оси x и находя их соответствующее изображение через функцию, чтобы облегчить процесс нахождения функции
график функции
.
вы получите корни квадратного уравнения, а когда корни действительны, они представляют собой точки, в которых парабола пересекает ось x.
Особый случай имеет место, когда корни комплексные, в этом случае парабола не пересекает ось x.
Типы квадратичных графиков
Как мы уже говорили, ВСЕ одномерные квадратичные функции будут представлены параболами, но в зависимости от того, a > 0 или a
Другое различие типов парабол может быть для тех, которые «центрированы» (т.е
вершина
это происхождение), и те, которые не являются таковыми.
2+2x-3\), из чего следует, что соответствующие коэффициенты являются:
\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]
Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]
Теперь нам нужно подставить значение \(x_V = \displaystyle -3\) в квадратичную функцию, чтобы получить:
\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]
Таким образом, координата x вершины равна \(x_V = \displaystyle -3\), а координата y вершины равна \(y_V = \displaystyle -6\).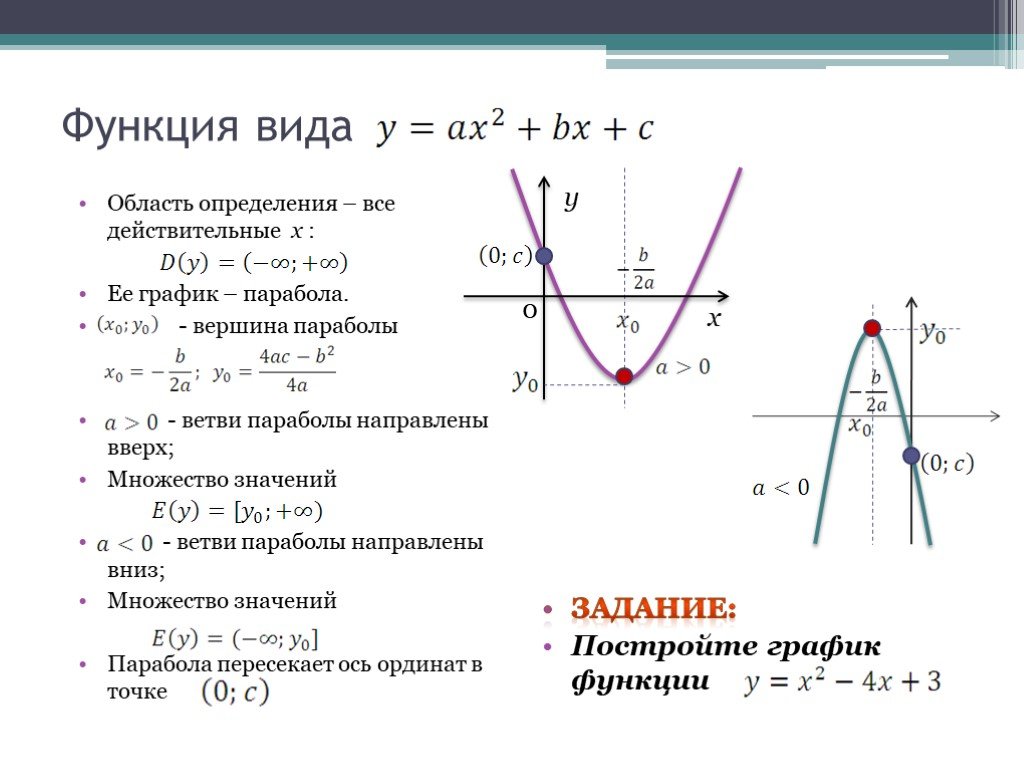
2+3x-2\), из чего следует, что соответствующие коэффициенты являются:
\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]
Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]
Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{9}{8}\) в квадратичную функцию, чтобы получить:
\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]
Таким образом, координата x вершины равна \(x_V = \displaystyle -\frac{9}{8}\), а координата y вершины равна \(y_V = \displaystyle -\frac{59}{16}\).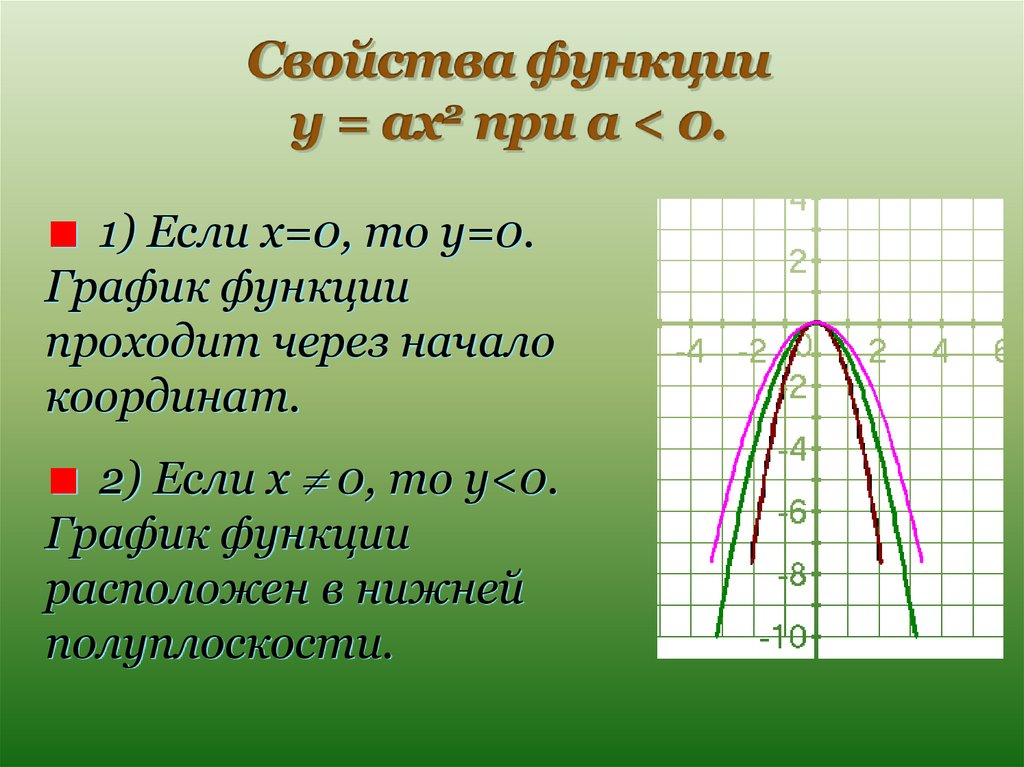
Это означает, что точка, обозначающая вершину, равна \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).
Графически получается следующее:
Больше квадратичных калькуляторов
Большинство всех приложений в базовой алгебре основаны на решении некоторого рода Квадратное уравнение , поэтому у него есть сильная педагогическая цель узнать об этом.
квадратичная формула
является одним из самых печально известных учебных предметов в математике.
Дело не в том, что кубические или квартовые уравнения не существуют, а в том, что
квадратные уравнения
это те, которые мы можем легко объяснить.
Исследовать функцию и построить график онлайн калькулятор с решением. Калькуляторы для построения графика функции
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.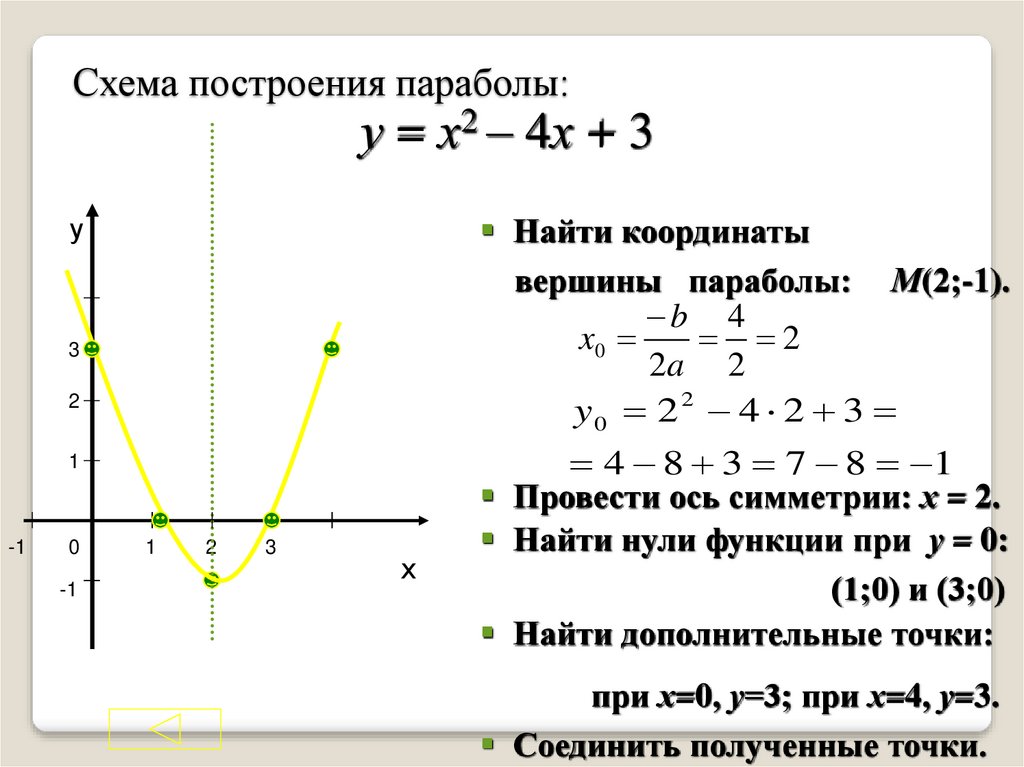
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см.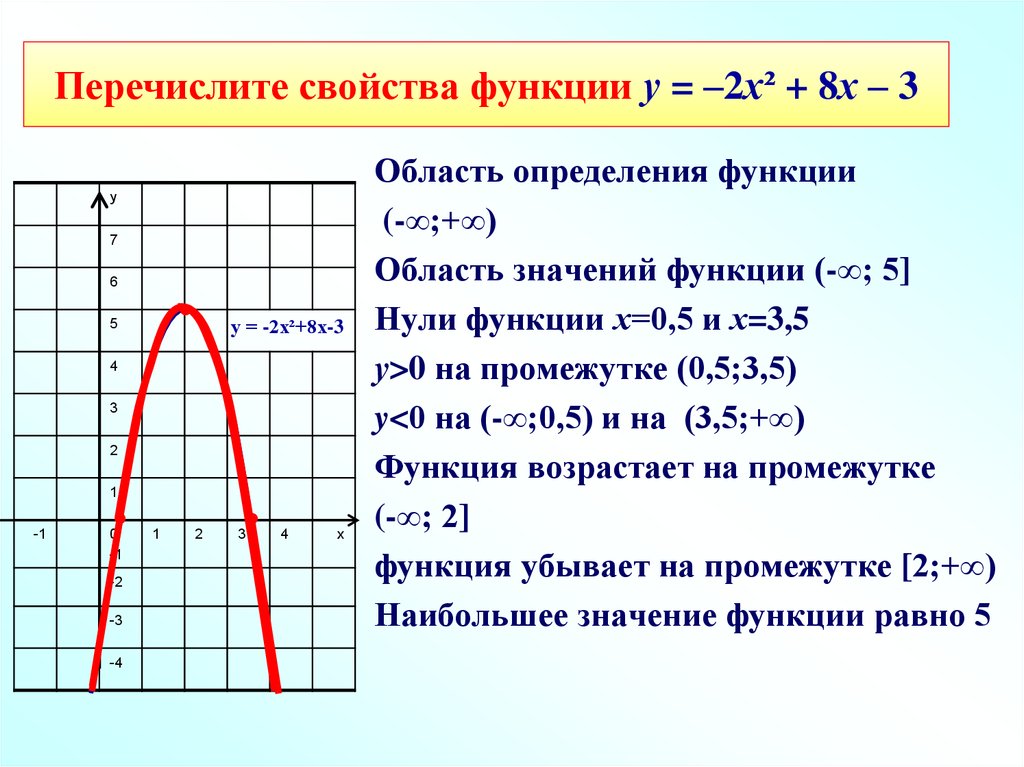
также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3).
Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны.
Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
д.Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2.
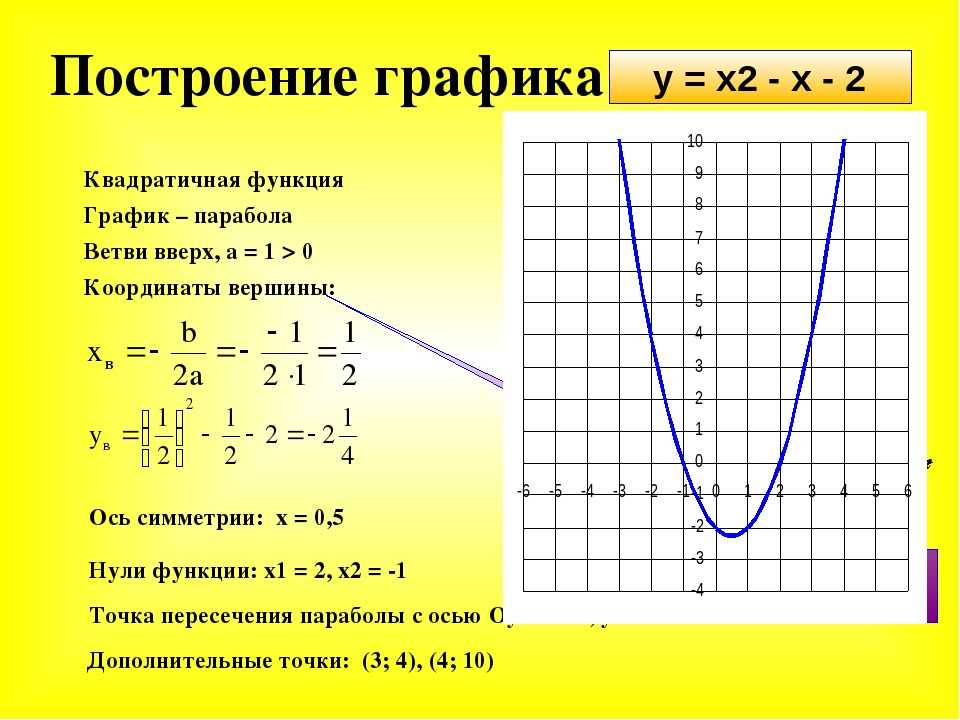
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
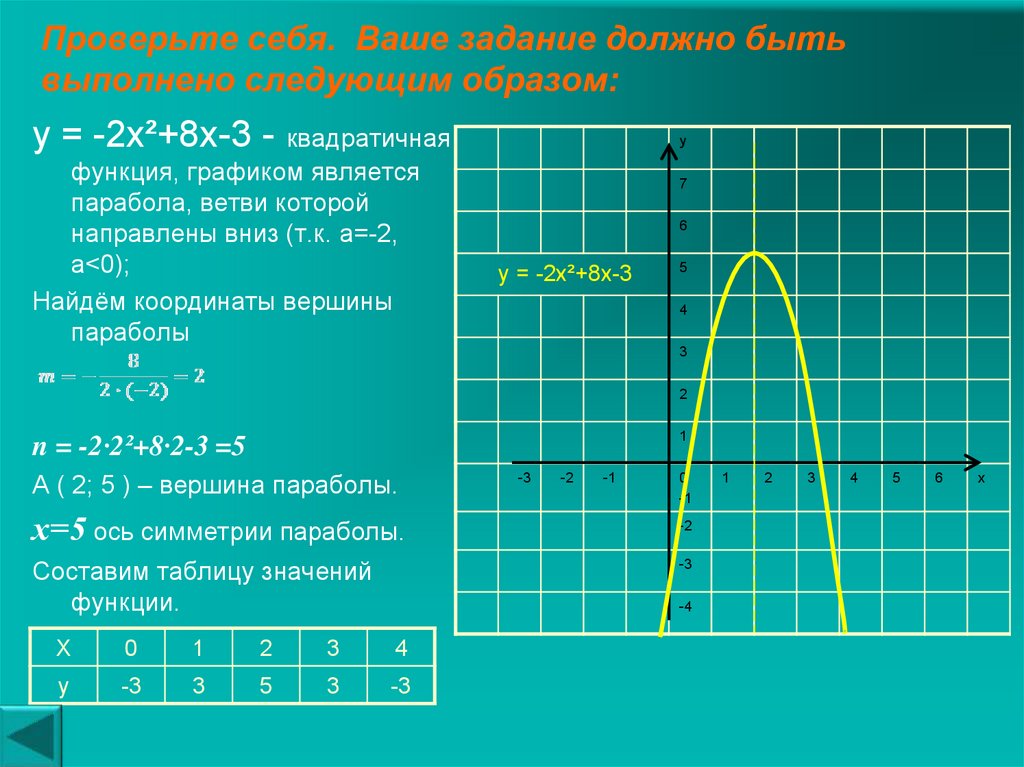
Квадратичный график — MathCracker.com
Инструкции: Используйте этот калькулятор Quadratic Graph, чтобы построить график любой предоставленной вами квадратичной функции, показывающий все шаги.
Пожалуйста, введите квадратичную функцию, которую вы хотите изобразить в форме ниже.
92 — 1/5, при условии, что это правильный квадратичный
функция.
После того, как вы введете действительное квадратное выражение, вы можете нажать кнопку «Рассчитать», и будет построен график функции, показывающий вам шаги вычисления вершины параболы и также ось симметрии.
Квадратичные функции играют преобладающую роль в основах алгебры, так как они часто используются в контексте решения квадратные уравнения и прикладные задачи. По сути, это базовые полиномы, в которых есть много интересного. характеристики.
Как построить график квадратичных уравнений?
Сделать квадратичный график просто, в том смысле, что вы знаете, что ВСЕ квадратичные функции будут иметь форму параболы.
Но все же есть
бесконечные параболы. Нам нужно знать немного больше, чтобы определить точную параболу, которая представляет данную квадратичную функцию.
Шаги по нахождению графика квадратичной функции
- Шаг 1: Четко определите заданную квадратичную функцию и при необходимости упростите
- Шаг 2: После упрощения определите функцию в виде f(x) = ax² + bx + c. Обратите внимание, что a не может быть нулевым
- Шаг 3: Если a > 0, вы знаете, что график будет представлять собой параболу, направленную вверх, тогда как если a
- Шаг 4: Ось симметрии находится в точке x* = -b/(2a), что говорит вам о «центре» параболы
- Шаг 5: обратите внимание, что x* = -b/(2a) является координатой x вершины параболы, а y* = f(x*) = a(x*)² + b(x*) + c координата y вершины
Этого должно быть достаточно, чтобы иметь четкое представление о соответствующем квадратичном графе. Следующим шагом было бы нанести несколько точек на график,
выбор различных точек на оси x и нахождение их соответствующего изображения с помощью функции, чтобы помочь процессу нахождения
график функции.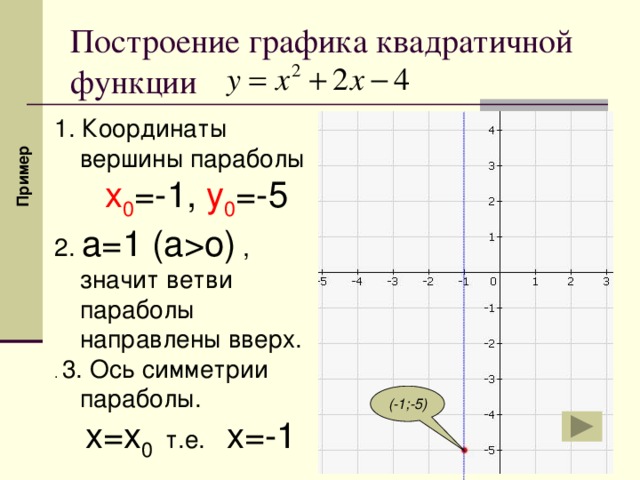
Квадратичная формула
Связана ли квадратичная формула с графиком квадратичной функции? Вы держите пари! Геометрически говоря, при решении квадратное уравнение 92 + Ьх + с = 0 \]
вы получаете корни квадратного уравнения, и когда корни действительны, они представляют собой точки, в которых парабола пересекает ось x.
Особый случай возникает, когда корни комплексные, и в этом случае парабола не пересекает ось x.
Типы квадратичных графиков
Как мы упоминали ранее, ВСЕ одномерные квадратичные функции будут представлены параболами, но в зависимости от того, a > 0 или a
92+2x-3\), из чего следует, что соответствующие коэффициенты равны:\[а = \фракция{1}{3}\] \[б = 2\] \[с = -3\]
Подставив известные значения \(a\) и \(b\) в формулу координаты x вершины, получим:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]
Теперь нам нужно подставить значение \(x_V = \displaystyle -3\) в квадратичную функцию, так что мы получим: 92+3x-2\), из чего следует, что соответствующие коэффициенты равны:
\[а = \фракция{4}{3}\] \[б = 3\] \[с = -2\]
Подставив известные значения \(a\) и \(b\) в формулу координаты x вершины, получим:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]
Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{9}{8}\) в квадратичную функцию, так что мы получим: 92+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\ frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]
Следовательно, координата x вершины равна \(x_V = \displaystyle -\frac{9}{8}\), а координата y вершины равна \(y_V = \displaystyle -\frac{59 {16}\).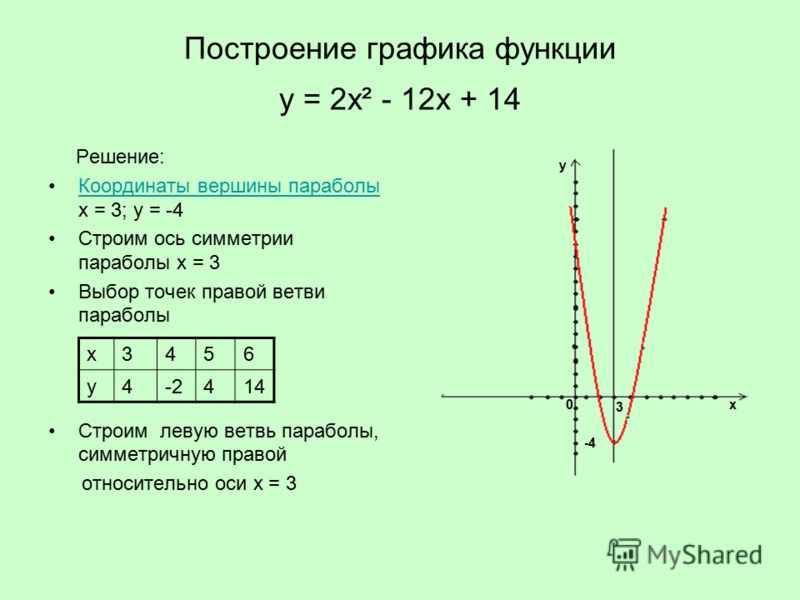
Это указывает на то, что точкой, представляющей вершину, является \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).
Графически получается следующее:
Другие квадратичные калькуляторы
Большинство приложений базовой алгебры основаны на решении какого-либо квадратного уравнения, поэтому оно имеет сильное педагогическое значение. Цель узнать об этом.
Квадратичная формула — один из самых печально известных обучаемых объектов в математике. Дело не в том, что уравнений кубической или четвертой степени не существует, дело в том, что квадратные уравнения — это те, которые мы можем легко объяснить.
Решение квадратных уравнений с помощью таблиц
Приступим к работе. Введение. Использование таблиц для представления решений. Использование таблиц для оценки решений.
Стандарты TEKS и ожидания учащихся
A(8) Квадратичные функции и уравнения.
Учащийся применяет стандарты математического процесса для решения квадратных уравнений с помощью технологий и без них и оценивает обоснованность их решений. Студент формулирует статистические зависимости и оценивает их обоснованность на основе реальных данных. Студент должен:
A(8)(B) решать квадратные уравнения, имеющие действительные решения, путем разложения на множители, извлечения квадратных корней, завершения квадрата и применения квадратной формулы функции, которые обеспечивают разумную подгонку данных для оценки решений и прогнозирования реальных проблем
Ресурс Цели
Используйте таблицу значений и заданный график, чтобы найти решение квадратного уравнения.
Основные вопросы
Как можно найти решение(я) квадратного уравнения по таблице значений?
Как найти решение(я) квадратного уравнения по графику?
Как можно оценить решение(я) квадратного уравнения по таблице?
Словарь
- Уравнение
- Функция
- x -Перехват
- Парабола
- Квадратное уравнение
- Ноль
Таблицу и график можно использовать для отображения решений квадратного уравнения.
График и таблица ниже показывают точки для квадратичной функции
y = x2- x — 6.
Для нахождения решения можно использовать оба представления квадратного уравнения.
Решения квадратных уравнений называются корнями. Корни – это 90 181 x 90 182 отрезков (нули) квадратичной функции.
Каждому квадратному уравнению соответствует квадратичная функция. Например, если вам дано квадратное уравнение
x2 + 5x + 4 = 0,
соответствующая квадратичная функция равна
f(x) = x2 + 5x + 4.
Квадратное уравнение может иметь два решения, одно решение или не иметь решения.
Ответьте на следующие вопросы о квадратных уравнениях и функциях.
Таблица значений может быть сгенерирована из квадратичной функции путем подстановки значений x и вычисления значений для f(x).
При просмотре таблицы значений квадратичной функции x 90 182 – значения 90 181 x 90 182, где 90 181 y = 0.
Это соответствует 90 181 x – значениям, где f(x) равно 0 в функциональном обозначении.
Подстановку можно использовать для проверки решений функции
f(x)=x2-x-6.
Иногда, когда у вас есть таблица значений функции, решения соответствующего уравнения не очевидны. Например, рассмотрим функцию
y = x2 — 2
и связанное с ним уравнение
x2 — 2 = 0.
В таблице ниже показано соотношение из уравнения.
Если вы хотите решить связанное уравнение
x2 — 2 = 0
из этой таблицы, нет значений y, равных 0 для использования. В этом случае мы должны оценить, где находятся нули из таблицы.
Щелкните изображение ниже, чтобы просмотреть видео об оценке нулей квадратичной функции по таблице. Во время просмотра подумайте, как можно использовать приведенную выше таблицу для оценки решений уравнения 9.0005
x2 — 2 = 0,
Вы изучили различные способы определения решений квадратных уравнений с помощью таблиц значений.