Как найти k и b по графику линейной функции?
В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти \(k\) и \(b\) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти \(k\) и \(b\), если известен график линейной функции.
Способ 1
Первый способ основывается на трех фактах:
-
Линейная функция пересекает ось \(y\) в точке \(b\).
Примеры:Но не советую определять так \(b\), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Примеры:
-
Если функция возрастает, то знак коэффициента \(k\) плюс, если убывает – минус, а если постоянна, то \(k=0\).
Примеры:
-
Чтоб конкретнее определить \(k\) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить \(k\) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.
Примеры:
Пример (ЕГЭ)
Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
\(b=3\) – это сразу видно. Функция идет вниз, значит \(k<0\).
Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.
\(k=-\frac{AC}{BC}=-\frac{1}{3}\).
Получается \(g(x)=-\frac{1}{3}x+3\).
Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.
Способ 2
Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу \(f(x)=kx+b\) и решить получившуюся систему уравнений.
Пример (ЕГЭ)
Обозначим жирные точки какими-нибудь буквами и найдем их координаты.
\(A(-2;2)\) и \(B(2;-5)\) подставим эти значения вместо \(x\) и \(f(x)\) в формулу \(f(x)=kx+b\):
Получим:
\(\begin{cases}2=-2k+b\\-5=2k+b\end{cases}\)
Теперь найдем \(k\) и \(b\), решив эту систему.
Для этого сложим уравнения друг с другом, чтобы исчезло \(k\):
\(2+(-5)=-2k+b+2k+b\)
\(-3=2b\)
\(b=-1,5\)
Теперь подставим найденное \(b\) во второе уравнение системы и найдем \(k\):
\(-5=2k-1,5\)
\(-5+1,5=2k\)
\(-3,5=2k\)
\(k=-1,75\)
Получается \(f(x)=-1,75x-1,5\).
Остается последний шаг – вычислим при каком иксе функция, то есть \(f(x)\), равна \(16\):
\(16=-1,75x-1,5\)
\(17,5=-1,75x\)
\(x=-10\).
Ответ: \(-10\).
Пример (ЕГЭ)
Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.
Функция \(f(x)\) возрастает, значит \(k>0\). \(k=+\frac{AC}{BC}=\frac{4}{4}=1,b=1\). \(f(x)=x+1\).
Теперь перейдем к функции \(g(x)\). Найдем координаты точек \(D\) и \(E\): \(D(-2;4)\), \(E(-4;1)\). Можно составить систему:
\(\begin{cases}4=-2k+b\\1=-4k+b\end{cases}\)
Вычтем второе уравнение из первого, чтоб убрать \(b\):
\(4-1=-2k+b-(-4k+b)\)
\(3=2k\)
\(k=1,5\)
Найдем \(b\):
\(4=-2\cdot 1,5+b\)
\(4=-3+b\)
\(b=7\)
\(g(x)=1,5x+7\).
\(x+1=1,5x+7\)
\(x-1,5x=7-1\)
\(-0,5x=6\)
\(x=6:(-0,5)\)
\(x=-12\).
Ответ: \(-12\).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Смотрите также:
Как определить a, b и c по графику параболы
Скачать статью
Linear function calculator
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Решить
- График
- Система
- Математический решатель на вашем сайте
Связанные темы:
вычисление квадратного корня | тесты по математике в девятом классе | линейные диофантовые уравнения | glencoe mcgraw — Алгебра Хилла 1 бесплатных вопросов и ответов | алгебра для чайников бесплатно онлайн | смешанная дробь → проценты | предметная область и диапазон рабочих листов графа функций | бесплатная алгебра 1 решение задач
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| dmj81 Зарегистрирован: 24. |
| ||||||
| Наверх | |||||||
| ИльбендФ Дата регистрации: 11.03.2004 |
| ||||||
| Вернуться к началу | |||||||
| Долкнанки Зарегистрирован: 24.10.2003 |
| ||||||
| Наверх | |||||||
| saavirsa Зарегистрирован: 04.11.2004 |
| ||||||
| Наверх | |||||||
| Mibxrus Зарегистрирован: 19.10.2002 | |||||||
| Наверх | |||||||
| Mibxrus Зарегистрирован: 19.10.2002 |
| ||||||
| Наверх | |||||||
04.2005 
Если кто-то знает о калькуляторе линейных функций, не могли бы вы мне помочь? Спасибо !
Он не только решит вопрос за вас, но и объяснит каждый шаг, который был предпринят для достижения определенного решения. И это лучшая функция на мой взгляд. У меня было много проблем с ответами на вопросы, основанные на калькуляторе линейных функций, но с тех пор, как я начал использовать программное обеспечение, математика была для меня как кусок пирога.
Algebrator — действительно отличная программа для алгебры. Я использовал его в нескольких математических классах — Промежуточная алгебра, Алгебра 1 и Алгебра 1. Я просто вводил проблему, и, нажимая «Решить», появлялось пошаговое решение. Программа настоятельно рекомендуется.Решение линейных функций — SAT II Math I
Все ресурсы SAT II Math I
6 диагностических тестов 113 практических тестов Вопрос дня Карточки Learn by Concept
SAT II Math I Help » Функции и графики » Решающие функции » Решение линейных функций
Решите для с точки зрения .
Возможные ответы:
Правильный ответ:
Пояснение:
Сначала вычтите по 7 с обеих сторон.
Фактор y в левой части.
Разделите обе части на 3 – x.
Сделайте дополнительный шаг, разложив знак минус в знаменателе.
Отменить знак минус.
Сообщить об ошибке
Найдите уравнение для прямой, проходящей через две указанные ниже точки.
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть .
Сначала рассчитайте уклон между двумя точками.
Затем используйте форму пересечения наклона для вычисления пересечения. Мы можем подставить наше значение для наклона, а также значения для .
Используя форму пересечения наклона, где мы знаем и , мы можем видеть, что уравнение для этой линии .
Сообщить об ошибке
Найдите уравнение прямой, проходящей через точки и .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы вычислить прямую, проходящую через две точки, нам сначала нужно вычислить наклон, .
Теперь, когда у нас есть наклон, мы можем подставить его в наше уравнение для линии в форме пересечения наклона.
Чтобы найти , мы можем подставить одну из точек, которые нам дали. Для этого примера давайте использовать , но поймите, что любая точка даст один и тот же ответ.
Теперь, когда мы решили для b, мы можем вставить это в нашу форму пересечения наклона и получить ответ
Отчет о ошибке
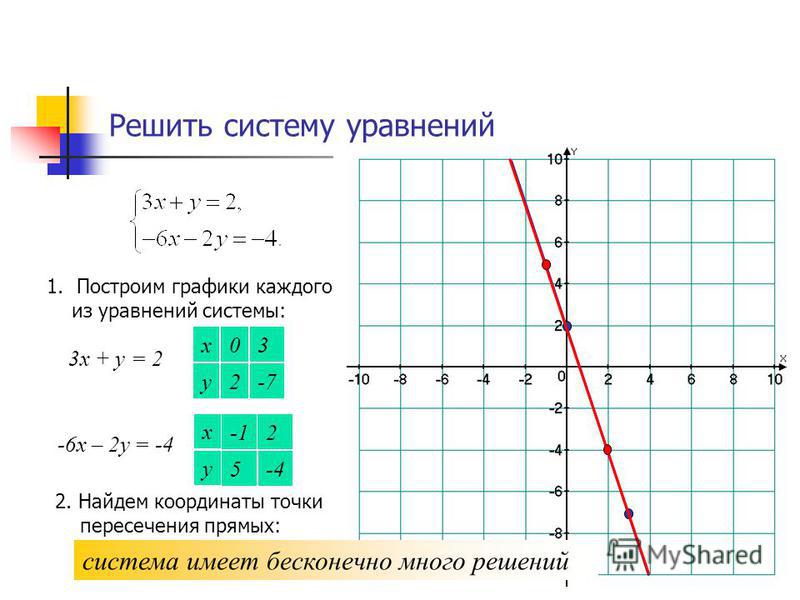
Найдите точку, в которой эти две строки пересекают:
Возможные ответы:
Правильный ответ:
446.
Объяснение:
Мы ищем точку, где эти две прямые пересекаются. Несмотря на то, что существует множество способов решения для двух уравнений, самый простой способ, который я вижу, — это использовать метод исключения, поскольку, складывая два уравнения вместе, мы можем исключить переменную.
Разделив обе части на 7, мы изолируем y.
Теперь мы можем снова подставить y в любое уравнение и найти x.
Далее мы можем найти x.
Следовательно, точка пересечения этих двух линий равна .
Сообщить об ошибке
Решите для когда .
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что нужно сделать, это подставить заданное значение, чтобы ваше уравнение было
.
Затем вы должны вычесть с обеих сторон, чтобы получить само по себе.
Теперь у вас есть
, и вы должны умножить на для каждой стороны, и вы получите .
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Добавить с обеих сторон.
Вычтите 2 с обеих сторон.
Разделите на 10 с обеих сторон.
Сократите дроби.
Ответ:
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Пояснение:Распределите правую сторону.
Перепишите уравнение.
Вычесть с обеих сторон.
Добавьте 4 с обеих сторон.