Онлайн решение производных сложных: Дифференциальные уравнения онлайн

Содержание

Производная сложной функции. Примеры решений

На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятия Как найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.

На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.

Смотрим в таблицу на правило (№5) дифференцирования сложной функции:

Разбираемся.

Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.

Функцию я буду называть внешней функцией, а функцию – внутренней (или вложенной) функцией.

! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.

Для того, чтобы прояснить ситуацию, рассмотрим:

Пример 1

Найти производную функции

Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:

В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.

Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.

В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.

Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).

Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией : Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией: После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .

Начинаем решать. С урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:

Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что .

Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:

Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем.

Ну и совершенно очевидно, что

Результат применения формулы в чистовом оформлении выглядит так:

Далее мы берем производную внутренней функции, она очень простая:

Постоянный множитель обычно выносят в начало выражения:

Готово

Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.

Пример 2

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Пример 3

Найти производную функции

Как всегда записываем:

Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция: И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция: Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции следующий:

Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется: Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:

Готово.

Пример 4

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?

Пример 5

а) Найти производную функции

б) Найти производную функции

Пример 6

Найти производную функции

Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:

Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :

Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:

Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).

Пример 7

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть как извращение забавно. Вот характерный пример:

Пример 8

Найти производную функции

Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:

Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:

Косинус – внутренняя функция, возведение в степень – внешняя функция.

Используем наше правило :

Находим производную внутренней функции, косинус сбрасываем обратно вниз:

Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.

Пример 9

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.

Пример 10

Найти производную функции

Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?

Сначала нужно найти , значит, арксинус – самое глубокое вложение:

Затем этот арксинус единицы следует возвести в квадрат :

И, наконец, семерку возводим в степень : То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.

Начинаем решать

Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:

Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени:

Теперь все просто, находим по таблице производную арксинуса и немного «причесываем» выражение:

Готово.

Пример 11

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

На практике правило дифференцирования сложной функции почти всегда применяется в комбинации с остальными правилами дифференцирования.

Пример 12

Найти производную функции

Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :

В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :

Замечаем, что под некоторыми штрихами у нас находятся сложные функции , . Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно. А пока запишем подробно, согласно правилу , получаем:

Готово.

! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.

Пример 13

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Пожалуй, хватит на сегодня. Хочется еще привести пример с дробью и сложной функцией, но такой пример принципиально ничем не отличается от двух последних заданий, единственное отличие – вместо правила применяем правило .

Для закрепления темы рекомендую статью Сложные производные. Логарифмическая производная. Помимо рассмотрения дополнительных примеров, есть и новый материал! После изучения третьего урока вы будете очень уверенно себя чувствовать в ходе дальнейшего изучения математического анализа. Если задания покажутся слишком трудными (у всех разный уровень подготовки), то сначала посетите страницу Простейшие типовые задачи с производной, там рассмотрено ещё порядка 15-ти производных.

Желаю успехов!

Ответы:

Пример 2:

Пример 4: Указание: перед дифференцированием необходимо перенести степень наверх, сменив у показателя знак .

Пример 7:

Пример 9:

Пример 11:

Пример 13:

Заказать контрольную работу по теме производная функции – онлайн решение и выполнение на заказ

Если у вас нет времени на выполнение контрольной работы по производной функции, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.

Ответы на вопросы по заказу контрольной работы по производной функции:

Сколько стоит помощь с контрольной работой?

Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения контрольной работы?

Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

Оценка стоимости бесплатна.

Каким способом можно оплатить?

Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

Присылайте в любое время! Я стараюсь быть всегда онлайн.

Ниже размещён теоретический и практический материал, который вам поможет разобраться в выполнении контрольной работы по предмету «производная функции», если у вас есть желание и много свободного времени!

Содержание:

Ответы на вопросы по заказу контрольной работы по производной функции:
Производные функций. Производные высших порядков
Производная высших порядков от сложных функций
Производные высших порядков от обратных функций
Механический смысл второй производной
Параметрически заданные функции
Дифференцирование функций, заданных параметрически
Дифференцирование неявно заданных функций

Пусть функция определена на интервале (a,b) и для функция , тогда на интервале (a,b) существует производная .

Определение 1. Если функция f(x) имеет производную в точке называется второй производной в точке x₀ , если существует эта производная.

Обозначение:

Определение 2. Производная n-го порядка функции в точке называется производная от производной порядка.

Обозначение:

Условимся, что

По этой ссылке вы сможете узнать как я помогаю с контрольными работами:

Помощь с контрольными работами

Определение 2’ Пусть ф-я . Полагаем для тех , для которых ф-я f (x) диф-ма; и, вообще (если функция определена в некоторой окрестности полагаем точек в некоторых функциядифференцируема.

Замечание 1. Для того чтобы n-я производная

производная должна в некоторой окрестности U(x₀) точки 0 и должна быть диф-мой в (.) x₀. При этом функция дxолжна быть дифмой в окр-ти U(x₀) (где производная

Замечание 2. Совокупность всех внутренних (…) множества E называется внутренностью E и обозначается

Пример:

Определение 3. Функция y = f (x) называется «n»-раз непрерывно дифференцируемой на интервале (a,b), если существует непрерывная на интервале (a,b) функция .

Обозначение:

Справедливо следующее утверждение: если функция

Замечание. Если ф-я ff (x) диф-ма «n» раз В некотором промежутке то это значит, что конечная производная в каждой (.) данного промежутка. Тогда производная дxиф-ма, а следовательно, и непрерывна в промежутке (a,b) Итак из конечной «n»-й производной в каждой (. ) пром-ка диф-ть (и стало быть непрерывность) во всем промежутке любой производной более низкого порядка, чем «n»,и сама функция. Пусть f(x) определена на . Скажем, что f(x) n -раз непрерывно диф-ма на (a,b). (Запись:

По этой ссылке вы сможете научиться оформлять контрольную работу:

Теоретическая контрольная работа примеры оформления

Теорема 1 (правило вычисления производных n-го порядка): пусть непрерывны на . Тогда справедливы следующие правила (утверждения):

Эта формула позволяет вычислять n-ую производную произведения двух функций. Она называется формулой Лейбница. Следует иметь ввиду, что

Тогда по определению

Доказательство: (математическая индукция)

База:

Индукция: пусть формула справедлива для n. Тогда докажем, что она справедлива для (n +1) .

По этой ссылке вы сможете заказать контрольную работу:

Заказать контрольную работу

Примеры:

Частный случай: если

Частный случай:

Закономерность, по которой составлена каждая з этих производных:

все производные содержат множителем число (-1) степени, которая на единицу меньше порядка производной.
Числитель дроби есть произведение натуральных чисел, начиная с единицы и кончая числом на единицу меньшем порядка производной.
1 x в степени равной порядку производной. Считаем, что эта закономерность сохраняется для производной любого порядка, получаем:

Выпишем следующие формулы:

Производная высших порядков от сложных функций

Теорема: Если функция при соблюдении условий теоремы о производной сложной функции имеют конечные производные второго порядка, то сложная функция также имеет производную второго порядка и эта производная имеет вид:

Доказательство: имеем

Рассмотрим первый множитель

Поэтому по теореме о сложной функции. Тогда, по теореме о сложной функции,

Рассмотрим второй множитель

По предположению , тогда мы можем получить, что

Замечание: предполагая, что, если функция сложная функция также трижды дифференцируема в точке и еѐ производная будет иметь вид:

Путѐм последовательного дифференцирования можно вывести формулы для любого порядка от сложной функции. В предположении, что функции имеют соответствующие производные.

Производные высших порядков от обратных функций

Теорема: если функция y = f (x)в некотором промежутке (a,b) (строго монотонна) имеет конечную производную, то обратная функция в соответствующем промежутке имеет обратную производную:

Доказательство: В силу теоремы о производной сложной функции . Поэтому производная будет вычисляться по следующему правилу:

! Если функция , то аналогично получим производную

Механический смысл второй производной

Рассмотрим движение точки по какой-нибудь траектории. При этом будем считать, что t – время, S – пройденный путь за это время, V – скорость точки, a ускорение.

, т.е. механическим смыслом второй производной является какое-нибудь ускорение в момент времени t.

Дифференциалы n-го порядка.

Пусть дана функция

Для

Тогда . Если фиксировать, то dy будет являться функцией только независимой переменной . Тогда:

Определение 1. Вторым дифференциалом функции в точке x = x₀ называется дифференциал от первого дифференциала, если он существует. При этом:

Приращение независимой переменной считается постоянным
Новые приращения независимой переменной, которые даются при вычислении второго дифференциала, считаются равными старому.

По определению 1:

2 Т.о. мы получили дифференциал второго порядка от дифференциала первого порядка при выполнении всех условий теоремы, наложенных на

Определение 2. Дифференциалом n -го порядка в точке по определению будет

Тогда

Т.о. в случае х – независимая переменная и y = f (x) , то имеем, что

Замечание: дифференциалы высшего порядка не обладают инвариантностью формы при замене переменной.

Доказательство:

Дана функция

Тогда

y = f (x)x независимая переменная.

Из определения дифференциалов второго порядка:

Найдѐм дифференциал третьего порядка:

Параметрически заданные функции

Их дифференцирование. Рассмотрим функцию заданную в некотором промежутке

Параметрически, посредством системы непрерывных функций

где , определѐнных в соответствующем промежутке строго монотонная. Предположим, что t имеет обратную функцию При этих условиях каждому значению х соответствует некоторое t, а значению t соответствует значение у, тогда у будет представлять собой функцию

Таким образом, система (1) определяет функцию у как функцию х. А, с законом соответствия:

Областью определения функции есть множество значений функции

Задание функции посредством уравнения (1), на некотором множестве есть параметрическое задание этой функции, где t – параметр.

Примеры:

1) Параметрическое уравнение окружности:

t – центральный угол

2) Эллипс

3) Циклоида

Рассмотрим три функции . Если каждому значению t в рассмотренной области определения этих функций отнести точку с координатами , то совокупность этих точек будет некоторая пространственная кривая:

Пример:

Дифференцирование функций, заданных параметрически

Рассмотрим функцию , заданную на некотором промежутке. Тогда параметрически, посредством системы непрерывных функций:

определѐнных на I₁, и функция строго монотонна (т.е. возрастает или убывает), причѐм

Теорема: если функции

Доказательство: взаимно обратные функции взаимно однозначны и непрерывно отображают другие промежутки:

Представим отношение:

По теореме о сложной функции, предел левой части в точке х равен пределу правой части в точке t, но последний предел равен отношению производных.

В обозначениях Лейбница:

Возможно вам пригодятся эти страницы:

Контрольная работа по комбинаторике заказать

Контрольная работа по психологии заказать

Контрольная работа по двоичному счислению заказать

Контрольная работа по теме матрицы заказать

Замечания:

Если функция удовлетворяет условию теоремы о существовании обратной функции:

На основании этой теоремы и теоремы о существовании обратной функции согласно инвариантности дифференциала первого порядка, на основании равенства:

При соблюдении условия теоремы:

Найдѐм производные высших порядков.

Теорема: если при соблюдении условий теоремы о производной функции заданной параметрически функция f(x) имеет производные более высоких порядков.

Доказательство:

По такому же принципу вычисляются производные третьего порядка.

Замечание: если функции tимеют производные четвѐртого порядка и т.д., то путѐм последовательного дифференцирования можно получить соответствующие выражения через параметр для производной четвѐртого порядка.

Пример 1: Астроида

Пример 2.

Найти

Циклоида представляет собой траекторию некоторой фиксированной (.) окружности, катящейся без скольжения по прямой линии.

Пример 3. Кривая – декартов лист

Дифференцирование неявно заданных функций

Пример:

Матричное дифференцирование · Учебник по ML от ШАД

Автор: Станислав Федотов

Основные обозначения
Простые примеры и свойства матричного дифференцирования
Простые примеры вычисления производной
Примеры вычисления производных сложных функций
Вторая производная
Примеры вычисления и использования второй производной

Любая задача машинного обучения — это задача оптимизации, а задачи оптимизации удобнее всего решать градиентными методами (если это возможно, конечно). n\). Функция $f(x)$ дифференцируема в точке $x_0$, если

\[f(x_0 + h) = f(x_0) + \color{#348FEA}{\left[D_{x_0} f \right]} (h) + \bar{\bar{o}} \left(\left| \left| h\right|\right|\right),\]

где $\color{#348FEA}{\big[D_{x_0} f\big]}$ — дифференциал функции $f$: линейное отображение из мира $x$-ов в мир значений $f$. Грубо говоря, он превращает «малое приращение $h=\Delta x$» в «малое приращение $\Delta f$» («малые» в том смысле, что на о-малое можно плюнуть):

\[f(x_0 + h) — f(x_0)\approx\color{#348FEA}{\left[D_{x_0} f \right]} (h)\]

Отметим, что дифференциал зависит от точки $x_0$, в которой он берётся: $\color{#348FEA}{\left[D_{\color{red}{x_0}} f \right]} (h)$. Под $\vert\vert h\vert\vert$ подразумевается норма вектора $h$, например корень из суммы квадратов координат (обычная евклидова длина).

Давайте рассмотрим несколько примеров и заодно разберёмся, какой вид может принимать выражение $\color{#348FEA}{\big[D_{x_0} f\big]} (h)$ в зависимости от формы $x$. T H\right).\]

Можно заметить, что здесь, по аналогии с примерами, где $x$ — скаляр и где $x$ — вектор (и $f(x)$ — скалярная функция), получилось на самом деле скалярное произведение градиента функции $f$ по переменным $X_{ij}$ и приращения. Этот градиент мы записали для удобства в виде матрицы с теми же размерами, что матрица $X$.

В примерах выше нам дважды пришлось столкнуться с давним знакомцем из матанализа: градиентом скалярной функции (у нескалярных функций градиента не бывает). Напомним, что градиент $\color{#FFC100}{\nabla_{x_0} f}$ функции в точке $x_0$ состоит из частных производных этой функции по всем координатам аргумента. При этом его обычно упаковывают в ту же форму, что и сам аргумент: если $x$ — вектор-строка, то и градиент записывается вектор-строкой, а если $x$ — матрица, то и градиент тоже будет матрицей того же размера. Это важно, потому что для осуществления градиентного спуска мы должны уметь прибавлять градиент к точке, в которой он посчитан.

Как мы уже имели возможность убедиться, для градиента скалярной функции $f$ выполнено равенство

\[\left[D_{x_0} f \right] (x-x_0) = \langle\color{#FFC100}{\nabla_{x_0} f}, x-x_0\rangle,\]

где скалярное произведение — это сумма попарных произведений соответствующих координат (да-да, самое обыкновенное).

Посмотрим теперь, как выглядит дифференцирование для функций, которые на выходе выдают не скаляр, а что-то более сложное.

Примеры конкретных форм $\big[D_{x_0} f\big] (h)$, где $f$ — это вектор или матрица

$f(x) = \begin{pmatrix} f(x_1)\\ \vdots\\ f(x_m) \end{pmatrix}$, $x$ — вектор. Тогда
\[f(x_0 + h) — f(x_0) = \begin{pmatrix} f(x_{01} + h_1) — f(x_{01})\\ \vdots \\ f(x_{0m} + h_m) — f(x_{0m}) \end{pmatrix} \approx \begin{pmatrix} f'(x_{01}) h_1\\ \vdots \\ f'(x_{0m}) h_m \end{pmatrix} = \begin{pmatrix} f'(x_{01}) \\ \vdots \\ f'(x_{0m}) \end{pmatrix} \odot h. \]
В последнем выражении происходит покомпонентное умножение:
\[\color{#348FEA}{\big[D_{x_0} f\big]} (h) = f'(x_0) \odot h = h \odot f'(x_0)\]
$f(X) = XW$, где $X$ и $W$ — матрицы. Тогда
\[f(X_0 + H) — f(X_0) = (X_0 + H) W — X_0 W = H W,\]
то есть
\[\color{#348FEA}{\big[D_{X_0} f\big]} (H) = H W\]
$f(W) = XW$, где $X$ и $W$ — матрицы. Тогда
\[f(W_0 + H) — f(W_0) = X(W_0 + H) — XW_0 = X H,\]
то есть
\[\color{#348FEA}{\big[D_{W_0} f\big]} (H) = X H\]
$f(x) = (f_1(x),\ldots,f_K(x))$ — вектор-строка, $x = (x_1,\ldots,x_D)$ — вектор-строка. Тогда
\[\color{#348FEA}{\big[D_{x_0} f\big]}(h) = \left(\sum_j \left. \frac{\partial f_1}{\partial y_j} \right|_{y=x_0}h_j, \ldots, \sum_j \left. \frac{\partial f_K}{\partial y_j} \right|_{y=x_0}h_j \right) = \\ = h \cdot \begin{pmatrix} \left. \frac{\partial f_1}{\partial y_1} \right|_{y=x_0} & \ldots & \left. \frac{\partial f_k}{\partial y_1} \right|_{y=x_0} \\ \vdots & & \vdots \\ \left. \frac{\partial f_1}{\partial y_D} \right|_{y=x_0} & \ldots & \left. \frac{\partial f_k}{\partial y_D} \right|_{y=x_0}\\ \end{pmatrix} = h \cdot \left. \frac{\partial f}{\partial y}\right|_{y = x_0}\]
Матрица, выписанная в предпоследней выкладке, — это знакомая вам из курса матанализа матрица Якоби.

Производная константы. Пусть $f(x) = a$. Тогда
\[f(x_0 + h) — f(x_0) = 0,\]
то есть $\color{#348FEA}{\big[D_{x_0} f\big]}$ — это нулевое отображение. А если $f$ — скалярная функция, то и $\color{#FFC100}{\nabla_{x_0} f} = 0.$
Производная линейного отображения. Пусть $f(x)$ — линейное отображение. Тогда
\[f(x_0 + h) — f(x_0) = f(x_0) + f(h) — f(x_0) = f(h)\]
Поскольку справа линейное отображение, то по определению оно и является дифференциалом $\color{#348FEA}{\big[D_{x_0} f\big]}$. Мы уже видели примеры таких ситуаций выше, когда рассматривали отображения умножения на матрицу слева или справа. Если $f$ — (скалярная) линейная функция, то она представляется в виде $\langle a, v\rangle$ для некоторого вектора $a$ — он и будет градиентом $f$.
Линейность производной. Пусть $f(x) = \lambda u(x) + \mu v(x)$, где $\lambda, \mu$ — скаляры, а $u, v$ — некоторые отображения, тогда
\[\color{#348FEA}{\big[D_{x_0} f\big]} = \lambda \color{#348FEA}{\big[D_{x_0} u\big]} + \mu \color{#348FEA}{\big[D_{x_0} v\big]}\] Попробуйте доказать сами, прежде чем смотреть доказательство.
\[f(x_0 + h) — f(x_0) = (\lambda u(x_0 + h) + \mu v(x_0 + h)) — (\lambda u(x_0) + \mu v(x_0)) =\] \[= \lambda(u(x_0 + h) — u(x_0)) + \mu(v(x_0 + h) — v(x_0)) \approx\]
$\approx \lambda \color{#348FEA}{\big[D_{x_0} u\big]}(h) + \mu \color{#348FEA}{\big[D_{x_0} v\big]}(h)$
Производная произведения. Пусть $f(x) = u(x) v(x)$, где $u, v$ — некоторые отображения, тогда
\[\color{#348FEA}{\big[D_{x_0} f\big]} = \color{#348FEA}{\big[D_{x_0} u\big]} \cdot v(x_0) + u(x_0) \cdot \color{#348FEA}{\big[D_{x_0} v\big]}\] Попробуйте доказать сами, прежде чем смотреть доказательство.
Обозначим для краткости $x = x_0 + h$. Тогда
\[u(x)v(x) — u(x_0)v(x_0) = u(x)v(x) — u(x_0)v(x) + u(x_0)v(x) — u(x_0)v(x_0) =\] \[(u(x) — u(x_0))v(x) + u(x_0)(v(x) — v(x_0))\approx\] \[\approx \color{#348FEA}{\big[D_{x_0} u\big]}(h) \cdot v(x) + u(x_0)\cdot \color{#348FEA}{\big[D_{x_0} v\big]}(h)\]
И всё бы хорошо, да в первом слагаемом $v(x)$ вместо $v(x_0)$. Придётся разложить ещё разок:
\[\color{#348FEA}{\big[D_{x_0} u\big]}(h) \cdot v(x) \approx\] \[\color{#348FEA}{\big[D_{x_0} u\big]}(h) \cdot \left(v(x_0) + \color{#348FEA}{\big[D_{x_0} v\big]}(h) + o(\vert\vert h\vert\vert)\right) =\]
$\color{#348FEA}{\big[D_{x_0} u\big]}(h) \cdot v(x_0) + \bar{\bar{o}}\left(\vert\vert h\vert\vert\right)$
Это же правило сработает и для скалярного произведения:
\[\color{#348FEA}{\big[D_{x_0} \langle u, v\rangle\big]} = \langle\color{#348FEA}{\big[D_{x_0} u\big]}, v\rangle + \langle u, \color{#348FEA}{\big[D_{x_0} v\big]}\rangle\]
В этом нетрудно убедиться, повторив доказательство или заметив, что в доказательстве мы пользовались лишь дистрибутивностью (= билинейностью) умножения.
Производная сложной функции. Пусть $f(x) = u(v(x))$. Тогда
\[f(x_0 + h) — f(x_0) = u(v(x_0 + h)) — u(v(x_0)) \approx\] \[\approx\left[D_{v(x_0)} u \right] (v(x_0 + h) — v(x_0)) \approx \left[D_{v(x_0)} u \right] \left( \left[D_{x_0} v\right] (h)\right)\]
Здесь $D_{v(x_0)} u$ — дифференциал $u$ в точке $v(x_0)$, а $\left[D_{v(x_0)} u \right]\left(\ldots\right)$ — это применение отображения $\left[D_{v(x_0)} u \right]$ к тому, что в скобках. Итого получаем:
\[\left[D_{x_0} \color{#5002A7}{u} \circ \color{#4CB9C0}{v} \right](h) = \color{#5002A7}{\left[D_{v(x_0)} u \right]} \left( \color{#4CB9C0}{\left[D_{x_0} v\right]} (h)\right)\]
Важный частный случай: дифференцирование перестановочно с линейным отображением. Пусть $f(x) = L(v(x))$, где $L$ — линейное отображение. Тогда $\left[D_{v(x_0)} L \right]$ совпадает с самим $L$ и формула упрощается:
\[\left[D_{x_0} \color{#5002A7}{L} \circ \color{#4CB9C0}{v} \right](h) = \color{#5002A7}{L} \left( \color{#4CB9C0}{\left[D_{x_0} v\right]} (h)\right)\]

Вычислим дифференциал и градиент функции $f(x) = \langle a, x\rangle$, где $x$ — вектор-столбец, $a$ — постоянный вектор.
Попробуйте вычислить сами, прежде чем смотреть решение.
Вычислить производную можно непосредственно:
\[f(x_0 + h) — f(x_0) = \langle a, x_0 + h\rangle — \langle a, x_0\rangle = \langle a, h\rangle\]
Но можно и воспользоваться формулой дифференциала произведения:
\[\color{#348FEA}{\big[D_{x_0} \langle a, x\rangle\big]} (h) =\] \[=\langle\color{#348FEA}{\big[D_{x_0} a\big]}(h), x\rangle + \langle a, \color{#348FEA}{\big[D_{x_0} x\big]}(h)\rangle\] \[= \langle 0, x\rangle + \langle a, h\rangle = \langle a, h\rangle\]
Сразу видно, что градиент функции равен $a$.
Вычислим производную и градиент $f(x) = \langle Ax, x\rangle$, где $x$ — вектор-столбец, $A$ — постоянная матрица.
Попробуйте вычислить сами, прежде чем смотреть решение.
Снова воспользуемся формулой дифференциала произведения:
\[\color{#348FEA}{\big[D_{x_0} \langle Ax, x\rangle\big]}(h) =\] \[= \langle\color{#348FEA}{\big[D_{x_0} Ax\big]}(h), x_0\rangle + \langle Ax_0, \color{#348FEA}{\big[D_{x_0} x\big]}(h)\rangle\] \[= \langle Ah, x_0\rangle + \langle Ax_0, h\rangle\]
Чтобы найти градиент, нам надо это выражение представить в виде $\langle ?, h\rangle$. 2,\]
что, конечно, меньше нуля для любой ненулевой $H$.

▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно. Пройдите курсы по математике, естественным наукам и бизнесу

Подготовка к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—


95% купили больше ПРИЛОЖЕНИЙ.	97% сообщили об улучшении результатов.	Рейтинг: 4,89 из 5 звезд.	Доступно 46 ПРИЛОЖЕНИЙ.

КОВИД СПЕЦИАЛЬНЫЙ

Купите 3 приложения Made Easy по цене 2 приложений.

Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenie ur Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyPhysik Leicht EasyPhysik Research Made EasyPhysik Research Made Easy GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometr ia de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.

Находится в разделе 5:Настройки → 4:Статус → О программе

ID может выглядеть так: 1008000007206E210B0 BD92F455 . ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.

или на международном уровне:

В конце оплаты PayPal вам будет отправлено электронное письмо, содержащее ваш ключ и программное обеспечение.

Хотите купить TI-калькулятор?

Получите самые низкие цены на TI-Calculators
(со сравнением цен)

СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.

Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Установите оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, восстановленные, подержанные калькуляторы.
Посмотрите обучающие видео и прочитайте руководства по калькуляторам.
Прочтите последние новости о калькуляторах в Интернете.

БЕСПЛАТНАЯ загрузка:
Решатель квадратных уравнений (шаг за шагом)

Загрузите пошаговый решатель квадратных уравнений

. Этот решатель является частью приложения Algebra Made Easy.

— Загрузите бесплатные пробные версии здесь.

— Срок действия пробных и платных приложений неограничен.

— Будущие обновления бесплатны — навсегда!

Онлайн-репетиторство по математике

Получите онлайн-репетиторство.

Репетиторы с отличными оценками по математике будут рады помочь вам.

Получите индивидуальную помощь по математике.

Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.

Репетиторы в настоящее время преподают алгебру, алгебру 2, предварительное исчисление, исчисление AP и BC, статистику AP, тригонометрию, дискретную математику.

Репетиторы работали более 10 лет в качестве читателей AP Calculus (те люди, которые оценивают экзамены AP Calculus).

Репетиторы также обучают навыкам сдачи тестов, которые так же важны, как и само содержание.

Наши преподаватели имеют более 20 лет опыта преподавания.

1. урок стоит 50$, после этого 100$ в час.
оптом: 540 долларов за 6 часов, 1000 долларов за 12 часов.

Забронируйте сеанс репетиторства по электронной почте: [email protected]

Для вопросов, заказов и т. д.: ОБЩАЙТЕСЬ С НАМИ.

Первый урок (50 долларов США)	Один урок (100 долларов США)	Несколько уроков

Искусство решения проблем

Голоморфная функция — это дифференцируемая сложная функция. То есть просто как и в вещественном случае, голоморфна в, если существуют. Это намного сильнее чем в реальном случае, так как мы должны допустить приближение к нулю от любое направление комплексной плоскости.

Обычно мы говорим о функциях как о голоморфных на (открытых) множествах, а не в точках, поскольку, когда мы рассматриваем поведение функции в точке, мы предпочитаем рассматривать ее в контексте точек рядом, поблизости.

Содержание

1 Уравнения Коши-Римана
- 1.1 Доказательство теоремы
2 Аналитические функции
- 2.1 Эквивалентность аналитических и голоморфных функций
- 2.2 Странные последствия расширения
3 См. также

Уравнения Коши-Римана

Мы можем получить эквивалентное определение, если на действительную и мнимую составляющие.

В частности, пусть будет определено по Если , то

Оказывается, мы можем выразить идею «голоморфна» полностью в терминах частных производных от и .

Теорема. Позвольте быть открытым, связным подмножеством . Сокращаем и. Тогда функция голоморфна на тогда и только тогда, когда все частные производные от и относительно к и непрерывны на , и справедлива следующая система для каждой точки: Эти уравнения называются уравнениями Коши-Римана .

Для удобства мы можем сократить С этим злоупотреблением обозначениями мы можем переписать уравнение Коши-Римана. уравнения таким образом:

Доказательство теоремы

Сначала предположим, что комплексно-дифференцируемый при . Тогда при , Разбивая на действительную и мнимую составляющие, мы видим Приравняв действительную и мнимую компоненты, получим Уравнения Коши-Римана. Это следует из Интегральная формула Коши, у которой существует вторая производная в ; таким образом, производная непрерывна в , и поэтому являются частными производными от и .

Теперь предположим, что уравнения Коши-Римана содержат точку , и что частные производные от и существуют и непрерывны в районе . Пусть произвольно маленькое комплексное число, с . затем с первым приближением из определения частных производных а второй из непрерывности частных производных. Мы можем заставить быть достаточно малыми, чтобы оба приближения произвольно точны. Теперь, по уравнениям Коши-Римана, Следовательно В частности, предел существует, поэтому дифференцируем при . Поскольку было произвольным, отсюда следует, что дифференцируемо везде в .

Аналитические функции

Родственным понятием гомоморфности является понятие аналитичности. А говорят, что функция аналитическая в если имеет сходящийся степенной ряд на некоторых окрестности . Удивительно, но оказывается, что функция голоморфна в тогда и только тогда, когда она аналитична в . Более того, его радиус сходимости является наибольшей нижней границей расстояния от до сингулярности.

Это не относится к реальным функциям. Рассмотрим, например, реальная функция Он бесконечно дифференцируем вдоль всей действительной прямой, но его степенной ряд расходится при . Но в комплексной плоскости мы видим, что имеет особенности при , поэтому степенной ряд, очевидно, должен расходятся, когда .

Эквивалентность аналитических и голоморфных функций

Теперь докажем, что все голоморфные функции ведут себя в этом упорядоченный путь.

Теорема. Позвольте быть связным, открытым подмножеством , и пусть — голоморфная функция на . Тогда для любого , разложение в ряд по степеням сходится, а его радиус сходимости есть наибольшая величина, для которой существует голоморфное продолжение на множество

Доказательство. Так как есть в , есть такие голоморфна внутри . Предположим, что . Пусть будет простым, положительно ориентированный круг радиуса о , и пусть быть верхняя граница для . Посредством Интегральная формула Коши, Таким образом, ряд сходится геометрически. Отсюда следует, что если существует голоморфное расширение на множество тогда степенной ряд примерно сходится с радиусом не менее .

Наоборот, предположим, что разложение в степенной ряд расходится ибо на некотором расстоянии меньшем, чем от . затем по предыдущему абзацу не существует голоморфного расширения ко всем точкам на расстоянии менее . Отсюда следует, что радиус сходимости разложения в ряд Тейлора около действительно является величиной, указанной в теореме.

Странные последствия расширения

В некоторых случаях повторное расширение функции может привести к к странным последствиям. Например, мы можем определить функция квадратного корня, голоморфная и определенная везде, кроме множества неположительных действительных чисел. Любой разложение степенного ряда без начала координат будет сходиться. Однако, если мы попытаемся пересечь отрицательную вещественную ось степенным рядом расширение, мы обнаружим, что наше расширение ряда мощности дает отличные результаты от нашей исходной функции с другой стороны оси! Это потому, что «функция» квадратного корня находится в на самом деле мультифункция, которая может ограничиться голоморфным функция на любом открытом подмножестве, которое не включить закрытый путь о происхождении. x$] [триггерные производные] [правило произведения] [частное правило] [цепное правило]

Обновление: По состоянию на октябрь 2022 года у нас есть гораздо более полных материалов, чтобы вы могли изучить и попрактиковаться в вычислении производных. Пожалуйста, посетите нашу главу «Вычисление производных», чтобы получить этот материал для себя. Все это бесплатно и предназначено для того, чтобы помочь вам преуспеть в вашем курсе.

Если вам сейчас просто нужно попрактиковаться в вычислении производных задач, предыдущие ученики сочли нижеприведенную информацию очень полезной. А если у вас есть вопросы, задавайте их на нашем форуме! 92\right) + \dfrac{d}{dx}(\cos x) = \, …$

Правило произведения для производных

\begin{align*}
\dfrac{d}{dx}(fg)& = \left(\dfrac{d}{dx}f \right)g + f\left(\dfrac{d}{dx}g \right)\\[8px]
&= \Big[\text{ (производное 1-го) } \times \text{ (2-го) }\Big] + \Big[\text{ (1-го) } \times \text{ (производного 2-го)}\Big]
\end{align *}

IV.

2} \\[8px]
&=\dfrac{{\Big[\text{(производная числителя) } \times \text{ (знаменатель)}\Big] – \Big[\text{ (числитель) } \times \text{ (производная знаменатель)}}\Big]}{\text{все разделить на [знаменатель в квадрате]}}
\end{align*}

Многие студенты помнят правило частного, думая о числителе как о «привет», демонинаторе как «lo», производная как «d», а затем пение

«lo d-hi минус hi d-lo over lo-lo»

[свернуть]

Чтобы получить доступ к другим проблемам и решениям, включая AP- создавайте вопросы с несколькими вариантами ответов, бесплатно войдите в свою учетную запись Google, Apple или Facebook или создайте специальный Matheno за 60 секунд. Вы также сможете отметить задачи 9{46}.$

Два конкретных случая, которые вы быстро запомните:
$$\dfrac{d}{dx}\text{(константа)} = 0$$
$$\dfrac{d}{dx}( x) = 1$$

Задача дифференцирования по степенному правилу #1

Дифференцировать $f(x) = 2\pi$.

Нажмите, чтобы просмотреть решение исчисления

$2\pi$ — это просто число: это константа. И производная любой константы равна 0:
\[ \begin{align*}
\dfrac{d}{dx}(2\pi) &= \dfrac{d}{dx}(\text{constant}) \ \[8px]
&= 0 \quad \cmark 9{x+1} \quad \cmark
\end{align*} \]
Обратите внимание, что последние две строки полностью эквивалентны. Любой правильный ответ.

[свернуть]

Чтобы получить доступ к другим проблемам и решениям, включая вопросы с несколькими вариантами ответов в стиле AP, войдите бесплатно с помощью своей учетной записи Google, Apple или Facebook или создайте специальный Matheno за 60 секунд. Вы также сможете отмечать задачи , которые вы хотите обязательно просмотреть перед экзаменами. Просто используйте область входа в систему в нижней части этого экрана. 92 x
\end{align*}} \]
Обратите внимание, что перед производными кофункций: косинуса, косеканса и котангенса стоит знак минус.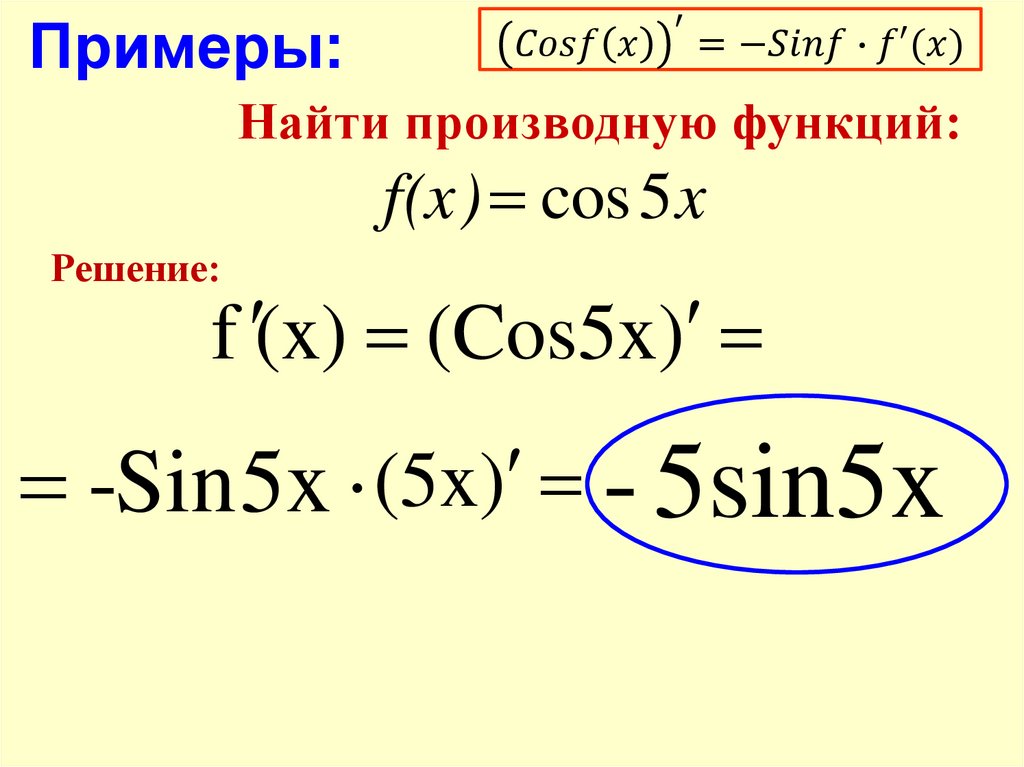

Триггерная задача дифференцирования #1

Дифференцировать $f(x) = \sin x – \cos x$.

Нажмите, чтобы просмотреть расчетное решение

Напомним из таблицы, что $\dfrac{d}{dx}(\sin x) = \cos x,$ и $\dfrac{d}{dx}(\cos x) = -\sin x.$
\[ \begin{align*}
\dfrac{d}{dx} \left(\sin x – \cos x \right) &= \dfrac{d}{dx}(\ sin x) – \dfrac{d}{dx}(\cos x) \\[8px] 92 x \quad \cmark
\end{align*} \]

[свернуть]

IV. Правило продукта

\[\bbox[yellow,5px]{
\begin{align*}
\dfrac{d}{dx}(fg)&= \left(\dfrac{d}{dx}f \right )g + f\left(\dfrac{d}{dx}g \right)\\[8px]
&= [{\small\text{(производное первого)} \times\text{(второе) }}]\, + \,[{\small \text{ (1-й) } \times \text{ (производный от 2-го)}}]
\end{align*}}\]

Дифференциация правила продукта Проблема №1

Дифференцировать $f(x) = x\sin x. $

Щелкните, чтобы просмотреть решение исчисления

Поскольку функция является произведением двух отдельных функций, $x$ и $\sin x$, мы должны использовать произведение Правило. Напомним, что $\dfrac{d}{dx}x = 1,$ и что $\dfrac{d}{dx}\sin x = \cos x.$
\[ \begin{align*}
\dfrac{d }{dx} \left( x\sin x\right)&= \left(\dfrac{d}{dx}x\right)\sin x + x \left( \dfrac{d}{dx}\sin x \right) \\[8px]
&= (1)\sin x + x \,(\cos x) \\[8px]
&= \sin x + x\cos x \quad \cmark 92} \\[8px]
&=\dfrac{{[{\small \text{(производная числителя) } \times \text{ (знаменатель)}]}\\ \quad – \, [{\ small \text{ (числитель) } \times \text{ (производная знаменателя)}}]}}{{\ small \text{все разделить на [знаменатель в квадрате]}}}
\end{align* }}\]
Многие учащиеся запоминают правило частных, представляя числитель как «привет», демонинатор как «ло», производную как «д», а затем напевая

«ло д-при минус привет д-ло». 2 x$$ 92} \quad \cmark
\end{align*} \]

[свернуть]

VI. Цепное правило

Цепное правило — большая тема, поэтому у нас есть отдельная страница для задач, требующих цепного правила.

Нужно использовать производную, чтобы найти уравнение касательной (или уравнение нормальной линии)? У нас есть отдельная страница на эту тему здесь.

Есть вопрос, предложение или пункт, который вы хотели бы, чтобы мы включили? Пожалуйста, дайте нам знать на нашем форуме!

Хотите получить доступ к всем нашим задачам и решениям исчисления? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд). Затем посетите наш главный экран исчисления.

Производная сложной функции. Примеры решений

Заказать контрольную работу по теме производная функции – онлайн решение и выполнение на заказ

Ответы на вопросы по заказу контрольной работы по производной функции:

Производная высших порядков от сложных функций

Производные высших порядков от обратных функций

Механический смысл второй производной

Параметрически заданные функции

Дифференцирование функций, заданных параметрически

Дифференцирование неявно заданных функций

Матричное дифференцирование · Учебник по ML от ШАД

▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно. Пройдите курсы по математике, естественным наукам и бизнесу

Подготовка к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—

Искусство решения проблем

Содержание

Уравнения Коши-Римана

Доказательство теоремы

Аналитические функции

Эквивалентность аналитических и голоморфных функций

Странные последствия расширения

Правило произведения для производных

IV.

Добавить комментарий Отменить ответ