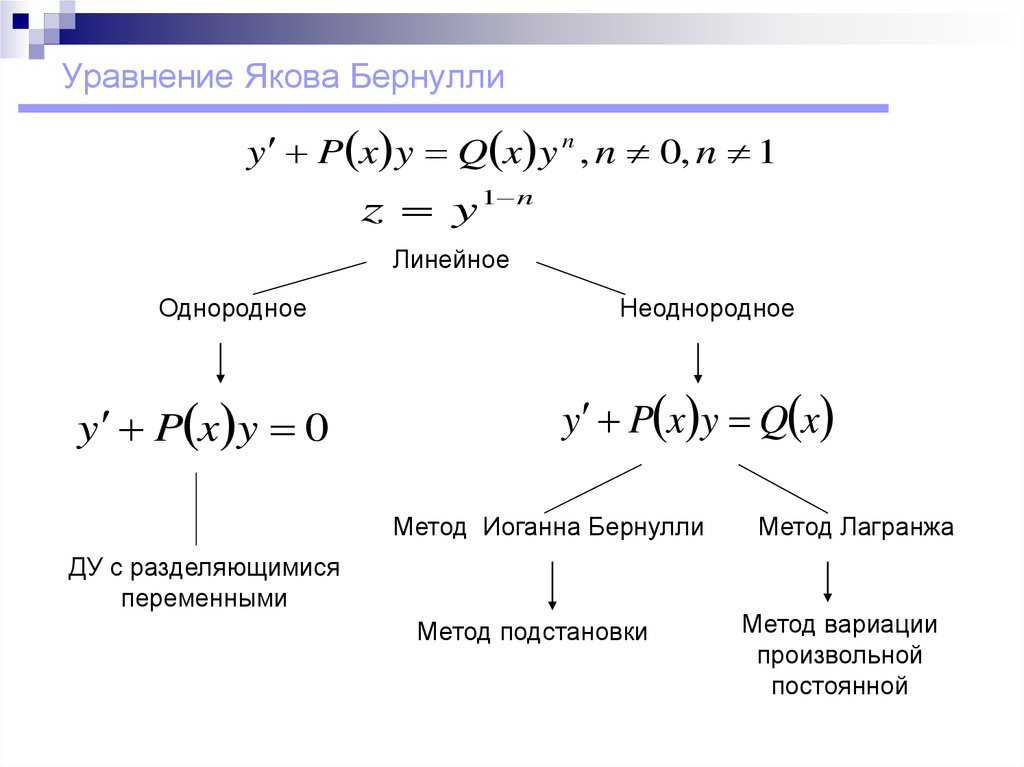
Онлайн решение уравнения бернулли: Дифференциальные уравнения онлайн

Уравнение Бернулли

Уравнение Бернулли в первую очередь, уравнение дифференциальное первого порядка. Выглядит как :

dy/dx + Py = Qy^a,

в нем Q и P не прерывающаяся данная функция исходящая из Х.
а — неизменное число. Если ввести новую функцию z = у -0+1, то уравнение Бернулли придет к аналогичному линейному уравнению. Выведен данное вычисление в 1695 году.

Во вторую очередь является основой в уравнениях гидродинамики, она связывает (уже в готовой движущейся жидкости): V скорость + Р давление + h высота минимальной величины жидкости к участку отсчета. Данный метод был выведен в 1738 году, применяется для не горящим жидкостям имеющие постоянную плотность Р и которые находятся исключительно под силой тяжести. Выглядит данное уравнение как:

v²/2 + p/p + gh = const.

в нем g есть ускорение. При умножении данного уравнения на p, первый член выступит в качестве кинетической энергии в единице количества жидкости, другие два члена — в качестве потенциальной энергии.

частично обусловленной с одной стороны как сила тяжести (крайнее значение) и давление с другой стороны. В этом виде и выходит закон о сохранении энергии. Во время когда по струе жидкости одна энергия к примеру кинетическая, возрастает, в это же время также падает потенциальная. Так когда поток в трубопроводе сужается, а его скорость возрастает (потому что за одинаковое время как через большое так и через маленькое сечение протекает одинаковый объем жидкости) и падает давление.

В уравнении Бернулли есть несколько важных моментов:

— Когда под силой тяжести из не закрытой емкости вытекает жидкость (изображено на первом рисунке)

v²/2g=h либо V=?2gh

что доказывает единую скорость как во время падения жидкость, так и при выходе в выходное отверстие.

-Когда в спокойном потоке со скоростью V0 и давлением р0, встречается на пути проблема или препятствие, как изображено на втором рисунке, то жидкость по действием давления подпирает данное препятствие и как следствие замедляется сам поток; что интересно в подпоре, во время давления потока жидкости, в самом центре (назовем его — критическая точка) скорость равна 0. Вывод давление на критическую точку р₁=р₀+рV²₀/2. Присоединяем давление к ней, которое равно р₁ + р₀ = рv²₀/2, является динамическое давление либо напор скорости. Струя любой жидкости в потоке не сохраняет механическую энергию, расходует ее на силы трения и рассеивает на тепло. Нужно брать во внимание потери сопротивления, при использовании уравнения Бернулли в реальной жидкости.

Если ты молод и ищешь дополнительный заработок, но не знаешь где. Перейди по ссылке, заработок в интернете для подростка (http://odostatke.ru/zarabotat-podrostok.html) , там все подробно написано.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Дифференциальное уравнение Бернулли с примерами решения

Содержание:

Примеры с решением
Линейные дифференциальные уравнения первого порядка. уравнение бернулли

Линейным дифференциальным уравнением первого порядка называется уравнение первой степени относительно и , т. е. уравнение вида

(14.19)

или . (14.20)

Решение линейного уравнения ищется в виде

. (14.21)

Подстановка выражений для и в уравнение (14.20) приводит его к виду . (14.22) В качестве выбирают одну из функций, удовлетворяющих уравнению , (14.23) тогда функция определяется из уравнения . (14.24)

Если функция , то уравнение (14.20) принимает вид (14.25) и называется линейным однородным, его общее решение выражается формулой . (14.26)

Для решения неоднородного линейного уравнения (14.20) можно применять метод вариации произвольной постоянной.

Этот метод состоит в том, что сначала находят общее решение уравнения (14.25), т. е. соотношение (14.26).

Далее, полагая в этом соотношении величину функцией от , ищут решение неоднородного уравнения (14. 20) в виде (14.26). Для этого подставляют в уравнение (14.20) и , определяемые из формулы (14.26), и из полученного дифференциального уравнения находят функцию . Общее решение уравнения (14.20) получается в виде . (14.27)

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Уравнением Бернулли называется уравнение вида , (14.28) где — действительное число. В случае уравнение (14.28) является линейным. Во всех других случаях оно сводится к линейному с помощью подстановки . (14.29)

Примеры с решением

Пример 1.

Найти общее решение линейного дифференциального уравнения . Данное уравнение является уравнением вида (14.20), где . Положим , тогда . Подставляя эти выражения в исходное уравнение, получим или . (A) В качестве выберем одну из функций, удовлетворяющих уравнению . (В) Интегрируя это уравнение, получим . Уравнение (А) с учетом (В) перепишем так: .

Подставляя сюда значение , получим .

Интегрируя полученное уравнение, находим . Подставим выражения для в формулу : . Следовательно, общее решение данного дифференциального уравнения таково: .

Возможно вам будут полезны данные страницы:

Нормальный закон распределения

Нормальный закон распределения случайной величины

Уравнение Бернулли дифференциальные уравнения

Физический смысл производной

Пример 2.

Найти общее решение линейного уравнения . Положим , тогда . Уравнение перепишем в виде . (A) Выберем так, чтобы выражение в скобках обратилось в нуль, тогда . Уравнение (А) при запишем так: , откуда . Следовательно,

общее решение.

Пример 3.

Проинтегрировать линейное уравнение . Пусть , тогда . Подставляя выражения для и в уравнение, получим , и . (А) Потребуем, чтобы , тогда . Если , то уравнение (А) принимает вид Подставляя сюда значение , перепишем уравнение в виде . Интегрируя последнее уравнение, получим .

Следовательно, . Таким образом, общее решение дается формулой .

Пример 4.

Найти решение уравнения , (А) удовлетворяющее начальному условию: при . По виду это уравнение не является линейным, так как содержит произведение искомой функции и ее производной . Однако, если рассматривать как функцию от , то, учитывая, что

, получим линейное уравнение . (В) Применим подстановку , тогда . Подставляя эти выражения в уравнение (В), получим

или . (С) Выберем функцию так, чтобы обратился в нуль коэффициент при в последнем уравнении . (D) Интегрируя, получим . (Е) Подставляя это значение в уравнение (С), в силу равенства (D) находим (F) Таким образом, общее решение уравнения (В) есть: или . Полагая и , получим , т. е. . Следовательно, искомое частное решение имеет вид .

Пример 5.

Проинтегрировать линейное уравнение . (А)

Применим метод вариации произвольной постоянной. Решим сначала линейное однородное уравнение , (В) Решение неоднородного уравнения ищем в виде . (С) Дифференцируя, находим . (D) Подставляя (С) и (D) в уравнение (А), получим: откуда . Осуществляя подстановку , найдем . Итак,

. (Е) Подставляя (Е) в (С), получим .

Пример 6.

Проинтегрировать уравнение . (А) Данное уравнение можно привести к виду . (А’) Это уравнение Бернулли, т. е. уравнение вида (14.28). Здесь . Подстановка (14.29) в данном случае принимает вид , т. е. , (В) откуда . (С) Подставляя (В) и (С) в уравнение (А), получим линейное неоднородное уравнение относительно :

. (D) Решим соответствующее однородное линейное уравнение: . (Е)

Так как

то

откуда

. (F)

Общее решение уравнения (D) ищем с помощью метода вариации произвольной постоянной. Полагаем . (G)

Дифференцируя функцию , получим . (Н)

Подставляя (Н) в уравнение (D), находим

или

(J)

Подставляя (J) в (G), получим общее решение уравнения (D):

Переходя к переменной , получим:

Следовательно, общее решение исходного уравнения.

Линейные дифференциальные уравнения первого порядка. уравнение бернулли

Уравнение (11.13)

линейное относительно неизвестной функции и ее производной (а также любое уравнение, с помощью алгебраических преобразований приводящееся к виду (11.13)), называется неоднородным линейным дифференциальным уравнением первого порядка. Функции и должны быть непрерывными в некоторой области, например на отрезке , для того, чтобы выполнялись условия теоремы Коши существования и единственности решения (см. теорему 2 из § 11.1). Общее решение уравнения (11.13) всегда можно записать в виде

, (11.14)

где — произвольная постоянная. Таким образом, общее решение уравнения (11.13) всегда представимо в квадратурах, т. е. выражается через интегралы от известных функций . Отметим, что при нахождении интегралов из уравнения (11.14) произвольные постоянные можно считать равными нулю или, что то же самое, считать их включенными в произвольную постоянную . Если в уравнении (11.13) или , то получим дифференциальные уравнения с разделяющимися переменными, общее решение которых определяется из уравнения (11.14) при или соответственно. В случае, когда , уравнение (11.13) называют однородным линейным дифференциальным уровнением,

Пример 7.

Найти общее решение уравнения . Решить задачу Коши при начальном условии . Приведем данное уравнение к виду (11.13), разделив обе его части на . Получим

Здесь

Общее решение исходного уравнения в соответствии с формулой (11.14) имеет вид

. (11.15)

Найдем входящие в это решение интегралы. Имеем:

где знаки « + » и « — » появляются в силу равенства . Подставляя найденные интегралы в решение (11.15), окончательно получаем общее решение исходного уравнения:

Из него выделяем частное решение, соответствующее начальному условию :

Полезно иметь в виду, что иногда дифференциальное уравнение является линейным относительно как функции , т. е. может быть приведено к виду

. (11.16)

Его общее решение находится по формуле

. (11.17)

Пример 8.

Найти общий интеграл уравнения . Данное уравнение является линейным относительно функции . Действительно,

т. е. получили уравнение вида (11.16). Согласно формуле (11.17), общее решение исходного уравнения имеет вид

Отметим, что линейное дифференциальное уравнение (11.13) можно также проинтегрировать методом Бернулли, суть которого заключается в следующем. Введем две неизвестные функции и по формуле (подстановка Бернулли). Тогда . Подставив выражения для и в уравнение (11.13), получим уравнение , которое преобразуем к виду . (11.18)

Пользуясь тем, что одна из неизвестных функций, например , может быть выбрана достаточно произвольно (поскольку только произведение должно удовлетворять исходному уравнению (11.13)), выбираем в качестве любое частное решение уравнения , обращающее в нуль коэффициент перед в уравнении (11. 18)). После этого уравнение (11.18) превращается в уравнение .

Найдя общее решение последнего уравнения, придем к общему решению уравнения (11.13): . Таким образом, интегрирование уравнения (11.13) сводится к интегрированию двух уравнений с разделяющимися переменными.

Пример 9.

Проинтегрировать уравнение

методом Бернулли и решить задачу Коши при начальном условии . Сделав подстановку Бернулли , получим: . Находим частное решение уравнения : ,

Полагая , выбираем частное решение . Далее ищем общее решение уравнения , где . Имеем: . Общее решение исходного уравнения .

Из него выделяем частное решение, удовлетворяющее начальному условию , откуда . Подставляя значение в общее решение, получаем частное решение исходного уравнения: . Дифференциальное уравнение , (11.19)

где , а также любое уравнение, с помощью алгебраических преобразований приводящееся к уравнению (11.19), называется уравнением Бернулли. Путем введения новой функции по формуле уравнение Бернулли сводится к линейному уравнению относительно этой функции: . (11.20)

Решив уравнение (11.20) одним из описанных выше методов, найдем , а затем и . Уравнение Бернулли, как и линейное уравнение (11.13), можно решить с помощью подстановки Бернулли (см. пример 3).

Пример 10.

Найти общее решение уравнения Бернулли . Так как.для данного уравнения , можно сделать замену . Согласно уравнению (11.20), получим уравнение , общее решение которого в соответствии с формулой (11.14) имеет вид Общее решение исходного уравнения .

Теорема Бернулли Калькулятор расчетных уравнений Формулы

Теорема Бернулли Калькулятор формул расчетных уравнений — Потеря напора Гидромеханика

Входы:

Преобразования:

Статическая головка или высота (Z1)

= 0

МЕТР

Статическая головка или высота (Z2)

= 0

Давление (P1)

= 0

Давление (P1)

= 0

паскаль

давление (P2)

= 0

паскаль 92

Решение:

потеря напора (ч)

= НЕ РАСЧЕТНО

Другие единицы:

Изменить уравнение
Примечание Бернулли Уравнение предполагает:

Поток — это оптимизация

Устойчивое состояние

IVISCID

INVISCID FLUID

IVISCID FLUID

Выберите для поиска другого неизвестного

	Solve for head loss
	Solve for static head or elevation at point 1
	Solve for pressure at point 1
	Solve for velocity at point 1

, где

H	=	Потеря головки
Z	=	Статическая головка или возвышение
P	или элева.0076	=	Pressure
V	=	fluid velocity
p	=	fluid density
g	=	acceleration of gravity
Q	=	расход

Справочник — Книги:
1) П. Аарне Весилинд, Дж. Джеффри Пирс и Рут Ф. Вайнер. 1994. Экологическая инженерия. Баттерворт Хайнеманн. 3-е изд.

Графики роста младенцев — Процентили для младенцев Калькулятор оплаты сверхурочной работы Конвертер зарплаты в почасовую оплату — Вакансии Скидка в процентах — Калькулятор скидок при продаже Калькулятор повышения заработной платы Калькулятор линейной интерполяции Калькулятор возраста собаки Калькулятор закона идеального газа Калькулятор формул Эйлера Калькулятор насоса — водная гидравлика Калькуляторы уравнений гидромеханики расходомер Вентури Калькулятор уравнений давления жидкости Калькулятор числа Рейнольдса Калькулятор теоремы Бернулли Калькулятор расхода отверстия Калькулятор уравнений Хазена Вильямса Калькулятор уравнения непрерывности Калькулятор уравнений закона Дарси Калькулятор возраста кошки в человеческий возраст Калькулятор уравнения энергии Эйнштейна Калькулятор подъемной силы крыла самолета Калькулятор уравнений гравитации Калькулятор идеальной конструкции реактора Кирпич Время концентрации Калькулятор коэффициента операционных расходов Расчетные формулы переменного тока

Онлайн-веб-приложения, Богатое интернет-приложение, Технические инструменты, Спецификации, Практические руководства, Обучение, Приложения, Примеры, Учебники, Обзоры, Ответы, Ресурсы для просмотра тестов, Анализ, Решения для домашних заданий, Рабочие листы, Справка, Данные и информация для инженеров, Техники, преподаватели, репетиторы, исследователи, образование K-12, учащиеся колледжей и старших классов, проекты научных выставок и ученые

Джимми Рэймонд

Контакт: aj@ajdesigner. com

Политика конфиденциальности, отказ от ответственности и условия

Гидравлическая механика Уравнения Формулы Калькуляторы

Калькулятор конструкции акустического расходомера

Решение задач, связанных с расходомерами, средней осевой скоростью потока воды, датчиками, временем прохождения акустического сигнала вверх и вниз по течению, длиной акустического пути между поверхностями преобразователей и углом между акустическими пути и продольной оси трубы.

Калькулятор теоремы Бернулли

Онлайн-скрипт для решения любой переменной в уравнении теоремы Бернулли. Решите для потери напора, статического напора, высоты, энергии давления, энергии скорости, плотности и ускорения свободного падения. Помогает в расчетах сброса утечек, трубопроводных сетей, резервуаров, шлюзовых затворов, водосливов, пилотных труб, насадок и потока в открытом канале. Течение предполагается обтекаемым, стационарным, невязким и несжимаемым.

Калькулятор числа Коши

Решение задач, связанных со значением Коши, скоростью потока, объемным модулем упругости и плотностью.

Калькулятор числа кавитации

Решение задач, связанных с числом кавитации, локальным давлением, давлением паров жидкости, плотностью жидкости и характеристической скоростью потока.

Калькулятор уравнения Шези

Решение задач, связанных с уравнением Шези, скоростью потока, коэффициентом Шези, коэффициентом шероховатости, гидравлическим радиусом и уклоном трубопровода.

Калькулятор уравнения Коулбрука

Решение задач, связанных с уравнением Коулбрука, турбулентным потоком, коэффициентом трения Дарси, абсолютной шероховатостью и числом Рейнольдса.

Калькулятор непрерывности

Решите для расхода, площади и скорости в уравнении непрерывности.

Калькулятор Дарси Вайсбаха

Онлайн-решатель для любой переменной в уравнении Дарси-Вейсбаха. Решите для потери напора, коэффициента трения, диаметра трубы, длины трубы, скорости потока и ускорения свободного падения

Калькулятор уравнения закона Дарси

Решение задач, связанных с расходом, гидравлической проводимостью, гидравлическим градиентом, объемом твердых частиц, фазовой диаграммой насыщенного грунта, площадью поперечного сечения потока, дарси-скоростью или потоком, скоростью просачивания, эффективной площадью поперечного сечения пустот, брутто-потоком площадь поперечного сечения, напор, твердые частицы, пористость, коэффициент пустотности и длина колонны.

Калькулятор уравнений плотности

Решите уравнение плотности для любой переменной. Переменные включают плотность, массу и объем.

Калькулятор числа Эйлера

Решение задач, связанных с безразмерным значением числа Эйлера, гидродинамикой, изменением давления, плотностью и характеристической скоростью потока.

Калькулятор давления жидкости

Расчет различных переменных, связанных с силой, площадью, модулем всестороннего сжатия, сжимаемостью, изменением объема, верхним и нижним давлением столба жидкости, плотностью, ускорением свободного падения, глубина, высота, абсолютное, атмосферное и избыточное давление.

Калькулятор гравитационных уравнений

Решает задачи, связанные с законом всемирного тяготения Ньютона, универсальной гравитационной постоянной, массой, силой, периодом обращения спутника, массой планеты, средним радиусом орбиты спутника, ускорением, критической скоростью, скоростью убегания, радиусом от центра планеты и третьим законом Кеплера.

Калькулятор Хазена Вильямса

Решите любую переменную в уравнении Хазена Вильямса. Переменные включают расход, расход, среднюю скорость, диаметр трубы, гидравлический радиус, уклон гидравлической линии уровня и коэффициент трения.

Калькулятор гидравлического радиуса

Решение уравнений, связанных с гидравлическим радиусом, площадью сечения потока, смоченным периметром, средней глубиной, шириной поверхности воды, числом Фруда, скоростью потока, ускорением свободного падения, круговым сегментом, центральным углом, частично, полностью и наполовину заполненная труба и длина дуги.

Калькулятор числа Маха

Решает задачи, связанные с числом Маха, скоростью звука, скоростью объекта, дозвуковой, сверхзвуковой, гиперзвуковой, трансзвуковой, механикой высокоскоростной жидкости и безразмерными величинами.

Калькулятор Мэннинга

Определите скорость потока, коэффициент шероховатости, гидравлический радиус и наклон линии энергетического класса.

Калькулятор незначительных убытков

Решите для любой переменной уравнение незначительного убытка. Переменные включают коэффициент потерь энергии в закрытом трубопроводе, скорость и потери напора. Включены значения K для дисковых затворов, обратных клапанов, задвижек, шаровых клапанов, колен, входов и выходов.

Калькулятор расхода диафрагмы

Решает задачи, связанные с диафрагмой, расходом, коэффициентом расхода, площадью диафрагмы, гравитационной постоянной и осевой линией напора.

Калькулятор проектирования лотков Паршалла

Решает проблемы, связанные с лотками Паршалла, скоростью потока, глубиной вверх по течению и шириной горловины.

Калькулятор пермеаметра

Решение задач, связанных с пермеаметрами, коэффициентом проницаемости, расходом пористого материала, площадью поперечного сечения, изменением напора и изменением длины.

Калькулятор расхода в трубах

Онлайн-программа на языке Java для решения задач механики потока жидкости в трубах типа I, II и III с использованием уравнений Swamee & Jain, Darcy-Weisbach, Colebrook и Hazen-Williams. Решите для скорости потока, потери напора, коэффициента трения и диаметра трубы.

Расчетный калькулятор Прандтля

Решает задачи, связанные с безразмерной величиной Прандтля, теплопередачей, гидромеханикой, диффузией тепла и импульса, кинематической вязкостью и температуропроводностью.

Калькулятор давления

Расчет различных переменных, связанных с силой, площадью, модулем объемного сжатия, сжимаемостью, изменением объема, верхним и нижним давлением столба жидкости, плотностью, ускорением свободного падения, глубиной, высотой, абсолютным, атмосферным и манометрическим давлением.

Калькулятор насосов

Решение задач, связанных с кавитацией, положительным кавитационным запасом (NPSH), скоростью жидкости, давлением на входе по осевой линии рабочего колеса, давлением паров, удельным весом жидкости, силой тяжести, нагнетанием насоса, общим напором, КПД насоса, водяной лошадиной силой и тормозом Лошадиные силы.

Калькулятор числа Рейнольдса

PHP-скрипт для решения любой переменной в уравнении числа Рейнольдса для анализа ламинарного, турбулентного и переходного течения. Число Рейнольдса анализирует пропорцию гидравлического эффекта силы инерции и силы вязкости. Переменные включают число Рейнольдса, плотность, скорость, характеристическую длину и вязкость.

Калькулятор числа Шмидта

Решение задач, связанных с безразмерными значениями числа Шмидта, гидромеханикой, массопереносом, кинематической вязкостью и диффузией массы.

Калькулятор закона Стокса

Решение задач, связанных с конечной скоростью, скоростью падения и осаждения, диаметром и плотностью частиц, плотностью и вязкостью среды (например, воды, воздуха, масла) и ускорением свободного падения.

Калькулятор преобразования температуры

Решает проблемы, связанные с термометрами, градусами Фаренгейта, Цельсия и Кельвина.

Калькулятор времени концентрации

Решает задачи, связанные со временем концентрации, Иззардом, Кирби, Кирпичем, кинематической волной, Службой охраны природных ресурсов, Брансби Уильямсом, площадью водосбора, длиной канала, временем задержки водосбора, гидравлической длиной водосбора, потенциальным водосбором водохранилище, средний уклон водораздела, длина пути, расстояние сухопутного течения, интенсивность осадков, уклон, коэффициент шероховатости замедления, коэффициент шероховатости сухопутного течения Мэннинга, средний уклон пути сухопутного течения и длина течения.

Калькулятор конструкции скважины безнапорного водоносного горизонта

Решение задач, связанных с законом Дарси для откачки через центр цилиндра, коэффициентом проницаемости, напором в наблюдательных и добывающих скважинах, радиусом, депрессией и конусом депрессии.

Калькулятор расходомера Вентури

Интерактивное программное обеспечение для расчета расхода и перепада давления с использованием уравнения Бернулли для манометра Вентури.

Калькулятор гидравлического удара

Решает проблемы, связанные с максимальным ударным давлением гидравлического удара, скоростью волны давления, изменением скорости жидкости, ускорением свободного падения, повышением давления, длиной трубы вверх по течению, временем закрытия клапана, давлением на входе и удельным весом жидкости.

Калькулятор числа Вебера

Решает задачи, связанные с числом Вебера, механикой жидкости, безразмерным значением, плотностью, скоростью, характеристической длиной и силой поверхностного натяжения.