Симплекс метод с искусственным базисом
Решение задачи линейного программирование симплекс методом искусственного базиса (М-метод)
Рассмотрим метод искусственного базиса на примере
Дана целевая функция
Z=3x1+2x2+x3→max
Ограничения в виде системы линейных уравнений
x1,x2,x3 ≥0
Для коэффициентов базисных переменных надо учитывать, что знак неравенства «≤» эквивалентен «+», а знак неравенства «≤» — «–»
В целях построения начального опорного плана ведём дополнительные переменные и приведем уравнение к каноническому виду
Далее, в полученную линейную систему введем также искусственные переменные
Также целевая функция при максимизации примет вид
F(x)=3x1+2x2+x3-Mx9-Mx10-Mx11
Под символом M, будем понимать очень большое неотрицательное число.
Так как необходимо максимизировать max функцию, то знак перед M ставится «-», то есть коэффициент равен -M.
Далее, из системы линейных уравнений из уравнений 3,4,5 выразим искусственные переменные x9,x10,x11, они равны
x9=200-x1+x6
x10=200-x2+x7
x11=100-x3+x8
Подставим полученные значения в целевую функцию
Составим 1-ый опорный план
Первая итерация
Данный опорный план не оптимален в связи с тем, что в индексной строке имеются отрицательные значения.
По модулю из индексной строки выбираем наибольшее значение, и оно равно -3-1М.
По строкам найдем минимальное значение по формуле
2000/2=1000
3000/1=3000
200/1=200
min{1000,3000,200,-,-}=200
Вторая итерация
Имеем на второй итерации следующий опорный план
Вторая итерация
Полученный опорный план не оптимален имеются отрицательные значения в индексной строке.
Выбираем по модулю наибольшее значение -2-1М
1600/2=800
2800/2=1400
200/1=200
min{1600,1400,-,200,-}=200
Решаем аналогично
Третья итерация
min{1200,800,-,-,100}=100
Четвертая (заключительная) итерация
План не оптимален, в индексной строке имеются отрицательные значения
min{550,2100,-,-,-}=650
X1=750
X2=200
X3=100
F(x)=3*750+2*200+100=2750
Пример решения задачи симплекс М-методом
Условие задачи
Найти оптимальные величины производства продукции видов А, Б и В. Затраты сырья на единицу продукции: А – 5, Б – 2, В – 4. Объем сырья – 2000 единиц. Затраты оборудования на единицу продукции: А – 4, Б – 5, В – 4. Объем оборудования – 1000 единиц.
Прибыль от реализации единицы продукции: А – 10, Б – 8, В – 12. Критерий – максимум прибыли предприятия. Производство продукции А должно быть не менее 100 ед. Производство продукции Б должно быть не менее 50 ед.
Решение задачи симплекс методом
1) Определение оптимального плана производства
Пусть x1, x2, x3 — количество произведенной продукции вида А, Б, В, соответственно. Тогда математическая модель задачи имеет вид:
F = 10·x1 + 8·x2 + 12·x3 –>max
Решаем симплекс методом.
Вводим дополнительные переменные x4 ≥ 0, x5 ≥ 0, x6 ≥ 0, x7 ≥ 0, чтобы неравенства преобразовать в равенства.
Чтобы выбрать начальный базис, вводим искусственные переменные x8 ≥ 0, x9 ≥ 0 и очень большое число M (M –> ∞).
Решаем М методом.
F = 10·x1 + 8·x2 + 12·x3 + 0·x4 + 0·x5 + 0·x6 + 0·x7– M·x8– M·x9 –>max
В качестве базиса возьмем x4 = 2000; x5 = 1000; x8 = 100; x9 = 50.
Данные заносим в симплекс таблицу
Симплекс таблица № 1
Целевая функция:
Вычисляем оценки по формуле:
.
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ1 = – M – 10
Вводим переменную x1 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x1:
Наименьшее неотрицательное: Q3 = 100.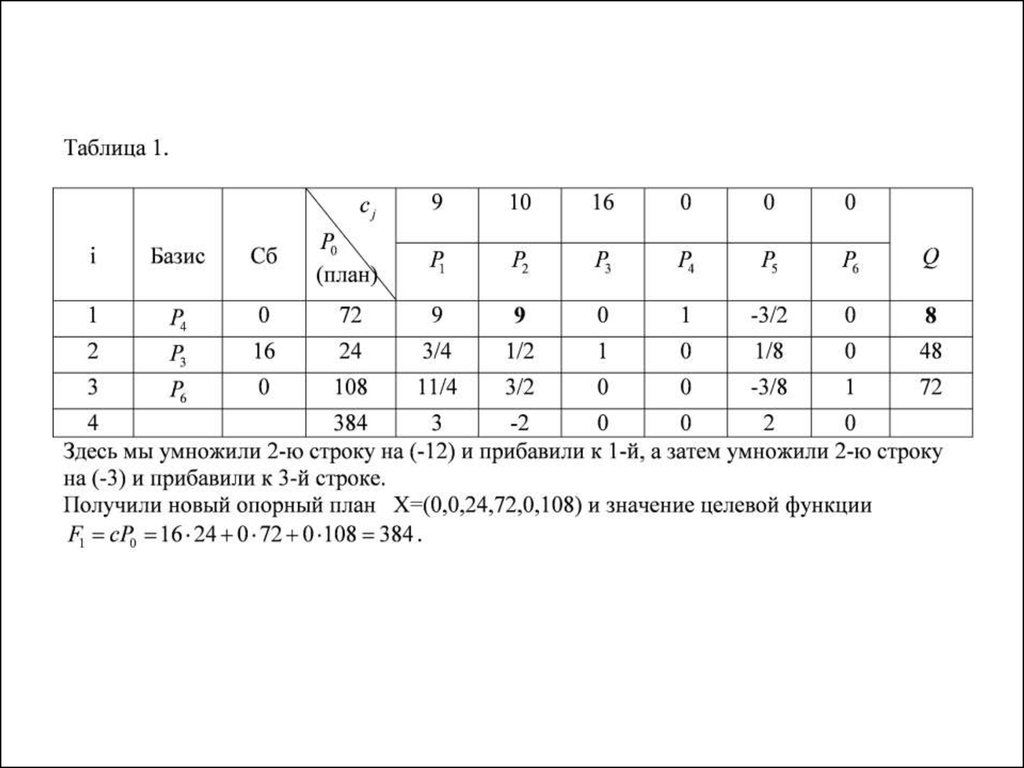
Выводим переменную x8 из базиса. Для этого над строками таблицы выполняем линейные преобразования .
Из 1-й строки вычитаем 3-ю строку, умноженную на 5
Из 2-й строки вычитаем 3-ю строку, умноженную на 4
Получаем новую таблицу.
Симплекс таблица № 2
Целевая функция:
Вычисляем оценки по формуле:
.
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ2 = – M – 8
Вводим переменную x2 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x2:
Наименьшее неотрицательное: Q4 = 50. Выводим переменную x9 из базиса и удаляем искусственные переменные. Выполняем линейные преобразования .
Из 1-й строки вычитаем 4-ю строку, умноженную на 2
Из 2-й строки вычитаем 4-ю строку, умноженную на 5
Получаем новую таблицу.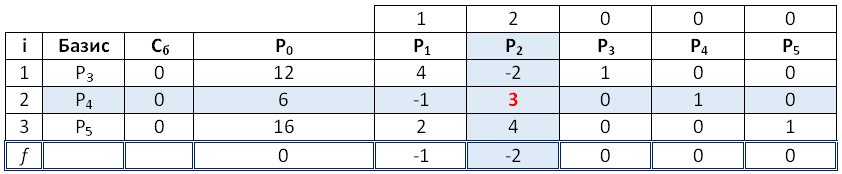
Симплекс таблица № 3
Целевая функция:
Вычисляем оценки по формуле:
.
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ3 = – 12
Вводим переменную x3 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x3:
= 87.5
Наименьшее неотрицательное: Q2 = 87.5. Выводим переменную x5 из базиса.
2-ю строку делим на 4.
Из 1-й строки вычитаем 2-ю строку, умноженную на 4
Вычисляем:
Получаем новую таблицу.
Симплекс таблица № 4
Целевая функция:
Вычисляем оценки по формуле:
.
Поскольку отрицательных оценок нет, то план оптимален.
Решение задачи: x1 = 100; x2 = 50; x3 = 175/2 = 87.
5; x4 = 1050; x5 = 0; x6 = 0; x7 = 0; Fmax = 2450
Ответ
x1 = 100; x2 = 50; x3 = 175/2 = 87.5; x4 = 1050; x5 = 0; x6 = 0; x7 = 0; Fmax = 2450
То есть необходимо произвести x1 = 100 единиц продукции вида А, x2 = 50 единиц продукции вида Б и x3 = 87,5 единиц продукции вида В. Максимальная прибыль при этом составит Fmax = 2450 единиц.
Калькулятор симплексного методашаг за шагом.
Пример 5. Решение задачи линейного программирования с использованием симплекс-метода.
Решение не единственное
Это решение было сделано с помощью калькулятора, представленного на сайте.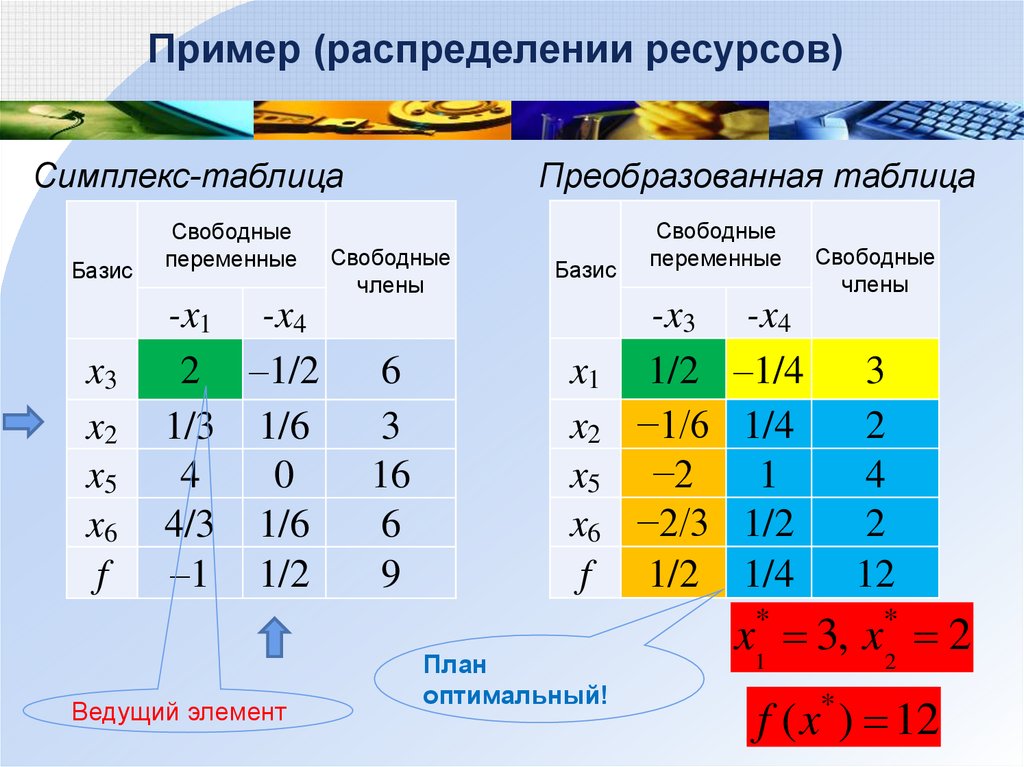
Пример 1. Нахождение максимального значения функции
Пример 2. Нахождение минимального значения функции
Пример 3. Нахождение максимального значения функции (искусственные переменные)
Пример 4. Нахождение минимального значения функции ( искусственные переменные)
Пример 6. Функция неограниченно возрастает
Пример 7. Функция неограниченно убывает
Пример 8. Область допустимых решений — пустое множество
Задача:
Найти максимальное значение функции
| F | = | 3 | x 1 | + | 2 | x 2 |
с ограничениями:
| 9.0048 | x 1 | 2 | x 2 | ≤ | 6 | ||
| 2 | x 1 | + | x 2 | ≤ | 8 | ||
| x 2 | ≤ | 2 |
Решение:
1.
Это необходимое условие решения задачи:
числа в правых частях системы ограничений должны быть неотрицательны.
Это условие выполнено.
2. Это необходимое условие решения задачи:
все ограничения должны быть уравнениями.
| x 1 | + | 2 | x 2 | ≤ | 6 | |||
| 2 | x 1 | + | x 2 | ≤ | 8 | |||
| x 2 | ≤ | 2 |
| x 1 | + | 2 | x 2 | + | S 1 | = | 6 | ||||||||||
| 2 | x 1 | + | x 2 | + | С 2 | = | 8 | ||||||||||
| x 2 | + | S 3 | = | 2 |
S 1 ≥ 0 , S 2 ≥ 0, S 3 ≥ 0.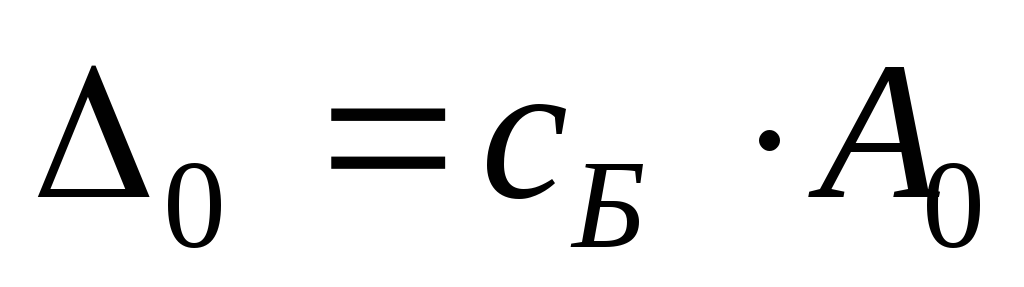
Введенные переменные S 1 , S 2 , S 3 называются переменными резерва.
3. Нахождение начального базиса и значения функции F, соответствующего найденному начальному базису.
Что такое базис?
Переменная называется основной переменной уравнения, если она входит в это уравнение с коэффициентом, равным единице, и не входит в другую систему уравнений (при условии, что в правой части уравнения стоит неотрицательное число).
Если в каждом уравнении есть базисная переменная, то говорят, что система имеет базис.
В чем заключается идея симплекс-метода?
Каждому основанию соответствует одно значение функции. Одно из них — максимальное значение функции F.
Мы будем двигаться от одной основы к другой.
Следующий базис будет выбран таким образом, чтобы значение функции F было не меньше, чем мы имеем сейчас.
Очевидно, что количество возможных оснований для любой задачи не очень велико.
Так что рано или поздно ответ будет получен.
Как мы будем переходить от одного базиса к другому?
Решение удобнее записывать в виде таблиц. Каждая строка таблицы эквивалентна системному уравнению. Выделенная строка состоит из коэффициентов функции (см. таблицу ниже). Это позволяет нам не переписывать переменные каждый раз. Это экономит время.
Это необходимо для того, чтобы получить значение функции F не меньше, чем у нас.
Колонка выбрана.
Для положительных коэффициентов выбранного столбца считаем коэффициент Θ и выбираем минимальное значение.
Это необходимо для того, чтобы получить неотрицательные числа в правой части уравнений после перехода на другой базис.
Строка выбрана.
Найден элемент, который будет основным. Далее нам нужно будет произвести расчет.
Есть ли у нашей системы основа?
| x 1 | + | 2 | x 2 | + | S 1 | = | 6 | ||||||||||
| 2 | x 1 | + | x 2 | + | S 2 | = | 8 | ||||||||||
| x 2 | + | S 3 | = | 2 |
В нашей системе есть основа.
| F | = | x 1 | + | 2 | x 2 |
. Не-Basic Variables. В уме мы можем найти значения основных переменных. (см. систему)
Функция F содержит только неосновные переменные. Поэтому значение функции F для этого базиса можно найти в уме.
| x 1 = 0 x 2 = 0 S 1 = 6 S 2 = 8 S 3 2 900 300 = 02 900 300 = 02 => F = 0 | |
Исходная база найдена. Найдено значение функции F, соответствующее исходному базису.
4. Нахождение максимального значения функции F.
Шаг 1
| x 1 | x 2 | S 1 | S 2 | S 3 | Const. | Θ |
| 1 | 2 | 1 | 0 | 0 | 6 | 6 : 2 = 3 |
| 2 | 1 | 0 | 1 | 0 | 8 | 8 : 1 = 8 |
| 0 | 1 | 0 | 0 | 1 | 2 | 2 : 1 = 2 |
| 1 | 2 | 0 | 0 | 0 | F — 0 | |
| 1 | 0 | 1 | 0 | -2 | 2 | |
| 2 | ||||||
| 2 | ||||||
| 2 | -1 | 6 | ||||
| 0 | 1 | 0 | 0 | 1 | 2 | |
| 1 | 0 | 0 | 0 | -2 | F — 4 |
Неосновные переменные равны нулю.
В уме мы можем найти значения основных переменных. (см. таблицу)
Функция F содержит только неосновные переменные. Поэтому значение функции F для этого базиса можно найти в уме. (см. выделенную строку в таблице)
| x 1 = 0 S 3 = 0 x 2 = 2 S 1 = 2 S 2 = 0 6 | => F — 4 = 0 => F = 4 |
Шаг 2
| x 1 | x 2 | S 1 | S 2 | S 3 | Const. | Θ |
| 1 | 0 | 1 | 0 | -2 | 2 | 2 : 1 = 2 |
| 2 | 0 | 0 | 1 | -1 | 6 | 6 : 2 = 3 |
| 0 | 1 | 0 | 0 | 1 | 2 | |
| 1 | 0 | 0 | 0 | -2 | F — 4 | |
| 1 | 0 | 1 | 0 | -2 | 2 | |
| 0 | 0 | -2 | 1 | 3 | 2 | |
| 0 | 1 | 0 | 0 | 1 | 2 | |
| 0 | 0 | -1 | 0 | 0 | F — 6 |
Неосновные переменные равны нулю.
Функция F содержит только неосновные переменные. Поэтому значение функции F для этого базиса можно найти в уме. (см. выделенную строку в таблице)
| S 1 = 0 S 3 = 0 x 1 = 2 x 2 = 2 2 0 S 2 9 | => F — 6 = 0 => F = 6 |
В выделенной строке нет положительных коэффициентов. Таким образом, было найдено максимальное значение функции F.
Коэффициент равен нулю на позиции 5 в выделенной строке. В столбце 5 нет базовой переменной.
Это позволяет нам найти другое решение, в котором F = 6.
Шаг 3
| х 1 | х 2 | S 1 | S 2 | S 3 | конст. | Θ |
| 1 | 0 | 1 | 0 | -2 | 2 | |
| 0 | 0 | -2 | 1 | 3 | 2 | 2 : 3 ≈ 0,67 |
| 0 | 1 | 0 | 0 | 1 | 2 | 2 : 1 = 2 |
| 0 | 0 | -1 | 0 | 0 | F — 6 | |
| 1 | 0 | 1 | 0 | -2 | 2 | |
| 0 | 0 | -2/3 | 1/3 | 1 | 2/3 | |
| 0 | 1 | 0 | 0 | 1 | 2 | |
| 0 | 0 | -1 | 0 | 0 | F — 6 | |
| 1 | 0 | -1/3 | 2/3 | 0 | 10/3 | |
| 0 | 0 | -2/3 | 1/3 | 1 | 2/3 | |
| 0 | 1 | 2/3 | -1/3 | 0 | 4/3 | |
| 0 | 0 | -1 | 0 | 0 | F — 6 |
Non -основные переменные равны нулю. В уме мы можем найти значения основных переменных. (см. таблицу)
Функция F содержит только неосновные переменные. Поэтому значение функции F для этого базиса можно найти в уме. (см. выделенную строку в таблице)
| S 1 = 0 S 2 = 0 x 1 = 10/3 x 2 = 4/3 3 S | 0 3 => F — 6 = 0 => F = 6 |
С геометрической точки зрения оба решения являются точками пространства, т.е. образуют отрезок.
Любая точка (любое решение) на этом отрезке также будет решением.
Результат:
X
1 = 2 * t + 10/3 * (1 — t)X
2 = 2 * t + 4/3 * (1 — t)0 ≤ t ≤ 1
F
max = 6Об инициализации симплексного алгоритма
На этой странице
АннотацияВведениеЗаключениеБлагодарностиСсылкиАвторское правоСтатьи по теме
В этом документе обсуждается важность начальной точки в симплексном алгоритме. Три разных метода нахождения базового допустимого решения сравниваются в выполненных численных тестовых примерах. Покажем, что наши два метода на Тестовые задачи Netlib имеют лучшую производительность, чем классический алгоритм поиска начального решения. Сравнение представленных оптимизационных программ основано на количестве итерационных шагов и требуемом процессорном времени. Отмечается, что в среднем для определения начальной точки требуется больше итераций, чем количество итераций, необходимое симплексному алгоритму для нахождения оптимального решения.
1. Введение
Существует два основных метода решения задачи линейного программирования: симплекс-метод и метод внутренних точек. В обоих этих двух методах необходимо определить начальную точку. Известно, что для применения симплексного алгоритма требуется хотя бы одно базисное допустимое решение. Для метода внутренних точек в большинстве случаев достаточно, чтобы точка принадлежала так называемому центральному пути. Также обратите внимание, что в большинстве алгоритмов, основанных на методах внутренних точек, начальная точка не обязательно должна быть достижимой. Однако при практической реализации показано, что численная устойчивость алгоритма все же зависит от выбора начальной точки. Эти вопросы исследованы в работах [1, 2].
Два классических алгоритма генерации начальной точки для симплекс-алгоритма — это двухфазный симплекс-алгоритм и метод Big-M . Главный недостаток этих алгоритмов — необходимость введения искусственных переменных, увеличивающих размерность задачи. По этой причине разрабатываются алгоритмы, не требующие введения искусственных переменных. В [3] предложена эвристика для нахождения начальной точки задачи линейного программирования, основанная на методе минимальных углов. К сожалению, эти эвристики можно использовать только для определенных классов задач. Подобные эвристики исследуются в работах [4–6]. Различные варианты алгоритма без введения искусственных переменных приведены в работах [7–12]. Один из вариантов этих алгоритмов представлен и обсуждается в статье [11], которая послужила источником вдохновения для нашей статьи. Мы сравниваем три разных метода нахождения начального базового допустимого решения (отправной точки для симплексного алгоритма) во всех выполненных численных тестовых примерах. Два метода, названные и , введены в [13], а третий метод, названный NFB, установлен в [11].
2. Симплекс-метод и модификации
Рассмотрим задачу линейного программирования (ЛП) в стандартной матричной форме: где – полная матрица рангов строк (), , а система определяется как , . Предполагается, что -я запись в обозначается через , , , и .
Затем выбираем основные переменные , выражаем их в виде линейной комбинации неосновных переменных и получаем каноническую форму задачи (2.1). Запишем эту каноническую форму в табл. 1.
Коэффициенты преобразованной матрицы и преобразованного вектора без ограничения общности снова обозначаются через и соответственно.
Для полноты изложения переформулируем один вариант двухфазного симплекс-алгоритма максимизации из [12, 14] для задачи (2.1), представленный в табл. 1.
В каждой итерации симплекс-метода ровно одна переменная переходит от небазового к базовому, и ровно одна переменная переходит от базового к небазовому. Обычно существует более одного выбора для входных и выходных переменных. Следующий алгоритм описывает переход от текущей базы к новой базе, когда выбраны исходящая базовая и входящая небазовая переменные.
Алгоритм 2.1 (рассмотреть обмен базовой переменной и неосновной переменной).
Следующий алгоритм находит оптимальное решение задачи ЛП при выполнении условия.
Алгоритм 2.2.
Шаг . Если , то базовое решение является оптимальным решением.
Шаг . Выбирайте по правилу Бланда [15].
Шаг . Если , остановите алгоритм. Максимум есть.
В противном случае перейдите к следующему шагу.
Шаг . Вычислить
Если условие не выполняется, используем алгоритм из [12, 14] для поиска начального базового допустимого решения. В отличие от подхода, использованного в [16], он не использует искусственных переменных и, следовательно, не увеличивает размер задачи. Здесь он переформулирован как следующий Алгоритм 2.3.
Алгоритм 2.3.
Шаг . Выберите последний.
Шаг . Если , то СТОП. Проблема ЛП неразрешима.
Шаг . В противном случае найти, вычислить
выберите в качестве входной неосновной переменной, а в качестве исходящей базовой переменной примените алгоритм 2.1 и перейдите к шагу .
Обратите внимание, что алгоритм 2.3 и алгоритм NFB из [11] эквивалентны. Как показано в работе [13], недостаток алгоритма из [12] заключается в том, что при его применении для преобразования выбранной координаты из базового решения в положительную может увеличиваться количество отрицательных координат.
Задача выбора уходящей базовой переменной и соответствующей входной неосновной переменной в двухфазном симплекс-методе содержится в шаге алгоритма 2.2 и шаге алгоритма 2.3. Мы заметили два недостатка Step . Через обозначим индекс последнего отрицательного .(1)Если для каждого индекса такого, что на следующей итерации становится отрицательным: (2) Если на следующей итерации отрицательно: Хотя могут существовать и такие, что В таком случае можно выбрать опорный элемент и получить Кроме того, так как каждый остается удобным для следующего основного допустимого решения:
Таким образом, возможно, что выбор входящей и выходящей переменной, определяемый Step, уменьшает количество положительных ‘s после применения алгоритма 2. 1. Наша цель — устранить наблюдаемые недостатки в Step . Для этой цели мы предлагаем модификацию Step , которая дает лучшую эвристику для выбора базовых и небазовых переменных.
Предложение 2.4 (см. [13]). Пусть задача (2.1) разрешима и пусть есть основное недопустимое решение с , . Рассмотрим набор индексов.
Верны следующие утверждения. (1) Новое базисное решение с не более чем отрицательными координатами можно получить только за один шаг симплекс-метода в следующих двух случаях: (а), (б) и существуют и такие, что
(2) Можно получить новое основное решение с точно отрицательными координатами за один шаг симплекс-метода, если ни условие (а), ни условие (б) не выполняется.
Доказательство. Переформулируем доказательство из [13] для полноты.
(1) (a) Если для произвольного опорного элемента мы получаем новое базовое решение хотя бы с одной положительной координатой:
Существование отрицательного обеспечивается предположением о разрешимости задачи (2. 1).
(b) Теперь предположим, что выполнены условия , , и (2.11). Выберите опорный элемент и примените алгоритм 2.1. Выберите произвольное , .
В случае очевидно, что
В случае , используя , делаем вывод сразу
С другой стороны, поскольку из алгоритма 2.1 получаем
Поэтому все неотрицательные остаются неотрицательными и становятся неотрицательными.
(2) Если ни условие (a), ни условие (b) не выполняются, пусть и таковы, что
Выбирая в качестве опорного элемента и применяя преобразования, определенные в алгоритме 2.1, мы получаем такое же количество отрицательных элементов в векторе . Этот факт доказывается аналогично части 1 (б).
Замечание 2.5. Из предложения 2.4 мы получаем три правильных выбора опорного элемента в шаге : (i) произвольный в случае ; (ii) произвольное, удовлетворяющее (2. 11), когда выполняются условия ,; (iii) произвольное, удовлетворяющее (2.16) при , а в предыдущем случае нет удовлетворяющих условиям.
В соответствии с предложением 2.4 и соображениями из замечания 2.5 мы предлагаем следующее улучшение алгоритма 2.3.
Алгоритм (модификация Алгоритма 2.3)
Шаг 1. Если , выполнить Алгоритм 2.2. В противном случае продолжайте.
Шаг 2. Выберите первый .
Шаг 3. Если , то СТОП. Проблема ЛП неразрешима.
В противном случае построить набор
инициализировать переменную и продолжить.
Шаг 4. Вычислить
Шаг 5. Если , то поменять местами входящую неосновную переменную и выходящую базовую переменную (применить Алгоритм 2.1) и перейти к Шагу 1. Иначе перейти к Шагу 6.
Шаг 6. Если , поменять местами и (применить Алгоритм 2.1 ) и перейти к шагу 1. В противном случае поставить и перейти к шагу 3.
Алгоритм выбирает одно фиксированное (первое) значение, удовлетворяющее условиям предложения 2.4. Но может существовать и такое, что выполняются условия предложения 2.4, и на следующей итерации мы можем получить базовое решение с меньшим числом отрицательных . По этой причине в [13] мы привели улучшенную версию Алгоритм , названный .
Алгоритм
Шаг 1. Если , выполнить Алгоритм 2.2. В противном случае построить множество
Шаг 2. Установите и выполните следующие действия. Шаг 2.1. Если то СТОП. Проблема ЛП неразрешима. В противном случае построить множество
поставить и продолжить. Шаг 2.2. Найдите минимумы:
Если , то выбираем в качестве опорного элемента применяем алгоритм 2.1 и переходим к шагу 1. (на следующей итерации становится положительным.) шаг 2.3. Если , то поставить и перейти к шагу 2.2, в противном случае продолжить. Шаг 2.4. Если , то поставить и перейти к шагу 2.1, в противном случае продолжить.
Шаг 3. Если и не существуют и такие, что
Шаг 3.1. Выбирать . Шаг 3.2. Вычислить
Шаг 3.3. Выберите опорный элемент, «примените алгоритм 2.1» и перейдите к шагу 1.
Алгоритм и Алгоритм хорошо определены. Если нет такого, что выполняется условие (2.11), выбираем опорный элемент в соответствии с замечанием 2.5, чтобы получить решение с тем же числом отрицательных ‘. Чтобы избежать зацикливания в этом случае, мы приведем правило антициклирования, основанное на следующем результате из [13].
Предложение 2.6 (см. [13]). Предположим, что не существует такого, что выполняются условия (2.11) предложения 2.4. После выбора опорного элемента согласно (2.16) получаем новую базу, где , выполняется для всех .
Поскольку на шаге 2 алгоритм зафиксирован, алгоритм может выполнять цикл только в том случае, если . По этой причине, если минимум в (2.18) неоднозначен, выбираем по правилу Бланда, гарантирующему, что симплекс-метод всегда обрывается [15] и [17, теорема 3.3]. Следовательно, согласно предложению 2.6, за конечное число итераций значение начнет возрастать, иначе мы придем к выводу, что задача неразрешима (положительны для всех ).
В дальнейшем мы покажем, что наши методы имеют лучшие характеристики, чем метод НОС Набли из [11]. Алгоритмы и реализованы в программном комплексе MarPlex , повторно использованном из [13] и протестированном на некоторых стандартных тестовых задачах линейного программирования.
3. Результаты сравнения
Мы уже упоминали, что статья [11] побудила нас рассмотреть количество итераций, необходимых для нахождения начальной точки. Это дает точный показатель качества применяемых решателей линейного программирования. В работе [11] показано, что частное от общего числа итераций, необходимых для определения начального решения, и числа переменных равно для НФБ, для для двухфазного алгоритма и для метода Big-M . Очевидно, что по этому критерию алгоритм NFB лучше, чем методы Two-phase и Big-M .
Отметим, что результаты работы [11] получены на небольшой выборке тестовых задач, в которых число переменных относительно невелико. Чтобы устранить этот недостаток, мы применили алгоритм NFB к задачам тестирования коллекции Netlib. Кроме того, мы протестировали два наших алгоритма, отмеченных и . В данной работе мы рассматриваем результаты практического применения этих алгоритмов в соответствии с методологиями, использованными в работах [11, 18].
Сравнение различных программ оптимизации из [11] основано на количестве итерационных шагов. В приведенных ниже таблицах столбцы с пометкой содержат количество переменных в задаче, а столбцы с пометкой NFB, и содержат количество итераций, необходимое для соответствующего алгоритма. Имена проблем Netlib приведены в столбце LP. Количество итераций, необходимое для нахождения начальных базовых допустимых решений в конкретных тестовых примерах, представлено в табл. 2.9.0006
Частное от общего количества итераций, необходимых для определения начального решения. Симплексный алгоритм и общее количество переменных равно для алгоритма NFB, для алгоритма равно , а для метода равно . Для алгоритма NFB мы получаем более высокое значение по сравнению с результатом из [11] как следствие большего размера и вычислительных усилий для решения тестируемых задач. Алгоритм показывает чуть лучшую эффективность, но дает значительно меньшее частное.
В таблице 3 мы приводим сравнительные результаты общего количества итераций, необходимых для решения одних и тех же тестовых задач.
Из таблицы 3 видно, что это лучший алгоритм. Интересно отметить, что алгоритм требует меньшего общего количества итераций по сравнению с NFB, хотя симплекс-алгоритм после применения алгоритма требует больше итераций. Следовательно, выбор алгоритма определения начальной точки очень важен для общей эффективности программного обеспечения для решения задач ЛП.
Из табл. 2 и 3 следует, что общее количество итераций, затраченных в Симплекс-алгоритме на выработку оптимального решения, равно 15409,16400,14170 для ООС, , и методов соответственно. Таким образом, ясно, что общее количество итераций, необходимых для исходного базового допустимого решения, больше, чем количество итераций, требуемых симплекс-алгоритмом для нахождения оптимального решения. Этот факт очень важен, особенно если из табл. 2 заметить, что около 25% рассмотренных задач подходят для определения исходной точки за один шаг. С учетом результатов работы [11], из которых следует, что число итераций классического двухэтапный метод определения начальной точки значительно превышает количество итераций алгоритмов, не вводящих искусственных переменных, факт становится более важным. Это означает, что поиск отправной точки представляет собой очень важную часть решения задач LP.
Лучшие характеристики метода в первую очередь (и особенно метода) по сравнению с методом NFB также могут быть подтверждены с помощью так называемого профиля производительности, введенного в [18]. Базовая метрика определяется количеством итерационных шагов. Следуя обозначениям, данным в статье [18], имеем, что количество решателей равно (NFB, , и ), а число численных экспериментов равно . Для показателей производительности мы используем количество итерационных шагов. Через мы обозначаем количество итераций, необходимых для решения задачи решателем. Количество
называется коэффициентом полезного действия. Наконец, производительность решателя определяется следующей кумулятивной функцией распределения
где и представляет собой набор задач. На рис. 1 показаны профили производительности для NFB, и относительно количества итераций. Рисунок 1(а) (соответственно, Рисунок 1(б)) иллюстрирует данные, расположенные в Таблице 2 (соответственно, Таблице 3).
Из рисунка 1(а) видно, что и методы показывают лучшие характеристики по сравнению с NFB. Сравнение алгоритмов и дает несколько противоречивые результаты. А именно, вероятность быть оптимальным решателем относительно количества итерационных шагов, необходимых для создания начальной точки, в пользу алгоритма, что подтверждается . С другой стороны, вероятность алгоритма больше, чем вероятность для всех значений. С другой стороны, всегда доволен.
Из рисунка 1(b) видно, что неравенство всегда выполняется, а это означает, что алгоритм имеет наибольшую вероятность быть оптимальным решателем по отношению к общему количеству итераций, необходимых для решения задачи.
В дальнейшем общее время процессора является критерием сравнения. Требуемое процессорное время для NFB и методы приведены в таблице 4. Соотношение времени и количество итераций алгоритмов и по отношению к алгоритму NFB также приведены в таблице 4.
Ситуация в данном случае не совсем ясна. А именно, сравнивая отношение времени по отношению к количеству итераций, указанному в столбцах с метками и , мы заключаем, что количество необходимых итераций и алгоритмов для задач czprob, share1b, ship04l и ship08l меньше, чем количество итераций алгоритма NFB, но это не соответствует требуемому соотношению процессорного времени. Это является следствием наибольшего количества условий, которые необходимо проверять в алгоритмах и по отношению к алгоритму NFB. Трудности этого типа могут возникнуть, особенно когда задача ЛП имеет плотную матрицу. Обратите внимание, что для всех остальных тестовых задач соответствие соотношения количества итераций требуемому соотношению процессорного времени существует.
На рис. 2 показаны профили производительности для NFB относительно требуемого процессорного времени.
Из рисунка 2 видно, что вероятность того, что решатель окажется оптимальным относительно требуемого процессорного времени, в пользу алгоритма, что подтверждается неравенствами . С другой стороны, дальнейшее сравнение при увеличении дает противоречивые результаты. К сожалению, алгоритм не является лучшим решением для всех значений. В этом случае следует, что алгоритм является лучшим вариантом, за исключением случаев, когда алгоритм NFB использует преимущество. Далее, для имеем , а значит, рассматриваемые решатели эквивалентны. Наконец, для значений Алгоритм снова лучший.
4. Заключение
Важность выбора исходной точки известна из теории линейного программирования. В этой статье мы исследовали эту проблему с точки зрения количества итераций, необходимых для нахождения начальной точки и оптимальной точки, а также с точки зрения требуемого процессорного времени.
Мы заметили, что наш алгоритм достиг наименьшего общего количества итераций для нахождения начальной точки для симплекс-метода, а также минимальное общее количество итераций для определения оптимальной точки. С другой стороны, алгоритм имеет наибольшую вероятность достижения минимального количества итераций для нахождения начального базового допустимого решения. Алгоритм имеет наибольшую вероятность быть оптимальным решателем по отношению к общему количеству итераций, необходимых для решения задачи.
Сравнение требуемого процессорного времени показывает, что вероятность того, что будет оптимальным решателем, в пользу алгоритма для и для . Понятно, что процессорное время в основном зависит от количества итераций, но очевидно, что есть и другие важные факторы. Дальнейшие исследования будут в этом направлении.
Благодарности
Авторы хотели бы поблагодарить анонимных рецензентов за полезные предложения. П. С. Станимирович, Н. В. Стойкович и М. Д. Петкович благодарят за поддержку Исследовательский проект 174013 Министерства образования и науки Сербии.
Ссылки
Станимирович П.С., Стойкович Н.В., Ковачевич-Вуйчич В.В., «Стабилизация первично-двойственного алгоритма Мехротры и его реализация», European Journal of Operational Research , vol. 165, нет. 3, стр. 598–609, 2005 г.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
Н. В. Стойкович и П. С. Станимирович, «Начальная точка в методе первичной-двойственной внутренней точки», Facta Universitatis, Series Machine Engineering , том.
3, стр. 219–222, 2001.Посмотреть по адресу:
Google Scholar | Zentralblatt MATH
Н. В. Стойкович и П. С. Станимирович, «Два прямых метода в линейном программировании», European Journal of Operational Research , vol. 131, нет. 2, стр. 417–439, 2001.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
H. W. Corley, J. Rosenberger, W. C. Yeh, and T. K. Sung, «Алгоритм косинусного симплекса», Международный журнал передовых производственных технологий , том. 27, нет. 9–10, стр. 1047–1050, 2006 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
П. К. Пан, «Правило поворота строки с наибольшим тупым углом для достижения двойной осуществимости: вычислительное исследование», European Journal of Operational Research , vol.
101, нет. 1, стр. 164–176, 1997.Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
В.-К. Йех и Х. В. Корли, «Простой симплексный алгоритм прямого косинуса», Applied Mathematics and Computation , vol. 214, нет. 1, стр. 178–186, 2009 г.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
Х. Аршам, «Алгоритм свободного решения с большим M для общих линейных программ», International Journal of Pure and Applied Mathematics , vol. 32, нет. 4, стр. 37–52, 2006 г.
Посмотреть по адресу:
Google Scholar
H. Jian-Feng, «Примечание об улучшенной начальной основе для симплексного алгоритма», Computers & Operations Research , vol. 34, нет. 11, стр.
3397–3401, 2007.Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
Х. В. Джуниор и М. П. Е. Линс, «Улучшенная исходная основа для алгоритма Simplex», Computers & Operations Research , vol. 32, нет. 8, стр. 1983–1993, 2005.
Просмотр:
Сайт издателя | Google Scholar
Н. Хан, С. Инаятулла, М. Имтиаз и Ф. Х. Хан, «Новый симплексный метод фазы 1 без искусственных добавок», Международный журнал фундаментальных и прикладных наук , том. 9, нет. 10, стр. 97–114, 2009.
Посмотреть по адресу:
Google Scholar
H. Nabli, «Обзор симплексного алгоритма», Applied Mathematics and Computation , vol. 210, нет. 2, стр. 479–489, 2009.
Просмотр:
Сайт издателя | ученый Google | Zentralblatt MATH
J.
K. Strayer, Linear Programming and Its Applications , Springer, 1989.View at:
Publisher Site
N. V. Stojković, P. S. Stanimirović, and M. D. Petković, “Modification and implementation of two -фазовый симплекс-метод», International Journal of Computer Mathematics , vol. 86, нет. 7, стр. 1231–1242, 2009.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
E. D. Nering and A. W. Tucker, Linear Programs and Related Problems , Academic Press, New York, NY, USA, 1993.
R. G. Bland, «New final pivoting method» для симплексного метода. Математика исследования операций , том. 2, нет. 2, стр. 103–107, 1977.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
J.