Онлайн умножение корней: Калькулятор корней онлайн

Как вынести из-под знака корня: число, множитель, букву

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Вынесение из под знака корня

В данной публикации мы рассмотрим, как выносить числа (множители) и буквы из-под знака корня второй и более старших степеней. Информация сопровождается практическими примерами для лучшего понимания.

• Правило вынесения из-под корня
  • Квадратный корень
  • Корень n-ой степени
  • Допустимые действия под корнем
• Вынесение буквы

Правило вынесения из-под корня

Квадратный корень

Вынести число (множитель) из-под знака корня – это значит извлечь корень из подкоренного выражения (т. е. того, что находится под знаком корня).

Если a² = b, то √b = a.

Например:

• √4 = 2, т.к. 2² = 4;
• √36 = 6, т.к. 6² = 36.

Примечание: чтобы было проще выносить числа и множители из-под знака квадратного корня, рекомендуется выучить квадраты натуральных чисел, хотя бы до 20.

Корень n-ой степени

Для вынесения подкоренного выражения из-под корня третьей и более старших степеней, извлекаем корень в соответствующей степени.

Например:

Пример 1
Вынесем множитель из-под корня √25 · 3.

Решение:
В данном случае извлечь квадратный корень можно только из числа двадцать пять, что мы и сделаем.

Пример 2
Вынесем множитель из √45.

Решение:
1. Сперва разложим подкоренное выражение (число 45) на множители. В нашем случае – это 9 и 5.
2. Из полученных чисел извлечь квадратный корень можно только из девяти.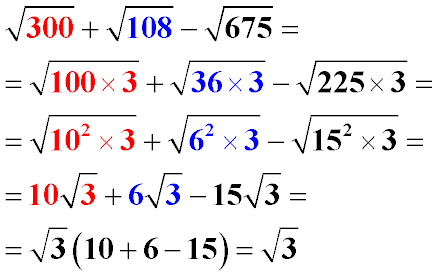

Таким образом получаем:

Допустимые действия под корнем

Если требуется вынести из-под корня выражение, то это можно сделать только в отношении произведения.

Например:

• √16 · 5 = √16 · √5 (правильно)
• √25 + 11 ≠ √25 + √11 (неправильно)
• √47 – 38 ≠ √47 – √38 (неправильно)
• √8 : 2 ≠ √8 : √2 (неправильно)

За исключением первого варианта, в остальных случаях сперва необходимо выполнить действия под корнем, а потом уже извлечь его.

• √25 + 11 = √36 = 6
• √47 – 38 = √9 = 3
• √8 : 2 = √4 = 2

Вынесение буквы

Вынести букву из-под корня – это то же самое, что и возвести ее в дробь, где в числителе – степень подкоренного выражения, в знаменателе – самого корня.

Примечание: этой же формулой можно пользоваться, подставляя вместо буквы конкретные числа.

Например:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор умножения радикалов

jpg»>   Учебники по алгебре!       года.   Воскресенье, 18 декабря

Дом Вычисления с отрицательными числами Решение линейных уравнений Системы линейных уравнений Решение линейных уравнений графически Алгебра Выражения Вычисление выражений и решение уравнений Правила дробей Факторинг квадратных трехчленов Умножение и деление дробей Деление десятичных дробей на целые числа Сложение и вычитание радикалов Вычитание дробей Факторинг полиномов по группировке Наклоны перпендикулярных линий Линейные уравнения Корни — Радикалы 1 График линии Сумма корней квадратного числа Написание линейных уравнений с использованием наклона и точки Факторинг трехчленов со старшим коэффициентом 1 Написание линейных уравнений с использованием наклона и точки Упрощение выражений с отрицательными показателями Решение уравнений 3 Решение квадратных уравнений Родительские и семейные графики Сбор похожих терминов -й Корень Степень частного свойства показателей Сложение и вычитание дробей Проценты Решение линейных систем уравнений методом исключения Квадратичная формула Дроби и смешанные числа Решение рациональных уравнений Умножение специальных биномов Округление чисел Факторинг по группам Полярная форма комплексного числа Решение квадратных уравнений Упрощение сложных дробей Алгебра Общие журналы Операции с числами со знаком Умножение дробей в общем Разделение многочленов Полиномы Высшие степени и переменные показатели Решение квадратных неравенств с помощью графика знаков Написание рационального выражения в минимальных терминах Решение квадратных неравенств с помощью графика знаков Решение линейных уравнений Квадрат бинома Свойства отрицательных показателей Обратные функции дроби Вращение эллипса Умножение чисел Линейные уравнения Решение уравнений с одним логарифмическим членом Объединение операций Эллипс Прямые линии Графики неравенств с двумя переменными Решение тригонометрических уравнений Сложение и вычитание дробей Простые трехчлены как произведения двучленов Соотношения и пропорции Решение уравнений Умножение и деление дробей 2 Рациональные числа Разность двух квадратов Факторизация полиномов по группировке Решение уравнений, содержащих рациональные выражения Решение квадратных уравнений Деление и вычитание рациональных выражений Квадратные корни и действительные числа Порядок действий Решение нелинейных уравнений подстановкой Формулы расстояния и средней точки Линейные уравнения Графики с использованием точек пересечения x и y Свойства показателей степени Решение квадратных уравнений Решение одношаговых уравнений с использованием алгебры Относительно простые числа Решение квадратного неравенства двумя решениями Квадратика Операции над радикалами Факторизация разности двух квадратов Прямые линии Решение квадратных уравнений методом факторинга Графики логарифмических функций Упрощение выражений, включающих переменные Сложение целых чисел Десятичные числа Факторинг полностью общих квадратных трехчленов Использование шаблонов для умножения двух двучленов Сложение и вычитание рациональных выражений с отличающимися знаменателями Рациональные показатели Горизонтальные и вертикальные линии     Калькулятор умножения радикалов Похожие темы: Калькулятор упрощения радикалов | спасатель математика 5 класс | алгебра 1 понятие и навыки даже ответы | программа 3 точки для решения параболы | квадратное уравнение с помощью решателя свойства квадратного корня | абсолютные значения PowerPoint | Рабочие листы/тесты по математике с множественным выбором для 6-го класса | калькулятор символьных методов | кошачьи перестановки и комбинации учебники | mcdougallittell математический ключ ответа | разложение третьих корней | Промежуточная алгебра четвертое издание — тусси онлайн Автор Сообщение mattr0x Дата регистрации: 21. 05.2003 От кого: Размещено: Четверг, 28 декабря, 11:06 Завтра днем ​​у меня тест. Но я застрял с проблемами, основанными на калькуляторе умножения радикалов. Я сталкиваюсь с проблемами понимания вычитания дробей и рациональных выражений, потому что я просто не могу найти способ решать задачи на их основе. Я позвонил своим друзьям и попробовал в Интернете, но ни одно из этих действий не помогло. Я все еще пытаюсь, но время истекает, и я, кажется, не могу понять это. Может кто-нибудь, пожалуйста, направьте меня? Мне очень нужна помощь от вас, ребята, для завтрашнего задания. Пожалуйста, ответьте. Наверх кфир Дата регистрации: 07.05.2006 Откуда: Египет Размещено: Пятница, 29 декабря, 12:49 Вам не нужно никого просить решить какие-либо типовые вопросы за вас; на самом деле все, что вам нужно, это Algebrator. Я пробовал довольно много таких программ для математического моделирования, но Algebrator намного лучше, чем большинство из них. Он решит любой ваш вопрос и даже объяснит каждый шаг, связанный с достижением этого решения. Вы можете привести столько примеров, сколько захотите, и, в отличие от нас, людей, он никогда не скажет: «О! Мне хватило на день! 😉 Даже у меня были некоторые проблемы с решением вопросов по построению графиков неравенств и сложных дробей, но эта программа действительно помогла мне их преодолеть. Наверх фвенгал Зарегистрирован: 11.07.2001 Откуда: Земля Размещено: Суббота, 30 декабря, 09:18 Эй, Алгебратор — потрясающая штука! Я начал использовать его, когда учился в старшей школе. С тех пор прошло много лет, но я до сих пор иногда им пользуюсь. Помяните мое слово, это действительно поможет вам. Наверх nea2c Зарегистрирован: 12.11.2002 От кого: Размещено: Воскресенье, 31 декабря, 09:50 Для начала, спасибо за ответы, ребята! Я очень хочу купить эту программу. Подскажите, пожалуйста, как приобрести эту программу? Можем ли мы заказать его онлайн, или мы покупаем его в каком-то розничном магазине? Наверх ДВХ Дата регистрации: 20.12.2001 От кого: Размещено: Понедельник, 01 января, 07:44 Я рад, что вам интересно использовать эту программу. Это лучшая программа, которую я когда-либо пробовал, и я не хочу, чтобы вы пропустили ее использование. Попробуйте посетить https://polymathlove.com/adding-and-subtracting-fractions.html. Удачи тебе в тестировании, друг! Наверх такси Зарегистрирован: 05.12.2002 Откуда: Бостон, Массачусетс, США Размещено: Среда, 03 января, 07:19 Я бы посоветовал использовать Алгебратор. Он не только поможет вам решить математические задачи, но и подробно предоставит все необходимые шаги, чтобы вы могли лучше понять предмет. Наверх

Авторские права © 2005-2022

Квадратные корни? | Wyzant Спросите эксперта

Показатели математической алгебры упрощают квадратный корень Индекс квадратных корней

Кортни Дж.

спросил 11.04.13

Я не могу понять это, буду признателен за любую помощь! Спасибо!

1.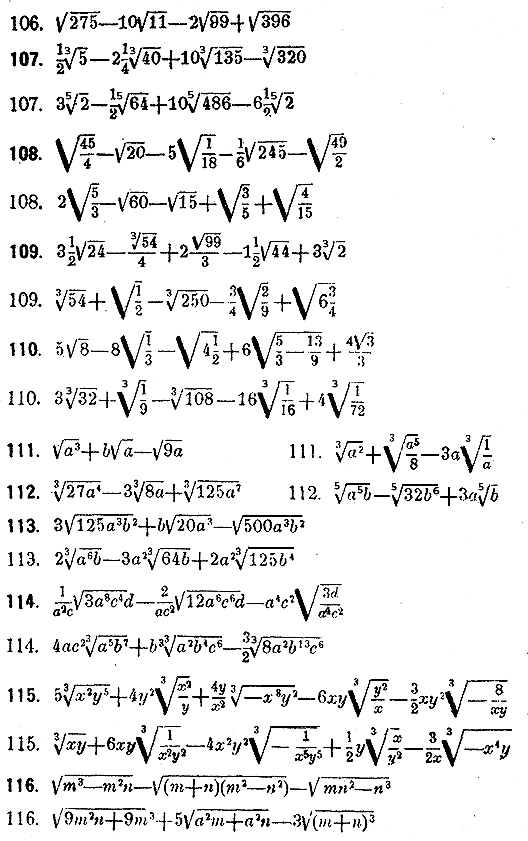    9(√6-2)

2.   (6√2+8√3)(√2+9√3)

3.   (√6+x) ²

4.   ( ³ √4-6)( ³ √2+6)

5.   (√x-3+5) ²

6.   7y√20y+9√20y ³

 

Подписаться І 2

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСтарые

Киша К. ответил 12.04.13

Репетитор

4.7 (22)

Учиться УДОБНО И ЛЕГКО!!!

Смотрите таких репетиторов

Смотрите таких репетиторов

Привет, Кортни,

Я не собираюсь давать вам ответы на все эти проблемы, потому что это ваша домашняя работа, а не моя :), но я помогу вам научиться решать такие проблемы, поэтому я проиллюстрирую их # 2. Может показаться, что я переборщил со скобками, но из-за ограничений этого форума мне нужно будет использовать их, чтобы внести ясность и обеспечить точность.

(6√(2)+8√(3))(√(2)+9√(3))

Эта задача одновременно и на умножение квадратных корней, и на сложение… так что давайте сначала обсудим правила.

1. Вы можете складывать или вычитать квадратные корни, только если число под корнем ( √() ) одинаково, например.

√(2) + √(2) = 2√(2).

Это означает, что квадратный корень из 2 плюс квадратный корень из 2 равен 2-кратному квадратному корню из 2… или 2 копиям квадратного корня из 2, как 2x равно x + x .

Вычитание будет таким же образом…

2√(2) — √(2) = √(2)

Нельзя складывать непохожие вещи… например. тот же # не находится под радикалом, поэтому…

√(2) + 9√(3) = √(2) + 9√(3)    ==> Это должно оставаться как — потому что √(2)  и √(3) не одно и то же, это яблоки и апельсины. .. РАЗНЫЕ !

2. При умножении и делении квадратных корней правила немного меняются…

==> Вы можете умножать только числа, находящиеся под радикалом ( √() ), например.

√(2) * √(3) = √(6)

… но проще это понять: √(2) * √(2) = √(4), что равно 2…но мы знаем это.

Попробуйте это на своем калькуляторе, чтобы проверить, найдя квадратный корень из 2, а затем возведите его в квадрат. Вы можете получить 3,99999 с чем-то, но это потому, что калькулятор округлил квадратный корень из 2.

3. Деление работает так же, как умножение, за исключением того, что вы можете получить дробь, которая должна остаться.

  √(4) ÷ √(2) на самом деле √(4/2) = √(2) … помните, что √(4) можно записать как √(2)*√(2).. .это облегчает отмену

…но что, если это был √(2) ÷ √(4) ?

Тогда ответ был бы

√(2)

   2

Даже если бы было хуже. .. √(8) ÷ √(6) …Я знаю гадость!

Но используйте те же принципы, и вы получите…

2√(2)

√(6)

Помните, что 4*2 = 8, а √(4) равно 2, поэтому мы можем убрать это из радикала.

Если мы факторизуем √(6), мы получим √(2) * √(3)… ну, как мы это делали до того, как мы смогли сделать отмену

2       *  √(2)   = 2     * √(2)  = 2  

√(3) * √(2)   = √(3) * √(2)   = √(3)

Этот ответ правильный, но мы обычно не любим квадратные корни или корни любого вида в знаменателе… так что мы умножаем на то же самое, что в знаменателе, чтобы мы могли получить ответ, который выглядит следующим образом:

   2  * √(3)  = 2 √(3)

√(3) * √(3) =    3

Возвращаясь к задаче… ), концепции из FOIL, или просто помните, что каждый член должен быть умножен на другие члены, основанные на свойстве дистрибутива .