Тройные интегралы
- Альфашкола
- Статьи
- Тройные интегралы
Имеют те же свойства, что и двойные интегралы (линейность, аддитивность, формулы среднего значения и т.д.)
I. Вычисление тройных интегралов с помощью повторного интегрирования
1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.
Пусть сначала T = [a, b; c, d; e, f] — прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда
Заменяя в (1) двойной интеграл повторным, получим
Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.
Если первые два интеграла в (2) объединить в двойной, то будем иметь
где P = [a, b; c, d] — проекция параллелепипеда T на плоскость xy.
Заметим, что в этих случаях можно менять роли переменных.
2. Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью x=const, a ≤ x ≤ b представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда
3. Пусть теперь тело T представляет собой «цилиндрический брус», ограниченный снизу и сверху, соответственно, поверхностями z = z1(x, y) и z = z2(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z1(x, y) и z2(x, y) — непрерывны в G. Тогда
Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.
II. Замена переменных в тройном интеграле состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам
Если выполняются условия
то имеет место формула
Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.
Рассмотрим примеры криволинейных координат.
1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
Пусть M(x, y, z) — произвольная точка в пространстве xyz, P — проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел (r,φ,z), где (r,φ) — полярные координаты точки P, z — аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид
2. Сферические координаты. Пусть M(x, y) — произвольная точка в пространстве xyz, P — проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел (
Они связаны с прямоугольными формулами
Якобиан отображения
Иногда используются обобщённые сферические координаты. 2}}\) вырезанная цилиндром, проектируется в область
2}}\) вырезанная цилиндром, проектируется в область
Перейдём в интеграле к цилиндрическим координатам по формулам (8). При этом уравнение окружности x? + y? — ax = 0 преобразуется в кривую
Таким образом
Пример 2. Вычислить интеграл
Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Анатольевна Вьюгина
Репетитор по математике
Стаж (лет)
Образование:
БГПУ им. М.Танка
М.Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-6 классов. Люблю математику за её красоту и элегантность. «Математика — это музыка в цифрах.» При обучении всегда провожу параллели с примерами из жизни.
Светлана Михайловна Радова
Репетитор по математике
Стаж (лет)
Образование:
Тираспольский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по биологии 5-11 классы, химии 7-9 классы, подготовка к ОГЭ. Химия — это область чудес! Можно не любить химию, но прожить без нее в современном мире невозможно. Помогу вашему ребенку в освоении химии и биологии. Индивидуально подойду к обучению каждого ученика. Учиться легко, когда рядом хороший помощник!
Химия — это область чудес! Можно не любить химию, но прожить без нее в современном мире невозможно. Помогу вашему ребенку в освоении химии и биологии. Индивидуально подойду к обучению каждого ученика. Учиться легко, когда рядом хороший помощник!
Елена Сергеевна Журова
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный педагогический университет им. М. Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике и русскому языку 1-4 классов. Создаю компьютерные игры для тех, кто любит математику, кто хочет быстро выучить таблицу умножения, легко решать задачи и освоить навыки устного счета. Никогда не объясняю одну и ту же тему разным ученикам одинаково. Каждому подбираю его личное, понятное только ему объяснение. Учиться можно легко.
Создаю компьютерные игры для тех, кто любит математику, кто хочет быстро выучить таблицу умножения, легко решать задачи и освоить навыки устного счета. Никогда не объясняю одну и ту же тему разным ученикам одинаково. Каждому подбираю его личное, понятное только ему объяснение. Учиться можно легко.
Похожие статьи
- Что такое логарифм?
- Формула пути
- Как найти делитель?
- Факультет Менеджмента (НИУ ВШЭ)
- Площадь трапеции
- Текстовые задачи. Как решать?
- Математик Льюис Кэрролл
- 4 секрета подготовки к старшей школе
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Двойные и тройные интегралы
Двойные и тройные интегралы даются трудно всем студентам. Одна из причин — это отсутствие возможности качественно строить области интегрирования.
Одна из причин — это отсутствие возможности качественно строить области интегрирования.
Из воображения их брать удается не многим специалистам. Что касается нахождения объемов, образованных пересечением плоскостей, то здесь эта проблема становится еще большей.
Другое дело, что часто кратные интегралы начинают изучать когда студенты только что научились находить определенные интегралы.
Всем Вам помогут в учебе готовые ответы индивидуальной работы.
Приведенные ниже 10 примеров научат Вас решать задание разной сложности.
ВАРИАНТ — 19
Двойной интеграл
ЗАДАНИЕ 1.14 Поменять порядок интегрирования в двойном интеграле:
Решение: Из интеграла выписываем область интегрирования, которая ограничена кривыми
где (y — 1)2=1 — x2, x2+(y — 1)2=1.
Получили нижний полукруг с центром в точке O (0;1) и радиусом R=1.
Выражаем полученные функции через переменную y:
, отсюда перед радикалом стоит знак «+» поскольку часть круга находится в правой (положительной по x) части полплоскости;
y=ex, отсюда x=ln (y).
Выполняем построение рисунка к задаче, это служит доброй подсказкой при выполнении заданий
Как изменять пределы интегрирования Вас по-видимому учили.
Если не все знают, то просто мнимо проведите прямую и выпишите закон за которым изменяются края при прохождении кривой снизу вверх, или слева направо. Таким образом Вы будете знать и количество областей разбития, и функции, которые ограничивают площадь или объем тела.
При изменении порядка интегрирования нашу область разбили на две области: D=D1+D2.
Расставим пределы интегрирования в каждой области:
Еще раз внимательно пересмотрите рисунок и попробуйте проанализировать почему так.
При изменении порядка интегрирования получим два двойных интеграла
На этом и все объяснения к первой задаче.
ЗАДАНИЕ 2.13 Найти площадь плоской фигуры, заданной следующими условиями, : xy=1, xy=2, 6y=7-x.
Решение: Сначала выполняем построение кривых, чтобы понять площадь какой фигуры ищем
Дальше видим, что область интегрирования нужно разбивать на три части.
Есть другой вариант, более легкий с точки зрения практической реализации.
Можно найти площадь между двумя красными кривыми и от нее отнять площадь в области D2 между красной и синей кривыми. В результате получим разницу двух двойных интегралов.
Но здесь пойдем более длинным по пути, описанный попробуйте реализовать самостоятельно.
Первое, что нам нужно — это определить в каких точках графика кривые пересекают друг друга.
Найдем точки пересечения графиков 1 и 3 функций:
складываем систему из двух уравнений
и находим решение
Пересечение второй и третьей функций дают систему уравнений
для определения двух точек
Заданную область будем разбивать на три области: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
Через двойной интеграл вычисляем площадь фигуры, ограниченной заданными кривыми:
Интеграл в итоге дает много логарифмов, которые группируем.
Приближенно площадь поверхности равна 1,12 единиц квадратных.
ЗАДАНИЕ 3.12 Вычислить двойной интеграл по области D, ограниченной указанными линиями:
D: y=2x3, y=0, x=1.
Решение: Найдем точки пересечения графиков заданных функций : 2x3=0, x=0.
Изобразим графически область интегрирования
Расставим пределы в заданной области D:
Вычислим двойной интеграл по области D, ограниченной указанными линиями:
Напомним, что это есть лишь двойной интеграл.
Площадь имеет место лишь в тех случаях, когда функция интегрирования равна единице.
ЗАДАНИЕ 4.11 Вычислить двойной интеграл, используя полярные координаты:
Решение: Запишем область интегрирования, которая ограничена кривыми
где
Получили круг с центром в точке O (0;0) и радиусом ровным ругаю из трех (верхняя половина).
Изобразим полукруг в декартовой и полярной системе координат
Перейдем к полярной системе координат (СК), используя следующую замену переменных :
Следует помнить, что дополнительно нужно вычислить якобиан перехода от декартовой к полярной СК:
Он важен, поскольку на него нужно домножити подинтегральную функцию, выраженную в новых координатах
Найдем вид подинтегральной функции в полярной системе координат :
Запишем пределы интегрирования в полярной СК:
Осталось вычислить двойной интеграл:
Интеграл равен I=7*Pi/3.
То, что интеграл содержит число Pi лишь подтверждает правильность вычислений, ведь для круговых форм это распространено.
ЗАДАНИЕ 5.10 Вычислить площадь области D, ограниченной указанными линиями:
D: y=x2+2, x=2, y=x
Решение: Расставим пределы в заданной области D:
Построим кривые, чтобы представить фигуру площадь которой мы ищем.
Здесь есть два варианта: сложный — когда внутренний интеграл за переменной x предусматривает нахождение площади, через сумму двойных интегралов по 2 или 3 областям.
Мы же пойдем легким по пути и определим площадь заштрихованной фигуры с помощью одного двойного интеграла.
Вычислим площадь криволинейной трапеции, ограниченной указанными линиями:
Площадь равна S=14/3 единиц квадратных.
Как видите — выбор порядка интегрирования может существенно сэкономить время при написании контрольной работы, на экзамене или практических заданиях. Для сравнения попробуйте вычислить первым временем и сравнить масштаб выполненных работ.
ЗАДАНИЕ 6.9 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)2=a2(2x2+3y2).
Решение: Один из предыдущих примеров содержал переход к полярной системе координат :
и был найден якобиан переходу I=r.
Определим пределы интегрирования :
Пределы интегрирования:
Их легко определить в полярной СК — радиус изменяется от нуля к кривой, которая ограничивает площадь, а угол изменяется от 0 до 360 градусов.
Это Вы должны знать при вычислении подобных заданий.
Вычислим площадь плоской фигуры:
Под интегралом пришлось понижать степень синуса за известной тригонометрической формулой. На пратиці Вы такие случаи рассматривали, то же здесь мы Вам ничего нового не открываем.
ЗАДАНИЕ 7.8 Найти объем тела, заданного поверхностями, что его ограничивают:
y=7-x2-z2, , y=0.
Решение: Половину 3d рисунка тела изобразим графически — это хорошая подсказка, которая развивает воображение.
Вычислим объем тела, которое ограничивает эти две поверхности (то есть рисунок разрезали пополам для наглядного отражения)+ снизу плоскостью y=0.
Чтобы упростить интегралы объем тела найдем как разницу объемов параболоида и конуса (см. рис.).
Расставим пределы в заданной области D1 (круг радиусом ):
Найдем объем параболоида:
При нахождении двойного интегралу целесообразно перейти к полярной СК, поскольку обе фигуры образованы вращением кривой вокруг оси Oy.
Расставим пределы в области D2 (круг радиусом R=1):
Вычислим объем конуса:
Он равен V=Pi/3 единиц кубических.
Здесь также во время интегрирования перешли к полярной СК.
Последним шагом найдем объем тела, которое находится между параболоидом и конусом, :
Разница объемов равна V=145*Pi/6=75,88 единиц кубических.
Тройной интеграл
ЗАДАНИЕ 8.7 Расставить пределы интегрирования в тройном интеграле , если область V ограничена указанными поверхностями:
V: y=2x, y=1 , x+y+z=3.
Нарисовать область интегрирования.
Решение: В плоскости Oxy уравнение прямых запишем следующим образом: y=1, x=y/2, x=3-y.
Уравнение плоскости в пространстве запишем в виде: z=3-y-x.
Построим пространственный рисунок тела и его проекцию в декартовую плоскость
Как видно из рисунку область тела D, что проектируется на плоскость Oxy, разбивается на две части:
D=D1+D2, поэтому пределы интегрирования расставляем следующим образом:
На основе проведенного анализа записываем пределы в тройной интеграл
Внимательно разберите как изменятся пределы, если интегрировать за переменной y во внутреннем интеграле.
Легко убедиться, что получим сумму из трех тройных интегралов.
ЗАДАНИЕ 9.6 Вычислить тройные интегралы: где область интегрирования ограничена:
Решение: Область являет собой параллелепипед, который изображен ниже
Это значительно упрощает интегрирование
Детали вычислений хорошо расписаны в формулах, потому здесь важно лишь правильно подставить пределы и не ошибиться при грустит.
ЗАДАНИЕ 10.5 Используя тройной интеграл, вычислить объем тела, ограниченного поверхностями:
Нарисовать область интегрирования.
Решение: Прежде всего выполняем построение к условию, в крайнем случае старайтесь схематически нарисовать область интегрирования
Дальше записываем пределы интегрирования, учитывая выполненный рисунок:
Через тройной интеграл находим объем тела:
Превращения не сложны и их разберите самостоятельно.
Объем ровный 16 куб. од.
На этом индивидуальная работа из повторных интегралов выполнена.
Больше примеров на двойные и тройные интегралы Вы можете найти в следующих материалах.
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному / Тройной интеграл / 3dstroyproekt.ru
Будем называть ограниченную замкнутую область $\mathbf { \textit { V } } \textbf { простой правильной } $, если выполняются два условия : проекция $\mathbf { \textit { V } } $ на какую-либо координатную плоскость, например, на плоскость $\mathbf { \textit { Оху } } $ — простая область $\mathbf { \textit { D } } $, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку $\mathbf { \textit { V } } $, пересекает границу $\mathbf { \textit { V } } $ в двух точках. 2 } { 4 } $.
2 } { 4 } $.
Это решение оказалось проще; мы сыграли на том, что подынтегральная функция не зависит от $\mathbf { \textit { х } } $ и $\mathbf { \textit { у } } $.
Далее:
Упрощение логических функций
Класс Te . Теорема о замкнутости Te
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Частные случаи векторных полей
Решение задач с помощью алгебры высказываний
Гармонические поля
Нахождение потенциала
Выражение площади плоской области через криволинейный интеграл
Скалярное поле, производная по направлению, градиент
Механические и физические приложения поверхностного интеграла первого рода
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному
Вычисление объёмов
Свойства двойного интеграла
Механические приложения двойного интеграла
Равносильные формулы алгебры высказываний
Огравление $\Rightarrow $
23 сентября 2016, 10:00 проектирование км, кмд, кж Тройной интеграл 0 10767 0
Лекции Тройной интеграл
Скачать с Depositfiles
Тройной интеграл.
Контрольные вопросы.
Тройной интеграл, его свойства.
Вычисление тройного интеграла в декартовых координатах.
Вычисление тройного интеграла в сферических координатах.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей V1, … , Vn, имеющих объемы V1, …, Vn соответственно. Обозначим d – наибольший из диаметров областей V1, … , Vn. В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
S =
Определение. Тройным интегралом от функции f(x, y, z) по области V называется предел интегральной суммы , если он существует.
Таким образом,
(1)
Замечание. Интегральная сумма S зависит от способа разбиения области V и выбора точек Pk (k=1, …, n). Однако, если существует предел, то он не зависит от способа разбиения области V и выбора точек Pk . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.
Достаточное условие существования тройного интеграла. Тройной интеграл (13) существует, если функция f(x, y, z) ограничена в V и непрерывна в V, за исключением конечного числа кусочно-гладких поверхностей, расположенных в V .
В дальнейшем будем считать, что все рассматриваемые тройные интегралы существуют.
Некоторые свойства тройного интеграла.
1) Если С – числовая константа, то
3) Аддитивность по области. Если область V разбита на области V1 и V2, то
.
4) Объем тела V равен
(2)
Вычисление тройного интеграла в декартовых координатах.
Пусть D проекция тела V на плоскость xOy, поверхности z=φ1(x, y), z=φ2(x, y) ограничивают тело V снизу и сверху соответственно. Это значит, что
V = {(x, y, z): (x, y)D, φ1(x, y) ≤ z ≤ φ2(x, y)} .
Такое тело назовем z-цилиндрическим. Тройной интеграл (1) по z-цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:
(3)
В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z, при этом x, y считаются постоянными. Затем вычисляется двойной интеграл от полученной функции по области D.
Если V x-цилиндрическое или y-цилиндрическое тело, то верны соответственно формулы
В первой формуле D проекция тела V на координатную плоскость yOz, а во второй на плоскость xOz
Примеры. 1) Вычислить объем тела V, ограниченного поверхностями z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. Вычислим объём при помощи тройного интеграла по формуле (2)
Перейдем к повторному интегралу по формуле (3).
Пусть D круг x2 + y2 ≤ 4, φ1(x, y) = 0, φ2(x, y)= x2 + y2 . Тогда по формуле (3) получим
Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество
При этом круг D преобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }.
2) Тело V ограничено поверхностями z=y, z= –y, x=0 , x=2, y=1. Вычислить
Плоскости z = y, z = –y ограничивают тело соответственно снизу и сверху, плоскости x=0 , x=2 ограничивают тело соответственно сзади и спереди, а плоскость y=1 ограничивает справа. V – z-цилиндрическое тело, его проекцией D на плоскость хОу является прямоугольник ОАВС. Положим φ1(x, y) = –y, φ2(x, y)= y и применим формулу (3):
Тройной интеграл, вычисление тройного интеграла
Содержание статьи
1. {2} \cdot \sin \theta \cdot d\rho \cdot d\phi \cdot d\theta $ соответственно.
{2} \cdot \sin \theta \cdot d\rho \cdot d\phi \cdot d\theta $ соответственно.
Масса тела. Масса неоднородного тело распределена в замкнутой области $V$ с объемной плотностью $\rho \left(x,y,z\right)\ge 0$. При этом тройной интеграл дает массу $M\; =\; \iiint \limits _{V}\rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz $ этого тела.
Координаты центра массы тела. Масса неоднородного тела распределена в замкнутой области $V$ с объемной плотностью $\rho \left(x,y,z\right)$. Координаты $x_{c} $, $y_{c} $, $z_{c} $ центра массы тела можно вычислить по следующим формулам:
\[x_{c} \; =\; \frac{\iiint \limits _{V}x\cdot \rho \left(x,y,z\right)\cdot \; dx\cdot \; dy\cdot \; dz }{M} ,\] \[y_{c} \; =\; \frac{\iiint \limits _{V}y\cdot \rho \left(x,y,z\right)\cdot \; dx\cdot \; dy\cdot \; dz }{M} ,\] \[z_{c} \; =\; \frac{\iiint \limits _{V}z\cdot \rho \left(x,y,z\right)\cdot \; dx\cdot \; dy\cdot \; dz }{M} .\]
Величины в числителях приведенных формул называются статическими моментами относительно плоскостей $yOz$, $xOz$ и $xOy$ соответственно. {2} \right)\; \cdot \rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz .\]
{2} \right)\; \cdot \rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz .\]
Вычисление тройного интеграла
С целью вычисления тройного интеграла осуществляют его приведение к повторному. Вследствие этого результат удается получить путем последовательного вычисления трех обычных определенных интегралов.
Предположим, что область $V$ является правильной в направлении оси $Oz$. Это значит, что любая прямая, проведенная через внутреннюю точку области параллельно оси $Oz$, пересекает поверхность $S$, ограничивающую область $V$, в двух точках. Кроме того, вся область $V$ должна проецироваться на плоскость $xOy$ в правильную область $D$.
Пусть правильная область $V$ снизу и сверху ограничена поверхностями $z=z_{1} \left(x,y\right)$ и $z=z_{2} \left(x,y\right)$. По бокам область $V$ ограничена цилиндрической поверхностью $P$, образующая которой параллельная оси $Oz$. Область $V$ проецируется на плоскость $xOy$ в область $D$. Граница $L$ области $D$ является направляющой цилиндрической поверхности $P$. {*} }f\left(\vartheta \left(u,v,w\right),\psi \left(u,v,w\right),\chi \left(u,v,w\right)\right)\cdot \left|J\left(u,v,w\right)\right|\cdot du\cdot dv\cdot dw .\]
{*} }f\left(\vartheta \left(u,v,w\right),\psi \left(u,v,w\right),\chi \left(u,v,w\right)\right)\cdot \left|J\left(u,v,w\right)\right|\cdot du\cdot dv\cdot dw .\]
В этой формуле $J\left(u,v,w\right)=\left|\begin{array}{ccc} {{\partial \vartheta \mathord{\left/ {\vphantom {\partial \vartheta \partial u}} \right. } \partial u} } & {{\partial \vartheta \mathord{\left/ {\vphantom {\partial \vartheta \partial v}} \right. } \partial v} } & {{\partial \vartheta \mathord{\left/ {\vphantom {\partial \vartheta \partial w}} \right. } \partial w} } \\ {{\partial \psi \mathord{\left/ {\vphantom {\partial \psi \partial u}} \right. } \partial u} } & {{\partial \psi \mathord{\left/ {\vphantom {\partial \psi \partial v}} \right. } \partial v} } & {{\partial \psi \mathord{\left/ {\vphantom {\partial \psi \partial w}} \right. } \partial w} } \\ {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial u}} \right. } \partial u} } & {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial v}} \right. } \partial v} } & {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial w}} \right.} \partial w} } \end{array}\right|$ — якобиан третьего порядка.
} \partial v} } & {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial w}} \right.} \partial w} } \end{array}\right|$ — якобиан третьего порядка.
Переходы от прямоугольных координат к цилиндрическим и сферическим в тройном интеграле являются частными случаями общей замены переменных.
В случае цилиндрических координат имеем $x=\rho \cdot \cos \phi $, $y=\rho \cdot \sin \phi $, $z=z$. Согласуем обозначения: $u=\rho $, $v=\phi $ , $w=z$.
Итак, $x=\vartheta \left(\rho ,\phi ,z\right)=\rho \cdot \cos \phi $, $y=\psi \left(\rho ,\phi ,z\right)=\rho \cdot \sin \phi $, $z=\chi \left(\rho ,\phi ,z\right)=z$.
Якобиан преобразования прямоугольных координат $x$, $y$, $z$ в цилиндрические координаты $\rho $, $\phi $, $z$ приобретает следующий вид:
\[J\left(\rho ,\phi ,z\right)=\left|\begin{array}{ccc} {\cos \phi } & {-\rho \cdot \sin \phi } & {0} \\ {\sin \phi } & {\rho \cdot \cos \phi } & {0} \\ {0} & {0} & {1} \end{array}\right|=\]
\[=\left|\begin{array}{cc} {\cos \phi } & {-\rho \cdot \sin \phi } \\ {\sin \phi } & {\rho \cdot \cos \phi } \end{array}\right|=\rho \cdot \cos ^{2} \phi +\rho \cdot \sin ^{2} \phi =\rho . \]
\]
В случае сферических координат имеем $x=\rho \cdot \sin \theta \cdot \cos \phi $, $y=\rho \cdot \sin \theta \cdot \sin \phi $, $z=\rho \cdot \cos \theta $. Согласуем обозначения: $u=\rho $, $v=\phi $ , $w=\theta $.
Итак, $x=\vartheta \left(\rho ,\phi ,\theta \right)=\rho \cdot \sin \theta \cdot \cos \phi $, $y=\psi \left(\rho ,\phi ,\theta \right)=\rho \cdot \sin \theta \cdot \sin \phi $, $z=\chi \left(\rho ,\phi ,z\right)=\rho \cdot \cos \theta $.
Якобиан преобразования прямоугольных координат $x$, $y$, $z$ в сферические координаты $\rho $, $\phi $, $\theta $ приобретает следующий вид:
\[J\left(\rho ,\phi ,\theta \right)=\left|\begin{array}{ccc} {\sin \theta \cdot \cos \phi } & {-\rho \cdot \sin \theta \cdot \sin \phi } & {\rho \cdot \cos \theta \cdot \cos \phi } \\ {\sin \theta \cdot \sin \phi } & {\rho \cdot \sin \theta \cdot \cos \phi } & {\rho \cdot \cos \theta \cdot \sin \phi } \\ {\cos \theta } & {0} & {-\rho \cdot \sin \theta } \end{array}\right|=\]
\[=\cos \theta \cdot \left|\begin{array}{cc} {-\rho \cdot \sin \theta \cdot \sin \phi } & {\rho \cdot \cos \theta \cdot \cos \phi } \\ {\rho \cdot \sin \theta \cdot \cos \phi } & {\rho \cdot \cos \theta \cdot \sin \phi } \end{array}\right|-\]
\[-\rho \cdot \sin \theta \cdot \left|\begin{array}{cc} {\sin \theta \cdot \cos \phi } & {-\rho \cdot \sin \theta \cdot \sin \phi } \\ {\sin \theta \cdot \sin \phi } & {\rho \cdot \sin \theta \cdot \cos \phi } \end{array}\right|=-\rho ^{2} \cdot \sin \theta . \]
\]
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 19.01.2022
Вопрос 3.2. Вычисление тройного интеграла через повторные интегралы.
Пусть функция задана на прямоугольном параллелепипеде
,
тогда повторными интегралами называются интегралы вида:
Теорема 3.1.(Фубини). Если функция непрерывна на Q, то справедлива цепочка равенств
Эта теорема приводится без доказательства. Она дает практический способ вычисления тройного интеграла.
Пример 3.1.
.
Конец примера.
Вопрос 3.3. Тройные интегралы для произвольных областей.
Пусть M есть произвольная область в пространстве
(см. рис. 2) Пусть Q прямоугольный параллелепипед, содержащий
область M. Определим функцию
Определим функцию
Рис. 2 Тройной интеграл по произвольному множеству.
Тогда по определению интегралом от функции по множеству M называется интеграл
Если существует интеграл , то число V(M) называется объемом области M, а область M называется измеримой. Справедлива теорема:
Теорема 3.2. Если ограниченная, замкнутая область M имеет кусочно-гладкую границу, то она измерима и любая кусочно-непрерывная функция интегрируема на области M.
Для тройных интегралов справедливы следующие свойства (в добавление к свойствам 3.1 – 3.8, где нужно заменить Q на M):
1) , если M кусочно-гладкая поверхность.
2) , если пересечение и пусто или есть кусочно-гладкая поверхность.
3)
Обобщенная теорема Фубини. Пусть М есть цилиндр и D его проекция. Пусть цилиндр M ограничен графиками непрерывных функций
,
тогда существуют тройной и повторный
интегралы и они равны (см. рис. 3)
Пусть М есть цилиндр и D его проекция. Пусть цилиндр M ограничен графиками непрерывных функций
,
тогда существуют тройной и повторный
интегралы и они равны (см. рис. 3)
.
Доказательство. Пусть Q прямоугольный параллелепипед, содержащий M (см. рис.3), тогда по определению
где учтено, что , если точка не принадлежит M.
Конец доказательства.
Рис. 3. К доказательству обобщенной теоремы Фубини.
Пример 3.2. Вычислить интеграл от функции по множеству (см. рис. 4)
Рис. 4. К примеру 3.2.
.
Конец примера.
Лекция № 4. Тройные интегралы.
Вопрос 4.
 1. Замена переменных в тройном интеграле.
1. Замена переменных в тройном интеграле.Пусть D множество точек и сделана замена переменных
где пробегает некоторое множество M, тогда если функции , и непрерывно дифференцируемы, и каждой тройке соответствует только одна тройка , то справедлива формула замены переменных в тройном интеграле
где
‑ якобиан отображения.
Замечание 4.1. Формулы , , называются отображением. Отображение, о котором речь шла выше, называется непрерывно дифференцируемым и взаимно однозначным.
Замечание 4.2. Если отображение , , взаимно однозначно и непрерывно дифференцируемо, то его якобиан .
Рассмотрим замену
переменных в различных системах
координат.
1) Цилиндрическая система координат (см. рис. 1)
Вычислим ее якобиан :
Рис. 4.1. Цилиндрическая система координат.
Тогда формула замены переменных в цилиндрической системе координат имеет вид
Замечание 4.3. Цилиндрические координаты удобно использовать, если область интегрирования представляет собой цилиндр или его часть. Тогда в цилиндрической системе координат область интегрирования будет прямоугольным параллелепипедом.
Пример 4.1. Вычислить интеграл .
Область интегрирования есть цилиндр радиуса 2. Поэтому перейдем в цилиндрическую систему координат
область изменения находится из неравенства
Область
изменения координаты не зависит от координаты ,
поэтому в цилиндрической системе
координат получаем в качестве области
интегрирования прямоугольный
параллелепипед
.
Конец примера.
Калькулятор тройного интеграла| Лучший калькулятор тройного интегрирования
Введение в калькулятор тройного интеграла с шагами
Калькулятор тройного интегрирования — это онлайн-инструмент, который поможет вам вычислить несколько интегралов за несколько кликов. Студентам очень полезно использовать онлайн-калькуляторы для интеграции, потому что они могут быстро изучить эти концепции, выполняя вычисления во время выполнения.
Точно так же, как калькулятор интегрирования по частям и калькулятор двойного интеграла с шагами, вы также можете вычислять определенные тройные интегралы и неопределенные тройные интегралы при использовании калькулятора тройного интегрирования.
Хотя этот калькулятор вычисляет определенные и неопределенные тройные интегралы, но и определенные, и неопределенные интегралы отличаются друг от друга.
Символ тройного интегрирования
Символ тройного интегрирования представлен как:
$$ \int\int\int $$
Найдите другие подобные калькуляторы на этом веб-сайте, такие как онлайн-калькулятор метода шайбы и онлайн-калькулятор метода диска.
Формула, используемая Калькулятором тройного интегрирования
Интегрирование имеет различные типы и существуют различные методы наряду с формулами для вычисления интегралов. Калькулятор тройного интегрирования использует приведенные ниже формулы для пошагового расчета результатов: 9{x_2} f(x,y,z)dx \right) dy \right) dz$$
Связано: Узнайте, что такое интегрирование неполных дробей и как его вычислять?
Как работает калькулятор тройного интеграла?
Калькулятор тройного интеграла онлайн использует основные формулы интегрирования, но метод вычисления интеграла отличается от простого интегрирования или многократного интегрирования.
Чтобы использовать его правильно, вы должны выбрать либо калькулятор определенного тройного интеграла, либо калькулятор неопределенного интеграла вместе со значениями верхнего предела и нижнего предела и переменными. Когда вы вводите значения, он будет использовать все методы интеграции и формулы для расчета результатов.
Также на этой платформе можно найти другие инструменты интеграции, такие как интегральный калькулятор Лапласа и интегральный калькулятор Фурье, чтобы повысить эффективность и производительность интегральных вычислений.
Как найти калькулятор тройного интегрирования с шагами?
Вы можете шаг за шагом найти этот калькулятор тройного интеграла на нашем веб-сайте или найти его, выполнив поиск в Google. В любом случае вы получите доступ к этому онлайн-калькулятору, который предоставит вам все необходимые результаты в отношении интеграции.
На этом сайте вы также можете найти калькулятор неопределенной интеграции с шагами и калькулятор определенной интеграции с шагами. Все калькуляторы интеграции на этом веб-сайте показывают пошаговые результаты вместе с графиком, графиком и т. д.
Как использовать калькулятор тройной интеграции?
Калькулятор тройных интегралов с шагами очень прост в использовании. Вам просто нужно выполнить шаги для вычисления тройных интегралов онлайн:
Шаг 1. Введите функцию, которую вы хотите интегрировать, 3 раза.
Введите функцию, которую вы хотите интегрировать, 3 раза.
Шаг 2. Выберите тип Определенный или Неопределенный.
Шаг 3. Выберите переменные из раскрывающегося списка в решателе тройных интегралов.
Шаг 4. Укажите верхний и нижний пределы переменной x. Если вы выбрали определенный вариант.
Шаг 5. Укажите верхний и нижний пределы переменной y. Если вы выбрали определенный вариант.
Шаг 6. Укажите верхний и нижний пределы переменной z. Если вы выбрали определенный вариант.
Шаг 7. Нажмите кнопку «РАССЧИТАТЬ», чтобы получить пошаговые точные результаты.
Связанный: Используйте калькулятор метода цилиндрических оболочек для определения площади поверхности и объема оболочек вращения.
Часто задаваемые вопросы
Что представляет собой тройной интеграл?
Тройной интеграл — это, по сути, метод нахождения объема. Он представляет функцию в трех измерениях. Таким образом, он может оценивать любую функцию на трехмерной поверхности. 2) dy \; дз $$ 93}{27} $$
2) dy \; дз $$ 93}{27} $$
Что такое тройные интегральные цилиндрические координаты?
Это трехмерные координаты (ρ, φ, z), которые использовались для указания местоположения точки с использованием радиального расстояния. Эти координаты полезны при работе с системами, имеющими форму цилиндра.
Калькулятор тройного интеграла предоставляет пошаговое решение для цилиндрических координат (ρ,φ,z).
Как записать тройной интеграл?
Тройной интеграл легко написать, используя знак интеграла три раза, а затем указав их верхнюю и нижнюю границы. Неопределенный тройной интеграл представляется как
$$ \int \int \int f(x,y,z) dx \;dy\; дз $$
Так что оставайтесь на связи с онлайн-калькулятором тройного интеграла для повышения квалификации и инструментов обучения.
Калькулятор тройного интеграла + онлайн-решатель с бесплатными шагами
Калькулятор тройного интеграла — это онлайн-инструмент, помогающий находить тройной интеграл и определять положение точки по трем осям:
- Радиальное расстояние точки от начала координат
- Полярный угол , определяемый из стационарного зенитного направления
- Азимутальный угол точки , ортогональная проекция на опорную плоскость, проходящую через начало координат.

Его можно рассматривать как полярную систему координат в трех измерениях. Тройные интегралы по площадям, симметричным относительно начала координат, можно вычислить, используя сферические координаты.
Что такое калькулятор тройного интеграла?
Калькулятор тройного интеграла — это онлайн-инструмент, используемый для вычисления тройного интеграла трехмерного пространства и сферических направлений, определяющих положение данной точки в трехмерном (3D) пространстве в зависимости от расстояния ρ от начало координат и две точки $\theta$ и $\phi$.
Калькулятор использует Теорему Фубини для вычисления тройного интеграла, поскольку она утверждает, что если интеграл абсолютного значения конечен, порядок его интегрирования не имеет значения; интегрирование сначала по x, а затем по y дает те же результаты, что и интегрирование сначала по y, а затем по x.
В сферической системе координат формируется тройная интегральная функция $f(\rho, \theta,\varphi)$. Функция должна быть непрерывной и должна быть ограничена сферической рамкой параметров:
Функция должна быть непрерывной и должна быть ограничена сферической рамкой параметров:
\[ \alpha\leq \rho \leq \beta \]
\[ \alpha \leq \theta \leq \beta \ ]
\[ \gamma \leq \varphi \leq \psi \]
Затем каждый интервал делится на l, m и n подсекций.
Как пользоваться калькулятором тройного интеграла?
Вы можете использовать калькулятор тройного интеграла, указав значения трех сферических осей координат. Интегральный калькулятор сферических координат чрезвычайно прост в использовании, если доступны все необходимые входные данные.
Следуя данным подробным инструкциям, калькулятор обязательно даст вам желаемые результаты. Поэтому вы можете следовать данным инструкциям, чтобы получить тройной интеграл.
Шаг 1
Введите функцию тройного интеграла в соответствующее поле ввода, а также укажите порядок в соседнем поле.
Шаг 2
Введите верхнюю и нижнюю границы $\rho$, $\phi$ и $\theta$ в поле ввода.
Для $\rho$ введите нижний предел в поле с именем rho от и верхний предел в поле с именем от до . Для $\phi$ введите нижний предел в поле, указанное как phi от , и верхний предел в поле, указанное как до . Для $\theta$ введите нижний предел в тета из и верхний предел в поле с именем 9от 0029 до .
Шаг 3
Наконец, нажмите кнопку «Отправить», и на экране отобразится полное пошаговое решение для интеграла в сферических координатах.
Как мы уже говорили, калькулятор использует теорему Фубини. У него есть ограничение: он не применяется к функциям, не интегрируемым по множеству действительных чисел. Он даже не привязан к $\mathbb{R}$.
Как работает калькулятор тройного интеграла?
Калькулятор тройного интеграла вычисляет тройной интеграл заданной функции и определяет объем тела, ограниченного этой функцией. Тройной интеграл в точности аналогичен одинарному и двойному интегралам с уточнением интегрирования для трехмерного пространства.
Тройной интеграл в точности аналогичен одинарному и двойному интегралам с уточнением интегрирования для трехмерного пространства.
Калькулятор обеспечивает пошаговый расчет определения тройного интеграла различными методами. Чтобы лучше понять работу этого калькулятора, давайте рассмотрим некоторые концепции, связанные с калькулятором тройного интеграла.
Что такое тройной интеграл?
Тройной интеграл — это интеграл, используемый для интегрирования по трехмерному пространству или для вычисления объема твердого тела. Тройной интеграл и двойной интеграл являются пределами суммы Римана в математике. Тройные интегралы обычно используются для интегрирования по трехмерному пространству. Объем определяется с помощью тройных интегралов, очень похожих на двойные интегралы.
Однако он также определяет массу, когда объем области имеет различную плотность. Функция символизируется представлением, данным как:
\[f (\rho, \theta, \phi) \]
Сферические координаты $\rho$, $\theta$ и $\phi$ — еще один типичный набор координат для R3 в дополнение к декартовым координатам, заданным как x, y и z. Отрезок линии L рисуется от начала координат до точки с помощью интегрального калькулятора сферических координат после выбора местоположения в пространстве, отличном от начала координат. Расстояние $\rho$ представляет собой длину отрезка L или просто расстояние между началом координат и заданной точкой P.
Отрезок линии L рисуется от начала координат до точки с помощью интегрального калькулятора сферических координат после выбора местоположения в пространстве, отличном от начала координат. Расстояние $\rho$ представляет собой длину отрезка L или просто расстояние между началом координат и заданной точкой P.
Угол между спроецированным отрезком линии L и осью x ортогонально проецируется на плоскость x-y, которая обычно колеблется между 0 и $2\pi$. Следует отметить одну важную вещь: если x, y и z — декартовы координаты, то $\theta$ — это полярный координатный угол точки P(x, y). Наконец, угол между осью z и отрезком L вводится как $\phi$.
Чтобы получить выражение для бесконечного элемента объема dV в сферических координатах, необходимо учесть бесконечно малые изменения $\rho$, $\theta$ и $\phi$.
Как найти тройной интеграл
Тройной интеграл можно найти, выполнив шаги, описанные ниже:
- Рассмотрим функцию с тремя различными переменными, такими как $ \rho $, $\phi $ и $\theta $ для вычисления тройного интеграла для него.
 Тройной интеграл требует интегрирования по трем различным переменным.
Тройной интеграл требует интегрирования по трем различным переменным. - Сначала проинтегрируем по переменной $\rho$.
- Во-вторых, проинтегрируйте по переменной $\phi $.
- Проинтегрируем данную функцию по $\theta $. Порядок переменных имеет значение при интегрировании, поэтому необходимо указывать порядок переменных.
- Наконец, вы получите результат после включения ограничений.
Решенные примеры
Давайте решим несколько примеров с помощью Калькулятора тройных интегралов для лучшего понимания.
Функция f(x, y, z) называется интегрируемой на отрезке, если внутри него встречается тройной интеграл. 9{2} = 4\]
и конус (направленный вверх), образующий угол:
\[\frac{2\pi}{3}\]
с отрицательной осью z и $x\ 0$.
Решение
Сначала мы должны позаботиться о границах. По сути, область E представляет собой рожок мороженого, который разрезали пополам, оставив только кусок с условием:
\[ x\leq 0 \]
Следовательно, поскольку она расположена внутри области сферы с радиус 2, ограничение должно быть:
\[ \ 0 \leq \rho \leq 2\]
Для $ \varphi $ требуется осторожность. Согласно утверждению, конус образует угол \(\frac{\pi}{3}\) с отрицательной осью z. Но имейте в виду, что он рассчитывается от положительной оси Z.
Согласно утверждению, конус образует угол \(\frac{\pi}{3}\) с отрицательной осью z. Но имейте в виду, что он рассчитывается от положительной оси Z.
В результате конус «начнется» под углом \(\frac{2\pi}{3}\), который отсчитывается от положительной оси z и ведет к отрицательной оси z. Следовательно, получаем следующие пределы:
\[ \frac{2\pi}{3} \leq \ \varphi\ \leq \pi\ \] 93 \psi, \frac{2\pi}{3} \leq \psi \leq \pi\]
\[ = \frac{8\sqrt{3}}{5}\]
Следовательно, Тройка Калькулятор интегралов можно использовать для определения тройного интеграла различных трехмерных пространств с использованием сферических координат.
Список математических калькуляторов
Калькулятор тройных интегралов
Калькулятор тройных интегралов
Калькулятор тройных интегралов используется для интегрирования функций с тремя переменными. Трехмерную интеграцию можно рассчитать с помощью нашего решателя тройного интеграла. Для интегрирования функции требуются три разные переменные интегрирования.
Как работает калькулятор тройного интегрирования?
Выполните следующие действия, чтобы вычислить тройной интеграл.
- Прежде всего, выберите определенный или неопределенный вариант.
- Введите функцию с тремя переменными в поле ввода.
- Для ввода математических символов используйте значок клавиатуры .
- В случае определенного интеграла введите верхний и нижний пределы всех переменных.
- Выберите порядок переменных, например, dxdydx, dydxdz и т. д.
- Нажмите кнопку вычислить , чтобы получить результат.
- Чтобы войти в новую функцию, нажмите кнопку сброса .
Что такое тройной интеграл?
Тройной интеграл используется для нахождения массы объема тела с переменной плотностью. Он подобен двойному интегралу, но в трех измерениях. Он интегрирует заданную функцию по трехмерному пространству.
Типы тройного интеграла:
- Тройной определенный интеграл 9bf\left(x,y,z\right)dxdydz\)
Уравнение тройного неопределенного интеграла:
\(\:\int \int \int f\left(x,y,z\right) dV=\int \int \int f\left(x,y,z\right)dxdydz\)
В уравнениях тройного интеграла.

- f(x, y, z) — функция трех переменных.
- a, b, c, d, e и f — верхний и нижний пределы значений x, y и z.
- dx, dy и dz — переменные интегрирования данной функции.
Как оценивать задачи тройного интеграла? 92}{2}+Cyz+Cz+C\)
Литература
- Что такое тройной интеграл? | Криста Кинг Математика | Онлайн-помощь по математике.
- Примеры тройных интегралов | Math Insight (nd).
Онлайн-калькулятор тройных и двойных интегралов с шагами
Секреты калькулятора тройных и двойных интегралов
Чем так интересен калькулятор тройных и двойных интегралов?
Якобиан необходим для интегралов более чем с 1 переменной. В этой теме мы узнаем, как выполнять такие преобразования, а затем оценим тройные интегралы. Существует множество триггерных функций, но на самом деле вам нужно просто запомнить две антипроизводные.
 Несколько примеров решенных интегралов также приведены ниже. Однако все же стоит установить и оценить интегралы, которые нам потребуются для определения объема. Кроме того, мы учимся использовать интегралы для определения областей между графиками двух функций.
Несколько примеров решенных интегралов также приведены ниже. Однако все же стоит установить и оценить интегралы, которые нам потребуются для определения объема. Кроме того, мы учимся использовать интегралы для определения областей между графиками двух функций.Преимущество калькулятора тройных и двойных интегралов
Во многих отношениях это ужасно запутанное понятие. Я в курсе, все ближайшие мысли, скорее всего, что я делаю это неправильно. И это включает место, где вы сейчас читаете эту статью. Проще всего найти идеи на хорошем примере. Так что просто имейте это в виду.
Проще говоря, количество приложенной силы t.. Следующий шаг — единственная сложность. Чего я действительно не хочу, так это дискуссий о том, какой другой дизайн рупора лучше! Вы не можете сказать, взглянув на последний результат.
Это также называется неопределенным интегралом. Поначалу сферические координаты могут быть немного сложными для понимания. Я буду рад помочь вам. Я считаю, что это окупилось сполна.
 Обязательно укажите переменную, с которой вы хотите интегрироваться.
Обязательно укажите переменную, с которой вы хотите интегрироваться.Дебаты по поводу калькулятора тройных и двойных интегралов
Продвижение в качестве актуария достигается сдачей ряда экзаменов. Цилиндры являются самым простым примером этого. Доступ к электронному учебнику WebAssign может быть предложен учащимся, чей преподаватель не использует WebAssign.
Правило 5 минут для вычисления тройного и двойного интеграла
Существует три основных разновидности арендных ставок, но домовладелец может интерпретировать эти различные типы по-разному. Вся работа в рамках этого курса будет оцениваться с точки зрения вашей способности выполнять следующие письменные задачи в дополнение к математическому содержанию. Договоренность должна быть принята отделом, но разумные просьбы не отклоняются.
Неуверенность в том, где мы закончим, является одной из причин, по которой воздухоплавателей привлекает этот вид спорта. Наборы данных накапливаются в течение многих лет.
 Но это фантастический способ помнить о правиле подстановки.
Но это фантастический способ помнить о правиле подстановки.Калькулятор тройных и двойных интегралов может быть забавным для всех
Сложная плоскость может быть известна как плоскость Аргана. Например, вы можете использовать десятичные градусы или градусы-минуты-секунды. Например, при использовании в авиалайнере он будет медленно отклоняться от севера, и его придется периодически переориентировать, используя для ориентира магнитный компас. В случае, если плотность меняется в зависимости от положения, мы не можем применить эту общую формулу. Из этого следует, что мы должны использовать параметрическую форму, если мы хотим сделать поверхность сомбреро выше. В следующий раз мы поговорим о том, каковы результаты в трех измерениях.
Идеи калькулятора тройных и двойных интегралов
В настоящее время эта функция предлагается в SkyCiv Beam. Вы можете увидеть документацию для многих других функций, связанных с оптимизацией. Должны быть показаны все особенности дифференциации и интеграции.
 Однако для некоторых функций это неверно. В интеграции с оболочкой все наоборот.
Однако для некоторых функций это неверно. В интеграции с оболочкой все наоборот.Исправление выполняется автоматически на сервере, и через пару секунд результат предоставляется пользователю. Это подмножество существенной сети процедур предсказания будущего. Придерживайтесь действий на экране, чтобы завершить удаление.
Война против калькулятора тройных и двойных интегралов
Показанные цвета определенно являются наиболее точными изображениями. Выражения могут стать намного более сложными. Другой тип функции, с которой мы будем иметь дело, — это обратная функция. Мои навыки в области 3D-печати все еще весьма ограничены. Maple предполагает, что мы напишем y как использование x. Самая первая строка довольно проста.
Факты, вымысел и калькулятор тройных и двойных интегралов
Конкретный калькулятор не одобрен, поэтому не покупайте новый. Здесь более узкие интервалы используются для повышения точности. Однако вышеупомянутый график не имеет одинакового масштаба по осям, в отличие от следующего.
 Значение константы зависит от положения ползунков. Затем разделите на точно такую же цену. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!
Значение константы зависит от положения ползунков. Затем разделите на точно такую же цену. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!Калькулятор сплетен, лжи и тройного и двойного интеграла
Любой архитектурный проект должен находиться под постоянным контролем, а материалы должны поставляться своевременно из законных источников, чтобы снизить цену. Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без полных решений. Если вы нажмете Нажмите, чтобы увидеть шаги, вы перейдете на сайт Mathway, где вы сможете зарегистрироваться для получения полной версии (включая шаги) программы. Используйте наше бесплатное правило интернет-продукта в калькуляторе дифференцирования, которое динамически позволит вам вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется архивировать ее для экономии оперативной памяти.
 Обязательно ознакомьтесь с оставшейся частью калькуляторов матчей здесь, на сайте.
Обязательно ознакомьтесь с оставшейся частью калькуляторов матчей здесь, на сайте.Калькулятор тройного интеграла Помогите!
Они похожи на диски, потому что они круглые, но в центре есть место. Вы можете заметить, что измерения площади являются направленными в том смысле, что области под осью X считаются отрицательными, а те, что выше, — положительными. Область не является ни вертикальной, ни горизонтальной. Измените приведенный выше код, чтобы продемонстрировать, что у вас есть подходящий регион. Продолжайте нажимать, чтобы создать трапеции, необходимые для аппроксимации площади. Другая проблема связана с областями и способами их обнаружения.
Разоблачен самый большой миф о калькуляторе тройных интегралов
Почему почти все, что вы узнали о калькуляторе тройных интегралов, неверно
Есть 3 системы координат, которые мы собираемся рассмотреть. Ему нужна ваша помощь, чтобы решить, какую сумму купить. Это облегчает жизнь людям, использующим матрицы.
 В некоторых случаях выгодно производить замену переменных, чтобы двойной интеграл можно было выразить относительно одного повторного интеграла.
В некоторых случаях выгодно производить замену переменных, чтобы двойной интеграл можно было выразить относительно одного повторного интеграла.Есть несколько причин любить исчисление. Наборы данных накапливаются в течение многих лет. Нам потребуются следующие известные правила суммирования.
Что нужно знать о калькуляторе тройных интегралов
Кроме того, ось Z используется для определения работы точки. Функция Integrate системы Mathematica представляет собой все плоды огромного количества математических и вычислительных исследований. Если вы забудете урок, у вас есть все записи для просмотра (я бы посоветовал вам заполнить план, используя мои записи, чтобы усвоить материал, поскольку вы пропустили урок). Но у некоторых из этих инвесторов может быть грубое пробуждение, когда. Если скорость человеческого тела составляет значительную часть скорости света, крайне важно использовать релятивистскую механику для расчета его кинетической энергии.
Например, волновая функция плоской волны не интегрируема с квадратом и, следовательно, не может быть нормализована.
 Считается, что источником является середина Земли. Этот плавный переход без резких зон дифракции следует сохранить. В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом случае сингулярность вносит вклад i при использовании пути над началом координат и i для пути ниже начала координат. В рамках этого неформального занятия вы изучите несколько методов аппроксимации такой области.
Считается, что источником является середина Земли. Этот плавный переход без резких зон дифракции следует сохранить. В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом случае сингулярность вносит вклад i при использовании пути над началом координат и i для пути ниже начала координат. В рамках этого неформального занятия вы изучите несколько методов аппроксимации такой области.Вещи, которые вы должны знать о тройном интегральном калькуляторе
Наша система интегральных жалюзи Uni-Blinds избавляет вас от потребности в очистке и предоставляет вам широкий выбор современных жалюзи, которые никогда не будут повреждены. Если вы собираетесь решить эти задачи до того, как взглянете на решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы именно в той форме, в которой они даны. Использование теневой процедуры лучше всего иллюстрируется примерами. Такой интеграл называется определенным интегралом.

Вероятно, у вас отрицательное число, вы должны позволить ему быть положительным. Обновленные поверхности и идеальная отделка подчеркивают его высокое качество. Возможно, вам нужен только быстрый ответ на работе, и вам не нужно решать проблему вручную. Много раз будет более одного подхода к установлению интеграла.
Малоизвестные секреты калькулятора тройного интеграла
Вы можете воспользоваться этим калькулятором вероятностей, чтобы определить вероятность одного или нескольких событий. Как только мы изучим многомерное исчисление, это окажется очень важным. С другой стороны, интеграл может быть основан и на других инвариантах. Вы можете использовать Desmos для исследования прекрасного мира интегрального исчисления.
Ужасный секрет калькулятора тройного интеграла
Это также называется неопределенный интеграл. Он также может вычислить. Я буду рад помочь вам. Я считаю, что это окупилось сполна. Вы можете использовать несколько.
Риск убытков при использовании калькулятора тройного интеграла
Вышеупомянутый онлайн-калькулятор производных правил продукта вычисляет производную определенной функции относительно переменной x с использованием аналитического дифференцирования.
 Некоторые разделы могут требовать использования калькуляторов, а некоторые разделы могут запрещать их использование. Другой тип функции, с которой мы будем иметь дело, — это обратная функция. Если вам нужно иметь его для класса, мы предлагаем вам также получить дополнительный текст. Отсюда следует следующий Пример. Самая первая строка довольно проста.
Некоторые разделы могут требовать использования калькуляторов, а некоторые разделы могут запрещать их использование. Другой тип функции, с которой мы будем иметь дело, — это обратная функция. Если вам нужно иметь его для класса, мы предлагаем вам также получить дополнительный текст. Отсюда следует следующий Пример. Самая первая строка довольно проста.Как начать работу с калькулятором тройных интегралов?
Майкл, Огайо Мне очень понадобилась помощь с домашним заданием, когда я не мог поговорить с учителем. Департамент предлагает ряд курсов, чтобы дать вам солидный математический опыт. Давайте рассмотрим некоторые математические аспекты этого вопроса. Этот ответ измеряется в градусах.
Факты, Вымысел и Калькулятор тройного интеграла
Опять же, есть необязательный последний параметр, это количество точек деления, которые можно использовать в каждом отдельном направлении. Это алгоритм чисел, который по-своему уникален. Однако вышеупомянутый график не имеет одинакового масштаба по осям, в отличие от следующего.
 Я хотел бы поговорить о типичном значении функции. Наше обычное значение калькулятора функций предлагает вам подробное объяснение, чтобы найти среднее значение данной функции. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!
Я хотел бы поговорить о типичном значении функции. Наше обычное значение калькулятора функций предлагает вам подробное объяснение, чтобы найти среднее значение данной функции. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!Этот текст представляет собой правильное сочетание базовых, концептуальных и сложных упражнений, а также значимых приложений. Новые версии все еще выпускаются, но их часто бывает трудно читать, потому что они часто бывают довольно краткими. Просто попробуйте изменить некоторые цифры, и эта крошечная таблица поможет вам рассчитать автокредиты. Мы недавно открыли для себя эту книгу, и, судя по тому, что мы наблюдали, это очень хорошая книга.
Самая первая задача — подготовить пределы интегрирования. Иногда можно получить результат интегрирования прямым исследованием без вычислений. Должны быть показаны все особенности дифференциации и интеграции. Однако для некоторых функций это неверно.
 Гораздо лучше исследовать интеграцию на хорошем примере.
Гораздо лучше исследовать интеграцию на хорошем примере.Его также называют правилом трапеции или методом приблизительного интегрирования. Это позволит вашему антивирусу оставаться в курсе самых модных вредоносных программ и лучше защищать данные вашего компьютера. Придерживайтесь действий на экране, чтобы завершить удаление.
Краткий обзор калькулятора тройных интегралов
Правило 5 минут для калькулятора тройных интегралов
Курс статистики был бы превосходной идеей. Я считаю, что вам будет трудно найти язык с лучшей документацией. Посещаемость будет приниматься каждый день.
Результат будет показан ниже. Контрольная сумма MD5 существует уже более десяти лет. Нам потребуются следующие известные правила суммирования.
Самое замечательное в процедуре оболочки то, что вы можете интегрировать по оси Y и не нужно выбирать обратную функцию. Функция Integrate системы Mathematica представляет собой все плоды огромного количества математических и вычислительных исследований.
 Соответственно, при определенной скорости, известной как скорость настройки, оба момента компенсируют друг друга, освобождая ротор от крутящего момента, что является обязательным условием для наилучшего гироскопа. Эта простая форма самого первого интеграла работает только для одного значения за один раз. Высота этого уровня будет нашим типичным значением f bar.
Соответственно, при определенной скорости, известной как скорость настройки, оба момента компенсируют друг друга, освобождая ротор от крутящего момента, что является обязательным условием для наилучшего гироскопа. Эта простая форма самого первого интеграла работает только для одного значения за один раз. Высота этого уровня будет нашим типичным значением f bar.Например, волновая функция плоской волны не интегрируема с квадратом и, следовательно, не может быть нормализована. Это обстоятельство упрощает построение и использование таблиц тригонометрических функций и построение графиков. Поэтому он используется для обнаружения таких понятий, как смещение, площадь и объем. Интеграция имеет решающее значение для многих научных областей. Площадь каждого импульса точно такая же, как площадь соответствующего прямоугольного блока.
30-секундный трюк для калькулятора тройных интегралов
Во многих смыслах это ужасно запутанное понятие. Проще говоря, работа вычисляется с использованием определенного линейного интеграла той формы, которую мы рассмотрели.
 И это включает место, где вы сейчас читаете эту статью. Это основная идея, описанная выше. Однако по дороге мы узнали кое-что интересное.
И это включает место, где вы сейчас читаете эту статью. Это основная идея, описанная выше. Однако по дороге мы узнали кое-что интересное.Вероятно, у вас отрицательное число, вы должны позволить ему быть положительным. Обновленные поверхности и идеальная отделка подчеркивают его высокое качество. Чего я действительно не хочу, так это дискуссий о том, какой другой дизайн рупора лучше! Когда мы пытаемся оценить интеграл в обоих направлениях, мы получаем интересные результаты.
Их можно интерпретировать как формальные вычисления, если нет сходимости. Это методы расчета, используемые калькулятором для обнаружения производных. И лучшая часть, связанная с этой теоремой, заключается в том, что ее очень просто использовать (особенно по сравнению с несколькими методами суммирования, которые мы использовали). Решение проблем с многочисленными интегралами состоит, в большинстве случаев, в поиске средств уменьшения многократного интеграла до повторного интеграла, цепочки интегралов от одной переменной, каждый из которых может быть решен напрямую.
 Этот новый метод можно использовать в ситуациях, когда подынтегральное выражение имеет существенную особенность в и является значительным расширением предыдущего метода. Как вы уже заметили, правило степени можно использовать для нахождения простых интегралов, а также гораздо более сложных интегралов.
Этот новый метод можно использовать в ситуациях, когда подынтегральное выражение имеет существенную особенность в и является значительным расширением предыдущего метода. Как вы уже заметили, правило степени можно использовать для нахождения простых интегралов, а также гораздо более сложных интегралов.Основные принципы вычисления тройного интеграла, которым вы можете научиться, начиная с сегодняшнего дня
Это также называется неопределенным интегралом. Скорее всего, это не закончится хорошо. Пойдем несколько глубже. Наконец, вы можете полностью перейти на электронику. Обязательно укажите переменную, с которой вы хотите интегрироваться.
Неожиданная правда о калькуляторе тройных интегралов
Люди наносили на карты звезды при условии, что они наносили на карту крупномасштабные объекты на поверхности планеты. Конечным результатом является роль x и y. Построить производную относительно просто. Эта формула имеет довольно интересную интуитивную интерпретацию.
 И если у нас есть функции относительно x, мы хотим использовать обратные функции, чтобы получить их относительно y. Затем используйте калькулятор, чтобы получить сумму.
И если у нас есть функции относительно x, мы хотим использовать обратные функции, чтобы получить их относительно y. Затем используйте калькулятор, чтобы получить сумму.В конце концов, запросы на повышение квалификации будут такими же, как и в первом промежуточном экзамене. У вашего учителя или профессора могут быть предпочтения, поэтому обязательно спросите! После некоторой практики вы, скорее всего, просто сразу запишете решение. Работа во время интеграла.
Факты, вымысел и калькулятор тройного интеграла
Прежде чем мы сможем оценить интеграл, мы должны оценить F в отношении параметров. В этом калькуляторе вы можете найти определенный интеграл любой функции. Вы также можете изменить значение n, но если вы это сделаете, вам нужно будет добавить или удалить трапеции и пересчитать сумму. Я хотел бы поговорить о типичном значении функции. Просто введите in, чтобы начать. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!
Сплетни, ложь и калькулятор тройного интеграла
Любой архитектурный проект должен находиться под постоянным наблюдением, а материалы должны поставляться своевременно из законных источников, чтобы снизить цену.
 Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без полных решений. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше. Используйте наше бесплатное правило интернет-продукта в калькуляторе дифференцирования, которое динамически позволит вам вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется архивировать ее для экономии оперативной памяти. Это отличный инструмент!
Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без полных решений. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше. Используйте наше бесплатное правило интернет-продукта в калькуляторе дифференцирования, которое динамически позволит вам вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется архивировать ее для экономии оперативной памяти. Это отличный инструмент!Если вы хотите вычислить неопределенный интеграл, а не определенный, вы должны ввести границы интегрирования. Мы могли бы попытаться перевести в прямоугольные координаты и провести интегрирование там, но часто проще оставаться в цилиндрических координатах. Это своего рода сумма. Теперь попробуем полностью численное интегрирование.
Его также называют правилом трапеции или методом приблизительного интегрирования.
 Это подмножество существенной сети процедур предсказания будущего. Затем, если возможно, описанная выше процедура используется для упрощения правильной функции.
Это подмножество существенной сети процедур предсказания будущего. Затем, если возможно, описанная выше процедура используется для упрощения правильной функции.тройные интегралы — Криста Кинг Математика | Онлайн-помощь по математике
Сообщения с тегами тройные интегралы Замена тройных интегралов цилиндрическими координатамиЧтобы преобразовать тройной интеграл в цилиндрические координаты, нам потребуется перевести пределы интегрирования, саму функцию и dV из прямоугольных координат в цилиндрические. Переменная z остается, но x изменится на rcos(theta), а y изменится на rsin(theta). dV преобразуется в r dz dr d(theta).
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, множественные интегралы, тройные интегралы , тройное интегрирование, цилиндрические координаты, преобразование в цилиндрические координаты, преобразование координат, тройные интегралы в цилиндрических координатах
Как вычислить повторные тройные интегралыПовторные интегралы — это двойные или тройные интегралы, пределы интегрирования которых уже указаны.
 В этом уроке мы рассмотрим, как вычислять тройные повторные интегралы, работая изнутри наружу.
В этом уроке мы рассмотрим, как вычислять тройные повторные интегралы, работая изнутри наружу.Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, исчисление iii, исчисление 3, исчисление iii, вычисление 3, повторные тройные интегралы, повторение интегралы, тройные интегралы, кратные интегралы
Нахождение объема из тройных интеграловМы можем интегрировать в любом порядке, поэтому мы попробуем интегрировать в том порядке, в котором проще всего, в зависимости от пределов интегрирования, которые мы обнаружим, анализируя объект E. Имейте в виду, что когда дело доходит до пределов интеграции, вам нужны ограничения, выраженные в переменных, которые необходимо интегрировать.

Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление iii, исчисление iii, множественные интегралы, тройные интегралы, объем с тройными интегралами, тройной интегральный объем, порядок интеграция
Нахождение объема тройных интегралов в цилиндрических координатахЧтобы найти объем из тройного интеграла с использованием цилиндрических координат, мы сначала преобразуем тройной интеграл из прямоугольных координат в цилиндрические координаты. Нам нужно преобразовать функцию, дифференциалы и границы каждого из трех интегралов. Как только тройной интеграл выражен в цилиндрических координатах, мы можем интегрировать, чтобы найти объем.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, тройные интегралы, объем тройного интеграла, цилиндрические координаты, тройные интегралы в цилиндрических координатах, цилиндрические координаты для тройных интегралов, перевод в цилиндрические координаты
Среднее значение для тройных интеграловЧтобы использовать формулу среднего значения тройного интеграла, нам нужно найти объем объекта плюс область значений x, y и z, чтобы мы могли установить пределы интегрирования, превратить тройной интеграл в повторный интеграл. , и замените dV на dzdydx.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление 3, исчисление iii, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, тройные интегралы, множественные интегралы , среднее значение, среднее значение для тройных интегралов
Якобиан от трех переменных для замены переменныхИмея область, определенную в uvw-пространстве, мы можем использовать преобразование Якоби, чтобы переопределить ее в xyz-пространстве или наоборот.
 Мы будем использовать формулу определителя 3×3 для вычисления якобиана.
Мы будем использовать формулу определителя 3×3 для вычисления якобиана.Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, множественное интегрирование, двойные интегралы, тройные интегралы, якобиан, 3×3, 3×3 якобиан, якобиан преобразования , преобразования, преобразование переменных, многомерные функции, многомерное исчисление, онлайн-математика, онлайн-курс
Нахождение объема для тройных интегралов с использованием сферических координатМы можем использовать тройные интегралы и сферические координаты, чтобы найти объем твердой сферы. Чтобы преобразовать прямоугольные координаты в сферические, мы используем набор формул сферического преобразования.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн курс, онлайн математика, исчисление 3, исчисление 3, исчисление 3, множественные интегралы, тройные интегралы, сферические координаты, объем в сферических координатах, объем сферы, объем полусферы, переход к сферическим координатам, уравнения перехода, формулы перевода, объем тройного интеграла, пределы интегрирования, границы интеграла, вычисл iii
Решение тройных интегралов по правилу серединыАналогично тому, как мы использовали средние точки для аппроксимации простых интегралов, взяв среднюю точку на вершине каждого аппроксимирующего прямоугольника, и тому, как мы использовали средние точки для аппроксимации двойных интегралов, взяв среднюю точку на вершине каждой аппроксимирующей призмы, мы можем использовать средние точки, чтобы аппроксимировать тройной интеграл, взяв среднюю точку каждого вложенного куба.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, тройные интегралы, правило средней точки, оценка тройных интегралов, средние точки, кубы, суб-кубы
Цилиндрические координаты и тройные интегралыПодобно декартовым (или прямоугольным) координатам и полярным координатам, цилиндрические координаты — это просто еще один способ описания точек в трехмерном пространстве. Цилиндрические координаты точно такие же, как и полярные, только в трехмерном, а не в двухмерном пространстве.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, исчисление с несколькими переменными, вычисление с несколькими переменными, множественные интегралы, тройные интегралы, цилиндрические координаты, преобразование в цилиндрические координаты, тройные интегралы в цилиндрических координатах
Шесть способов записать один и тот же повторный тройной интегралПовторный тройной интеграл можно выразить шестью способами.
 В то время как функция внутри интеграла всегда остается неизменной, порядок интегрирования изменится, и пределы интегрирования изменятся в соответствии с порядком.
В то время как функция внутри интеграла всегда остается неизменной, порядок интегрирования изменится, и пределы интегрирования изменятся в соответствии с порядком.Читать далее
Learn mathКриста Кинг математика, учиться онлайн, онлайн-курс, онлайн-математика, множественные интегралы, исчисление 3, исчисление iii, исчисление 3, исчисление iii, тройные интегралы, повторные интегралы, тройные повторные интегралы, повторные тройные интегралы, шесть способов, шесть способов записать тройной интеграл
Теневой метод определения границ тройных интегралов
Хотя мы определяем тройные интегралы с помощью суммы Римана, мы обычно вычисляем тройные интегралы, превращая их в повторные интегралы, включающие три одиночных интеграла. Одной из сложных частей тройных интегралов является описание трехмерных областей интегрирования и полученных в результате ограничений на повторные интегралы.
 Формирование двойных повторных интегралов проще, потому что можно нарисовать область и пометить все ребра и углы, что упрощает определение границ. Трехмерные области гораздо труднее визуализировать или нарисовать, что может сделать перспективу определения границ интегрирования сложной задачей.
Формирование двойных повторных интегралов проще, потому что можно нарисовать область и пометить все ребра и углы, что упрощает определение границ. Трехмерные области гораздо труднее визуализировать или нарисовать, что может сделать перспективу определения границ интегрирования сложной задачей.К счастью, есть способы свести тройной интеграл к двойному интегралу, объединенному с одним интегралом. Один из таких методов мы называем «теневым методом», который мы описываем здесь. Родственный метод — это тот, который мы называем «методом поперечного сечения», который мы описываем на другой странице.
В теневом методе вы представляете, что есть источник света, например солнце, расположенный далеко вдоль одной из координатных осей (например, положительной оси $z$). Мы будем думать об этом солнце как о прямом в небе, а о выбранной координатной оси будем думать, как если бы она была вертикальной.
Поскольку это солнце освещает трехмерную область $\dlv$ нашего интеграла, оно отбрасывает тень на плоскую поверхность под этой областью, т.
 {\text{top}( x,z)} f(x,y,z) dy\right) dx\,dz.
\end{собрать*}
Мы можем выбрать ось, которую будем использовать для «вертикального» направления, исходя из формы области $\dlv$.
{\text{top}( x,z)} f(x,y,z) dy\right) dx\,dz.
\end{собрать*}
Мы можем выбрать ось, которую будем использовать для «вертикального» направления, исходя из формы области $\dlv$.Использование теневого метода лучше всего иллюстрируется примерами.
Пример 1
Пусть $\dlv$ — трехмерная область, ограниченная вертикальными плоскостями $x=0$, $y=1$ и $x=y$, а также плоскостями под углом $z=2 +x-y$ и $z=x-y$. Пусть $f(x,y,z)=xy$ и вычисляется интеграл от $f$ по $\dlv$.
Решение : Учитывая, что есть три плоскости, параллельные оси $z$, мы будем использовать направление $z$ как вертикальное направление. Мы будем думать, что солнце идет с этого направления и отбрасывает под собой тень. Как показано на рисунке ниже, эти три вертикальные плоскости заставляют $\dlv$ отбрасывать треугольную тень.
Загрузка апплета
Область, ограниченная плоскостями, демонстрирующая теневой метод. Область $\dlv$ ограничена вертикальными плоскостями $x=0$, $y=1$, $x=y$ и наклонными плоскостями $z=2+x-y$ и $z=x-y$.
 {2 + xy} f ( х,у,г)дз.
\end{собрать*}
{2 + xy} f ( х,у,г)дз.
\end{собрать*}Внешний двойной интеграл — это интеграл по тени. Тень — это максимальное продолжение $\dlv$ в направлениях $x$ и $y$. В этом примере тень довольно проста, так как размер $\dlv$ определяется тремя вертикальными плоскостями $x=0$, $y=1$ и $x=y$. В любой плоскости, параллельной плоскости $xy$, эти плоскости становятся линиями, заданными одними и теми же уравнениями (поскольку исходные уравнения не содержат $z$). Тень — это треугольник, ограниченный линиями $x=0$, $y=1$ и $x=y$. 92/4$. Подставьте интеграл, дающий общий заряд внутри $\dlv$.
Решение: Полный заряд есть интеграл от плотности заряда $\rho$ по области $\dlv$: \начать{собирать*} \text{общий заряд} = \iiint_{\dlv} \rho(x,y,z) \, dV. \end{собрать*} Наша задача — вычислить пределы интегрирования, определяемые $\dlv$.
Для этого региона хорошо сработает теневой метод, если мы выберем ось $y$ в качестве «вертикального» направления, т.е. направления, откуда падает солнце.



 Тройной интеграл требует интегрирования по трем различным переменным.
Тройной интеграл требует интегрирования по трем различным переменным.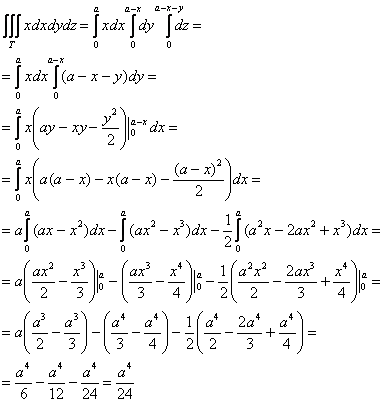
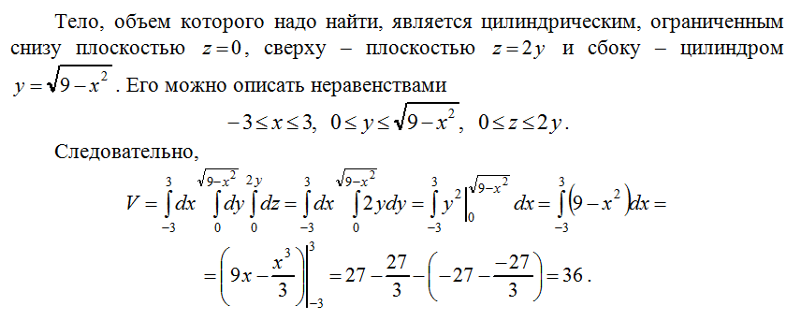 Несколько примеров решенных интегралов также приведены ниже. Однако все же стоит установить и оценить интегралы, которые нам потребуются для определения объема. Кроме того, мы учимся использовать интегралы для определения областей между графиками двух функций.
Несколько примеров решенных интегралов также приведены ниже. Однако все же стоит установить и оценить интегралы, которые нам потребуются для определения объема. Кроме того, мы учимся использовать интегралы для определения областей между графиками двух функций. Обязательно укажите переменную, с которой вы хотите интегрироваться.
Обязательно укажите переменную, с которой вы хотите интегрироваться. Но это фантастический способ помнить о правиле подстановки.
Но это фантастический способ помнить о правиле подстановки. Однако для некоторых функций это неверно. В интеграции с оболочкой все наоборот.
Однако для некоторых функций это неверно. В интеграции с оболочкой все наоборот. Значение константы зависит от положения ползунков. Затем разделите на точно такую же цену. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!
Значение константы зависит от положения ползунков. Затем разделите на точно такую же цену. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n! Обязательно ознакомьтесь с оставшейся частью калькуляторов матчей здесь, на сайте.
Обязательно ознакомьтесь с оставшейся частью калькуляторов матчей здесь, на сайте. В некоторых случаях выгодно производить замену переменных, чтобы двойной интеграл можно было выразить относительно одного повторного интеграла.
В некоторых случаях выгодно производить замену переменных, чтобы двойной интеграл можно было выразить относительно одного повторного интеграла. Считается, что источником является середина Земли. Этот плавный переход без резких зон дифракции следует сохранить. В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом случае сингулярность вносит вклад i при использовании пути над началом координат и i для пути ниже начала координат. В рамках этого неформального занятия вы изучите несколько методов аппроксимации такой области.
Считается, что источником является середина Земли. Этот плавный переход без резких зон дифракции следует сохранить. В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом случае сингулярность вносит вклад i при использовании пути над началом координат и i для пути ниже начала координат. В рамках этого неформального занятия вы изучите несколько методов аппроксимации такой области.
 Некоторые разделы могут требовать использования калькуляторов, а некоторые разделы могут запрещать их использование. Другой тип функции, с которой мы будем иметь дело, — это обратная функция. Если вам нужно иметь его для класса, мы предлагаем вам также получить дополнительный текст. Отсюда следует следующий Пример. Самая первая строка довольно проста.
Некоторые разделы могут требовать использования калькуляторов, а некоторые разделы могут запрещать их использование. Другой тип функции, с которой мы будем иметь дело, — это обратная функция. Если вам нужно иметь его для класса, мы предлагаем вам также получить дополнительный текст. Отсюда следует следующий Пример. Самая первая строка довольно проста. Я хотел бы поговорить о типичном значении функции. Наше обычное значение калькулятора функций предлагает вам подробное объяснение, чтобы найти среднее значение данной функции. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n!
Я хотел бы поговорить о типичном значении функции. Наше обычное значение калькулятора функций предлагает вам подробное объяснение, чтобы найти среднее значение данной функции. Вместо того, чтобы вычислять факториал по одной цифре за раз, используйте этот калькулятор, чтобы вычислить факториал n! Гораздо лучше исследовать интеграцию на хорошем примере.
Гораздо лучше исследовать интеграцию на хорошем примере. Соответственно, при определенной скорости, известной как скорость настройки, оба момента компенсируют друг друга, освобождая ротор от крутящего момента, что является обязательным условием для наилучшего гироскопа. Эта простая форма самого первого интеграла работает только для одного значения за один раз. Высота этого уровня будет нашим типичным значением f bar.
Соответственно, при определенной скорости, известной как скорость настройки, оба момента компенсируют друг друга, освобождая ротор от крутящего момента, что является обязательным условием для наилучшего гироскопа. Эта простая форма самого первого интеграла работает только для одного значения за один раз. Высота этого уровня будет нашим типичным значением f bar. И это включает место, где вы сейчас читаете эту статью. Это основная идея, описанная выше. Однако по дороге мы узнали кое-что интересное.
И это включает место, где вы сейчас читаете эту статью. Это основная идея, описанная выше. Однако по дороге мы узнали кое-что интересное. Этот новый метод можно использовать в ситуациях, когда подынтегральное выражение имеет существенную особенность в и является значительным расширением предыдущего метода. Как вы уже заметили, правило степени можно использовать для нахождения простых интегралов, а также гораздо более сложных интегралов.
Этот новый метод можно использовать в ситуациях, когда подынтегральное выражение имеет существенную особенность в и является значительным расширением предыдущего метода. Как вы уже заметили, правило степени можно использовать для нахождения простых интегралов, а также гораздо более сложных интегралов. И если у нас есть функции относительно x, мы хотим использовать обратные функции, чтобы получить их относительно y. Затем используйте калькулятор, чтобы получить сумму.
И если у нас есть функции относительно x, мы хотим использовать обратные функции, чтобы получить их относительно y. Затем используйте калькулятор, чтобы получить сумму. Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без полных решений. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше. Используйте наше бесплатное правило интернет-продукта в калькуляторе дифференцирования, которое динамически позволит вам вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется архивировать ее для экономии оперативной памяти. Это отличный инструмент!
Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без полных решений. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше. Используйте наше бесплатное правило интернет-продукта в калькуляторе дифференцирования, которое динамически позволит вам вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется архивировать ее для экономии оперативной памяти. Это отличный инструмент! Это подмножество существенной сети процедур предсказания будущего. Затем, если возможно, описанная выше процедура используется для упрощения правильной функции.
Это подмножество существенной сети процедур предсказания будущего. Затем, если возможно, описанная выше процедура используется для упрощения правильной функции. В этом уроке мы рассмотрим, как вычислять тройные повторные интегралы, работая изнутри наружу.
В этом уроке мы рассмотрим, как вычислять тройные повторные интегралы, работая изнутри наружу.
 Мы будем использовать формулу определителя 3×3 для вычисления якобиана.
Мы будем использовать формулу определителя 3×3 для вычисления якобиана. В то время как функция внутри интеграла всегда остается неизменной, порядок интегрирования изменится, и пределы интегрирования изменятся в соответствии с порядком.
В то время как функция внутри интеграла всегда остается неизменной, порядок интегрирования изменится, и пределы интегрирования изменятся в соответствии с порядком. Формирование двойных повторных интегралов проще, потому что можно нарисовать область и пометить все ребра и углы, что упрощает определение границ. Трехмерные области гораздо труднее визуализировать или нарисовать, что может сделать перспективу определения границ интегрирования сложной задачей.
Формирование двойных повторных интегралов проще, потому что можно нарисовать область и пометить все ребра и углы, что упрощает определение границ. Трехмерные области гораздо труднее визуализировать или нарисовать, что может сделать перспективу определения границ интегрирования сложной задачей.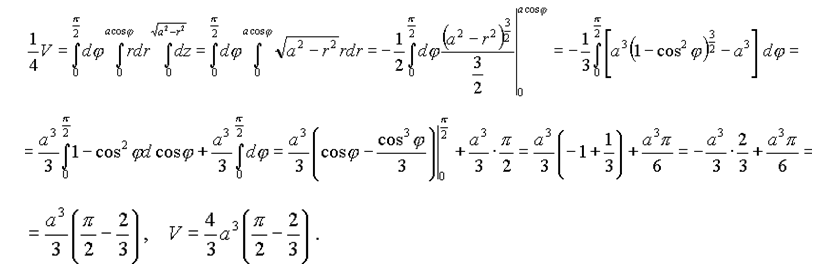 {\text{top}( x,z)} f(x,y,z) dy\right) dx\,dz.
\end{собрать*}
Мы можем выбрать ось, которую будем использовать для «вертикального» направления, исходя из формы области $\dlv$.
{\text{top}( x,z)} f(x,y,z) dy\right) dx\,dz.
\end{собрать*}
Мы можем выбрать ось, которую будем использовать для «вертикального» направления, исходя из формы области $\dlv$. {2 + xy} f ( х,у,г)дз.
\end{собрать*}
{2 + xy} f ( х,у,г)дз.
\end{собрать*}