Несмещенная оценка дисперсии — исправленная выборочная дисперсия. Решение задач и контрольных работ теории вероятностей и статистике онлайн
Краткая теория
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена повторная выборка объема :
| Значения признака | … | |||
| Частоты | … |
При этом
Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию
.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой
,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить на дробь . Сделав это, получим исправленную дисперсию, которую обычно обозначают через :
Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии. Действительно:
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию:
Для оценки среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
При достаточно больших значениях
объема выборки выборочная и исправленная
дисперсия отличаются мало.
На практике используются исправленной дисперсией,
если примерно
.
Пример решения задачи
Найти несмещенную выборочную дисперсию на основании данного распределения выборки.
| 16 | 20 | 22 | 30 | |
| 14 | 26 | 17 | 3 |
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма частот:
Вычислим среднюю:
Средняя квадратов:
Несмещенная выборочная дисперсия:
Ответ:
Кроме этой задачи на другой странице сайта есть пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда
Калькулятор дисперсии для покера — онлайн-инструкция по использованию
В покере дисперсия — это отклонение реального результата от математически ожидаемого. Онлайн-калькуляторы показывают, насколько большим может быть это отклонение. Его определяют игровая дистанция и уровень игрока. Чем больше раздач или турниров сыграно, тем меньше фактический результат зависит от удачи.
И чем сильнее игрок, тем меньше его график отклоняется от математического ожидания.
Содержание
- Коротко о дисперсии
- Что дает игроку калькулятор дисперсии
- Как использовать калькулятор покерной дисперсии
- Как анализировать график калькулятора дисперсии
- Безопасный банкролл-менеджмент с калькулятором дисперсии
- Как учитывать кешауты при расчете в калькуляторе дисперсии
- Заключение
Коротко о дисперсии
Профессионалы играют в покер, используя теорию вероятностей. Но прибыльная игра не дает 100% шансы на выигрыш в каждой раздаче. Например, если вы пойдете олл-ин с KK против J7, выиграете в ~86% случаев. Это очень выгодно. Но время от времени будет побеждать оппонент — примерно 1 раз из 7. Это произойдет не в каждой 7-й раздаче. Иногда он выиграет такой олл-ин 2, 3 или даже 5 раз подряд. Иногда — не победит 10 или 15 раз подряд.
Например, проведено 100 таких ситуаций. По математическому ожиданию, оппонент должен был выиграть 14 из них, но удача на его стороне — он победил 20 раз.
Это отклонение и есть дисперсия.
Но оппоненту не будет везти всегда. Если он продолжит играть с 14% на победу, со временем фактический результат вернется к ожидаемому. И на большой дистанции — после 1,000, 10,000, 1,000,000 таких ситуаций — вы будете побеждать в 86% раздач.
Чтобы узнать, насколько дисперсия может увести график от математического ожидания, используют калькуляторы.
Читайте нашу подробную статью о дисперсии в покере.
Что дает игроку калькулятор дисперсии
Викторина
Хорошо ли ты знаешь покерные программы?
Получи в подарок PDF-книгу о покере. В ней ты найдешь:
- Правила, изложенные подробно и доступно.
- Советы по стратегии.
- Лайфхаки от профессионалов.
Лучший онлайн-калькулятор дисперсии в покере, по нашему мнению, — это популярный Primedope Calculator. Покажем, как им пользоваться и как анализировать график.
Программа симулирует большое количество раздач, показывая возможные варианты отклонения графика в обе стороны.
Primedope Calculator показывает 20 возможных результатов — сэмплов. Чем длиннее дистанция, тем меньше реальный результат отличается от математического.
Посмотрим, какой график инструмент покажет для винрейта -2 bb/100 при игре за короткими столами Холдема на дистанции 100,000 рук.
Винрейт -2 bb/100 — показатель убыточной стратегии. Но все равно есть шансы выиграть за 100,000 рук 7,500 больших блайндов. Это показывает первая линия — жирная синяя. Худший возможный проигрыш показан нижней линией: -12,500 больших блайндов.
Математическое ожидание — жирная черная линия. Она показывает проигрыш 2,000 больших блайндов и соответствует винрейту -2 bb/100.
Покерные профессионалы не считают дистанцию в 100,000 рук показательной. На таком количестве раздач влияние удачи на выигрыш все еще велико. В нашем примере минусовый участник провел ее в плюс. А что будет, если рассчитать 10 миллионов рук?
Никаких шансов сыграть в плюс.
Результат самого удачного расчета: -104,500 больших блайндов.
Как использовать калькулятор покерной дисперсии
Для симуляции необходимо в онлайн-форме на сайте калькулятора ввести данные:
- Winrate in BB/100: винрейт на 100 BB.
- Observed winrate in BB/100: наблюдаемый винрейт (заполнять не обязательно). Укажите там значение, если предполагаете, что винрейт на дистанции изменится.
- Standard deviation in BB/100: стандартное отклонение. Оно зависит от формата покера. Узнать показатель можно в Holdem Manager, там он называется Std Dev bb per 100 hands. Можно использовать параметры Primedope Calculator. Для Холдема: 9-max — 60-80, 6-max — 75-120. Для Омахи ПЛ: 9-max 100-140; 6-max — 120-160.
- Number of hands to simulate
Заполнив поля, нажмите Calculate. Под формой появится график симуляции, таблица с расшифровкой показателей, график даунстриков и таблица их вероятности.
Как анализировать график калькулятора дисперсии
Линии на графике — это 20 возможных результатов. От наибольшего выигрыша до худшего проигрыша. Расшифровка линий:
- Черная (средняя). Математическое ожидание.
- Две жирные темно-зеленые. 95% возможных результатов.
- Две жирные светло-зеленые. 70% возможных результатов.
- Тонкие линии. 20 случайных расчетов.
Если снова нажать Calculate, программа выдаст 20 других линий. Линии 95%, 70% и EV останутся, поменяются только возможные выигрыши и проигрыши.
Под графиком есть таблица с числовой расшифровкой — Variance in numbers. Для банкролл-менеджмента она важнее, чем график. Помимо заданных пользователем данных, здесь можно посмотреть:
- Вероятность отрицательного результата на данной дистанции.
- Вероятность, что винрейт будет выше значения observed win rate.
- Вероятность, что винрейт будет выше observed win rate.
- Минимальный банкролл, при котором риск проиграть все меньше 5%.
Если для симуляции задан отрицательный винрейт, минимальный банкролл считается неправильно.
Безопасный банкролл-менеджмент с калькулятором дисперсии
Представим, что вы играете на лимите NL20 с винрейтом 5 bb на 100 рук. С калькулятором можно посчитать, какой банкролл нужен, чтобы вероятность проиграть его за 100,000 раздач была меньше 5%.
Расчет на 100,000 рукТаблица показывает, что для риска меньше 5% нужно 2,996 больших блайндов. Это 30 бай-инов по 100 bb. Для лимита NL20 это $600. И остается вероятность 5.7%, что этот отрезок игры закончится в минус.
Вероятности в расчете справедливы только для введенных дистанции и винрейта. Если указать больше или меньше рук, цифры изменятся. Например, шанс сыграть в минус 10,000 рук равен 30.8%.
Расчет на 10,000 рукПокеристы не оценивают уровень своей игры на короткой дистанции, так как он сильно зависим от удачи. Например, при 5 bb/100 нулевая вероятность сыграть в минус отображается только при симуляции 960,000 раздач.
Планирование игры с калькулятором дисперсии
Абстрактные графики с симуляциями миллионов раздач не помогут в покерной карьере. Но калькулятор можно использовать на реальных выборках. Например, вы играете 50,000 рук в месяц. Узнаем вероятность сыграть в минус.
Например, вы выигрываете 6 больших блайндов за 100 рук. Вводим данные в Primedope и читаем таблицу.
В 9% случаев месяц закончится в минус. Риск не большой, но при планировании игры на год стоит подготовиться к тому, что один месяц должен быть отрицательным.
Моделирование даунсвинга
График detailed sample with downswing показывает, в какой даунсвинг может попасть игрок. Он считается по данным заполненной формы. А количество симуляций можно задать ползунком над графиком. Вот возможные даунсвинги на 100,000 раздач при 6 bb/100.
Самые большие даунсвинги в расчете на 100,000 рукВертикальная ось — большие блайнды. Горизонтальная — сыгранные руки. На фоне — расчет, по которому смоделированы даунсвинги.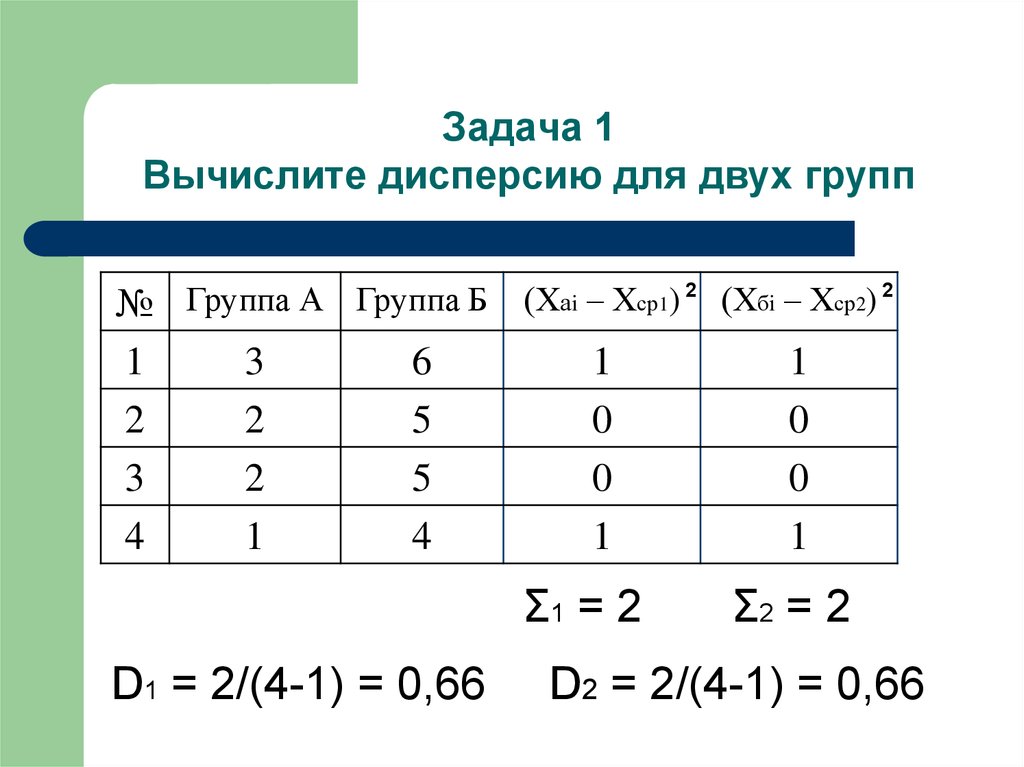
В примере с 24,000 до 55,000 игрок фактически ничего не получал, а постепенно ушел в минус на 2.254 больших блайнда. Потом он быстро отыгрался, но тут же попал в новый даунсвинг — на 1.453 больших блайнда.
График на фоне показывает, что из-за отклонений дисперсии участник по факту ничего не получил на отрезке примерно в 50,000 рук: с 24,000 до 75,000.
Таблица под графиком показывает даунсвинги в цифрах:
- Downswing extents — вероятность даунсвинга размером в X BB;
- Downswing stretches — вероятность даунсвинга на дистанции в X рук.
Ключевой показатель для расчета свингов — винрейт. Чем выше преимущество игрока над оппонентами, тем меньше отклонение его результата от математического ожидания и короче даунсвинги.
Как учитывать кешауты при расчете в калькуляторе дисперсии
Primedope Calculator рассчитывает график так, будто все выигранные деньги остаются в банкролле.
Но профессиональные покеристы играют, чтобы выводить деньги и жить на них. Стандартный размер банкролла в этом случае должен быть выше на сумму, которая будет отниматься каждый месяц.
Например, минимальный банкролл, при котором риск проиграть все ниже 5%, равен 2.496 bb. А вы будете каждый месяц выводить 1,000 bb. Значит, ваш минимум — 3.496 больших блайндов.
Заключение
Понимание дисперсии крайне важно для профессионального покериста. Это помогает уйти от желания выигрывать в каждой раздаче, всегда принимать долгосрочные прибыльные решения и оставаться в психологической форме. Но важно объективно оценивать свою игру в покер-румах, анализировать и улучшать стратегию, чтобы поддерживать винрейт и не списывать проигрыши на длинные серии неудач.
15 апреля 2020
2676
У Вас есть вопросы и желание их обсудить?
Тогда переходите на наш форум, где каждый пользователь может проявить себя!
Обсудить на форуме
Материал подготовлен
Приветствую читателей Poker.
ru! Я Катя Осипова, эксперт Poker.ru. Являюсь профессиональной покеристкой, люблю онлайн и офлайн-покер. Выиграла несколько живых турниров и регулярно участвую в онлайн-сериях.
Игровая карьера началась летом 2001 с покера против казино. При помощи покерных симуляторов и собственных расчетов удалось вывести стратегии обыгрыша казино. Результат — закрытие на вход к 2009 году в 25+ московских казино и в таком же количестве по стране.
Хотите поделиться своим мнением или оставить комментарий?
Написать
Калькулятор дисперсии| Определение и формула
Создано Jasmine J Mah
Отзыв от Dominik Czernia, PhD и Jack Bowater
Последнее обновление: 01 октября 2022 г.
Содержание:- Что такое определение дисперсии?
- Формула дисперсии
- Формула дисперсии населения и выборки
- Пример расчета
- Как рассчитать дисперсию вручную?
- Сводка переменных и уравнений
Калькулятор дисперсии — отличный образовательный инструмент, который научит вас вычислять дисперсию набора данных.
Калькулятор работает как для совокупности, так и для выборочных наборов данных.
Читайте дальше, чтобы узнать:
- Определение дисперсии в статистике;
- Формула дисперсии;
- Примеры расчета дисперсии; и
- Быстрый метод расчета дисперсии вручную.
Что такое определение дисперсии?
Дисперсия является мерой изменчивости значений в наборе данных.
Высокая дисперсия указывает на то, что набор данных на более разбросан .
Низкая дисперсия указывает на то, что данные более плотно сгруппированы вокруг среднего значения или менее разбросаны .
Обучение вычислению дисперсии является ключевым шагом в вычислении стандартного отклонения. Эти две меры являются основой для расчета относительного стандартного отклонения и доверительных интервалов.
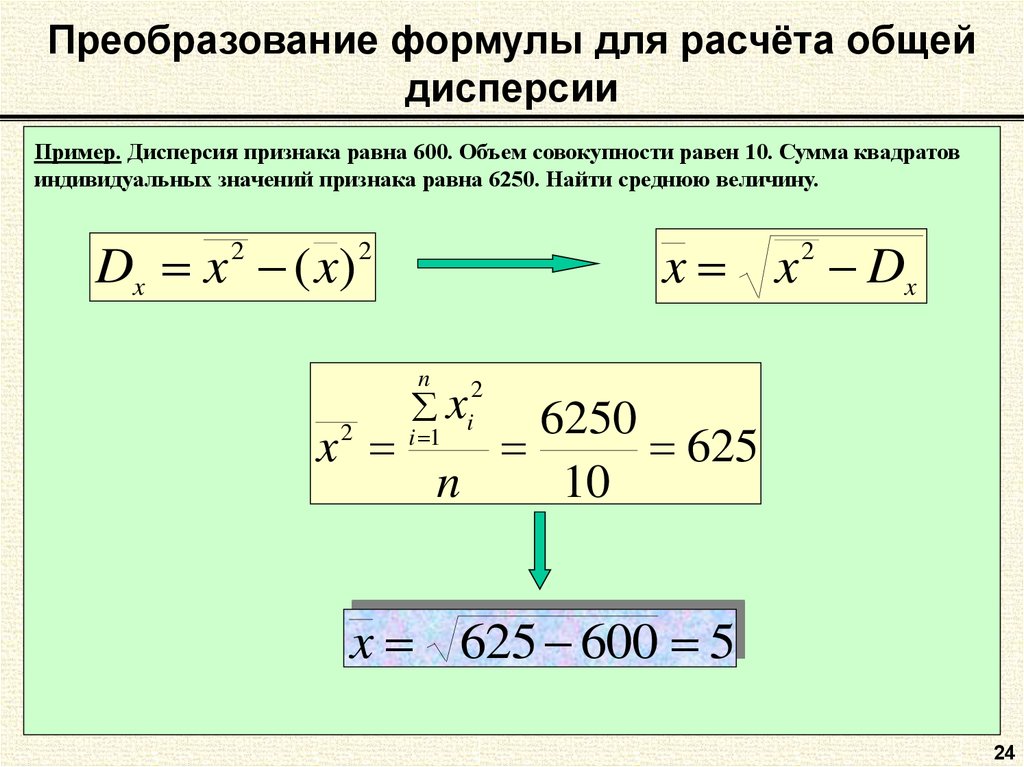
Не уверены в двух последних понятиях, которые мы использовали? Откройте для себя их, посетив наши специальные инструменты: калькулятор относительного стандартного отклонения и калькулятор доверительного интервала! 92 σ2=N1∑i=1N(xi−µ)2
где,
- σ 2 — дисперсия;
- μ — среднее значение; и
- xᵢ представляет i th точек данных из N точек данных. 2 σ2=N1∑i=1N(xi−µ)2 недооценивает дисперсию населения. 92 s2=N−11∑i=1N(xi−xˉ)2
где,
- s 2 — оценка дисперсии;
- x̄ (произносится как «x-bar») — среднее значение выборки; и
- x i i th точек данных из N точек данных.
Пример расчета
Рассчитаем дисперсию результатов восьми учащихся за тест: 5, 5, 5, 7, 8, 8, 9, 9 . Выполните следующие действия:
1. Вычислите среднее значение
Чтобы вычислить среднее значение (x̄), разделите сумму всех чисел на количество точек данных:
x‾=18(5+5+5+7+8+8+ 9+9)\overline{x} = \frac 18 (5 + 5 + 5 + 7 + 8 + 8 + 9 + 9)x=81(5+5+5+7+8+8+9+9 )
x‾=7\overline{x} = 7x=7
2. Вычислить разность от среднего и квадрат разности от среднего
Теперь, когда мы знаем, что среднее равно 7 , мы вычислит разницу от среднего по формуле: 92= 4(5−7)2=(−2)2=4
В приведенной ниже таблице показаны рассчитанные квадраты отклонений от среднего значения для всех результатов викторины.
Столбец «Отклонение» представляет собой оценку минус 7, а столбец «Отклонение 2 » представляет собой предыдущий столбец в квадрате.Оценка
Отклонение
Отклонение 2
5
-2
4
5
-2
4
5
-2
4
7
0
0
8
1
1
8
1
Теперь, когда вы знаете, как найти дисперсию, попробуйте вычислить ее самостоятельно, а затем проверьте свой ответ с помощью нашего калькулятора!
Вам может показаться интересным, что дисперсию можно использовать для расчета дисперсии данных.
Как рассчитать дисперсию вручную?
Если вы рассчитываете дисперсию с помощью портативного калькулятора, вам следует использовать более простую формулу. Эта альтернативная формула математически эквивалентна, но ее легче ввести в калькулятор. 92) \\ = &\tfrac 13 (57 — \tfrac {169}4) \\ = &4,9167 \end{align*}s2===31((12+22+42+62)−41(1+2+4+6)2)31(57−4169)4.9167
Попробуйте сделайте это самостоятельно, а затем проверьте свой ответ с помощью нашего калькулятора дисперсии!
Сводка переменных и уравнений
Таблица 1. Переменные для данных о населении
Переменная
Символ
Уравнение
Средняя численность населения
μ
∑(х я ) / N
Сумма квадратов
нержавеющая сталь
∑(х i — мк) 2
Разница
о 2
Нерж.
сталь / НСтандартное отклонение
о
√(σ 2 )
Таблица 2. Переменные для выборочных данных
Переменная
Символ
Уравнение
Выборочное среднее
х
∑(х я ) / N
Сумма квадратов
нержавеющая сталь
∑(х я — х̄) 2
Выборочная дисперсия
с 2
нерж. сталь / (N — 1)
Стандартное отклонение
с
√(с 2 )
Jasmine J Mah
Данные (можно ввести до 30 чисел)
Настройки
Тип набора данных
Шаги для отображения
Результаты
Ознакомьтесь с 39 похожими калькуляторами описательной статистики 📊
5 числовых сводок5★ рейтинг среднийКоэффициент вариации… Еще 36
Калькулятор дисперсии онлайн — выборка и совокупность (шаг за шагом) 🥇
Дисперсия является важным компонентом статистики и представляет изменчивость ряда данных относительно его среднего значения.
В этой статье в вашем распоряжении будет онлайн-калькулятор для получения дисперсии и порядок ее расчета.Калькулятор дисперсии
Десятичный разделитель:
Запятая (,)
Точка (.)
Разделитель данных:
Запятая (,)
Точка с запятой (;)
Пробел ( )
Введите набор данных:
Что такое дисперсия?
Дисперсия — это мера дисперсии, которая оценивает, насколько далеко каждое число в наборе данных от своего среднего значения. Дисперсия равна квадрату стандартного отклонения.
Формулы для расчета совокупности и выборочной дисперсии приведены ниже:
(a) Дисперсия населения:
(b) Дисперсия выборки:
Где:
- σ 2 3 3 Дисперсия.
- s 2 : Выборочная дисперсия.
- x̄ : Среднее значение.
- N : Количество оцененных значений.
- x i : Каждое из значений.
Дисперсия играет центральную роль в статистике, в таких темах, как описательная статистика, проверка гипотез, статистический вывод, выборка методом Монте-Карло и т. д.
Как пользоваться онлайн-калькулятором дисперсии?
Чтобы использовать онлайн-заявку на отклонение, выполните следующие действия:
- Выберите десятичный разделитель и разделитель данных.
- Введите значения набора данных.
- Нажмите «Решить».
- В нижней части формы вы сможете визуализировать процедуру расчета отклонения.
Пример показан ниже:
Пример расчета дисперсии
Рассчитать выборочную и совокупную дисперсию следующих данных: 10, 12, 13, 16, 16, 9, 8, 8, 12, 8, 6, 16 .
Решение
Мы записываем набор данных:
Нажатие кнопки «Решение».
Процедура:Дисперсия популяции: 11,4722
Отправление выборки: 12.5152
.0693 3.3871
Стандартное отклонение выборки: 3,5377
Среднее значение: 11.1667
Счет данных: 12
В соответствии с данными проблемы.
- N = 10
- x̄ = 110/10 = 11
х я x i – x̄ (х я – х̄) 2 10 -1,1667 1.3612 12 0,8333 0,6944 13 1,8333 3,361 16 4,8333 23.3608 16 4,8333 23.3608 9 -2,1667 4,6946 8 -3,1667 10.028 8 -3,1667 10.
2 σ2=N1∑i=1N(xi−µ)2 недооценивает дисперсию населения. 92 s2=N−11∑i=1N(xi−xˉ)2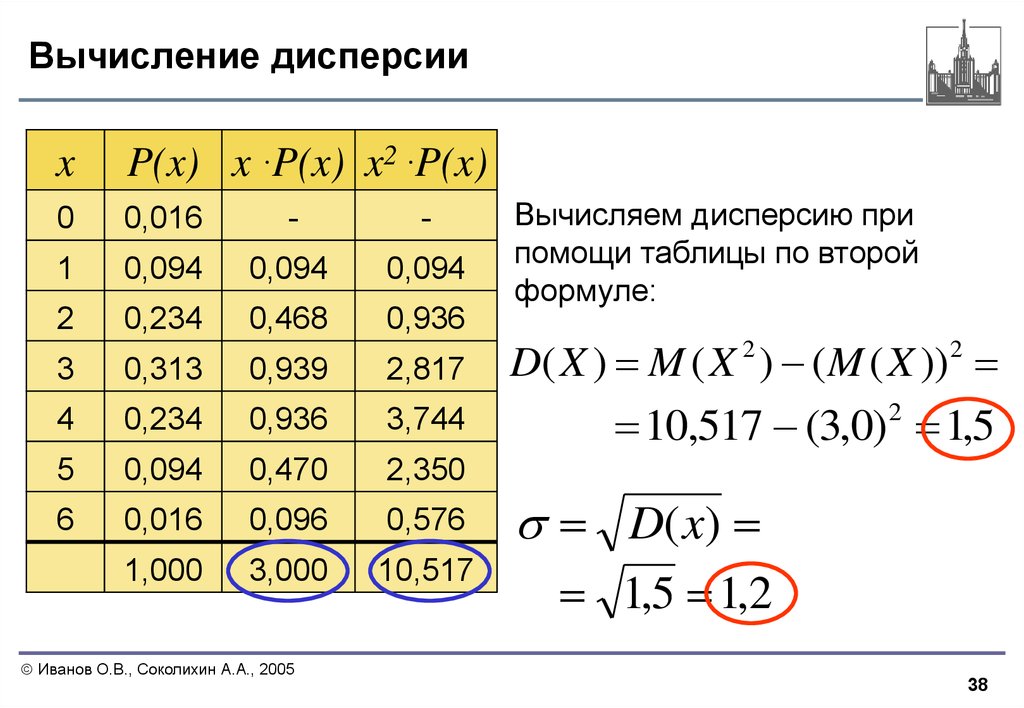
Столбец «Отклонение» представляет собой оценку минус 7, а столбец «Отклонение 2 » представляет собой предыдущий столбец в квадрате.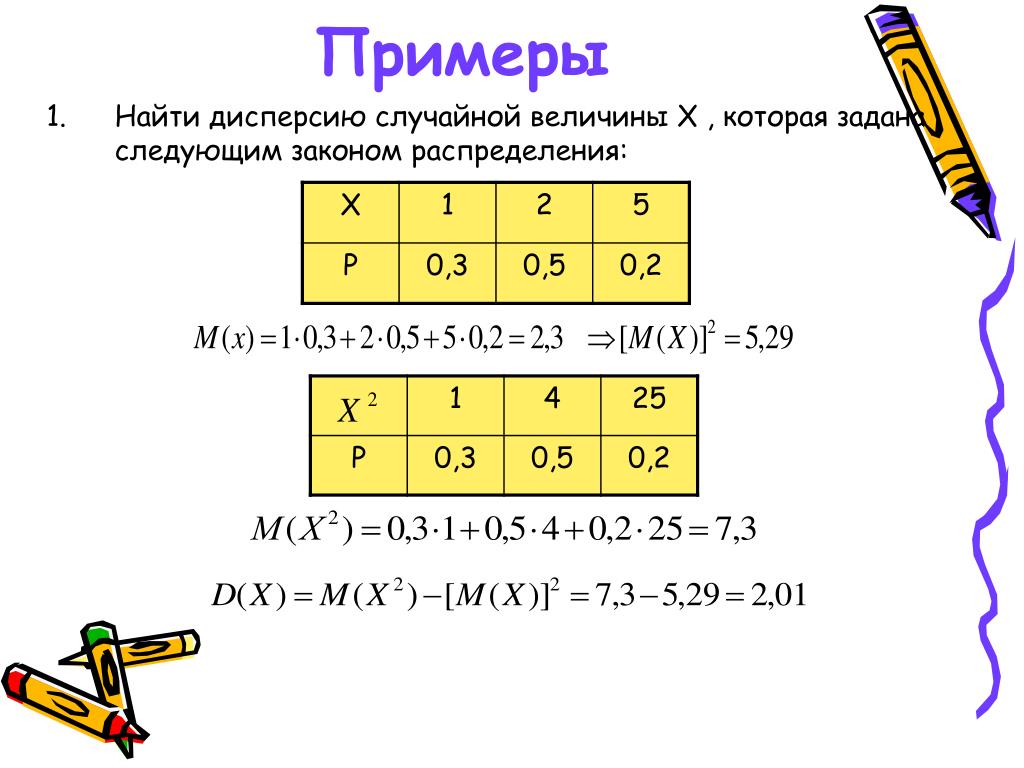
сталь / Н
В этой статье в вашем распоряжении будет онлайн-калькулятор для получения дисперсии и порядок ее расчета.
Процедура: