Урок геометрии в 10 классе «Перпендикулярные плоскости»
Материал опубликовала
0
#10 класс #Геометрия #ФГОС #Методические разработки #Урок #Все учителя #Учитель-предметник #Школьное образование #УМК другой
10 кл. Геометрия
19.01.23г. Тема: «Перпендикулярные плоскости»
Цели урока:
Предметные: ввести понятие угла между плоскостями, познакомить учащихся с определением перпендикулярных плоскостей, признаком перпендикулярности двух плоскостей, формировать умение применять его при решении задач.
Личностные: развивать познавательный интерес к предмету, формировать умение представлять результат своей деятельности.
Метапредметные: формировать умение ставить и формулировать для себя новые задачи в учебе и познавательной деятельности.
Планируемые результаты: учащийся научится применять новую теорему при решении несложных задач.
Оборудование: компьютер, телевизор, карточки с заданиями.
Тип урока: закрепление изученного материала.
Ход урока
1. Организационная часть
Приветствие. Готовность класса к уроку. Проверка домашнего задания.
2.Актуализация пройденного материала
А) Фронтальный опрос.
Учитель: Что изучает планиметрия? Стереометрия?
Ответ учащихся.
Учитель: Какое взаимное расположение 2х прямых возможно на плоскости?
Ответ учащихся.
Учитель: Какое взаимное расположение плоскостей в пространстве?
Ответ учащихся.
Мы с вами повторили основные понятия необходимые для дальнейшего изучения темы.
3.
Мотивация учебной деятельности, сообщение темы и постановка цели занятия
Девизом нашего урока является высказывание: “Мудр не тот, кто знает много, а тот, чьи знания полезны” (Эсхил), так как на уроках геометрии очень важно уметь, смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. Мы сегодня на уроке будем развивать и тренировать свое геометрическое зрение, доказывать свои выводы.
В процессе изучения темы нам предстоит ознакомиться с признаками перпендикулярности двух плоскостей.
4. Закрепление раннее изученного материала:
Открываем тетради записываем число и тему урока: «Перпендикулярные плоскости». Вспомним определение: Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90.
О чем гласит признак перпендикулярности двух плоскостей? Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Урок 11. перпендикулярность плоскостей — Геометрия — 10 класс — Российская электронная школа (resh.edu.ru)
5.Подведение итогов урока и выставление оценок за урок:
В процессе изучения темы мы повторили признаки перпендикулярности двух плоскостей и решили задачи.
Сейчас вы на столе возьмете карточку, на которой написаны утверждения. Против каждого утверждения нужно поставить «+», если оно верно, и «-» , если неверно. Приложение 1.
Опросник. (Нужное подчеркнуть)
1. Моё восприятие темы «Перпендикулярность плоскостей».
а) усвоил всё;
б) почти всё;
в) усвоил частично.
2. Как я работал на уроке:
а) отлично;
б) хорошо;
в) удовлетворительно;
г) неудовлетворительно.
6.Задание на дом:
Повторить признак перпендикулярности двух плоскостей. Решить задачи
№
Опубликовано в группе «УРОКИ, КИМы, ИГРЫ, практикумы, творческие задания по ИНФОРМАТИКЕ, МАТЕМАТИКЕ и другим дисциплинам.»
Перехваты и асимптоты тангенциальных функций — Концепция
Касательная идентичность такова: tan(theta)=sin(theta)/cos(theta), что означает, что всякий раз, когда sin(theta)=0, tan(theta)=0, и всякий раз, когда cos(theta)=0, tan(theta) не определен (делится на ноль). Когда функция тангенса равна нулю, она пересекает ось x.
Следовательно, чтобы найти точки пересечения, найдите момент, когда sin(theta)=0. Чтобы найти вертикальные асимптоты, определите, когда cos(theta)=0.
синус косинус касательная нули х перехватывает вертикальные асимптоты
Иногда в домашнем задании или задаче вас спросят о точках пересечения и асимптотах касательной функции. Что ж, давайте исследуем это. Начнем с тождественного тангенса тета, равного синусоидальному тета над косинусным тета. Сначала найдем нули тангенса. Из-за этого тождества нули тангенса будут точно такими же, как нули синуса. То есть тангенс тета равен нулю, а синус тета равен нулю. Теперь синус тета равен нулю при целых числах, кратных пи. Таким образом, тета равна, например, 0, пи 2 пи и так далее.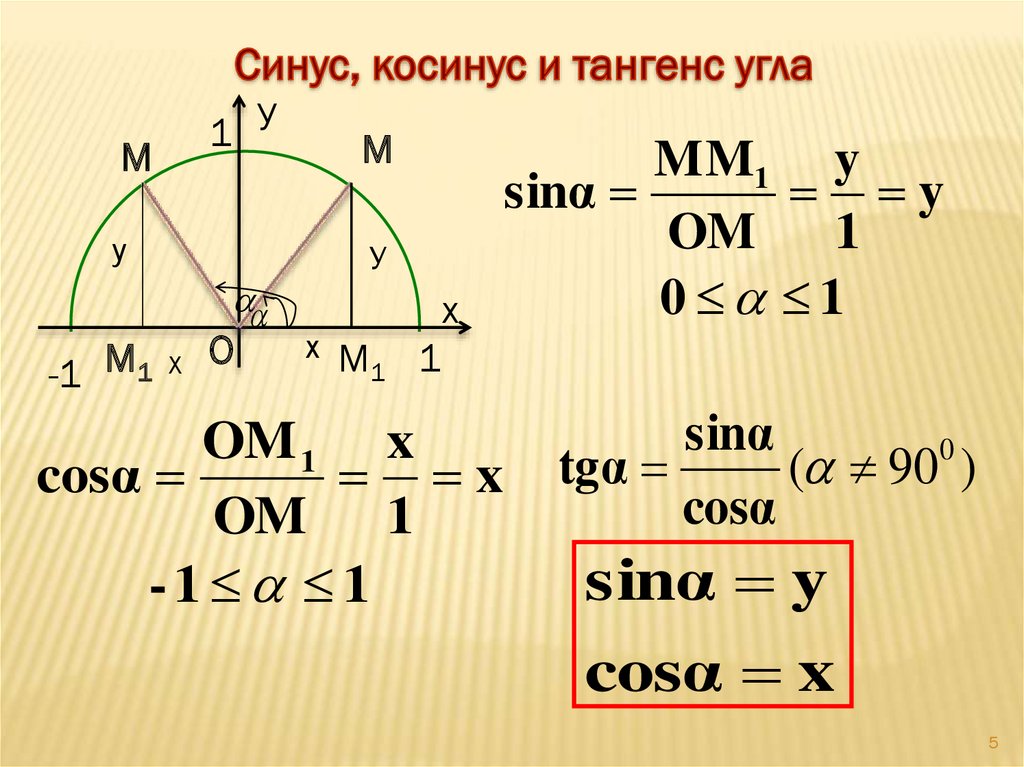
Один из способов выразить это более компактно — назвать это n pi, где n — целое число n, т. е. целое число, кратное числу pi. Какое отношение это имеет к x перехватам? Ну, нули становятся x перехватами, когда вы рисуете. Таким образом, x перехватывает, я буду сокращать это так: 0 0, pi 0, 2 pi 0 и так далее. это нули касательной, и, конечно, вторая координата точки пересечения x будет равна 0. Это точки пересечения x. А асимптоты?
х равно отрицательному пи больше 2,. отрицательные 3 пи на 2, отрицательные 5 пи на 2 и так далее. Если вас когда-нибудь спросят о домене функции тангенса, поскольку это места, где тангенс не определен, вы бы назвали все действительные числа, кроме этих. Если вас когда-нибудь спрашивали о диапазоне функции тангенса, то это все действительные числа. Вы можете получить любое число из функции тангенса, потому что помните, что тангенс представляет собой наклон конечной стороны угла на единичной окружности, который может быть любым.
Итак, снова нули тангенсов и точки пересечения x, целые числа, кратные числу пи. Неопределенные вертикальные асимптоты тангенса — это число пи больше 2 плюс целое число, кратное числу пи.
Объяснение урока: Знаки тригонометрических функций в квадрантах
В этом объяснении мы узнаем, как определить, в каком квадранте лежит угол и являются ли его синус, косинус и тангенс положительными или отрицательными.
Чтобы определить знак функций синуса и косинуса для данного угла, мы начнем с точного напоминания того, что мы подразумеваем под функциями синуса и косинуса данного угла.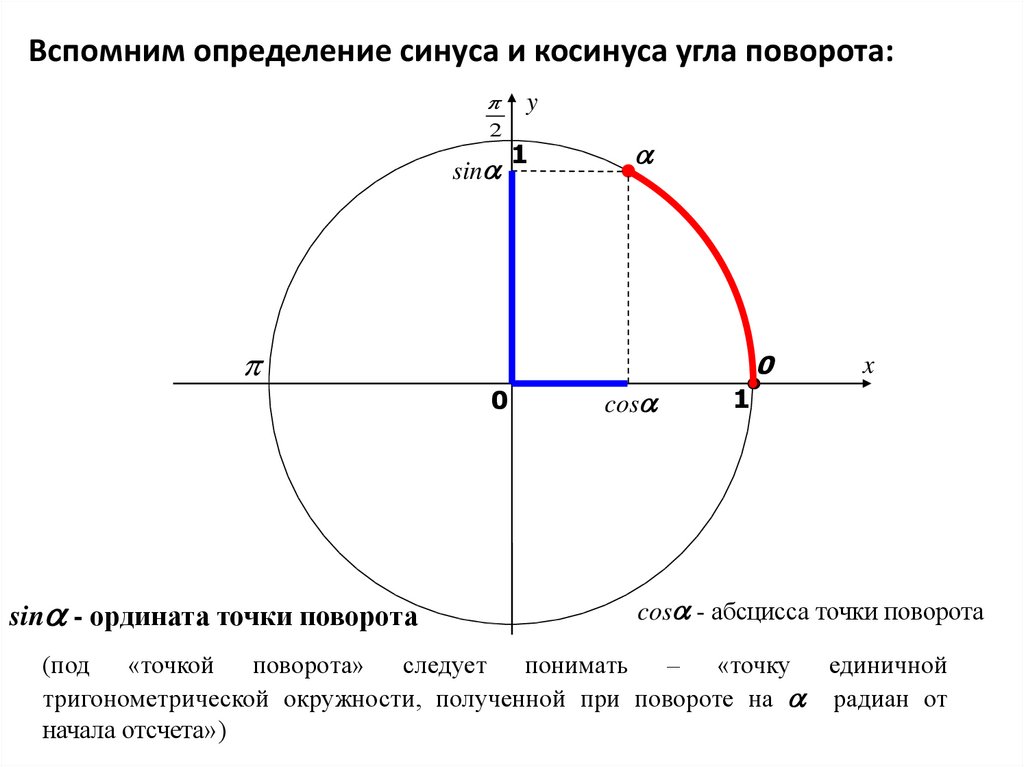
Для этого сначала нужно вспомнить, что именно мы понимаем под синусом и косинусом угла. Синус и косинус угла можно определить, используя точки на единичной окружности.
𝑥-координата этой точки будет cos𝜃, где 𝜃 — угол, измеренный против часовой стрелки от положительной 𝑥-оси. Точно так же 𝑦-координата этой точки будет sin𝜃. Когда наш угол 𝜃 острый, у нас есть прямоугольный треугольник, где функции синуса и косинуса являются отношениями длин сторон этого прямоугольного треугольника. Однако этот метод позволяет определить синус и косинус любого угла от 0∘ до 360∘.
Мы можем расширить это еще больше, разрешив направленные углы. В этом случае угол, измеренный по часовой стрелке, задается отрицательным числом. Мы также можем расширить это, разрешив углы, представляющие больше, чем полный оборот.
Например, угол −120∘ можно представить следующим образом.
Этот угол равен 120∘ и направлен по часовой стрелке.
Следовательно, чтобы найти синус и косинус заданного угла 𝜃, мы можем измерить угол 𝜃 от положительной оси 𝑥, а затем найти координаты соответствующей точки на единичной окружности.
Давайте посмотрим на примере, как применить это к углу 150∘. Начнем с измерения угла 150 ∘ против часовой стрелки от положительной оси 𝑥 на диаграмме с центром единичной окружности в начале координат.
Координаты точки пересечения окружности и отрезка сообщают нам синус и косинус угла 150∘. На диаграмме видно, что 𝑦-координата этой точки положительна; следовательно, sin150∘ также положителен. Точно так же 𝑥-координата этой точки отрицательна; следовательно, cos150∘ также отрицательна.
Давайте посмотрим на примере, как мы можем использовать это, чтобы найти знак косинуса угла больше 360∘.
Пример 1. Определение знака тригонометрической функции заданного угла
Кос400∘ положительный или отрицательный?
Ответ
Существует множество различных методов, которые мы можем использовать для определения знака косинуса заданного угла. Например, мы могли бы использовать различные тригонометрические тождества для вычисления этого выражения.
Однако мы сосредоточимся на графической интерпретации.
Для этого сначала напомним, что косинус любого угла равен 𝑥-координате точки 𝑃 на единичной окружности, где 𝑂𝑃 составляет угол 𝜃 с положительной 𝑥-осью.
Следовательно, нам нужно найти точку 𝑃 такую, что 𝑂𝑃 образует угол 400∘ с положительной 𝑥-осью. Так как 400=360+40∘∘∘, то получаем следующее.
Мы видим, что coscos400=40∘∘, поскольку эти два угла представляют одну и ту же точку на единичной окружности. Косинус этого угла будет равен 𝑥-координате 𝑃.
На диаграмме видно, что 𝑥-координата 𝑃 положительна, так как она лежит правее начала координат.
Следовательно, cos400∘ положителен.
В предыдущем примере мы видели, что знак косинуса угла полностью определяется значением 𝑥-координаты точки пересечения конечной стороны угла с единичной окружностью. Мы можем использовать это, чтобы определить знак функций синуса и косинуса для любого угла.
Если угол соответствует точке на единичной окружности справа от начала координат, то его 𝑥-координата положительна и, следовательно, его косинус также положителен.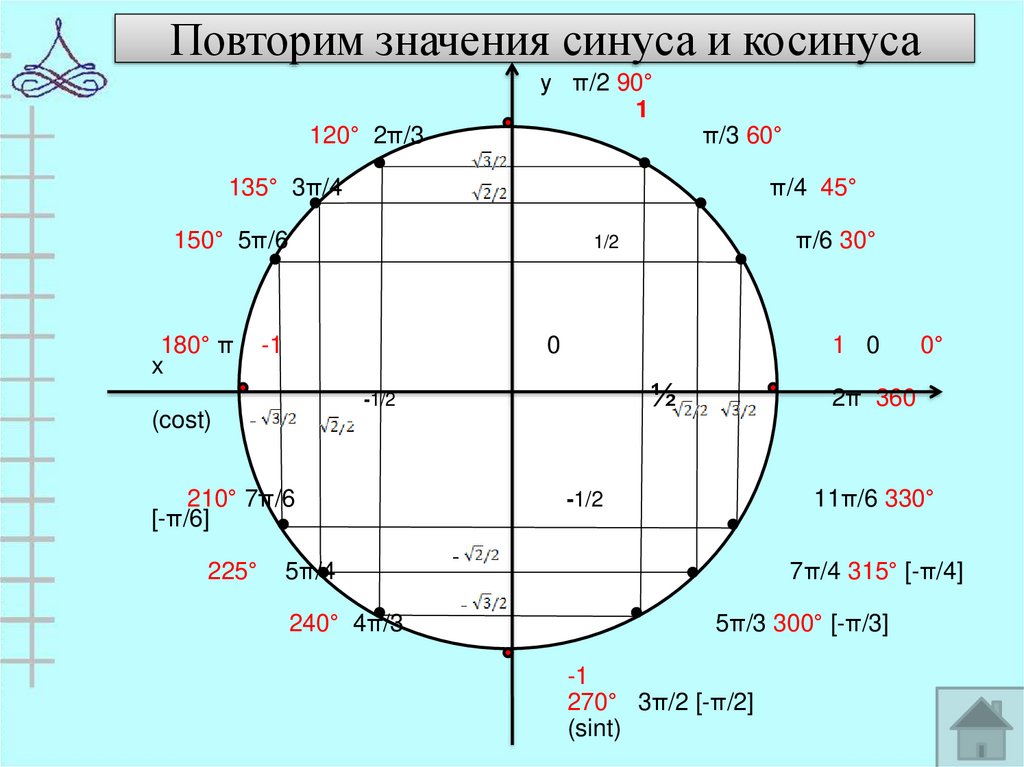
Точно так же, когда он соответствует точке слева от начала координат, его 𝑥-координата отрицательна, и, следовательно, его косинус также должен быть отрицательным. Мы также можем сделать это с 𝑦-координатами.
Если угол соответствует точке на единичной окружности, лежащей выше начала координат, то его 𝑦-координата положительна и, следовательно, его синус также должен быть положительным. Точно так же, когда он соответствует точке ниже начала координат, его 𝑦-координата отрицательна, и, следовательно, его синус также должен быть отрицательным.
Было бы полезно иметь терминологию, чтобы говорить о том, где в координатной плоскости лежит точка, а также угол относительно осей. Поскольку плоскость естественным образом делится осями на четыре секции, мы можем сделать это, пометив эти секции, которые мы назовем квадрантами. Мы начнем с верхнего правого квадранта и пронумеруем их против часовой стрелки.
Мы обычно обозначаем их римскими цифрами, и стоит подчеркнуть, что сами оси не являются частью какого-либо квадранта.
Это позволяет нам описать, где в координатной плоскости лежит точка, не лежащая на осях.
Например, (1,2) лежит в первом квадранте, (−3,2) лежит во втором квадранте, (−3,−3) лежит в третьем квадранте, а (1,−2) лежит в четвертый квадрант.
Определение: квадранты в координатной плоскости — точки
Для любых положительных действительных чисел 𝑥 и 𝑦 мы говорим, что
- (𝑥,𝑦) лежит в первом квадранте;
- (−𝑥,𝑦) лежит во втором квадранте;
- (−𝑥,−𝑦) лежит в третьем квадранте;
- (𝑥,−𝑦) лежит в четвертом квадранте.
Точки на осях не лежат ни в каком квадранте.
Точно так же мы можем сказать, что некоторые углы, измеренные от положительной оси 𝑥, лежат в определенном квадранте.
Определение: квадранты в координатной плоскости — углы
Учитывая угол 𝜃 в стандартном положении, мы говорим, что 𝜃 лежит в том же квадранте, что и его конечная сторона.
Давайте посмотрим на примере, как определить квадрант, в котором будет лежать заданный угол.
Пример 2. Определение, в каком квадранте лежит заданный угол
В каком квадранте лежит угол 288∘?
Ответ
Для того, чтобы определить квадрант, в котором будет лежать угол, напомним, что квадранты — это 4 сечения координатной плоскости, разделенные осями, а квадрант угла определяется квадрантом, в котором лежит его конечная сторона дюймов, если мы измеряем от положительной оси 𝑥.
Мы можем сделать это в эскизе, где мы помним, что 288∘ положительно, поэтому наш угол измеряется в направлении против часовой стрелки, и мы нумеруем квадранты сверху справа также в направлении против часовой стрелки.
Поскольку 288=270+18∘∘∘, мы видим, что крайняя сторона будет лежать в четвертом квадранте. Следовательно, мы также можем сказать, что 288° лежит в четвертом квадранте.
Мы знаем, что знак синуса и косинуса угла полностью определяется его положением на координатной плоскости. На самом деле мы можем определить знак, исключительно рассматривая квадрант, в котором лежит угол.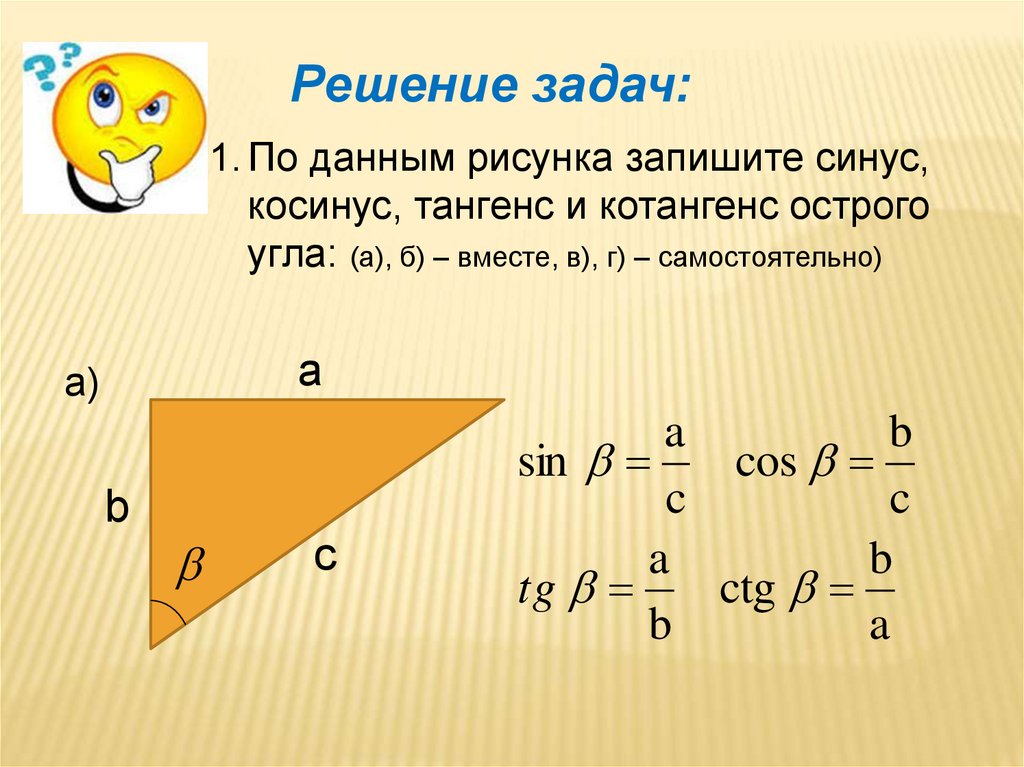
Во-первых, когда наш угол лежит в первой или четвертой четверти, 𝑥-координаты всех точек на его конечной стороне положительны. В частности, это означает, что 𝑥-координата точки пересечения терминальной стороны с единичной окружностью также положительна. Следовательно, косинус этого угла положителен. Точно так же, если угол лежит во второй или третьей четверти, его косинус отрицателен.
Во-вторых, когда наш угол лежит в первом или втором квадранте, 𝑦-координаты всех точек на его конечной стороне положительны. В частности, это означает, что 𝑦-координата пересечения концевой стороны и единичной окружности также положительна. Следовательно, синус этого угла положителен. Точно так же, если угол лежит в третьей или четвертой четверти, его синус отрицателен.
Мы можем обобщить это следующим образом.
Определение: Знаки тригонометрических функций в разных квадрантах
- cos𝜃>0, когда 𝜃 находится в первом или четвертом квадранте;
- cos𝜃0, когда 𝜃 находится во втором или третьем квадранте;
- sin𝜃>0, когда 𝜃 находится в первом или втором квадранте;
- sin𝜃0, когда 𝜃 находится в третьем или четвертом квадранте.
Мы можем использовать их, чтобы найти знак функции тангенса в разных квадрантах. Напомним следующее тригонометрическое тождество: tansincos𝜃≡𝜃𝜃.
Поскольку функция тангенса представляет собой частное функций синуса и косинуса, ее знак определяется знаком этих функций. Нам не нужно беспокоиться о случаях, когда cos𝜃=0, поскольку они будут происходить на самих осях, а не в квадранте.
Когда 𝜃 находится в первом квадранте, синус и косинус положительны; следовательно, tan𝜃 — это частное двух положительных чисел. Следовательно, tan𝜃>0.
Когда 𝜃 находится во втором квадранте, синус положительный, а косинус отрицательный; следовательно, tan𝜃 — это частное положительного числа и отрицательного. Следовательно, tan𝜃0.
Когда 𝜃 находится в третьем квадранте, синус отрицательный, а косинус отрицательный; следовательно, tan𝜃 — это частное двух отрицательных чисел. Следовательно, tan𝜃>0.
Наконец, когда 𝜃 находится в четвертом квадранте, синус отрицательный, а косинус положительный; следовательно, tan𝜃 — это частное отрицательного числа и положительного числа.
Следовательно, tan𝜃0.
Это дает нам следующее.
Определение: Знаки касательной функции в разных квадрантах
- tan𝜃>0, когда 𝜃 находится в первом или третьем квадранте;
- tan𝜃0, когда 𝜃 находится во втором или четвертом квадранте.
Ту же информацию мы можем определить для обратных тригонометрических функций. Однако, поскольку взятие обратной величины не меняет знака, обратные тригонометрические функции будут иметь тот же знак, что и соответствующие им тригонометрические функции.
Существует полезная диаграмма, называемая диаграммой CAST, которую можно использовать для запоминания знаков этих тригонометрических функций в разных квадрантах. Мы находим это, помечая каждый квадрант тригонометрическими функциями, положительными для лежащих там аргументов.
Используя аббревиатуру CAST для обозначения квадрантов в направлении против часовой стрелки, мы можем быстро вспомнить, что все тригонометрические функции положительны в первом квадранте, только функция синуса положительна во втором квадранте, только функция тангенса положительна в третьем квадранте, и, наконец, только функция косинуса положительна в четвертом квадранте.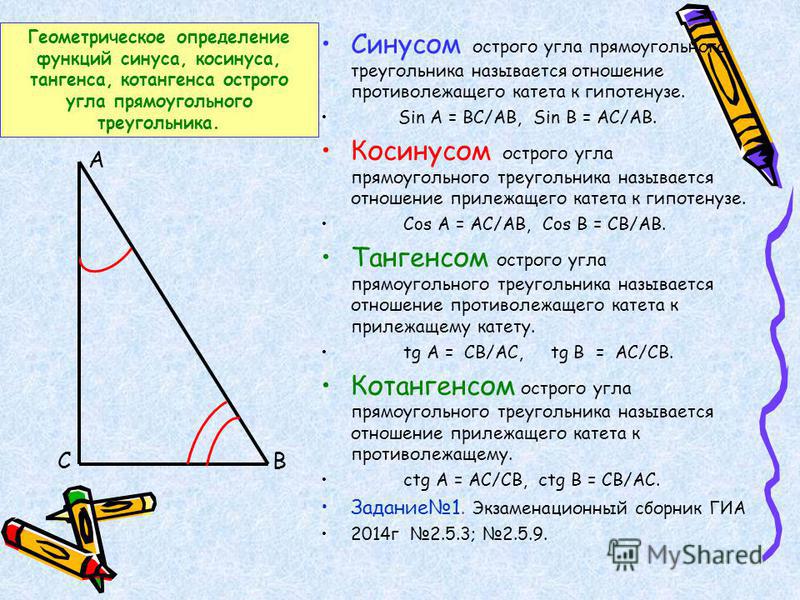
Давайте рассмотрим пример того, как мы можем использовать эту диаграмму для определения квадранта, в котором должен лежать угол, учитывая информацию о синусе и косинусе угла.
Пример 3. Определение квадранта, в котором лежит угол при данных двух его тригонометрических отношениях
В каком квадранте лежит 𝜃, если sin𝜃=1√2 и cos𝜃=1√2?
Ответ
Мы хотим определить квадрант угла, лежащего в заданной информации о синусе и косинусе этого угла. Для этого напомним, что квадранты — это 4 сечения координатной плоскости, разделенные осями, а квадрант угла определяется квадрантом, в котором лежит его конечная сторона, отсчитываемым от положительной 𝑥-оси.
Мы могли бы сделать это, используя определения функций синуса и косинуса. Однако более простой метод предполагает использование диаграммы CAST. Мы обозначаем квадранты координатной плоскости буквами аббревиатуры, начиная с четвертого квадранта и двигаясь против часовой стрелки.
Буквы затем сообщают нам квадранты, для которых выход каждой тригонометрической функции положителен, где A означает все, а C, S и T означают косинус, синус и тангенс соответственно.
В вопросе нам говорят, что sin𝜃 и cos𝜃 равны 1√2. Другими словами, и синус, и косинус положительны. Это происходит только в первом квадранте. Следовательно, 𝜃 находится в первом квадранте.
Ответ: Первый.
В нашем следующем примере мы определим квадрант, в котором лежит угол, учитывая знак функций косинуса и синуса.
Пример 4. Определение квадранта, в котором находится угол, по двум его тригонометрическим отношениям
Определите квадрант, в котором находится 𝜃, если cos𝜃>0 и sin𝜃0.
Ответ
Чтобы определить квадрант, в котором будет лежать данный угол, мы могли бы использовать определения функции синуса и косинуса. Однако диаграмма CAST может сэкономить нам время.
Диаграмма CAST показывает нам квадранты, в которых результат каждой тригонометрической функции положителен. Нам нужно определить, где косинус положительный, а где отрицательный.
Начнем с положительного значения косинуса. Диаграмма CAST говорит нам, что косинус положителен для углов в квадрантах «C» или «A», то есть в четвертом и первом квадрантах соответственно.
Точно так же диаграмма CAST говорит нам, что, поскольку синус положительный в квадрантах «А» и «С», он будет отрицательным в других квадрантах. Другими словами, синус угла отрицателен для любого угла в третьем или четвертом квадранте.
Поскольку нам нужно, чтобы оба эти утверждения были истинными, 𝜃 должно лежать в четвертом квадранте.
В нашем последнем примере мы увидим, как применить это для определения знака обратной тригонометрической функции при заданном угле.
Пример 5. Определение знака обратной тригонометрической функции заданного отрицательного угла
Является ли значение csc(−225)∘ положительным или отрицательным?
Ответ
Существует ряд методов, которые мы могли бы использовать для определения знака функции косеканса заданного угла. Например, мы могли бы использовать различные тригонометрические тождества или сделать это непосредственно из определения функции синуса. Однако вместо этого мы сосредоточимся на графической интерпретации с помощью диаграммы CAST.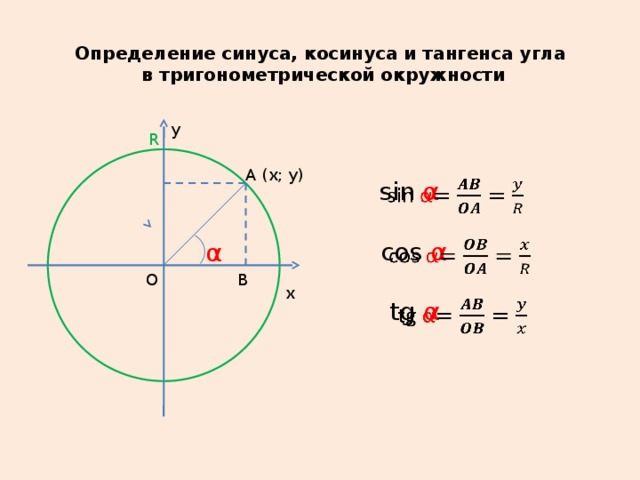
Диаграмма CAST показывает нам квадранты, для которых различные тригонометрические функции положительны. Чтобы использовать эту диаграмму, нам сначала нужно записать csc(−225)∘ в терминах синуса и косинуса. Напомним следующее обратное тригонометрическое тождество: cscsin𝜃≡1𝜃; следовательно, cscsin(-225)=1(-225).∘∘
Это означает, что мы можем определить знак csc(-225)∘ по знаку sin(-225)∘. Для этого нам нужно определить, в каком квадранте находится −225∘, и мы можем добиться этого, нарисовав угол на нашей диаграмме CAST. Помните, поскольку этот угол отрицателен, нам нужно измерять угол по часовой стрелке.
Поскольку −225=−180−45∘∘∘, мы видим, что этот угол лежит во втором квадранте. Диаграмма CAST говорит нам, что функция синуса положительна во втором квадранте. Следовательно, sin(−225)>0.∘
В частности, это означает, что 1(−225)sin∘ является частным двух положительных чисел. Следовательно, csc(−225)∘ положительно.
Давайте закончим повторением некоторых важных моментов этого объяснения.