Основные понятия комбинаторики: Основные понятия комбинаторики.

Содержание

Основные понятия комбинаторики.

n – факториал ‒ произведение первых n ‒ натуральных чисел (обозначается n!).

Основными понятиями комбинаторики являются ‒ размещения, перестановки и сочетания.

Определение 1. Пусть имеется множество, содержащее n ‒ элементов.

Размещением из n ‒ элементов по m ‒ элементов (m ≤ n) ‒ называются все подмножества, содержащие m ‒ элементов и отличающиеся друг от друга или составом своих элементов или порядком их следования.

‒ число размещений из n ‒ элементов по m ‒ элементов.

Определение 2. Перестановками из n ‒ элементов называются размещения из n ‒ элементов по n ‒ элементов.

–число перестановок из n ‒ элементов.

Определение 3. Сочетаниями из n ‒ элементов по m ‒ элементов (m≤n) называются все m‒ элементные подмножества n ‒ элементного множества, отличающиеся друг от друга только составом своих элементов.

‒ число сочетаний из n ‒ элементов по m ‒ элементов.

Свойства сочетаний:

Доказательство:

Так как

Следовательно,

Примеры:

Доказательство:

Примеры:

Доказательство:

Примеры:

Бином Ньютона и его свойства.

Воспользуемся формулами:

=+2ab+=+

Используя принцип математической индукции (от частных примеров к общей формуле), получим формулу Ньютона:

Или кратко:

– формула Ньютона для степени бинома или бином Ньютона.

Свойства:

1. Формула содержит (n+1) ‒ слагаемое.

2. Показатель степени a ‒ убывает от n до 0; Показатель степени b – возрастает от 0 до n.

3. Любой член разложения можно найти по формуле:

4. Коэффициентыназываются – биноминальными. Биноминальные коэффициенты, равноудаленные от концов разложения, равны между собой.

5. Сумма всех биноминальных коэффициентов находятся по формуле:

Доказательство:

Пусть a = b = 1.

Тогда

Примеры на формулу Ньютона и ее свойства:

Пример 1.

Где

Следовательно,

Пример 2.

Найти: .

Решение:

В комбинаторных задачах удобно пользоваться следующей таблицей:

Выбор

Сочетания

Размещения

Перестановки

Без повторения

С повторением

2.Понятие случайного события. Виды случайных событий.

Случайным событием, связанным с некоторым опытом (испытанием) называется всякое событие, которое при осуществлении опыта может произойти, а может и не произойти.

Случайные события обозначаются, заглавными буквами латинского алфавита A,B,C….

Виды случайных событий:

1. Событие, которое всегда происходит в результате опыта, называется достоверным. Обозначается .

2. Событие, которое никогда не происходит в результате опыта, называется – невозможным. Обозначается .

3. Событие, состоящее в том, чтобы событие A не произошло называется противоположным событию А. Обозначается .

4. События A и B называются несовместными, если они не могут произойти одновременно.

5. Событияназываютпопарно несовместными, если никакие два из них не могут произойти одновременно.

6. События образуютполную группу событий, если в результате опыта непременно произойдет, хотя бы одно из них.

7. События

A и B называются равновероятными, если в результате опыта нет оснований считать одно из них более возможным, чем другое.

8. Событие, приводящее к наступлению события A, называется благоприятствующим событию А.

9. События , образующие полную группу попарно несовместных равновероятных событий, называютсяэлементарными событиями.

Конспект урока на тему «Основные понятия комбинаторики» (1 курс)

Урок ________

Тема программы: Комбинаторика

Тема: «Основные понятия комбинаторики».

Тип урока: урок усвоения новых знаний.

Цели:

— формирование основных понятий комбинаторики: размещения из m элементов по n, сочетания из m элементов по n, перестановки из n элементов; формирование умений и навыков вычисления значений комбинаторных выражений по формулам, решения простейших комбинаторных задач;

— развитие умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности;

— воспитание интереса к дисциплине, честности, аккуратности, эстетического отношения к оформлению математических решений, воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда; прививать чувство патриотизма;

Обучающийся должен

знать:

определения трех важнейших понятий комбинаторики:

— размещения из n элементов по m;

— сочетания из n элементов по m;

— перестановки из n элементов, а также, формулы вычисления их количества.

уметь:

— отличать задачи на «перестановки», «сочетания», «размещения» друг от друга;

— применять основные комбинаторные формулы при решении простейших комбинаторных задач.

Развитие общих компетенций:

ОК 4. Осуществлять поиск и использовать информацию, необходимую для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 6. Работать в коллективе и команде, взаимодействовать с руководством, коллегами, социальными партнерами

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий

Используемые методы обучения:

словесный: устный опрос, эвристическая беседа, публичное выступление студентов;

наглядный: показ иллюстраций;

практический: решение задач.

ХОД УРОКА

I. Организационный момент

Преподаватель проверяет готовность к уроку.

Я рада приветствовать всех Вас на сегодняшнем уроке. Все мы с вами пришли на урок с разным настроением, но я надеюсь, что в конце нашего занятия у нас у всех будут только положительные эмоции. Девизом нашего занятия я предлагаю взять слова английского математика Д. Сильвестра

«Число, положение и комбинация —

три взаимно пересекающиеся,

но различные сферы мысли,

к которым можно отнести

все математические идеи»

Английский математик

Джеймс Джозеф Сильвестр
(1814-1897)

II. Мотивация

Ребята, каждая группа в течении года дежурит по колледжу и в столовой.

Являются ли бригады дежурных в группах постоянными? Скажите, а сколько всего существует способов назначить из n студентов группы m дежурных. В математике есть раздел, который занимается решением подобных задач. Этот раздел называется комбинаторикой.

III. Сообщение темы, целей урока

Тема сегодняшнего урока «Основные понятия комбинаторики». Давайте вместе попробуем сформулировать цели урока:

— ознакомиться с основными понятиями комбинаторики (размещения, сочетания, перестановки без повторов)

— научиться решать простейшие комбинаторные задачи

IV. Актуализация знаний, умений и навыков

Прежде чем перейти к изучению нового материала, проведем небольшую разминку по ранее изученному материалу.

1) Дайте определение факториала числа. (Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число).

Как обозначается факториал? ( восклицательным знаком).

3) Запишите формулу факториала. ( n! = 1*2*…*(n-1)*n.)

4) А чему равен 1! ? 0! ? (Факториал 0 и 1 равен единице.)

5) Вычислите факториалы следующих чисел: 2!, 3!, 4!, 5!, 6!

V. Изучение нового материала.

Введение общих понятий

Сейчас я предлагаю Вам решить задачу.

Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

Ответ: ВРФ ВФР РФВ РВФ ФРВ ФВР (6)

Как называются задачи такого типа?

Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными.

Как называется раздел математики, в котором решаются задачи на составление различных комбинаций?

Раздел математики, занимающийся их решением, — комбинаторикой

Определение:

Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.

(Комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам. )

Определение: Группы, составленные из каких-либо элементов, называются соединениями.

Вы сейчас предложили несколько способов решения выше указанной задачи. Но есть более простой способ решения данной задачи – это решение с использованием основных понятий комбинаторики. Различают три вида соединений: размещения, перестановки и сочетания.

— Давайте более подробно остановимся на каждом понятии и рассмотрим формулы вычисления их количества.

1. Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.

Число перестановок из n элементов обозначается символом P_nи вычисляется по формуле:

P_n = n!

— Вернемся к нашей задаче. Нам известно, что туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

P_n = n! = 3! = 1*2*3=6 (способов)

Ответ: 6 способов.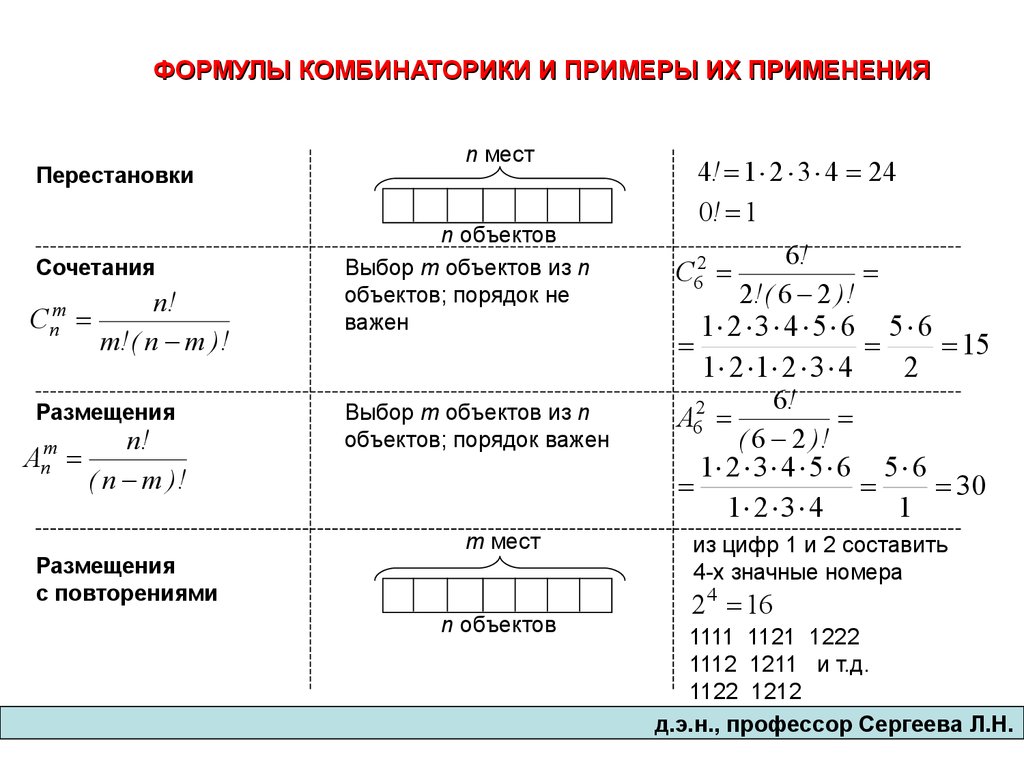

Рассмотрим еще одну задачу.

В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

2. Сочетания. Сочетаниями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Количество сочетаний обозначается и вычисляется по формуле:

Вернемся к задаче.

Мы рассмотрели два основных понятия комбинаторики. Скажите, о каком понятии мы еще не говорили.

Размещения.

Совершенно верно – размещения.

3. Размещения. Размещениями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения. Количество размещений обозначается и вычисляется по формуле

Предлагаю Вам составить задачу на нахождения количества размещений.

Пример. Сколько различных двузначных чисел можно составить из множества цифр , причем так, чтобы цифры числа были различны?
Искомое число чисел

VI.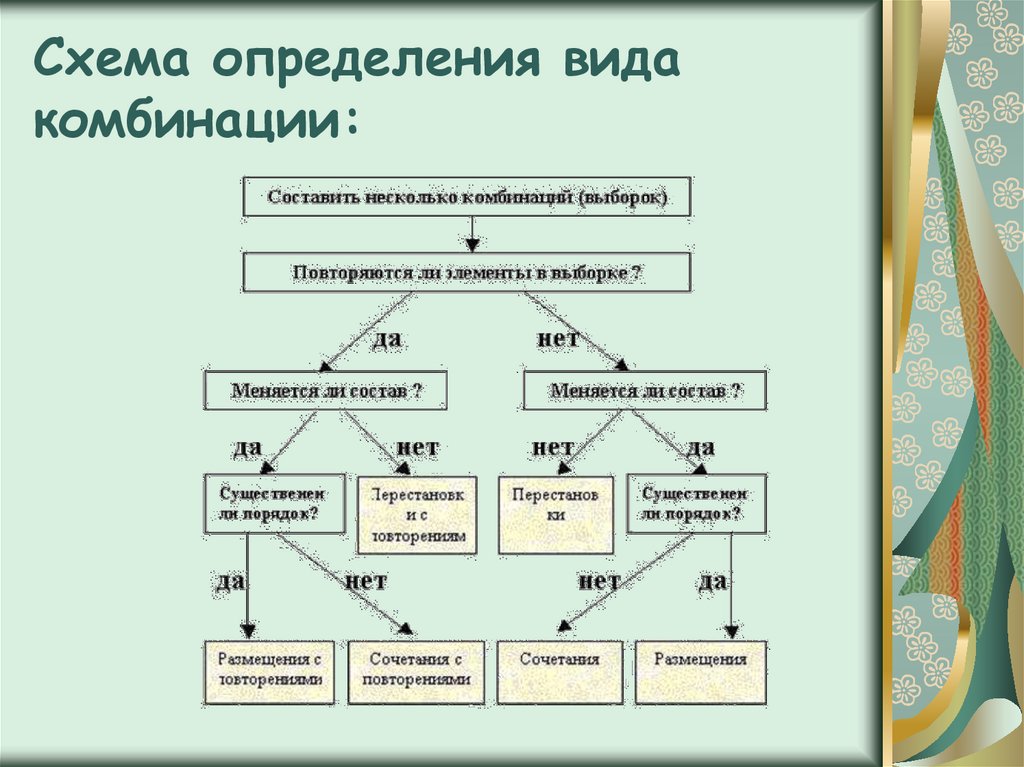 Первичный контроль знаний

(Студенты работают у доски, решают простейшие комбинаторные задачи.)

Решение простейших комбинаторных задач:

№1. Сколькими способами можно рассадить 5 человек за столом?

№2. В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

способами.

№3. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

VII. Закрепление

Студенты работают самостоятельно по вариантам. Взаимопроверка.

1 вариант.

Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6?

Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4

2 вариант.

В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?

Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента:

Ответ : 120

Самостоятельная работа, работа в парах, публичное выступление раздаточный материал (карточка с задачами)

VIII. Подведение итогов занятия. Рефлексия.

(Обобщаются новые знания, делаются выводы о достигнутых целях урока. Поощряются активные студенты, выставляются обоснованные преподавателем оценки.)

1) Подведем итоги нашего занятия.

Проверь себя:

1.Определите вид соединений:

а) Соединения из n элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются __________перестановки

б) Соединения из m элементов по n, отличающихся друг от друга только составом элементов, называются _______________сочетания

в) Соединения из m элементов по n, отличающихся друг от друга составом элементом и порядком их расположения, называются _________ размещения

2. Восстановите соответствие типов соединений и формул для их подсчёта

А. 1) сочетания	В. 2) размещения	С. 3) перестановки

2) Обсуждение и выставление оценок за урок.

3) Рефлексия:

Достиг ли ты своих целей? ______________

Оцени степень усвоения: _______________

Продолжи одно из предложений:

“Мне понятно…

“Я запомнил…

“Мне на уроке…

“Я думаю…

IX. Домашнее задание

Решить задачу (дифференцированные задачи)

Задача на «3»

1.Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.

Задачи на «4»

2. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

3.Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?

Задача на «5»

4.Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

Вы молодцы!

Каждый из вас «научился тому, что следует знать».

Спасибо за урок!

Раздаточный материал по теме «Основные понятия комбинаторики».

1. Задания к изучению новой темы

№1. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

№2. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

№3. Сколько различных двузначных чисел можно составить из множества цифр, причем так, чтобы цифры числа были различны?

2. Задания на первичный контроль знаний

Комбинаторные задачи:

№1. Сколькими способами можно рассадить 5 человек за столом?

№2. В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

№3. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

3. Задания на закрепление

1 вариант.

Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6?

2 вариант.

4. Задания «Подведение итогов»

1. Определите вид соединений:

а) Соединения из n элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются __________

б) Соединения из m элементов по n, отличающихся друг от друга только составом элементов, называются _______________

в) Соединения из m элементов по n, отличающихся друг от друга составом элементом и порядком их расположения, называются _________

2. Восстановите соответствие типов соединений и формул для их подсчёта

А.	В.	С.

1) сочетания	2) размещения	3) перестановки

5. Домашнее задание

Решить задачу (дифференцированные задачи)

Задача на «3»

1. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.

Задачи на «4»

2. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

3. Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?

Задача на «5»

4. Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

Community — Competitive Programming — Competitive Programming Tutorials в реальных жизненных ситуациях. Множество способов подсчета количества элементов в наборе — одна из основных задач комбинаторики, и в этом уроке я попытаюсь описать некоторые ее основные аспекты. Эти методы используются в ряде приложений, от дискретной математики и теории вероятностей до статистики, физики, биологии и т. д.

Комбинаторные примитивы
Давайте начнем с краткого обзора основных правил и объектов, на которые мы обратимся позже.

Правило суммы

Правило произведения

Например, если у нас есть три города — A, B и C — и есть 5 дорог из A в B и дороги из B в C, то мы можем добраться из A в C через B 3*5=15 различными способами.

Эти правила можно использовать для конечных наборов наборов.

Перестановка без повторения

Когда мы выбираем k объектов из n -элемент, установленный таким образом, что порядок имеет значение, и каждый объект может быть выбран только один раз:

Например, предположим, что мы планируем следующие 3 задачи, и у нас есть набор из 10 простых задач на выбор. В каждом соревновании мы будем использовать только одну простую задачу, поэтому мы можем выбирать задачи по-разному.

Перестановка (вариация) с повторением

Количество возможных вариантов k объектов из набора n объектов, когда важен порядок и один объект может быть выбран более одного раза:

Например, если у нас есть 10 разных призов которые нужно разделить между 5 людьми, мы можем сделать это 510 способами.

Перестановка с повторением

Количество различных перестановок n объектов, из которых n1 неразличимых объектов типа 1, n2 неразличимые объекты типа 2,… и nk неразличимые объекты типа k (n1+n2+…+nk=n), это:

Например, если у нас есть 97 кодировщиков и мы хотим назначить их на 5 комнат (в комнатах 1-4 по 20 кодеров, а в 5-й комнате по 17), то есть возможные способы это сделать.

Комбинации без повторения

В комбинациях мы выбираем набор элементов (а не расположение, как в перестановках), поэтому порядок не имеет значения. Количество различных подмножеств k-элементов (когда каждый элемент можно выбрать только один раз) множества n-элементов равно:

Например, если у нас есть 7 разноцветных шаров, мы можем выбрать любые 3 из них разными способами.

Комбинация с повторением

Допустим, мы выбираем k элементов из n-элементного набора, порядок не имеет значения и каждый элемент может быть выбран более одного раза. В этом случае количество различных комбинаций равно:

Например, допустим, у нас есть 11 одинаковых шаров и 3 разных лузы, и нам нужно посчитать количество различных делений этих шаров на лузы. Были бы разные комбинации.

Полезно знать, что это также число целых решений этого уравнения:

Почему? Это легко доказать. Рассмотрим вектор (1, 1, …, 1), состоящий из (n+k-1) единиц, в котором мы хотим заменить n-1 единицами нули таким образом, чтобы получить n групп единиц (некоторые из которое может быть пустым), а количество единиц в i-й группе будет равно значению xi:

Сумма xi будет равна k, так как после подстановки осталось k единиц.

Основы

Двоичные векторы

Некоторые задачи, и сложные задачи не являются исключением, могут быть переформулированы в терминах двоичных векторов. Соответственно, некоторое знание основных комбинаторных свойств бинарных векторов весьма важно. Давайте посмотрим на некоторые простые вещи, связанные с ними:

1. Количество двоичных векторов длины n: 2n.

2. Количество двоичных векторов длины n и с k ‘1’ равно
.

Мы просто выбираем k позиций для наших единиц.

3. Количество упорядоченных пар (a, b) бинарных векторов, расстояние между которыми (k) можно вычислить следующим образом: .
Расстояние между a и b — это количество компонентов, которые различаются между a и b — например, расстояние между (0, 0, 1, 0) и (1, 0, 1, 1) равно 2).

Пусть a = (a1, a2, …an), b = (b1, b2, …bn) и расстояние между ними равно k. Далее рассмотрим последовательность пар (a1, b1), (a2, b2), … (an, bn). Имеется ровно k индексов i, в которых ai ≠ bi. Они могут быть (0,1) или (1,0), поэтому есть 2 варианта, а n-k может быть либо (0,0), либо (1,1), еще 2 варианта. Для вычисления ответа мы можем выбрать k индексов, в которых векторы различаются способами, затем мы выбираем компоненты, которые отличаются 2k способами, и компоненты, которые равны 2n-k способами (все они используют формулу перестановки с повторением), и в в конце мы просто перемножаем все эти числа и получаем .

Копнем глубже
Теперь давайте рассмотрим очень интересную и полезную формулу, называемую принципом включения-исключения (также известным как принцип решета):

Эта формула является обобщением: различные задачи, которые можно решить с помощью принципа решета, поэтому остановимся на одной из них. Эта проблема наиболее известна как «Психические расстройства». Разложением конечного множества X называется биекция из X в X, не имеющая неподвижных точек. Небольшой пример: для множества X = {1, 2, 3} биекция {(1,1), (2,3), (3,2)} является не расстройством из-за (1,1), а биекцией { (1,2), (2,3), (3,1)} — расстройство. Итак, вернемся к задаче, цель которой — найти количество нарушений n-элементного множества.

Имеем X = {1, 2, 3,…, n}. Пусть:

A множество всех биекций из X в X, | А |= н! ,
A0 — множество всех нарушений X,
Ai ( i ∈ X ) — множество биекций из X в X, которые имеют (i,i),

I ⊆ X

В формуле есть суммы , в нашем случае будет , посчитаем их:

(поскольку существует ровно i-элементных подмножеств X).

Теперь мы просто подставляем этот результат в формулу принципа решета:

И теперь последний шаг, из которого мы получим ответ:

И последнее замечание:

Эта задача может не выглядеть очень удобен для использования в задачах TopCoder, но идея, стоящая за ним, довольно важна, и эти идеи могут найти широкое применение.

Еще один интересный метод комбинаторики — и один из моих любимых из-за его элегантности — называется методом путей (или траекторий). Основная идея состоит в том, чтобы найти геометрическую интерпретацию задачи, в которой мы должны вычислить количество путей специального типа. Точнее, если у нас есть две точки А, В на плоскости с целочисленными координатами, то мы будем оперировать только кратчайшими путями между А и В, которые проходят только через линии целочисленной сетки и что можно сделать только в горизонтальной или вертикальные движения с длиной, равной 1. Например:

Все пути между A и B имеют одинаковую длину, равную n+m (где n — разница между координатами x, а m — разница между координатами y). Мы можем легко вычислить количество всех путей между A и B следующим образом:

или .

Давайте решим известную задачу, используя этот метод. Цель состоит в том, чтобы найти количество слов Дейка длины 2n. Что такое слово Дайка? Это строка, состоящая только из n X и n Y и соответствующая следующему критерию: в каждом префиксе этой строки больше X, чем Y. Например, «XXYY» и «XYXY» — это слова Дайка, а «XYYX» и «YYXX» — нет.

Начнем процесс расчета. Мы собираемся построить геометрический аналог этой задачи, поэтому рассмотрим пути, которые ведут из точки A(0, 0) в точку B(n, n) и не пересекают отрезок AB, но могут касаться его (см. примеры для n =4).

Очевидно, что эти две задачи эквивалентны; мы можем просто построить биекцию так: шаг вправо — «X», шаг вверх — «Y».

Основная идея решения: найти количество путей из A в B, пересекающих отрезок AB, и назвать их «неправильными». Если путь «неправильный», он имеет точки на отрезке CD, где C = (0, 1), D = (n-1, n). Пусть E — ближайшая к A точка, принадлежащая CD (и пути). Просимметрируем AE, часть нашего «неправильного» пути относительно прямой CD. После этой операции мы получим путь из F = (-1, 1) в B.

Нетрудно заметить, что для каждого пути из F в B мы можем построить только один «неправильный» путь из A в B, так что у нас есть биекция. Таким образом, количество «неправильных» путей из А в В равно . Теперь мы можем легко получить ответ, вычитая количество «неправильных» путей из всех путей:

Это число также известно как каталонское число n: Cn — это количество слов Дайка длиной 2n. Эти числа также появляются во многих других задачах, например, Cn подсчитывает количество правильных расположений n пар скобок в выражении, а Cn также является количеством возможных триангуляций многоугольника с (n + 2) вершинами, и скоро.

Использование рекуррентных соотношений
Рекуррентные соотношения, наверное, заслуживают отдельной статьи, но я должен отметить, что они играют большую роль в комбинаторике. В частности, что касается TopCoder, кажется, что большинство вычислительных задач требуют от кодировщиков использования некоторого рекуррентного соотношения и поиска решения для значений параметров.

Если вы хотите узнать больше, ознакомьтесь с этими руководствами: Введение в рекурсию, Рекурсия, часть 2 и динамическое программирование: от новичка до продвинутого. Закончил читать? Давайте посмотрим на некоторые примеры.

ChristmasTree (SRM 331 Division Two — Level Three):

Для решения этой проблемы мы воспользуемся DP — возможно, это не лучший способ решить эту проблему, но его проще всего понять. Пусть cnt[lev][r][g][b] будет количеством возможных способов украсить первые lev уровней дерева, используя r красных, g зеленых и b синих безделушек. Для рекуррентного шага вычисления cnt[lev][r][g][b] рассмотрим 3 варианта:

cnt[lev][r][g][b]=

мы заполняем последний уровень одним цветом (красным, зеленым или синим), поэтому просто:

= cnt [lev-1] [r-lev][g][b]+ cnt[lev-1][r][g-lev][b]+ cnt[lev-1][r][g][b-lev]+ ;

если (lev%2 == 0) мы заполняем последний уровень двумя цветами (красный+зеленый, зеленый+синий или красный+синий), то мы вычисляем количество возможных украшений с помощью Перестановка с повторением формула. Мы получим возможные варианты для каждых двух цветов, поэтому всего

(cnt[lev-1][r-lev/2][g-lev/2][b]+…+cnt[lev-1][r][g-lev/2][b- лев/2])+;

если (lev%3 == 0) мы заполним последний уровень тремя цветами и снова по формуле Перестановка с повторением получим возможные варианты, то получим:

(все cnt[l][i][j][k] с отрицательными индексами равны 0).

DiceGames (SRM 349 Division One — Level Two):

Сначала мы должны немного подготовиться к основной части решения, отсортировав стороны массива в возрастающем порядке и вычисление только тех образований, в которых числа на костях идут в неубывающем порядке. Эта подготовка избавляет нас от необходимости вычислять одни и те же формации несколько раз (дополнительные пояснения см. в SRM 349 – Постановка задач и анализ). Теперь нам нужно только построить рекуррентное отношение, так как реализация довольно проста. Пусть ret[i][j] — количество различных раскладок первых i игральных костей, причем последняя игральная кость равна 9. 0005 j (так что , где n — количество элементов в сторонах ). Теперь мы можем просто написать рекуррентное соотношение:

Ответ будет .

Заключение
Поскольку эта статья была написана для новичков в комбинаторике, основное внимание в ней уделялось основным аспектам и методам счета. Чтобы узнать больше, я рекомендую вам ознакомиться со справочниками, перечисленными ниже, и продолжать практиковаться — как в SRM TopCoder, так и в чисто математических задачах. Удачи!

Каталожные номера:

Холл М. «Комбинаторная теория»
Кэмерон П. Дж. «Комбинаторика: темы, методы, алгоритмы»
en.wikipedia.org 🙂
8 8 9004 Основы комбинаторики — GeeksforGeeks
Комбинаторика — это раздел математики, занимающийся изучением конечных или счетных дискретных структур. Он включает в себя перечисление или подсчет объектов, обладающих определенными свойствами. Подсчет помогает нам решить несколько типов проблем, таких как подсчет количества доступных адресов IPv4 или IPv6.

Принципы подсчета –
Существуют два основных принципа подсчета: правило суммы и правило произведения.
Правило суммы – Если задачу можно выполнить одним из способов или одним из способов, где ни один из наборов способов не совпадает ни с одним из наборов способов, то есть способы выполнить задачу.
Правило продукта — Если задачу можно разбить на последовательность подзадач, где каждая подзадача может выполняться соответственно, то общее количество способов выполнения задачи равно .
- Пример 1 – Сколькими способами можно получить 3 выигрышных приза 3 лучшим игрокам в игре, в которой участвуют 12 игроков?
- Решение – Нам нужно распределить 3 приза между 12 игроками. Эту задачу можно разделить на 3 подзадачи назначения единого приза определенному игроку.
  Выдать первый приз можно 12 различными способами. После выдачи первого приза остается два приза и остается 11 игроков. Точно так же второй приз и третий приз можно получить 11 и 10 способами. Общее количество способов по правилу произведения равно 12 * 11 * 10 = 1320.
- Пример 2 – Сколькими способами человек может выбрать проект из трех списков проектов размеров 10, 15 и 19 соответственно?
- Решение – Человек может выбрать проект из любого из трех списков. Таким образом, человек может выбирать из 10 проектов, 15 проектов или 19 проектов. Поскольку выбор из одного списка отличается от выбора из другого списка, общее количество способов выбора проекта по правилу сумм равно 10 + 15 + 19.= 44.
- Пример 3 – Сколько различных номерных знаков возможно в данном формате – Два алфавита в верхнем регистре, за которыми следуют две цифры, затем дефис и, наконец, четыре цифры. Образец- АВ12-3456.
- Решение – Есть 26 вариантов для каждой из двух букв и 10 вариантов для каждой из цифр. Следовательно, общее количество возможностей равно – 26 * 26 * 10 * 10 * 10 * 10 * 10 * 10 = 676000000.
- Пример 4 – Сколько существует имен переменных длиной до 3, если имена переменных буквенно-цифровые и чувствительны к регистру с ограничением, что первый символ должен быть алфавитом?
- Решение – Обозначим количество возможных имен переменных длины 1, 2 и 3. Следовательно, общее количество имен переменных равно .
  Для есть только 52 возможности, поскольку первый символ должен быть алфавитом.
  Для существует 52 * 62 = 3224 возможности
  Для существует 52 * 62 * 62 = 199888 возможностей
  Следовательно, общее количество имен переменных = 52 + 3224 + 199888 = 203164
Принцип включения-исключения :
8 Упомянутая выше сумма правил 90 что если существует несколько наборов способов выполнения задачи, не должно быть никакого общего способа между двумя наборами способов, потому что, если он есть, он будет учитываться дважды, и перечисление будет неправильным.
Принцип включения-исключения говорит, что для подсчета только уникальных способов выполнения задачи мы должны сложить количество способов выполнить ее одним способом и количество способов выполнить ее другим, а затем вычесть количество способов выполнить задачу, которая являются общими для обоих наборов способов.
Принцип включения-исключения также известен как принцип вычитания . Для двух наборов путей и перечисление будет выглядеть следующим образом:
```
 
```
- Пример 1 – Сколько двоичных строк длины 8 начинаются с бита «1» или заканчиваются двумя битами «00»?
- Решение — Если строка начинается с единицы, остается 7 символов, которые можно заполнить разными способами.
  Если строка заканчивается на «00», то можно заполнить 6 символов способами.
  Теперь, если мы добавим вышеуказанные наборы способов и придем к выводу, что это окончательный ответ, то это будет неправильно. Это связано с тем, что существуют строки, начинающиеся с «1» и заканчивающиеся на «00», и поскольку они удовлетворяют обоим критериям, они учитываются дважды.
  Таким образом, нам нужно вычесть такие строки, чтобы получить правильный подсчет.
  Строки, начинающиеся с «1» и заканчивающиеся на «00», содержат пять символов, которые можно заполнять разными способами.
  Таким образом, по принципу включения-исключения мы получаем:
  Всего строк = 128 + 64 – 32 = 160
- Пример 2 – Сколько чисел от 1 до 1000, включая оба, делятся на 3 или 4?
- Решение – Количество чисел, делящихся на 3 = =.
  Количество чисел, кратных 4 = = .
  Количество чисел, делящихся на 3 и 4 = = .
  Таким образом, количество чисел, кратных 3 или 4 = = 333 + 250 – 83 = 500
Угловые вопросы GATE CS
Реализация следующих вопросов поможет вам проверить свои знания. Все вопросы были заданы в GATE в предыдущие годы или в пробных тестах GATE.
No related posts.