Страница 35 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 35. Математика 3 класс учебник 2 часть. Автор: М.И. Моро.
Решебник — страница 35Готовое домашнее задание
Номер 15.
Найди на рисунке прямые, острые и тупые углы. Выпиши их номера.
Ответ:
Прямые углы: 8, 9, 10, 11, 13, 14, 12, 15. Острые углы: 1, 2, 3, 4, 6. Тупые углы: 5, 7.
Номер 16.
Выполни деление с остатком.
Ответ:
36 : 7 = 5 (ост. 1) 44 : 5 = 8 (ост. 4) 60 : 8 = 7 (ост. 4) 80 : 12 = 6 (ост. 8) 44 : 18 = 2 (ост. 8)
Номер 17.
Запиши по 3 числа, при делении которых на 8 в остатке получается 5; 6; 2; 0.
Ответ:
29 : 8 = 3 (ост. 5)
45 : 8 = 5 (ост. 5)
61 : 8 = 7 (ост. 5)
22 : 8 = 2 (ост. 6)
38 : 8 = 4 (ост. 6)
54 : 8 = 6 (ост. 6)
18 : 8 = 2 (ост. 2)
58 : 8 = 7 (ост. 2)
82 : 8 = 10 (ост. 2)
16 : 8 = 2 (ост. 0)
64 : 8 = 8 (ост. 0)
72 : 8 = 9 (ост. 0)
Номер 18.
Выйдет ли квадратная проволочная рамка со стороной 7 см из треугольной рамки, каждая сторона которой равна 9 см?
Ответ:
Номер 19.
На юношеских соревнованиях по плаванию на 100 м Косте осталось проплыть четвертую часть дистанции, а Вите – пятую ее часть. Кто из них ближе к финишу и на сколько метров?
Ответ:
1) 100 : 4 = 25 (м) – осталось проплыть Косте.
2) 100 : 5 = 20 (м) – осталось проплыть Вите.
3) 25 – 20 = 5 (м) – на столько ближе Витя.
Номер 20.
Ответ:
7 м 8 дм = 78 дм 95 см > 8 дм 9 см 6 дм 5 см < 7 дм 18 мм = 1 см 8 мм
Номер 21.
Что больше и на сколько:
Ответ:
1) 45 : 9 < 42 : 6 8 ∙ 8 > 9 ∙ 7
42 : 6 – 45 : 9 = 2 8 ∙ 8 – 9 ∙ 7 = 1
2) 18 : 2 > 27 : 9 56 : 7 > 24 : 6
18 : 2 – 27 : 9 = 6 56 : 7 – 24 : 6 = 4
Номер 22.
Ответ:
99 : 9 + 32 : 2 = 11 + 16 = 27
96 : 8 + 75 : 5 = 12 + 15 = 27
Номер 23.
1) Ломаная состоит из четырех одинаковых звеньев, длиной 3 см каждое. Найди длину этой ломаной.
Ответ:
1) 4 ∙ 3 = 12 (см) — длина ломаной.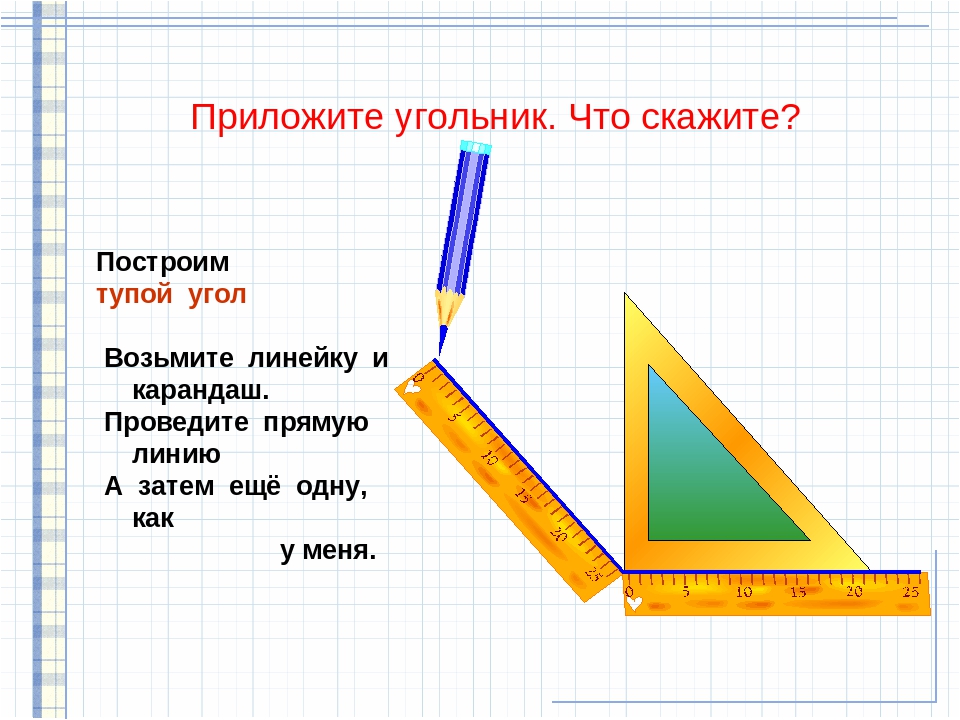
Ответ: 12 см длина ломаной.
2)
Номер 24.
Начерти в тетради пятиугольник, в котором будет 2 прямых угла, 2 тупых и 1 острый угол.
Ответ:
Номер 25.
Переставь карточки так, чтобы равенство стало верным.
Ответ:
96 : 4 = 24
Номер 26.
Найди разными способами площадь данной фигуры.
Ответ:
Ответ: 6 см2 площадь фигуры
РейтингВыберите другую страницу
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
Ваше сообщение отправлено!
+
2d — Решение столкновений с тупыми внутренними углами
Я предполагаю, что вы хотите смоделировать «мяч движется в определенном направлении.
Если он сталкивается с препятствием, он будет скользить вдоль препятствия. Он никогда не будет двигаться против направления». оно движется».
Чтобы решить эту проблему, я сначала притворюсь, что мои две линии, с которыми я сталкиваюсь, бесконечно длинные. Каждая линия описывается как некоторая точка \$p\$, единичный вектор \$u\$ и диапазон кратных этому единичному вектору вдоль линии \$\lambda\$: \$p + \lambda u\$ .
Движение мяча можно описать параметром \$t\$. Если бы не было препятствия, центр шара оказался бы в точке \$x_0 + t v\$ через \$t\$ времени.
Затем я решаю, «при каких \$(t, \lambda)\$-значениях мой мячик пересекает эти бесконечные линии».
Решение задачи «Я (почти) параллелен линии» — это одна из подзадач. Для непараллельных траекторий мы можем найти, когда центр пересекает линию, а затем вычислить, «откатившись», когда это сделал круг.
Мы можем спроецировать скорость нашего мяча вдоль линии с помощью простого скалярного произведения: \$v .
u\$, и его нормальная скорость через векторное произведение \$v x u\$. Разделите величину векторного произведения на радиус мяча, чтобы узнать, как давно (в \$t\$ единицах) мяч впервые коснулся линии. Чтобы найти разницу между центральным столкновением и первым пересечением мячом за \$\lambda\$, умножьте вычисленное значение delta-\$t\$ на \$v . у\$.
Теперь у вас есть интервал вдоль бесконечной линии, когда ваш мяч находится в пределах радиуса линии, а также интервал времени, когда это происходит. Вы на самом деле хотите шариковую линию сегмент пересечение , но это хорошее начало.
Если вас не беспокоит попадание в концы отрезков (и если вы «знаете», что входите в такой угол, это остается в силе), вы можете пропустить проблему с отрезками.
Если вы беспокоитесь, вы должны сделать пересечения мяч-шар на концах сегментов линии и обрезать ваши значения \$t\$ и \$lambda\$ на основе этого.
Обычно вас волнует только то, когда вы впервые попадаете в линию, поскольку вселенная меняется, когда вы это делаете.
Итак, возьмите минимальное положительное t в этом интервале. (если он равен 0, это означает, что вы либо касаетесь линии, либо пересекаетесь с ней).
Начиная с этого момента времени \$t\$, вам будет запрещено скользить по линии, которой вы касаетесь. Будь осторожен! Если вы хотите смоделировать «движение по определенному пути», простое рекурсивное решение с этим новым направлением приведет к странным отскокам. С другой стороны, вы можете захотеть этого — может быть, вы хотите, чтобы столкновение с «круговым разворотом» могло заставить ваш мяч вращаться и лететь в другом направлении.
Предполагая, что вы этого не хотите, вы должны относиться к этому как к ограничению вашей скорости, а не как к новой скорости. Этот ограниченный вектор (по линии) следует за линией (пока не столкнется с ней). И вы сравниваете со всеми другими линиями во вселенной.
Используйте тот же алгоритм, чтобы узнать, с какими другими линиями вы сталкиваетесь, но при определении конечной скорости применяйте каждую линию как ограничение, а не полное перенаправление; не берите начальную скорость, отклоняйтесь по первому ограничению, затем отклоняйте результат по второму (и третьему и т.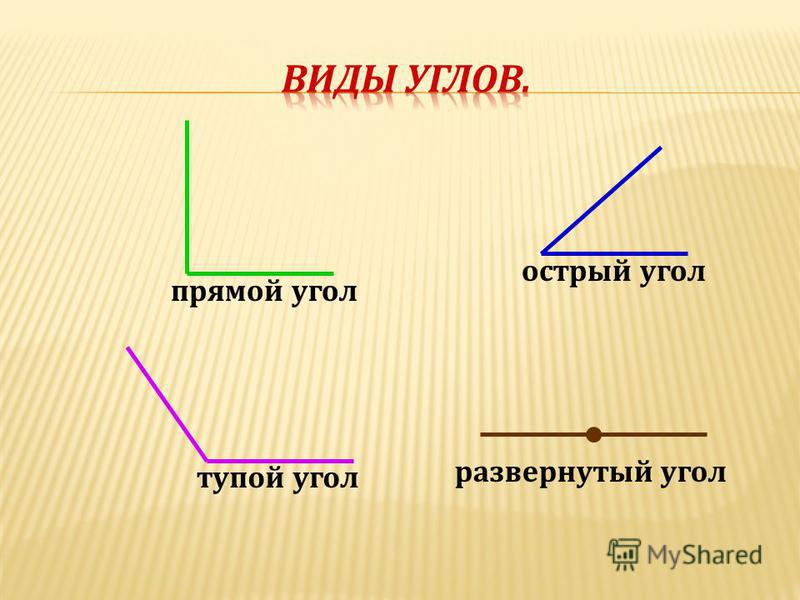
д.), если только вы не играете в бильярд.
Вместо этого у вас есть вектор скорости и куча ограничений «вы не можете двигаться в этом направлении».
Учитывая угол движения шаров, каждое ограничение будет либо слева, либо справа (т. е. оно ударяет по мячу левой или правой стороной, когда тот движется). Если у вас есть ограничение с обеих сторон, ваш мяч останавливается. Если вы этого не сделаете, вы заботитесь только о максимальное ограничение активно, и вы применяете его.
Это позволяет вам попасть в линию справа от вас, а затем в линию, которая толкает вас еще дальше вправо. Только когда ваша левая сторона касается линии, вы останавливаетесь.
Чтобы определить левое и правое, посмотрите на время столкновения; центр мяча и точка на линии, которой касается радиус мяча. Они образуют линию с радиусом мяча, перпендикулярную вектору движения мяча, и позволяют избежать проблемы числовой ошибки округления (ваш мяч касается двух линий, почти полностью параллельных с одной стороны.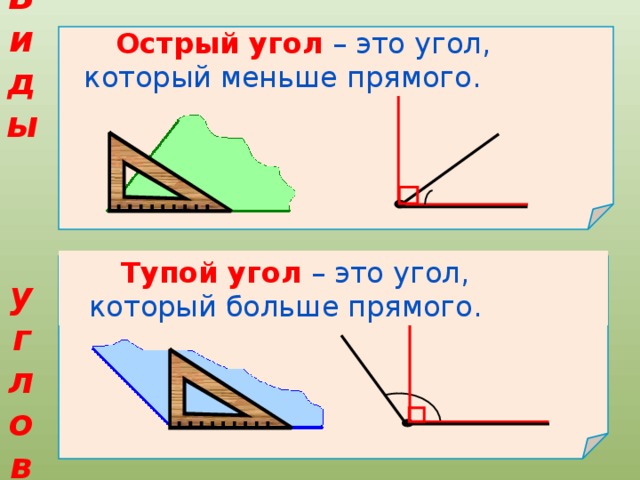
Ошибка с плавающей запятой может поставить их на противоположные стороны, если вы не будете осторожны.)
Kee Safety 55-7 Kee Klamp Колено с тупым углом
Фитинг типа 55 идеально подходит для использования в качестве альтернативы гибке или когда требуется соединение между наклонной трубой и концевой стойкой, например, ограждения и лестницы. .
Компоненты из оцинкованной стали Kee Klamp®
Стальная труба по своей сути является эффективным конструкционным элементом. Он прочный, не имеет острых углов и легко доступен по всему миру. Сложность использования стальной трубы для формирования конструкций возникает при соединении. Труба с резьбой должна поставляться заданной длины, что исключает гибкость при установке. Сварка трудоемкая, требует высококвалифицированной рабочей силы и специального оборудования. Ответ — компоненты KEE KLAMP®. Основополагающий принцип прост, но очень эффективен: используйте надеваемые компоненты для создания универсальных и жестких трубчатых конструкций.
Особенности:
- Высокая коррозионная сопротивление
- Нет сварки или резьбы
- Оцинкованные для длительной защиты
- Уточненные винты для плавного вида
- Краткая инсталляция
- Большие винтовые винты. ® Фитинг
Простой, но эффективный инженерный принцип фитинга Kee Klamp® является основой самой универсальной доступной системы соединения труб. Существует множество вариантов фитингов, подходящих для широкого спектра применений, что обеспечивает универсальность для достижения практически любой структурной конфигурации.
Фитинги Kee Klamp® представляют собой отливки из чугуна, изготовленные в соответствии с требованиями ASTM A47-77-32510. Доступен ряд фитингов для восьми размеров труб. Винты с шестигранной головкой прочно фиксируют трубу в фитинге.
Установочные винты изготовлены из закаленной стали и защищены от коррозии Kee Koat®.
Фитинг Kee Klamp® (размеры от 5 до 9) может выдерживать осевую нагрузку *2000 фунтов. на установочный винт с затяжкой установочного винта с крутящим моментом 29 фунтов/фут. Обычно это достигается при полной затяжке установочного винта с помощью ключа с храповым механизмом.
Компоненты Kee Safety одобрены TÜV, ведущим в Европе независимым испытательным центром. Максимальная нагрузка каждого типа фитингов указана в сертификате TÜV.
| Weight(LBS) | 1.800000 |
|---|---|
| Pipe A Size | 7 |
| Pipe B Size | N/A |
| Pipe C Size | N/ A |
| Размер D | 2,17 дюйма |
| Dimension E | 6. |