Отрицательное минус отрицательное число: Вычитание отрицательных чисел — Kid-mama

Правила сложения отрицательных чисел.

С начала разберем правила сложения отрицательных чисел. Всего таких вариантов 6.

К сожалению, эти все 6 вариантов, не подчиняются одному правилу!

1.1.) Сложение отрицательных чисел

Для двух вариантов, когда 2 слагаемых отрицательные, для них одно правило на двоих :

Правило сложения двух отрицательных чисел звучит так: при сложении двух отрицательных чисел, минус выводится за скобки, числа внутри скобок складываются, и перед суммой остается минус.

1.2.) Правило сложения отрицательного и положительного числа

Второй пункт правил для сложения отрицательного и положительного звучит так : «Если первое отрицательное число a(без минуса), меньше второго слагаемого b, то слагаемые просто меняются местами».

1.3.) Правило сложения положительного и отрицательного числа

Если первое число a больше второго b(без минуса), то знак сложения меняется на минус, и происходит обычное вычитание двух чисел.

Если первое число a меньше второго b(без минуса), то минус выносится за скобки, большое число ставится на первое место, и знак внутри скобок меняется на минус.

Скопировать ссылку

Сложить отрицательное число с отрицательным числом.

Пример сложения двух отрицательных чисел

Для того, чтобы нам сложить два отрицательных числа нам потребуется пример, пусть это будут два числа:

Первое отрицательное число : -15.

Второе отрицательное число : -12.

Далее нам нужно эти два отрицательных числа сложить и это сложение, должно записываться примерно так, второе число записываем в скобках, потому, что оно отрицательное и впереди него есть другой знак :

Далее выносим минус за общую скобку :

Как проверить сложение двух отрицательных числе!?

Скопировать ссылку

Сложить отрицательное число с положительным числом.

Закрепим и рассмотрим эти два правила сложения отрицательного числа на примерах:

Нам нужен опять пример, далеко не будем ходить и пусть это будет вот такое выражение:

Как было уже выше сказано, что это первый вариант, 15 больше 12, т.е, знак выносим за скобки, внутри скобок меняем на противоположный :

Второй пример, вычтем по второму пункту правил :

Видим, что наше первое слагаемое 12 меньше 15, меняем их местами :

Скопировать ссылку

Сложить положительное число с отрицательным числом.

Рассмотрим выше приведенные правила на примерах :

Скопировать ссылку

Сложить отрицательное число с отрицательным числом на калькуляторе.

Набираем число 15.

Делаем его отрицательным с помощью кнопки : «±». нажимаем кнопку плюс : «+»

Набираем число 12.

Делаем его отрицательным с помощью кнопки : «±».нажимаем кнопку равно: «=»

И получаем результат сложения двух отрицательных чисел на калькуляторе :

Скопировать ссылку

Сложить отрицательное число с положительным числом на калькуляторе.

Если в правилах для этого варианта существует два подпункта, то в случае с калькулятором- калькулятору все равно, он посчитает, хоть так, хоть так:

Набираем первое слагаемое 12.

Нажимаем кнопку смены знака -«±».

Нажимаем плюс «+»

Набираем второе число — 15.

Нажимаем равно «=».

Получаем результат сложения отрицательного числа с положительным :

Скопировать ссылку

Сложить положительное число с отрицательным числом на калькуляторе.

Набираем первое число 12.

Далее плюс «+».

Длаее 15.

Нажимаем кнопку смены знака -«±».

Нажимаем равно «=».

Получаем результат сложения положительного и отрицательного числа :

отрицательное число

Отрицательное число — это число, указывающее на противоположное. Если положительное число — это расстояние вверх, то отрицательное — это расстояние вниз. Если положительное число — это расстояние справа, то отрицательное — это расстояние слева. Если положительное число — это депозит на банковский счет, то отрицательное число — это снятие средств с этого банковского счета. Если положительное число — это количество минут в будущем, то отрицательное число — это количество минут в прошлом. Если положительное число означает сложение, то отрицательное — вычитание.

Счетные числа (1, 2, 3 и т.д.) — это все положительные числа. Положительные числа, отрицательные числа и вместе взятое нулевое число называются «знаковыми числами» или целыми числами.

Число ноль не является ни положительным, ни отрицательным. Ноль — это его собственная противоположность, то есть +0 = -0. То есть нулевой шаг вправо — это то же самое, что нулевой шаг влево.

Отрицательное число всегда меньше нуля.

Отрицательное число записывается путем проставления знака минуса «-» перед положительным числом. Например, 3 — положительное число, а -3 — отрицательное. Оно читается как «отрицательная тройка» или «минус тройка»; это означает противоположность знаку 3.

Отрицательные числа в числовой строке оставляют ноль. Число и его противоположность всегда находятся на одном и том же расстоянии от нуля. Отрицательное число -3 находится слева от нуля, а 3 справа от нуля:

Иногда для выделения мы пишем пару противоположных чисел как -3 и +3.

Число и его противоположность всегда складываются к нулю. Таким образом, сумма -3 и +3 равна 0. Можно записать это либо как -3 + 3 = 0, либо как 3 + (- 3) = 0. Кроме того, число и его противоположность говорят, что «аннулируют друг друга».

арифметика с отрицательными числами

• Добавление отрицательного числа к чему-то — это то же самое, что и вычитание положительного числа из него. Например, прибавление отрицательного числа «-1» к числу «9» равнозначно вычитанию одного из девяти. В символах:

9 + (−1) = 9 − 1 = 8

• Вычитание отрицательного числа из чего-то — то же самое, что и добавление к нему положительного числа. Например, вычитание отрицательного числа «-8» из числа «6» равнозначно сложению числа «6» и числа «8». В символах:

6 − (−8) = 6 + 8 = 14

• Отрицательное число, умноженное на другое отрицательное число, дает положительное число. Например, умножить отрицательное число «-3» на отрицательное число «-2» то же самое, что умножить число «3» на число «2». В символах:

(−3) × (−2) = 3 × 2 = 6

• Отрицательное число, умноженное на положительное, дает отрицательное число. Например, умножение отрицательного числа «-4» на положительное число «5» аналогично умножению числа «4» на число «5», но ответ отрицательный. В символах:

(−4) × 5 = −(4 × 5) = −20

Использование отрицательных чисел

Когда человек беден, люди иногда говорят, что у него отрицательная сумма денег. Отрицательные числа используются в бухгалтерии и науке.

Вопросы и ответы

В: Как записывается отрицательное число?
О: Отрицательное число записывается путем постановки знака минус, «-«, перед положительной версией того же числа. Например, 3 — это положительное число, а -3 — его соответствующая отрицательная версия.

В: Что такое знаковые числа?
О: Знаковые числа или целые числа — это множество всех положительных чисел, отрицательных чисел и нуля вместе взятых. Сам ноль не имеет определенного знака, так как его можно рассматривать как свою противоположность; поэтому +0 = -0.

В: Где мы находим отрицательные числа на вещественной прямой?
О: Отрицательные числа находятся слева от нуля на вещественной прямой.

В: Что происходит, когда Вы складываете два противоположных знаковых числа вместе?
О: Когда Вы складываете два противоположных знаковых числа вместе, они всегда аннулируют друг друга и дают в результате 0; например, -3 + 3 = 0 или 3 + (-3) = 0.

В: Есть ли другой способ представить все отрицательные действительные числа?
О: Да, все отрицательные действительные числа можно также представить в виде R-{\displaystyle \mathbb {R} _{-}}. .

Автор

Библиографические ссылки

Вычитание отрицательных чисел Number Talk

Исследуйте вычитание отрицательных чисел, находя разницу в температуре, используя термометр как линию линейного номера модели.

Учащиеся будут изучать вычитание целых чисел в реальных контекстных ситуациях, связанных с повышением и понижением температуры.

Цепочка связанных задач

Представьте следующие предложения на вычитание по одному. Создайте контекст, который побуждает учащихся использовать структуру вычитания различий. Например, температура поднялась с 5 градусов до 12 градусов. Насколько теплее? Температура поднялась до -9градусов до -2 градусов, насколько теплее? Предложите учащимся использовать открытую числовую строку для защиты своего ответа. Смоделируйте мышление студента на открытой числовой прямой.

В этом наборе визуальных числовых подсказок мы рассмотрим первые две (2) из ​​пяти (5) связанных задач из 5-го дня модуля, основанного на задаче «Поднимающаяся вода»:

12–5

7 – 0 

3 – (-4)

-2 – (-9)

-3 – (-10) 

Примечание для ведущего . Первые четыре выражения являются частью строки. Студенты быстро поймут, что все четыре выражения имеют одинаковую разницу, они просто корректируются вниз по числовой строке путем вычитания одинаковой суммы как из уменьшаемого, так и из вычитаемого.

Пятое уравнение уникально. Предложите учащимся скорректировать эти значения по числовой прямой, чтобы защитить свой ответ. Например, если я прибавлю 10 к -3 и -10, мое уравнение будет 7 — 0. 

Учащимся будет предложено:

Составьте предложение с вычитанием, чтобы представить и определить разницу температур. Используйте числовую линию, чтобы защитить свой ответ.

В этом наборе визуальных бесед о числах мы даем учащимся еще одну возможность побороться с вычитанием целых чисел, используя линейный контекст температуры.

Как и в День 3 этого реального математического блока, мы начинаем с повышения температуры от одной положительной температуры до другой положительной температуры, что приводит к положительной разнице.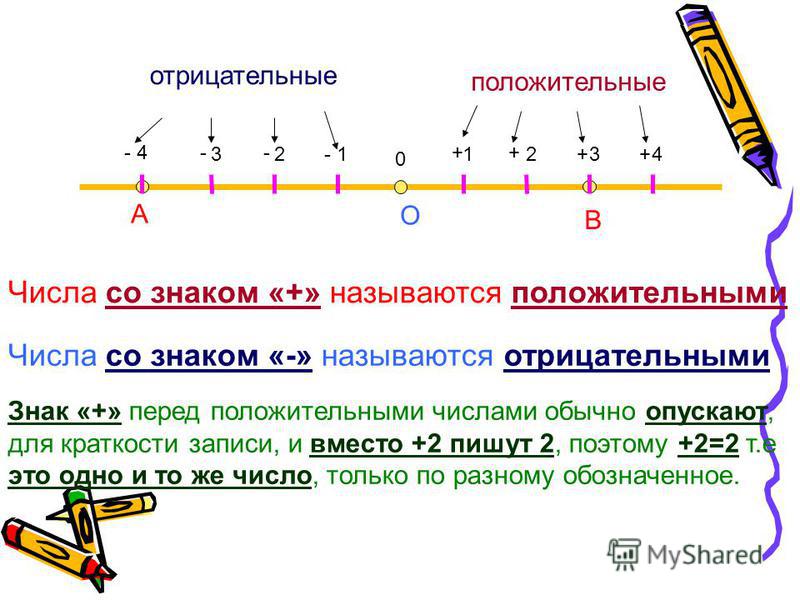 Опять же, мы хотим смоделировать это с помощью числовой прямой, несмотря на то, что большинство студентов твердо знают и понимают, что разница составляет 7 градусов Цельсия, чтобы стимулировать использование инструмента для более сложных различий, которые появятся позже в строке.

Учащимся будет предложено:

Постройте предложение с вычитанием для представления и определения разницы температур. Используйте числовую линию, чтобы защитить свой ответ.

Опять же, учащимся предоставляется очень низкая возможность не только найти разницу между более высокой и более низкой температурой, используя числовую прямую как инструмент для представления своего мышления.

Важно смоделировать мышление учащихся с помощью числовой прямой, чтобы впоследствии они могли использовать числовую инструмент для мышления , когда мы начнем работать с отрицательными температурами.

Стоит отметить, что разница между 7 градусами и 0 градусами такая же, как разница между 12 градусами и 5 градусами.

Предлагайте дополнительные предложения с вычитанием, где разница составляет 7 градусов, например:

3 – (-4)

-2 – (-9)

-3 – (-10)

После этой строки учащиеся должны почувствовать больше начальной температуры, разница должна быть положительной.

Можно ли обобщить правило вычитания целых чисел, когда уменьшаемое больше вычитаемого?

Хотите продолжить изучение этих концепций и навыков?

Доступны три (3) дополнительных подсказки с номером в 5-м дне математического блока, основанного на задаче «Поднимающаяся вода», в который вы можете погрузиться прямо сейчас.

Почему бы не начать с самого начала этого контекстуального 6-дневного блока реальных уроков со страницы «Моменты по математике».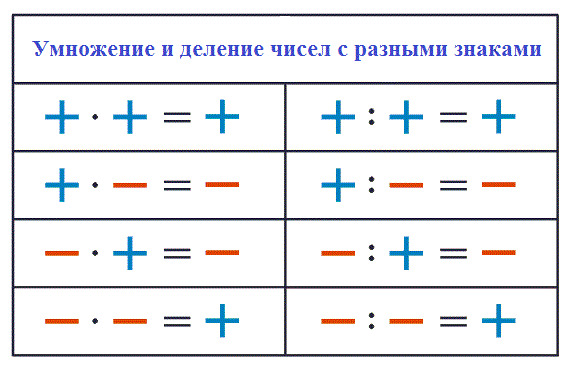

Вы использовали это в классе или дома? Как дела? Пишите в комментариях!

Math IS Visual. Давайте учить так.

Класс 5 Класс 6 Класс 7 Класс 8 Класс 9

Вычитание отрицательных чисел

В этом уроке мы рассмотрим вычитание отрицательных чисел как сложение обратного сложения.

В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.

Тест:

Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!

равнопротивоположноеотрицательноенулевое вычитание

Сумма, аддитивная обратнаяСложение обратная, вычитаниеВычитание, аддитивная обратнаяСумма, вычитание

(-5), 55, (-5)13, ( -13)(-13), 13

-12 — 10 = -210- 12 = -2-2 — 12 = 10

-7-337

-7-337

-7-337

Этот тест включает изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудио описание.

Тест:

Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!

равнопротивоположноеотрицательноенулевое вычитание

Сумма, аддитивная обратнаяСложение обратная, вычитаниеВычитание, аддитивная обратнаяСумма, вычитание

Выберите одну (1) ячейку

-12 — 10 = -210- 12 = -2-2 — 12 = 10

-7-337

-7-337

-7-337

Эти слайды помогут вам выполнить некоторые задания урока. Если вам нужно повторно воспроизвести видео, нажмите значок «Возобновить видео». Если вас попросят добавить ответы на слайды, сначала загрузите или распечатайте рабочий лист. После того, как вы выполнили все задачи, нажмите «Далее» ниже.

В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.

Викторина:

Попробуйте ответить на вопросы ниже!

двадцать восемь то же самое отрицательное нулевое вычитание Противоположное число.

Сложение, сложение, вычитание, сложение, вычитание, вычитание

-15-5-82

9 — (-12)9- 12(-9)-12-9-(-12)

9 — (-12)9- 12(-9)-12-9-(-12)

В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет вам помочь. аудио описание.

Викторина:

Попробуйте ответить на вопросы ниже!

двадцать восемь то же самое отрицательное вычитание нуля

Сложение, сложение, вычитание, сложение, вычитание, вычитание

-15-5-82