Умножение отрицательных и положительных чисел. Умножение отрицательных чисел: правило, примеры
В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.
Правило деления чисел с разными знаками
Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.
Правило деления чисел с разными знаками
При делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.
В буквенном виде это выглядит так:
a ÷ — b = — a ÷ b
A ÷ b = — a ÷ b .
Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.
Еще одна эквивалентная математическая формулировка данного правила имеет вид:
a ÷ b = a · b — 1
Чтобы разделить числа a и b , имеющие разные знаки, нужно число a умножить на число, обратное числу b , то есть b — 1 . Данная формулировка применима на множестве рациональных и действительных чисел, она позволяет перейти от деления к умножению.
Рассмотрим теперь, как применять описанную выше теорию на практике.
Как делить числа с разными знаками? Примеры
Ниже мы рассмотрим несколько характерных примеров.
Пример 1. Как делить числа с разными знаками?
Разделим — 35 на 7 .
Сначала запишем модули делимого и делителя:
35 = 35 , 7 = 7 .
Теперь разделим модули:
35 7 = 35 7 = 5 .
Допишем перед результатом знак минус и получим ответ:
Теперь воспользуемся другой формулировкой правила и вычислим число, обратное 7 .
Теперь проведем умножение:
35 · 1 7 = — — 35 · 1 7 = — 35 7 = — 5 .
Пример 2. Как делить числа с разными знаками?
Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.
Пример 3. Как делить числа с разными знаками?
Разделим смешанное число — 3 3 22 на десятичную дробь 0 , (23) .
Модули делимого и делителя соответственно равны 3 3 22 и 0 , (23) . Переводя 3 3 22 в обыкновенную дробь, получаем:
3 3 22 = 3 · 22 + 3 22 = 69 22 .
Делитель также представим в виде обыкновенной дроби:
0 , (23) = 0 , 23 + 0 , 0023 + 0 , 000023 = 0 , 23 1 — 0 , 01 = 0 , 23 0 , 99 = 23 99 .
Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:
69 22 ÷ 23 99 = — 69 22 · 99 23 = — 3 2 · 9 1 = — 27 2 = — 13 1 2 .
В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д.
В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается. При необходимости вычисляется его приближенное значение с необходимой точностью.
Пример 4. Как делить числа с разными знаками?
Разделим числа 5 7 и — 2 3 .
По правилу деления чисел с разными знаками, запишем равенство:
5 7 ÷ — 2 3 = — 5 7 ÷ — 2 3 = — 5 7 ÷ 2 3 = — 5 7 · 2 3 .
Избавимся от иррациональности в знаменателе и получим окончательный ответ:
5 7 · 2 3 = — 5 · 4 3 14 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.
Деление отрицательных чисел. Правило
Напомним, в чем суть операции деления. Данное действие представляет собой нахождение неизвестного множителя по известному произведению и известному другому множителю. Число с называется частным от деления чисел a и b , если верно произведение c · b = a . При этом, a ÷ b = c .
Правило деления отрицательных чисел
Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.
Пусть a и b — отрицательные числа. Тогда
a ÷ b = a ÷ b .
Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.
Приведем еще одну формулировку данного правила, подходящую для рациональных и действительных чисел. Она дается с помощью взаимно-обратных чисел и гласит: для деления отрицательного числа a на число undefined умножить на число b — 1 , обратное числу b .
a ÷ b = a · b — 1 .
Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками.
Равенство a ÷ b = a · b — 1 можно доказать, используя свойство умножения действительных чисел и определение взаимно обратных чисел. Запишем равенства:
a · b — 1 · b = a · b — 1 · b = a · 1 = a .
В силу определения операции деления, данное равенство доказывает, что есть частное от деления числа на число b.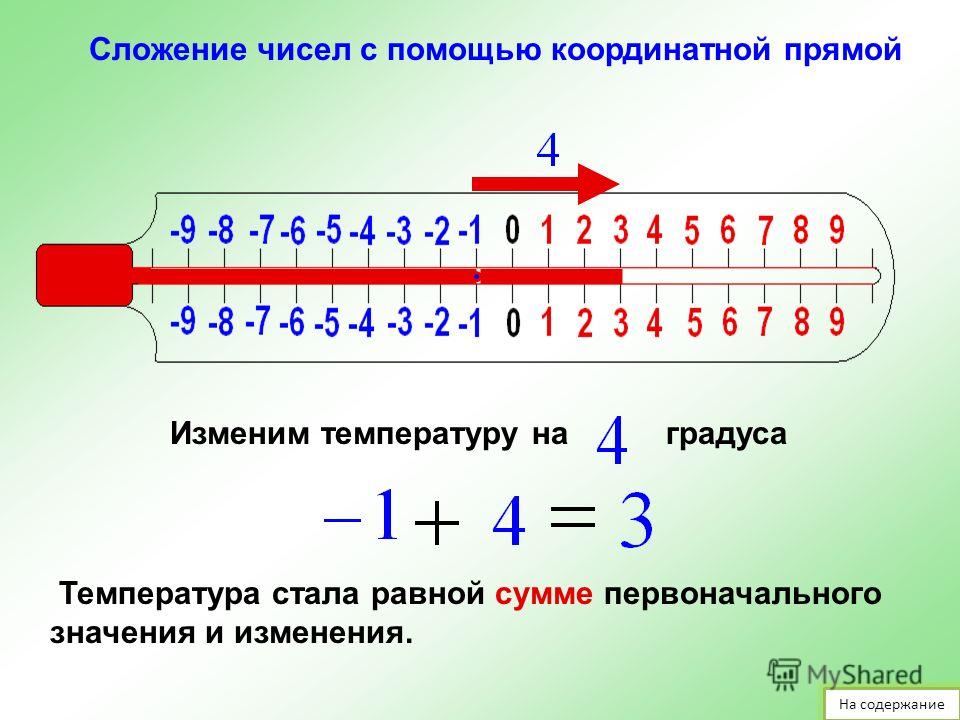
Перейдем к рассмотрению примеров.
Начнем с простых случаяв, переходя к более сложным.
Пример 1. Как делить отрицательные числа
Разделим — 18 на — 3 .
Модули делителя и делимого соответственно равны 3 и 18 . Запишем:
18 ÷ — 3 = — 18 ÷ — 3 = 18 ÷ 3 = 6 .
Пример 2. Как делить отрицательные числа
Разделим — 5 на — 2 .
Аналогично, записываем по правилу:
5 ÷ — 2 = — 5 ÷ — 2 = 5 ÷ 2 = 5 2 = 2 1 2 .
Такой же результат получится, если использовать вторую формурировку правила с обратным числом.
5 ÷ — 2 = — 5 · — 1 2 = 5 · 1 2 = 5 2 = 2 1 2 .
Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.
Пример 3. Как делить отрицательные числа
Разделим — 0 , 004 на — 0 , 25 .
Сначала записываем модули этих чисел: 0 , 004 и 0 , 25 .
Теперь можно выбрать один из двух способов:
- Разделить десятичные дроби столбиком.
- Перейти к обыкновенным дробям и выполнить деление.
Разберем оба способа.
1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.
Ответ: — 0 , 004 ÷ 0 , 25 = 0 , 016
2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.
0 , 004 = 4 1000 ; 0 , 25 = 25 100 0 , 004 ÷ 0 , 25 = 4 1000 ÷ 25 100 = 4 1000 · 100 25 = 4 250 = 0 , 016
Полученные результаты совпадают.
В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.
Пример 4. Как делить отрицательные числа
Вычислим частное от деления чисел — 0 , 5 и — 5 .
0 , 5 ÷ — 5 = — 0 , 5 ÷ — 5 = 0 , 5 ÷ 5 = 1 2 · 1 5 = 1 2 5 = 5 10 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
На этом уроке мы повторим правила сложения положительных и отрицательных чисел.
Также научимся умножать числа с разными знаками и узнаем правила знаков для умножения. Рассмотрим примеры умножения положительных и отрицательных чисел.
Свойство умножения на ноль остается верным и в случае отрицательных чисел. Ноль умножить на любое число — будет ноль.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.
Домашнее задание
- Интернет-портал Mnemonica.ru ().
- Интернет-портал Youtube.com ().
- Интернет-портал School-assistant.ru ().
- Интернет-портал Bymath.net ().
Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?
Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд.
По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
(+ 4) ∙ (+ 5) = + 20.
Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?
Ответ ясен: точка находилась влево от A на расстоянии 20 дм.
Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:
(+ 4) ∙ (– 5) = – 20.
Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?
Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:
(– 4) ∙ (+ 5) = – 20.
Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A.
Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:
(– 4) ∙ (– 5) = + 20.
Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:
1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.
Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).
Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.
Упражнения.
Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.
Чтобы не спутать порядка действий, обратим внимание на формулу
Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить.
Также в формуле
надо сперва число b умножить на c и затем полученное произведение вычесть из a.
Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).
Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).
Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.
Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:
Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:
Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:
Теперь останется выполнить умножение и вычитание:
16. Произведение нескольких множителей. Пусть требуется найти
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).
Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.
Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен
напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),
то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.
Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.
Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:
Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.
Итак, теперь мы легко узнаем, что
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.
(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.
Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.
Удобно, когда имеем дело с дробными числами, находить произведение сразу:
Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.
Сложение и вычитание отрицательных чисел, правила. Урок в 6 классе
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Примеры сложения и вычитания отрицательных чисел (PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 6 класса
Электронная рабочая тетрадь по математике для 6 класса
Интерактивный тренажер к учебнику Виленкина Н.Я.
Ребята, давайте повторим пройденный материал.
Сложение – это математическая операция, после выполнения которой, мы получим сумму исходных чисел (первого слагаемого и второго слагаемого).
Модуль числа – это расстояние на координатной прямой от начала координат до какой-либо точки.
У модуля числа есть определенные свойства:
1.
Модуль числа нуль равен нулю.
2. Модуль положительного числа, например, пяти есть само число пять.
3. Модуль отрицательного числа, например, минус семь есть положительное число семь.
Сложение двух отрицательных чисел
При сложении двух отрицательных чисел, можно использовать понятие модуля. Тогда можно отбросить знаки чисел и сложить их модули, а сумме присвоить отрицательный знак, поскольку изначально оба числа были отрицательными.
Например, необходимо сложить числа: — 5 + (-23)=?
Отбрасываем знаки и сложим модули чисел. Получим: 5 + 23 = 28.
Теперь присвоим полученной сумме знак минус.
Ответ: -28.
Ещё примеры сложения.
-39 + (-45) = — 84
-193 + (-205) = -398
Пример: -0,12 + (-3,4) = -3,52
Сложение положительного и отрицательного чисел
Сложение чисел с разными знаками немного отличается от сложения чисел с одинаковыми знаками.
Рассмотрим пример: 14 + (-29) =?
Решение.
1. Отбрасываем знаки, получаем числа 14 и 29.
2. Из большего по модуля числа вычитаем меньшее: 29 — 14.
3. Перед разностью ставим знак числа, у которого больше модуль. В нашем примере – это число -29.
14 + (-29) = -15
Ответ: -15.Сложение чисел с помощью числовой прямой
Если при сложении отрицательных чисел у вас возникают трудности, то можно использовать метод числовой прямой. Он нагляден и удобен для маленьких чисел.
Например, сложим два числа: -6 и +8. Отметим на числовой прямой точку -6.
Затем переместим точку, обозначающую число -6, на восемь позиций вправо, т.к. второе слагаемое равно +8 и попадем в точку, обозначающую число +2.
Ответ: +2.
Пример 2.
Сложим два отрицательных числа: -2 и (-4).
Отметим на числовой прямой точку -2.
Затем переместим её на четыре позиции влево, т.к. второе слагаемое равно -4 и попадем в точку -6.
Ответ -6.
Этот метод удобен, но он громоздкий, ведь нужно рисовать числовую прямую.
Полосатая пиковая школа
Приносим извинения за неудобства, но страница, на которую вы пытались попасть, находится не по этому адресу. Вы можете использовать приведенные ниже ссылки, чтобы помочь вам найти то, что вы ищете. Если вы уверены, что у вас правильный веб-адрес, но столкнулись с ошибкой, пожалуйста, связаться с Администрацией Сайта. Спасибо. Возможно, вы искали…
|
Смотрите прикрепленный файл.
..- Работает на Plone и Python
- Карта сайта
- Доступность
- Контакт
- Политика конфиденциальности
- Условия обслуживания
Манипулятор для целочисленных операций
Работа с отрицательными целыми числами всегда была камнем преткновения для моих студентов, независимо от того, изучают ли они только отрицательные целые числа или решают уравнения или вычисляют квадратные числа.
Почему?
Отношения между положительными и отрицательными числами скользкие с нечеткими правилами. Когда мы умножаем и делим, у нас есть строгие правила, которые, кажется, очень нравятся конкретным мыслителям. При добавлении и вычитании «правила» становятся намного более абстрактными.
Я разработал этот инструмент как часть своей диссертации, чтобы помочь своим студентам увидеть взаимосвязь между отрицательными и положительными числами, и это значительно сократило количество ошибок, которые они допускали.
Вот краткое видео, показывающее, как работает манипуляция:
Этот манипулятор представлял собой гибкую числовую линию с точкой опоры в нуле. По сути, это позволяло учащимся использовать абсолютные значения чисел, которые они складывали или вычитали, для поиска различий.
Пример:
Если мы используем 7-12 в качестве примера, мы можем думать о 7 и -12 как о целых числах (существительных), а не о двух целых числах с вычитанием (глаголом) между ними.
Это обычно очень хорошо воспринимается студентами, потому что делает цифры более конкретными.
Находим на числовой прямой 7 и -12 и выясняем, какое целое число дальше от нуля. Поскольку -12 дальше, наш ответ будет отрицательным.
Далее идет самое интересное. Как только мы определяем, что наш ответ будет отрицательным, мы складываем числовую прямую пополам.
А затем мы считаем пробелы между двумя числами, чтобы получить 5. Это, в сочетании с нашим предыдущим шагом, дает нам 7 — 12 = -5.
Способность моих студентов работать с отрицательными целыми числами, даже после того, как манипуляции были удалены, улучшилась на 62%, и моя диссертация [в конце концов, после многих, многих правок] была принята в мае 2011 года.
Когда я сижу у доски и возникает задача типа «7 — 12», у меня не всегда есть время остановиться и показать ученикам на линейке, как мы получаем -5.
Итак, я задаю ряд вопросов:
«[В 7 — 12] Какое число дальше от нуля?»
-12
«Хорошо, наш ответ будет отрицательным. Насколько дальше?»
5
«ОК, так что наш ответ будет? …»
-5
Эти вопросы действительно хорошо работают в мгновение. Когда ученики работают над классной работой и у них есть больше времени, я люблю показывать им задачу на линейке, если у них возникают проблемы. Обычно это происходит 1 к 1.
Поскольку манипулятивные методы очень практичны, они позволяют учащимся видеть и чувствовать числа, которые, кажется, всегда лучше запоминаются.
ОБНОВЛЕНИЕ: Я добавил цифровую версию манипуляции, которая работает в Google Slides. Вы можете увидеть, как это работает в этом видео:
youtube.com/embed/14tOebi_p9E»/> Как и манипулятивная версия для печати, цифровая версия работает с абсолютным значением. Учащиеся перетаскивают стрелки к своим двум целым числам и подсчитывают расстояние между ними (сравнивая абсолютные значения двух целых чисел). Простые инструкции напечатаны на слайде.
Вы можете сделать несколько копий слайда, чтобы создать задание для учащихся. Затем они могут использовать числовую прямую для решения целочисленных уравнений.
| Манипуляции с целыми числами — печатные и цифровые |
Если вы обнаружите, что ваши учащиеся испытывают затруднения с операциями с целыми числами, вы можете скачать это пособие по манипуляциям с целыми числами. И печатная, и цифровая версии включены в одну и ту же загрузку. Мне нравится ламинировать версию для печати, чтобы ученики могли писать на ней маркерами.
Это помогает некоторым учащимся вести точный подсчет пробелов между числами.
| Квест-комната для цифровой математики с целыми числами |
Чтобы удовлетворить потребности классов с технологиями, я создал квест-комнаты для цифровой математики, такие как эта, для сложения и вычитания целых чисел. В каждом квесте ученики должны открыть 5 замков, ответив на 20 вопросов. В этой квест-комнате с целыми числами учащиеся должны объединить три целых числа в каждой задаче
| Целочисленные математические вымпелы |
Вам может понравиться этот математический вымпел с целыми числами для забавного занятия с целочисленными операциями, которое можно использовать в качестве декора для классной комнаты, созданного учениками.