Парабола график функции y ax2 bx c: Квадратичная функция y = ax² + bx + c. Алгебра, 8 класс: уроки, тесты, задания.

alexxlab / / Разное

Функция y=ах2+bx+c, ее свойства и график

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. ФУНКЦИЯ y=ах2+bx+c, ЕЕ СВОЙСТВА И ГРАФИК

2
ФУНКЦИЯ y=ах +bx+c,
ЕЕ СВОЙСТВА И ГРАФИК
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
Квадратный трехчлен
ax 2 bx c
a, b, c – числа (коэффициенты), a 0.
ах2 – старший член квадратного трехчлена.
а – старший коэффициент квадратного трехчлена.
3 x 2 2 x a = 3, b = 2, c = 0.
Функцию y ax 2 bx c, где a, b, c – произвольные
числа, причем a 0, называют квадратичной функцией.
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
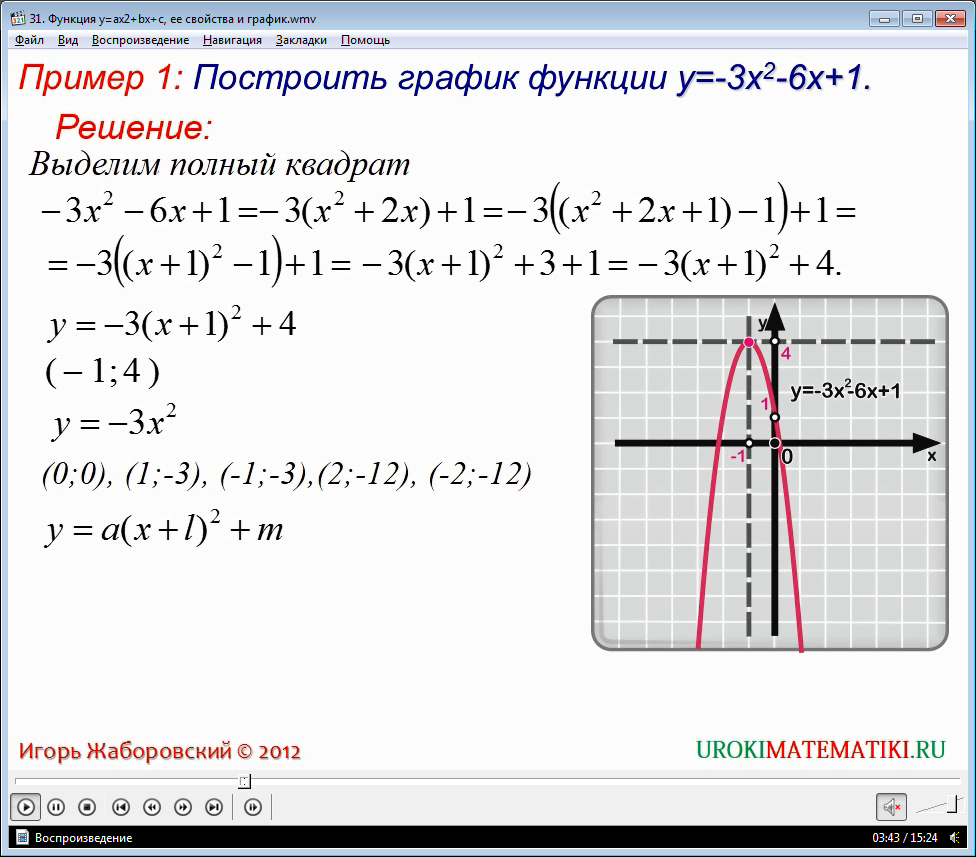
Пример 1: Построить график функции y=-3×2-6x+1.
Решение:
Выделим полный квадрат
3x 2 6 x 1 3( x 2 2 x) 1 3 ( x 2 2 x 1) 1 1
3 ( x 1) 2 1 1 3( x 1) 2 3 1 3( x 1) 2 4.
y 3( x 1) 2 4
( 1;4)
y 3x 2
(0;0), (1;-3), (-1;-3),(2;-12), (-2;-12)
y a( x l ) 2 m
График любой квадратичной
функции y=ax2+bx+c можно
получить из параболы y=ax2
параллельным переносом.
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
Теорема: Графиком квадратичной функции y=ax2+bx+c
является парабола, которая получается из параболы
y=ax2 параллельным переносом.
Доказательство:
Метод выделения полного квадрата
b
2
2
2
ax bx c (ax bx) c a( x x) c
a
2
2
2
2
2
b
b b
b
b
a
x
a x 2 x 2
c
c
2
2a
4a 4a
2a 4a
2
b 4ac b 2
a x
.
2a
4a
ax 2 bx c a x l 2 m,
Игорь Жаборовский © 2012
b
l ,
2a
4ac b 2
m
.
4a
UROKIMATEMATIKI.RU
Теорема: Графиком квадратичной функции y=ax2+bx+c
является парабола, которая получается из параболы
y=ax2 параллельным переносом.
Доказательство:
2
y a x l m
y ax 2
( l ; m)
y ax 2 bx c
b
x l ; x .
2a
b
Осью параболы
служит прямая x
;
2a
2
абсцисса х0 вершины параболы y=ax +bx+c вычисляется
2
b
4
ac
b
по формуле
x0 . y0
.
2a
4a
y=ax2+bx+c
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
Пример 2: Не выполняя построения графика функции
y=-3×2-6x+1, ответить на следующие вопросы:
а) Какая прямая служит осью параболы?
б) Каковы координаты вершины параболы?
в) Куда (вверх или вниз) направлены ветви параболы?
Решение:
а) a 3, b 6
b
x , x 1.
2a
б) x0 1,
y0 f ( x0 ) f ( 1) 4.
( 1;4)
2
y
3
x
6x 1
в)
y 3x 2
Игорь Жаборовский © 2012
UROKIMATEMATIKI. RU
Ветви параболы y=ax2+bx+c направлены вверх,
если а>0, и вниз, если a<0.
b
x
2a
b
x0 ,
2a
y0 f ( x0 ), f ( x) ax 2 bx c
4ac b 2
y0
.
4a
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
Пример 3: Построить график функции y=2×2-6x+1.
Решение:
2 – положительное число
a 2, b 6,
b
6
x0
1,5.
2a
2 2
2
f
(
x
)
2
x
6x 1
y0 f ( x0 ) f (1,5),
y0 f (1,5) 2 1,5 6 1,5 1 3,5.
2
(1,5; 3,5)
x 0, x 3, f (0) f (3)
f (0) 1,
f (3) 1
(0;1), (3;1)
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU
Алгоритм построения параболы y = аx2 + bx + c :
1. Найти координаты вершины параболы, построить на
координатной плоскости соответствующую точку,
провести ось параболы.
2. Отметить на оси х две точки, симметричные
относительно оси параболы (чаще всего в качестве одной
из таких точек берут точку х=0), найти значения
функции в этих точках; построить на координатной
плоскости соответствующие точки. 2+4x-3$ на отрезке $[-5;2]$.

Биоматематика: квадратичные функции

Определение и символическое представление

Квадратичные функции могут быть представлены символически уравнением,

у ( х ) = ах 2 + бх + с ,

, где a , b и c — константы, а a ≠ 0. Эта форма называется стандартной. Коэффициент

a в этой форме называется старшим коэффициентом, потому что он связан с наибольшей степенью x (т. е. квадратом члена).

Графическое представление

Квадратичные функции — это нелинейные функции, графически представленные параболами. Параболы имеют характерную ∪-форму и открываются либо вверх, либо вниз, как показано ниже,

На эти графики следует обратить внимание:

  • Нижняя точка параболы, которая открывается вверх, называется вершиной параболы. Термин вершина также относится к высшей точке параболы, которая открывается вниз.
  • Параболы симметричны относительно вертикальной линии, проходящей через вершину. Параболы, открывающиеся вверх, слева от вершины уменьшаются, а справа от вершины возрастают. Параболы, открывающиеся вниз, увеличиваются слева от вершины и уменьшаются справа от вершины.
  • Хотя вершина находится в начале координат на каждом из этих графиков, важно понимать, что вершина параболы не обязательно должна находиться в начале координат или лежать на одной из осей.

 

Стандартная форма дает представление о том, как будет выглядеть график квадратичной функции.

Анализируя квадратное уравнение в стандартной форме,

у ( х ) = ах 2 + бх + с ,

вы можете получить представление о том, как будет выглядеть график. Старший коэффициент говорит вам, в каком направлении открывается парабола, а именно

.

если a > 0, парабола открывается вверх

, если a < 0, парабола открывается вниз.

Кроме того, константа c является точкой пересечения y квадратичной функции. Этот факт можно вывести математически, установив x = 0 (помните, что точки, лежащие на оси Y, должны иметь координату x , равную нулю) в стандартной форме квадратного уравнения, что дает

y (0) = a · 0 2 + b · 0 + c

y (0) = c .

Обратите внимание, что квадратичная функция всегда будет пересекать ось y , но может не пересекать ось x (позже мы обсудим эту тему более подробно).

Наконец, изучив стандартную форму квадратного уравнения, вы увидите, что областью определения квадратных функций являются все действительные числа (т.

е. нет значения x , которое нельзя было бы подставить в уравнение y ( x ) = ах 2 + bx + c ). Однако диапазон квадратичных функций составляет , а не всех действительных чисел, а скорее варьируется в зависимости от формы кривой. В частности,

  • Для квадратичной функции, открывающейся вверх, диапазон состоит из всех y , больших или равных y -координата вершины.
  • Для квадратичной функции, открывающейся вниз, диапазон состоит из всех y меньше или равно y -координата вершины.

Пример

Простейшая квадратичная функция задается как

y = x 2 . Чтобы построить график этой функции вручную, вы можете использовать следующую таблицу значений:

Изучив эту таблицу значений, вы увидите, что функциональные значения симметричны относительно вертикальной линии x = 0. Вы можете нанести эти точки на плоскость xy- и провести через них плавную кривую, чтобы сформировать параболу, как показано ниже,

 

*****

В следующем разделе мы рассмотрим, как найти вершину параболы.

Вершина квадратичной функции

Как найти точку поворота параболы?

Когда квадратное уравнение представлено графически в виде буквы U, оно называется параболой. Парабола также может быть определена как плоская кривая, где любая точка на этой кривой равноудалена от фиксированной точки, фокуса. Точка поворота любой кривой или параболы — это точка, в которой ее направление меняется с восходящего на нисходящее или наоборот. Точка поворота параболы называется вершиной. Стандартная форма параболы: y = ax 2 + бх + в. Форма вершины параболы с вершиной (h, k) равна y = a(x – h) 2 + k.

 

Точка поворота параболы

Чтобы получить точку поворота или вершину (h, k) параболы, мы можем преобразовать это уравнение в форму вершины параболы: y = a(x – h) 2 + к.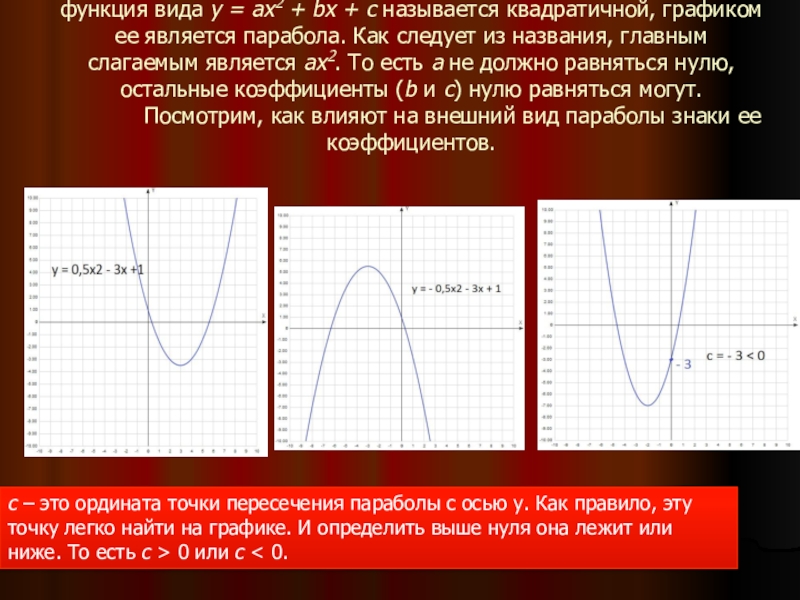 Мы можем сделать это, используя метод «Завершение квадратов».

  • Вычтите c из левой и правой сторон.

y – c = ax 2 + bx

  • Возьмем «a» в качестве общего множителя в правой части.

y – c = a(x 2 + (b/a)x)

  • Добавьте член a(b / 2a) 2 как к правой, так и к левой стороне.

y – c + (b 2 /4a) = a(x 2 + (b/a)x + (b/2a) 2 )

  • Теперь уравнение на RHS имеет вид форма (м + п) 2 .

у – (с + (б 2 /4а)) = а(х + (б/2а) 2 )

Сравнивая это уравнение с вершинной формой параболы, мы можем наблюдать следующую связь между значениями a, b, c и h, k.

Vertex (H, K) = (-B /2A, C-(B 2 /4A))

Проблемы выборки

Проблем уравнение y = 5x 2 + 3x + 2.

Решение:

Дано, y = 5x 2 + 3x + 2: a = 5 b = 3 c = 2

Используя приведенную выше формулу, (h, k) = (-b/2a, c – (b 2 /4a))

⇒ h = -3/(2 × 5) = -3/10 = 0,3 

⇒ k = 2 – (3 × 3)/(4 × 5) = 2 – (9/20) = 1,55 

Итак, (h, k) = (0,3, 1,55)

Задача 2. Для функции F(x) = 7x 2 + 5x + 8 найти значение x, при котором оно возрастает.

Решение:

Уравнение 7x 2 + 5x + 8 имеет форму параболы.

Где, a = 7, b = 5 и c = 8

Мы знаем, что при a > 0 парабола имеет восходящее или возрастающее направление при x > h.

Используя приведенную выше формулу, (h, k) = (-b/2a, c – (b 2 /4a))

⇒ h = -5/(2 × 7) = -5/14 = -0,357

Итак, функция возрастает при (x > -0,357)

Задача 3: Каково минимальное значение функции y = 3x 2 + 8x + 1?

Решение:

Уравнение y = 3x 2 + 8x + 1 имеет форму параболы.

Где, a = 3, b = 8 и c = 1

Мы знаем, что при a > 0 парабола имеет минимальное значение в вершине.

Используя приведенную выше формулу, вершина V (h, k) = (-b/2a, c – (b 2 /4a))

⇒ h = -8/(2 × 3) = -8/ 6 = -1,33

⇒ k = 1 – (8 × 8/(4 × 3)) = 1 – (64/12) = -4,33

Следовательно, минимальное значение функции находится при (-1,33, — 4. 33).

Задача 4. Найти точку поворота параболы, определяемой уравнением y = 1x 2 + 2x + 3.

Решение:

Дано, y = 1x 2 + 2x + 3,

 a = 1  

 b = 2  

 c = 3

Используя приведенную выше формулу, точка поворота или вершина равна

(h, k) = (-b/2a, c – ( b 2 /4a))

⇒ h = -2/(2 × 1) = -1

⇒ k = 3 – (2 × 2/4) = 2

Итак, (h, k) = (-1, 2)

Задача 5. Для заданной функции F(x) = -2x 2 + 2x + 1 найти значение x, для которого она уменьшение.

Решение:

Уравнение -2x 2 + 2x + 1 имеет форму параболы.

Где, a = -2, b = 2 и c = 1

Мы знаем, что при a < 0 парабола имеет нисходящее или убывающее направление при x > h.

Используя приведенную выше формулу,

(h, k) = (-b/2a, c – (b 2 /4a))

⇒ h = -2/(2 × (-2)) = 1/2 = 0,5

Итак , функция возрастает при (x > 0,5).

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *