Преобразовать в Десятичные градусы (DD)
Быстро конвертируйте широту и долготу в формат Десятичные градусы (DD)
На базе aspose.com и aspose.cloud
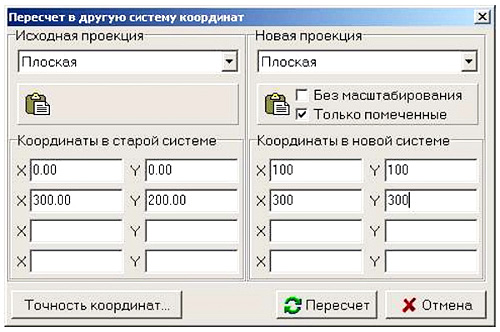
Преобразовать координаты
Разобрать текст
Преобразовать координаты
Широта:
Долгота:
Разобрать координаты
Положение:
Форматировать как
Gpx Viewer онлайн Конвертировать GPX в KML Преобразовать Координаты Изображения с Геотегами
Мы уже обработали файлов общим размером МБ
Aspose.Gis Coordinates FacebookПоделиться в Facebook Поделиться в Facebook
Aspose.Gis Coordinates TwitterПоделиться в Twitter Поделиться в Twitter
Aspose.Gis Coordinates LinkedInПоделиться в LinkedIn Поделиться в LinkedIn
Aspose. Gis CoordinatesДругие приложения
Другие приложения
Gis CoordinatesДругие приложения
Другие приложения
Aspose.Gis Coordinates GitHubGitHub GitHub
GIS Конвертер координат
Обзор
- Инструкция
- Вопросы
Преобразовать координаты в Десятичные градусы (DD)
Преобразовать координаты в Десятичные градусы (DD) strong > преобразует введенные координаты в систему Десятичные градусы (DD) . Просто введите свою широту и долготу и нажмите кнопку «Преобразовать». Наше приложение автоматически распознает вашу систему координат и преобразует их в желаемую.
Это бесплатное онлайн-приложение для преобразования предоставляется Aspose.Gis. Мы даем вам возможность получать доступ и управлять географической информацией из векторных форматов геопространственных данных. API поддерживает чтение, запись и преобразование большинства популярных форматов файлов ГИС, таких как Shapefile, GeoJSON, FileGDB, KML и OSM XML, а также отображение карты из поддерживаемых форматов в SVG.
Десятичные градусы (DD) выражают географические координаты широты и долготы как десятичные доли градуса. DD используются во многих географических информационных системах (ГИС), веб-картографических приложениях, таких как OpenStreetMap, и устройствах GPS.
Read More
Как преобразовать координаты в Десятичные градусы (DD) с помощью Convert Coordinates
- Чтобы преобразовать координаты, выберите режим «Преобразовать координаты» на панели рабочего режима.
- Введите широту и долготу в соответствующие поля Широта и Долгота.
- Выберите желаемый формат.
- Нажмите кнопку «Преобразовать», и результат отобразится на карточке «Преобразованные координаты» в поле «Положение».
- Чтобы проанализировать данные, выберите режим анализа текста на панели рабочего режима.
- Вставьте строку в поле «Позиция» на карточке «Анализ координат».

- Нажмите кнопку «Анализировать», и результат отобразится на карточке «Преобразованные координаты» в соответствующих полях.
Вопросы
С более подробной информацией вы можете ознакомиться перейдя convert to dd
-
❓ Как я могу преобразовать свои координаты в разные форматы?
Сначала выберите режим работы «Преобразовать координаты». Затем введите широту и долготу в соответствующие поля в разделе «Преобразовать координаты». Далее выберите желаемый формат, в который будут преобразованы ваши координаты. Затем просто нажмите «Конвертировать» и дождитесь результата конвертации. Когда координаты преобразованы, результат будет отображаться в разделе «Преобразованные координаты».
-
❓ Как я могу получить координаты из строки?
Сначала выберите режим работы «Анализ текста».
 Затем введите строку в поле «Позиция». Затем нажмите кнопку «Разобрать» и дождитесь завершения процесса. Координаты отображаются в окне Разобранное положение.
Затем введите строку в поле «Позиция». Затем нажмите кнопку «Разобрать» и дождитесь завершения процесса. Координаты отображаются в окне Разобранное положение.
-
❗ Могу ли я увидеть преобразованные координаты на карте?
Да, ты можешь! После получения результата появится кнопка «Открыть карту». Если вы нажмете на эту кнопку, откроется карта с вашими координатами.
-
❗ Нужно ли указывать ожидаемый формат для анализа координат?
Нет необходимости. Наше приложение автоматически определит формат.
-
📁 Какие форматы поддерживаются?
Мы поддерживаем десятичные градусы (DD), градусы минут и секунд (DMS), десятичные градусы минут (DDM), GeoRef, USNG, MGRS.

-
💻 Могу ли я конвертировать и анализировать координаты в Linux, Mac OS или Android?
Да, вы можете использовать бесплатное приложение «Координаты» в любой операционной системе, в которой есть веб-браузер. Наш конвертер работает онлайн и не требует установки программного обеспечения.
-
🌐 Какой браузер использовать для преобразования/анализа координат?
Для преобразования/анализа координат вы можете использовать любой современный браузер, например, Google Chrome, Firefox, Opera, Safari.
Другие поддерживаемые преобразования и синтаксический анализ координат
Вы также можете преобразовать координаты, используя многие другие пространственные привязки. См. cписок популярных ниже.
См. cписок популярных ниже.
Версия: 22.34.2
(Заметки о выпуске)
Email:
Сделайте этот форум закрытым, чтобы он был доступен только вам и нашим разработчикам
Вы успешно сообщили об ошибке, Вы получите уведомление по электронной почте, когда ошибка будет исправлена
Новый взгляд на координаты точек. Перевод чисел из различных систем счисления в десятичную и обратно
- Копытова Светлана Алексеевна, учитель информатики
Разделы: Информатика
Ещё один способ перевода чисел из десятичной
системы счисления в двоичную систему
заключается в подборе чисел, которые должны
входить в состав ряда степеней двойки, и,
просуммировав которые, мы получим заданное
десятичное число.
Ещё раз запишем полученные результаты степень
двойки по возрастанию для лучшего визуального
восприятия данного ряда чисел:
Рассмотрим этот способ перевода на конкретном примере: переведём число 567 из десятичной системы счисления в двоичную систему.
Видно, что первое значение, которое входит в ряд степеней двойки и меньше заданного числа 567, это 512. Записываем 1 для данного разряда и выполняем вычитание: 567512.
Получилось число 55. Следующее число, входящее в
заданный ряд и меньшее теперь уже числа 55 это 32:
в соответствующем данному числу разряде тоже
надо поставить 1. Но между 512 и числом 32
располагаются в записанном нами ряду степеней
двойки числа 64, 128, 256. Мы их не можем миновать
просто так и оставить без внимания: запишем в
соответствующих им разрядах нули. Итого, запись
нашего двоичного числа преобразуется уже в
следующий вид: 10001 (первая единица соответствует
512ти, нули 256, 128, 64, и последняя единица 32м)
 Следующее после 32
число 16 сразу подходит нам, так как оно меньше 23.
Следовательно, в разряде, соответствующем 16, мы
тоже записываем 1. Двоичное число приобретает
вид: 100011.
Следующее после 32
число 16 сразу подходит нам, так как оно меньше 23.
Следовательно, в разряде, соответствующем 16, мы
тоже записываем 1. Двоичное число приобретает
вид: 100011.Вновь выполняем действие: 2316=7. Следующее, подходящее для результата число ряда это 4. В разряде, соответствующем числу 8 (которое мы миновали), мы ставим 0, а в разряде, соответствующем 4, пишем 1. Двоичное число приобретает вид: 10001101.
Вновь выполняем действие: 74=3. Следующее подходящее число 2 . Ставим в соответствующем разряде 1.
Выполняем действие: 32=1. Ставим последнюю единицу в разряде, соответствующем 1. Законченная запись числа приобретает вид: 1000110111.
Все объяснения можно было свести к следующей записи:
1 0 0 0 1 1 0 1 1 1
512 256 128 64 32 16 8 4 2 1
из которой явственно видно, суммированием
каких чисел ряда степеней двойки можно получить
заданное число 567. Над нужными числами стоят 1, над
числами, не используемыми при суммировании,
ставится 0.
Ну а теперь, для закрепления, переведём число 736 в двоичную систему счисления:
1 0 1 1 1 0 0 0 0 0
512 256 128 64 32 16 8 4 2 1
При изучении темы о переводе чисел различных систем счисления перед преподавателями возникает проблема как заинтересовать учащихся процессом перевода: ведь просто выполнять арифметические действия представляется малоинтересным. Можно предложить им задание на закрепление, суть которого заключается в переводе координат точек, представленных в недесятичных системах счисления, в их обычный десятичный вид записи числа. Затем эти координаты использовать при построении рисунка в графическом редакторе Microsoft Paint (на рис.1 представлена сетка для построения, которую учитель должен приготовить заранее).
Перевод чисел двоичной, восьмеричной, шестнадцатеричной систем счисления в десятичную систему (варианты заданий)
Вариант №1
Координаты точек представлены в
недесятичной системе счисления. Выполните
перевод координат в десятичную систему
счисления и отметьте точки на координатной
плоскости. Правильно сделав перевод и соединив
последовательно все точки, получите некий
рисунок.
Выполните
перевод координат в десятичную систему
счисления и отметьте точки на координатной
плоскости. Правильно сделав перевод и соединив
последовательно все точки, получите некий
рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
X |
100002 |
11102 |
11102 |
11002 |
11002 |
11012 |
11102 |
11102 |
1116 |
1416 |
1416 |
1516 |
Y |
1002 |
1002 |
102 |
102 |
10102 |
11002 |
10102 |
101102 |
1816 |
1616 |
А16 |
С16 |
продолжение таблицы
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
X |
1616 |
1616 |
1416 |
248 |
228 |
228 |
208 |
208 |
218 |
228 |
228 |
Y |
А16 |
216 |
216 |
48 |
48 |
28 |
28 |
128 |
148 |
128 |
48 |
Результат построения на рис. 2
2
Вариант №2
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
X |
10102 |
10002 |
100102 |
100102 |
11102 |
228 |
128 |
128 |
228 |
Y |
102 |
10002 |
1102 |
101102 |
101012 |
248 |
208 |
148 |
108 |
продолжение таблицы
10 |
11 |
12 |
13 |
14 |
15 |
|
X |
168 |
1216 |
1216 |
1С16 |
1А16 |
А16 |
Y |
168 |
1416 |
616 |
816 |
216 |
216 |
Результат построения на рис. 3
3
Вариант №3
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
X |
100002 |
100002 |
10102 |
100002 |
11002 |
208 |
168 |
228 |
Y |
102 |
1002 |
1002 |
10102 |
10102 |
168 |
168 |
248 |
продолжение таблицы
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
X |
268 |
248 |
1816 |
1416 |
1А16 |
1416 |
1416 |
1016 |
Y |
168 |
168 |
А16 |
А16 |
416 |
416 |
216 |
216 |
Результат построения на рис.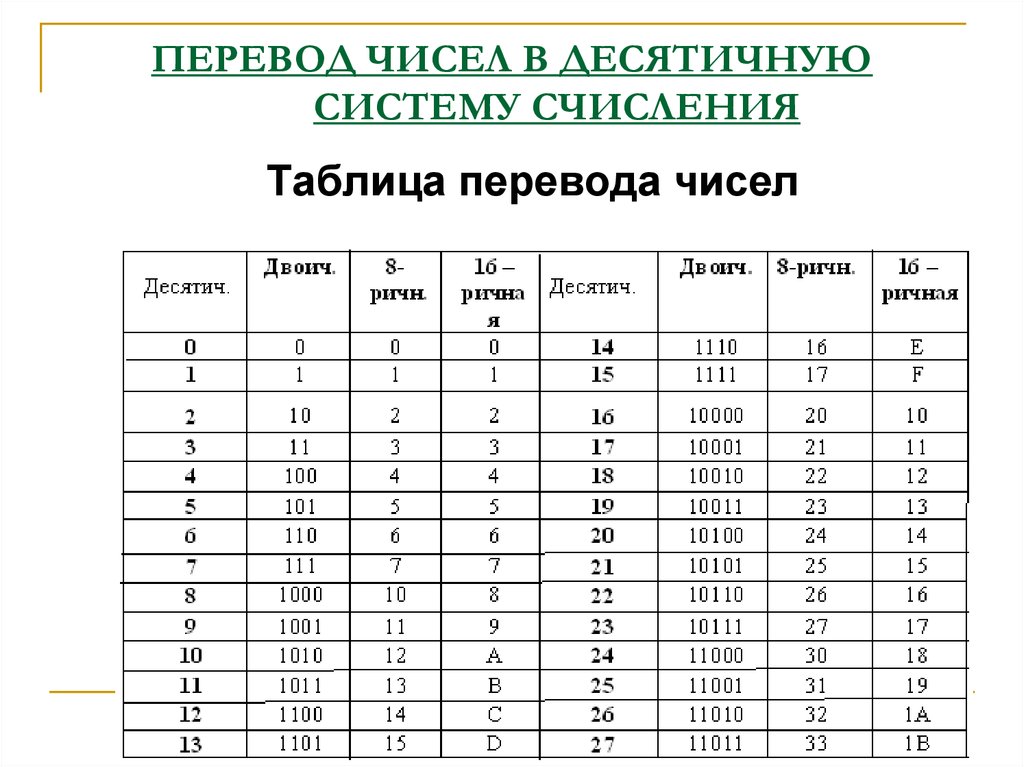 4
4
Вариант №4
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
X |
1102 |
10102 |
100002 |
100102 |
1416 |
1616 |
1416 |
1316 |
1A16 |
Y |
11102 |
100002 |
11102 |
11112 |
F16 |
E16 |
E16 |
D16 |
816 |
продолжение таблицы
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
X |
1D16 |
348 |
348 |
328 |
158 |
138 |
11002 |
10002 |
1102 |
Y |
916 |
78 |
48 |
68 |
118 |
108 |
10102 |
11002 |
11102 |
Результат построения на рис. 5
5
Перевод чисел из десятичной системы счисления в двоичную
Цели урока:
Обучающая
Обобщить способ перевода десятичных чисел в двоичную систему счисления, двоичных чисел в десятичную систему счисления, расширить представления учащихся о возможностях приложения Калькулятор.
Развивающая
Продолжить развитие у учащихся умения самостоятельно делать выводы, обосновывать и высказывать свое мнение.
Воспитывающая
Продолжить формирование навыков самостоятельной работы на компьютере. Развивать культуру общения, умение работать в паре.
Задачи:
Повторить способ перевода десятичных чисел в двоичную систему счисления, показать другие способы перевода двоичных чисел в десятичную систему счисления: использование приложения Калькулятор, перевод чисел в программе Excel
Оборудование:
Презентация к данному уроку, компьютер, мультимедийный проектор
Карточки
Тип урока:
Комбинированный урок
Форма работы: фронтальная, групповая, индивидуальная.
Знания и навыки учащихся:
Уметь переводить целые десятичные числа в двоичную систему счисления и обратно. Умение работать на компьютере с приложением Калькулятор.
Ход урока
1.Организационный момент.
2.Актуализация опорных знаний учащихся.
Учитель:
Здравствуйте. На прошлых занятиях мы занимались с вами Перевод чисел из десятичной системы счисления в двоичную и наоборот, используя алгоритм перевода. Какие возникли у вас вопросы при выполнении домашнего задания?
(Проверка домашнего задания. Выяснить, какие задания вызывали затруднения, какие вопросы возникли у учеников. )
Давайте вспомним некоторые понятия. Скажите, пожалуйста, что такое система счисления?
Ответ: система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса:
Учитель: А, что такое алфавит системы счисления?
Ответ: знаки, с помощью которых записываются числа, называют цифрами, а их совокупность алфавитом системы счисления.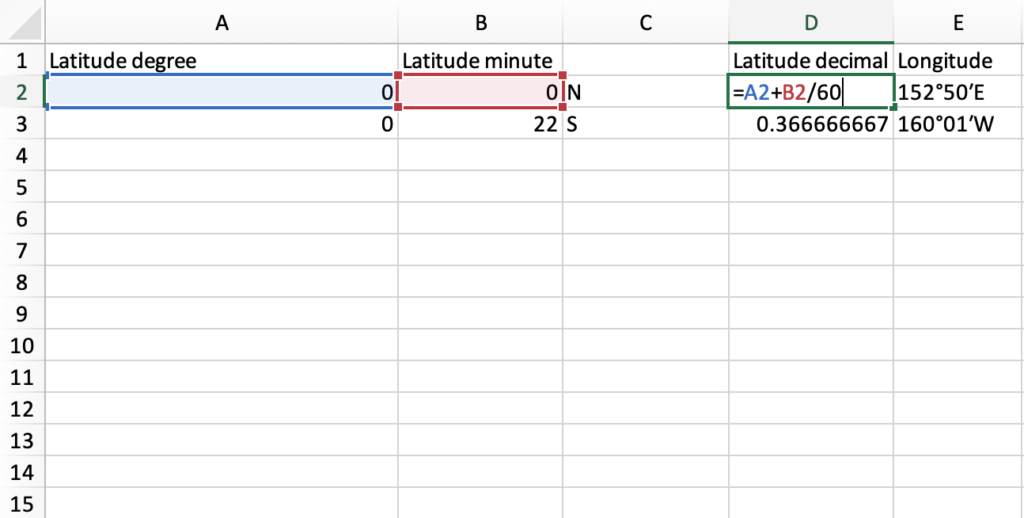
Учитель: почему система счисления называется двоичной, десятичной?
Ответ: система счисления называется двоичной, потому что алфавит системы счисления состоит из двух цифр: 0 и 1, а алфавит десятичной системы составляют цифры 0,1,2,3,4,5,6,7,8,9.
Учитель: что называют основанием системы счисления?
Ответ: для записи чисел в различных системах счисления используется определенное количество знаков или цифр. Число таких знаков в позиционной системе счисления называется основанием системы счисления.
Учитель: а теперь вспомним алгоритм перевода чисел из десятичной в двоичную и наоборот.
Двое учащихся показывают алгоритм перевода на слайде№3
Учитель: я предлагаю вам несколько заданий, решив устно, вы должны выбрать правильный ответ слайды №4-11
1.Двоичное число 1010000 в десятичной записи имеет вид:
А) 81
Б) 92
В) 80
Г) 78
2. Десятичное число 118 в двоичной записи имеет вид:
Десятичное число 118 в двоичной записи имеет вид:
А) 1110010
Б) 1110011
В) 1110110
Г) 1111001
3.Двоичное число 1001 в десятичной записи имеет вид:
А) 9
Б) 8
В) 17
Г) 10
Значит, чтобы перевести числа из двоичной системы в десятичную и наоборот мы должны ….
Слайды 12-13
Учитель: Мы с вами повторили, как переводятся десятичные числа в двоичную систему счисления и наоборот. Сейчас мы рассмотрим с вами другие способы перевода чисел из десятичной системы в двоичную и наоборот с помощью приложения Калькулятор, и в программе Exsel
Для этого вы должны включить компьютеры. Работая на компьютере, ребята, помните правила техники безопасности и давайте будем следовать им при работе за компьютером (вспомнить некоторые правила по ТБ). Сейчас мы будем работать с приложением Калькулятор. Давайте посмотрим, как его найти и как настроить для работы. (Слайд 14-17)
Пуск/ Стандартные/Калькулятор
Запускаем приложение Калькулятор и выполняем команду (Вид- инженерный). Обратите внимание на группу переключателей, определяющих систему счисления:
Обратите внимание на группу переключателей, определяющих систему счисления:
·Hex ·Dec · Oct · Bin
Десятичная система счисления
Двоичная система счисления
Убедимся, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши вводим в поле ввода произвольное число. Активизируем переключатель Bin и в поле ввода видим новое число в двоичной системе счисления.
Настроим Калькулятор на работу в двоичной системе счисления. Обратите внимание, какие кнопки и цифровые клавиши нам доступны. Вводим двоичное число и с помощью переключателя Dec переводим его в десятичную систему счисления.
Пример №1 ( 128)10=(?)2
Пример№2 (1110111)2=(?)10
Закрепление.
Учитель: Теперь можно приступить вам к выполнению практической работы
Нарисуй фигуру
Каждой паре выдается карточка, содержащая таблицу с координатами точек, записанными в двоичной системе счисления, и система координат. Для выполнения задания необходимо:
Для выполнения задания необходимо:
а) перевести координаты точек в десятичную систему с помощью приложения Калькулятор
б) построить по ним фигуру в координатной плоскости
Для выполнения этого задания вам понадобятся не только знания, полученные сегодня на уроке, но и математические знания. Каждому ученику выдается тетрадный лист с нанесенной на нем системой координат (заранее подготавливается учителем)
Пояснение к заданию: каждая координата точки записана в двоичной системе координат. Вам надо перевести координаты точек в десятичную систему счисления и, применяя знания по математике, построить точки на системе координат, соединить их.
I вариант (буква Г)
Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления.
№ точки | Двоичный код | Десятичный код |
1 | (101;101) |
|
2 | (101;101000) |
|
3 | (11001;101000) |
|
4 | (11001;100011) |
|
5 | (1010;100011) |
|
6 | (1010;101) |
|
7 | (101;101) |
|
Ответ: (5;5), (5;40), (25;40), (25;35), (10;35), (10;5), (5;5).
2 вариант. Звезда
№ точки | Двоичный код | Десятичный код |
1 | (10; 1111) |
|
2 | (1000; 10000) |
|
3 | (1011; 10110) |
|
4 | (1110; 10000) |
|
5 | (10100; 1111) |
|
6 | (10000; 1010) |
|
7 | (10010; 100) |
|
8 | (1011; 111) |
|
9 | (100; 100) |
|
10 | (110; 1010) |
|
11 | (10; 1111) |
|
Ответ: (2;15), (8;16), (11; 22), (14; 16), (20; 15), (16; 10), (18; 4), (11; 7), (4;4), (6;10), (2;15)
Учитель: давайте немного отдохнем (физминутка) слайд№21
Учитель: Откройте все программу Excel. Посмотрим, как легко перевести числа в этой программе слайд№22-23
Посмотрим, как легко перевести числа в этой программе слайд№22-23
Выполните задание в программе Excel
3 вариант. Ракета
№ точки | Двоичный код | Десятичный код |
1 | (1000; 10) |
|
2 | (101; 10) |
|
3 | (1000; 1010) |
|
4 | (1000; 10101) |
|
5 | (1011; 11001) |
|
6 | (1110; 10101) |
|
7 | (1110; 1010) |
|
8 | (10001; 10) |
|
9 | (1110; 10) |
|
10 | (1110; 111) |
|
11 | (1100; 111) |
|
12 | (1101; 10) |
|
13 | (1001;10) |
|
14 | (1010; 111) |
|
15 | (1000; 111) |
|
16 | (1000; 10) |
|
Ответ: (8;2), (5;2), (8;10), (8;2), (11;25), (14;21), (14;10), (17;2), (14;2), (14;7), (12;7), (13;2), (9;2), (10;7), (8;7), (8;2).
Ну а сейчас, ребята, поиграем «Попробуй открой открытку»(PROEKT 1и PROEKT 2). Можете пользоваться любым способом перевода
Слайд №24
Итог урока.
Что нового узнали на уроке? (В виде беседы с классом.)
Рефлексия.
Вам понравился урок? Чтобы узнать мнение учащихся, учесть их интересы и лучше подготовиться к следующему уроку, можно подготовить два вида смайликов. Учащиеся выбирают тот смайлик, который соответствует их настроению.
Слайд25
Домашнее задание слайд №26
Вывод:
Данный урок сопровождается презентацией. С помощью мультимедийного проектора на экране учащиеся наглядно видят весь теоретический и практический материал данного урока, что повышает результативность и усвояемость данного материала.
Данная методическая разработка урока предназначена в помощь учителю, работающему по новому учебно-методическому комплекту по информатике
(автор Босова Л. Л., издательство «Бином. Лаборатория знаний»), имеющему гриф «Допущено» Министерства образования РФ.
Л., издательство «Бином. Лаборатория знаний»), имеющему гриф «Допущено» Министерства образования РФ.
Учебное пособие:
Информатика: Учебник
/Л.Л. Босова. – 4-е изд., испр. – М.: Бином. Лаборатория знаний, 2006.
Используемая методическая литература:
Уроки информатики в 8-9 классах: Методическое пособие/ Л.Л. Босова, А.Ю. Босова. – М.:Бином. Лаборатория знаний, 2004.
Занимательные задачи по информатике
/ Л.Л.Босова, А.Ю.Босова, Ю.Г. Коломенская. – 2-е изд., испр. – М.: Бином. Лаборатория знаний, 2006.
8
Конвертер координат| Широта и долгота
Автор: Julia Żuławińska
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 22 сентября 2022 г.
Содержание:- Что такое широта и долгота?
- Как написать координаты?
- Как преобразовать координаты широты и долготы?
- Как преобразовать координаты в DD в DMS или DDM?
Этот преобразователь координат преобразует координаты широты и долготы в желаемый формат: DD, DMS или DDM. Что такое широта и долгота? Это воображаемые линии, которые проходят вокруг и от полюса к полюсу на земном шаре соответственно. Зная широту и долготу, можно найти любое место на Земле. Для этого вам нужно знать , как читать и записывать координаты . Мы объясним, как это сделать, в тексте ниже. Также мы покажем вам принципы преобразования координат и приведем пошаговых примеров для Сиднейского оперного театра и Эмпайр Стейт Билдинг.
Что такое широта и долгота? Это воображаемые линии, которые проходят вокруг и от полюса к полюсу на земном шаре соответственно. Зная широту и долготу, можно найти любое место на Земле. Для этого вам нужно знать , как читать и записывать координаты . Мы объясним, как это сделать, в тексте ниже. Также мы покажем вам принципы преобразования координат и приведем пошаговых примеров для Сиднейского оперного театра и Эмпайр Стейт Билдинг.
Хотите знать, как координаты широты и долготы связаны с часовыми поясами? Проверьте ответ в конвертере lat long to UTM!
Что такое широта и долгота?
С помощью координат вы можете найти любое место на Земле с высокой степенью точности. Географическая система координат основана на сферической системе координат для эллипсоида — формы Земли. Он берет начало от пересечения нулевого меридиана (Гринвич, Англия) с Экватор . Мы указываем координаты, используя широту и долготу. Но какие именно?
Но какие именно?
Широта — это угол между плоскостью экватора и линией, проходящей от центра Земли до определенной точки на ее поверхности. Он ссылается на положение север-юг на Земле. Он представлен окружностью широты или параллелями — линиями, огибающими земной шар. Центральная линия широты называется .Экватор . Он имеет широту 0 градусов. Максимальное значение широты — 90 градусов — встречается на полюсах.
Долгота , с другой стороны, относится к позиции восток-запад на Земле. Линии долготы или меридиана соединяют Северный и Южный полюса. Они простираются к востоку и западу от нулевого меридиана , достигая 180 градусов. Все меридианы имеют одинаковую длину — 12 429,9 миль (20 003,93 км).
Знаете ли вы, что можно рассчитать кратчайшее возможное расстояние между двумя точками с известными географическими координатами, используя широту и долготу? Узнайте больше об этом в калькуляторе расстояния широты и долготы. Кроме того, с помощью калькулятора азимута вы можете оценить направление, в котором вам нужно указать компас, чтобы добраться из одной точки в другую!
Кроме того, с помощью калькулятора азимута вы можете оценить направление, в котором вам нужно указать компас, чтобы добраться из одной точки в другую!
Теперь, когда вы знаете, что такое широта и долгота, давайте посмотрим, как записать координаты в GPS, наш конвертер широты и долготы или любой другой инструмент.
Как записать координаты?
Первое правило записи координат:
Сначала идет широта, затем долгота.
Иногда для облегчения различия между широтой и долготой включаются соответствующие символы: φ (фи) для широты и λ (лямбда) для долготы. Для формулировки координат можно использовать:
- DD (десятичные градусы — °)
- ДМС (градусы -°, минуты -‘, секунды — «)
- DDM (градусы (°), десятичные минуты (‘))
Чтобы указать кардинальное направление, вы можете использовать буквы или положительные и отрицательные числа. Для широты северные направления могут быть обозначены буквой N или положительным числом , а южные направления могут быть отмечены либо буквой S, либо отрицательным значением . Для долготы вы можете использовать букву E или положительное число для восточного направления, а западное направление может быть обозначено цифрой 9.0019 буква W или отрицательное число . Помните — не смешивайте формы! Если вы используете буквы, значения всегда должны быть положительными.
Для долготы вы можете использовать букву E или положительное число для восточного направления, а западное направление может быть обозначено цифрой 9.0019 буква W или отрицательное число . Помните — не смешивайте формы! Если вы используете буквы, значения всегда должны быть положительными.
Выражение направления с положительными или отрицательными значениями распространено в формате координат DD. Это менее популярно с DMS или DDM.
Например, посмотрим, как записать координаты двух мест: Эмпайр Стейт Билдинг в Нью-Йорке — города, расположенного к западу от нулевого меридиана и в северном полушарии, — и Сиднейского оперного театра — к востоку от нулевого меридиана и в южное полушарие.
Вот некоторые допустимые формы координат широты и долготы:
- Empire State Building:
- 40.748417, -73.985833 (ДД)
- 40.748417 С, 73.985833 Ш (ДД)
- 40 44 54,3 φ N, 73 59 9 λ W (DMS)
- Сиднейский оперный театр:
- -33,858611 φ, 151,214167 λ (DD)
- 33 51,5167 Ю, 151 12,8500 В (ДДМ)
- 33° 51′ 31″ ю.
 ш., 151° 12′ 51″ в.д. (DMS)
ш., 151° 12′ 51″ в.д. (DMS)
Обратите внимание, что ° , ' , " символы не являются обязательными. Если вы их не используете, числа градусов, минут и секунд разделяются пробелами.
Как преобразовать координаты широты и долготы?
В одном градусе 60 минут, а в одной минуте 60. Это означает, что в одном градусе 3600 секунд. Когда вы понимаете это, формула DMS to DD очевидна:
Десятичные градусы = градусы + минуты/60 + секунды/3600
Преобразуем координаты широты и долготы Эмпайр Стейт Билдинг. Координаты: 40° 44′ 54,3″ северной широты, 73° 59′ 9″ западной долготы. Таким образом, его широта в десятичных градусах равна:
DD = 40 + 44/60 + 54,3/3600 = 40,748417
И долгота3:
DD = 73 + 59/60 + 9/3600 = 73,985833
Координаты в северном полушарии имеют положительные значения. Координаты к западу от нулевого меридиана имеют отрицательные значения.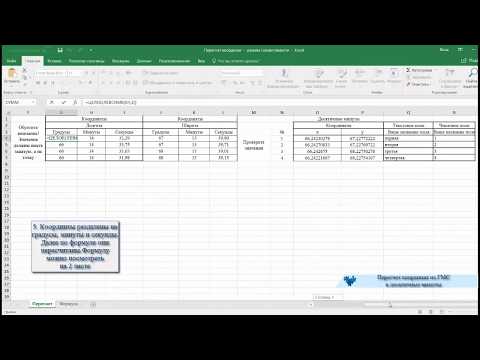 Итак, географические координаты Эмпайр Стейт Билдинг:
Итак, географические координаты Эмпайр Стейт Билдинг: 40.748417 -73.985833 .
Преобразование из градусов с десятичными минутами в десятичные градусы сокращает формулу:
DD = градусы + десятичные минуты / 60
Преобразование в обратном направлении немного сложнее. Но не волнуйтесь. Мы объясним это шаг за шагом ниже.
Как преобразовать координаты в DD в DMS или DDM?
Для преобразования координат широты и долготы в десятичных градусах в градусы с минутами и секундами или градусы с десятичными минутами выполните следующие три шага :
- Возьмите целое число — это градусы.
- Умножить десятичную часть на 60.
- Если вы хотите иметь десятичные минуты — вот они! Не обращайте внимания на третий пункт.
- Если вы хотите получить координаты в DMS, берите только целое число — это минуты. Перейти к третьему пункту.
- Умножьте остаток на 60. Вот секунды.

Например, давайте преобразуем координаты Сиднейского оперного театра из DD в DMS. Координаты -33.858611 151.214167.
Например, давайте преобразуем координаты Сиднейского оперного театра из DD в DMS. Координаты -33.858611 151.214167.
Широта:
- Целое число от 33,858611 равно 33. Градусы равны 33.
- Десятичная часть:
0,858611умножить на60равно51,51666. Возьмем целое число —минут = 51'. - Снова возьмем десятичную часть —
0,51666и умножим на60. Вы получите суммусекунд = 31 дюйм.
Теперь повторите шаги для долготы:
- Градусы равны 151°.
-
0,214167 * 60 = 12,85: минуты равны 12′. -
0,85002 * 60 = 51: секунды = 51″.
Осталось определить стороны света. Широта отрицательная, так что это на юге. Долгота положительная. Это указывает на положение на востоке. Итак, координаты Сиднейского оперного театра:
Итак, координаты Сиднейского оперного театра: 33° 51′ 31″ ю.ш. 151° 12′ 51″ в.д. .
Теперь вы знаете, как считать, как наш конвертер широты и долготы!
Джулия Жулавиньска
Координатные форматы:
DD — Десятичные градусы
DMS — DEGREES с минутными и десятичными секундами
9000 2 DDMINES -минуты и десятичные секунды. В координатах есть буквы?
Широта
Долгота
Проверить 167 похожих калькуляторов конвертации
Преобразование широта долгота географические координаты во всех форматах: десятичный, шестидесятеричный, GPS DD DM DM DMS градусы минуты секунды, поиск по клику на карте.
| Наверх Содержание | Карта | Результат | скачать PDF-файл | | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Вернуться к началу Содержание | Карта | Результат | скачать PDF-файл |
Как преобразовать из десятичного в секс -личность
Как преобразовать от сексиагримальной в десятичную десятичную Содержание | Карта | Результат | скачать PDF-файл |
Как преобразовать десятичный вид в шестидесятеричный
# У вас есть десятичные градусы (-73,9874°) вместо градусов, минут и секунд (-73° 59′ 14,64″)
# Целые единицы измерения градусов останутся прежними (-73,9874° долготы, начните с 73°)
# Умножьте десятичную дробь на 60 (0,9874 * 60 = 59,244)
# Целое число станет минутами (59′)
# Возьмите оставшуюся десятичную дробь и умножьте на 60. (0,244 * 60 = 14,64)
(0,244 * 60 = 14,64)
# Полученное число станет секунд (14,64 дюйма). Секунды могут оставаться десятичными.
# Возьмите три набора чисел и соедините их вместе, используя символы градусов (°), минут (’) и секунд («) (-73° 59′ 14,64» долготы)
Вернуться к началу Содержание | Карта | Результат | скачать PDF-файл |
Как преобразовать шестидесятеричный вид в десятичный
# У вас есть градусы, минуты и секунды (-73° 59’ 14,64″) вместо десятичных градусов (-73,9874°)
# Целые единицы измерения градусов останутся прежними
# Разделите секунды на 60 (14,64/60 = 0,244)
# Полученное значение сложите в минуты и разделите на 60 (59,244/60 = 0,9874)
# Полученное десятичное значение градусов (0,9874)
# Просуммируйте градусов до десятичной точки с использованием символов градусов (°) (-73,9874°)
Вернуться к началу Содержание | Карта | Результат | скачать PDF-файл |
Формат
Диапазон значений
Допустимые значения широты от -9От 0,0° до 90,0° для долготы от -180,0° до 180,0°, знак + должен быть опущен, а знак минус не нужен, если есть радиокомпонент для выбора направления С-Ю или З-В (градусный и десятичный формат) .
Десятичный
Необходимо выбрать направление (север-юг или запад-восток) и ввести число от 0 до 90 для широты или от 0 до 180 для долготы (пример 45.12345).
Градусы
Формат градусов состоит из направления (север-юг или запад-восток) и трех наборов чисел, разделенных символами градусов (°), минут (’) и секунд («).
Градус — это целое число без знака, от 0 до 90 для широты или от 0 до 180 для долготы. Минута — это целое число без знака, от 0 до 59. Секунды — это двойное значение без знака, от 0 (или 0,0000) до 59,9999.
Координаты
Формат координат представляет собой пару широты и долготы со знаком минус (-) для направления южной широты и западной долготы, разделенными запятой (,), вот пример:
52.5163 , 13.3779
40.7389 , -7816
-22.9708 , -43.1830
Поиск на карте
Нажмите на поиск, чтобы открыть веб-страницу Координаты Земли, здесь вы получите широту и долготу, просто нажав на карту, и сохраните значение, нажав кнопку сохранить.
Вернуться к началу Содержание | Карта | Результат | скачать PDF-файл |
Точность
Широта и долгота имеют максимальную ошибку на экваторе, потому что радиус Земли максимален.
Земля не сфера, а неправильная форма, близкая к эллипсоиду. Точность долготы увеличивается по мере удаления от экватора. Точность широты остается практически неизменной.
Радиус Земли на экваторе: 6378,160 км, длина окружности: (2*π*r) 40075,1612 км, каждый градус: (40075,1612/360) 111,319 км.
Выбор точности 5 знаков после запятой с точностью до 1,11 метра (+/- 55,5 см) на экваторе.
| разряда | десятичных град. | градусов | Расстояние |
| 0 | 1,0 | 1 ° 0’0 « | 111,319 км | 3 11. 132 km 132 km |
| 2 | 0.01 | 0°0’36» | 1.113 km |
| 3 | 0.001 | 0°0’3.6″ | 111.3 m |
| 4 | 0.0001 | 0°0’0.36″ | 11.13 m |
| 5 | 0.00001 | 0°0’0.036″ | 1.11 m |
| 6 | 0.000001 | 0°0’0.0036″ | 11,1 см |
| 7 | 0,0000001 | 0°0’0,00036″ | 1,11 см |
Вернуться к началу Содержание | Карта | Результат | скачать PDF-файл |
Комментарий
Если вы обнаружите ошибку или другую неточность, захотите предложить новую функцию или просто захотите высказать мнение о сайте, не стесняйтесь сделать это в разделе «Комментарии» (или напрямую по электронной почте). Администрация сайта ценит все комментарии, поскольку мы стремимся создать точный и конструктивный ресурс.
Заранее спасибо за ваш вклад в улучшение этого сайта (пожалуйста, исправьте грамматические ошибки и ошибки перевода).
Вернуться к началу Содержание | Карта | Результат | скачать PDF-файл |
Ссылки
http://en.wikipedia.org/wiki/Долгота
http://en.wikipedia.org/wiki/Широта
http://en.wikipedia.org/wiki/Geographic_coordinate_system
http: //en.wikipedia.org/wiki/Википедия:Получение_географических_координат
Вернуться к началу Содержание
| Карта | Результат | скачать PDF-файл |
| # Преобразование координат из форматов DMS или DdM в десятичные | |
| # DMS = «градусы минуты секунды»; DdM = «градусы десятичной минуты» | |
| # ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ | |
dg2dec <- function(varb, Dg=NA, Min=NA, Sec=NA, SW. Hemisphere=»S|W») { Hemisphere=»S|W») { | |
| # Dg=десятичное, Min=минуты и Sec=секунды; | |
| # ПРИМЕЧАНИЕ 1 — если формат «градусы десятичные минуты — DdM» (например, 40° 26,767′ с. ш.), а не | |
| # «градусы минуты секунды — DMS» (например, 40° 26′ 46″ с.ш.), затем вызовите функцию только с | |
| # Аргументы Dg и Min, например dg2dec(varb, Dg=»°», Min=»′N»). | |
| # То же самое, если нет символа секунд (например, 45°12’7.38). | |
| # Обратите внимание, что нельзя использовать пробелы в аргументах Dg, Min или Sec (вернет NA). | |
| # Подробнее о форматах см.: | |
# https://en. wikipedia.org/wiki/Geographic_coordinate_conversion#Coordinate_format_conversion wikipedia.org/wiki/Geographic_coordinate_conversion#Coordinate_format_conversion | |
| # Используйте paste0(«[«, Dg, Min, Sec, «]») для создания шаблона регулярного выражения [] | |
| # следовательно, strsplit() разделит строку «varb» по символам, которые вы укажете на Dg, Min, Sec | |
| DMS <- sapply(strsplit(varb, paste0('[', Dg, Min, Sec, ']')), as.numeric) | |
| # DMS — это матрица; первая строка содержит степени; секунда — минуты; третий — секунды. | |
| # Если формат «градусы десятичные минуты» (например, 40° 26,767′ северной широты), а не | |
| # «градусы минуты секунды» (например, 40° 26′ 46″ северной широты), тогда матрица имеет только две допустимые строки: | |
| # первая строка содержит градусы; второй — минуты; | |
| # поэтому вычисляйте конверсию за секунды, только если в DMS более 2 строк | |
| # и Sec отличается от NA (если в формате DMS есть секунды) | |
decdg <- abs(DMS[1, ]) + DMS[2, ]/60 + ifelse(dim(DMS)[1] > 2 & !is. na(Sec), DMS[3, ]/3600, 0 ) na(Sec), DMS[3, ]/3600, 0 ) | |
| # все координаты Южного или Западного полушария становятся отрицательными в десятичном формате | |
| SW <- grepl(pattern = SW.Hemisphere, x = varb, ignore.case = TRUE) | |
| возврат(ifelse(SW, -1, 1) * decdg) | |
| } | |
| # Ссылки: | |
| # http://stackoverflow.com/questions/14404596/converting-geo-coordinates-from-grade-to-decimal | |
| # https://en.wikipedia.org/wiki/Geographic_coordinate_conversion#Coordinate_format_conversion | |
# https://en. wikipedia.org/wiki/Десятичные_градусы wikipedia.org/wiki/Десятичные_градусы | |
| # протестировано преобразование с http://www.pgc.umn.edu/tools/conversion | |
| # ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ | |
| # Примеры | |
| x <- read.table(text="DdM DMS_lat DMS_lon DMS | |
| 45°12’7,38» 45°12’7,38»ю.ш. 45°12’7,38»з.д. 45°12’7,38 | |
| 31°29,17′ 31°29’10,2»N 31°29’10,2»E 31°29’10,2″, | |
| заголовок = ИСТИНА, stringsAsFactors = ЛОЖЬ) | |
| х | |
| # DdM DMS_широта DMS_lon DMS | |
# 1 45°12’7,38» 45°12’7,38»ю. ш. 45°12’7,38»з.д. 45°12’7,38 ш. 45°12’7,38»з.д. 45°12’7,38 | |
| # 2 31°29,17′ 31°29’10,2»с.ш. 31°29’10,2»в.д. 31°29’10,2 | |
| # регистр «градусы десятичные минуты» (DdM) | |
| dg2dec(varb=x$DdM, Dg=»°», Min=»‘») | |
| # [1] 45.20205 31.48617 | |
| # случай «градусов минут секунд» (DMS) для широты | |
| # с символом для Северного (N) и Южного (S) полушарий | |
| # использовать метасимвол регулярного выражения | для обозначения логической операции «ИЛИ» | |
| dg2dec(varb=x$DMS_lat, Dg=»°», Min=»‘», Sec=»»S|N») | |
#[1]-45. 20205 31.48538 20205 31.48538 | |
| # случай «градусов минут секунд» (DMS) для долготы | |
| # с символом для восточного (E) и западного (W) полушарий | |
| dg2dec(varb=x$DMS_lon, Dg=»°», Min=»‘», Sec=»»E|W») | |
| #[1]-45.20205 31.48538 | |
| # случай «градусов минут секунд» (DMS) без символа секунд. | |
| # Обратите внимание, что возвращаются только положительные координаты! | |
| dg2dec(varb=x$DMS, Dg=»°», Min=»‘») | |
# [1] 45. 20205 31.48538 20205 31.48538 | |
| # Иногда метасимвол регулярного выражения | |
| # может появиться в формате DMS (например, при чтении данных с веб-страниц) | |
| # вот как с этим справиться: | |
| тест <- "43°37'42\" с.ш. | |
| # где секунды обозначаются (\» N) или (\» W), | |
| # потому что \ является метасимволом в регулярном выражении, | |
| # в R нужно экранировать как \\\\, | |
| # вот почему вы видите ниже Sec=’\\\\» N’ | |
| dg2dec(test, Dg=’°’, Min=»‘», Sec=’\\\\» N’) | |
| # Примеры таблиц данных: | |
библиотека (данные. |

 Затем введите строку в поле «Позиция». Затем нажмите кнопку «Разобрать» и дождитесь завершения процесса. Координаты отображаются в окне Разобранное положение.
Затем введите строку в поле «Позиция». Затем нажмите кнопку «Разобрать» и дождитесь завершения процесса. Координаты отображаются в окне Разобранное положение.

 ш., 151° 12′ 51″ в.д. (DMS)
ш., 151° 12′ 51″ в.д. (DMS)