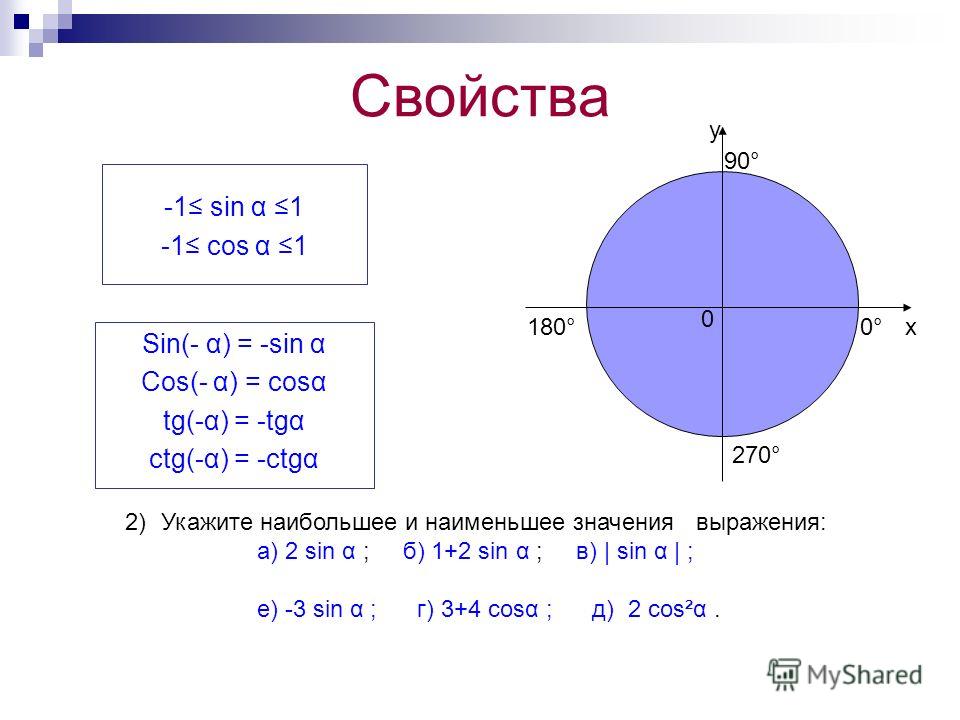
Как сделать тангенс в excel?
Содержание
- 1 Вычисление значения арктангенса
- 1.1 Способ 1: ручной ввод функции
- 1.2 Способ 2: вычисление при помощи Мастера функций
- 1.3 Помогла ли вам эта статья?
- 2 Функция РАДИАНЫ в Excel
- 3 Функция ГРАДУСЫ в Excel
- 4 Альтернативный способ перевода
Дата: 23 сентября 2016 Категория: Excel Поделиться, добавить в закладки или статью
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel.
Еще одна функция – ПИ(), не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Конечно, Вы знаете эти функции:
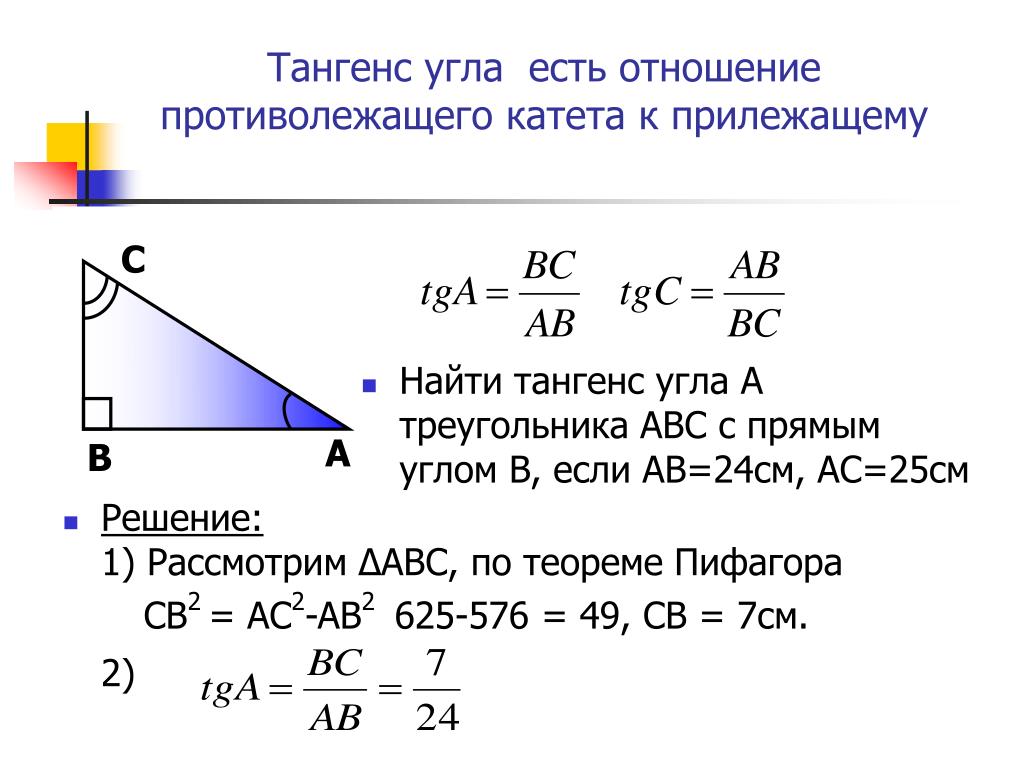
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.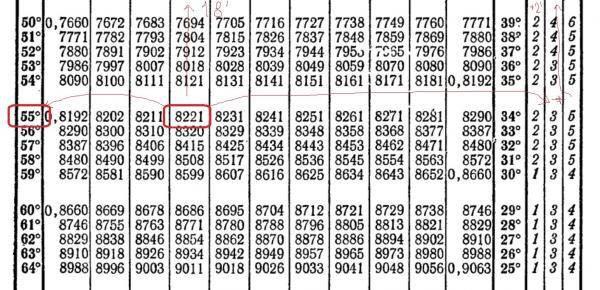
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса).
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса).
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса).
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ.
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Поделиться, добавить в закладки или статью
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
=ATAN(число)
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.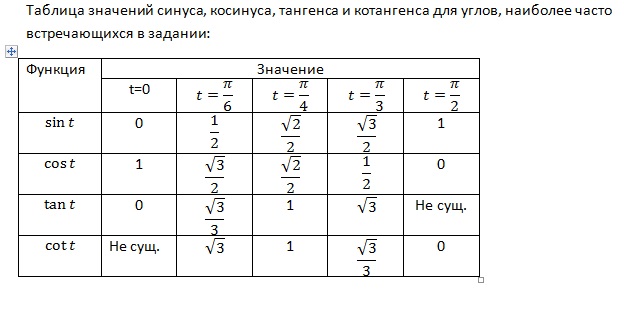
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
=ATAN(число)Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
=ATAN(4)Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
- Для вывода результатов расчета на экран нажимаем на кнопку Enter.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
- Происходит открытие Мастера функций.
 В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK». - После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
- После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.
Урок: Мастер функций в Excel
Как видим, нахождение из числа арктангенса в Экселе не является проблемой.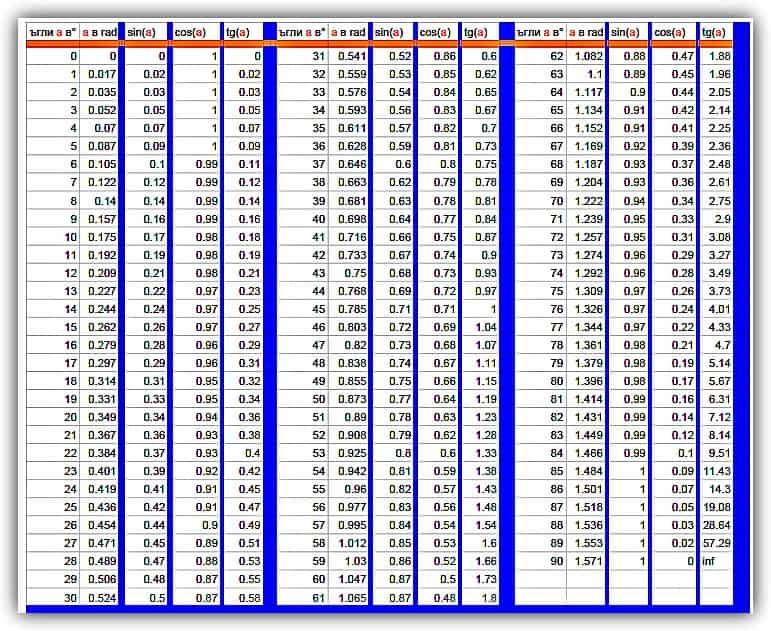 Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.
В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов.
Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.
Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы.
И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.
Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:
В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот.
Давайте подробно остановимся на особенностях применения каждой из них.
Функция РАДИАНЫ в Excel
Синтаксис и описание:
РАДИАНЫ(угол)
Преобразует градусы в радианы.
- Угол (обязательный аргумент) — угол в градусной мере, преобразуемый в радианы.

В качестве аргумента задаем угол в градусной мере, в результате преобразования получаем радианную:
Функция ГРАДУСЫ в Excel
Синтаксис и описание:
ГРАДУСЫ(угол)
Преобразует радианы в градусы.
- Угол (обязательный аргумент) — угол в радианной мере, преобразуемый в градусы.
Функция по сути аналогична описанной выше, но в данном случае на входе мы задаем радианы, а на выходе получаем градусы:
Альтернативный способ перевода
Перевести угол из градусной меры в радианную можно и без использования стандартных формул перевода углов в Excel.
Действительно, мы уже выяснили, что в развернутом угле (180°) содержится π радиан, поэтому умножая угол выраженный в градусах на коэффициент π/180 (с помощью константы Пи) получим радианную меру угла:
Аналогично умножая на обратный коэффициент 180/π можно сделать перевод из радианной меры в градусную:
Удачи вам и до скорых встреч на страницах блога Tutorexcel. ru!
ru!
Как найти угол по тангенсу
Как перевести тангенс в градусы?
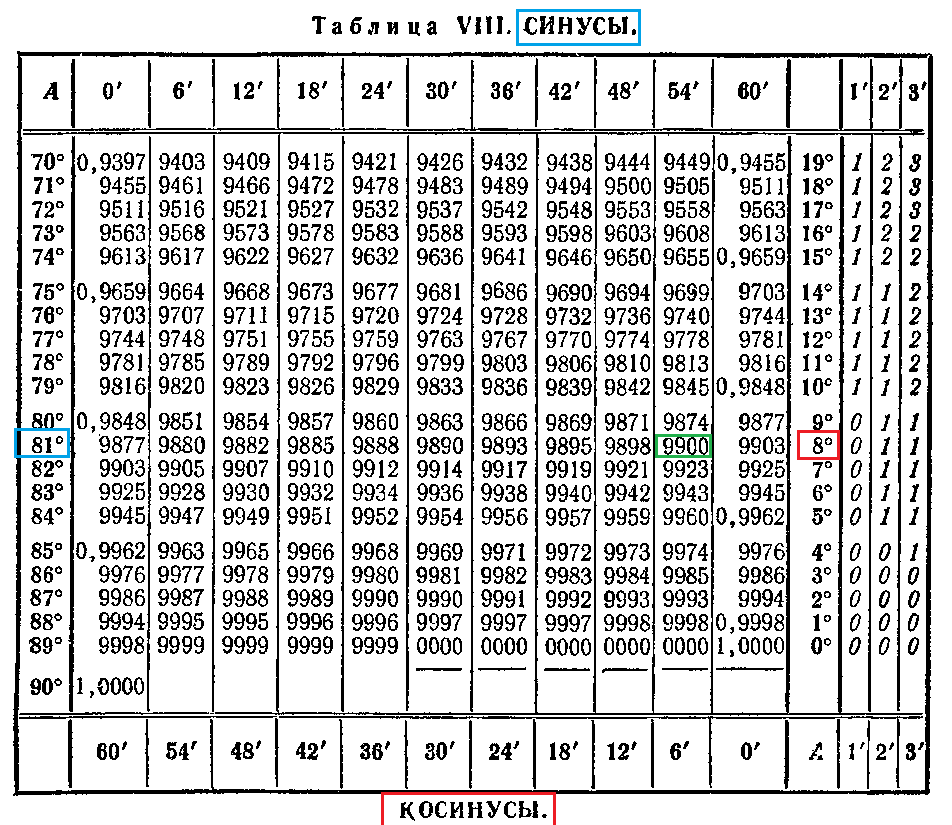
Итак, мы знаем все стороны прямоугольного треугольника. => мы знаем тангенс любого угла (отношение противолежащего катета к прилежащему) . Теперь вопрос. Зная Тангенс угла, как его перевести в Градусы? Надо это делать математически! Т. е. Таблица Брадиса не подходит.
По тангенсу угла можно найти величину угла. Для этого надо вычислить арктангенс тангенса, получится величина угла в радианах, потом ее можно перевести в градусы, умножив на 180 и разделив на пи.
ты же сам сказал отношение вот и дели
получишь радианы а там и не далеко к градусам
ты что в школе головой об парту стучался
Есть формула для арктангенса
градусы вычесть по таблице брадиса. ей еще пользоваться надо уметь
по другому никак
долго не мог найти ответ, но в итоге нашёл.
и решил тут написать вдруг кто тоже будет искать
нужно умножить на 180 и поделить на ПИ
тоесть сторону А делим на сторону Б
получаем тангенс в радианах
далее полученное значение умножаем на 180 и делим на 3. 14
14
в итоге получаем градусы
Как найти угол имея цифровое значение синуса, косинуса, тангенса?
Как найти угол имея цифровое значение синуса, косинуса, тангенса,котангенса? например есть значение sin a=0,3452 какой угол этому соответствует?
Функции: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), называются тригонометрическими. Они выражают зависимости длин сторон от углов треугольника при гипотенузе. Определяются отношением какой-либо из сторон треугольника к другой. То есть, показывают, насколько одна сторона больше другой. Это отношение может быть характерно только для строго определенного угла. Выражаются тригонометрические функции в безразмерных единицах.
Если известно значение какой-либо тригонометрической функции (в данном случае, синуса — sin), а требуется найти соответствующий ему угол в градусах, то нужно:
- найти обратную тригонометрическую функцию, так называемую «arc»: arcsin, arccos, arctg, arcctg.
 . Эти функции находятся: по таблицам Брадиса, в которых для каждого угла приведены свои — строго определенные значения тригонометрических функций (таблицами Брадиса пользовались в «докомпьютерный век»), с помощью «инженерных» калькуляторов или компьютерными программами, в частности — Excel. Для того, чтобы определить значение угла по таблицам Брадиса, нужно водить пальцем по их строкам (с тысячами значений), где найти нужную величину (то ли 5, то ли 6 знаков после запятой). И увидеть соответствующее ему значение угла. Так что, с помощью Excel это делается несравненно быстрее и точнее.
. Эти функции находятся: по таблицам Брадиса, в которых для каждого угла приведены свои — строго определенные значения тригонометрических функций (таблицами Брадиса пользовались в «докомпьютерный век»), с помощью «инженерных» калькуляторов или компьютерными программами, в частности — Excel. Для того, чтобы определить значение угла по таблицам Брадиса, нужно водить пальцем по их строкам (с тысячами значений), где найти нужную величину (то ли 5, то ли 6 знаков после запятой). И увидеть соответствующее ему значение угла. Так что, с помощью Excel это делается несравненно быстрее и точнее. - Однако функции arc показывают значение в радианах. Искомый угол равен 0,35245 радиан. Если нужно в градусах, то следуют применить еще и формулу перевода радиан в градусы.
Определение значения arcsin угла (в радианах) и значения в градусах — с помощью функций Excel
Итак, ответ получен:
Синусу угла альфа со значением 0,3452 соответствует угол 20,194 градуса.
Данному значению синуса соответствует угол- немногим более 20 градусов, это- по таблице, а если есть значение гипотенузы, то- по отношению- можно найти катет и другие элементы треугольника и- возможно- все улы, здесь- главное- зацепка- кончик ниточки, чтобы размотать весь клубочек,( а имея в
хозяйстве инженерный калькулятор, можно сразу- по функции найти угол с точностью до н- ого знака после запятой. )
Можно без компьютера, без калькулятора, без таблиц Брадиса найти этот угол. Для этого нужен такой инструмент, как транспортир. Можно воспользоваться угломером. Если есть чертежный прибор, который еще называют кульман, то и им. Но сначала высисляют катет и гипотенузу. Чем больше длина, тем точгее. Допустим, гипотенуза 100 мм, тогда противолежащий катет будет равен 100*0,3452=34,52мм. Берем клетчатую бумагу, по вертикали откладываем 35 мм от горизонтальной линии вверх. Из верхней точки циркулем с разведенными ножками на 100 мм делаем засечку на глризонтальной линии. Соединяем три точки линиями и измеряем угол.
Если честно, то в повседневной жизни не припомню, чтобы приходилось определять углы по синусу или тагенсу. Вот строить углы приходится постоянно. Например, нужно обрезать плинтуса под углом 45 градусов. Никакой транспортир или угломер не нужен. На заводе плинтус обрезан под прямым углом, тогда просто отмеряешь два одинаковых катета и проводишь гипотенузу, угол получантся сам собой. Так же легко строить углы 30 и 60 градусов, так как гипотенуза равна двум противолежащим катетам.
Еще углы можно измерять смартфоном илитпланшетом, если в нем установлено приложение по измерению углов, очень удобная штука, не надо покупать строительный уровень.
Таблица тангенсов
Тангенс, как отношение катетов в прямоугольном треугольнике, представляет собой функцию которая выглядит как дуга окружности внутри данного треугольника с центром в вершине угла и прилежащим катетом в качестве радиуса.
Значение тангенса показывает не только раскрытие угла α , но и насколько один катет больше другого. При тангенсе угла α , равном 1 , катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
При тангенсе угла α , равном 1 , катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
Как перевести sin в cos?
Как перевести sin в cos?
Перевод синуса в косинус и обратно выполняется посредством решения основного тригонометрического тождества sin2(x) + cos2(x) = 1. Смотрите также: — калькулятор вычисления синуса угла; — калькулятор вычисления косинуса угла.
Чему равен косинус и синус?
Синус, косинус острого угла треугольника Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Что такое cos в математике?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.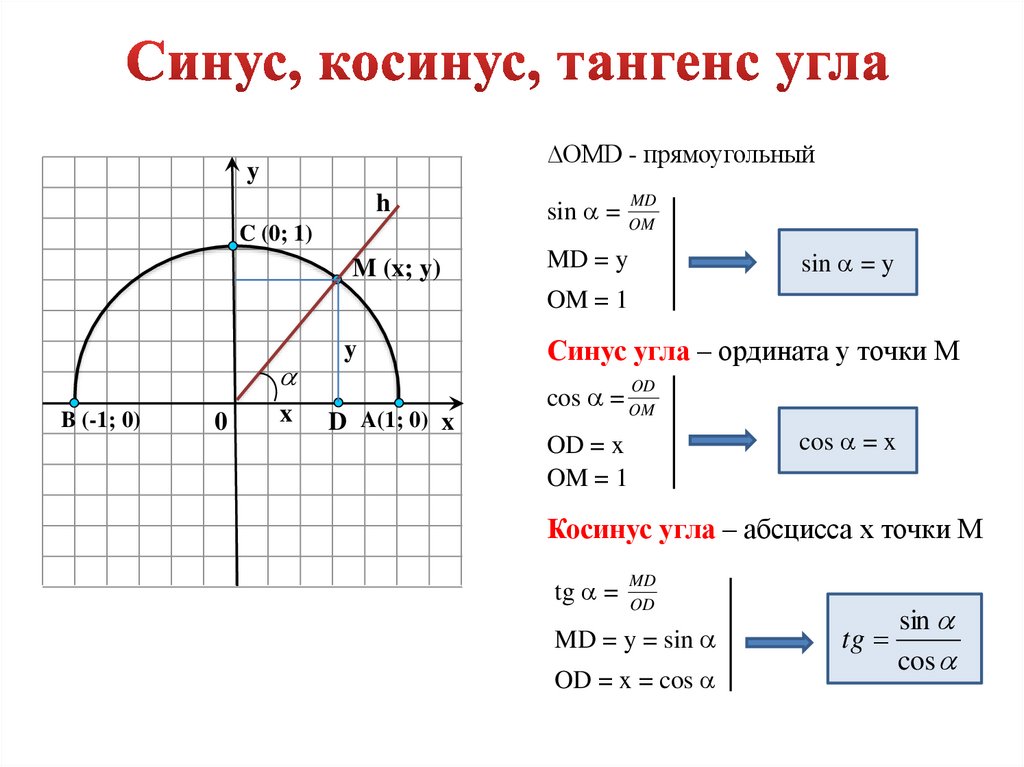 Синус угла (sin α ) — отношение противолежащего этому углу катета к гипотенузе. Косинус угла (cosα ) — отношение прилежащего катета к гипотенузе.
Синус угла (sin α ) — отношение противолежащего этому углу катета к гипотенузе. Косинус угла (cosα ) — отношение прилежащего катета к гипотенузе.
Как найти косинус какого то числа?
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе. Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.
Как найти косинус по 3 сторонам?
Формулировка теоремы косинусов Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Как найти угол треугольника зная его 2 стороны?
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.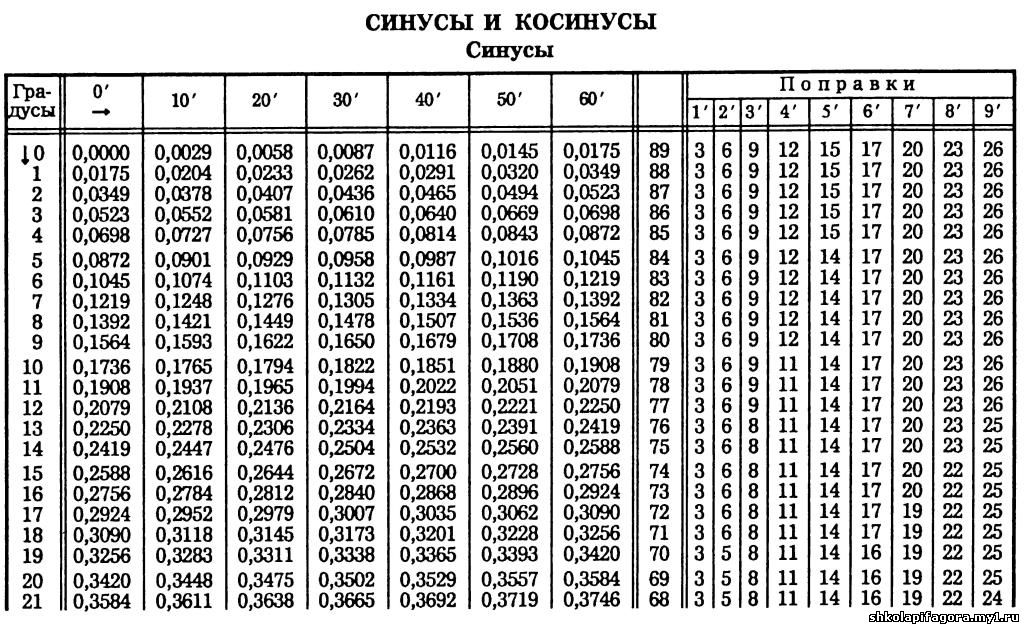
Как найти косинус через стороны?
Формула теоремы косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Теорема косинусов является обобщением теоремы Пифагора.
Как найти стороны треугольника если известна одна сторона и угол?
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов. Если известны одна сторона и два прилежащих угла, то с помощью теоремы синусов можно вычислить остальные две стороны треугольника.
Как в прямоугольном треугольнике найти катет если известна гипотенуза и угол?
Если вам задан один из острых углов, например, A, и гипотенуза, то катеты можно найти из определений основных тригонометрических : a= c*sin(A), b= c*cos(A). Если задан один из острых углов, например, A, и один из катетов, например, a, то гипотенуза и другой катет вычисляются из соотношений: b=a*tg(A), c=a*sin(A).
Как найти катет в прямоугольном треугольнике через угол?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Как найти одну сторону прямоугольного треугольника?
По теореме Пифагора, для того чтобы вычислить гипотенузу прямоугольного треугольника, нужно извлечь квадратный корень из суммы квадратов катетов. Катетами считаются стороны a и b, образующие друг с другом прямой угол, а гипотенузой – сторона, лежащая напротив него.
Как вычислить гипотенузу зная катеты?
Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Как найти второй катет в прямоугольном треугольнике?
Теорема Пифагора, чтобы найти катет прямоугольного треугольника Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора.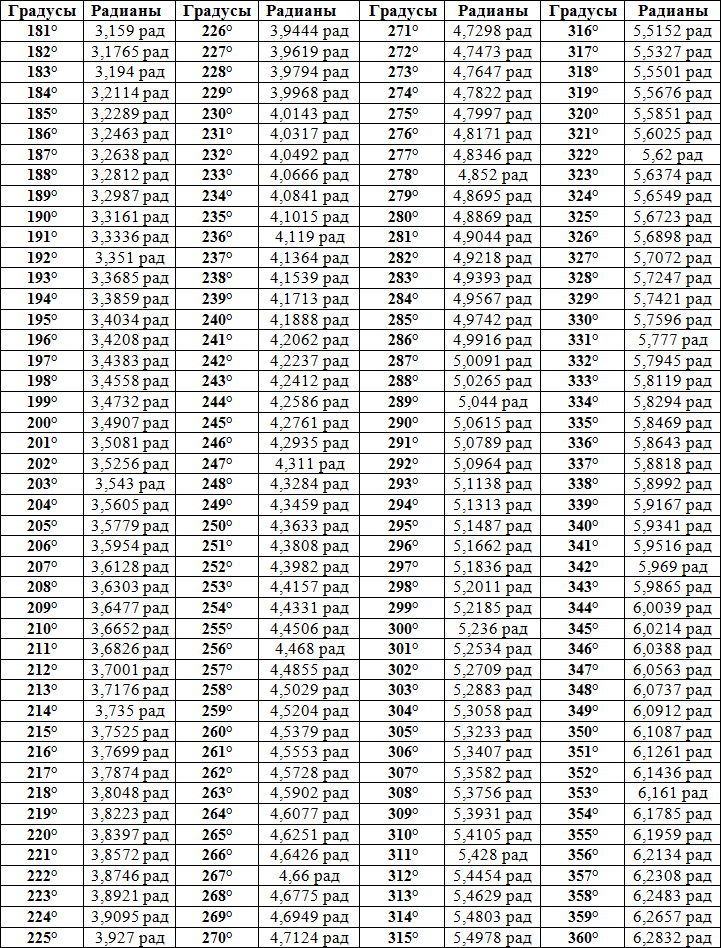 Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты.
Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты.
Как найти катет в прямоугольном треугольнике 8 класс?
Правило нахождения катета через гипотенузу: Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего ему угла или на косинус прилежащего ему угла.
Как найти катет в прямоугольном треугольнике если известна площадь?
Ответ, проверенный экспертом Площадь прямоугольного треугольника равна половине произведения его катетов. Поэтому ab=2S(a и b — катеты(пусть b — катет с прилежащим к нему углом 30 градусов)).
Как найти площадь прямоугольного треугольника если известна гипотенуза?
Площадь прямоугольного треугольника через гипотенузу можно найти по формуле для площади треугольника через 2 стороны и синус угла между ними: S = 1 2 ⋅ a ⋅ c ⋅ sin (1).
Чему равна площадь треугольника?
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.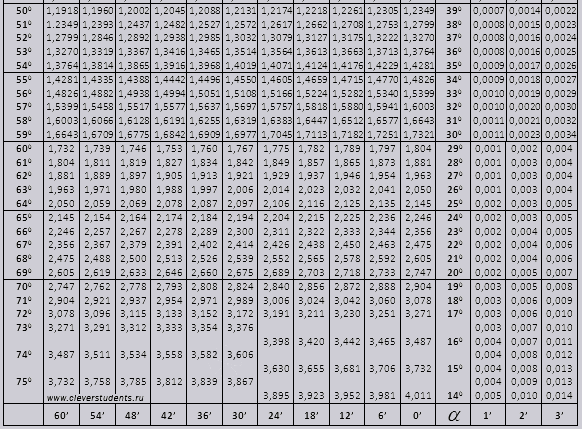
Как определить площадь треугольника в 4 классе?
Площадь прямоугольного треугольника равна половине произведения его катетов. 4.
Можно ли найти площадь треугольника по трем сторонам?
Площадь треугольника по формуле Герона (по трем сторонам) Один из способов расчета площади треугольника — использование формулы Герона. Для того, что бы найти площадь треугольника, необходимо знать три его стороны.
Как найти площадь треугольника 7 класс?
площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S ABC = a ⋅ h 2 .
Урок — Версия для печати
Урок — Версия для печати| Урок 3: Тригонометрия |
1 Обзор тригонометрии
| Урок 3: Тригонометрия | |||
| < Уроки | | |||
Тригонометрические функции часто используются в технических дисциплинах.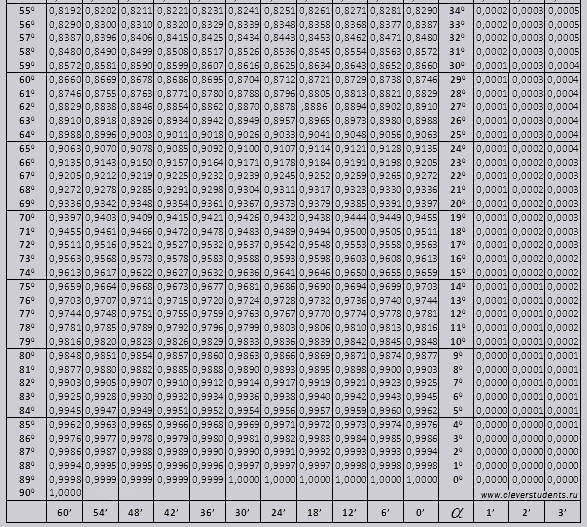 например, природные ресурсы. Особое значение имеет их использование в
землеустройство и измерения. например, природные ресурсы. Особое значение имеет их использование в
землеустройство и измерения.Фундаментальной концепцией тригонометрии является угол . Угол – это мера количества вращения между двумя линии. Углы обычно измеряются в градусов или радиан . Сейчас мы сосредоточимся на понимании степеней, минут и секунд . Углы работают так же, как наша система времени. работает. То есть градус () делится на 60 минут () и минута делится на 60 секунд (). Мы можем записать это как DMS . Мы также можем выразить DMS в виде десятичной дроби. ПримерДавайте решим проблему с преобразованием DMS в десятичное число. степени:
ПримерТеперь давайте попробуем преобразовать десятичные градусы обратно в DMS .
|
Урок для печати | ||
| < Уроки | | |||
2 Синус, косинус и тангенс
| Урок 3: Тригонометрия | |||
Когда у нас есть прямоугольный треугольник , как показано ниже, мы можем
назовите каждую сторону ангела o следующим образом:
Мы можно определить три тригонометрических отношения как синус θ , косинус θ и тангенс θ следующим образом: Чтобы запомнить их, вы можете использовать SOHCATOA
|
Урок для печати | ||
3 Косеканс, секанс и котангенс
| Урок 3: Тригонометрия | |||
Во многих случаях нам потребуется знать обратных отношений тригонометрические функции. Обратное значение находится путем поворота
дробь вверх ногами. Обратное значение находится путем поворота
дробь вверх ногами.Таким образом, обратная функция синуса называется косекансом и равна гипотенузе/противоположной. Обратная величина косинуса Функция называется секансом и равна гипотенузе / смежный, и обратный тангенс функция называется котангенс и равен прилежащему/противоположному. Важно отметить, что существует большая разница между обратное значение csc θ и sin -1 x. косеканс функция означает 1/sin θ, а вторая включает в себя нахождение угла синус которого равен х. |
Урок для печати | ||
4 Представление тригонометрических функций на плоскости x-y
| Урок 3: Тригонометрия | |||
Давайте теперь посмотрим, как мы можем определить тригонометрические функции в терминах
букв вместо слов.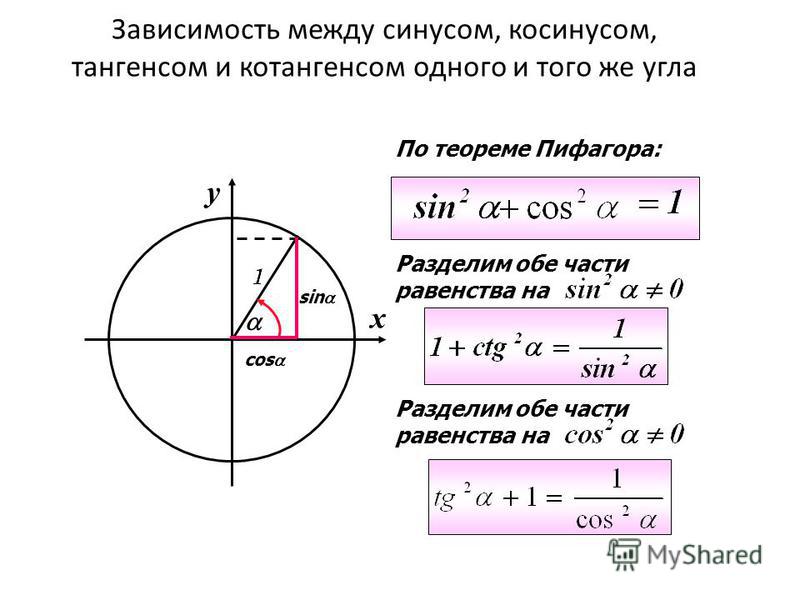 Мы начнем с рассмотрения правого
треугольник вдоль плоскости x-y. Обратите внимание, что гипотенуза теперь
обозначена буквой R, противоположная сторона теперь обозначена буквой Y, а соседняя
сторона теперь помечена как X. Мы начнем с рассмотрения правого
треугольник вдоль плоскости x-y. Обратите внимание, что гипотенуза теперь
обозначена буквой R, противоположная сторона теперь обозначена буквой Y, а соседняя
сторона теперь помечена как X.Теперь мы можем переписать наши тригонометрические функции следующим образом: Точно так же мы можем переписать обратные соотношения в терминах плоскость x-y следующим образом: Переписывая эти отношения, используя определенные значения x, y и r, мы
определили каждую точку, через которую проходит крайняя сторона. Мы
теперь можно использовать теорему Пифагора для решения R. Эта теорема утверждает, что длина стороны R равна квадрату корень из стороны х в квадрате плюс сторона у в квадрате. |
Урок для печати | ||
5 Пример тригонометрических задач
| Урок 3: Тригонометрия | |||||||||||||
| Найдите точные значения для sin θ, cos θ и tan θ, если терминал
боковые проходы (5,12) Сначала посмотрим, что мы знаем.
Мы можем найти R, используя теорему Пифагора , как показано здесь:
Теперь мы знаем длину каждой стороны, X= 5, Y= 12 и R=13 Вспомните следующие уравнения: Все, что нам нужно сделать сейчас, это подставить значения и найти каждый. Sin θ = 0,923 Кос θ = 0,385 Тан θ = 2,4 Теперь давайте воспользуемся той же задачей и решим для CSC θ, SEC θ, и СОТ θ Помните, что мы знаем, что X = 5, Y = 12 и R = 13, также вспомните следующие уравнения: Теперь давайте подставим правильные значения и решим. |
Урок для печати | ||||||||||||
6 Контрольные вопросы
| Урок 3: Тригонометрия | |||
|
Урок для печати | ||
Ищете таблицу преобразования триггеров? Ознакомьтесь с нашим полезным руководством!
Вы ищете таблицу преобразования триггеров , которая поможет вам легко найти необходимые измерения? Если это так, вы пришли в нужное место! Мы составили это краткое руководство по всем наиболее распространенным преобразованиям между различными тригонометрическими функциями и их метриками, включая синус, косинус, тангенс и другие.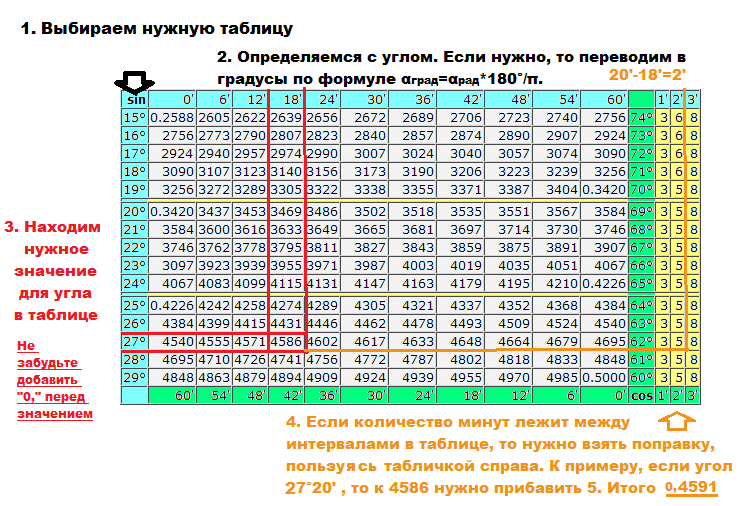 Вам не нужно быть экспертом в тригонометрии, чтобы понять это руководство, просто следуйте инструкциям, пока мы познакомим вас с этими основами! Давайте начнем!
Вам не нужно быть экспертом в тригонометрии, чтобы понять это руководство, просто следуйте инструкциям, пока мы познакомим вас с этими основами! Давайте начнем!
Если вы только начинаете работать с триггером, возможно, вы чувствуете себя немного подавленным. Ведь столько соотношений нужно запомнить! Но не волнуйтесь, мы здесь, чтобы помочь. В этом сообщении блога мы предоставим вам таблицу преобразования триггеров , которая значительно упростит задачу. Поверьте нам, как только вы увидите, как легко пользоваться этой таблицей, вы сразу же станете профессионалом. Итак, давайте взглянем на основы: во-первых, есть три типа углов — острые углы (меньше 90 градусов), прямые углы (90 градусов) и тупые углы (более 90 градусов). Числа внутри треугольника представляют отношение прилежащей стороны к гипотенузе; в то время как значения вне треугольника представляют функции синуса и косинуса. Пока вы помните, что они означают, все будет готово.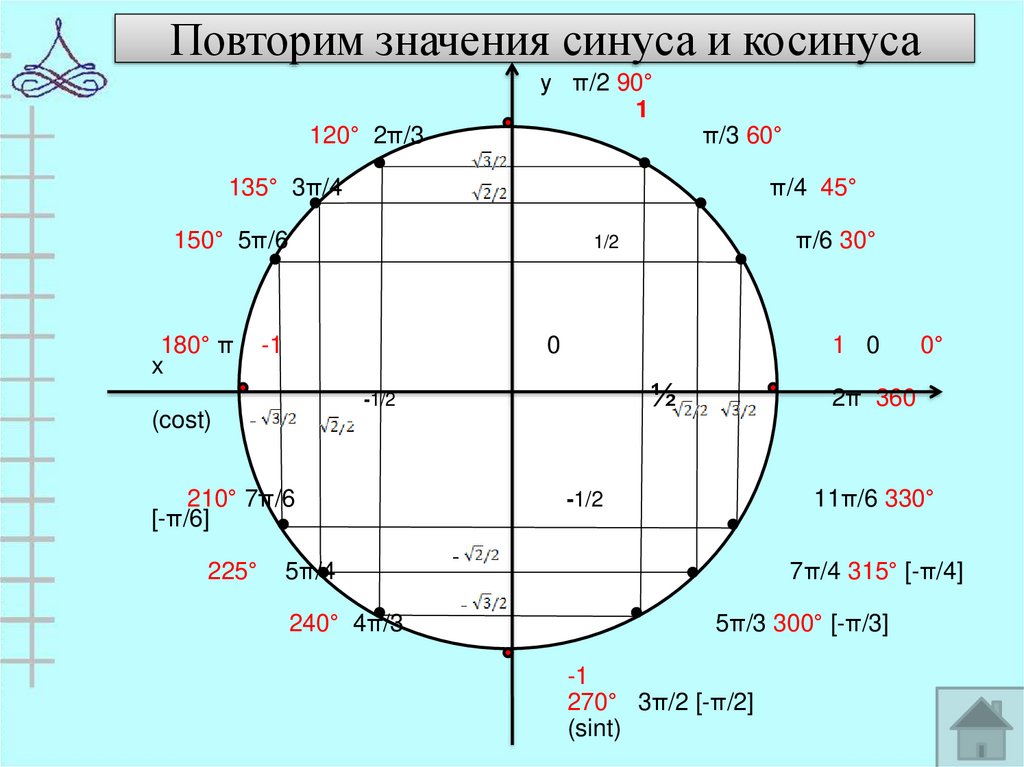
В тригонометрии радиан — это единица измерения, используемая для представления углов. Один радиан равен 57,29.578 градусов. Чтобы преобразовать радианы в градусы, просто умножьте количество радианов на 57,29578. Например, если у вас есть 2 радиана, вы должны умножить 2 на 57,29578, чтобы получить 114,59156 градусов. В качестве альтернативы, чтобы узнать, сколько градусов в радиане, разделите градус на 57,29578. Например, если вы хотите узнать, сколько градусов в 1 радиане, разделите 1 на 57,29578, а затем умножьте результат на 180 градусов. Итак, если у вас есть 1 радиан и вы хотите узнать, сколько в нем градусов, возьмите (1/57,29578) * 180, что равно 0,011727460176961 или примерно 1 градус. Если вам нужно преобразовать радианы в десятичные градусы, используйте следующую формулу: (градусы*57,29578)/радиан. Если вам нужна помощь в преобразовании любых других единиц измерения, ознакомьтесь с нашей полной таблицей преобразования ниже.
Вы можете добавить углы в триггерную таблицу преобразования , найдя сумму их отношений. Для этого вам понадобится таблица преобразования триггеров. Вы можете найти их в Интернете или в учебниках по математике. Получив таблицу, просто найдите отношения углов, которые вы пытаетесь сложить, и сложите их вместе. Например, если вы хотите добавить 45 градусов и 30 градусов, тогда соотношение будет 1:2. Если мы посмотрим на нашу таблицу, то увидим, что добавление 1:2 эквивалентно умножению 45 градусов на 2, что равно 9.0 градусов (1 х 2 = 2). Итак, 45+30=90. Чтобы вычесть углы, вам нужно найти разницу между двумя вычитаемыми углами, а затем поставить отрицательный знак перед одним из них, чтобы это стало проблемой сложения. Например, допустим, я хочу вычесть 35 градусов из 135 градусов. Сначала я бы нашел их разницу, приняв 135-35=100. Затем я бы взял 100 градусов и применил его как отрицательное значение перед прямым углом, поскольку 100 становится -100 при преобразовании в радианы. Теперь моя задача на вычитание будет 130-35=-9.5, но при применении к нашей таблице преобразования он показывает как 130-25=-105 из-за того, что sin(-x) является обратным от sin(x). Последнее, о чем мы хотим знать, — это умножение углов вместе с тригонометрией.
Теперь моя задача на вычитание будет 130-35=-9.5, но при применении к нашей таблице преобразования он показывает как 130-25=-105 из-за того, что sin(-x) является обратным от sin(x). Последнее, о чем мы хотим знать, — это умножение углов вместе с тригонометрией.
Чтобы вычесть триггерную таблицу преобразования , нам просто нужно найти разницу между двумя углами. Для этого воспользуемся формулой: Угол 1 – Угол 2 = Угол 3. Итак, если мы хотим вычесть угол в 45 градусов из угла в 60 градусов, мы будем использовать следующее уравнение: 60 – 45 = 15. Это дало бы нам ответ 15 градусов. Мы также можем складывать и вычитать углы по отношению друг к другу, используя приведенную выше формулу и обращая ее. Например, если мы хотим добавить угол 180 градусов к углу 360 градусов, мы просто воспользуемся формулой 360 + 180 = 540. Однако если мы хотим вычесть угол 180 градусов из угла 360 градусов , мы бы сначала использовали формулу 540 – 180 = 360. Хитрость в том, что когда вы вычитаете любое значение из 360, вы прибавляете его к 360. Итак, каким был бы ответ, если бы мы складывали угол 180 градусов с Угол 1440 градусов? Самый простой способ — вычислить 1440 — 180 = 1260. Однако, если вы возьмете любое число (например, 1440) и разделите его на 8, а затем умножите это число на 10 (1440/8 x 10), вы получите именно такой результат. должно быть, потому что 1440 ÷ 8 = 200 х 10 = 1200
Хитрость в том, что когда вы вычитаете любое значение из 360, вы прибавляете его к 360. Итак, каким был бы ответ, если бы мы складывали угол 180 градусов с Угол 1440 градусов? Самый простой способ — вычислить 1440 — 180 = 1260. Однако, если вы возьмете любое число (например, 1440) и разделите его на 8, а затем умножите это число на 10 (1440/8 x 10), вы получите именно такой результат. должно быть, потому что 1440 ÷ 8 = 200 х 10 = 1200
Таблица преобразования триггеров — это раздел математики, изучающий отношения между сторонами и углами треугольников. Самыми основными отношениями в тригонометрии являются отношения синуса, косинуса и тангенса. Эти соотношения используются для нахождения недостающих сторон и углов треугольников. Коэффициент синуса определяется как отношение длины стороны, противоположной углу, к длине гипотенузы. Отношение косинусов определяется как отношение длины стороны, прилежащей к углу, к длине гипотенузы. Отношение тангенса определяется как отношение длины стороны, противоположной углу, к длине стороны, примыкающей к нему. Слово тангенс происходит от латинского слова tangere, что означает касаться. Имея дело с любым треугольником, важно помнить, что при решении уравнения можно использовать только одно тригонометрическое соотношение.
Отношение тангенса определяется как отношение длины стороны, противоположной углу, к длине стороны, примыкающей к нему. Слово тангенс происходит от латинского слова tangere, что означает касаться. Имея дело с любым треугольником, важно помнить, что при решении уравнения можно использовать только одно тригонометрическое соотношение.
Соотношения синуса, косинуса и тангенса также имеют соответствующие функции arcsin, arccos и arctan. Чтобы вычислить таблицу преобразования триггеров в градусах или радианах, умножьте ее аргумент на 180/π. Чтобы преобразовать градусы в радианы, разделите на 180/π. Чтобы преобразовать радианы в градусы, умножьте на 180/π. Например: Sin(22°) = Sin(ArcTan (1/2)) = ArcTan (1/2) x 180/π = 90°.
6.7 Скорости изменения тригонометрических функций
6.7 Скорости изменения тригонометрических функций
Полезные видео
youtube.com/embed/K_bYVQElows?wmode=transparent&autoplay=0&mute=0&theme=dark&controls=1&autohide=0&loop=0&showinfo=0&rel=0&enablejsapi=0″ frameborder=»0″ title=»External YouTube» aria-label=»External YouTube» data-testid=»youtube» allowfullscreen=»»>Определите среднюю скорость изменения функции
y = 4 cos (x) + 3 для 0 <π/3
. значения y для x = 0 и x = π/3
y = 4 cos (0) + 3 y = 4 cos ( π/3) + 3
= 4(1) + 3 = 4 (1/2) +3
= 7 = 2 + 3
= 5
m = (y2 — y1) ÷ (x2 -x1)
= (5 — 7) ÷ (π/3- 0)
= -2 ÷ π/3
= — 1,91
1 0Следовательно, средняя скорость изменения на этом интервале составляет -1,91
Шаг 2) Используя формулу наклона, рассчитайте среднюю скорость изменения.
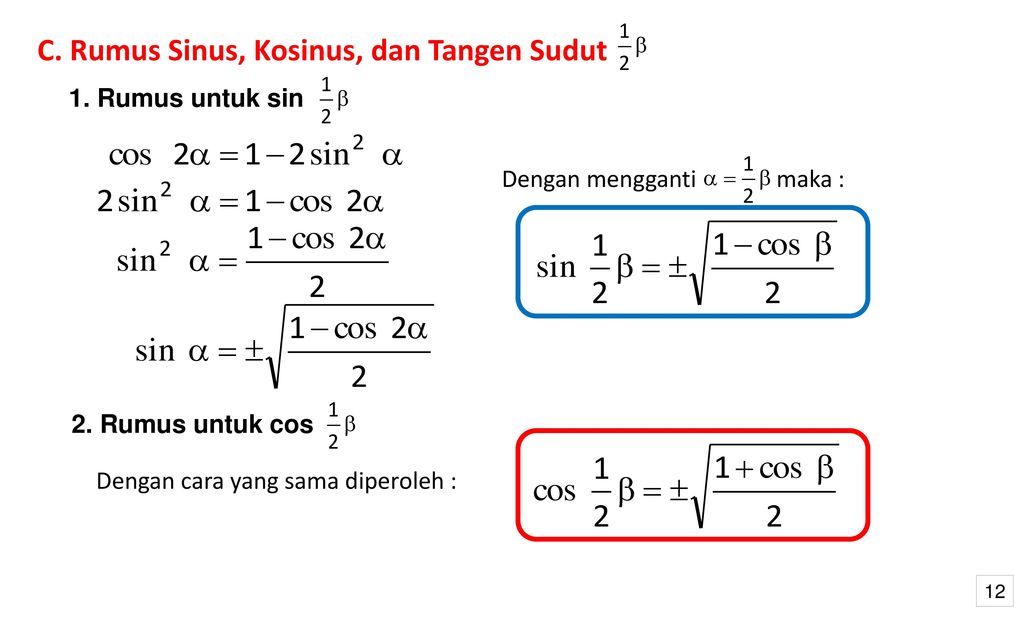 (ПРИМЕЧАНИЕ. Прежде чем продолжить, проще преобразовать угол из радианов в градусы.)
(ПРИМЕЧАНИЕ. Прежде чем продолжить, проще преобразовать угол из радианов в градусы.)Средняя скорость изменения тригонометрических функций находится путем подстановки значений x в уравнение и определения значений y. Получив обе координаты, просто используйте формулу наклона: m=(y2 — y1)÷(x2 — x1). Полученное значение m представляет собой среднюю скорость изменения этой функции за этот интервал.
Мгновенная скорость изменения тригонометрических функций определяется с помощью формулы наклона с координатами, полученными из значений x, которые немного выше и ниже рассматриваемого значения x на долю.
Ознакомьтесь с нашим руководством ниже, чтобы предоставить подробный пример того, как определить среднюю и мгновенную скорость изменения тригонометрических функций.
Скорость изменения тригонометрических функций определяется с помощью методов и стратегий, аналогичных тем, которые используются при работе с другими функциями.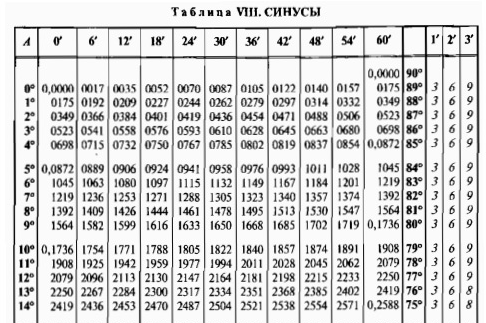
Не помните? Хорошо, давайте кратко рассмотрим их!
Пример 1
Шаг 1) Определите значения y для случаев, когда t= 8,001 и t= 7,999. (ПРИМЕЧАНИЕ: используйте калькулятор для оценки). Не забудьте сохранить несколько (если не все) знаков после запятой.
y = 3 sin 6 (7.999) + 11 y = 3 sin 6 (8.001) + 11
= 13,22922425 = 13,229644468
M = (Y2-Y1) ÷ (x2 -x)
= (13,22964468 -13,22922425) ÷ (8,001-7,999)
= (0,000420428 ÷ 0,002)
= 0,21
= 0,21
0,10 мгновенная скорость изменения
1 90
Шаг 2) Используя формулу наклона, рассчитайте мгновенную скорость изменения.
Определите мгновенную скорость изменения следующей функции при t=8: y = 3 sin 6(t) + 11.
Примеры вопросов
Уровень 1/2
1. Определить среднюю скорость изменения функции y =6 cos 2(x-π/3) + 5 для интервала π/3 x 2π/3.
2. Как мы можем определить, является ли средняя скорость изменения синусоидальной функции положительной или отрицательной для интервала, прежде чем найти среднюю скорость изменения? Объяснять.
Как мы можем определить, является ли средняя скорость изменения синусоидальной функции положительной или отрицательной для интервала, прежде чем найти среднюю скорость изменения? Объяснять.
Уровень 3
Определите мгновенную скорость изменения при t = 14 для следующей функции: H(t) = 4 sin 5 (t) -10.
Проверить ответы
Уровень 4
4. Этой весной температура в Торонто, Онтарио, была аномальной. Температура увеличилась с 0°C до 15°C и снова снизилась с 15°C до 0°C. Этот цикл повторялся каждые 12 часов. Выразите температуру как функцию времени и найдите мгновенную скорость изменения при t = 22.
Наверх
Другие полезные ссылки
Проверьте свою работу!
Ключевые понятия/советы
Определение средней скорости изменения или мгновенной скорости изменения ничем не отличается от расчета с помощью других функций. Те же стратегии используются и для других типов функций. Касательные линии встречаются в точках максимума и минимума функции, из-за ее периодического характера мгновенная скорость изменения равна 0 во многих областях, здесь также наклон касательных равен нулю.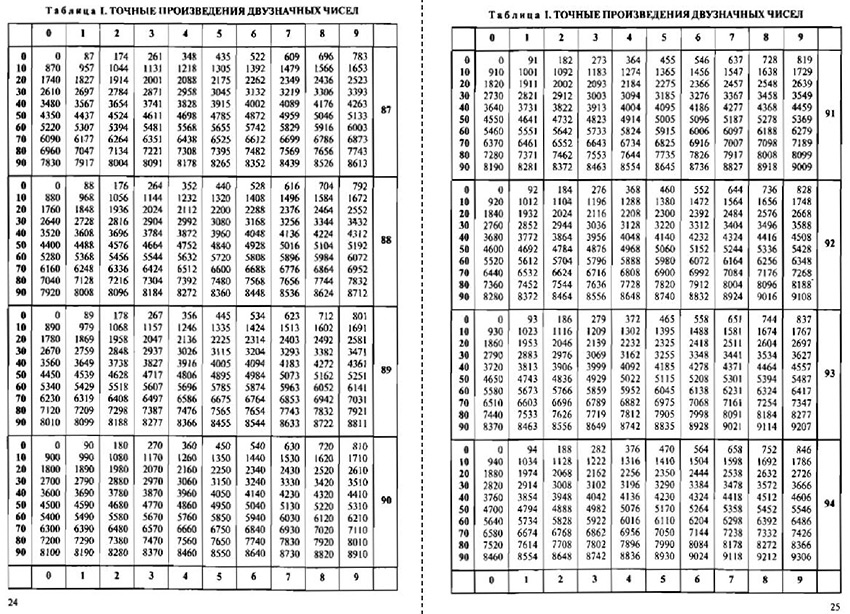

 В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
 . Эти функции находятся: по таблицам Брадиса, в которых для каждого угла приведены свои — строго определенные значения тригонометрических функций (таблицами Брадиса пользовались в «докомпьютерный век»), с помощью «инженерных» калькуляторов или компьютерными программами, в частности — Excel. Для того, чтобы определить значение угла по таблицам Брадиса, нужно водить пальцем по их строкам (с тысячами значений), где найти нужную величину (то ли 5, то ли 6 знаков после запятой). И увидеть соответствующее ему значение угла. Так что, с помощью Excel это делается несравненно быстрее и точнее.
. Эти функции находятся: по таблицам Брадиса, в которых для каждого угла приведены свои — строго определенные значения тригонометрических функций (таблицами Брадиса пользовались в «докомпьютерный век»), с помощью «инженерных» калькуляторов или компьютерными программами, в частности — Excel. Для того, чтобы определить значение угла по таблицам Брадиса, нужно водить пальцем по их строкам (с тысячами значений), где найти нужную величину (то ли 5, то ли 6 знаков после запятой). И увидеть соответствующее ему значение угла. Так что, с помощью Excel это делается несравненно быстрее и точнее. Итак, мы получаем ответ
0,25.
Итак, мы получаем ответ
0,25. Для этого вы
умножьте 0,4 на 60 и вы получите 24 секунды.
Для этого вы
умножьте 0,4 на 60 и вы получите 24 секунды.
 текст
текст  текст
текст