Периметр четверти круга Калькулятор | Вычислить Периметр четверти круга
✖Радиус четверти круга — это длина линии, соединяющей центр и любую точку на изогнутом краю четверти круга.ⓘ Радиус четверти круга [r] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Периметр четверти круга — это общая длина всех граничных ребер четверти круга. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
ⓘ Периметр четверти круга [P]
👎
Формула
сбросить
👍
Периметр четверти круга Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Радиус четверти круга: 5 метр —> 5 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
17.8539816339745 метр —> Конверсия не требуется
< 5 Периметр четверти круга Калькуляторы
Периметр четверти круга формула
Периметр четверти круга = 2*Радиус четверти круга*(1+pi/4)
Что такое четверть круга?
Если мы разрежем круг через любые два перпендикулярных диаметра на четыре равные части, то одна такая часть на самом деле называется четверть круга. Слово «четверть» означает долю одной четверти или 1 из 4. Таким образом, название «четверть круга» связано с тем, что она содержит одну четвертую часть полного круга.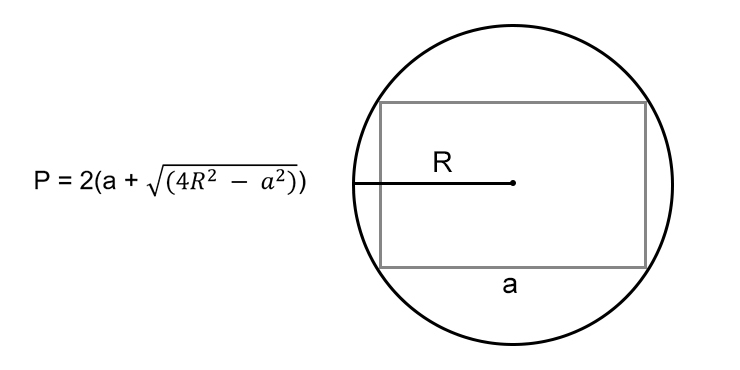
То есть и площадь, и длина дуги составляют одну четвертую долю исходного круга.
Share
Copied!
что это такое, чему равно, история, как округлить
Представляете, мы живем в эпоху технологического прорыва, но до сих пор не можем точно рассчитать площадь съеденного круглого торта? Все потому, что в формуле вычисления площади круга используется число π.
От автомобильного колеса до орбиты спутника, от часового механизма до электромагнитных и звуковых волн. В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.
Что такое число пи
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. Если записать это отношение математическими символами, то выглядит оно так: π = C/d, где C — это длина окружности, а d — диаметр окружности.
То есть π — это результат деления длины окружности на ее диаметр. Но само по себе число пи не является каким-то параметром окружности. Это математическая постоянная, или константа (то есть неизменная), которая нужна для расчета определенных данных. Например, число пи необходимо, чтобы посчитать площадь круга.
Чему равно число пи
Число пи не имеет точного значения. Это легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора. У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.
Число π примерно равно 3,14, или, если точнее, 3,1415926535. Именно значение с десятью знаками после запятой принято использовать. Но все дело в округлении.
Там, где не нужны максимально точные расчеты, за число пи часто берут 3. А вот для точных расчетов в науке ученые используют число пи с 38-ю знаками десятичного разложения (после запятой в десятичной дроби).
Итак:
π = 3,14 или π = 3,1415926535
Как посчитать число пи самостоятельно
Возьмите несколько круглых предметов разного размера, например тарелку, блюдце и крышку от кастрюли. Измерьте окружность каждого. Для этого используйте сантиметровую ленту. Или можно обернуть их по окружности ниткой или веревкой, а потом полученную длину нитки или веревки измерить линейкой. С помощью сантиметровой ленты или линейки измерьте и диаметр каждого предмета. Длина окружности и диаметры у каждого будут разные, ведь предметы разные по размеру.
Теперь для каждого предмета разделите его длину окружности на диаметр. Вы увидите, что во всех случаях, какого бы размера ни был круглый предмет, полученное значение будет 3 целых и далее десятые и сотые доли.
Оно необязательно соответствует принятому значению в 3,14, но всегда будет около него.
Практическое применение числа пи
В школе нас учат использовать число пи для вычисления площади круга. Рассчитывается она по следующей формуле: S = πr², где S — площадь, π — число пи, r² — радиус в квадрате. Можно использовать эту формулу: S = d²/4*π, где d² — диаметр.
Зная число пи и диаметр, можно посчитать длину окружности. Для этого вспомним школьные уравнения. Если π = C/d, то C (длина окружности) высчитывается по формуле C = π*d.
Но применение числа пи в науке гораздо шире. Оно используется практически для любых расчетов в любой области, будь то архитектура, авиация и даже статистика. Например, число π нужно для расчета времени полета самолета и расстояния, которое он должен преодолеть. А в статистике с помощью числа пи рассчитывают значения ниже так называемой кривой нормального распределения. Это нужно для того чтобы, например, выяснить, как распределялись голоса респондентов при опросе.
S (площадь круга) = πr²
История числа пи
Считается, что первым обозначать число пи буквой греческого алфавита π (pi) стал британский математик Уильям Джонс в 1706 году, а популяризировал обозначение его швейцарский коллега Леонард Эйлер в 1737 году. Есть версия, что эта буква выбрана не случайно, а как начальная в греческом слове perijereia, что означает «окружность», «периферия».
Как и на многие явления, известные науке сегодня, на существование некой постоянной, с помощью которой можно посчитать площадь круга, обратили внимание еще в Древнем мире. Но ученые того времени приходили к разному мнению относительно значения этой постоянной: одни использовали значение 3,125, другие — 3,16, третьи — 3,139. Но всегда это значение было 3 с небольшим.
На точное вычисление числа пи ушли тысячелетия. Первым, кто определил более-менее приблизительное значение π, был древнегреческий ученый Архимед. По его расчетам пи равно 3,142857142857143. Как мы знаем сейчас, верными оказались только первые два десятичных числа.
это интересно
Натуральные числа
Их разряды, классы и свойства
подробнее
Точнее оказались расчеты китайского математика 480-х годов нашей эры — 3,1415927. Именно это значение числа пи считалось самым верным до 1420-х годов, пока ученые не расширили этот ряд до 16 цифр после запятой, затем до 20-ти, 32-х и так далее.
В XX веке с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
Популярные вопросы и ответы
Отвечают Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике; Ирина Ходакова, учитель математики.
Как округлить число пи?
Чтобы не запоминать число пи с большим количеством десятичных значений, его принято округлять, — говорит Вячеслав Смольняков. — В математике все округления проводятся по строгим правилам. Для округления значения числа пи применяют метод округления к ближайшему целому. Если перед округляемым числом стоит число 5 и большее, то число округляется в большую сторону. Например, 12,513. Другой пример: 12,5812,613.
Если перед округляемым числом стоит число менее 5, то число округляется в меньшую сторону. Например, 12,412. Или: 12,3412,312.
Итак, возьмем π — 3,1415. Округление начинают с последнего значения, в данном случае это 5. Значит, следующая за ним единица округляется до двух: 3,14153,142. Последнее число 2 меньше пяти, значит, последующее 4 остается неизменным: 3,1423,14. Вот мы и пришли к общепринятому значению числа пи.
По тому же принципу давайте продолжим округление до целого числа: 3,143,23.
И вот у нас получилось значение числа пи 3.
Как запомнить число пи?
Чтобы запомнить значение числа π, — советует Ирина Ходакова, — используют один из самых популярных способов — запомнить фразу, в которой количество букв в каждом слове совпадает с цифрами числа π.
Например, «Что(3) я(1) знаю(4) о(1) круге(5)?»
Чтобы запомнить больше знаков числа π, пользуются различными приемами мнемотехники (совокупность приемов, облегчающих запоминание информации). Например, существует стихотворение С. Боброва «Волшебный двурог» для запоминания числа π, которое совсем не сложно выучить:
«Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь»
Где используется число пи?
Изначально число π было необходимо для применения в строительстве.
Ведь порой из-за погрешности в значении числа π падали башни и рушились целые дворцы. Сейчас π используется в различных сферах нашей жизни.
Мы уже выяснили, что число π позволяет нам рассчитывать и создавать окружности. Если колеса на вашем автомобиле будут немного отличаться друг от друга, то поездки для вас станут как минимум не очень удобными. Но применение числа π этим не ограничивается. Например, без числа π нельзя было бы обеспечить качественную работу телевизоров, радио и телефонов, так как инженеры используют π для расчета и оптимизации звуковых волн. Также π играет важную роль в расчете времени и расстояния путешествия на самолете, так как на большие расстояния самолеты летят по округлой дуге. Не было бы даже многих игр, таких как футбол, баскетбол, теннис, ведь мячи должны быть абсолютно круглыми.
какова площадь круга диаметром 28 ярдов?
Вот ответ на вопросы типа: как найти площадь круга диаметром 28 ярдов?
Круговой калькулятор
| ||||||||||||
Площадь круга диаметром 28 равна 615,8 | |
Изображение кружка = 14d = 28C = 88 | А = πr 2 = π(d2) 2 А = С 2 4π π = 3,1415A = площадь C = окружность или периметр r = радиус , d = диаметр |
Площадь круга в пересчете на
радиусов :Площадь = π·r 2 = 3,14·14 2 = 615,8 квадратных ярдов (*)
Площадь круга относительно
диаметра :Площадь = π·(d2) 2 = 3,14·(282) 2 = 3,14·(14) 2 = 615,8
квадратных ярдов (*)Площадь круга относительно
длины окружности :Площадь = С 2 4π = 87,96 2 4π = 7736,96(4·3,14) = 7736,9612,56 = 615,8 квадратных ярдов (*)
(*) 615,7521601036 ярдов, точно или ограничено точностью этого калькулятора (13 знаков после запятой).
Примечание: для простоты указанные выше операции были округлены до 2 знаков после запятой, а число π округлено до 3,14.
Круг радиусом = 14 или диаметром = 28 или окружностью = 87,96 ярда имеет площадь:
- 0 квадратных километров (км²)
- 0 квадратных метров (м²)
- 0 квадратных сантиметров (см²)
- 0 квадратных миллиметры (мм²)
- 0 квадратных миль (ми²)
- 0 квадратных ярдов (ярдов²)
- 0 квадратных футов (фут²)
- 0 квадратных дюймов (дюйм²)
Используйте калькулятор площади этого круга ниже, чтобы найти площадь круга, учитывая его диаметр или другие параметры. Для расчета площади вам достаточно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть в нижней части калькулятора пошаговое решение.
Формула площади круга
Вот три способа нахождения площади круга (формулы):
Формула площади круга в пересчете на радиус
A = πr 2
Формула площади круга в пересчете на радиус диаметр
A = π(d2) 2
Формула площади круга в пересчете на длину окружности
A = C 2 4π
См.
ниже некоторые определения, относящиеся к формулам: расстояние вокруг края круга.
Радиус
Радиусом круга является любой из отрезков линии от его центра до периметра. Радиус равен половине диаметра или r = d2.
Диаметр
Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности. Диаметр в два раза больше радиуса или d = 2·r.
Греческая буква π
π обозначает число Пи, которое определяется как отношение длины окружности к ее диаметру или π = Cd . Для простоты можно использовать Pi = 3,14 или Pi = 3,1415. Пи — иррациональное число. Первые 100 цифр числа Пи: 3,14159.26535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
. Замечание. (дюйм²) и т. д. …
Окружность часто неправильно пишется как окружность.
Пример расчета площади круга
- Площадь круга диаметром 19,5 единиц
- Площадь круга с окружностью 90,8 километра
- Площадь круга с радиусом 15,6 метра
- Площадь круга с окружностью 15,4 единиц
- Площадь круга с окружностью 13,3
- Площадь круга с радиусом 40 миль 181818 Круг диаметром 25 ярдов
- Площадь круга радиусом 1 фут
- Площадь круга радиусом 5,1 сантиметра
Отказ от ответственности ни этот веб-сайт, ни его авторы не несут ответственности за любые ошибки или упущения.
Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.Научитесь вычислять периметр круга с помощью уравнений
В уроке Периметр круга мы собираемся обсудить,
- Периметр полукруга
- Периметр четверти круга
- Периметр сектора
Что такое периметр круга
Прежде чем перейти к периметру, давайте вспомним некоторые сведения об основных свойствах круга.
- Центр окружности
- Диаметр круга
- Радиус окружности
Центр круга
Центр — это точная середина окружности.
Другими словами, мы также можем определить Центр как точку, в которой ось симметрии окружности пересекается с центром.
Диаметр окружности
Диаметр – это прямой отрезок, соединяющий две точки окружности и проходящий через центр окружности.
В этом круге AB — диаметр.
Радиус окружности
Отрезок прямой линии, соединяющий центр с любой точкой окружности, называется радиусом окружности.
Если центр — «О», а точка на окружности — «В», то OB — это радиус окружности.
OB и OD — это «Радиусы» (множественное число от радиуса) круга.
Существует связь между диаметром и радиусом
Диаметр – AB
Радиусы – AO и BO
AB = AO + BO
АВ = АО + АО ; потому что BO = AO
AB = 2 AO
Диаметр = 2 x радиус
Диаметр круга в два раза больше его радиуса.
Простое значение периметра – это длина вокруг замкнутой плоской фигуры
Когда дело доходит до кругов, мы также называем его окружностью круга
Формула окружности
Для полного круга
Если «O» — центр, а «r» — радиус этой окружности.
Окружность ‘c’ будет,
c = 2πr
Здесь π — постоянная величина.
Пример 01:
Найдите длину окружности радиусом 14см.
Длина окружности c = 2πr
Следовательно, длина окружности равна 88 см.
Когда вместо радиуса указан диаметр, мы получаем другое уравнение окружности.
Пусть « d » — диаметр, а « r » — радиус.
д = 2πr (удвоенный радиус равен диаметру)
Если длину окружности обозначить как ‘ c ‘
c = 2πr
Мы также можем записать формулу длины окружности как
c = π x d (d = 2πr)
c = πd
Пример 02:
Найдите длину окружности диаметром 21см.
В этом примере речь идет об отношении диаметра к окружности.
Следовательно, окружность равна 66 см.
Упражнение 01
Найдите длину окружности по измерениям, указанным ниже.
- Радиус 7 см
- Диаметр 28 м (подсказка: преобразуйте в смешанное число)
- Диаметр 17 1/2 см
- Радиус 10,5 м
*Ответы даны в конце статьи.
Периметр полукруга
Когда круглая пластинка разделена на две равные части по диаметру, каждая часть называется полукругом.
Длина дуги полукруга радиусом
Из рисунка видно, что для нахождения периметра полукруга к длине дуги нужно прибавить диаметр.
Периметр полукруга радиусом
Пример 03:
Найдите периметр полукруга, если его диаметр равен 21см.
Вы можете обратиться к статье об умножении дробей, чтобы узнать об упрощениях.
2r = диаметр = 21 см
Следовательно, периметр полукруга
= 33см + 21см
= 54см
Упражнение 02:
Найдите периметр полукруглой пластинки с размерами, указанными ниже.
- Радиус = 14 см
- Диаметр = 7 см
*Ответы даны в конце статьи.
Периметр четверти круга
Длина дуги четверти окружности
Из рисунка видно, что для нахождения периметра четверти круга к длине дуги нужно прибавить два радиуса.
Периметр четверти круга
Пример 04:
Если радиус равен 28 см, найдите периметр четверти окружности.
Следовательно, периметр четверти круга
= 44см + 56см
= 100см
Периметр сектора круга
Область, ограниченная двумя радиусами и дугой, называется сектором окружности.
Угол, образуемый дугой в центре окружности, называется центральным углом.
Здесь центральный угол равен ‘ θ ‘
Угол в центре окружности равен 360 o . Длина дуги, относящаяся к углу 360 o , равна 2π r .
Глядя на приведенную выше диаграмму, мы можем сказать, что
Для 360 o длина дуги будет 2π r .
Длина дуги сектора круга радиусом r ’ и центральный угол ‘ π ’.
Пример 05:
Найдите периметр
Длина дуги 11см.