Периодические функции — подготовка к ЕГЭ по Математике
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.
Дадим определение периодической функции:
Функция называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения
Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.
Например, — периодические функции.
Для функций и период ,
Для функций и период
Но не только тригонометрические функции являются периодическими.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:
1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения
График функции может выглядеть, например, вот так:
Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.
Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.
Значения функции в точках -3 и 7 равны пяти. Мы получим:
2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).
Построим график функции при
Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.
Период функции равен 2. Повторим периодически участок длины 2, который уже построен.
Найдем
3. Найдите наименьший положительный период функции
Наименьший положительный период функции равен
График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).
Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен . Значит, на отрезке укладывается ровно 3 полных волны функции
Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции
Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен .
4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции
По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через .
Если мы выберем любую точку на графике функции то через значение функции будет такое же, как и в точке
Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке
На каком же расстоянии от точки расположена точка, в которой значение функции такое же, что и в точке ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, .
Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.
Период суммы тригонометрических функций : Чулан (М)
| Alexey1 |
| |||
08/09/07 |
| |||
| ||||
04.2009, 07:03 | gris |
| |||
13/08/08 |
| |||
| ||||
04.2009, 07:13 | Alexey1 |
| |||
08/09/07 |
| |||
| ||||
04.2009, 07:34 | gris |
| |||
13/08/08 |
| |||
| ||||
04.2009, 08:00 | Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 4 ] |
Модераторы: Модераторы Математики, Супермодераторы
Амплитуда, период, фазовый сдвиг и частота
Некоторые функции (такие как синус и косинус) повторяются вечно
и называются периодическими функциями.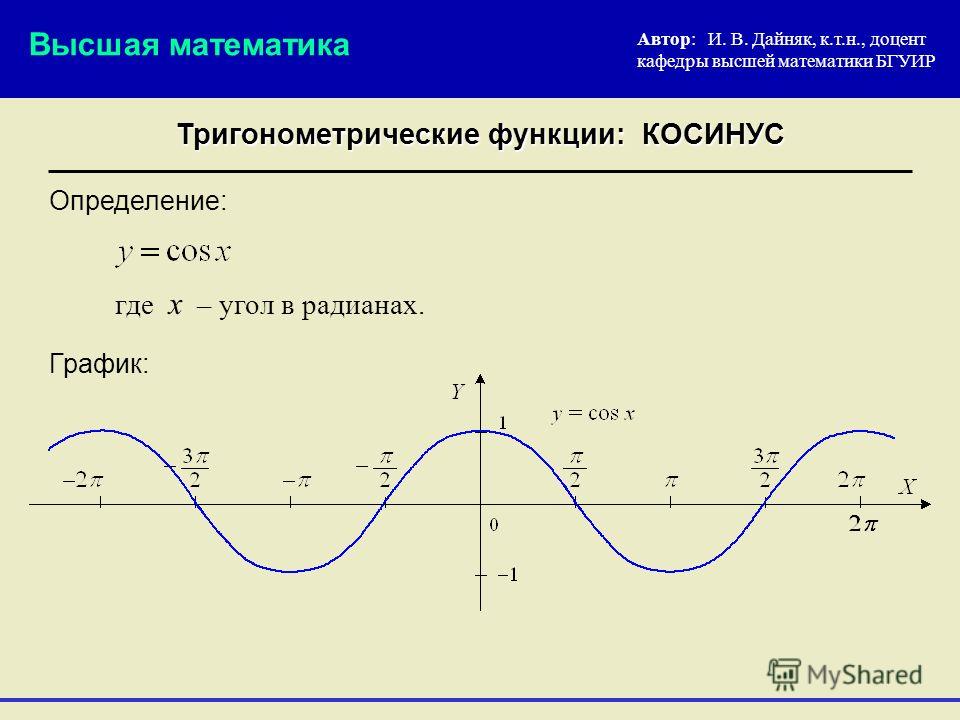
Период идет от одного пика к другому (или от любой точки к следующей точке совпадения):
Амплитуда — это высота от центральной линии до пика (или до впадины). Или мы можем измерить высоту от самой высокой до самой низкой точки и разделить ее на 2.
Фазовый сдвиг показывает, насколько функция сдвинута по горизонтали от обычного положения.
Сдвиг по вертикали показывает, насколько функция смещена по вертикали от обычного положения.
Все вместе!
Мы можем получить их все в одном уравнении:
у = А грех(В(х + С)) + D
- амплитуда A
- период равен 2π/B
- фазовый сдвиг C (положительный слева )
- вертикальное смещение D
А вот как это выглядит на графике:
Обратите внимание, что здесь мы используем радианы, а не градусы, и на один полный оборот приходится 2π радиан.
Пример: sin(x)
Это основная формула неизменного синуса. А = 1, В = 1, С = 0 и D = 0
Итак, амплитуда 1 , период 2π , фазового или вертикального сдвига нет:
Пример: 2 sin(4(x − 0,5)) + 3
- амплитуда A = 2
- период 2π/B = 2π/4 = π/2
- фазовый сдвиг = −0,5 (или 0,5 вправо)
- вертикальное смещение D = 3
Прописью:
- 2 говорит нам, что он будет в 2 раза выше, чем обычно, поэтому Амплитуда = 2
- обычный период равен 2 π , но в нашем случае он «ускорен» (укорочен) 4 в 4 раза, поэтому период = π/2
- и −0,5 означают, что он будет сдвинут на вправо на 0,5
- , наконец, +3 говорит нам, что центральная линия равна y = +3, поэтому вертикальное смещение = 3
Вместо x у нас может быть t (для времени) или другие переменные:
Пример: 3 sin(100t + 1)
Сначала нам нужны скобки вокруг (t+1), поэтому мы можем начать с деления 1 на 100:
3 sin(100t + 1) = 3 sin(100 (t + 0,01))
Теперь мы можем видеть:
- амплитуда равна A = 3
- период равен 2π/100 = 0,02 π
- фазовый сдвиг равен C = 0,01 (влево)
- вертикальное смещение равно D = 0
И получаем:
Частота
Частота — это то, как часто что-то происходит в единицу времени (на «1»).
Пример: Здесь функция косинуса повторяется 4 раза между 0 и 1:
Таким образом, Частота равна 4
А Период равен
На самом деле Период и Частота связаны:
Частота = 1 Период
Период = 1 Частота
Пример из предыдущего: 3 sin(100(t + 0,01))
Период равен 0,02 π
Таким образом, частота равна 1 0,02π знак равно 50 №
Еще несколько примеров:
| Период | Частота |
|---|---|
| 1 10 | 10 |
| 1 4 | 4 |
| 1 | 1 |
| 5 | 1 5 |
| 100 | 1 100 |
Когда частота равна в секунду , это называется «Герц».
Пример: 50 Гц означает 50 раз в секунду
Чем быстрее он отскакивает, тем больше «Герц»!
Анимация
../алгебра/изображения/wave-sine.js
7784,7785,7788,7789,9863,7793,7794,7795,7796,7792
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домен y=cos x