1. Первообразная и неопределенный интеграл
Определение: Функция F(x) называется первообразной для функции
f(x) на интервале (a,b), если на этом интервале существует
производная F'(x) и F'(x)=f(x).
Теорема: Если F1(x) и F2(x) —
первообразные для одной и той же функции f(x), то их разность есть
величина постоянная.
Докозательство: По условию F’1(x)=F’2(x)=f(x)
обозначим: Ф(x)= F1(x) — F2(x). Очевидно, Ф'(x)
равняется нулю во всем промежутке (a,b), где определены первообразные F
1(x) и F2(x). Для любых х1, x2
,Î (a,b) по формуле Лагранжа Ф(х1)-Ф(х2
)=Ф'(c)(b-a).
1)=Ф(х2). Это означает, что Ф(х) сохраняет постоянное
значение на промежутке (a,b), т.е. F1(x) — F2(x)
=С.
Следствие: Если для функции f(x) первообразной на интервале (a,b) является
функция F(x), то ее любая другая первообразная для f(x) имеет вид F(x)+C, где
С — произвольная постоянная.
Определение: Неопределенным интегралом от функции f(x) называется совокупность
всех первообразных этой функции. Он изображается так: ∫ f(x)dx,
где ∫- знак интеграла, f(x)dx — подынтегральное выражение,f(x) —
подынтегральная функция.
Из определения вытекает, что
И следовательно d(∫f(x)dx)=f(x)dx. С другой стороны,
∫F'(x)dx=∫dF(x)=F(x)+C.
Если F(x) — какая-нибудь первообразная для f(x), то учитывая приведенное выше
следствие, можно написать: ∫ f(x) dx = F(x)+C, где С-
произвольная
постоянная.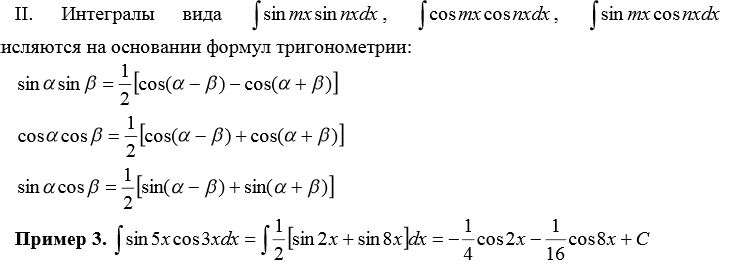 Путем дифференцирования
обеих частей равенства легко
Путем дифференцирования
обеих частей равенства легко
доказать справедливость следующих свойств:
1. ∫ Аf(x)dx = A ∫ f(x)dx (постоянный множитель можно
выносить за знак интеграла).
2. ∫[f(x)-f(x)]dx=∫f(x)dx+∫f(x)dx (интеграл от суммы
функций равен сумме интегралов от этих функций).
2. Основные методы интегрирования
Замена переменной.
Будем полагать функции f(u) и φ'(x) непрерывными. Замена переменной
производится по формуле:
Формула проверяется дифференциалом обеих частей равенства по x (правая часть
дифференцируется как сложная функция).
Интегрирование по частям:
Пусть u и v являются функциями x. Умножив обе части равенства (uv)’=u’v+uv’
на dx, получим d(uv)=vdu+udv. Интегрируя приходим к формуле интегрирования по
частям
3. Интегрирование тригонометрических уравнений
1) Интегрирование дифференциалов
В любом промежутке вида для интегрирования указанных дифференциалов можно применить универсальную подстановку
Таким образом,
интеграл всегда выражается в конечном виде.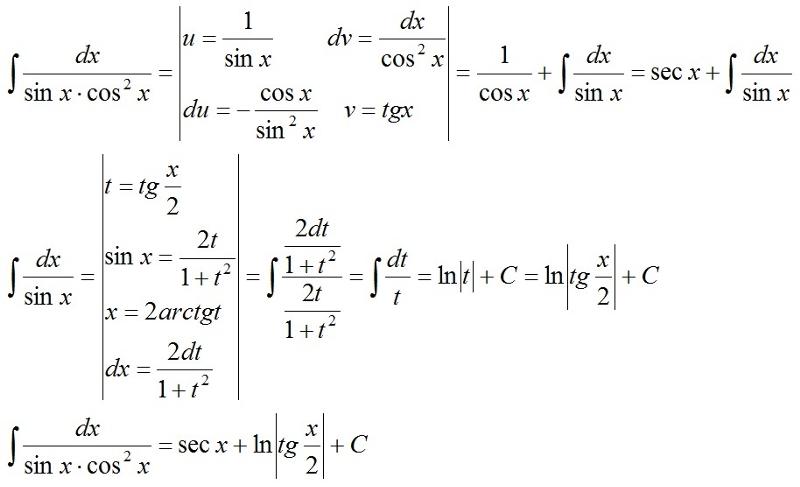 Для
их выражения кроме функций встречающихся
при интегрировании рациональных
выражений нужны лишь тригонометрические
функции.
Для
их выражения кроме функций встречающихся
при интегрировании рациональных
выражений нужны лишь тригонометрические
функции.
2) Универсальная подстановка всегда ведет к цели, но в силу своей общности, она часто не является лучшей в плане краткости.
Рассмотрим частные случаи:
, данный интеграл находится с помощью тригонометрических формул в зависимости от n и m.
а) Если хотя бы одно из n и m положительно и нечетно, то от нечетной степени отделяем множитель, а оставшийся, в четной степени, преобразуем через , отделенный множитель вместе с dx дают либо дифференциал синуса, либо косинуса.
б) Если n и m оба положительные и четные, то применяем формулы понижения порядка
в) Если выгодно выполнить
Математический анализ. Интегральное исчисление
Математический анализ. Интегральное исчисление
Интегральное исчисление
ОглавлениеПРЕДИСЛОВИЕГлава I. НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ 2. Первообразная функция. 3. Определения неопределенного и определенного интегралов. 4. Таблица основных интегралов. 5. Свойства неопределенного интеграла. 6. Свойства определенного интеграла. § 2. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ 2. Интегрирование по частям в определенном интеграле. § 3. ИНТЕГРИРОВАНИЕ МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ 2. Замена переменной в определенном интеграле. 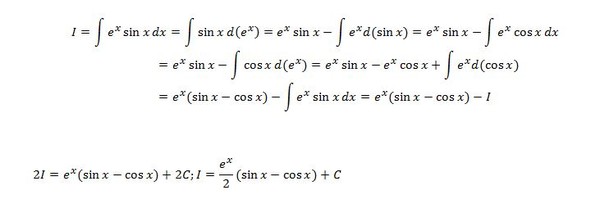 § 4. МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ § 5. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интегрирование правильных дробей. 3. Интегрирование неправильных дробей. § 6. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ § 7. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИ § 8. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ С ПОМОЩЬЮ ТАБЛИЦ Глава II. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА § 1. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ЧИСЛО, РАЗДЕЛЯЮЩЕЕ ДВА ЧИСЛОВЫХ МНОЖЕСТВА 2. Определенный интеграл как разделяющее число. 3. Свойства нижних и верхних сумм Дарбу. 4. Необходимое и достаточное условие интегрируемости функции. 5. Интегрируемость монотонных функций. 6. Интегрируемость непрерывных функций. § 2. СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ ДЛЯ НЕПРЕРЫВНОЙ ФУНКЦИИ 2. Среднее значение функции. 3. Дифференцирование определенного интеграла по верхнему пределу. 4. Формула Ньютона—Лейбница. § 3. СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Интегрирование четных, нечетных и периодических функций. 3. 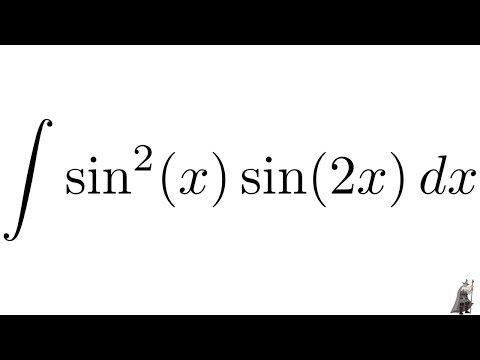 Интегрирование неравенств. Интегрирование неравенств.§ 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Признаки сходимости несобственных интегралов 1-го рода. § 5. ИНТЕГРАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ Глава III. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР 2. Квадрируемые области. 3. Свойства площадей квадрируемых фигур. 4. Вычисление площади плоской фигуры в декартовых координатах. 5. Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями. 6. Площадь в полярных координатах. § 2. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ 2. Объем прямого цилиндрического тела. 3. Вычисление объема тела по площадям параллельных сечений. 4. Принцип Кавальери. 5. Объем тела вращения. § 3. ВЫЧИСЛЕНИЕ ДЛИН ДУГ 2. Достаточное условие спрямляемости кривой. 3. Вывод формулы длины дуги регулярной кривой. 4. Частные случаи формулы длины кривой. 5. Необходимое и достаточное условие спрямляемости кривой.  § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ § 5. ПЛОЩАДЬ ПОВЕРХНОСТИ ВРАЩЕНИЯ § 6. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ К РЕШЕНИЮ ФИЗИЧЕСКИХ ЗАДАЧ 2. Вычисление статических моментов и координат центров тяжести плоских фигур. 3. Теоремы Гульдина—Паппа. 4. Вычисление моментов инерции. 5. Другие приложения интегрального исчисления к физике. ПРИЛОЖЕНИЕ 1. ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ ПРИЛОЖЕНИЕ 2. ПРИМЕРНЫЕ ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ ОТВЕТЫ |
Прикладные науки | Бесплатный полный текст
1. Введение
Нелинейные системы играют важную роль в обработке музыкальных сигналов. В частности, существует множество эффектов, классифицируемых как овердрайв, дисторшн или фузз, основной целью которых является введение гармонического искажения для обогащения сигнала. Обычно нелинейное поведение сочетается с (линейной) фильтрацией для спектрального формирования выходного сигнала или для того, чтобы количество вносимых искажений зависело от частоты.
Одной из основных проблем, возникающих в цифровых нелинейных системах, независимо от того, были ли они разработаны с нуля или получены с помощью виртуального аналогового моделирования, является искажение наложения. Как только дополнительные гармоники, вносимые нелинейностью, превышают предел Найквиста на половине частоты дискретизации, они возвращаются к более низким частотам, как если бы соответствующий аналоговый сигнал был дискретизирован без соответствующего ограничения полосы. В отличие от желаемого гармонического искажения, искажение наложения обычно воспринимается как неприятное. Следовательно, необходимы методы для подавления или уменьшения искажения наложения спектров.
Концептуально простейший метод уменьшения алиасинга — передискретизация. Однако, если гармоники медленно затухают с частотой, коэффициент передискретизации должен быть высоким, что делает этот подход непривлекательным из-за растущих вычислительных требований. Следовательно, были предложены различные альтернативы, например [5,6,7,8,9,10,11]. Однако эти методы обычно имеют определенные ограничения, чаще всего ограничения для систем без памяти. В этой работе представлено расширение [10], которое ослабляет ограничение от систем без памяти до определенного класса систем с состоянием.
Следовательно, были предложены различные альтернативы, например [5,6,7,8,9,10,11]. Однако эти методы обычно имеют определенные ограничения, чаще всего ограничения для систем без памяти. В этой работе представлено расширение [10], которое ослабляет ограничение от систем без памяти до определенного класса систем с состоянием.
Эта статья является продолжением нашего предыдущего доклада на конференции [12]. Основными отличиями являются обобщение метода на случай нескольких параллельных нелинейных функций и дополнительное обсуждение нелинейностей с векторным входом.
2. Уменьшение псевдонимов на основе первообразных для нелинейных вычислений без памяти Системы
Поскольку предлагаемый метод основан на подходе из [10], мы кратко резюмируем его. Концептуально цифровой сигнал преобразуется в сигнал непрерывного времени с использованием линейной интерполяции между последовательными выборками, применяется нелинейность, и результат подвергается фильтрации нижних частот путем интегрирования в течение одного интервала выборки перед повторной выборкой для получения цифрового выходного сигнала.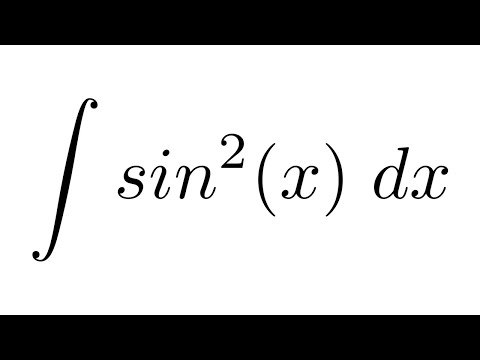 Таким образом, нелинейная система
Таким образом, нелинейная система
где f(u) обозначает нелинейную функцию, отображающую входную выборку u(n) в выходную выборку y(n), которая преобразуется в
Лишь в редких случаях интеграл будет иметь закрытое решение, а численное интегрирование во время выполнения непривлекательно, учитывая вычислительную нагрузку. Однако, переключая переменную интегрирования, мы получаем
где мы можем применить фундаментальную теорему исчисления и, дополнительно применив u(n) ≈ u(n−1), чтобы избежать числовых проблем, мы, наконец, придем к
где F(u)=∫f(u)du — первообразная функции f(u). Опять же, первообразная может не иметь закрытого решения, но будучи функцией одной переменной, она может быть предварительно вычислена и сохранена в таблице поиска.
Помимо уменьшения артефактов алиасинга, подход вводит полувыборочную задержку и ослабляет компоненты сигнала не только выше предела Найквиста, но и на высоких частотах ниже его, т. е. действует как фильтр нижних частот в звуковом диапазоне . Это можно легко увидеть, если использовать тождественную функцию f(u)=u вместо истинной нелинейности. В этом случае прямой расчет дает
е. действует как фильтр нижних частот в звуковом диапазоне . Это можно легко увидеть, если использовать тождественную функцию f(u)=u вместо истинной нелинейности. В этом случае прямой расчет дает
который представляет собой фильтр нижних частот с конечной импульсной характеристикой первого порядка с групповой задержкой, равной половине выборки. Эффекту нижних частот можно противодействовать небольшой передискретизацией (например, в два раза), и задержка обычно не вызывает беспокойства.
Многомерный случай
Прежде чем перейти к системам с состоянием, мы кратко обсудим, как снять ограничение на системы с одним скалярным входом u(n) и одним скалярным выходом y(n), которые до сих пор спокойно предполагались. Для краткости обозначений мы собираем входы u1(n),u2(n),…,uKu(n) системы со скалярными входами Ku во входной вектор u(n)=u1(n)u2(n) ⋯uKu(n) (жирным шрифтом обозначены векторы здесь и далее). Аналогично, несколько выходных данных собираются в выходной вектор y(n)=y1(n)y2(n)⋯yKy(n).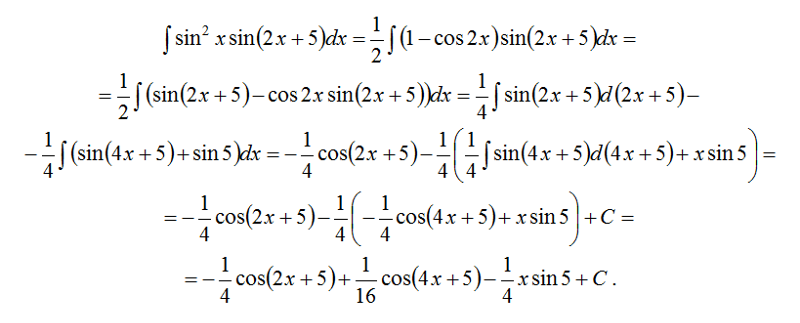 Сначала мы можем заметить, что расширение для векторнозначного вывода является прямым: приведенный выше вывод вообще не зависит от того факта, что нелинейная функция (или ее первообразная) является скалярнозначной.
Сначала мы можем заметить, что расширение для векторнозначного вывода является прямым: приведенный выше вывод вообще не зависит от того факта, что нелинейная функция (или ее первообразная) является скалярнозначной.
С другой стороны, с векторным вводом дела обстоят не так хорошо. В частности, мы больше не можем переписывать (2) как (3). Таким образом, если интеграл в (2) не имеет закрытого решения, чтобы избежать численного решения во время выполнения, мы почти застряли с предварительным вычислением и табулированием решения для всех комбинаций u(n) и u(n−1) при определенная плотность. Таким образом, если входные данные имеют Ku-размерность, то для формирования вектора поиска (индекса) необходимо использовать два последовательных входных вектора, наложенных один на другой, для формирования вектора поиска (индекса), нам потребуется таблица поиска размером 2Ku. Небольшое улучшение возможно, если понять, что мы всегда интегрируем по линиям, а линия может быть параметризована параметрами 2Ku−2 в Ku-мерном пространстве.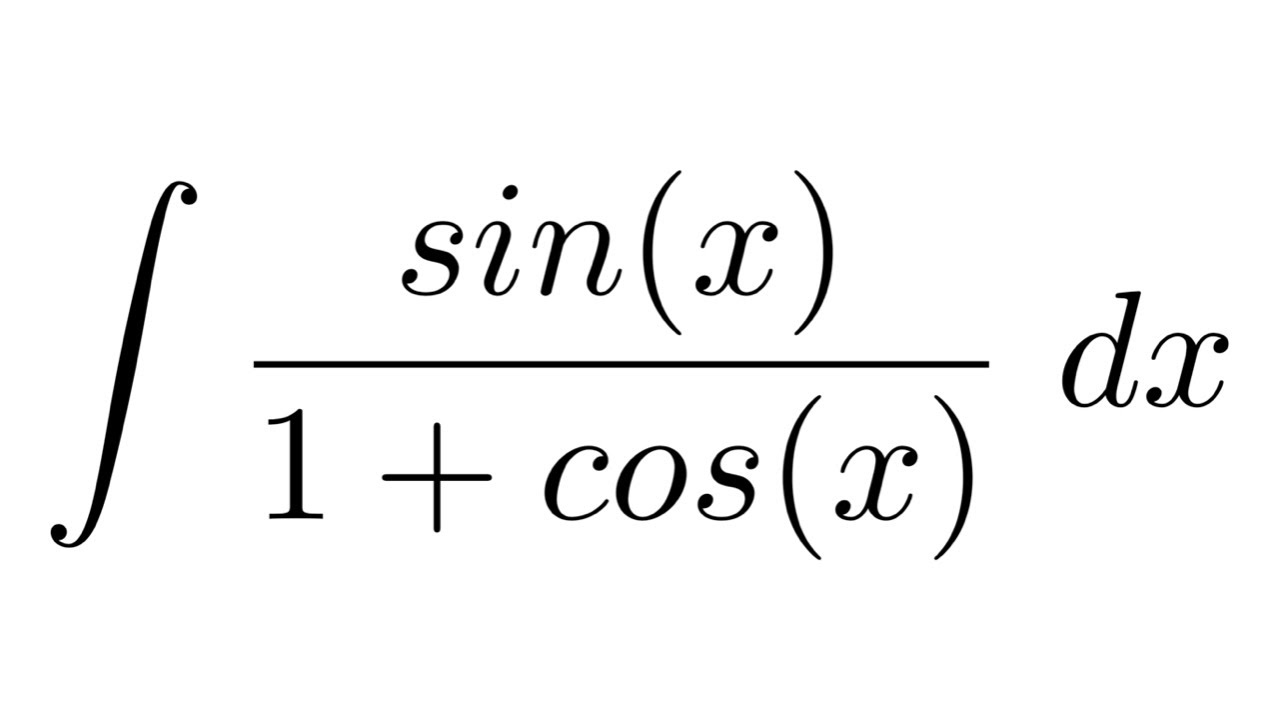 Вдоль линии мы можем предварительно вычислить первообразную относительно скалярной координаты вдоль линии. Эта первообразная с одномерным аргументом и параметрами 2Ku-2 может быть сохранена в 2Ku-1-мерной таблице поиска. Хотя это может быть разумным для Ku = 2, это быстро становится невозможным для больших Ku из-за непомерно высоких требований к памяти.
Вдоль линии мы можем предварительно вычислить первообразную относительно скалярной координаты вдоль линии. Эта первообразная с одномерным аргументом и параметрами 2Ku-2 может быть сохранена в 2Ku-1-мерной таблице поиска. Хотя это может быть разумным для Ku = 2, это быстро становится невозможным для больших Ku из-за непомерно высоких требований к памяти.
3. Расширение для систем с отслеживанием состояния
Задержка на полвыборки, введенная методом [10], становится проблематичной, если нелинейность встроена в контур обратной связи системы с отслеживанием состояния. Как отмечено в [10], для частного случая интегратора, следующего за нелинейностью и использующего правило трапеций для временной дискретизации, можно просто заменить числитель передаточной функции дискретизированного интегратора фильтром, введенным сглаживанием. Это слияние нелинейности со сглаживанием и интегратора не имеет дополнительной задержки по сравнению с системой без сглаживания, поэтому его можно без проблем использовать внутри системы с обратной связью.
Здесь мы рассматриваем системы, которые не обязательно имеют интегратор, следующий за нелинейностью. В частности, мы будем рассматривать общую дискретную нелинейную систему в пространстве состояний
с
где x(n)∈RKx — вектор состояния, u(n)∈RKu — входной вектор, y(n)∈RKy — выходной вектор. Нелинейность системы фиксируется (потенциально) нелинейными функциями fx,l:RKpx,l→RKx и fy,m:RKpy,m→RKy для обновления состояния и вывода соответственно. Их аргументы px,l(n)∈RKpx,l и py,m(n)∈RKpy,m вычисляются по (8) и (9) как линейную комбинацию предыдущих состояний и текущего входа, где матрицы коэффициентов Cpx,l∈RKpx,l×Kx, Dpx,l∈RKpx,l×Ku, Cpy,m∈RKpy,m×Kx и Dpy,m∈RKpy ,m×Ku зависят от системы. Несколько замечаний по порядку:
Мы допускаем не только множественные состояния, собранные в векторе x(n), но также множественные входы в u(n) и множественные выходы в y(n).
 Однако во многих приложениях ввод и вывод будут скалярными.
Однако во многих приложениях ввод и вывод будут скалярными.Хотя наличие только одной нелинейной функции в правой части, т. е. L=M=0, вполне допустимо, мы допускаем разложение на сумму нескольких функций. Мы делаем это потому, что, как обсуждалось выше, нелинейные функции со скалярным или очень низкоразмерным аргументом гораздо лучше подходят для предлагаемого метода, чем функции с многомерным аргументом. Таким образом, хотя мы теоретически допускаем векторные значения px,l(n) и py,m(n) произвольной размерности, с практической точки зрения их размерности Kpx,l и Kpy,m должны быть низкими. Следовательно, если нелинейность системы можно разложить на сумму нелинейных функций с малоразмерными аргументами, так и должно быть. Следует, однако, отметить, что, к сожалению, не все системы допускают такое разложение своей нелинейности.
Часто бывает желательно различать линейные и нелинейные части этой системы. Позволяя fx,0(px,0(n))=px,0(n) и fy,0(py,0(n))=py,0(n) быть тождественной функцией и далее переименовывая A=Cpx, 0∈RKx×Kx, B=Dpx,0∈RKx×Ku, Cy=Cpy,0∈RKy×Kx и Dy=Dpy,0∈RKy×Ku, поэтому мы перепишем нашу систему как
Визуальное представление представлено в виде блок-схемы на рисунке 1.

Если система получена в контексте виртуального аналогового моделирования, обычно нелинейные функции будут заданы только неявно (как решение того, что иногда называют в качестве контура без задержек), что делает необходимым решение нелинейного уравнения. Однако они, как правило, основаны на общем наборе функций fm, применяя только разное взвешивание к своим выходам, т. е.
с L=M и pm(n)=px,m(n)=py,m(n). Хотя эту избыточность следует иметь в виду для оптимизации реализации, мы выведем наш метод для более общего случая возможных независимых нелинейных функций для обновления состояния и вывода.
На первом этапе мы можем рассмотреть применение подавления алиасинга только к fy,m(py,m), поскольку они не являются частью какой-либо петли обратной связи. Однако мы должны быть осторожны и не можем просто заменить fy,m на f˜y,m в (11), поскольку это привело бы к смещению во времени линейных и сглаженных нелинейных членов. Вместо этого мы должны применить сглаживание также и к линейной части fy,0, хотя очевидно, что оно не вносит искажения алиасинга. К счастью, интеграл имеет замкнутое решение независимо от размерности, а именно
Вместо этого мы должны применить сглаживание также и к линейной части fy,0, хотя очевидно, что оно не вносит искажения алиасинга. К счастью, интеграл имеет замкнутое решение независимо от размерности, а именно
в результате чего
Однако любое искажение наложения спектров, вносимое в x(n) с помощью (10), не подвергается никакому смягчению (за исключением фильтрации нижних частот).
Теперь, если мы наивно перепишем (10), как мы сделали с (11), мы изменим нашу систему нежелательным образом, так как введем дополнительную задержку в обратной связи. Но мы делаем это очень контролируемым образом: единичная задержка обратной связи заменяется задержкой в 1,5 сэмпла. Поскольку задержка в 1,5 отсчета соответствует задержке в один отсчет при частоте дискретизации, равной 23, мы можем компенсировать дополнительную задержку в полвыборки, разработав нашу систему для этой уменьшенной частоты дискретизации, но затем работая с исходной частотой дискретизации. Таким образом, мы приходим к
Таким образом, мы приходим к
с
где все коэффициенты рассчитаны для приведенной частоты дискретизации f˜s=23fs. Мы можем сделать это только потому, что у нас нет цикла без задержек. Или, скорее, цикл без задержек скрыт внутри нелинейных функций: вместо того, чтобы беспокоиться о нелинейности внутри цикла без задержек, мы рассматриваем решение цикла без задержек как нелинейность, к которой нужно применить уменьшение наложения. Обратите внимание, что поведение для частот выше 12f˜s=13fs плохо определено, но в любом случае с умеренной передискретизацией, предложенной в [10], нам не нужно об этом беспокоиться.
Увеличенная задержка — не единственный эффект модификации. Также есть фильтр нижних частот. Чтобы изучить это более подробно, предположим, что все fx,l(px,l) и fy,m(py,m) линейны, так что мы имеем линейную систему, и пусть H(z) обозначает передаточную функцию, полученную из ( 8)–(11). Если мы вместо этого воспользуемся (16)–(19) без корректировки коэффициентов, то несложно проверить, что результирующая передаточная функция удовлетворяет
Если мы вместо этого воспользуемся (16)–(19) без корректировки коэффициентов, то несложно проверить, что результирующая передаточная функция удовлетворяет
Мы можем наблюдать два эффекта: известную фильтрацию с множителем снаружи и замену z ←12(z−1+z−2)−1 в аргументе H. Вычисляя последнюю при z=ejω, мы отмечаем, что
2.
В то время как в исходной системе H(z) оценивается по единичной окружности ejω (показана пунктиром) для получения частотной характеристики, для модифицированной системы исходная H(z) оценивается по траектории (21). Мы замечаем, что в дополнение к частотному масштабированию на 32 имеется дополнительное масштабирование от единичного круга, возрастающее с частотой. Важно отметить, что поскольку мы оцениваем H(z) только для z на единичной окружности или за ее пределами, мы сохраняем стабильность, т. е. если H(z) устойчива, то и H˜(z). Тем не менее, особенно для более высоких частот, это может вызвать значительное искажение частотной характеристики.
Крайним примером может служить полнопроходной фильтр с высокой добротностью, в котором преобразование может привести к перемещению нуля по оси частот, превращая плоскую частотную характеристику в характеристику с глубоким вырезом. Как продемонстрируют примеры, многие типичные системы довольно хорошо ведут себя при преобразовании, но нужно помнить об этой ловушке.
4. Вычислительные затраты
Помимо потенциального изменения поведения системы на высоких частотах, цена за применение предлагаемого подхода к сглаживанию — это вычислительные затраты. Очевидно, что точное общее количество необходимых операций зависит от реальной системы, к которой будет применяться метод, но мы можем наблюдать некоторые тенденции. Во-первых, из-за необходимой передискретизации в два раза вычислительные затраты удваиваются даже для операций, которые мы иначе не меняем. Это, конечно, все же лучше, чем просто использование более высокого коэффициента передискретизации и вообще никакого другого сглаживания. Если входная и выходная частоты дискретизации фиксированы, требуемая передискретизация требует интерполяционных и децимационных фильтров, что влечет за собой дополнительные затраты, но как для предлагаемого подхода, так и для наивной передискретизации.
Если входная и выходная частоты дискретизации фиксированы, требуемая передискретизация требует интерполяционных и децимационных фильтров, что влечет за собой дополнительные затраты, но как для предлагаемого подхода, так и для наивной передискретизации.
Чтобы оценить вычислительную стоимость модификаций, сделанных предлагаемым методом, предположим, что и нелинейные функции, и их первообразные хранятся в интерполяционных таблицах с одинаковым разрешением и методом интерполяции/интерполяции. Тогда замена нелинейных функций на (4) вводит деление и немного увеличивает количество необходимых обращений к таблице. Обратите внимание, что количество просмотров таблицы не удваивается, так как F(p(n)) может быть сохранено, чтобы избежать поиска F(p(n-1)) на следующем временном шаге. Только при переключении между двумя случаями в (4) требуется дополнительный поиск. Однако вычислительные затраты на интерполяцию при просмотре таблицы экспоненциально растут с ее размерностью.
Таким образом, если все нелинейные функции имеют только скалярные аргументы, дополнительные усилия на каждый временной шаг составляют количество сложений и умножений на 12 и одно деление на нелинейную функцию, а также случайный дополнительный поиск в таблице. Это почти наверняка будет более эффективным, чем дальнейшее увеличение частоты дискретизации. Однако, когда нелинейные функции имеют аргументы более высокой размерности, (почти) удвоенная размерность для первообразных приводит к быстрому увеличению вычислительных затрат для поиска в таблице, что делает метод непривлекательным в этом случае, в дополнение к взрывным требованиям к памяти, обсуждавшимся выше. .
Это почти наверняка будет более эффективным, чем дальнейшее увеличение частоты дискретизации. Однако, когда нелинейные функции имеют аргументы более высокой размерности, (почти) удвоенная размерность для первообразных приводит к быстрому увеличению вычислительных затрат для поиска в таблице, что делает метод непривлекательным в этом случае, в дополнение к взрывным требованиям к памяти, обсуждавшимся выше. .
5. Примеры
Мы проиллюстрируем метод на примере двух хорошо подходящих для него схем, так как они приводят к нелинейным функциям со скалярным входом. Исходный код Julia, реализующий производные модели, можно найти по адресу https://github.com/martinholters/ADAA_Examples.jl.
5.1. Диодный ограничитель
В качестве первого примера рассмотрим диодный ограничитель, показанный на рис. 3.
Схема достаточно проста, поэтому мы кратко повторим здесь процесс моделирования. Из законов Кирхгофа и Ома и iC=Cy˙ сразу получаем
Суммируя по двум последующим экземплярам выборки, получаем
Теперь воспользуемся правилом трапеций, чтобы заменить
и получить
Сбор всех величин с временного шага n−1 в канонические состояния
позволяет упростить
Используя уравнение Шокли для диодов, получаем
где ток насыщения и температурное напряжение выбраны IS=1 фА и vT=25 мВ соответственно. Подставляя (28) в (27) и вводя
Подставляя (28) в (27) и вводя
то приводит к неявному уравнению
для у (п). Обратите внимание, что мы не рассматриваем это как цикл без задержек и применяем сглаживание к функции sinh. Вместо этого мы позволяем fy(py(n))=y(n) обозначать решение неявного уравнения. Результирующая функция изображена на рисунке 4 (получена с помощью итеративного решателя).
Чтобы получить уравнение обновления состояния, мы преобразуем (27) в
и обратите внимание, сравнивая с (26), что левая часть равна x(n). Таким образом вводя
с px(n)=py(n), мы приходим к
желаемой формы.
В этом случае применение подавления алиасинга только к выходному уравнению особенно просто, что дает
с f˜y, определенной согласно (4). Требуемая первообразная Fy(py) для fy(py), изображенная на рисунке 5, должна быть определена численно. Для приведенных ниже результатов он был предварительно рассчитан для 1024 равномерно распределенных точек в соответствующем диапазоне и сохранен в таблице с использованием кубической интерполяции во время поиска.
Требуемая первообразная Fy(py) для fy(py), изображенная на рисунке 5, должна быть определена численно. Для приведенных ниже результатов он был предварительно рассчитан для 1024 равномерно распределенных точек в соответствующем диапазоне и сохранен в таблице с использованием кубической интерполяции во время поиска.
Чтобы также применить смягчение алиасинга к уравнению обновления состояния, мы должны изменить его на
и подставим f˜s=23fs вместо fs в (30) и (32). Обратите внимание, что это сразу приводит к
Для изучения эффективности метода рассмотрим рис. 6, где изображены выходные спектры при синусоидальном возбуждении для различных конфигураций модели. На рисунках 6a,b показан базовый уровень системы без какого-либо подавления наложения спектров при частотах дискретизации fs=44,1 кГц и fs=88,2 кГц соответственно. Только применение смягчения наложений к выходному уравнению в соответствии с (35) дает мало преимуществ, как видно при рассмотрении рис. 6c, d в сравнении. Однако мы отмечаем эффект нижних частот на рисунке 6c, где высшие гармоники демонстрируют затухание до 10 дБ.
6c, d в сравнении. Однако мы отмечаем эффект нижних частот на рисунке 6c, где высшие гармоники демонстрируют затухание до 10 дБ.
При применении уменьшения наложения к уравнению обновления состояния в соответствии с (36) мы наблюдаем значительное уменьшение наложения на рисунке 6e,f. Как объяснялось, уменьшение наложения частот должно сочетаться с (умеренной) передискретизацией. В этом конкретном случае, как показано на рисунке 6e, модель по-прежнему относительно хорошо подходит даже без избыточной выборки, что, однако, в основном должно быть связано с удачным совпадением. Более уместным является случай частоты дискретизации fs=88,2 кГц, показанный на рисунке 6f. По сравнению с передискретизацией до fs=220,5 кГц без дополнительных мер по уменьшению наложения, как показано на рисунке 6g, мы видим, что наложенные компоненты на низких частотах, где они наиболее легко воспринимаются, находятся на сравнимом уровне.
5.2. Схема искажения типа Tube Screamer
В качестве второго примера рассмотрим схему искажения на рис.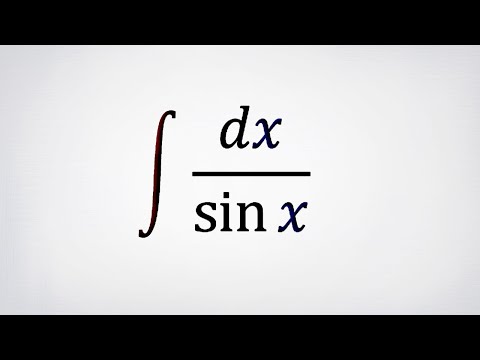 7, вдохновленную Ibanez Tube Screamer TS-808.
7, вдохновленную Ibanez Tube Screamer TS-808.
Мы не будем вдаваться в подробности процедуры моделирования, для которой мы использовали ACME.jl (https://github.com/HSU-ANT/ACME.jl), но заметим, что если позволить использовать три диода отличается, больше нельзя получить выражение в закрытой форме для их комбинированного поведения. Вместо этого нелинейное поведение определяется системой трех уравнений. Тем не менее, используя подход уменьшения размерности из [13], вход px(n)=py(n) в нелинейность можно привести к скалярной величине, образованной линейной комбинацией состояний входа и конденсатора. Следовательно, предлагаемый метод применим.
На рис. 8 снова показаны выходные спектры для синусоидального возбуждения. Как видно на рисунке 8a, при простой передискретизации до fs=88,2 кГц сигнал содержит сильные компоненты наложения спектров. Применение подавления алиасинга только к выходному уравнению уменьшает искажение алиасинга до ограниченной степени, как показано на рисунке 8b. Напротив, при одновременном применении смягчения наложения к уравнению обновления состояния наложение значительно уменьшается, как видно на рисунке 8c. Опять же, подавление алиасинга наиболее эффективно на низких частотах, где оно также наиболее актуально для восприятия. Как и в примере с диодным ограничителем, для низких частот система с подавлением наложения частот при fs=88,2 кГц работает как минимум так же хорошо, как и немодифицированная система при fs=220,5 кГц, см. рис. 8d.
Напротив, при одновременном применении смягчения наложения к уравнению обновления состояния наложение значительно уменьшается, как видно на рисунке 8c. Опять же, подавление алиасинга наиболее эффективно на низких частотах, где оно также наиболее актуально для восприятия. Как и в примере с диодным ограничителем, для низких частот система с подавлением наложения частот при fs=88,2 кГц работает как минимум так же хорошо, как и немодифицированная система при fs=220,5 кГц, см. рис. 8d.
6. Выводы и перспективы
Представленный подход к уменьшению алиасинга обобщает подход [10] ко всем нелинейным системам, которые могут быть преобразованы таким образом, что нелинейность принимает скалярные или очень низкоразмерные входные данные. Это включает, но не ограничивается, все модели схем с одним однопортовым нелинейным элементом. Если система содержит контур без задержек, его необходимо преобразовать таким образом, чтобы нелинейность определялась как решение контура без задержек. Тогда задержку, вносимую применением метода [10] к нелинейности, можно компенсировать путем настройки коэффициентов системы, даже если нелинейность является частью контура обратной связи.
Тогда задержку, вносимую применением метода [10] к нелинейности, можно компенсировать путем настройки коэффициентов системы, даже если нелинейность является частью контура обратной связи.
Как и следовало ожидать, достигнутое снижение алиасинга сравнимо с таковым в [10], что позволяет значительно уменьшить требуемую передискретизацию, особенно для систем, вносящих сильные искажения, при небольшой дополнительной вычислительной нагрузке. Предполагая, что таблицы поиска используются для f(u) (как правило, неявно определенного) и его производной F(u), основная цена, которую приходится платить, определяется используемой памятью.
Следует отметить, что расширения первообразных более высокого порядка, предложенные в [14] или [15], должны быть прямыми, следуя тому же принципу. Более интересным будущим направлением было бы снять ограничение на нелинейную функцию, чтобы иметь только скалярные или очень низкоразмерные входные данные. Если бы метод из [10] (или даже расширения более высокого порядка из [14] или [15]) можно было бы обобщить на нелинейные функции с несколькими входами, не требуя слишком больших интерполяционных таблиц, метод, предложенный в настоящей статье, немедленно обобщил бы ко всем нелинейным системам с состоянием.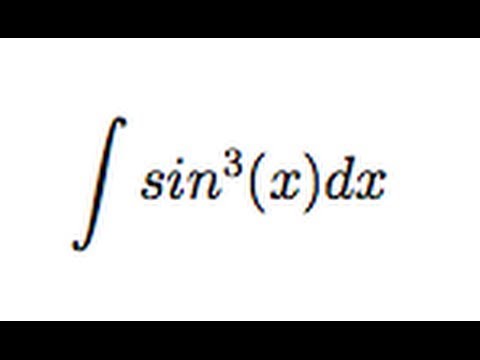
определенный
определенный
| Математика 122 — Математика для биологии II | |
|---|---|---|
Государственный университет Сан-Диего — Последнее обновление этой страницы: 21 апреля 2003 г. |
Определенный интеграл
- Дыхательная мертвая зона
- Основная теорема исчисления
- Примеры
- Примеры работы
- Том Мертвого Космоса
В предыдущем разделе показано, как приблизительно определить площадь под
кривой с помощью правила средней точки.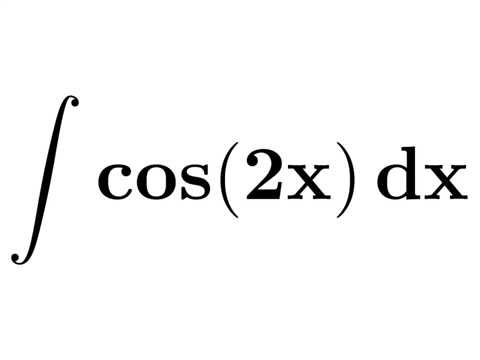 Однако эта техника довольно
скучный. В этом разделе используются наши методы из предыдущих разделов с
первообразную для нахождения площади под кривой. Основная теорема исчисления позволяет с помощью определенного интеграла найти точную площадь под
функция. Мы иллюстрируем использование наших методов интеграции с помощью
пример из физиологии дыхания.
Однако эта техника довольно
скучный. В этом разделе используются наши методы из предыдущих разделов с
первообразную для нахождения площади под кривой. Основная теорема исчисления позволяет с помощью определенного интеграла найти точную площадь под
функция. Мы иллюстрируем использование наших методов интеграции с помощью
пример из физиологии дыхания.
Респираторная мертвая зона
При вдыхании воздуха в легкие и из них воздух должен проходить через носовые ходы, глотку, трахею и бронхов, прежде чем он сможет попасть в альвеолы, где кислород и углерод обмен диоксида с кровеносной системой. Эти регионы, где жизненно важные газы не обмениваются, называются мертвых мест . Чтобы определить здоровье пациентов с респираторными заболеваниями, важно знать информацию обо всех аспектах их легких. Это включает в себя измерение мертвого пространства.
Существует довольно простой способ измерения мертвого пространства для
пациент. Больной дышит обычным воздухом, затем непосредственно перед
измерения, он или она делает один вдох чистого кислорода.
кислород будет смешиваться с нормальным воздухом в альвеолах, но мертвый
пространство будет заполнено почти исключительно чистым кислородом. Пациент
выдыхает смесь через быстро записывающий измеритель азота.
запись дает измерение количества
№ 2 и та часть, которая
включает только O 2 представляет
мертвое пространство. Ниже приведен график, показывающий типичную запись
пациент.
Больной дышит обычным воздухом, затем непосредственно перед
измерения, он или она делает один вдох чистого кислорода.
кислород будет смешиваться с нормальным воздухом в альвеолах, но мертвый
пространство будет заполнено почти исключительно чистым кислородом. Пациент
выдыхает смесь через быстро записывающий измеритель азота.
запись дает измерение количества
№ 2 и та часть, которая
включает только O 2 представляет
мертвое пространство. Ниже приведен график, показывающий типичную запись
пациент.
Область слева от кривой – чистая O 2 в мертвом пространстве, при этом область справа от кривой представляет смешанный воздух в алеволи, где фактический газ обменивается с циркуляторным система. Объем мертвого пространства определяется площадью слева кривой, умноженной на общий объем выдыхаемого воздуха, деленный на общая площадь под пунктирной линией.
Функция, которая близко соответствует собранным выше данным, предоставлено
, где N — процент
азота в выдыхаемом воздухе и х количество миллилитров с истекшим сроком годности.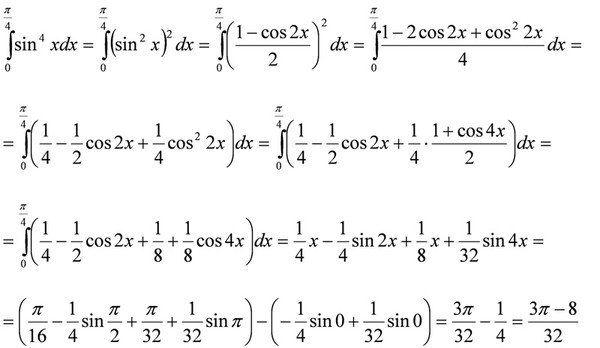 Мы легко можем видеть, что
общая площадь ( V ) под пунктиром
линия В = 0,6×500
= 300 мл, поэтому мы можем найти площадь слева от кривой по формуле
найти площадь под кривой и вычесть ее из общей
площадь, В . Мы хотели бы более простой
означает, чем суммы Римана, чтобы найти площадь под этой кривой, и
Фундаментальная теорема исчисления дает нам этот инструмент. Ниже мы
завершить наши вычисления, чтобы получить фактический объем мертвых
пространство, представленное приведенными выше данными.
Мы легко можем видеть, что
общая площадь ( V ) под пунктиром
линия В = 0,6×500
= 300 мл, поэтому мы можем найти площадь слева от кривой по формуле
найти площадь под кривой и вычесть ее из общей
площадь, В . Мы хотели бы более простой
означает, чем суммы Римана, чтобы найти площадь под этой кривой, и
Фундаментальная теорема исчисления дает нам этот инструмент. Ниже мы
завершить наши вычисления, чтобы получить фактический объем мертвых
пространство, представленное приведенными выше данными.
Основы Теорема исчисления
Пусть f ( x ) будет непрерывная функция на интервале [ а , b ] и предположим что F ( x ) любой производная от f ( x ). Определенный интеграл , который дает площадь под кривой f ( x ) между и и b , может быть вычислено следующая формула:
Пример 1: Используйте основную теорему исчисления для вычисления интеграла
из ф ( х ) = х 2 от
от 0 до 2.
Решение: Решение дается
Обратите внимание, что это представляет собой площадь под кривой x 2 от от 0 до 2.
Пример 2: Учитывать функции f ( x ) = x 2 — 2 х — 3 и г ( х ) = 1 — 2 х . Найдите x и y -перехваты и вершина параболы. Также найдите точки пересечения. Окончательно, определить площадь между кривыми.
Решение: Для f ( x ), y -intercept (0,
-3). По факторингу f ( x ) = x 2 — 2 х — 3 = ( х — 3)( х +1),
поэтому x -перехватов (-1,
0) и (3, 0).
вершина имеет значение x посередине между
два x -перехвата, так что легко увидеть, что
вершина этой параболы равна (1, -4). Для
прямая г ( х ) = 1 — 2 х , x и y — перехваты
являются (1/2, 0) и (0, 1),
соответственно.
Для нахождения точек пересечения функции устанавливаются равными друг друга. Таким образом, х 2 — 2 х — 3 = 1 — 2 х или x 2 — 4 = 0. Значения x пересечения равны х = + 2, поэтому точка пересечение (-2, 5) и (2, -3). Ниже приведен график двух кривых, показывающих область между их.
Из точек пересечения мы видим, что домен проценты равны -2 < x < 2. Обратите внимание, что г ( x ) > f ( x ) на интересующем интервале, что дает высоту при любом разрешении x как г ( x ) — f ( x ) = (1 — 2 х ) — ( x 2 — 2 х — 3) = 4 — х 2 . Таким образом, площадь находится с помощью следующего интеграла
Пример 3: Когда
интеграция требует подстановки, то подстановка, используемая в интеграции
также может использоваться на конечных точках интеграции для упрощения процесса
вычисление интеграла.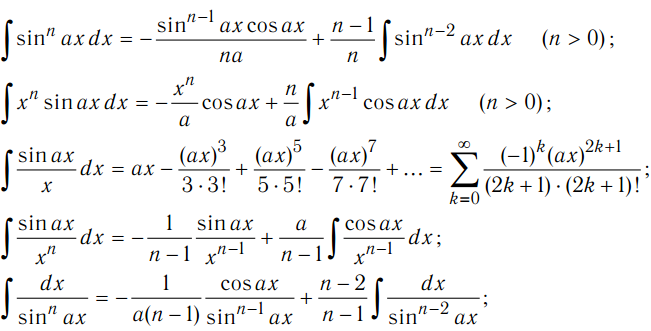 Оцените следующий определенный интеграл:
Оцените следующий определенный интеграл:
Решение: Для интеграции в этом интеграле нам нужно сделать замену u = 2 т + 1, значит ду = 2 дт . Конечные точки t = 0, что меняется на u = 1 и t = 4, что становится u = 9. Таким образом, интеграл выше решается следующим образом:
Как обычно есть в коллекции Работал Примеры , чтобы помочь с домашним заданием и дать дополнительные рекомендации по решению определенных интегралов.
Том Мертвых Космос
Как отмечалось в примечаниях выше, мертвое пространство для дыхания находится путем определения площади области слева от кривой на рисунок выше. Площадь этого региона может быть аппроксимирована определенный интеграл
Приведенный выше интеграл разбивается на два интеграла, которые необходимо решить.
первое достаточно элементарно, а второе требует подстановок.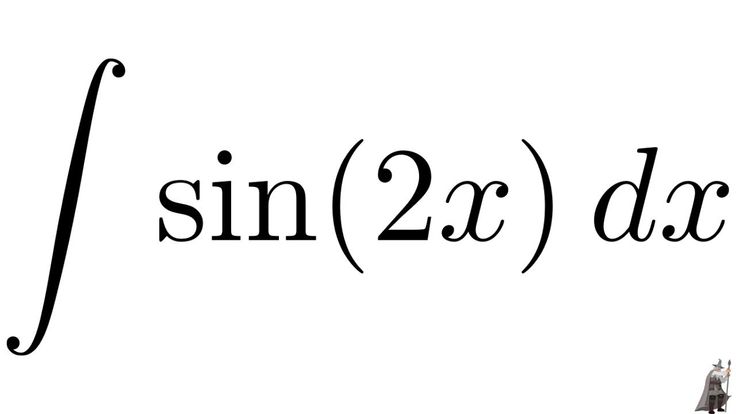

 Однако во многих приложениях ввод и вывод будут скалярными.
Однако во многих приложениях ввод и вывод будут скалярными.