Площадь фигуры калькулятор онлайн: Площадь фигур | Онлайн калькулятор

Онлайн расчеты и формулы площади для плоских фигур

Онлайн расчеты и формулы площади для объемных фигур

Площадь шара калькулятор нахождения площадь поверхности сферы или шара	Площадь куба как найти чему равна площадь поверхности куба
Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра	Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды
Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др.	Площадь конуса нахождение площади поверхностей конуса
Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса	Площадь тетраэдра площадь поверхности и грани тетраэдра
Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы

Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.

Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.

Вычисление площадей фигур востребовано для решения различных задач:
— строительных;
— кадастровых;
— инженерных и пр.

Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.

×

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Скачать калькулятор

Рейтинг: 3 (Голосов 150)

Сообщить об ошибке

Смотрите также

Площадь по периметру калькулятор. Как вычислить площадь по периметру. К разным фигурам применяйте различные формулы

Геометрия постигает свойства и колляции двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по знаменитым формулам либо выражается одно через другое.

Инструкция

1. Прямоугольник.Задача: вычислите площадь прямоугольника, если вестимо, что его периметр равен 40, а длина b в 1,5 раза огромнее ширины a.

2. Решение.Используйте знаменитую формулу периметра, он равен сумме всех сторон фигуры. В данном случае P = 2 a + 2 b. Из исходных данных задачи вы знаете, что b = 1,5 a, следственно, P = 2 a + 2 1,5 a = 5 a, откуда a = 8. Обнаружьте длину b = 1,5 8 = 12.

3. Запишите формулу для площади прямоугольника:S = a b,Подставьте вестимые величины:S = 8 *12 = 96.

4. Квадрат.Задача: обнаружьте площадь квадрата, если периметр равен 36.

5. Решение.Квадрат – частный случай прямоугольника, где все стороны равны, следственно, его периметр равен 4 a, откуда a = 8. Площадь квадрата определите по формуле S = a? = 64.

6. Треугольник.Задача: пускай дан произвольный треугольник ABC, периметр которого равен 29. Узнайте величину его площади, если знаменито, что высота BH, опущенная на сторону AC, делит ее на отрезки с длинами 3 и 4 см.

7. Решение.Для начала припомните формулу площади для треугольника:S = 1/2 c h, где c – основание и h – высота фигуры. В нашем случае основанием будет сторона AC, которая знаменита по условию задачи: AC = 3+4 = 7, осталось обнаружить высоту BH.

8. Высота является перпендикуляром, проведенным к стороне из противоположной вершины, следственно, она разделять треугольник ABC на два прямоугольных треугольника. Зная это качество, разглядите треугольник ABH. Припомните формулу Пифагора, согласно которой:AB? = BH? + AH? = BH? + 9 ? AB = ?(h? + 9).В треугольнике BHC по тому же тезису запишите:BC? = BH? + HC? = BH? + 16 ? BC = ?(h? + 16).

9. Примените формулу периметра:P = AB + BC + ACПодставьте величины, выраженные через высоту:P = 29 = ?(h? + 9) + ?(h? + 16) + 7.

10. Решите уравнение:?(h? + 9) + ?(h? + 16) = 22 ? [замена t? = h? + 9]:?(t? + 7) = 22 – t, возведите обе стороны равенства в квадрат:t? + 7 = 484 – 44 t + t? ? t?10,84h? + 9 = 117,5 ? h ? 10,42

11.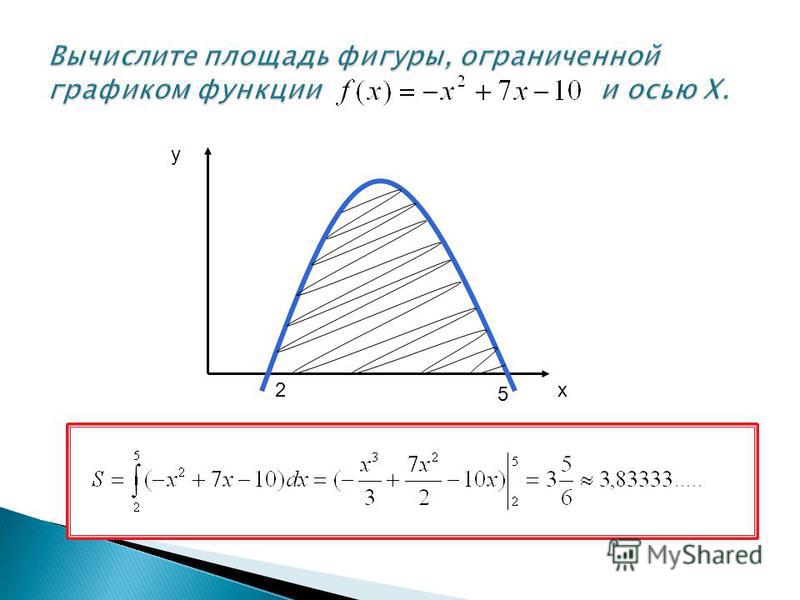 Обнаружьте площадь треугольника ABC:S = 1/2 7 10,42 = 36,47.

При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон

В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.

Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.

• Задача 4. Изменение длины сторон при сохранении площади прямоугольника

Задача 1. Найти стороны прямоугольника из площади

2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x 2 +2y 2 =260
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0

Задача 2. Найти стороны прямоугольника из периметра

Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.

Задача 3. Найти площадь прямоугольника из пропорции его сторон

Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.

Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.

Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2

Решение .
Площадь прямоугольника равна
S = ab

В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab

Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.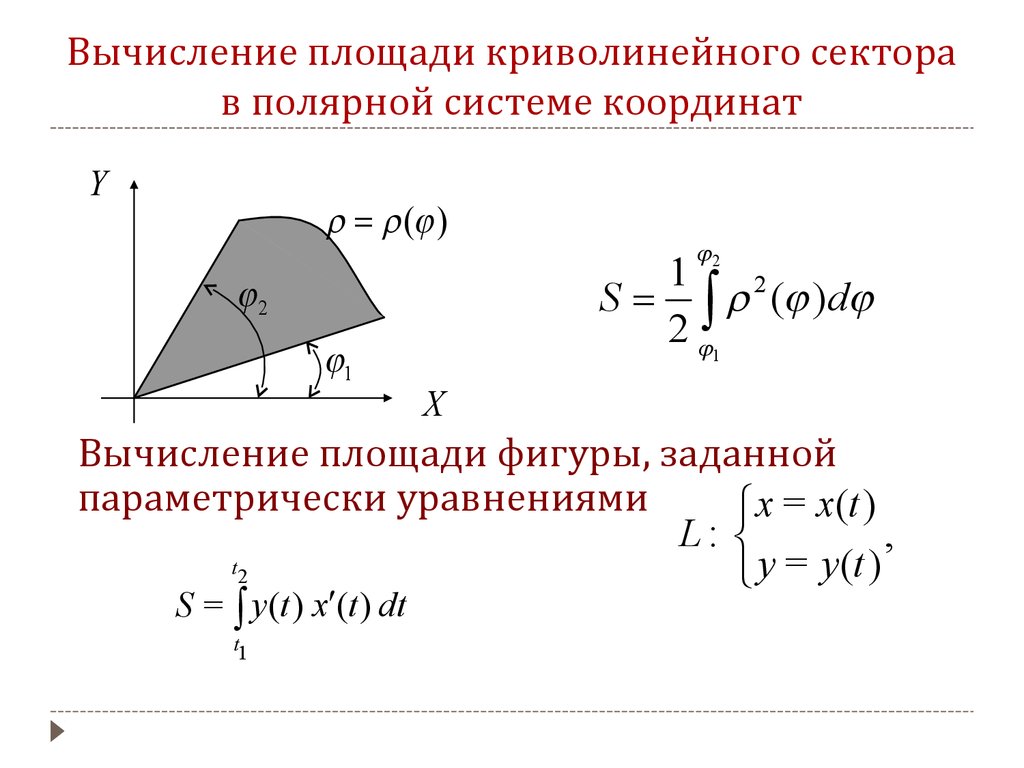 25
S 2 = 1,25ab / 1.25

Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25

1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%

Ответ : ширину нужно уменьшить на 20%.

Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Круг

Частные случаи

Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.

Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.

Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.

Многоугольник

Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:

• — пентагон;
• — гексагон;
• восемь — октагон;
• двенадцать — додекагон.

И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:

где n – количество сторон многоугольника, a – длина стороны.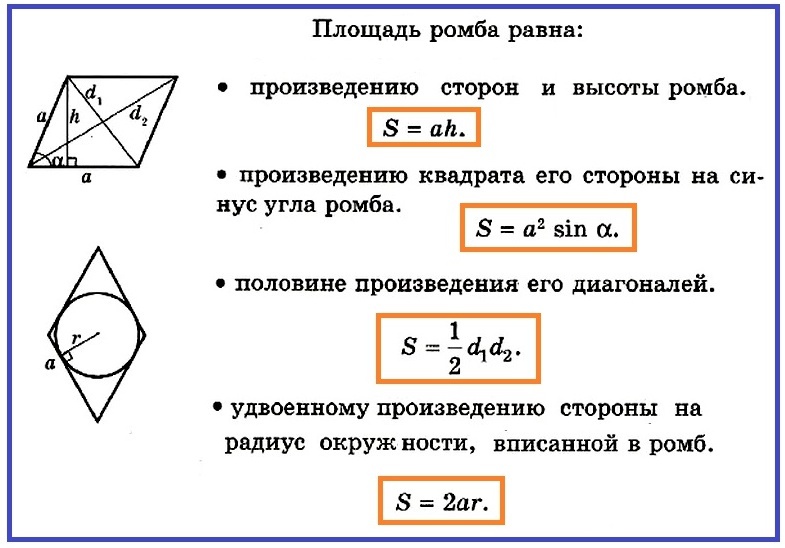

Для определения площади используется выражение:

S = n/4 × a 2 × ctg(pi/n).

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.

Примеры из реальной жизни

Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.

Покраска забора

Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.

Отделка бахромой

Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:

Таким образом, нам понадобится 4 м бахромы для отделки платка.

Заключение

Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.

Как вычислить площадь фигуры зная ее периметр? и получил лучший ответ

Ответ от Ёемен Аркадьевич[гуру]
В Компас 3D нанести план и автоматически посчитать площадь. По периметру площадь произвольного многоугольника не посчитать. Все равно придется разбивать на отдельные фигуры.
Будут вопросы — пиши в агент.

Ответ от Ѐамис Ш [новичек]
..

Ответ от Kiss(RUSS фор всех) ки (я) [гуру]
1.выбрать центр
2.измерить расстояние от центра до углов
3.измерить стороны вашего многоугольника
4.вычислить периметры получившихся N треугольников
5.вычислить площади всех треугольников, используя формулу Герона-через полупериметр.
6.суммировать все площади
7.выбрать мой ответ лучшим.
8.все

Ответ от Semrid [гуру]
попробуй разделить периметр на 4 и потом перемножить полученное друг на друга

Ответ от ScrAll [гуру]
Вырезаешь из бумаги и взвешиваешь.
Или разбиваешь на треугольники.
Половина основания на высоту…

Ответ от Алексей Зайцев [гуру]
Проще и безошибочнее начертить эскизик — вид сверху с размерами. Затем по этому эскизику площадь разделить на прямоугольники, посчитать и просуммировать их площади

Ответ от Мария Кемпель [активный]
нереально

Ответ от Nemo [гуру]
Нереально. По периметру вычисляется площадь только ПРАВИЛЬНЫХ фигур. Советую кусочным способом

Ответ от Djon [гуру]
лучше всего разбить сложную фигуру на несколько простых, и посчитать площадь отдельно, затем сложить

Ответ от Lavavoth [гуру]
Нереально.. . Лучше выложи план зала, есть другие способы подсчета, но нужно видеть план.

Ответ от 3 ответа [гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Как вычислить площадь фигуры зная ее периметр?

Петя хочет нарисовать фигуру, у которой периметр 12 см, а площадь 12 кв. см. Докажите, что у него ничего не получится
максимальная площадь по периметру у фигуры — Круг.
Если площадь круга с длинной окружности 12

— Примеры, Калькулятор площади онлайн

вычисляет площадь заданной геометрической формы в квадратных единицах. Площадь определяется как пространство, заключенное в границах двумерной формы. Существуют разные формулы для расчета площади различных двумерных фигур.

Что такое калькулятор площади?

Калькулятор площади — это онлайн-инструмент, который помогает вычислить площадь круга, квадрата, треугольника, прямоугольника и четырехугольника. Площадь любого объекта выражается в квадратных единицах. Чтобы использовать это Калькулятор площади введите значения в поля ввода.

Калькулятор площади

Как пользоваться калькулятором площади?

Чтобы найти площадь с помощью онлайн-калькулятора площади, выполните следующие действия:

• Шаг 1: Перейдите к онлайн-калькулятору площади Cuemath.
• Шаг 2: Выберите фигуру из раскрывающегося меню и введите значения в поля ввода калькулятора площади.
• Шаг 3: Нажмите на кнопку «Рассчитать» , чтобы найти площадь.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор площади?

Ниже приведены геометрические фигуры, площадь которых можно вычислить с помощью калькулятора:

1. Площадь треугольника: Треугольник – это замкнутый многоугольник с 3 углами, 3 вершинами и 3 сторонами. Площадь треугольника равна половине произведения основания на высоту. Формула для вычисления площади треугольника:

Площадь треугольника = 1/2 × (основание × высота) квадратных единиц.

2. Площадь квадрата: Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя прямыми углами.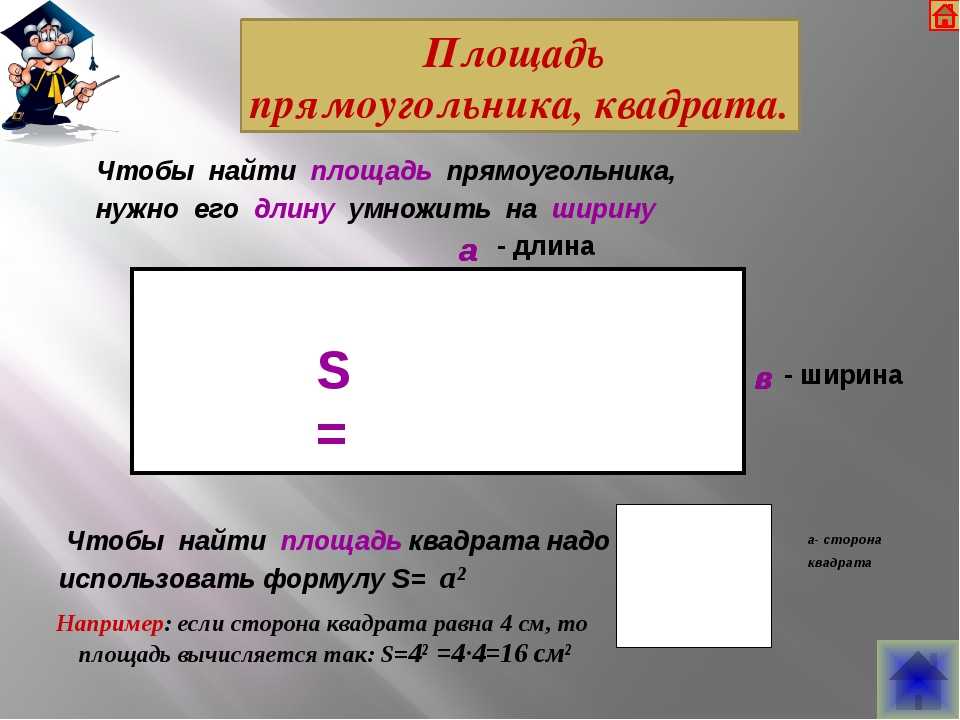 Площадь равна квадрату длины его стороны. Формула для вычисления площади квадрата:

Площадь квадрата = сторона × сторона = s ² квадратных единиц.

3. Площадь прямоугольника: Прямоугольником называется фигура, у которой противоположные стороны параллельны и равны по длине. Далее, все его углы равны 90 градусов. Площадь прямоугольника равна длине, умноженной на его ширину. Формула для вычисления площади прямоугольника:

Площадь прямоугольника = (длина × ширина) квадратных единиц

4. Площадь четырехугольника: Четырехугольник — это замкнутая фигура, которая получается путем соединения четырех точек, среди которых любые три точки не лежат на одной прямой. Формула для вычисления площади четырехугольника:

Площадь четырехугольника = диагональ × (сумма высот) квадратных единиц

5. Площадь круга: Кривая, описываемая точкой, движущейся относительно фиксированной точки, называется окружностью. Формула для вычисления площади круга:

Площадь круга = π r ² квадратных единиц

Где r — радиус круга, а π — константа, принимающая значение 3,14 или 22/7. .

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Заказать бесплатный пробный урок

Решенные примеры на площади

Пример 1: Найдите площадь треугольника, если высота = 4 единицы, а основание = 5 единиц, и проверьте это с помощью калькулятора площади.

Решение:
Дано: высота = 4 единицы и основание = 5 единиц
Площадь треугольника = 1/2 × основание × высота 90 109. = 1 / 2 × 5 × 4
= 10 квадратных единиц

Пример 2: Найдите площадь круга, радиус которого равен 5 единицам, и проверьте ее с помощью калькулятора площади.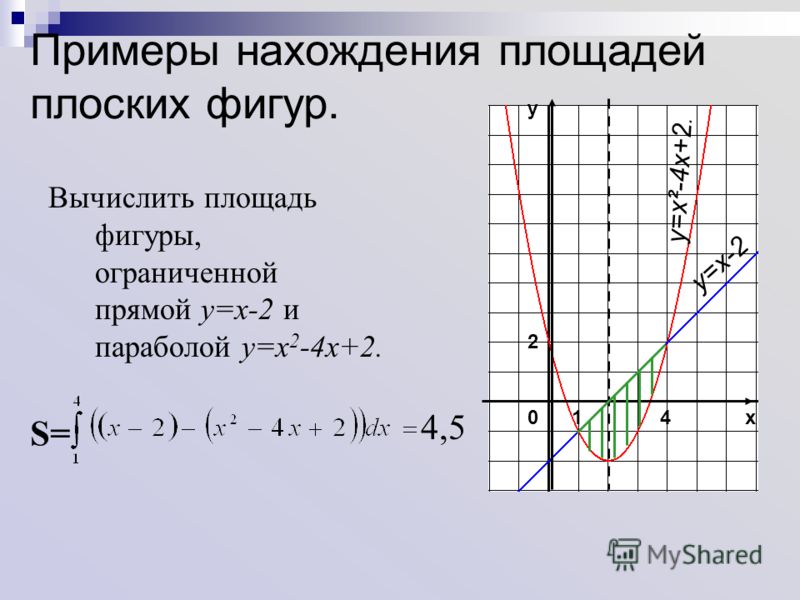

Решение:
Дано: r = 5 единиц
Площадь круга = π r ²
= 3,14 × 5 ²
= 78,5 квадратных единиц

Точно так же вы можете попробовать калькулятор площади, чтобы найти площадь для:

• Квадрата, сторона которого а = 2 единицы
• Прямоугольник, длина которого = 8 единиц, а ширина = 7 единиц

☛ Математические калькуляторы:

Калькулятор скидок — Примеры, Онлайн калькулятор скидок

Калькулятор скидок — это бесплатный онлайн-инструмент, который помогает рассчитать процентную скидку, когда указаны отмеченная цена и цена продажи. Скидка относится к уступке, предоставляемой покупателям по указанной цене продукта.

Что такое калькулятор скидок?

Калькулятор скидок поможет вам рассчитать скидку, предлагаемую на указанную цену товара, в процентах. Владельцы магазинов обычно предлагают покупателям скидки в качестве тактики увеличения продаж своих товаров. Чтобы использовать калькулятор скидок введите значения в поля ввода.

Калькулятор скидок

Как пользоваться калькулятором скидок?

Пожалуйста, следуйте шагам, приведенным ниже, чтобы найти процентную скидку, используя онлайн-калькулятор скидок.

• Шаг 1: Перейдите к онлайн-калькулятору скидок Cuemath.
• Шаг 2: Введите отмеченную цену и цену продажи в поля ввода.
• Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти ставку дисконтирования.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор скидок?

Существуют определенные термины, связанные со скидками, с которыми пользователи должны быть знакомы. Они даны следующим образом:

• Маркированная цена — Это также известно как прейскурантная цена. Это первоначальная цена товара, заявленная продавцом.
• Цена продажи — Цена, по которой продается продукт, называется продажной ценой.
• Ставка дисконтирования — Сумма денег, уменьшенная с указанной цены, выраженная в процентах, дает ставку дисконтирования.

Шаги для расчета ставки дисконтирования следующие:

• Цена продажи вычитается из указанной цены.
• Разделите это значение на отмеченную цену.
• Умножьте значение, полученное на шаге 2, на 100, чтобы выразить скидку в процентах.

Формула для ставки дисконтирования приведена ниже:

Ставка дисконтирования = (Маркированная цена — Цена продажи) / Маркировочная цена × 100%

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенные примеры со скидкой

Пример 1: Вы покупаете часы, прейскурантная цена которых составляет 400 долларов, а цена продажи — 380 долларов.