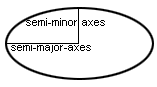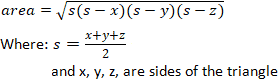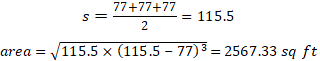Площадь прямоугольника
Площадь прямоугольника, формулы для вычисления площади прямоугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей прямоугольника. Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.
Таблица с формулами площади прямоугольника (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь прямоугольника через две стороны
… подготовка …
b — сторона
2
Площадь прямоугольника через периметр и одну из сторон
В указанной формуле, площадь периметра прямоугольника вычисляется:
… подготовка …
a (или b) — сторона
P — периметр
3
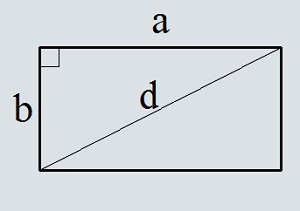
Площадь прямоугольника по диагонали и стороне
… подготовка …
a (или b) — сторона
d — диагональ
4
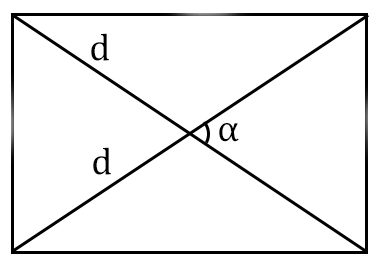
Площадь прямоугольника по диагоналям и углу между ними
… подготовка …
d — диагональ
α° — угол между диагоналями
5
Площадь прямоугольника через сторону и радиус описанной окружности
… подготовка …
a (или b) — сторона
6
Площадь прямоугольника через сторону и диаметр описанной окружности
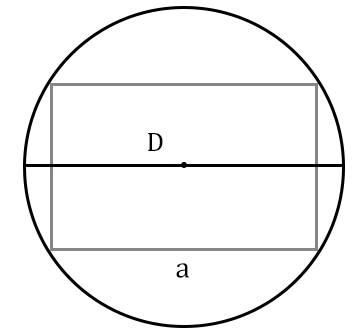
… подготовка …
a (или b) — сторона
D — диаметр описанной окружности
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади прямоугольника
Определения
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Презентация и конспект урока «Площадь. Формулы площади прямоугольника и квадрата» (5 класс)
План-конспект урока математики по теме: «Площадь. Формулы площади прямоугольника и квадрата»
5 класс
Составила : учитель математики
МБОУ гимназии № 9
г. Ставрополя
Косова Валентина Ивановна
План-конспект урока математики по теме: «Площадь. Формулы площади прямоугольника и квадрата»
5 класс
Цели: Обобщить знания учащихся о площади, полученные в начальной школе. Дать понятие равных фигур, формулы площади прямоугольника и квадрата. Совершенствовать вычислительные навыки.
Раздаточный материал: треугольники, прямоугольники, произвольные фигуры- равные и не равные; карточки (красная и зеленая у каждого ученика)
Организационный момент (слайд 3)
Лабиринт вопросов трудных
Разгадать помогут нам
Наши знанья и уменья
Со смекалкой пополам
Устный счет, определение темы урока (слайды 4,5)
Назовите числа, квадрат которых оканчивается цифрой 4, 6,1 (2 и 8, 4 и 6, 1 и 9)
Назовите цифры, которыми не могут оканчиваться квадраты чисел (2,3,7,8)
Вычислите удобным способом и прочитайте слово:
4.18.25 Шифр
8.14.125 Л(14 000) Щ(8500)
8.45.250 А(74 000) П(1800)
50.85.2 О(90 000) Д(1 000 000)
16.125.37 Ь(2100)
40.8.25.125
21.25.4
(площадь)
Слово «площадь» имеет несколько значений: (слайд 6)
Первую находим- вычисляем,
Много формул для нее мы знаем.
На второй же – митинги, парады,
Погулять по ней всегда мы рады.
Площадь- открытое, обрамленное какими –либо зданиями или зелеными насаждениями пространство, входящее в систему других городских пространств; нередко играет важную роль в градостроительстве. (Слайд 7)
Древние египтяне говорили, что площадью называется величина, характеризующая размер плоской фигуры (слайд 8)
Работа по теме урока
-Расскажите, что вызнаете о площади
-В каких единицах измеряется площадь?
-Что значит измерить площадь? (работа с учебником п.18, рис. 62,63)
Формулируем правило и закрепляем на примерах (слайд 9,10)
-Подумайте, какие фигуры можно назвать равными? (на столах раздаточный материал – треугольники, прямоугольники, произвольные фигуры- равные и не равные). Предлагаю среди них найти равные.
-Как находили равные фигуры?
Формулируем свойства площадей (слайд 11)
Выполняем из учебника № 709-712-устно
-Какая фигура называется прямоугольником, квадратом?
-Вспомните, чему равна площадь прямоугольника, квадрата? (записываем формулы) (слайд 12.13)
Выполняем из учебника № 716,719, 720
Закрепление материала
Проверочная работа (слайд 14)
Предлагаю обменяться тетрадями и проверить работы (ответы и решение озвучиваем)
Рефлексия
-Определите, что полезного узнали для себя на уроке, что нужно повторить;
-Оцените свое настроение (поднимают карточки –красную или зеленую)
Подводим итог урока (слайд 15)
Домашнее задание (слайд 16)
1.Начертить фигуру, площадь которой равна 10 см2
2. Начертить прямоугольник, измерить его длину и ширину, найти его площадь.
3.Начертить квадрат со стороной 6 см, найти его площадь.
формула по длине стороны, диагонали
Квадрат
– это геометрическая фигура; правильный четырехугольник, т.е. четырехугольник, имеющий равные стороны и углы (90°).Формула вычисления площади
1. По длине стороны:
Площадь квадрата (S) равняется квадрату длины его стороны:
S = a2
Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:
S = a*b
А т.к. все стороны квадрата равны, то вместо стороны b мы снова подставляем в формулу сторону a, т.е. S = a*a = a2.
2. По по длине диагонали
Площадь квадрата равняется половине квадрата длины его диагонали:
S = d2/2
Соотношение стороны и диагонали квадрата: d=a√2.
Примеры задач
Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.
Решение:
Используем формулу по длине стороны, т.е. S = 72 = 49 см2.
Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.
Решение 1:
Воспользуемся второй формулой (по длине диагонали): S = 42/2 = 8 см2.
Решение 2:
Мы можем выразить длину стороны через диагональ: a = 4/√2. И тогда, используя первую формулу, S = (4/√2)2 = 8 см2.
Площадь квадрата
Площадь квадрата – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.
Для вычисления площади квадрата применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь или проверить уже выполненные вычисления.
Таблица с формулами площади квадрата (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь квадрата через его сторону
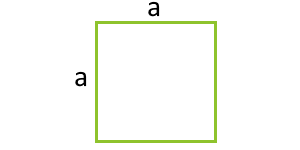
… подготовка …
a — сторона
2
Площадь квадрата через его диагональ
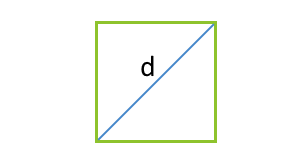
… подготовка …
d — диагональ
3
Площадь квадрата через периметр
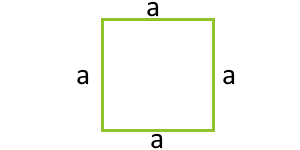
… подготовка …
P — периметр
4
Площадь квадрата через отрезок проведенный из вершины квадрата к середине противоположной стороны
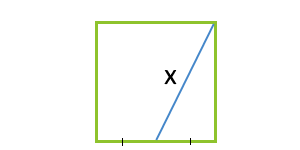
… подготовка …
k — отрезок
5
Площадь квадрата через радиус вписанной окружности
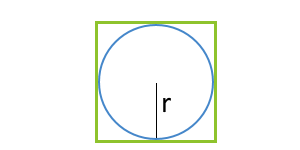
… подготовка …
r — радиус вписанной окружности
6
Площадь квадрата через радиус описанной окружности
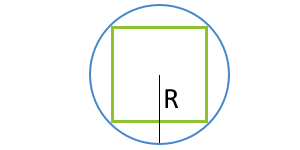
… подготовка …
R — радиус описанной окружности
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади квадрата
Определения
Квадрат – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Урок и презентация по теме «Площадь. Формула площади прямоугольника и квадрата»( 5 класс)
Муниципальное бюджетное общеобразовательное учреждение
«Тетюшская татарская средняя общеобразовательная школа»
Тетюшского муниципального района Республики Татарстан
Открытый урок на тему:
Учитель математики
Шайдуллина А.Ф.
2013-2014 учебный год
Тема: Площадь. Формула площади прямоугольника и квадрата
Цель урока: актуализировать навыки нахождения площади прямоугольника, квадрата;
сформировать навыки нахождения площади квадрата и треугольника;
развивать самостоятельность и усидчивость.
Задачи:
1)систематизировать знания учащихся о площадях прямоугольника и квадрата;
2)развивать умение работать в парах, умения работать в коллективе,
выполнять самоконтроль, логическое мышление
3)воспитывать толерантное отношение друг к другу, умение выслушивать собеседника
Оборудование: учебник Н.Я.Виленкин, 5 класс», карточки, мультимедийный проектор, презентация
I.Организационный момент. (Дети сидят в группе по 4 человека)
— Ребята, здравствуйте. Давайте поприветствуем друг друга и пожелаем всем успеха.
-Скажите, пожалуйста, какую тему мы с вами изучали на предыдущем уроке? (формула площади прямоугольника)
— Молодцы! Вот сейчас мы повторим и обобщим изученное .
II. Актуализация.
Проверка домашнего задания.
Два ученика пишут домашнее задание (№737, 738) на доске, решение № 745 на слайде. Далее ученики берут в руки тетради с домашним заданием и карандаши и встречаются с другом, с которым у него назначена встреча на 3 часа. (Данная структура называется Сlock Buddies. Дети заранее рисуют часы и назначают встречу на 12, 3, 6 и 9 часов с другом. Друзья должны быть разными.) В течении 1 минуты они разбирают домашнее задание и ставят карандашом оценку.
Повторение пройденного материала ( Применяется Ralli Robin)
— Сейчас вспомните правило и формулу вычисления площади прямоугольника . Сначала подумайте ( 10с)
Работаете с партнером по плечу. 1 листок на двоих. ( Ralli Robin)
Проверим, что у вас получилось .Отвечает стол №2 под №…
Отвечает стол №1 под №…
-Молодцы.
Вспомните формулу вычисления площади квадрата (дается 10 с)
Работаете с партнером по лицу.
Отвечает стол №1 под №…
Отвечает стол №2 под №…
На слайде фигуры прямоугольников и квадратов.
Вычислите площади этих фигур ( устно)
Какие из фигур можно назвать равными ? Почему ? Подумайте 10 с. применяется Single Round Robin — учащиеся по кругу в течение 1 минуты проговаривают правило равенства фигур)
Отвечает стол №1 ученик под №…
Отвечает стол№2 ученик под №..
Как вычислить площадь треугольника через площадь прямоугольника?
Дан треугольник со сторонами 3см и 4 см. Как найти его площадь?
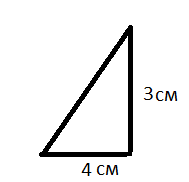
Как найти площадь всей фигуры, зная площади всех её частей?
— Работаете с партнером по лицу.
III .Решение задач по учебнику.
Стр. №717 (Один ученик работает у доски, остальные решают в тетрадях)
стр.110 № 718
N M
K T
-Прочитайте задачу.
— О чем говорится в данной задаче?
-Что надо знать, чтобы вычислить площадь?
-Что сказано про длину прямоугольника?
-Как ее найти?
-По какой формуле вычислим площадь прямоугольника?
-На какие фигуры делит отрезок КМ прямоугольник?
-Что вы можете сказать про площади треугольников?
-Как найти площадь треугольника?
-Решите задачу.
1) 26+14=40(см) – длина второй стороны прямоугольника
2) 26*40=1040(см2 )- площадь прямоугольника
3) 1040:2=520 (см2 )- площадь треугольника
IV. Работа с раздаточным материалом
Обучающимся раздаются наборы многоугольников (один конверт на двоих учеников по плечу). Из набора многоугольников нужно выбрать прямоугольники и квадраты. Сделать необходимые измерения и вычислить площадь прямоугольника и квадрата .Результаты записать в тетрадь.
Физкультминутка. Используется Mix Pair Share- обучающая структура, в которой ученики смешиваются под музыку, образовывают пару, когда музыка прекращается, задается вопрос по данной теме.
Площадь прямоугольника – 6 кв.см, длина – 3 см, чему равна ширина?
Сторона квадрата – 2 см, чему равна его площадь ?
Площадь квадрата – 16 кв.дм, чему равна его сторона?
V. Работа с карточками
На каждом столе лежит карточка с четырьмя заданиями. Учащиеся решают по очереди по одному заданию ,проговаривая решение. Начинает ученик №1, решает и передает карточку второму и т.д.( Применяется обучающая структура Round Table)
1. Дана площадь прямоугольника S=48 см2 и ширина a=12 см.
Найдите длину b.
2.Дан квадрат со стороной а= 8 дм. Найдите площадь квадрата.
3. Дан прямоугольник со сторонами a = 18 см,b = 3 см.Найдите площадь прямоугольника.
4. Дан треугольник со сторонами 5 дм и 6 дм. Найдите его площадь.
VI. Тесты ( тесты в четырех вариантах)
1 вариант
Начало формыКонец формы
Найти площадь прямоугольника со сторонами 8 см и 6 см
10
24
20
14
48
2 вариант Начало формыКонец формы
Найти площадь прямоугольника со сторонами 6 см и 4 см
10
24
20
14
28
3 вариант Начало формыКонец формы
Найти площадь прямоугольника со сторонами 4 см и 5 см
10
24
20
14
28
4 вариант Начало формыКонец формы
Найти площадь прямоугольника со сторонами 10 см и 2 см
10
24
20
14
28
VII. Домашнее задание.
П. 18 повторить правила, №722,733
VIII. Этап подведения итогов урока
Итог урока:
Какие выводы вы сделали на уроке?
Выводы:
1.Площадь прямоугольника равна произведению
ширины прямоугольника на его длину;
2. Площадь квадрата равна квадрату его стороны;
3. Площади равных фигур равны;
4.Площадь всей фигуры равна сумме площадей ее частей.
VI. Рефлексия
1.На уроке я работал активно / пассивно2.Своей работой на уроке я доволен / не доволен
3.Урок для меня показался коротким / длинным
4.За урок я не устал / устал
5.Мое настроение стало лучше / стало хуже
6.Материал урока мне был понятен / не понятен
-Молодцы, спасибо за урок!
Площадь прямоугольника. Онлайн-калькулятор
Онлайн-калькулятор площади прямоугольника поможет вам точно и быстро рассчитать или проверить расчеты по нахождению площади любого прямоугольника. Обычно площадь прямоугольника можно рассчитать двумя способами: через две стороны прямоугольника или через его диагонали. При первом способе расчета введите значения длин сторон a и b. При втором – длину диагоналей и значение угла между ними в градусах или радианах. Помимо ответа калькулятор покажет решение.
Способ расчета площади прямоугольника:
по двум сторонам через диагоналиРассчитать
Прямоугольник – это геометрическая фигура, представляющая собой четырехугольник, у которого все углы прямые (90° ). Диагонали прямоугольника равны между собой.
Как найти площадь прямоугольника?
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
a, b – стороны
2) через диагонали и угол
d – диагонали, α – угол между диагоналями.
Формула площади прямоугольника
Что такое прямоугольник? Прямоугольник — это параллелограмм, у которого все углы прямые (то есть равны 90 °).
1. Если задан прямоугольник со сторонами a и b. Тогда его площадь равна произведению сторон:
\[ \LARGE S = a \cdot b \]
2. Если заданы диагонали прямоугольника (их длины равны) и угол между ними, то площадь вычисляется по формуле::
\[ \LARGE S = \frac{1}{2} \cdot d^{2} \cdot sin(\alpha) \]
3. Если заданы диагонали параллелограмма и известен угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = \frac{1}{2} \cdot d_{1} \cdot d_{2} \cdot sin(\alpha) \]
Свойства прямоугольника
Поскольку прямоугольник является частным случаем параллелограмма, то он обладает всеми свойствами параллелограмма. Кроме этих свойств, прямоугольник имеет присущее только ему свойство — Диагонали прямоугольника равны (AC = DB).
Признаки прямоугольника
Если диагонали параллелограмма равны, то такой параллелограмм — прямоугольник.
Около любого прямоугольника можно описать окружность. Центром этой окружности будет точка пересечение диагоналей, а радиус будет равен:
\[ R = \frac{ AC }{2} \]
Калькулятор площади прямоугольника
Расчитать площадь фигуры онлайн
Калькулятор: Площадь прямоугольника
Входные данные
Результат
Площадь геометрической фигуры, или площадь фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади фигуры выражается числом заключающихся в него квадратных единиц.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Формулы площади
( пи = = 3,141592 …)
Площадь Формулы
Примечание: «ab» означает «а» умножить на «б». «a 2 » означает «квадрат», что то же самое, что «а» умножить на «а».
Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений. Примеры
квадрат = 2
прямоугольник = ab
параллелограмм = bh
трапеция = h / 2 (b 1 + b 2 )
круг = пи r 2
эллипс = pi r 1 r 2
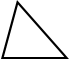
| треугольник = | , равная половине длины основания, умноженной на высоту треугольник |
| равносторонний треугольник = |
треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C
треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)
правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = длина от центра до угла
Квартир
Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол.
Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.
Если у квадрата одна сторона 4 дюйма, площадь будет 4 дюйма, умноженная на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в 2 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.
Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?
НЕ ПРАВИЛЬНО …. 4 раза 6 = 24
ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута.(или 2 кв. фута, или 2 фута 2 ).
.Площадь формулы прямоугольника в квадратных футах
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma класса 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел. для класса 12
- Классы
- CBSE — вопросник за предыдущий год
- CBSE — вопросник за предыдущий год, класс 10
- CBSE — за предыдущий год — вопросник, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7,
- , Cla
Площадь квадрата и калькулятор. Определение и формула
Площадь квадрата и калькулятор. Определение и формула — Открытый справочник по математике Количество квадратных единиц, необходимое для полного заполнения квадрата.
Формула: ширина × высота
Попробуйте это Перетащите оранжевые точки, чтобы переместить квадрат и изменить его размер. Как размер квадрата изменяется, пересчитывается площадь.
Формула площади
Площадь квадрата определяется по формуле Но поскольку ширина и высота по определению одинаковы, формула обычно записывается как где s — длина одной стороны.В строго правильной математической формулировке формулу выше следует произносить как «s в степени 2», то есть s умножается само на себя. Но мы обычно говорим это как «s в квадрате». Эта формулировка фактически взята из квадрат. Длина линии s, умноженная на себя, образует квадрат со стороной s. Отсюда «s в квадрате».
Калькулятор
Используйте калькулятор выше, чтобы рассчитать свойства квадрата.
Введите любое одно значение, и остальные три будут рассчитаны.Например, введите длину стороны, и площадь будет рассчитана.
Точно так же, если вы войдете в область, будет рассчитана длина стороны, необходимая для получения этой площади.
Метод «диагоналей»
Если вам известны длины диагоналей, то площадь равна половине произведения диагоналей. Поскольку обе диагонали равны конгруэнтно (одинаковой длины), это упрощается до: d — длина любой диагонали. Они оба одинаковой длины.Координатная геометрия
Если вы знаете координаты из вершины квадрата, вы можете рассчитать все остальные свойства, включая площадь.Подробнее об этом см. Площадь и периметр квадрата (координатная геометрия)Что попробовать
- На рисунке выше нажмите «скрыть детали»
- Перетащите оранжевые точки на вершинах, чтобы создать квадрат произвольного размера.
- Теперь попробуйте оценить площадь квадрата, просто глядя на маленькие единичные квадраты внутри него
Другие полигоны
Общие
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с полигонами
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Калькулятор площади
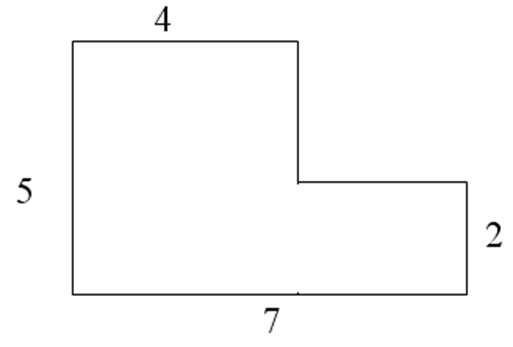
Ниже приведены калькуляторы для оценки площади семи распространенных форм. Площадь более сложных форм обычно можно получить, разбив их на совокупность простых форм и суммируя их площади. Этот калькулятор особенно полезен для оценки земельной площади.
Прямоугольник
 |
Треугольник
 Используйте калькулятор треугольника, чтобы определить |
Трапеция
 |
Круг
 |
Сектор
 |
Эллипс
 |
Параллелограмм
 |
Калькулятор площади сопутствующих поверхностей | Калькулятор объема
Площадь — это величина, которая описывает размер или размер двумерной фигуры или фигуры на плоскости.Его можно визуализировать как количество краски, которое потребуется для покрытия поверхности, и оно является двумерным эквивалентом одномерной длины кривой и трехмерного объема твердого тела. Стандартная единица площади в Международной системе единиц (СИ) — квадратный метр, или м 2 . Ниже приведены уравнения для некоторых наиболее распространенных простых форм и примеры расчета площади каждой из них.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами.Это одна из простейших форм, и для расчета ее площади необходимо только знать (или измерить) ее длину и ширину. Четырехугольник по определению — это многоугольник, имеющий четыре ребра и вершины. В случае прямоугольника длина обычно относится к двум более длинным краям четырехугольника, а ширина относится к более коротким из двух краев. Когда длина и ширина прямоугольника равны, форма представляет собой особый случай прямоугольника, называемый квадратом. Уравнение для вычисления площади прямоугольника выглядит следующим образом:
площадь = длина × ширина
Фермер и его дочь — непроданная земля
Представьте, что фермер пытается продать участок земли совершенно прямоугольной формы.Поскольку у него есть несколько коров, которые он не хотел бы свободно резвиться, он огородил участок земли и знает точную длину и ширину каждого края. Фермер также живет в Соединенных Штатах и, не знаком с использованием единиц СИ, все еще измеряет свой участок земли в футах. Стопа была определена как ровно 0,3048 метра в 1959 году после того, как она изменилась в течение длительного периода времени, поскольку исторически человеческое тело часто использовалось в качестве основы для единиц длины, и неудивительно, что оно было непостоянным в зависимости от времени и местоположения.В стороне, участок земли фермера имеет длину 220 футов и ширину 99 футов. Используя эту информацию:
площадь = 220 × 99 = 21780 кв. Футов
Земельный участок фермера площадью 21780 квадратных футов равен половине акра, где акр определяется как площадь 1 цепи на 1 фарлонг, которые определяются чем-то другим и т. Д., И почему СИ сейчас существует. К несчастью для фермера, он живет в районе, где преобладают иностранные инвесторы с более мелкими ногами, которые считали, что им следует получить больше квадратных футов за свои деньги, и его земля остается непроданной сегодня.
Треугольник
Существует множество уравнений для вычисления площади треугольника в зависимости от имеющейся информации. Как упоминалось в калькуляторе выше, используйте Калькулятор треугольников для получения дополнительных сведений и уравнений для расчета площади треугольника, а также для определения сторон треугольника с использованием любой доступной информации. Вкратце, уравнение, используемое в приведенном выше калькуляторе, известно как формула Герона (иногда называемая формулой Героя), относящаяся к герою Александрии, греческому математику и инженеру, которого некоторые считают величайшим экспериментатором древних времен.Формула выглядит следующим образом:
Фермер и его дочь — Triangle Daze
В этот момент, благодаря огромным усилиям и настойчивости, фермер, наконец, продал свой участок земли площадью 21 780 квадратных футов и решил использовать часть заработанных денег, чтобы построить бассейн для своей семьи. К несчастью для фермера, он не принимает во внимание тот факт, что одни только расходы на обслуживание бассейна в течение одного года, вероятно, могут покрыть посещение его детьми любого бассейна или аквапарка на долгие годы.Еще более печально для фермера, его 7-летняя дочь, которая недавно приехала в Египет через Дору-исследовательницу, влюбилась в треугольники и настаивает на том, чтобы бассейн имел не только треугольную форму, но и размеры должна включать только цифру 7, чтобы обозначить ее возраст и увековечить этот момент ее жизни в форме треугольного бассейна. Как любящий отец, фермер соглашается на просьбу дочери и приступает к планированию строительства своего треугольного бассейна.Теперь фермер должен определить, достаточно ли у него на заднем дворе площади для размещения бассейна. В то время как фермер начал узнавать больше об единицах СИ, он все еще испытывает дискомфорт от их использования и решает, что его единственный жизнеспособный вариант — построить бассейн в форме равностороннего треугольника со сторонами 77 футов в длину, поскольку любой другой вариант будет либо слишком большим, либо маленьким. Учитывая эти размеры, фермер определяет необходимую площадь следующим образом:
Поскольку наибольшее расстояние между любыми двумя точками равностороннего треугольника — это длина ребра треугольника, фермер резервирует края бассейна для плавания «кругов» в своем треугольном бассейне с максимальной длиной примерно вдвое меньшей, чем у олимпийского. бассейн, но с удвоенной площадью — все под бдительными глазами правящей королевы бассейна, его дочери и неодобрительного взгляда его жены.
Трапеция
Трапеция — это простой выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных сторон. Свойство быть выпуклым означает, что угол трапеции не превышает 180 ° (в отличие от вогнутого четырехугольника), в то время как простота отражает то, что трапеции не самопересекаются, то есть две несмежные стороны не пересекаются. В трапеции параллельные стороны называются основаниями трапеции, а две другие стороны называются ногами.Существует больше различий и классификаций для разных типов трапеций, но их площади по-прежнему рассчитываются таким же образом с использованием следующего уравнения:
где b 1 и b 2 — базы. h — высота или перпендикулярное расстояние между основаниями
Фермер и его дочь — попытки разгрома
Прошло два года с тех пор, как бассейн фермера был достроен, а его дочь выросла и повзрослела.Хотя ее любовь к треугольникам все еще сохраняется, она в конце концов пришла к осознанию того, что независимо от того, насколько хорошо она была «треугольной», сами по себе треугольники не могут заставить мир вращаться, и что мастерская Санты не может правдоподобно балансировать на Северном полюсе, если бы мир скорее пирамида, чем сфера. Постепенно она начала принимать другие формы в свою жизнь и преследовала множество различных интересов — в настоящее время — фристайл BMX. Таким образом, ей требуется пандус, но, к сожалению для фермера, не просто пандус.Пандус должен состоять только из форм, которые могут быть сформированы из нескольких треугольников, поскольку, как и ее рэп-идол Б.о.Б., дочери фермера все еще трудно принять реальность изогнутых поверхностей. Конечно, он должен использовать только цифру 9 в своих измерениях, чтобы отразить ее возраст. Фермер решает, что его лучший вариант — построить пандус, состоящий из нескольких прямоугольников, при этом боковая поверхность пандуса имеет форму трапеции. По мере того, как фермер теперь освоился с СИ, он может быть более креативным в использовании единиц и может построить пандус более разумного размера, соблюдая требования своей дочери.Он решает построить пандус с трапециевидной поверхностью высотой 9 футов, нижним основанием длиной 29,528 футов (9 м) и верхним основанием 9 футов. Площадь трапеции рассчитывается следующим образом:
| площадь = | × 9 = 173,376 кв. Футов |
Круг
Круг — это простая замкнутая форма, образованная множеством всех точек на плоскости, находящихся на заданном расстоянии от заданной центральной точки. Это расстояние от центра до любой точки на окружности называется радиусом.Более подробную информацию о кругах можно найти на странице «Калькулятор круга», но для вычисления площади необходимо только знать радиус и понимать, что значения в круге связаны математической константой π . Уравнение для вычисления площади круга выглядит следующим образом:
площадь = πr 2
Фермер и его дочь — Круг Ли (ж)
Прошло еще шесть лет, и его дочь превратилась в сильного, красивого, влиятельного, уверенного в себе 15-летнего неблагодарного человека, сосредоточенного исключительно на поиске внешнего подтверждения у знакомых и незнакомых людей в социальных сетях, при этом полностью игнорируя искреннюю поддержку со стороны ближайших родственников и друзей. ,После спора с отцом по поводу чрезмерного использования социальных сетей, она решает воспользоваться страхом отца перед неизвестным и его верой в сверхъестественное, чтобы разыграть его. Не зная, с чего начать, она ходит по городу, разговаривая с множеством незнакомцев, у каждого из которых, по-видимому, есть бесконечные источники мудрости и советов, где она узнает о кругах на полях и их связи с инопланетянами и неопознанными летающими объектами, а также на многие другие темы, которые игнорируйте все научные и логические объяснения.Убедившись, наконец, в сферической природе Земли, удалив все свои прошлые публикации в социальных сетях, касающихся BoB, и расширив свою любовь к треугольникам до принятия других форм, она решает сделать основной круг на полях, состоящий из ряда концентрических кругов и хочет определить площадь, необходимую для создания кругов на полях с внешним радиусом 15 футов. Она делает это, используя следующее уравнение:
площадь = π × 15 2 = 706,858 кв. Футов
К несчастью для фермера, он не только напуган кругами на полях, которые появились в ту ночь, когда его дочь сказала ему, что она была на вечеринке со своими друзьями, что по какой-то странной причине не привело к лишним постам в Instagram (он был, конечно, первым последователем своей дочери), но количество «исследователей круга» и «цереологов», появившихся на его ферме, чтобы изучить и впоследствии подтвердить подлинность кругов на полях как инопланетной конструкции, стоило ему значительного ущерба для его посевов ,
Сектор
Сектор круга — это по существу часть круга, заключенного между двумя радиусами и дугой. Учитывая радиус и угол, площадь сектора можно вычислить, умножив площадь всего круга на отношение известного угла к 360 ° или 2π радианам, как показано в следующем уравнении:
| площадь = | × πr 2 | , если θ в градусах |
или
| площадь = | × πr 2 | , если θ в радианах |
Фермер и его дочь — разделение семьи
Фермер и его семья столкнулись с самой серьезной дилеммой на сегодняшний день.Прошел год, дочери фермера исполнилось 16 лет, и в рамках празднования ее дня рождения ее мать испекла ее любимый десерт — ежевичный пирог. К несчастью для дочери фермера, ежевичный пирог также является любимой едой их домашнего енота, Утконоса, о чем свидетельствует отсутствие пирога на 180 ° с явными признаками виновника в виде крошек, ведущих к чрезмерно увлеченному еноту. Изначально пирог легко можно было разделить между тремя людьми и одним енотом, но теперь половину пирога приходится делить между тремя людьми, поскольку огорченный, но пресыщенный Утконос наблюдает издали.Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, можно рассчитать следующим образом:
площадь = 60 ° / 360 ° × π × 16 2 = 134,041 дюйм 2
В результате невнимательности Утконоса каждый получает на треть меньше, и дочь задумчиво вспоминает урок американской истории, где она узнала о битве при Аламо и изображении народного героя Дэви Крокетта и его шляпы из енотовидной шкуры.
Эллипс
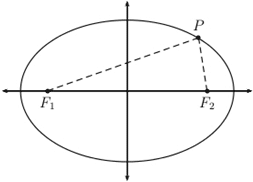
Эллипс — это обобщенная форма круга и кривая на плоскости, где сумма расстояний от любой точки кривой до каждой из двух ее фокальных точек постоянна, как показано на рисунке ниже, где P — любая точка эллипса, а F 1 и F 2 — это два фокусировки.
Когда F 1 = F 2 , полученный эллипс представляет собой круг. Большая полуось эллипса, как показано на рисунке, который является частью калькулятора, является самым длинным радиусом эллипса, а малая полуось — самым коротким.Большая и малая оси относятся к диаметрам, а не радиусам эллипса. Уравнение для вычисления площади эллипса аналогично уравнению для вычисления площади круга, с той лишь разницей, что используются два радиуса, а не один (поскольку фокусы находятся в одном месте для круга):
area = πab
, где a и b — мажор
и малые полуоси
Фермер и его дочь — падение с орбиты
Прошло два года с момента таинственного исчезновения домашнего питомца Утконоса и случайного выигрыша пушистого аксессуара дочери фермера в школьной лотерее, которая помогла заполнить пустоту потери их любимого питомца.Дочке фермера сейчас 18, и она готова сбежать из сельской Монтаны, чтобы жить в колледже, полной свободы и распутства, и, конечно же, немного поучиться на стороне. К несчастью для дочери фермера, она росла в среде, наполненной позитивным подкреплением, и, следовательно, с менталитетом, что нужно «стрелять на луну, [поскольку] даже если вы промахнетесь, вы приземлитесь среди звезд», а также утверждение всех окружающих, что она может делать абсолютно все, что захочет! Таким образом, с ее неоптимальными оценками, отсутствием каких-либо внеклассных занятий из-за ее бесчисленного множества различных интересов, отнимающих все ее свободное время, нулевого планирования и ее настойчивого стремления поступать только в самые лучшие из лучших университетов, шок, который возник, когда она не была принята ни в один из ведущих университетов, в которые она подавала документы, что можно было бы разумно сравнить с ее метафорической посадкой в глубоком космосе, надуванием, замерзанием и быстрым удушьем, когда она пропустила луну и приземлилась среди звезд.Наряду с ее легкими ее мечта стать астрофизиком была внезапно нарушена, по крайней мере, на время, и ей пришлось вычислить эллиптическую площадь, необходимую в ее комнате, чтобы построить модель почти эллиптической орбиты Земли вокруг Солнца размером с человека. чтобы она могла с тоской смотреть на солнце в центре своей комнаты и его олицетворение ее сердца, пылающего страстью, но окруженного холодными просторами космоса, с далеким вращением Земли, насмешливо представляющим расстояние между ее мечтами и твердой землей ,
площадь = π × 18 футов × 20 футов = 1130,97 кв. Футов
Параллелограмм
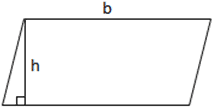
Параллелограмм — это простой четырехугольник, у которого есть две пары параллельных сторон, причем противоположные стороны и углы четырехугольника равны по длине и углам. Прямоугольники, ромбы и квадраты — это частные случаи параллелограммов. Помните, что классификация «простой» формы означает, что форма не является самопересекающейся. Параллелограмм можно разделить на прямоугольный треугольник и трапецию, которые в дальнейшем можно преобразовать в прямоугольник, что делает уравнение для вычисления площади параллелограмма по существу таким же, как и для вычисления прямоугольника.Однако вместо длины и ширины параллелограмм использует основание и высоту, где высота — это длина перпендикуляра между парой оснований. Основываясь на рисунке ниже, уравнение для расчета площади параллелограмма выглядит следующим образом:
площадь = b × h
Фермер и его дочь — Алмаз в небе
Еще два года прошли в жизни фермера и его семьи, и, хотя его дочь была причиной сильного беспокойства, она наконец преодолела расстояние между пылающим солнцем, которое является ее сердцем, и Землей, на которой настаивает общество. она должна оставаться на земле.В результате борьбы, которая последовала за ее самоизоляцией, в окружении воображаемых, осуждающих глаз, предполагающих ее неудачу со всех сторон, дочь фермера вышла из-под натиска земли, как алмаз, ярко и твердо сияя в своей решимости. Несмотря на все его недостатки, она решает, что у нее нет другого выбора, кроме как оставаться в астероидном поле жизни в надежде, что финал сказки Диснея существует. Наконец-то, к счастью для дочери фермера и ее семьи, надежда действительно появилась, но не в виде Прекрасного Принца, а скорее как знак с предполагаемых небес.Несмотря на все ее метафорические размышления и невзгоды, связанные с космосом, становится почти правдоподобным, что дочь фермера каким-то образом повлияла на массивный восьмигранный алмазный астероид, падающий прямо, но безопасно на их сельскохозяйственные угодья, что она интерпретирует как представление ее путешествия, становления и возможного возвращения домой. Дочь фермера приступает к измерению площади одного из ромбовидных лиц своего недавно найденного символа жизни:
площадь = 20 футов × 18 футов = 360 квадратных футов
К несчастью для дочери фермера, появление огромного алмаза привлекло внимание со всего мира, и после достаточного давления она уступает человеку внутри себя и продает алмаз, само изображение ее жизни и души, одному человеку. богатый коллекционер и продолжает жить остаток своей жизни в щедрых удовольствиях, отказываясь от своих убеждений и теряясь в черной дыре общества.
Единицы общего пользования
| Блок | Площадь, м 2 |
| квадратных метров | Единица СИ |
| га | 10,000 |
| квадратных километров (км 2 ) | 1000000 |
| квадратных футов | 0,0929 |
| двор | 0,8361 |
| акров | 4046.9 (43 560 квадратных футов) |
| квадратных миль | 2,589,988 (640 акров) |