Площадь круга и периметр: Площадь и периметр круга: формула, расчет, и калькулятор

Площадь круга кратко Планометрия

Привет, сегодня поговорим про площадь круга, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое площадь круга , настоятельно рекомендую прочитать все из категории Планометрия.

площадь круга — это численная характеристика, характеризующая размер плоскости, ограниченной линией окружности. Вычислить площадь круга можно с помощью числа Пи и радиуса окружности, или с помощью других известных исходных данных.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Теорема

Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

Доказательство

Построим два правильных n-угольника: P1 – вписанный в круг и P2 – описанный около круга.

Многоугольники P1 и P2 являются простыми фигурами. Многоугольник P2 содержит круг, а многоугольник P1 содержится в круге. Радиусы, проведенные в вершины многоугольника разбивают его на n треугольников, равных треугольнику AOD. Поэтому

где p – периметр многоугольника P1, R – радиус треугольника. Аналогично находим площадь многоугольника P2

Итак, многоугольник P1, содержащийся в круге, имеет площадь

И многоугольник P2, содержащий круг, имеет площадь

При достаточно большом n периметр p отличается сколь угодно мало от длины l окружности, а cos α сколь угодно мало отличается от единицы, поэтому площади многоугольников P1 и P2 сколь угодно мало отличаются от величины lR/2. Согласно определению площади произвольной фигуры это значит, что площадь круга

Теорема доказана.

Таблица с формулами площади круга

	исходные данные	Чертеж	формула для определения площади
1	радиус		​​
2	диаметр		​​​​
3	длина окружности		​​​​
4	сторона квадрата вписанного в круг		​​​​
5	сторона квадрата, в который вписан круг		​​​​
6	стороны треугольника		​​
7	сторона равностороннего треугольника		​​​​
8	высота равностороннего треугольника		​​
9	боковая сторона и основание равнобедренного треугольника
10	стороны при прямом угле треугольника
11	боковая сторона и основание равнобедренного треугольника
12	боковые стороны равнобедренного треугольника и угол между ними
13	стороны прямоугольного треугольника
14	сторона и угол при основании треугольника
15	сторона равностороннего треугольника
16	сторона и угол при основании трапеции
17	боковые стороны и диагональ трапеции
18	стороны прямоугольника
19	сторона и количество сторон многоугольника
20	сторона равностороннего шестиугольника		​​

---

См .

Об этом говорит сайт https://intellect.icu . также

• площадь прямоугольника , площадь квадрата ,
• площадь треугольника ,
• вычисление площадей плоских фигур в полярных координатах ,
• площадь трапеции ,
• вычисление площадей плоских фигур ,
• площадь параллелограмма ,
• площадь кругового сектора ,
• четырехугольник , четырехугольники ,
• площадь фигуры ,

• площадь боковой поверхности цилиндра ,
• площадь сферы ,

Понравилась статья про площадь круга? Откомментируйте её Надеюсь, что теперь ты понял что такое площадь круга и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия

Из статьи мы узнали кратко, но емко про площадь круга

Площадь круга, сектора

Разделим окружность на возможно большее число равных частей, все полученные точки деления соединим с центром окружности, а соседние — друг с другом хордами.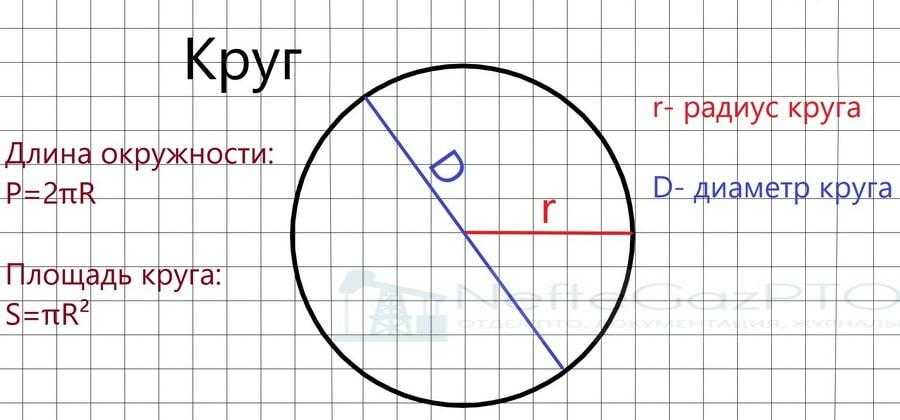

Таким образом получим ряд равных равнобедренных треугольников (черт. 339).

Площадь каждого треугольника равна ^ah/₂, где а — основание его, h — высота.

Обозначив через S’ сумму площадей всех полученных треугольников, получим формулу:

$$ S’=\frac{ah}{2}\cdot n \;\; или \;\; S’=\frac{an \cdot h}{2} $$, где n — число треугольников.

Сумма площадей всех треугольников (S’) весьма близка к площади круга (S), сумма оснований всех треугольников (an) весьма близка к длине окружности (C), а высота (h) каждого треугольника весьма близка к радиусу (r) круга.

Если пренебречь незначительными различиями в размерах, то получим формулу площади круга:

$$ S_{кр} = \frac{Cr}{2} $$

После преобразования получим \( S_{кр} = \frac{2\pi r \cdot r}{2} \), или S_кр = π r²; а обозначив через D диаметр круга, получим:
$$ S_{кр} = \frac{\pi D^2}{4} $$

Примечание. В формуле \(S_{кр} = \frac{Cr}{2}\) поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах доказывается, что равенство \(S_{кр} = \frac{Cr}{2}\) не приближённое, а точное.

Другое доказательство:

Впишем в круг, радиус которого обозначим R, какой-нибудь правильный многоугольник.

Пусть площадь этого многоугольника будет q, периметр — р, апофема — а.

По формуле вычисления площади правильного многоугольника имеем:

q = ¹/₂pa.

Вообразим теперь, что число сторон этого многоугольника неограниченно удваивается. Тогда периметр р и апофема а (следовательно, и площадь q) будут увеличиваться, причём периметр будет стремиться к пределу, принимаемому за длину C окружности, апофема будет стремиться к пределу, равному радиусу R круга. Из этого следует, что площадь многоугольника, увеличиваясь при удвоении числа сторон, будет стремиться к пределу, равному ¹/₂С • R.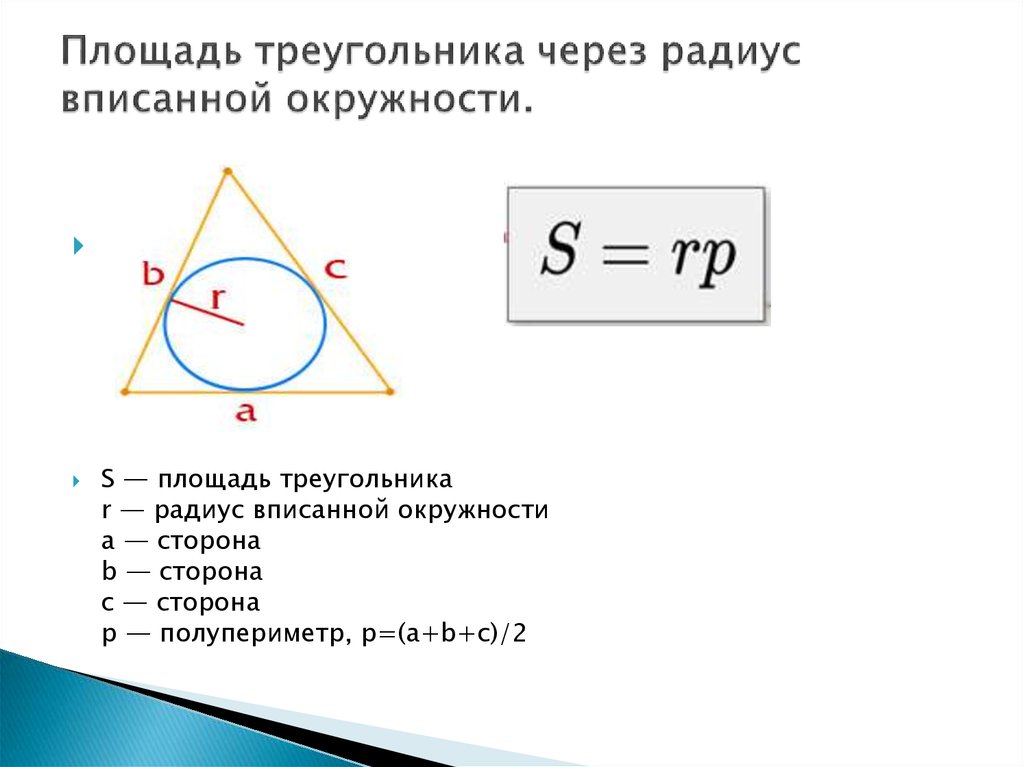 2 n}{360} $$ где S — площадь сектора.

Периметр и площадь круга: формула, диаграмма и многое другое

• Автор Кирти Кулкарни
• Последнее изменение 06-10-2022

Периметр и площадь круга: Круг — очень важная геометрическая фигура. В нашей повседневной жизни мы видим вокруг себя много круглых объектов, таких как кольцо, дно бутылки, руль и т. д. Длина границы круга называется периметром или окружностью круга. Пространство или область, окруженная кругом, называется площадью круга.

Архимеду, греческому математику, приписывают изобретение метода вычисления значения числа пи. Для аппроксимации он нарисовал правильный многоугольник внутри круга, и чем больше сторон он нарисовал у многоугольника, тем лучшего приближения он достиг. Отношение длины окружности (периметра) к ее диаметру было известно давно. Математическая константа — это число. Отношение длины окружности к диаметру любого круга равно. 3,14159 является близким приближением. Интерактив ниже показывает, как рассчитать значение числа Пи.

В этой статье мы подробно обсудим периметр и площадь круга и многое другое.

Геометрическое место множества всех точек плоскости, находящихся на равном расстоянии от фиксированной точки, называется окружностью. Круг – двумерная фигура.

Фиксированная точка называется центром окружности, а фиксированное расстояние называется радиусом окружности. Различные термины, связанные с кругом, обсуждаются ниже:

1. Центр
   Неподвижная точка окружности, из которой все точки взяты на одинаковом расстоянии, называется центром окружности.
2. Радиус
   Фиксированное расстояние от точки на окружности до центра окружности называется радиусом окружности. Можно сказать, что отрезок, соединяющий центр с точкой на окружности, называется радиусом окружности.
3. Диаметр
   Отрезок, соединяющий две точки окружности и проходящий через центр окружности, называется диаметром окружности.
4. Хорда
   Хорда окружности — это отрезок, соединяющий любые две точки на окружности окружности.
5. Касательная
   Линия, касающаяся окружности только в одной точке, называется касательной к окружности.
6. Секанс
   Прямая, пересекающая окружность в двух точках, называется секущей окружности.
7. Сектор:
   Область, ограниченная двумя радиусами и дугой окружности, называется сектором окружности.
8. Сегмент
   Область, образованная хордой и дугой окружности, называется сегментом окружности.
9. Дуга
   Дуга представляет собой непрерывную часть окружности окружности.

Периметр и площадь круга: Определение

Окружность (периметр)
Окружность круга или периметр круга — это мера длины границы круга.

Если круг разрезать на одном конце и разрезать, образуя отрезок, то его длина равна длине окружности.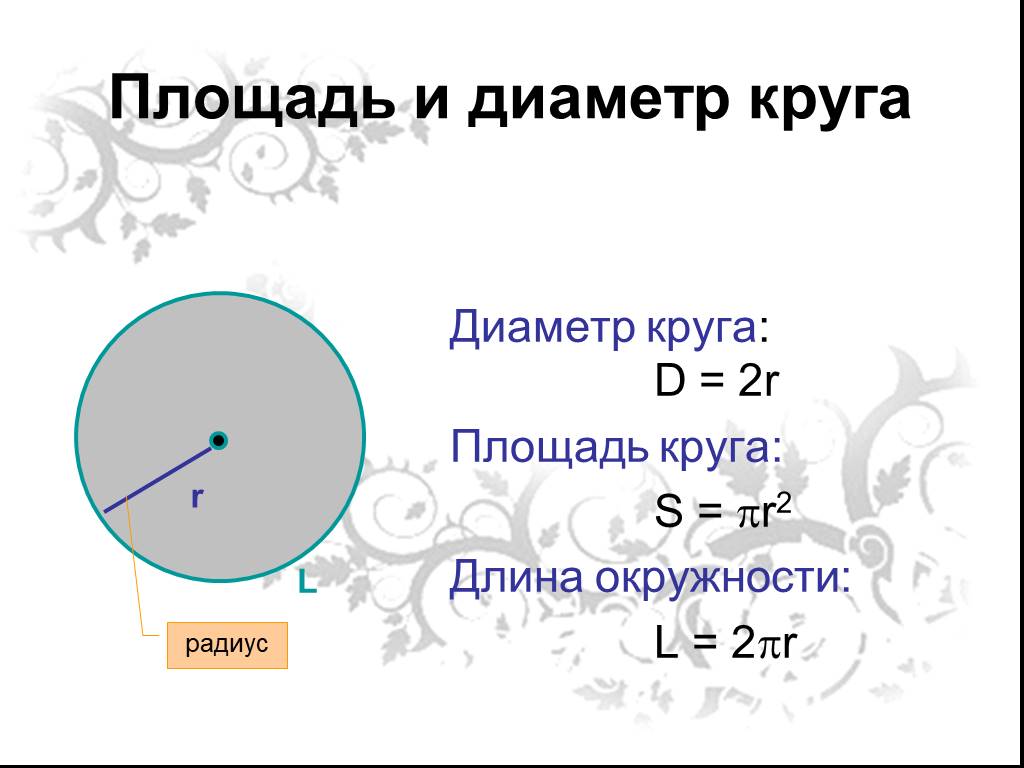 Обычно он измеряется в таких единицах, как \({\rm{см}}\) или \({\rm{м}}\). 9{\rm{o}}}\), тогда образуется окружность. Если дуга больше половины окружности, то это большая дуга. Если она меньше половины окружности, это малая дуга.

Диаметр делит круг ровно на две равные части, каждая из которых называется полукругом.

Малая дуга, полуокружность и большая дуга показаны на рисунках выше красным цветом.

Что такое

Формула периметра и площади круга ?

Рассмотрим окружность радиуса \(‘r’\). Есть несколько формул, связанных с площадью и периметром круга, которые объясняются ниже:

Периметр (окружность) окружности с радиусом

Если радиус окружности задан, то длину окружности можно рассчитать по формуле

Окружность \( = 2 \times {\rm{Радиус}} = 2\pi r\)

Где \(r\) представляет радиус окружности, а \(\pi \)  – математическая константа, значение которой примерно равно \(\frac{ {22}}{7}\) или \(3. 2}}}{4}\) , , где \(d\) представляет собой диаметр окружности.

Вывод формулы площади круга

Для вычисления площади круга используются следующие методы:

1. Использование площади прямоугольника
2. Использование площади треугольника.

Площадь круга с использованием площади прямоугольника

В этом методе круг делится на множество маленьких секторов, а расположение секторов выполнено в виде параллелограмма, как показано на рисунке ниже.

Понятно, что если круг разделить на большее количество секторов, то параллелограмм превратится в прямоугольник.

Как видно на рисунке, круг разделен на \(16\) секторов; \(8\) из них окрашены в синий цвет, а остальные \(8\) – в зеленый.

Синие и зеленые сектора расположены попеременно, как показано на рисунке выше.

Учитывая, что длина окружности равна \(2\pi r\), общая длина основания параллелограмма (прямоугольника по мере увеличения числа секторов) будет равна \(\pi r\) (общая длина оснований \(8\) синих секторов) и высота параллелограмма (или прямоугольника) будет \(r\). 92}\).

Площадь круга с использованием площади треугольника

В этом методе вся площадь круга считается состоящей из бесконечного числа концентрических окружностей. Если окружность разрезать по радиусу так, как показано на рисунке, и если все эти бесконечно много прямых (окружностей концентрических окружностей) расположить в виде прямоугольного треугольника или в виде равнобедренного треугольника, то прямоугольный получается равнобедренный или равнобедренный треугольник, основание которого равно \(2\pi r\) , а высота равна \(r\). 92}\)

Периметр и площадь концентрических окружностей

Окружности с одним центром и разными радиусами называются концентрическими окружностями.

Периметр (окружность)

\({C_1}\) и \({C_2}\) – длина окружности, а \(r\) и \(R\) – радиус внутренней и внешней окружности. круг соответственно.

Окружность внешнего круга \({C_1} = 2\pi r\)

\( \Rightarrow r = \frac{{{c_1}}}{{2\pi }}\)

92}} \справа)\).

Периметр и площадь полукруга

Если круг разделить на две половины, то каждая часть называется полуокружностью.

Периметр (окружность)
Длина окружности полукруга равна половине длины окружности круга.

Окружность полукруга \( = \frac{1}{2} \times 2\pi r = \pi r\).

Площадь
Длина диаметра в два раза больше длины радиуса. Итак, если \(r\) – радиус, а \(d\) – диаметр окружности, то \(d = 2r\) или \(r = \frac{d}{2}\). 92}}}{8}\).

Решенные примеры

Q.1. Раму и его друзьям подают пиццу \(15\) дюймов (диаметром). Вычислите его окружность.

Ответ :  Диаметр пиццы \((d) = 15\)
Формула длины окружности через диаметр \(C = \pi d\)
\(C = \ pi \times 15 = 15\pi \) дюймов
Следовательно, длина окружности пиццы равна \(15\pi \).

Q.2. Колесо инвалидной коляски имеет диаметр \(56\;\,{\rm{cm}}\). Если колесо сделает один оборот, на какое расстояние проедет кресло-коляска? (Используйте: \(\pi = \frac{{22}}{7}\))
Ответ :  Если колесо повернется один раз, кресло-коляска переместится на расстояние, равное окружности колеса.
Дан диаметр колеса \((d) = 56\;{\rm{см}}\)
Мы знаем, что длина окружности колеса \(C = \pi d\)
\(C = \ frac{{22}}{7} \times 56 = 176\;\,{\rm{см}} = 1\;\,{\rm{m}}\,76\;\,{\rm{см} }}\)
Таким образом, кресло-коляска движется \(1\;\,{\rm{m}}\,76\;\,{\rm{см}}\) за один оборот колеса.

2}\)

Q.5. Если радиус круга \(r\,{\rm{см}}\) и если его удвоить, то какой будет длина окружности нового круга .
Ответ : Дан радиус окружности \( = r\;{\rm{cm}}\)
Тогда длина окружности \( = 2\pi r\)
Если радиус круга удваивается, тогда новый радиус \(R = 2r\;{\rm{см}}\)
Следовательно, длина окружности нового круга \( = 2\pi R = 2\pi \times 2r = 4\pi r\)
Следовательно, длина окружности нового круга равна \(4\pi r\). 2}}}\).

Q.4.   В чем разница между площадью и периметром круга?
Ответ : Площадь круга – это пространство, занимаемое кругом в двумерной плоскости. Периметр – это длина границы окружности.

Q.5. Чему равна площадь и периметр круга?
Ответ : Окружность круга или периметр круга — это мера длины границы круга. Площадь круга определяется пространством или областью, занимаемой кругом в двумерной плоскости.

Мы надеемся, что эта подробная статья о периметре и площади круга поможет вам в подготовке. Если вы застряли, сообщите нам об этом в разделе комментариев ниже, и мы свяжемся с вами в ближайшее время.

Площадь и периметр круга

Решение : 

Площадь круга

Вы уже хорошо знакомы с концепцией круга. Вот, на этом уроке мы будем изучать площадь круга. В ходе изучения понятия площади круга мы столкнемся с формулой площади круга и формулой периметра круга. Вы также сможете поработать над примерами, на которых вы можете попрактиковаться в конце этой главы.

Что такое площадь круга?

Область, занимаемая кругом в двухмерной плоскости, называется площадью круга. Площадь круга можно определить по формуле A =2 πr² Здесь ‘r’ обозначает радиус окружности.  Измерение площади, занимаемой круглым полем или участком, становится проще, если использовать формулу площади. Также возможно вычислить периметр, а также площадь круга с использованием различных формул. Также важно понимать, что круг не имеет объема, создающего путаницу в сознании учащихся. Это потому, что объем не присутствует в круге, поскольку круг представляет собой двухмерную форму, а не объемную трехмерную фигуру.

Что такое формула площади круга?

Важно понимать, что такое формула площади круга.  Здесь мы постараемся обсудить это в хорошем и простом виде, чтобы вы получили правильные знания. Нарисуем окружность радиусом ‘r.’

На приведенном выше рисунке мы нарисовали окружность с радиусом ‘r’ от центра ‘o’ к границе. Вы должны понимать, что площадь приведенного выше круга A равна произведению квадрата радиуса и значения числа пи.

Площадь круга, A = πr² квадратных единиц (где ‘r’ радиус и значение π = 22/7 или 3,14)

Площадь и периметр

Важно понимать понятие площади и периметра.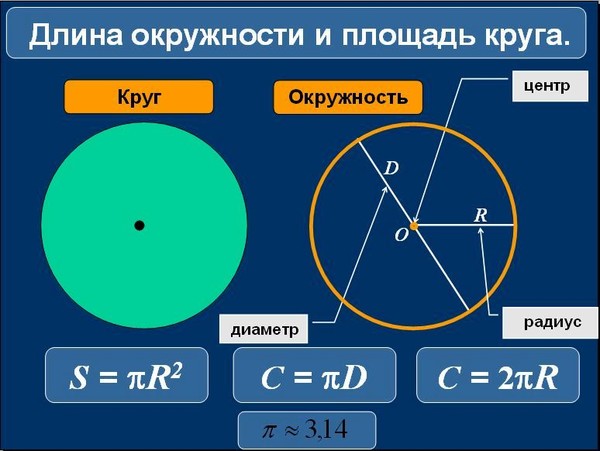

Итак, область, ограниченная формой объекта, называется формой объекта. Площадь фигуры относится к пространству, которое покрыто любыми геометрическими формами фигуры. Это зависит от свойств и размеров, когда речь идет о площади всех форм.

Обратите внимание, что и для квадрата, и для ромба есть разница в площади квадрата. Не обязательно, чтобы площадь двух объектов, имеющих одинаковую форму, была равна, если не установлено, что их размеры обеих форм равны. Мы можем понять это на примере. Предположим, что два прямоугольника имеют длину L1 и L2, и пусть B1 и B2 — ширина. Здесь площади прямоугольного ящика A1 и A2 будут равны, но только при условии, что L1 = L2 и B1 = B2.

Что касается периметра фигуры, то это общее расстояние вокруг фигуры. Следовательно, это длина любой формы при расширении в линейную форму. Приближаясь к периметру различных форм, они могут совпадать по длине друг с другом в соответствии с их размерами.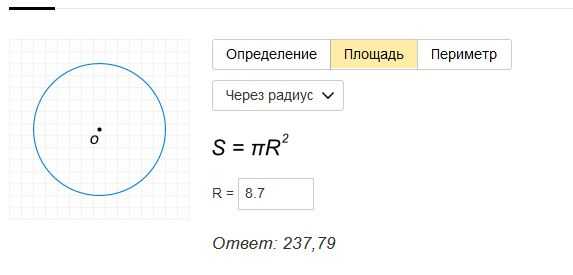 Например, если для изготовления круга используется металлическая проволока длиной L, то вы можете использовать ту же проволоку для построения квадрата со сторонами, равными по длине.

Похожие видео:

<ул>

Площадь и периметр квадрата

Площадь и периметр параллелограмма

Площадь и периметр треугольника

Площадь и периметр трапеции

Площадь и периметр ромба

Что такое периметр и площадь круга?

В круге длина окружности – это расстояние от внешней линии круга.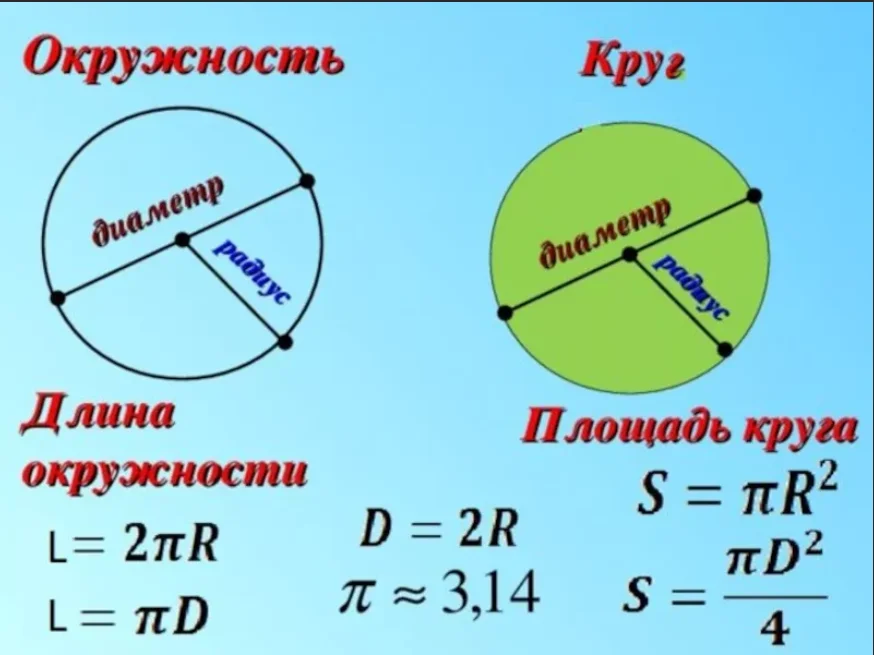 Итак, здесь длина окружности равна 2πr, а площадь круга равна πr²

В квадрате все четыре стороны равны, а все углы равны 90⁰.  В двумерной плоскости пространство, занимаемое квадратом, является площадью квадрата. Расстояние, пройденное по внешней линии, является ее периметром.

    Периметр квадрата = 4a

    Площадь квадрата = a²

Здесь длина стороны квадрата равна ‘a’ где a – длина стороны квадрата.

Диаграмма площади и периметра

Теперь мы проверим приведенную ниже диаграмму площади и периметра различных геометрических фигур, чтобы хорошо понять ее.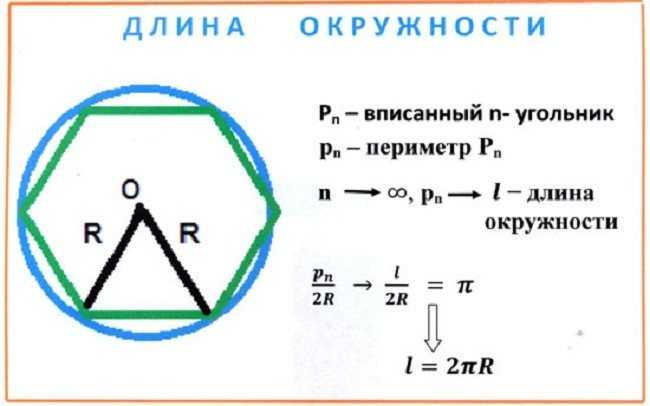

<граница таблицы="1" ячейкиспейсинг="0"> <тело> <тд>

Форма

<тд>

Область

<тд>

Периметр

<тд>

Условия

<тд>

Круг

<тд>

A = π &раз; р²

<тд>

Окружность = 2πr

<тд>

r = радиус окружности

<тд рядов = "3">

Треугольник

<тд рядов = "3">

A = ½ &раз; б & раз; ч

<тд рядов = "3">

S = a + b + c

<тд>

b = основание

<тд>

h = высота

<тд>

a, b и c – стороны треугольника

<тд>

Квадрат

<тд>

A = a²

<тд>

P = 4a

<тд>

a = длина стороны

<тд рядов = "2">

Прямоугольник

<тд рядов = "2">

A = l × ж

<тд рядов = "2">

P = 2(l + w)

<тд>

l = длина

<тд>

w = ширина

<тд рядов = "3">

Параллелограмм

<тд рядов = "3">

A = b × ч

<тд рядов = "3">

P = 2(b + h)

<тд>

b=база

<тд>

 

<тд>

h=высота по вертикали

Здесь мы поработаем над некоторыми примерами, которые помогут вам получить правильное представление о том, как решать различные вопросы о площади, диаметре, окружности и периметре круга.

Вопрос 1. Радиус окружности равен 6 см. Сможете ли вы узнать его диаметр, площадь и длину окружности?

Решение:

Здесь

Радиус, r = 6 см

Диаметр круга 2r

Итак, 2 × 6 см

Получаем = 12 см

Площадь круга составляет  π р²

Итак, мы получаем π &раз; 36

Получаем = 113,097 см²

Диаметр окружности равен 2 π р

= 2 × &Пи; &раз; 6

= 37,699 см

Проблема 2:  Радиус окружности равен 20 см. Сможете ли вы найти диаметр, площадь и длину окружности?

Решение

Здесь

Радиус круга, r = 20 см

Диаметр круга 2r

= 2 × 20

= 40 см

Площадь круга составляет πr²

= π &раз; 20²

= π &раз; 400

= 125,66 см²

Чтобы найти длину окружности, мы используем P= 2 πr

= 2 × &Пи; &раз; 20

= 125,66 см

Важные главы:

<ул>

No related posts.