Площадь прямоугольника квадрата треугольника: Площадь прямоугольника и квадрата | Геометрия

8 класс. Геометрия. Площадь. Площадь квадрата, прямоугольника, параллелограмма. — Площадь квадрата. Площадь прямоугольника.

Комментарии преподавателя

Площадь квадрата. Площадь прямоугольника

1. Теорема про площадь прямоугольника и её доказательство

На данном уроке мы докажем формулу для площади прямоугольника и решим несколько задач на её применение.

Теорема

Площадь прямоугольника равна произведению его смежных сторон (см. Рис. 1).

Если записать краткую формулировку этой теоремы, то она будет выглядеть так: .

Рис. 1

Доказательство:

Для доказательства данной теоремы достроим данный прямоугольник до квадрата со стороной  – см. Рис. 2.

Рис. 2

Площадь этого квадрата (по 4 свойству площадей) равна . Этот квадрат состоит из двух квадратов со сторонами  и  и двух прямоугольников со сторонами  и , площадь каждого из которых мы приняли за .

Воспользовавшись свойством площадей, составим следующее равенство:

.

Раскроем скобки в левой части:

Из этого равенства следует, что: .

Доказано.

2. Решение задач на применение формулы площади прямоугольника

Теперь решим несколько задач, используя данную теорему.

Задача 1

Смежные стороны прямоугольника равны  см и . Найдите площадь  этого прямоугольника (см. Рис. 3).

Решение

Рис. 3

Воспользуемся теоремой, которую мы только что доказали. В данном случае: , . Получаем: .

Ответ:.

3. Задача на применение свойства площадей

Задача 2

Как изменится площадь прямоугольника, если:

а) одну пару противоположных сторон увеличить в 3 раза;

б) одну пару противоположных сторон увеличить в 3 раза, а другую пару – уменьшить в 3 раза?

Решение:

а) На Рис. 4 изображена пара соответствующих прямоугольников.

 

Рис. 4

Воспользуемся формулой для площади прямоугольника: , . Таким образом, площадь прямоугольника увеличится в 3 раза.

б) На Рис. 5 изображена пара соответствующих прямоугольников.

 

Рис. 5

Воспользуемся формулой для площади прямоугольника: , . Таким образом, площадь прямоугольника не изменится.

Ответ: а) площадь прямоугольника увеличится в 3 раза; б) площадь прямоугольника не изменится.

Решим более сложную задачу, которая потребует от нас знания предыдущего материала.

Задача 3

Дан прямоугольник .  – середина , точка  – точка пересечения прямых  и . Найти площадь треугольника , если площадь прямоугольника : .

Решение:

Рис. 6

Рассмотрим треугольники:  и . Эти треугольники равны по второму признаку равенства треугольников (равенство сторон и двух углов). Действительно:

.

Из равенства треугольников следует равенство их площадей, то есть: .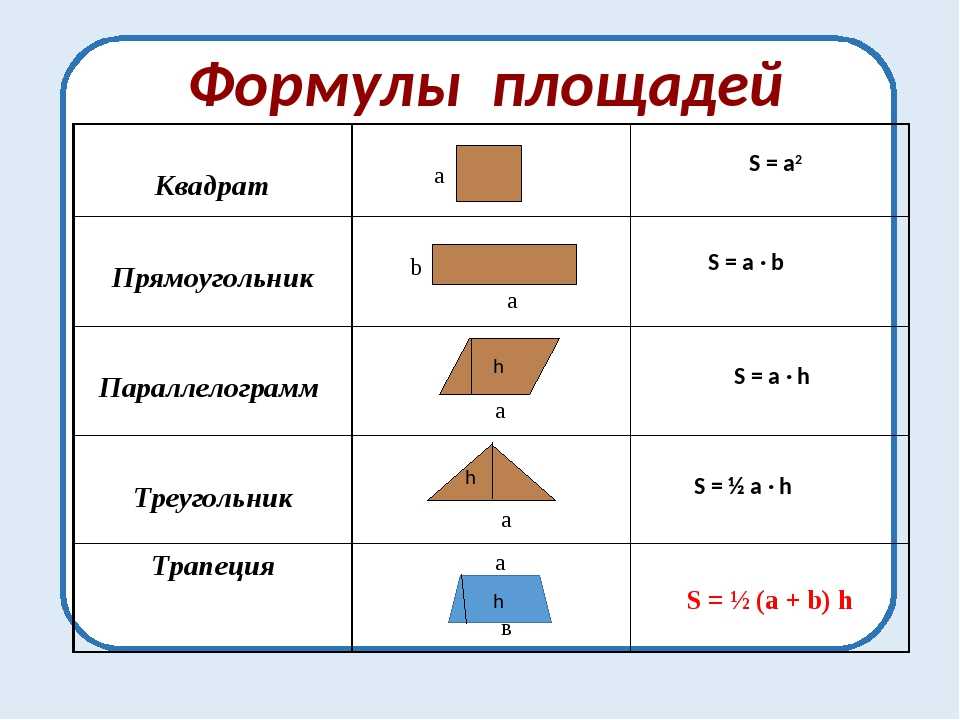

Кроме того, треугольник  состоит из треугольника  и четырёхугольника . Значит: .

Доказано.

ИСТОЧНИК

http://x-uni.com/geometriya/8-klass/video/ploschad-kvadrata-ploschad-pryamougolnika

http://www.youtube.com/watch?v=Jj9Xs2daB2k

http://www.youtube.com/watch?v=f4FYkfcvRho

http://fs00.infourok.ru/images/doc/302/301153/img16.jpg

http://frannersmicop.science/pic-www.uchportal.ru/_ld/224/86666795.jpg

http://static.zoobrilka.com/files/gdz/15693/291017.jpg

Площади треугольника и других плоских фигур

Что такое площадь?

Странный вопрос – не правда ли?

В обычной жизни мы привыкли к тому, что у всяких плоских фигур (таких как поверхность стола, стула, пол наших квартир и т.д.) есть не только длина и ширина, но и какая-то еще характеристика, которую мы, не задумываясь, называем площадью. {2}}\)? Ну например так:

Да и вообще, если мы возьмем прямоугольник, у которого стороны равны \( \displaystyle a\) метров и \( \displaystyle b\) метров, то в этом прямоугольнике…

…поместится ровно \( \displaystyle a\cdot b\) квадратных метров. Посмотри внимательно: у нас есть \( \displaystyle b\) «слоев», в каждом из которых ровно \( \displaystyle a\) квадратных метров.

Значит, всего в прямоугольнике размером \( \displaystyle a\)x\( \displaystyle b\) поместилось \( \displaystyle ab\) квадратных метров. Вот это число, сколько квадратных метров поместилось в прямоугольнике, и есть его площадь.

А если фигура – вовсе не прямоугольник, а какая-то абракадабра?

Можно ли узнать, сколько квадратных метров в ней находится? Можно ведь некоторые квадратные метры «порезать», переставить и т.д. ?..

Удивлю тебя – бывают такие ужасные абракадабры, для которых совершенно невозможно установить сколько там квадратных метров. Даже приблизительно! К сожалению, нарисовать такие фигуры – невозможно.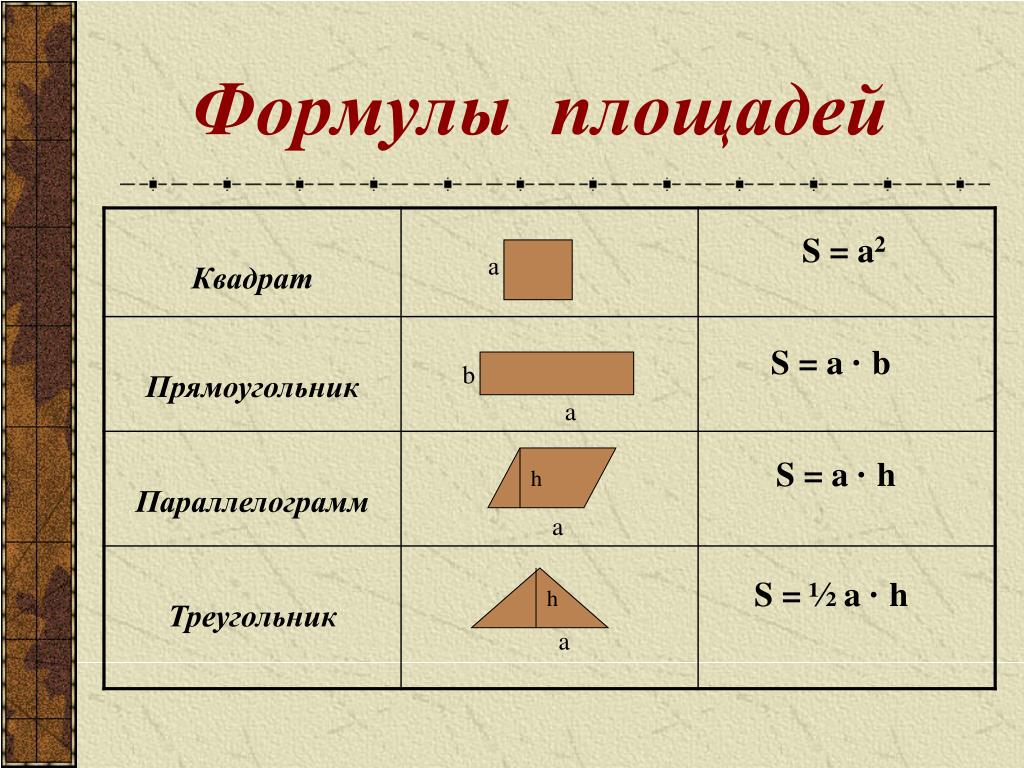

Но они есть! Они похожи, например, на такую «расческу» с очень мелкими зубьями.

Но мы такими «расческами» орудовать не будем, а будем рассматривать нормальные фигуры.

И вот, для нормальных фигур можно интуитивно (то есть для себя) считать, что площадь фигуры – это такое число, сколько в этой фигуре «поместится» квадратных единиц (метров, сантиметров и т.д.)

И представь себе, математики для многих фигур научились выражать площади через какие-то линейные (те, что можно измерить линейкой) элементы фигур. Эти выражения называются «формулы площади».

Формул этих довольно много – математики долго старались. Ты постарайся запомнить сначала самые простые и основные формулы, а потом уже те, что посложнее.

Хитрые вопросы о площадях

Кроме задачек, в которых просят просто найти площадь, встречаются еще всякие вопросики.

Ну вот например:

Во сколько раз увеличится площадь квадрата, если его сторону увеличить в три раза?

Давай ответим на этот вопрос двумя способами. {2}\) – площадь увеличилась в \( \displaystyle 9\) раз!

В случае с квадратами есть и второй способ «пощупать» и убедиться напрямую в этом числе \( \displaystyle 9\).

Рисуем:

Видишь, в квадрате со стороной \( \displaystyle 3a\) уместилось ровно \( \displaystyle 9\) квадратов со стороной \( \displaystyle a\).

Значит, формулам действительно можно верить 🙂

Если же у тебя не квадрат, то остается только подставлять новые значения в формулы – и не удивляйся, если вдруг числа получатся довольно большими.

Базовая геометрия — площадь (многоугольник, треугольник, круг, квадрат)

Предыдущий Следующий

Площадь (Многоугольник, Треугольник, Круг, Квадрат)

Площадь — это количество пространства внутри двумерной формы. Если вы думаете о полу вашей спальни, площадь будет максимальной площадью пола, на которую вы можете бросить свои вещи, прежде чем вы не сможете увидеть оставшийся пол.

Площадь всегда выражается в квадратных единицах ( единиц ² ). Это потому, что он двумерный (длина и высота).

Вы можете найти площадь фигур, посчитав клетки внутри фигур. На этих трех рисунках каждый прямоугольник представляет .

• Рисунок А занимает 25 маленьких ящиков, поэтому его площадь составляет
• Рисунок B занимает 36 маленьких ящиков, поэтому его площадь составляет
• Рисунок C занимает 21 полный ящик и 7 половинных ящиков, поэтому имеет площадь

Площадь прямоугольника = основание x высота

Вот файл .

Если разбить его на части шириной 1 см, то получится так:

В каждом ряду 10 квадратов, всего 6 рядов, что дает в сумме 10 × 6 квадратных см. Это то же самое, что умножить основание на высоту: .

Площадь треугольника = ½ (основание × высота)

Вот треугольник с основанием 5 см и высотой 6 см.

Если мы поместим другой треугольник с такой же высотой и основанием поверх этого треугольника, мы получим .

Теперь мы уже знаем, как вычислить площадь прямоугольника (основание × высота). Итак, площадь прямоугольника равна

. Однако нам нужен только треугольник, который составляет половину прямоугольника, . По сути, мы взяли ½ площади всего прямоугольника или ½ (основание × высота).

Площадь параллелограмма = основание × высота

Теперь рассмотрим параллелограмм с основанием 6 см и высотой 3 см.

Переместив маленький треугольник слева до упора вправо, эта фигура станет прямоугольником с основанием 6 и высотой 3 см.

Поскольку вы уже знаете, как найти площадь прямоугольника (основание × высота), у вас есть все инструменты, необходимые для нахождения площади этого параллелограмма.

Площадь трапеции = ½(основание ₁ + основание ₂ ) x Высота

Представьте себе, что отрезаем треугольный нижний левый угол и помещаем его в верхний правый угол, как показано ниже:

Теперь у нас есть еще один прямоугольник, но с новым основанием. Основание этой новой фигуры является средним значением исходных оснований. Площадь этой новой фигуры равна . Только будьте осторожны, потому что основание, которое мы используем, является средним значением двух первоначальных оснований!

Площадь круга = πr ²

Наконец мы осмотрим красивый круг. Вот один с радиусом 6 см.

Вот тот же круг, но с линиями, проведенными через каждый сантиметр.

Сначала мы объединили части квадрата, чтобы получить полный квадрат, затем мы очень тщательно и старательно пересчитали каждый из этих квадратов и обнаружили, что их примерно 113 квадратов. Это почти равно .

Предыдущий Следующий

Подробнее о базовой геометрии Навигация

Это продукт премиум-класса

Разблокировать эти функции

Устали от рекламы?

Присоединяйтесь сегодня и никогда больше их не увидите.

Начало работы

Найдите площадь квадрата, прямоугольника, треугольника и круга Рабочий лист

• Академики
• Ресурсы
• Безопасность
• Цены
• регистр
• Авторизоваться

Найдите площадь данного квадрата

8 дюймов 8 дюймов 8 дюймов

Найдите площадь данного прямоугольного треугольника

9

8 дюймов 3 дюйма

Найти площадь данного прямоугольника

9 дюймов 8 дюймов 9 дюймов 8 дюймов

Найти площадь данного круга площадь заданного квадрата

5 дюймов 5 дюймов 5 дюймов

Найти площадь заданного прямоугольного треугольника

8 дюймов 2 дюйма

Найти площадь заданного прямоугольника

4 дюйма 3 дюйма 4 дюйма

Показать все упражнения

7 Найти тренировку

7 площадь данного круга

9 дюймов

Площадь = 254,47 дюймов ₂

Решение

Площадь круга = π x r ²
Радиус (r) = 9 дюймов
x 9 x 3,194 ; где π = 3,14
область = 254,47 в ²

Найдите площадь данной квадратной

8 IN8 IN8 IN 8 в

Площадь = 64 в ₂

Решение

Площадь квадратной.
Сторона = 8 дюймов
Площадь = 8 x 8
Площадь = 64 дюйма ²

Найдите площадь данного правого треугольника

9 IN8 в

Площадь = 36 в ₂

Решение

Площадь треугольника =

12

x B x H

Базовая (B) = 8 в


X B x H

(B) = 8. (h) = 9 в

Область =

12

x 8 x

Площадь = 36 в ²

Найдите площадь данного прямоугольника

8 в 2 дюйма в 2 в

= 16 в ₂

Решение

Площадь прямоугольника = l x b
Длина (l) = 8 дюймов
Ширина (b) = 2 дюйма
Площадь = 8 x 2
Площадь = 16 дюймов ²

Найдите площадь данного прямоугольного треугольника

8 IN3 в

Область = 12 в ₂

Решение

Площадь треугольника =

12

x B x H

Основание (B) = 3 в
Высота (H) = 8 в

Область =

12 12 12.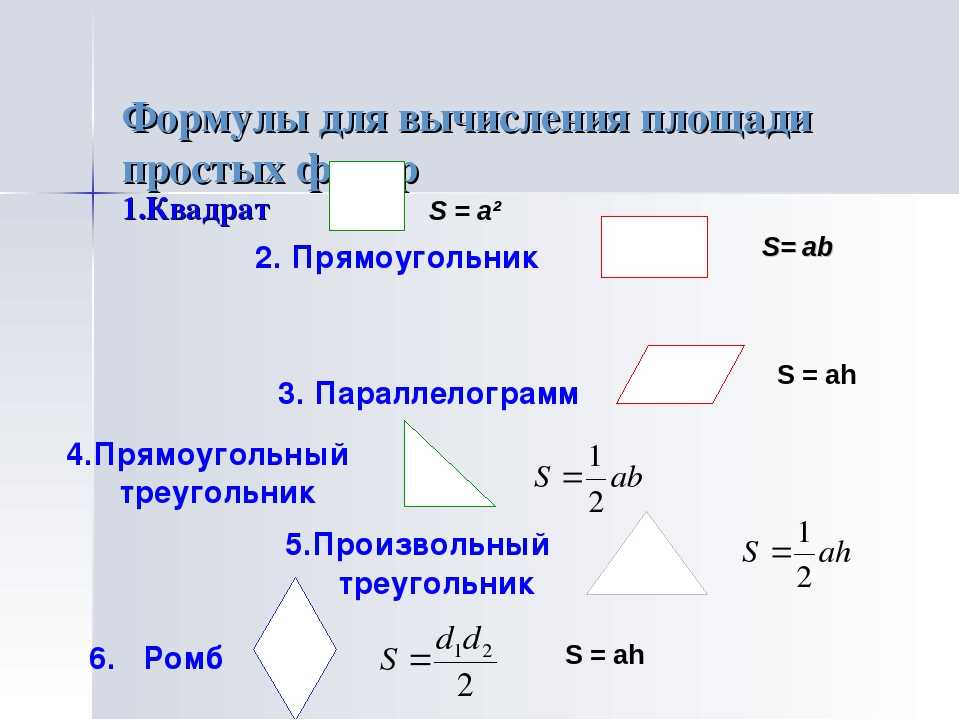

x 3 x 8

Площадь = 12 дюймов ²

Найдите площадь данного прямоугольника

9 дюймов 8 дюймов 9 дюймов 8 дюймов

Площадь = 72 дюйма ₂

Решение

Площадь прямоугольника = l x b
Длина (l) = 9 дюймов 8 (l) ширина
В области
= 9 x 8
Область = 72 в ²

Найдите область данного круга

8 в

Область = 201,06 в ₂

Решение

Область круга = π x R ²

.
Радиус (r) = 8 дюймов
Площадь = 3,14 x 8 x 8 ; где π = 3,14
Область = 201,06 в ²

Найдите площадь данной площади

5 в 5 в 5 в 5 в

Зона = 25 в ₂

Раствор

Площадь квадрата = сторона ²
. В площади
= 5 x 5
Площадь = 25 в ²

Найдите площадь данного правого треугольника

8 дюймов в 2 в

Площадь = 8 в ₂

Раствор

Площадь Трауриала =

12 12 120142.

х ш х в

Основание (b) = 2 дюйма
Высота (h) = 8 дюймов

Площадь =

12

х 2 х 8 дюйм3 дюйм4 дюйм3

Площадь = 12 дюймов ₂

Решение

Площадь прямоугольника = l x b
Длина (l) = 4 дюйма
Ширина (b) = 3 дюйма
Площадь = 4 x 3


Площадь = 112 в ²

Рабочий лист «Найти площадь квадрата, прямоугольника, треугольника и круга» с ответами для учебной программы по математике для 6-го класса доступен онлайн бесплатно в формате для печати и загрузки (pdf и изображение). Нажмите кнопку «ПЕЧАТЬ», «PDF» или «ИЗОБРАЖЕНИЕ», чтобы распечатать или загрузить эту таблицу геометрии для 6-го класса, чтобы попрактиковаться в нахождении площади двумерных фигур, таких как квадрат, прямоугольник, прямоугольный треугольник и круг.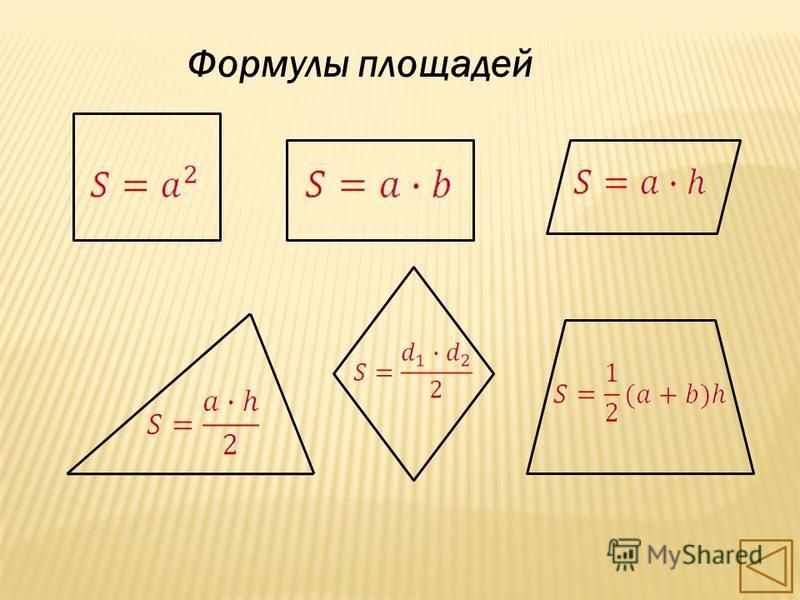

Как использовать этот рабочий лист

В этом рабочем листе по геометрии для шестого класса учащиеся должны найти площадь круга, прямоугольного треугольника, прямоугольника или квадрата, применяя соответствующие входные значения в соответствующих формулах. Ниже приведены формулы для Найдите
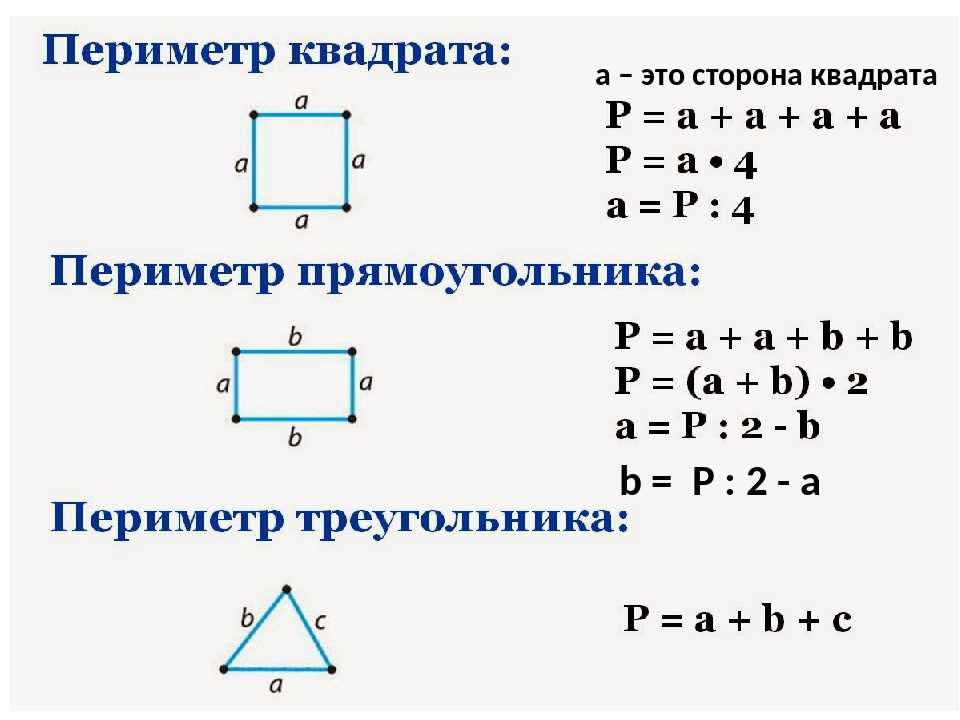
Площадь квадрата = сторона x сторона


Площадь прямоугольника = длина x ширина
Площадь треугольника = 1/2 x основание x высота
Площадь круга = π r ²

Ключ ответов

Учителя, воспитатели, родители или учащиеся могут проверять или подтверждать решенные вопросы, используя соответствующий ключ ответов, который содержит пошаговую работу по нахождению площади квадрата, прямоугольника, треугольника и круга.

Создать дополнительные рабочие листы

Учащиеся, учителя, репетиторы или родители могут создавать неограниченное количество вопросов и ответов с помощью кнопки « НОВЫЙ РАБОЧИЙ ТАБЛИЦ » для подготовки к экзаменам, заданиям, классным или домашним заданиям или пошаговым вычислениям.

No related posts.