Площадь трапеции расчет онлайн: Онлайн калькулятор. Площадь трапеции

Площадь трапеции — онлайн калькулятор

Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Через длины оснований и высоту

Чему равна площадь трапеции, если:

основание a =
основание b =
высота h =

Ответ: S =

ед.²

Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны основания a и b, а также высота h?

Формула

S = ½ ⋅ (a + b) ⋅ h

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Через среднюю линию и высоту

Чему равна площадь трапеции, если:

средняя линия m =
высота h =

Ответ: S =

ед. ²

Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны средняя линия m и высота h?

Формула

S = m ⋅ h

Пример

Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:

S = 6 ⋅ 4 = 24 см²

Через длины сторон и оснований

Чему равна площадь трапеции, если:

основание a =
основание b =
сторона c = сторона d =

Ответ: S =

ед.²

Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?

Формула

Пример

Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:

S ≈ 13. 555 см²

Через диагонали и угол между ними

Чему равна площадь трапеции, если:

диагональ d₁ =
диагональ d₂ =
угол α =

Ответ: S =

ед.²

Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны диагонали d₁ и d₂ и угол между ними α?

Формула

S = ½ ⋅ d₁ ⋅ d₂ ⋅ sin(α)

Пример

Если у трапеции одна диагональ d₁ = 5 см, другая диагональ d₂ = 7 см, а угол между ними ∠α = 30°, то её площадь:

S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²

Площадь равнобедренной трапеции

Через среднюю линию, боковую сторону и угол при основании

Чему равна площадь трапеции, если:

средняя линия m =
сторона c =
угол α =

Ответ: S =

ед. ²

Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

Формула

S = m ⋅ c ⋅ sin(α)

Пример

Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:

S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²

Через радиус вписанной окружности

Чему равна площадь трапеции, если:

радиус r =
угол α =

Ответ: S =

ед.²

Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?

Формула

S = ^4⋅r² ⁄ _sin(α)

Пример

Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:

S = 4 ⋅ 5² / sin (30) = 100 / 0. 5 = 200 см²

См. также

онлайн калькулятор, формула расчета, пример вычисления

Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.

Определение 1

Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.

Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.

Площадь прямоугольной трапеции

Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.

Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:

$S = \frac12 \cdot (a + c) \cdot b$, где

$a$ — малое основание;

$с$ — большее основание;

$b$ — перпендикулярная основаниям сторона.

Пример 1

Задача

Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2.42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?

Решение:

Воспользуемся приведённой выше формулой:

$S =\frac{(2.42 + 3.93) \cdot 2.32}{2} = 7.37$ кв. см.

Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.

Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.

Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:

$S = m \cdot h$, где

$S$ — площадь трапеции,

$m$ — средняя линия,

$h$ — высота трапеции.

Другой способ расчёта площади прямоугольной трапеции — через длины оснований и два угла, расположенных при одном основании. 2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где

$S$ — площадь трапеции,

$b$ — большее основание,

$g$ — малое основание,

$α$ — первый угол при основании,

$γ$ — второй угол при основании.

Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.

Площадь трапеции по диагонали и углу между диагоналями

Формула нахождения площади трапеции по диагонали и углу между диагоналями:

$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где

$S$ — площадь трапеции,

$d1$ — первая диагональ,

$d2$ — вторая диагональ,

$α$ — угол между диагоналями.

Рассмотрим пример.

Пример 2

Задача

Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2.22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?

Решение:

Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. 2}$, где

$S$ — площадь трапеции,

$a$ — малое основание,

$b$ — большее основание,

$c, d$ — боковые стороны.

Калькулятор площади трапеции

Автор Bogna Szyk

Отзыв Стивена Вудинга

Последнее обновление: 10 мая 2022 г.

Содержание:

• Что такое трапеция?
• Как найти площадь трапеции?
• Как найти периметр трапеции?
• Использование калькулятора площади трапеции: пример
• Часто задаваемые вопросы

Если у вас когда-либо возникали проблемы с запоминанием формул на уроках геометрии, эта область калькулятора трапеции обязательно вам поможет. Всего за несколько простых шагов вы сможете найти площадь трапеции и определить все остальные ее свойства, например длины сторон внутренних углов. Итак, если вас беспокоят такие вопросы, как «как найти периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!

Вы также можете воспользоваться нашим калькулятором длины окружности, чтобы более подробно проанализировать геометрию круга, или нашим калькулятором формулы окружности, чтобы узнать больше об уравнениях, лежащих в основе этой геометрии.

Что такое трапеция?

Трапеция – это четырехсторонняя геометрическая фигура, две стороны которой параллельны друг другу. Эти две стороны ( a и b на схеме) называются основаниями трапеции. Две другие стороны ( c и d ) называются ножками. h высота трапеции.

Сумма всех внутренних углов трапеции дает 360°. Кроме того, углы с одной и той же стороны катета называются смежными и всегда дают в сумме 180°:

α + β = 180°

γ + δ = 180°

Как найти площадь трапеции?

Чтобы найти площадь трапеции ( A ), выполните следующие действия:

1. Найдите длину каждого основания ( a и b ).
2. Найдите высоту трапеции
   ( h ).
3. Подставьте эти значения в формулу площади трапеции: A = (a + b) × h / 2 .

Вы можете заметить, что для трапеции с a = b (и, следовательно, c = d = h) формула упрощается до A = a × h , что в точности соответствует формуле площади прямоугольника.

Как найти периметр трапеции?

Чтобы быстро найти периметр трапеции, выполните следующие действия:

1. Найдите длины всех сторон трапеции ( a , b , c и

   7 8 ).

2. Сложите их вместе, чтобы получить периметр трапеции: P = a + b + c + d .
3. Вот оно! Это так просто.

В качестве альтернативы вы можете использовать калькулятор площади трапеции, который автоматически найдет для вас площадь и периметр трапеции.

Использование калькулятора площади трапеции: пример

Предположим, вы хотите вычислить площадь некоторой трапеции. Все данные приведены:

• α = 30°

• γ = 125°

• В = 6 см

• а = 4 см

• Р = 25 см

1. Вычислите оставшиеся внутренние углы. Как α + β = 180° , β = 180° - 30° = 150° .

2. Аналогично, как γ + δ = 180° , δ = 180° - 125° = 55° .

3. Найдите длины катетов трапеции, используя формулу синуса угла:

   sin 30° = c / h

   sin 55° = д / ч

   с = sin 30° × 6 = 12 см

   d = sin 55° × 6 = 7,325 см

4. Вычтите значения a, c и d из периметра трапеции, чтобы найти длину второго основания:

   b = P - a - c - d = 25 - 4 - 12 - 7,325 = 1,675 см

5. Наконец, применим формулу площади трапеции:

   A = (a + b) × h / 2 = (4 + 1,675) × 6 / 2 = 17,026 см²

Не забудьте также взглянуть на шестигранный калькулятор!

Часто задаваемые вопросы

Чем трапеция отличается от других четырехугольников?

Трапеции отличаются от других четырехугольников тем, что они имеют ровно одну пару параллельных сторон . Они, по сути, четырехугольники, как прямоугольники и квадраты, но не параллелограммы.

Какова площадь трапеции высотой 5 м и основаниями 8 м и 1 м?

Площадь этой трапеции равна 22,5 метра в квадрате . Для получения результата воспользуемся формулой площади трапеции: A = (a + b) × h / 2 и положим a = 8 м , b = 1 м , а h = 5 м внутри него.

Bogna Szyk

a (основание)

b (основание)

h (высота)

Периметр

Периметр

Углы

Посмотреть 23 похожих калькулятора 2d геометрии 📏

ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 20 четыре прямые линии), имеющие пару параллельных противоположных сторон. Противоположные параллельные стороны называются основанием, а непараллельные стороны называются сторонами трапеции. Это замкнутая плоская форма, имеющая четыре стороны и четыре угла.

Что такое Калькулятор площади трапеции?

‘ Калькулятор площади трапеции ‘ — это онлайн-инструмент, который вычисляет площадь трапеции за несколько секунд.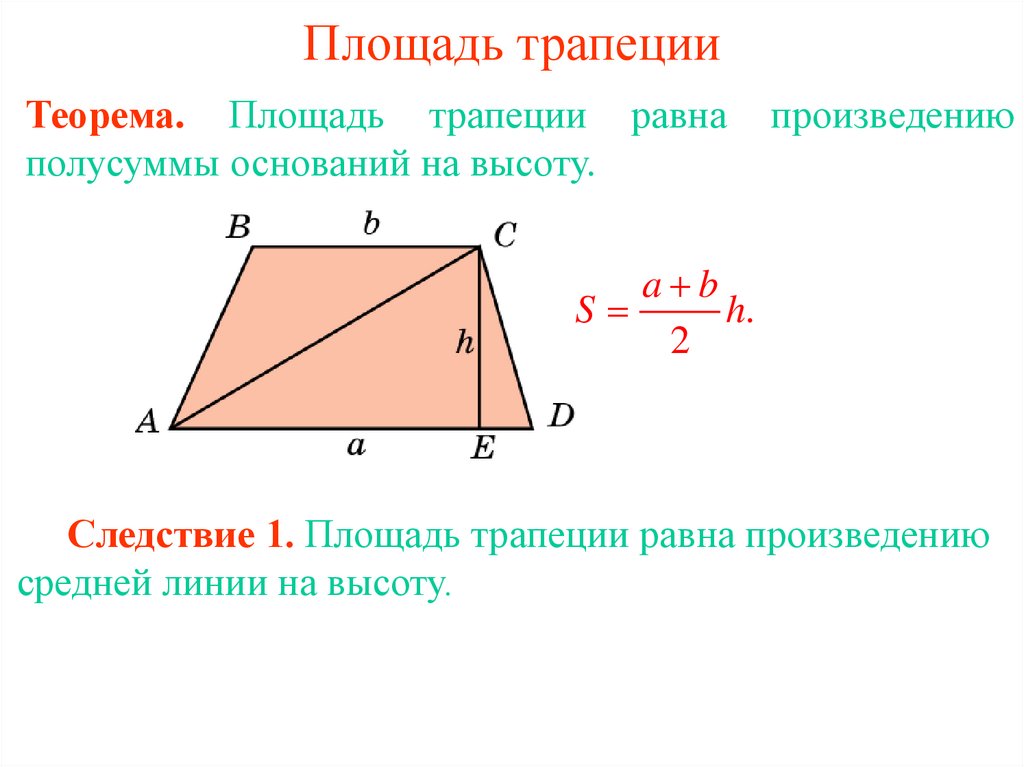 Площадь трапеции определяется путем вычисления среднего оснований и умножения его результата на высоту.

Калькулятор площади трапеции

 

Как пользоваться калькулятором площади трапеции?

Чтобы найти площадь трапеции, выполните следующие шаги:

• Шаг 1: Введите длину двух параллельных сторон трапеции (основание) и высоту в данное поле ввода.
• Шаг 2:  Нажмите кнопку  «Рассчитать» , чтобы найти площадь трапеции.
• Шаг 3:  Нажмите кнопку «Сброс» , чтобы найти площадь для разных длин параллельных сторон трапеции.

Как найти площадь трапеции?

Площадь трапеции определяется как половина произведения суммы длины двух ее параллельных сторон и высоты. Площадь трапеции – это количество единичных квадратов, которые можно в нее поместить, и измеряется она в квадратных единицах 

Площадь трапеции равна 1/2 × (a + b) × h 

Где «a» и «b» — длины двух параллельных сторон трапеции, а «h» — высота (перпендикулярное расстояние между a и b)

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.