Площадь треугольника определение: Площадь треугольника

формула, чему равна, как найти

Что такое площадь треугольника

Определение

Треугольник — это многоугольник с тремя сторонами и тремя вершинами.

Определение

Площадь треугольника — это величина плоскости, заключенной между сторонами этой геометрической фигуры.У треугольника она равна произведению половины основания на высоту.

Математически это выглядит так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(S=\frac12a\times h\)

где a — основание треугольника, а h — его высота.

Способы нахождения площади

Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.

Через две стороны и угол

Источник: lifehacker. ru

Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:

\(S=\frac12a\times b\times\sin\alpha\)

где a и b — стороны фигуры, а α — угол между ними.

Через радиус описанной окружности и три стороны

Источник: lifehacker.ru

Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:

\(S=\frac{a\times b\times c}{4\times R}\)

где a, b и c — стороны фигуры, а R — радиус описанной окружности.

Через радиус вписанной окружности и три стороны

Источник: lifehacker.ru

В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:

\(S=r\times\frac{a+b+c}2\)

где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.

Таким образом, формулу можно выразить всего двумя множителями:

\(S=r\times p\)

где p — полупериметр треугольника. \circ-(\alpha+\beta)\)

Для прямоугольного треугольника

В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.

По двум сторонам

Источник: lifehacker.ru

Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:

\(S=\frac{a\times b}2\)

где a и b — катеты прямоугольного треугольника.

Через гипотенузу и острый угол

Источник: spravochnick.ru

Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.

Начнем с поиска катета:

\(\cos\left(\alpha\right)=\frac ac\)

\(a=c\times\cos\left(\alpha\right)\)

где c — гипотенуза треугольника, a — его катет, а α —  угол между ними. 2\times\tan\left(\alpha\right)\)

Через радиус вписанной окружности и гипотенузу

Источник: mnogoformul.ru

Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:

\(S=r\times(r+c)\)

где r — радиус вписанной окружности, c — гипотенуза.

Через вписанную окружность

Источник: mnogoformul.ru

Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:

\(S=с_1\times с_2\)

где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.

По формуле Герона

Источник: mnogoformul.ru

Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:

\(S=(p-a)\times(p-b)\)

где \(p=\frac{a+b+c}2\) — полупериметр фигуры.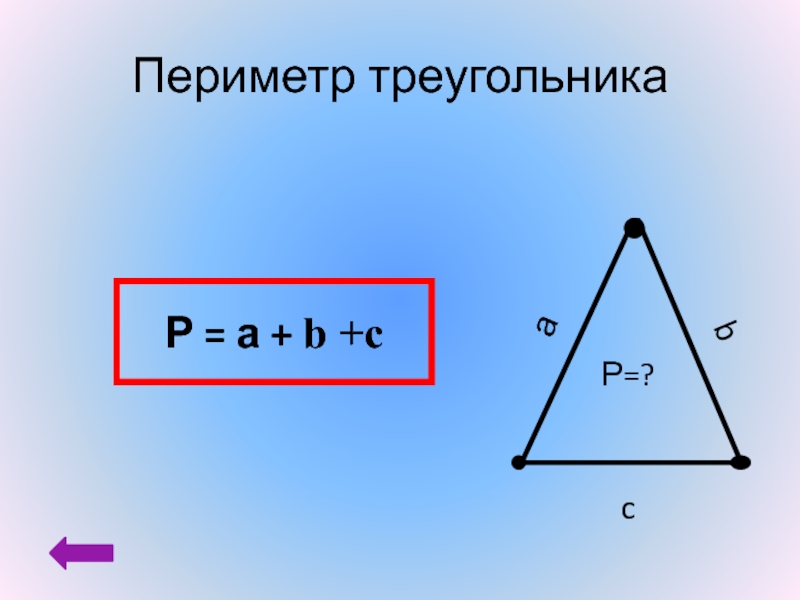 2\).

Площадь треугольника — все формулы

Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.

Содержание

Что такое треугольник

Треугольник – это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.

Сумма трех углов треугольника должна быть равна 180°.

Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту.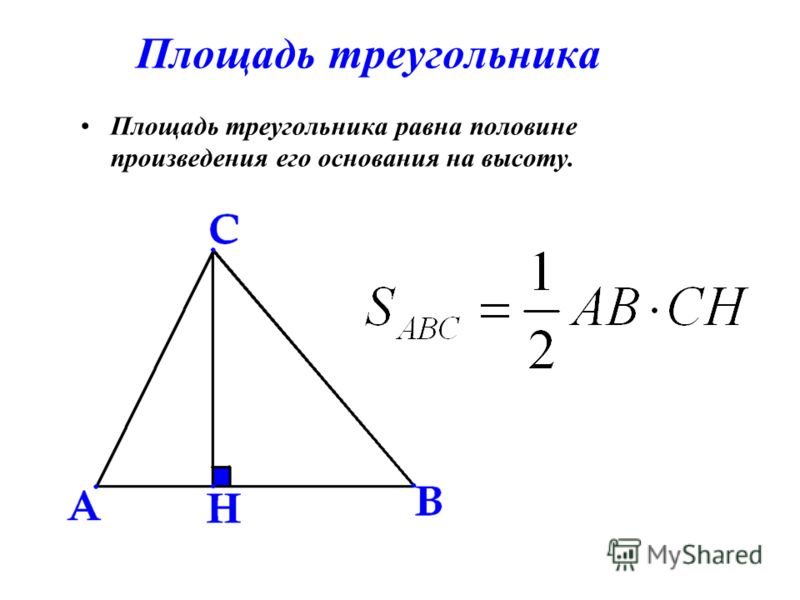 Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).

 

Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.

Различные типы треугольников в зависимости от длины их сторон

Разносторонний треугольник

Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.

Равнобедренный треугольник

Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.

Прямоугольный треугольник

Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.

Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.

Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.

Равносторонний треугольник

Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.

Площадь треугольника

Площадь разностороннего треугольника

Вычисляем площадь треугольника без особенностей – все его стороны разные и все углы разные.

Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле “площадь треугольника через две стороны и угол между ними”:

Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:

Формула Герона определения площади треугольника

Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.

, где

Площадь равнобедренного треугольника

Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.

К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:

Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.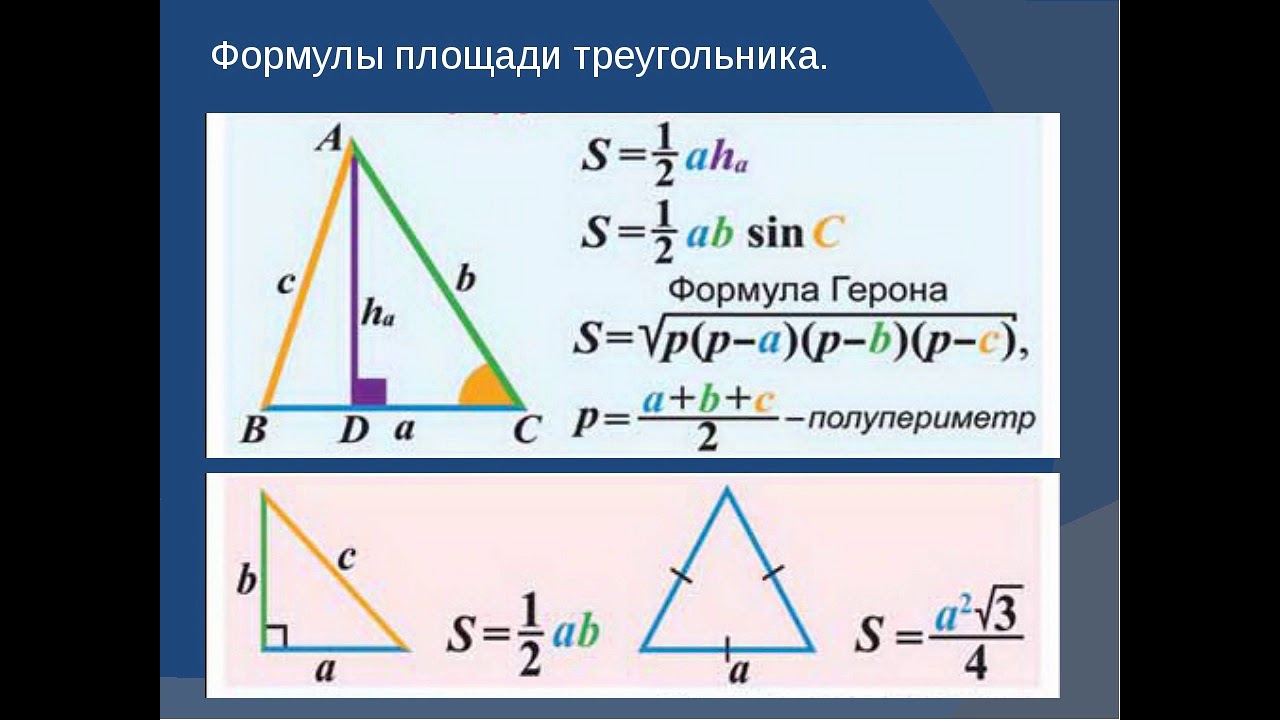

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:

Площадь прямоугольного треугольника

Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:

Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе

Площадь прямоугольного треугольника, если в него вписана окружность:

Площадь равностороннего треугольника

Площадь равностороннего треугольника можно найти через радиус описанной окружности.

Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:

Площадь равностороннего треугольника, если известна сторона треугольника:

Площадь равностороннего треугольника, если известна высота треугольника:

Площадь треугольника Определения и примеры

Площадь треугольника Определения и примеры

Введение

Определения треугольников и примеры важны для математики. В этом сообщении блога мы рассмотрим три различных определения треугольника площади и примеры. Таким образом вы сможете лучше понять, как работают эти концепции и как они могут помочь вашим математическим навыкам.

Какова площадь треугольника?

Площадь треугольника равна половине произведения основания на высоту.

Формула: A = 1/2 × b × h .

Определение треугольника

Треугольник — это трехсторонняя фигура с двумя углами, равными 90 градусам. Угол при вершине — это угол между основанием и вершиной треугольника, а два других угла называются боковыми углами. Прямоугольный треугольник имеет прямой угол при вершине и сумму углов, равных 180 градусам. В случае треугольника с острым углом, например, 90 градусов, один из его углов умножается на 3, чтобы найти его меру.

Площадь треугольника

Треугольник — это трехсторонняя геометрическая фигура с двумя равными сторонами и третьей стороной, которая короче двух других. Треугольник имеет шесть точек пересечения, которые называются вершинами. Три вершины одинакового размера образуют основание треугольника. Точка в середине основания называется вершиной треугольника.

Три вершины на одной стороне треугольника называются внутренними углами. Угол, противолежащий любому внутреннему углу с одной стороны, называется внешним углом. Внешний угол с одной стороны также считается внутренним углом, если он имеет общую вершину с другим внешним углом с той же стороны. 93

Если треугольник прямоугольный, то значение «base_a» равно 0, а все остальные значения равны 1. Если треугольник не прямоугольный, то «base_a» может быть любым действительным числом, а «height_a» всегда будет положительный.

Площадь треугольника с двумя сторонами и прилежащим углом (SAS)

Формула: Площадь = (a x b x sin c)/2 , где a, b — две стороны, а c — угол между ними.

Другим определением является сумма длин трех сторон, также известная как мера длины или линейная мера. Другой способ подумать об этом — представить, что каждая сторона отрезается посередине между двумя концами, и подсчитывается, сколько дюймов (или сантиметров) получаются разрезы. Это также называется базовой длиной или иногда просто базой.

Третье определение называется радиусом описанной окружности, и это как раз то, что вы ожидаете — радиус вокруг одного из углов треугольника. Наконец, есть особый тип треугольника, называемый равносторонним треугольником, у которого все углы равны 90 градусам. Все эти определения важны при работе с Треугольниками в задачах и расчетах, поэтому к ним стоит привыкнуть!

Площадь прямоугольного треугольника

Площадь прямоугольного треугольника равна сумме трех сторон. Основание всегда самая длинная сторона, а высота самая короткая.

Площадь треугольника можно найти, умножив длину основания на высоту. Например, если у вас есть треугольник с основанием 10 дюймов и высотой 12 дюймов, то его площадь составит 120 квадратных дюймов.

Типы треугольников

Существует много типов треугольников, некоторые из них более распространены, чем другие. Вот некоторые из них:

Равнобедренный треугольник

Равнобедренный треугольник имеет две равные стороны, а третья сторона имеет ту же длину, что и две другие.

Треугольник в правой вертикальной плоскости

В геометрии треугольник в правой вертикальной плоскости — это треугольник, вершины которого центрированы на верхнем, нижнем и левом краях листа. Прямоугольный треугольник в этом контексте имеет один угол, равный 90 градусам.

Заключение

В этой статье мы обсудили три наиболее распространенных типа треугольников и их определения. Прочитав это, вы должны лучше понять, что такое треугольник и как его идентифицировать в различных ситуациях. Надеюсь, вам понравится узнавать об этих важных формах!

---

Результат

Определение

Определяющие неравенства

Свойства пластин

Механические свойства

Свойства расстояния 900 05

Альтернативная форма

Альтернативные формы при условии, что a, b и c положительны

Площадь треугольника: формула Герона, решенные примеры

• Автор Асит Баранкар
• Последнее изменение 25-01-2023

Площадь треугольника: В двумерной плоскости площадь треугольника — это область, заключенная в нем.

Треугольник, как мы все знаем, представляет собой замкнутую форму с тремя сторонами и тремя вершинами. В результате площадь треугольника равна общему пространству, занимаемому тремя сторонами треугольника. Половина произведения основания треугольника на высоту — это обычная формула вычисления его площади.

Область, занимаемая внутри границы плоского объекта или фигуры, определяется как «площадь» в целом. Измерение производится в квадратных единицах, при этом квадратные метры являются обычной единицей измерения (м2). Существуют предопределенные формулы для вычисления площади квадратов, прямоугольников, кругов, треугольников и других фигур. В этом посте мы изучим формулы площади треугольников для нескольких видов треугольников, а также рассмотрим некоторые примеры задач.

Треугольник — это многоугольник с тремя сторонами. Его также можно определить фигурой, ограниченной или заключенной в трехлинейные отрезки. Ясно, что треугольник будет иметь три стороны и три вершины.

Узнайте о треугольниках здесь

Классификация треугольников

Треугольники классифицируются двумя основными способами:
а) классификация на основе длины сторон треугольника
б) классификация на основе внутренних углов треугольника.

Классификация треугольников по длине сторон

В зависимости от длины сторон треугольники делятся на три типа: разносторонний треугольник, равнобедренный треугольник и равносторонний треугольник.

Разносторонние треугольники

Если все три стороны треугольника различны по длине или если ни одна из сторон треугольника не равна, то такой треугольник называется разносторонним. Треугольник, приведенный ниже, является разносторонним треугольником. В этом треугольнике все три угла имеют разную величину.

Равнобедренные треугольники

Если любые две из трех сторон треугольника равны, то такой треугольник называется равнобедренным.

В приведенном выше треугольнике указаны две равные стороны. Это равнобедренный треугольник. В равнобедренном треугольнике два угла, противолежащие двум равным сторонам, равны по величине.

Равносторонний треугольник

Если все три стороны треугольника имеют одинаковую длину, то такой треугольник называется равносторонним. 9{\rm{o}}}\) называется тупоугольным треугольником.)

Термины, относящиеся к площади треугольника

Высота треугольника

Перпендикуляр, проведенный из любой вершины в сторону, противоположную вершине, называется высотой треугольника из этой вершины.

На приведенном выше рисунке перпендикуляр \(AD\) проведен из вершины \(A\) на сторону \(BC.\). Итак, \(AD\) называется высотой треугольника.

На приведенном выше рисунке перпендикуляры \(AD,\,BE\) и \(CF\) проведены из вершин \(A,\,B\) и \(C\) на противоположных сторонах \(BC ,\,CA\) и \(AB,\) соответственно. В этом случае \(AD\) считается высотой треугольника из вершины \(A\) относительно основания \(BC.\). Аналогично, \(BE\) и \(CF\) считаются высотами треугольника из вершины \(B\) и \(C\) относительно оснований \(CA\) и \(AB,\) соответственно. Три высоты треугольника всегда совпадают. Общая точка называется ортоцентром треугольника.

Иногда перпендикуляр, проведенный из вершины, не достигает противоположной стороны.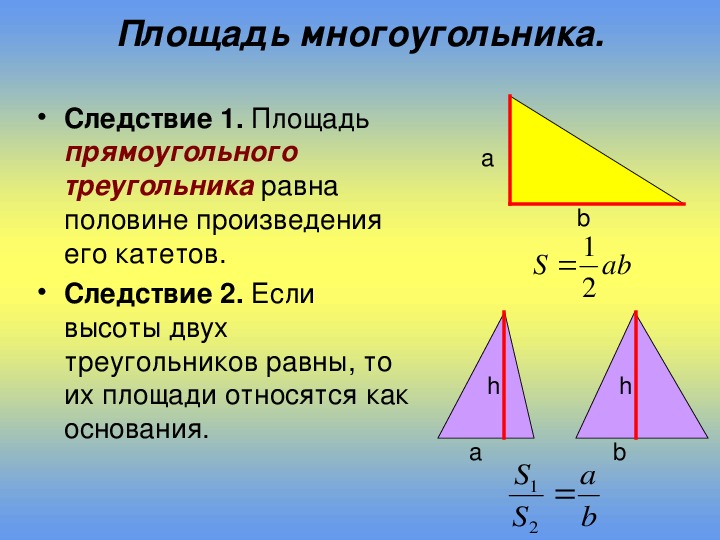 Он лежит на расширенной противоположной стороне.
На приведенном выше рисунке перпендикуляр \(AD\) проведен к продолжению \(BC.\). В этом случае \(AD\) считается высотой треугольника \(ABC\) относительно основания \(BC .\)

Медиана треугольника

Медиана определяется как отрезок, соединяющий вершину треугольника и среднюю точку противоположной стороны треугольника.

На приведенном выше рисунке, если \(D\) является серединой \(BC,\), то \(AD\) называется медианой, проведенной из вершины \(A\) на противоположной стороне \(BC .\)

В любом треугольнике из каждой вершины на противоположных сторонах можно провести три медианы, как показано на рисунке выше. В любом треугольнике три медианы пересекаются в одной точке. Точка пересечения медиан треугольника называется центром тяжести треугольника.

Какова площадь треугольника?

Площадь треугольника — это область или пространство, ограниченное тремя сторонами треугольника.

Формула площади треугольника

Существует несколько формул, используемых для расчета площади треугольника. Они обсуждаются ниже:

Площадь треугольника при заданных основании и высоте

Площадь треугольника \({\rm{ = }}\frac{{\rm{1}}}{{\rm{2} }}{\rm{ \times base \times height}}\)

Приведенная выше формула используется, когда известны или даны длина любой стороны и соответствующая высота.
Для приведенного выше рисунка площадь треугольника \(= \frac{1}{2} \times {\rm{основание \times height}} = \frac{1}{2} \times BC \times AD = \frac{1}{2} \times b \times h\)

Площадь прямоугольного треугольника

Приведенная выше формула используется непосредственно для прямоугольных треугольников.

Следовательно, формула, используемая для вычисления площади треугольника, выглядит следующим образом: \(\frac{1}{2} \times {\rm{основание \times height}} = \frac{1}{2} \times b \ раз h\), где \(b\) — основание, а \(h\) — высота.

Типы треугольников, для которых используется эта формула

Помимо прямоугольных треугольников, эта формула может использоваться для расчета площади любого типа треугольника, если длина основания и высота заданы или могут быть получены из заданных Информация о треугольнике.

Площадь треугольника с 3 сторонами: формула Герона

Эта формула используется для вычисления площади треугольника, если известны или даны длины всех трех сторон.

Согласно этой формуле площадь треугольника определяется выражением
\({\rm{площадь}} = \sqrt {s(s — a)(s — b)(s — c)} \), где , \(a,\,b\) и \(c\) — длины сторон треугольника, а \(s\) — полупериметр треугольника, определяемый выражением \(s = \frac{{a + b + c}}{2}.\)

Площадь равностороннего треугольника

Формулу Герона можно использовать для получения специальной формулы, применимой для расчета площади равностороннего треугольника.

В равностороннем треугольнике все три стороны равны по длине. Итак, в этом случае \(a = b = c.\)
Итак, \(s = \frac{{a + b + c}}{2} = \frac{{a + a + a}}{2 } = \frac{{3\,a}}{2}\)

Итак, \({\rm{площадь}} = \sqrt {s(s – a)(s – b)(s – c )}   = \ sqrt {\ frac {{3a}} {2} \ times \ left ( {\ frac {{3a}} {2} — a} \ right) \ times \ left ( {\ frac {{3a}) {2} – a} \right) \times \left( {\frac {{3a}}{2} – a} \right)} \) 92}}}{4}} \)

Площадь треугольника при заданных координатах его вершин

Площадь треугольника можно вычислить, если известны координаты трех вершин треугольника на декартовой плоскости.

В треугольнике \(ABC\), показанном выше, \(A\left( {{x_1},\,{y_1}} \right),\,B\left( {{x_2},\,{y_2} } \right)\) и \(C\left( {{x_3},\,{y_3}} \right)\) — координаты вершин треугольника.

Площадь этого треугольника можно рассчитать по формуле
\( {{площадь}} = \frac{1}{2}\left| { {x_1}\left({{y_2} – {y_3}} \right) + {x_2}\left({{y_3} – {y_1}} \right) + {x_3}\left({{y_1} – {y_2}} \right)} \right|\)

Связь между площадями двух треугольников, лежащих на одном основании и между одинаковыми параллелями

Существует интересная связь между площадями двух разных треугольников, если они лежат на одном основании и находятся между двумя одинаковыми параллельными прямыми. Можно доказать, что площади двух треугольников с одинаковым основанием, лежащих между двумя одинаковыми параллельными прямыми, равны.

Здесь прямая \(BC\) параллельна прямой \(DQ.\) Отсюда ясно, что \(\Delta ABC\) и \(\Delta PBC\) имеют одно и то же основание \(BC\) и они лежат между одними и теми же параллельными прямыми \(BC\) и \(DQ. \)
Итак, площади \(\Delta ABC\) и \(\Delta PBC\) равны. Следовательно, \({\mathop{\rm area}\nolimits} \Delta ABC = {\rm{area}}\Delta PBC.\)

Связь между площадью треугольника и площадью параллелограмма, лежащего на одном и том же треугольнике. Основание и между одинаковыми параллелями

Интересная связь также существует между площадью треугольника и площадью параллелограмма, если они лежат на одном основании и между одними и теми же двумя параллельными прямыми. Можно доказать, что площадь треугольника равна половине площади параллелограмма, если они имеют одно основание и лежат между одними и теми же двумя параллельными прямыми.

Здесь прямая \(AB\) параллельна прямой \(QD\) Отсюда, очевидно, \(\Delta ABC\) и параллелограмм \(ABDC\) и \(ABPQ\) имеют одно и то же основание \(AB\) и лежат между одними и теми же параллельными прямыми \(AB\) и \(QD\)

Значит, площадь \(\Delta ABC\) равна половине площади параллелограмма \(ABDC\) а также параллелограмм \(ABPQ\). 2}.\)

Q.2. Найдите площадь треугольника, длины сторон которого равны \({\rm{3\,см}}\).\({\rm{4\,см}}\) и \({\rm{ 5\,см}}\)
Ответ: Здесь даны длины трех сторон. Итак, воспользуемся формулой Герона для вычисления площади треугольника. Здесь \(a = 3\;{\rm{см}},b = 4\;{\rm{см}}\) и \(c = 5\,{\rm{см}}\) согласно по этой формуле площадь треугольника определяется выражением \({\rm{area}} = \sqrt {s(s — a)(s — b)(s — c)} ,\), где \(a ,\,b\) и \(c\) — длины сторон треугольника, а \(s\) — полупериметр треугольника, определяемый выражением \(s = \frac{{a + b + c }}{2}.\) Итак, \(s = \frac{{a + b + c}}{2} = \frac{{3 + 4 + 5}}{2} = \frac{{12} }{2} = 6\;{\rm{см}}\)Следовательно, площадь данного треугольника\( = \sqrt {s\left( {s – a} \right)\left( {\left( {s – b} \right)\left( {s – c} \right)} \right)} = \sqrt {6\left( {6 – 3} \right)\left( {6 – 4} \right )\left( {6 – 5} \right)} \)\(= \sqrt {6 \times 3 \times 2 \times 1} = \sqrt {36} = 6\;{\rm{c}}{ {\ гт {м}} ^ 2} \) 92}]\)

Резюме

В двумерной плоскости площадь треугольника определяется как общее пространство, занимаемое тремя его сторонами.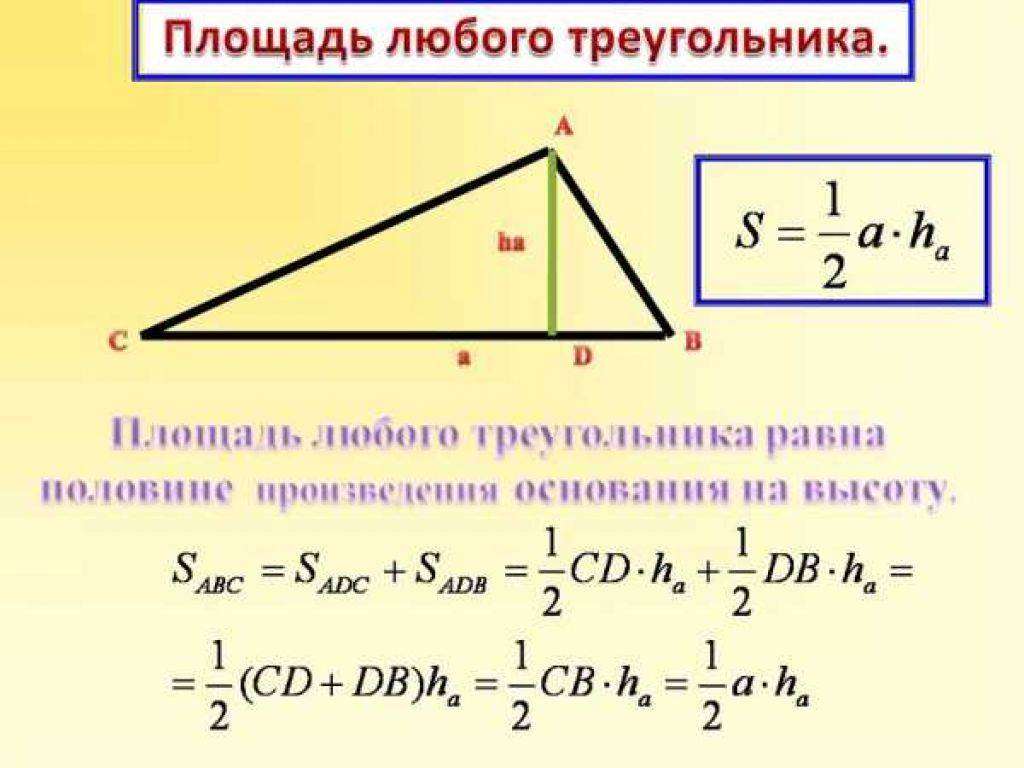 Площадь треугольника равна половине произведения его основания на высоту, поэтому A = 1/2bh — основная формула. Эта формула работает для любого треугольника, будь то разносторонний треугольник, равнобедренный треугольник или равносторонний треугольник. Важно помнить, что основание и высота треугольника перпендикулярны друг другу.

Эта статья поможет всесторонне узнать о том, как вычислить площадь различных видов треугольников в зависимости от того, какая информация доступна о треугольнике. Зная это, можно рассчитать площадь любой земли треугольной формы или любого другого предмета треугольной формы.

Это также помогает в вычислении площади любой земли правильной или неправильной многоугольной формы или любого другого объекта путем деления многоугольника на треугольники по диагоналям, а затем получения площади каждого треугольника и сложения их.

Часто задаваемые вопросы о площади треугольника

Q.1. Сколько высот может быть у треугольника?
Ответ: Треугольник может иметь \(3\) (три) высоты.

Q.2 . Как найти площадь треугольника, если не дана высота, но даны длины трех сторон?
Ответ: Если высота не дана, но даны длины трех сторон, то можно использовать формулу Герона.
Согласно этой формуле площадь треугольника определяется выражением
\({\rm{площадь}} = \sqrt {s(s — a)(s — b)(s — c)} ,\)
где \(a,b\) и \(c\) — длины сторон треугольника, а \(s\) — полупериметр треугольника, определяемый выражением \(s = \frac{{a + b + c}}{2}.\)

Q.3 .

Какая формула обычно используется для нахождения площади прямоугольного треугольника, если известны длина и высота?
Ответ: Если длина основания и высота известны, то можно использовать формулу \({\rm{area = }}\frac{{\rm{1}}}{{ \rm{2}}}{\rm{ \times base \times height}}{\rm{.}}\)

Q.4. Для расчета площади треугольника по формуле \(\frac{{\rm{1}}}{{\rm{2}}}{\rm{ \times base \times height}}\) 9{\rm{2}}}\)

Q.