Площадь треугольника равнобедренного формула онлайн калькулятор: Площадь равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Расчет площади равнобедренного треугольника — Онлайн калькулятор

Равнобедренным называется треугольник, у которого равны длины двух сторон. Для расчета площади используются значения длины двух неравных сторон a и  b:

S=b*a2-b242

Площадь равнобедренного треугольника по формуле в онлайн-калькуляторе высчитывается просто. Для получения ответа:

• введите значения стороны и высоты в соответствующие поля и установите единицы измерения;
• выберите единицу, в которой необходимо получить решение;
• воспользуйтесь кнопкой «Найти».

Расчет площади равнобедренного треугольника онлайн-калькулятором предполагает получение подробного решения и не требует оплаты.

Как найти площадь равнобедренного треугольника с помощью онлайн-калькулятора

Для нахождения площади равнобедренного треугольника нужно знать значения его двух неравных сторон.

Рассмотрим пример нахождения площади равнобедренного треугольника с помощью онлайн-калькулятора. Пусть нужно найти площадь такого треугольника со сторонами 4 см и 5 см соответственно:

1. Введем значения сторон в пустые поля:
   
2. Выберем единицы измерения:
   
3. Отметим, что онлайн калькулятор производит конвертацию величин. Например, стороны заданы в сантиметрах, а результат нам нужен в квадратных метрах. Укажем соответствующие размерности, нажмем «Найти» и получим ответ:
   
   Отметим также, что в калькуляторе существуют ограничения. Например, в поле для значений сторон нельзя вводить отрицательные числа. Если вы введете некорректное значение, калькулятор предупредит вас об этом.

Материалы, которые помогут вам лучше разобраться в теме:

• Площадь фигуры: понятие площади, свойства площади, квадрируемые фигуры
• Вычисление площади фигуры в полярных координатах

Ответ:

Решение

Ответ:

• list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

• Площадь треугольника (по 3 сторонам)
• Площадь треугольника (по 2 сторонам и углу)
• Площадь треугольника (по стороне и высоте)
• Площадь прямоугольного треугольника
• Площадь равностороннего треугольника
• Площадь квадрата (по стороне квадрата)
• Площадь квадрата (по диагонали)
• Площадь прямоугольника
• Площадь треугольника (по 3 сторонам и радиусу описанной окружности)
• Площадь треугольника (по 3 сторонам и радиусу вписанной окружности)
• Площадь треугольника (по полупериметру и радиусу вписанной окружности)
• Площадь треугольника (по двум сторонам и одному углу)
• Площадь треугольника (по одной стороне и двум углам)
• Площадь треугольника (по радиусу описанной окружности и двум углам)
• Площадь круга (по радиусу)
• Площадь круга (по диаметру)
• Площадь круга (по длине окружности)
• Площадь ромба (по сторонам и углу между ними)
• Площадь ромба (по стороне и высоте)
• Площадь ромба (по диагоналям)
• Площадь параллелограмма (по сторонам и углу между ними)
• Площадь параллелограмма (по стороне и высоте)
• Площадь параллелограмма (по диагоналям и углу между ними)
• Площадь трапеции (по основаниям и высоте)
• Площадь трапеции (по средней линии и высоте)
• Площадь трапеции (по диагоналям и углу между ними)
• Площадь эллипса
• Площадь поверхности куба
• Площадь поверхности параллелепипеда
• Площадь поверхности сферы
• Площадь поверхности цилиндра
• Площадь поверхности конуса

Вычисление площади равнобедренного треугольника онлайн-калькулятором

Сервис Zaochnik предоставляет возможность автоматических вычислений.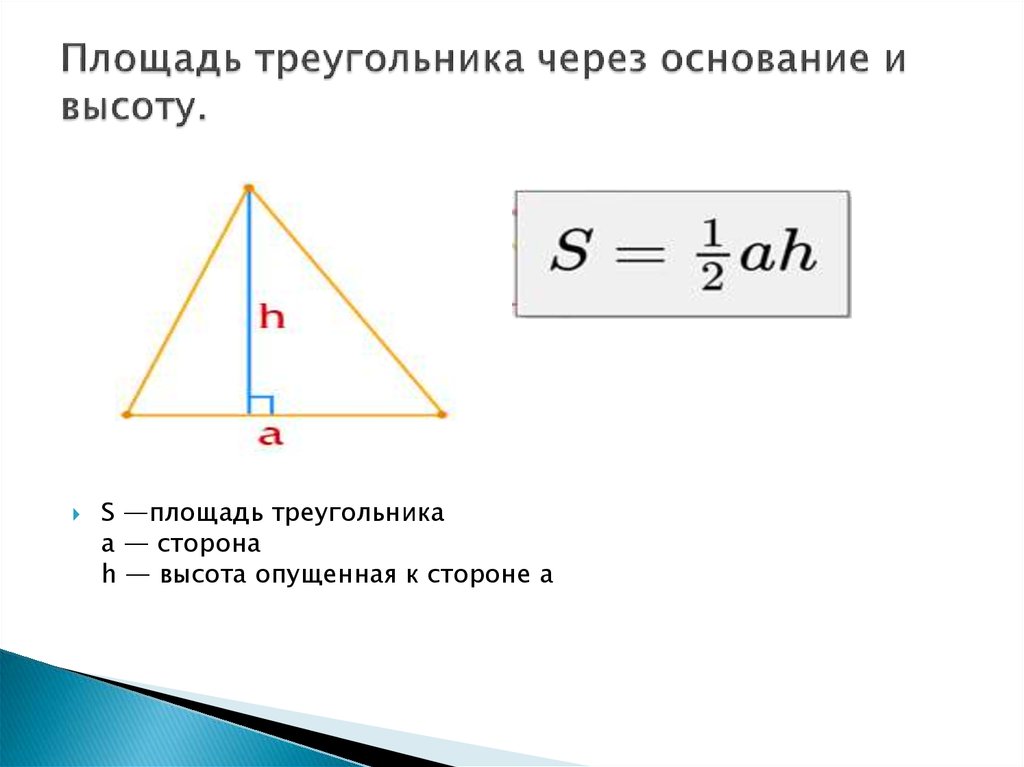 Площадь равнобедренного треугольника онлайн – это проверка при самостоятельной подготовке школьников к занятиям по геометрии. Помощь заключается в том, что ученик получает не просто готовый ответ, а пошаговое решение. Так быстрее запоминается формула. Полученный способ можно применять для решения аналогичных задач.

Причины рассчитать площадь равнобедренного треугольника онлайн-калькулятором:

• экономия времени;
• исключение ошибок и описок;
• наглядное решение; 
• автоматическое приведение единиц измерения к нужной величине.

На сайте собраны калькуляторы не только для вычисления площади треугольника, но и других фигур. Тренируйтесь в подсчетах и систематизируйте полученные знания.

Понравился калькулятор? Поделись с друзьями!

Площадь равнобедренного треугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь равнобедренного треугольника. Для нахождения площади равнобедренного треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

• Площадь равнобедненного треугольника по основанию и стороне
• Площадь равнобедненного треугольника по боковым сторонам и углу между ними
• Площадь равнобедненного треугольника по основанию и прилежащему углу
• Площадь равнобедненного треугольника по основанию и противолежащему углу
• Площадь равнобедненного треугольника по основанию и высоте

Площадь равнобедненного треугольника по основанию и стороне

Пусть в равнобедренном треугольнике известны основание a=BC и сторона b=AC (AC=BC) (Рис.1):

Найдем площадь треугольника. Проведем высоту h=AH. Поскольку в равнобедренном треугольнике высота являетcя также биссектрисой и медианой, то:

Применим теорему Пифагора для прямоугольного треугольника AHC:

то есть

или

Площадь треугольника по основанию и высоте имеет следующий вид:

или

Подставляя (2) в (3), получим:

Пример 1. Основание равнобедренного треугольника равна a=4.5, а боковая сторона − b=7. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (4). Подставляя значение a=5 и b=7 в (4), получим:

Ответ:

Площадь равнобедненного треугольника по боковым сторонам и углу между ними

Пусть в равнобедренном треугольнике известны боковые стороны b=c и угол между ними α (Рис.2).

Плошадь треугольника по сторонам и углу между ними вычисляется с помощью следующей формулы (см. теорему 2 статьи Площадь треугольника онлайн):

Учитывая, что b=c, получим:

Пример 2. Боковые стороны равнобедненного треугольника равны b=c=12, а угол между ними равна α=67°. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (5). Подставляя значения b=12 и α=67° в (5), получим:

Ответ:

Площадь равнобедненного треугольника по основанию и прилежащему углу

Пусть в равнобедренном треугольнике известны основание a и прилежащий угол γ (Рис. 3):

Найдем площадь треугольника. Проведем высоту AH. Для прямоугольного треугольника AHC можно записать:

Откуда:

Формулу вычисления площади по основанию и прилежащему углу получим подставляя (6) в (3):

Пример 3. Основание равнобедненного треугольника равна a=25.4, а прилежащий угол равен γ=27°. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (7). Подставляя значения a=25.4 и α=27° в (7), получим:

Ответ:

Площадь равнобедненного треугольника по основанию и противолежащему углу

Пусть в равнобедренном треугольнике известны основание a и противолежащий угол α=∠BAC (Рис.4):

Найдем площадь треугольника. Проведем высоту AH. Для прямоугольного треугольника AHC можно записать:

Откуда:

Формулу вычисления площади по основанию и противолежащему углу получим подставляя (8) в (3):

Пример 4. Основание равнобедненного треугольника равна a=17, а прилежащий угол равен γ=21.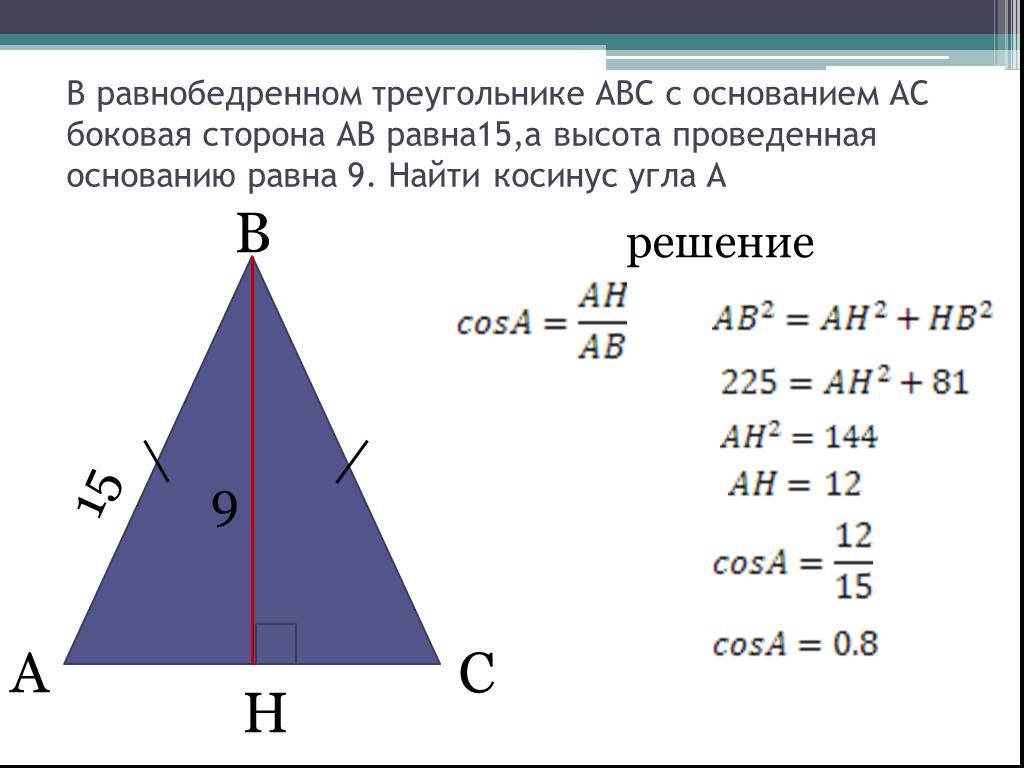 4°. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (9). Подставляя значения a=17 и α=21.4° в (9), получим:

Ответ:

Площадь равнобедненного треугольника по основанию и высоте

Пусть в равнобедренном треугольнике известны основание a и высота h (Рис.5):

Формула для вычисления площади треугольника имеет вид (3):

Пример 5. Основание равнобедненного треугольника равна a=18, а высота равна h=31. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения a=18 и h=31 в (10), получим:

Ответ:

Смотрите также:

• Площадь треугольника онлайн
• Площадь прямоугольного треугольника онлайн
• Площадь равностороннего треугольника онлайн

Калькулятор равнобедренного треугольника

Автор: Hanna Pamuła, PhD

Отзыв от Bogna Szyk и Adena Benn

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Что такое равнобедренный треугольник?
• Формулы площади и периметра для равнобедренного треугольника
• Что такое теорема о равнобедренном треугольнике?
• Калькулятор золотого треугольника
• Как найти площадь с помощью этого калькулятора равнобедренного треугольника?
• Часто задаваемые вопросы

Калькулятор равнобедренного треугольника — лучший выбор, если вы ищете быстрое решение ваших задач по геометрии. Найдите площадь равнобедренного треугольника, его периметр, внутренний радиус, радиус описанной окружности, высоты и углы — все в одном месте. Если вы хотите построить конуру, узнать площадь равнобедренного фронтона греческого храма или просто сделать домашнее задание по математике, этот инструмент для вас. Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника и теореме о равнобедренном треугольнике.

Что такое равнобедренный треугольник?

Равнобедренный треугольник представляет собой треугольник с двумя сторонами одинаковой длины, называемыми катетами. Третья сторона треугольника называется основанием. Угол при вершине — это угол между катетами. Углы, у которых основание является одной из сторон, называются углами при основании.

Вот важнейшие свойства равнобедренных треугольников:

• Имеет ось симметрии по высоте вершины;
• Два угла, противоположные сторонам, равны; и
• Равнобедренный треугольник может быть остроугольным, прямоугольным или тупоугольным, но зависит только от угла при вершине (углы при основании всегда острые)

Равносторонний треугольник является частным случаем равнобедренного треугольника. Вы можете узнать обо всех возможных типах треугольников в калькуляторе классификации треугольников. Кроме того, если вы хотите углубиться в характеристики равностороннего треугольника, ознакомьтесь с калькулятором равностороннего треугольника

Формулы площади и периметра равнобедренного треугольника

Для расчета площади равнобедренного треугольника можно использовать множество различных формул. Наиболее популярны уравнения:

1. Данная ножка a и основание b :

   площадь = (1/4) × b × √(4 × a² - b²)

2. Дано h высота от вершины и основания b или h3 высота от двух других вершин и ножки a :

   площадь = 0,5 × h × b = 0,5 × h3 × a

3. При любом угле и катете или основании

   площадь = (1/2) × a × b × sin(угол_базы) = (1/2) × a² × sin(угол_вершины)

Также вы можете проверить наш калькулятор площади треугольника, чтобы найти другие уравнения, которые работают для любого типа треугольника, а не только для равнобедренного.

Чтобы вычислить периметр равнобедренного треугольника, просто сложите все стороны треугольника:
периметр = a + a + b = 2 × a + b

Что такое теорема о равнобедренном треугольнике?

Теорема о равнобедренном треугольнике, также известная как теорема об углах при основании, утверждает, что если две стороны треугольника конгруэнтны, то углы, противоположные этим сторонам, равны .

Также существует обратная теорема, утверждающая, что если два угла треугольника равны, то стороны, противоположные этим углам, равны .

Калькулятор золотого треугольника

Золотой треугольник, который также называют возвышенным треугольником, представляет собой равнобедренный треугольник, в котором катет находится в золотом отношении к основанию:

a / b = φ ~ 1,618

Золотой треугольник обладает некоторыми необычными свойствами:

• Это единственный треугольник с тремя углами в соотношении 2:2:1
• Это форма треугольников, найденных в точках пентаграмм
• Используется для формирования логарифмической спирали

Как найти площадь с помощью этого калькулятора равнобедренного треугольника?

Давайте узнаем, как использовать этот инструмент на простом примере. Посмотрите на это пошаговое решение:

1. Определите первое значение . Предположим, мы хотим проверить свойства золотого треугольника. Введите 1,681 дюйма в поле ноги .
2. Введите второй известный параметр . Например, возьмем основание, равное 1 д.
.
3. Все остальные параметры рассчитываются в мгновение ока! Мы проверили, например, что периметр равнобедренного треугольника равен 4,236 дюйма и что углы в золотом треугольнике равны 72° и 36° — отношение действительно равно 2:2:1.

Вы можете использовать этот калькулятор для определения других параметров, чем в примере, но помните, что обычно есть два различных равнобедренных треугольника с заданной площадью и другими параметрами, например, длиной катета. Наш калькулятор покажет одно из возможных решений.

Часто задаваемые вопросы

Как рассчитать площадь равнобедренного треугольника по катету и основанию?

Чтобы вычислить площадь равнобедренного треугольника с катетом a и основанием b , выполните следующие действия:

1. Применить теорему Пифагора к найти высоту : √( a² - b²/4 ) .

2. Примените стандартную формулу площади треугольника , т. е. умножьте основание b на высоту, полученную в шаге 1, а затем разделите на 2 .

3. Вот и все. Окончательная формула у нас есть:

   площадь = ½ × b × √(a² - b²/4) .

Как вычислить периметр равнобедренного треугольника по катету и основанию?

Периметр равнобедренного треугольника с катетом a и основанием b вычисляем по формуле периметр = 2 × a + b . В этой формуле используется тот факт, что две стороны равнобедренного треугольника имеют одинаковую длину.

Какова площадь равнобедренного треугольника со стороной 4 и основанием 4?

Ответ: 6,93 . Чтобы получить его, мы можем использовать формулу площадь = ½ × b × √(a² - b²/4) с a = b = 4 .

В качестве альтернативы мы можем заметить, что здесь у нас есть равносторонний треугольник : формула площади упрощается до площадь = a² × √3 / 4 с a = 4 .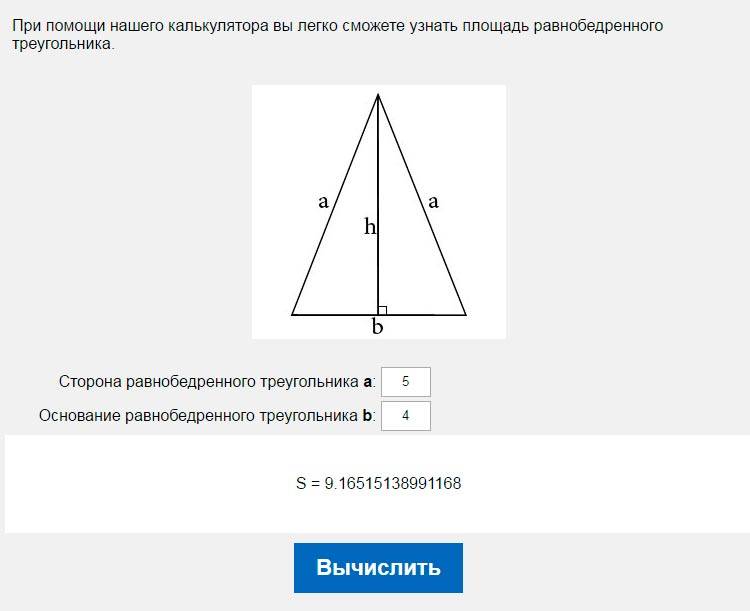

Ханна Памула, PhD

Ножка (a)

Основание (b)

Высота от вершины (hb)

Высота от основания (га)

Угол основания (β) 2α 3 900

Площадь и периметр

Периметр

Посмотреть 18 подобных калькуляторов треугольников 🔺

30 60 90 Triangle45 45 90 Trianglearea of ​​Right Triangle… 15 еще

Isosceles Triangle Calculator

, созданный Rijk de Wet

. Обзор Aleksandra Zają, MD

Последний :

• Как пользоваться калькулятором площади равнобедренного треугольника?
• Что такое равнобедренный треугольник?
• Как найти площадь равнобедренного треугольника?
• Связанные калькуляторы
• Часто задаваемые вопросы

Добро пожаловать в калькулятор площади равнобедренного треугольника , где мы научим вас всему, что нужно знать о площади равнобедренного треугольника! Мы специально покажем вам, как вычислить площадь равнобедренного треугольника, чтобы найти ее самостоятельно вручную.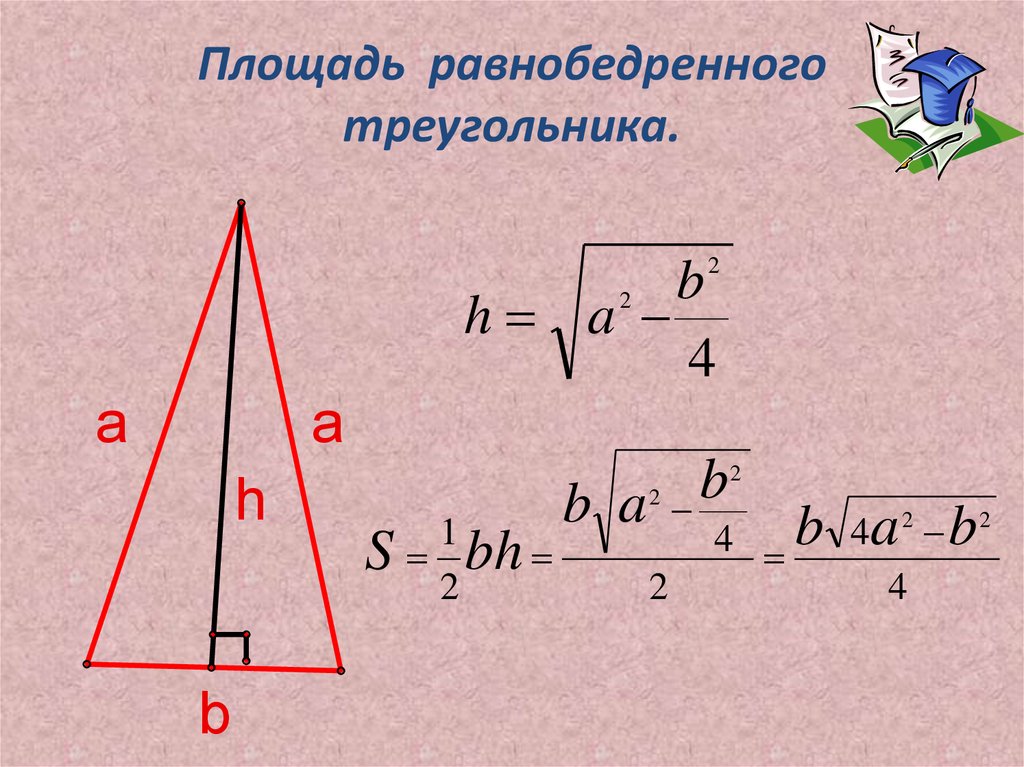

Как пользоваться калькулятором площади равнобедренного треугольника?

Пользоваться калькулятором площади равнобедренного треугольника очень просто:

1. Введите размеры, которые вы знаете из катетов, основания и высоты .
2. Найдите площадь описанного вами равнобедренного треугольника.
3. Калькулятор площади равнобедренного треугольника также может работать в обратном направлении — введите площадь и некоторые длины сторон, и калькулятор вычислит другие стороны.

Что такое равнобедренный треугольник?

Равнобедренный треугольник — это треугольник с двумя равными сторонами. Две равные стороны называются ножками и имеют длину ааа. Оставшаяся сторона называется база и имеет длину bbb. Равнобедренный треугольник обычно рисуется так, что основание лежит горизонтально внизу:

Равнобедренный треугольник. Обратите внимание, что стороны, отмеченные aaa, имеют одинаковую длину, а углы, отмеченные α\alphaα, имеют одинаковый угол.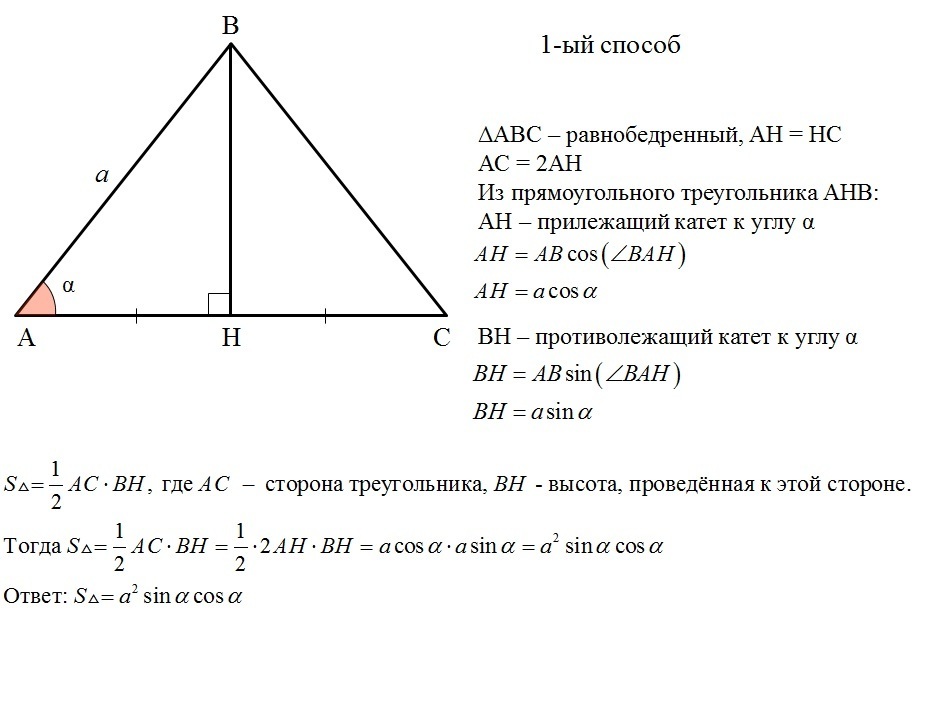

Как найти площадь равнобедренного треугольника?

Наш калькулятор площади равнобедренного треугольника великолепен, но на экзамене его не будет. Итак, давайте научимся вычислять площадь равнобедренного треугольника. Равнобедренный треугольник следует тому же формула площади как и любой другой треугольник:

A=12×b×hA = \frac{1}{2} \times b \times hA=21​×b×h

, где

• AAA — площадь равнобедренного треугольника;
• bbb — длина стороны основания; и
• hhh — высота треугольника.

Уловка для , как найти площадь равнобедренного треугольника , заключается в вычислении его высоты, потому что она обычно неизвестна. Если вы знаете длину катетов равнобедренного треугольника, вы можете легко вычислить hhh по теореме Пифагора: 92}h=a2−(2b​)2

​

Зная высоту, вы можете использовать стандартное уравнение площади треугольника , которое мы показали выше.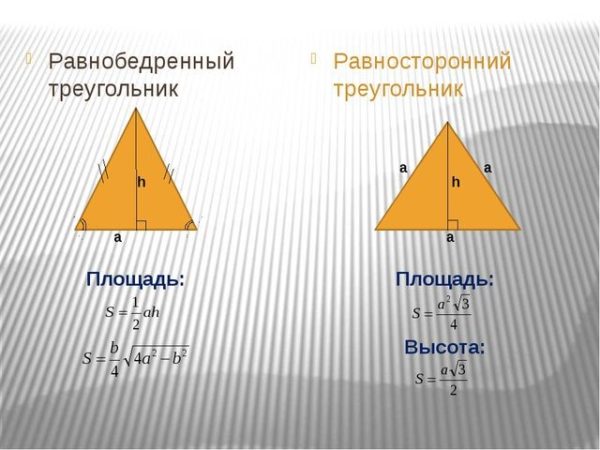

Вот и все! Теперь вы знаете, как вычислить площадь равнобедренного треугольника.

Если вы нашли этот калькулятор площади равнобедренного треугольника слишком тупым для ваших нужд, вы можете попробовать:

• Равнобедренный треугольник;
• Прямоугольный равнобедренный треугольник;
• Равнобедренный треугольник найти А;
• Углы равнобедренного треугольника;
• Сторона равнобедренного треугольника;
• Высота равнобедренного треугольника;
• Вершины треугольника.

Часто задаваемые вопросы

Как найти площадь равнобедренного треугольника без высоты?

Вы можете использовать другие методы нахождения высоты равнобедренного треугольника:

• Если у вас есть длины сторон a и b , вы можете использовать теорему Пифагора для вычисления высоты h :
  ч = √[ а² − (b/2)² ]
• Если у вас есть угол при основании α и длина стороны a или b , вы можете использовать тригонометрию для вычисления высоты:
  h = ½×a×tan(α) = b×sin(α)

Получив высоту, вы можете вычислить площадь с помощью A = ½ × b × h .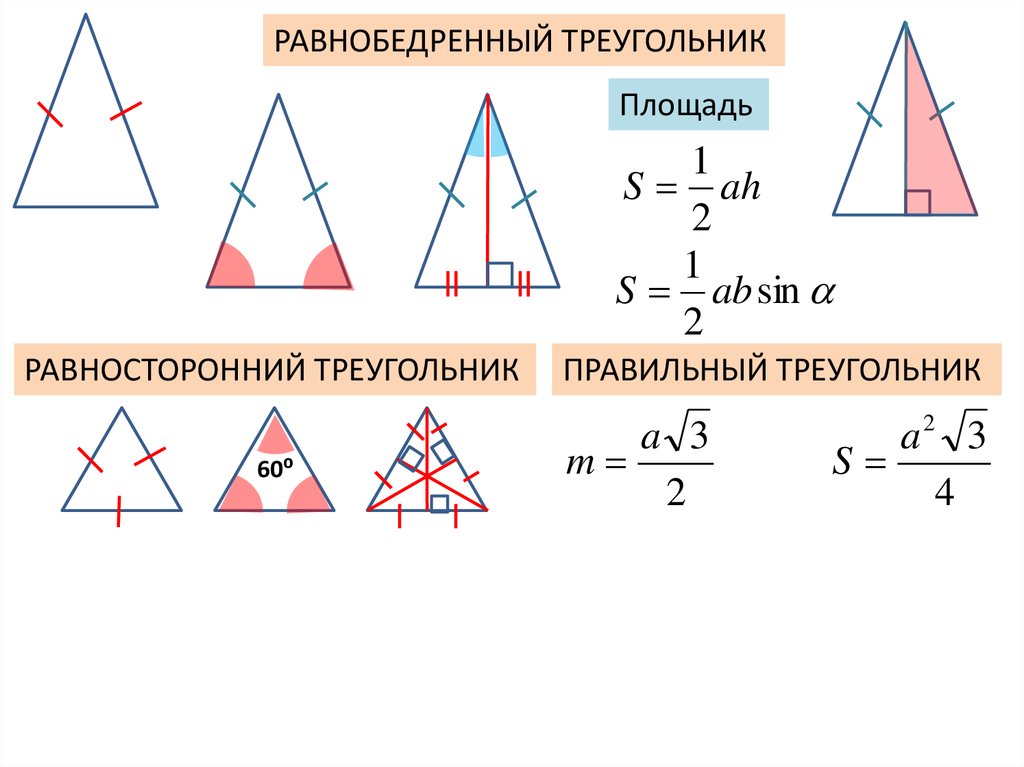

Какова площадь равнобедренного треугольника со сторонами 13, 13 и 24?

Площадь этого треугольника 60 см ² . Две ножки 13 см, а основание 24 см (хотя вы можете использовать любое устройство, какое захотите).

1. Вычислите высоту этого треугольника по теореме Пифагора:
   h = √[ a ² − (b/2) ² ]
   = √[ (13) ² − (24/2) ² ]
   = 5 см
2. Вычислите площадь этого треугольника по стандартной формуле:
   A = ½ × h × b
   = ½ × 24 × 5
   = 60 см ²

Все равносторонние треугольники равнобедренные?

Это зависит от точного определения , которое вы используете для равнобедренных треугольников. Некоторые говорят, что в равнобедренном треугольнике ровно две равные стороны, что лишает правосторонний треугольник считаться равнобедренным. Другие говорят, что у равнобедренного треугольника 90 124 по крайней мере 90 125 двух равных сторон.