Площади фигур найти: Как найти площадь фигуры, формула

Содержание

Разные способы вычисления площадей фигур

Авторы
Руководители
Файлы работы
Наградные документы

Боташева С.М. 1

1Дворец творчества детей и молодежи, г. Нальчик

Суншева З.Н. 1

1Дворец творчества детей и молодежи, г.Нальчик

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Математика – один из моих любимых школьных предметов. А самое сложное и одновременно самое интересное в математике — решение задач. Задачи в учебнике и сборниках попадаются самые разные и способов решения каждой задачи можно придумать несколько. Но один вид задач, как мне кажется, не похож на другие. Это задачи на клетчатой бумаге. Они кажутся необычными, более занимательными.

А встречаются ли такие задачи старшеклассникам? Я решила посмотреть открытый банк заданий ОГЭ и ЕГЭ по математике, посетить сайты по подготовке выпускников 9 и 11 классов к экзаменам. Оказалось, что задачи на нахождение площадей многоугольников на клетчатой бумаге достаются на экзаменах почти каждому выпускнику.

Вывод прост: уметь решать задачи на сетке (в т.ч. на нахождение площадей) разными способами нужно уметь каждому школьнику. В этом я вижу актуальность моей работы, а ее новизну в том, что один из рассматриваемых способов решения не разбирается в школьных учебниках математики.

Цель исследования – изучить способы вычисления площадей фигур на клетчатой бумаге, и выбрать самый эффективный.

Для достижения данной цели необходимо выполнить следующие задачи:

Подобрать литературу по данной теме.
Изучить способы нахождения площадей фигур на клетчатой бумаге.
Провести эксперимент.
Сделать выводы.

Предмет исследования: площади фигур на клетчатой бумаге.

Объект исследования: фигуры на клетчатой бумаге.

Гипотеза: самым эффективным способом вычисления площадей фигур на клетчатой бумаге является – формула Пика.

Глава 1. Способы нахождения площадей фигур на клетчатой бумаге. 1.1Площадь фигуры как сумма площадей ее частей

Задача №1. Найти площадь фигуры на рисунке 1 (клетки размером 1х1 см).

Разбиваем данную фигуру на четыре части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.

S=S1+ S2+ S3+S4

S1=2*3= 6 см2; S2= *2*1=1 см2;

S3= *2*1= 1 см2; S4= *3*1= 1,5 см2

S= 6+1+1+1,5= 9,5 см2.

Рис. 1. Ответ: 9,5 см2

Задача №2. Найти площадь фигуры на рисунке 2 (клетки размером 1х1 см).

S=S1+ S2+ S3+S4

S1= *1*5= 2,5 см2; S2=4*2=8 см2;

S3= *1*2= 1 см2; S4= *2*4= 4 см2;

S= 2,5+8+1+4= 15,5 см2.

Ответ: 15,5 см2.

Рис. 2.

Задача №3. Найти площадь фигуры на рисунке 3 (клетки размером 1х1 см).

Разбиваем данную фигуру на три части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.

S=S1+ S2+ S3

S1= *2*5= 5 см2;

S2=5*5=25 см2;

S3= *2*5= 5 см2;

S= 5+25+5= 35 см2

Рис. 3. Ответ: 35 см2.

1.2. Площадь фигуры как часть площади прямоугольника

Задача № 4. Найти площадь фигуры на рисунке 4 (клетки размером 1х1 см).

Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:

S=Sпр – S1 – S2 – S3

Sпр=5*5=25 см2; S1= *5*4=10 см2;

S2= *5*2=5 см2; S3= *1*3=1,5 см2;

S=25-10-5-1,5=8,5 см2

Ответ: 8,5 см2.

Рис.4.

Задача №.5. Найти площадь фигуры на рисунке 5 (клетки размером 1х1см).

S=Sпр – S1 – S2 – S3 – S4

Sпр=7*7= 49 см2; S1= *2*5=5 см2;

S2= *2*5=5 см2; S3= *2*5=5 см2;

S4= *2*5=5 см2;

S= 49-5-5-5-5= 29 см2

Ответ: 29 см2.

Рис.5.

Задача №.6. Найти площадь фигуры на рисунке 6 (клетки размером 1х1см).

S=Sпр – S1 – S2

Sпр=5*5=25 см2;

S1= *3*1=1,5 см2; S2= *4*5=10 см2;

S= 25-1,5-10=13,5 см2.

Ответ: 13,5 см2.

Рис. 6.

1.3. Формула Пика

Георг Александр Пик – австрийский математик. Родился Георг Пик в еврейской семье. Его отец Адольф Йозеф Пик возглавлял частный институт. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).

В 1900 – 1901 годах занимал пост декана философского факультета.

После того как Пик вышел в отставку в 1927 году, он получил звание почётного профессора и вернулся в Вену – город, в котором он родился. Однако в 1938 году после аншлюса Австрии 12 марта он вернулся в Прагу. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Круг математических интересов Георга Пика был чрезвычайно широк: 67 его работ посвящены многим темам, таким как линейная алгебра, интегральное исчисление, функциональный анализ, геометрия и др. Но больше всего он известен своей теоремой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года.

Эта теорема оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 году польский математик Гуго Штейнгауз включил теорему (или как её ещё называют – формулу) в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.

Пусть В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины, S – его площадь. Тогда справедлива следующая формула:

S = В+ – 1 ,

Это и есть формула Пика.

Задача №7. Вычислить площадь многоугольника на рисунке 7. Воспользуемся формулой Пика.

Отметим узлы:

Г=9 (синие)

В=48 (красные)

Подставив в формулы наши данные, получаем:

Рис.7. S=48 + – 1 = 51,5 см2 .

Задача №8. Вычислить площадь многоугольника на рисунке 8. Воспользуемся формулой Пика.

Отметим узлы:

Г=9 (синие)

В=16 (красные)

Подставив в формулы наши данные, получаем:

S=16 + – 1 = 19,5 см2 .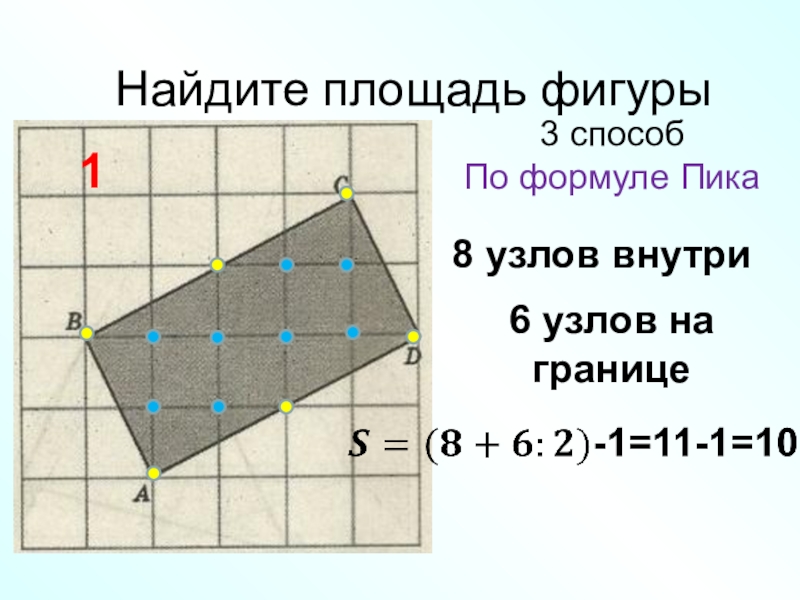

Рис. 8.

Задача № 9. Вычислить площадь многоугольника на рисунке 9. Воспользуемся формулой Пика.

Отметим узлы:

Г=8 (синие)

В=24 (красные)

Подставив в формулы наши данные, получаем

S=24 + – 1 = 19 см2 .

Рис. 9.

Глава 2. Проведение эксперимента

2.1. Результаты эксперимента

Изучив все способы нахождения площадей фигуры на клетчатой бумаге, мы решили провести эксперимент. Исследование проводилось в объединении «Знаю и считаю» Дворца творчества детей и молодежи, в котором я обучаюсь. Вместе с нашим педагогом, который также является моим научным руководителем, мы объяснили ребятам все способы вычисления площадей фигур. Затем, мы им раздали задания: по три задачи по каждому способу, и предложили решить их на время. Мы с моим научным руководителем засекали время, а ребята решали задачи.

В Таблице 1 представлены результаты каждого обучающегося по трем способам:

№	Ф. И. учащихся	Время, затраченное на решение задач 1-м методом (мин)	Время, затраченное на решение задач 2-м методом (мин)	Время, затраченное на решение задач 3-м методом (Формула Пика) (мин)
1	Алина	3,23	4,33	1,04
2	Дана	4,12	4,54	1,43
3	Дарина	5,07	4,46	2,15
4	Алина	2,32	2,45	1,12
5	Инал	2,17	2,34	0,52
6	Лалина	5,43	6,31	3,23
7	Залина	4,43	4,23	2,38
8	Руслан	2,34	3,43	1,15
9	Алина	3,56	4,52	2,43
10	Даяна	3,15	3,49	1,34
11	Алихан	2,24	2,15	0,54
12	Милена	3,12	4,37	1,32
13	Артур	5,34	5,12	2,33
14	Александр	4,47	5,42	2,46
15	Ислам	5,36	6,13	3,52
	Всего:	3,43	4,22	1,07

Как видно из таблицы, меньше всего времени ребята затратили, решая задачи формулой Пика. В среднем на три задачи ребята потратили 1 минуту, 7 секунд – формулой Пика, а на задача другими способами – 3 минуты 43 секунды и 4 минуты 22 секунды. Но быстро не всегда означает правильно, поэтому мы посчитали количество допущенных ошибок каждого обучающегося по всем способам. Результаты представлены в Таблице 2:

№	Ф.И. учащихся	Количество допущенных ошибок в задачах, решенных 1 методом	Количество допущенных ошибок в задачах, решенных 2 методом	Количество допущенных ошибок в задачах, решенных 3 методом
1	Алина	1	2	0
2	Дана	2	1	1
3	Дарина	2	3	2
4	Алина	0	0	0
5	Инал	0	0	0
6	Лалина	3	3	2
7	Залина	1	2	1
8	Руслан	1	1	0
9	Алина	2	2	1
10	Даяна	1	2	0
11	Алихан	0	0	0
12	Милена	1	1	0
13	Артур	2	3	2
14	Александр	2	2	1
15	Ислам	3	3	1
	Всего ошибок из 45 задач:	21	25	11

Из таблицы видно, что меньше всего ошибок ребята сделали, решая задачи формулой Пика. По первому методу 21неправильных задач из 45, по второму методу 25 неправильных, а по третьему методу всего 11 неправильных задач из 45, причем 7 учеников из 15 сделали все три задачи правильно, пользуясь этим методом. Это означает, что формула Пика не только сокращает время, но и помогает избежать ошибок.

Заключение

В данной работе мы рассмотрели все способы вычисления площадей фигур на клетчатой бумаге. В ходе исследования, наша гипотеза подтвердилась. В результате эксперимента, мы выяснили, что формула Пика является самым эффективным способом решения таких задач. Она проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника. Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.

Я уверена, что при сдаче выпускных экзаменов, задачи на вычисление площади фигур не будут вызывать затруднения, если ребята будут использовать формулу Пика.

Список использованной литературы

Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009
Математика? Легко!!! Площади фигур. – [Электронный ресурс].
Жарковская Н.М., Рисс Е.А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс].

Приложения

Приложение 1

Площадь фигуры равна сумме площадей ее частей.

Площадь фигуры как части площади прямоугольника.

Формулу Пика.

Просмотров работы: 880

Математика Таблица единиц площади. Измерение площади фигуры с помощью палетки

Материалы к уроку

Конспект урока

19. Таблица единиц площади. Измерение площади фигуры с помощью палетки

Организационный этап

Заливистый школьный звонок
Позвал нас опять на урок.
Тем, кто учит математику,
Тем, кто любит математику,
Тем, кто ещё не знает,
Что может полюбить математику,
Урок математики посвящается!

Сегодня на уроке мы познакомимся с единицами площади. Научимся измерять площадь фигуры с помощью палетки.

Этап подготовки учащихся к активному сознательному усвоению знаний

Устный счет

Задание

Вспомним, как найти площадь прямоугольника.

Чтобы найти площадь прямоугольника, нужно умножить его длину на ширину.

Не забывайте, что площадь будет выражена в соответствующих единицах измерения.

Решите задачи.

Задача 1. Вычислите площадь прямоугольника со сторонами 7 и 2 см.

7 · 2 = 14 (см²).

Чтобы найти площадь фигуры, надо длину умножить на ширину. Площадь прямоугольника 14 см².

Задача 2. Площадь прямоугольника 18 дм². Длина одной его стороны 6 дм. Найдите длину другой стороны.

18 : 6 = 3 (дм)

Чтобы найти длину неизвестной стороны, надо площадь разделить на длину известной стороны. Длина другой стороны 3 дм.

Задача 3. Площадь прямоугольника 72 м². Длина – 12 м. Во сколько раз ширина прямоугольника меньше его длины?

Сразу на вопрос задачи ответить нельзя, т.к. надо знать длины обеих сторон. Сначала узнаем длину второй стороны.

1) 72 : 12 = 6 (м) – ширина прямоугольника.

Потом сравним длины.

2) 12 : 2 = 2 (р.) – ширина меньше длины.

Мы видим, что ширина меньше длины в 2 раза.

Кто догадался, выполняя задания устного счета, чем мы сегодня будем заниматься на уроке?

Этап усвоения новых знаний

Какие единицы измерения площади вы знаете?

Помогите Мудрой Сове заполнить таблицу

Сколько в 1 кв. см квадратных миллиметров?

1 см² = 100 мм².

Сколько в 1 кв. дм квадратных сантиметров и квадратных миллиметров?

1 дм² = 100 см² = 10 000 мм².

Продолжайте заполнять таблицу по аналогии.

Запомните таблицу соотношения единиц площади.

1 см² = 100 мм²

1 дм² = 100 см² = 10 000 мм²

1 м² = 100 дм² = 10 000 см² = 1 000 000 мм²

1 км² = 10 000 дм² = 1 000 000 м²

1 а = 100 м² = 10 000 дм² = 1 000 000 см²

1 га = 100 а = 10 000 м² = 1 000 000 дм²

1 км² = 100 га= 10 000 а

Закончите предложение.

Чтобы найти площадь прямоугольника, нужно …

Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.

Как найти площадь фигуры, если длины сторон не указаны?

Прямоугольник со сторонами 6 см и 4 см.

Разделим фигуру на квадратные сантиметры. Получилось 24 квадрата со стороной 1 см. Площадь – 24 см.

Найдите площадь фигуры.

Эта фигура не прямоугольной формы. Как быть?

Можно как бы поместить нашу фигуру в прямоугольную форму, разбить на квадратные сантиметры и посчитать.

Не все квадраты целые. Что будем делать?

Ученые договорились складывать все неполные квадраты и делить их количество на 2. Если таких квадратов получится нечётное количество, то их надо увеличить или уменьшить на 1. Площадь таких фигур можно посчитать приблизительно.

Целых квадратов 1, нецелых – 8. Воспользуемся формулой, разделим 8 на 2, будет 4. 1 плюс 4 – 5. Площадь данной фигуры 5 см².

Вы заметили, что самим расчерчивать фигуру на квадраты очень долго? Чтобы сэкономить время и ускорить работу, люди придумали палетку.

Палетка – это прозрачная пластинка (плёнка), разделённая на равные квадраты (например, квадратные миллиметры, квадратные сантиметры, квадратные дециметры).

Мудрая Сова решила вывести алгоритм нахождения площади фигуры с помощью палетки. Проверьте, всё ли она сделала правильно.

1. Наложить палетку на фигуру.

2. Подсчитать количество целых квадратов.

3. Подсчитать количество нецелых квадратов.

4. Число нецелых квадратов разделить на 2 и прибавить к числу целых квадратов.

Закрепление материала

Выберите правильный ответ.

Что является единицей площади?

Сантиметр, километр, гектар, дециметр.

(Гектар)

В 1 дм² содержится…

100 мм², 10 000 мм², 1000 мм², 100 000 мм².

(В 1 дм² содержится 10 000 мм²)

Сколько квадратных сантиметров составляют 7900 кв. дм?

79 см², 790 см², 7900 см², 790 000 см².

(790 000 см²)

Площадь огорода 15 соток. Сколько это квадратных метров?

15 м², 150 м², 1500 м², 15 000 м².

(1500 м²)

Какова площадь квартиры, если площадь комнаты 18 м², площадь кухни в 2 раза меньше площади комнаты, площадь прихожей в 3 раза меньше площади комнаты, а площадь совместного санузла 4 м²?

Найдем площадь кухни: 18 : 2 = 9 (м²)

Найдем площадь прихожей: 18 : 3 = 6 (м²)

Вычислим площадь квартиры: 18 + 9 + 6 + 4 = 37 (м²)

Площадь квартиры 37 м².

Выразите в квадратных сантиметрах 7 дм², 54 м², 2 а.

Проверьте себя.

7 дм² = 700 см²

54 м² = 540 000 см²

2 а = 2 000 000 см²

Выразите в квадратных метрах 5 км², 31 а, 20 га.

Проверьте работу соседа по парте.

5 км² = 5 000 000 м²

31 а = 310 000 м²

20 га = 200 000 м²

Вычислите площадь фигуры.

Целых квадратов 6. Нецелых квадратов 8. Делим 8 на 2, получается 4. 4 плюс 6 – это 10. Площадь данной фигуры приблизительно 10 квадратных сантиметров.

Вычислите площадь фигуры.

Целых квадратов нет. Нецелых квадратов 10. Делим 10 на 2, получается 5. Площадь данной фигуры приблизительно 5 квадратных дециметров.

Этап подведения итогов

Чему научились на уроке?

Что такое палетка?

Для чего она служит?

Как измеряют площадь с ее помощью?

Какой формулой пользуются для измерения приблизительной площади фигур?

Рефлексия

Оцените свою работу на уроке.

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Площадь рисунков — прямоугольник и квадрат

Ключевые понятия

Площадь прямоугольника
Прямоугольники и квадраты

Предыдущие знания: . .
Сколько всего апельсинов?
Ответ:
Даны 5 групп апельсинов, по 5 апельсинов в каждой группе.
Из рисунка выше
5 групп по 5
= 5 × 5
= 5 + 5 + 5 + 5 + 5
= 25
∴∴
Всего 25 апельсинов.
13.1 Площадь прямоугольника
Площадь:
Площадь фигуры – это площадь поверхности, покрытая фигурой.
Как найти площадь?
Рассмотрим лист бумаги в клетку
Из этого листа бумаги в клетку мы делаем прямоугольник, как показано на следующем рисунке.
Чтобы найти площадь, посчитаем квадраты внутри прямоугольника.
Количество квадратов = 15
Итак, площадь равна 15 квадратным единицам.
Здесь площадь будет равна количеству квадратов.
Площадь = 15 квадратных единиц
Что означают квадратные единицы?
На нашем рисунке
Единица означает размер 1 квадрата
Единица измерения может быть любой, например см, м, км
Теперь квадратные единицы означают.
см × см = см ²
м   × м   = м ²
км × км = км ²
При вычислении площади путем подсчета квадратов следуем следующим правилам:
Если площадь меньше половины квадрата, игнорируем возьми 0)
Если площадь больше половины квадрата, прими ее за 1 квадратную единицу
Если площадь равна половине квадрата, возьми 12 квадратных единиц
Пример 1:
Найдите площадь квадрата фигура.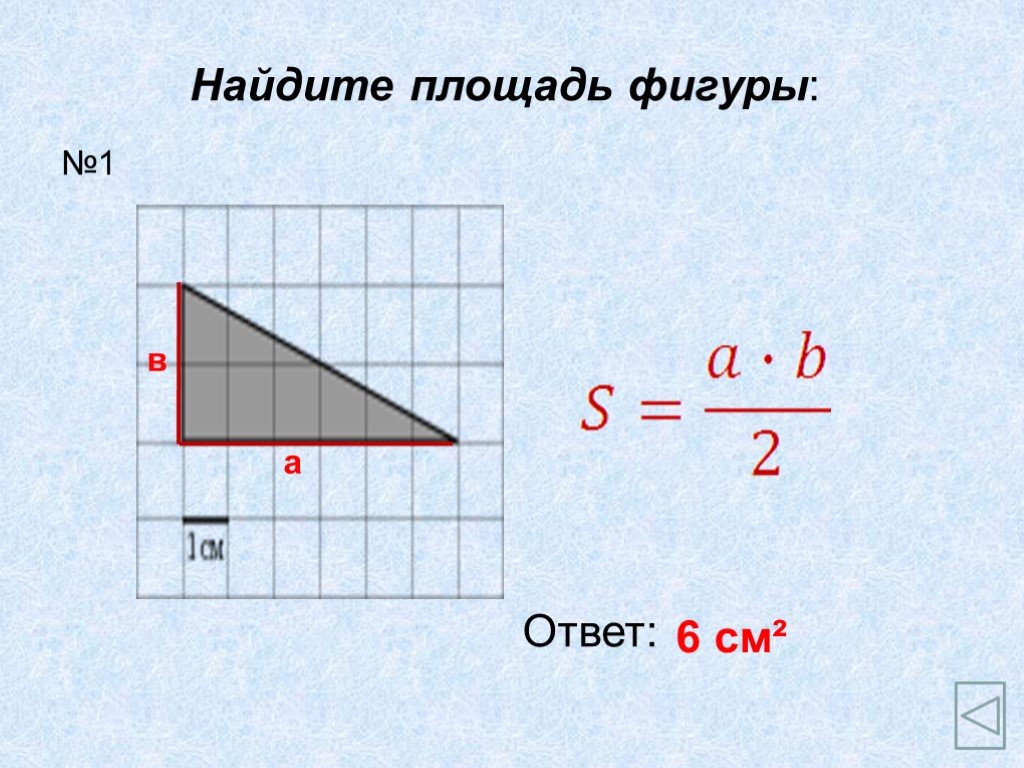
Из рисунка выше считаем квадраты.
Количество квадратов = 25
Итак, площадь = 25 квадратных единиц
Пример 2:
Найдите площадь круга.
Найдите площадь
круга.
Итак, площадь = 4 + 8 + 2
   = 14 квадратных единиц
Пример 3:
Найдите площадь пятиугольника.
Итак, площадь = 4 + 4 + 0
   = 8 квадратных единиц
13.2 Прямоугольники и квадраты
Прямоугольники и квадраты являются двумя наиболее распространенными формами.
Вот несколько примеров прямоугольных объектов:
Примеры квадратных объектов:
Площадь прямоугольника
Чтобы узнать площадь прямоугольника, мы посчитаем количество квадратов , которые он покрывает.
Другой способ — умножить длину сторон на .
В прямоугольнике противоположные стороны равны .
Длина сторон, идущих слева направо, называется шириной .
Длина сторон, идущих сверху вниз, называется высотой или длиной .
Чтобы найти площадь прямоугольника , умножьте ширину на высоту.
Площадь = ширина × высота
Воспользуемся этой формулой, чтобы найти ширину зеленого прямоугольника.
Во-первых, узнайте ширину и высоту.
Ширина равна 3 квадратным единицам, а высота — 2 квадратным единицам.
Теперь умножьте ширину на высоту.
3 × 2 = 6 квадратных единиц
Если 1 квадратная единица равна 1 квадратному метру, то 6 квадратных единиц составляют 6 квадратных метров (6 м²).
Площадь квадрата
У квадрата 4 равные стороны.
Это означает, что длина сторон одинакова.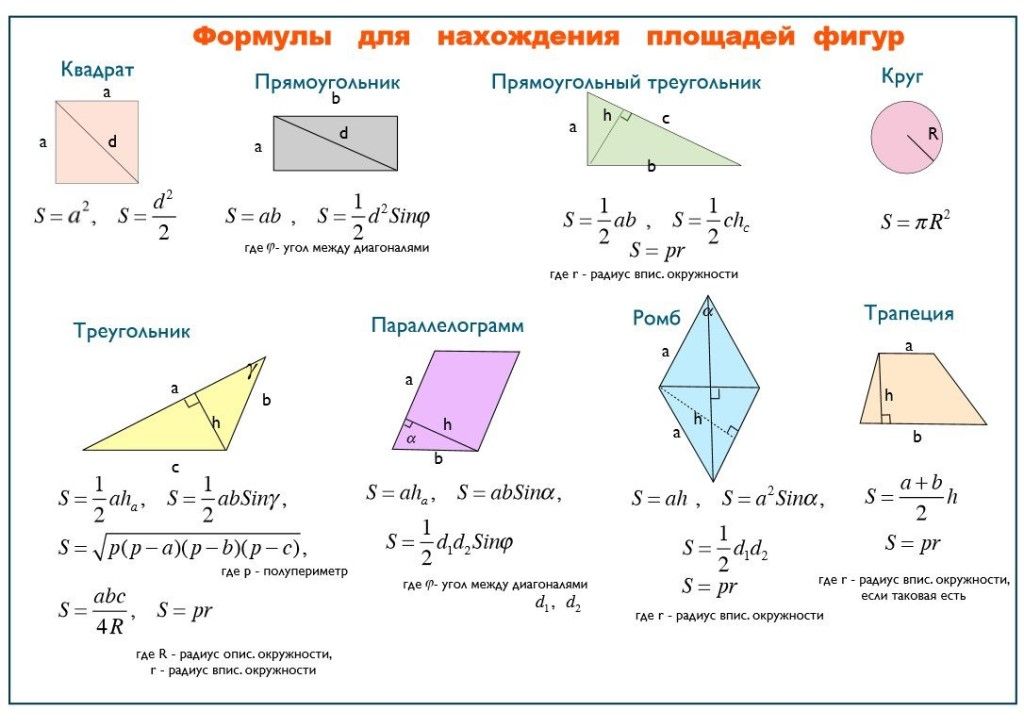
Чтобы найти площадь квадрата , умножьте длину 1 стороны на себя.
Какова площадь этого квадрата?
Длина каждой стороны равна 3.
3 × 3 = 9 квадратных единиц
Площадь квадрата равна 9 квадратных единиц.
Если 1 квадратная единица равна 1 сантиметру, то 9 квадратных единиц составляют 9 квадратных сантиметров (9 см²).
Нет сетки:
Если нет сетки с квадратами, чтобы помочь вам, вы все равно можете вычислить площадь фигуры.
, чтобы найти площадь прямоугольника ,
Длина ширины × Длина высоты
, чтобы найти площади квадратной ,
. любая сторона сама по себе.
Периметр
Периметр — это длина или расстояние вокруг фигуры.
Как найти периметр?
Чтобы найти периметр фигуры, сложите длины всех сторон
Пример 1:
Фигуры ниже имеют одинаковый периметр, но разную площадь.
Какова площадь прямоугольника B?
Из приведенных выше фигур у нас есть высота и ширина прямоугольника A. Мы можем использовать их, чтобы найти его периметр.
Мы делаем это, добавляя длины всех его сторон.
4 + 4 + 3 + 3 = 14 метров
т. е. периметр прямоугольника B также равен 14 метрам.
Мы еще не можем вычислить площадь B, потому что длина одной стороны все еще отсутствует.
Как найти недостающую сторону?
Мы знаем, что ширина 2 метра.
Так как противоположные стороны равны , мы удваиваем это, чтобы получить сумму двух сторон.
2 + 2 = 4
Теперь мы вычитаем полученную сумму из общего периметра.
14 – 4 = 10
Это означает, что сумма двух неизвестных сторон равна 10 м.
Делим на 2, чтобы получить длину каждой неизвестной стороны.
10 ÷ 2 = 5
Теперь мы знаем, что высота прямоугольника B равна 5 метров
Давайте посмотрим, верно ли это, сравнив его периметр с периметром прямоугольника A.
5 + 2 + 5 + 2 = 14 метров
Теперь мы получили недостающую сторону прямоугольника B.
Найдем площадь.
Чтобы найти площадь, умножаем длину и ширину прямоугольника B.
∴∴
Площадь прямоугольника B = 2 × 5 = 10 квадратных метров.
Пример 2:
Прямоугольники ниже имеют одинаковую площадь, но разный периметр.
Чему равен периметр прямоугольника А?
Чтобы найти периметр прямоугольника, нам нужно знать его высоту и ширину.
Из приведенных выше форм у нас есть ширина прямоугольника A, высота отсутствует.
Как найти высоту прямоугольника А?
Мы знаем, что площади двух прямоугольников равны.
Сначала нам нужно найти площадь прямоугольника B.
Площадь прямоугольника В = высота × ширина
Теперь нам нужно найти периметр прямоугольника A.
Мы знаем, что ширина прямоугольника A равна 3 дюймам, а его площадь равна 30 в ²
A = H × W
30 = H × 3
В = 30 ÷ 3 = 10 дюймов
Недостающая сторона равна 10 дюймам
∴∴
Периметр прямоугольника A = 3 + 3 + 10 + 10 = 26 дюймов.
Что у нас есть leanrt:
Понять значение площади
Сравнить площадь и периметр двух фигур
Найти площадь фигур для решения реальных задач
Выбрать подходящий инструмент и единицы длины для измерения площади
Измерение площади поверхностей предметов и мест
Упражнение
Найдите площадь заштрихованной области.
2. Найдите площадь заштрихованной области.
3. Школьная дорожка имеет форму прямоугольника с полукругом (полукругом) на каждом конце. Прямоугольник имеет длину 105 метров и ширину 68 метров. Найдите площадь, ограниченную дорожкой. Округлите ответ до сотых.
4. Найдите площадь заштрихованной области. Округлите ответ до двух знаков после запятой.
Ширина – 17 футов
Длина – 23 фута
5. Найдите площадь поверхности и объем прямоугольного тела длиной 15 ярдов, шириной 7 ярдов и
высота 8 ярдов.
6. Прямоугольный ящик имеет длину 14 дюймов, ширину 6 дюймов и высоту 10 дюймов. Найдите его объем как поверхность
площади.
7. Чему равен периметр этой фигуры?
8. Джордж хочет поставить небольшой забор вокруг своего сада. Сад имеет длину 17 футов и ширину 9 футов.
Сколько ограждений ему нужно купить?
9. Если правильный пятиугольник имеет длину стороны 7 дюймов, каков его периметр?
10. Периметр прямоугольной красочной подушечки составляет 20 сантиметров. Его ширина 6 сантиметров. Как долго это?
Концептуальная карта:
Формулы периметра различных форм:
Урок Видео: Площадь: целые и полуквадраты
Расшифровка видео
Площадь, целые и полуквадраты
9,0017 В этом видео учиться как измерить площади фигур, нарисованных на сетке целыми и половинными квадратами, счет и сопоставление половинок. Как мы могли найти площадь этого прямоугольник?
Площадь – это размер поверхности или количество пространства, которое он охватывает. Значит площадь этого прямоугольника количество пространства внутри розовых линий. Когда мы измеряем площадь форма, мы измеряем его в квадратных единицах. Это квадратная единица. Итак, чтобы найти площадь этого прямоугольник, нам просто нужно подсчитать количество квадратных единиц, которые он покрывает. Раз, два и еще два делают четыре, и еще четыре дают восемь. Площадь этого прямоугольника равна восьми квадратных единиц.
Как мы можем найти площадь этого форма кошки?
Начнем с подсчета числа квадратов, которые охватывает фигура. Вот два квадрата, четыре, шесть. Вот ряд из четырех квадратов. И мы знаем, что шесть и четыре 10. Еще один ряд из четырех дает 14. квадраты. И еще четыре дают 18, плюс еще три дают нам в общей сложности 21 квадрат. Мы посчитали все квадраты. Теперь нам нужно посчитать все треугольники.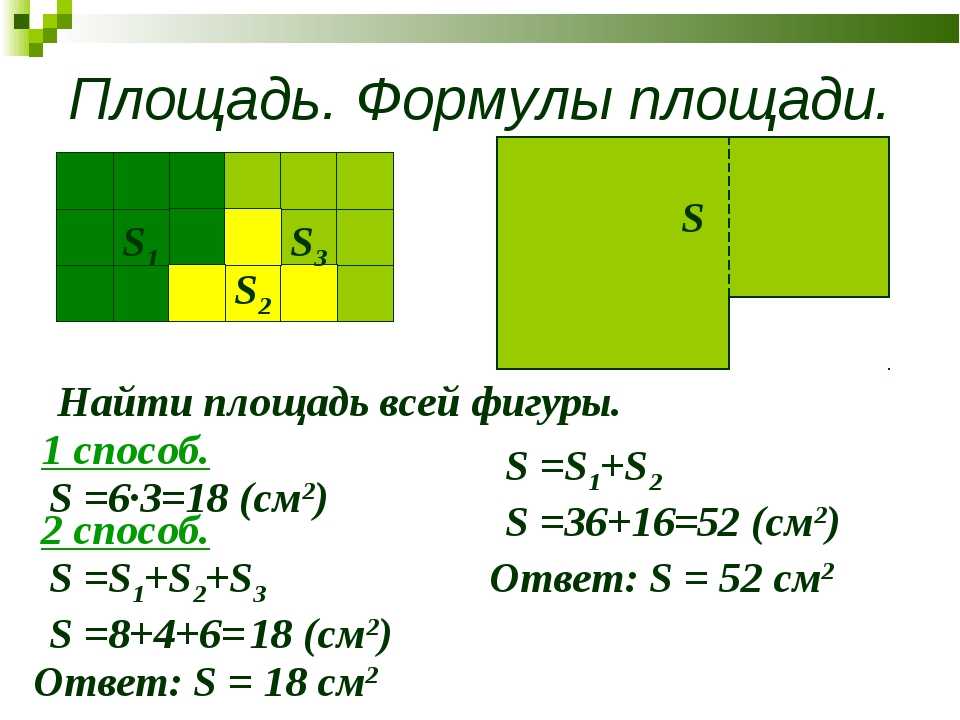 Вы заметили, что каждый треугольник половина квадрата? Если бы мы поместили два таких треугольники вместе, то получится целый квадрат. Итак, если мы соединим два треугольника вместе у нас получился один квадрат.
Мы можем поставить эти два треугольника вместе, чтобы сделать один квадрат. Мы можем соединить эти треугольники вместе, чтобы сделать еще один квадрат. Вот еще одна пара, дающая нам другой квадрат. Вот еще один квадрат. И мы можем положить наши последние две половинки вместе, чтобы сделать еще один квадрат. Посчитаем, сколько целых квадратов мы сделали из наших треугольников. Один два три четыре пять, шесть. Теперь мы можем добавить, чтобы найти общее количество количество квадратных единиц. 21 плюс шесть равно 27 квадратных единиц. Площадь фигуры кота равна 27. квадратных единиц.
Теперь, когда мы научились находить площадь фигур с целыми и половинными квадратами, давайте попробуем ответить на некоторые вопросы сейчас.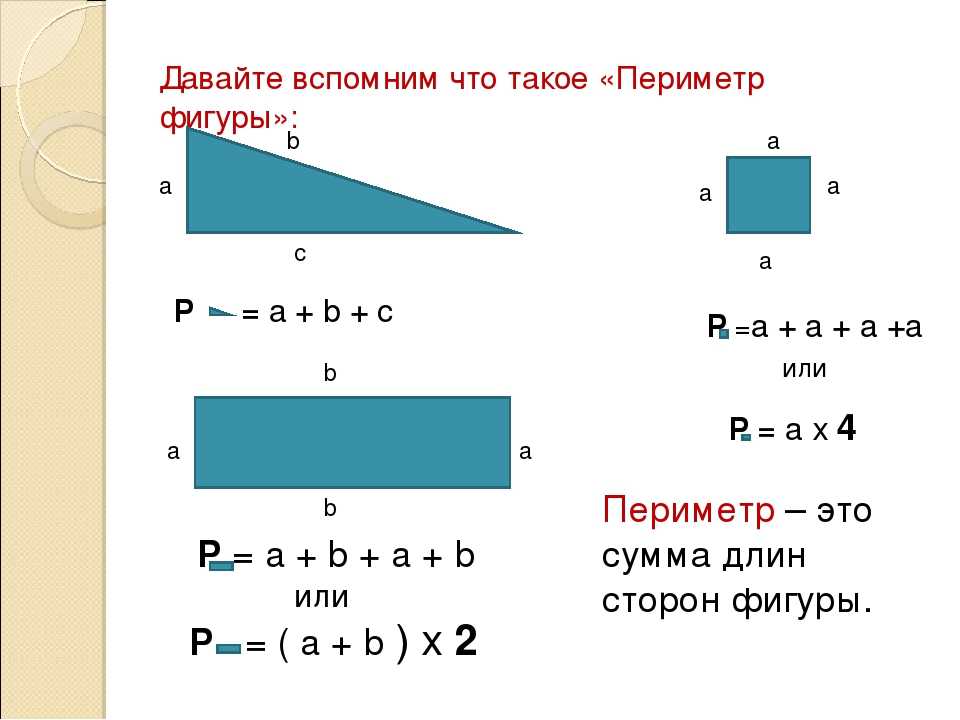
Найдите площадь фигуры.
В этом вопросе мы должны найти площадь заданной формы. Площадь — это количество пространства формы крышки или размер поверхности формы. Мы видим, что наша форма была рисуется на квадратной сетке. И мы измеряем площадь в квадрате единицы измерения. Итак, чтобы найти площадь этой фигуры, нам просто нужно подсчитать количество квадратных единиц, которые он покрывает. Вот две квадратные единицы, три, четыре, пять, шесть, семь, восемь, девять и еще три квадрата дают 12.
Но мы не посчитали все квадраты, которые покрывает фигура. Этот прямоугольник составляет половину квадрат. Если бы мы поместили эти две половинки квадраты вместе, мы бы сделали один полный квадрат. На один больше 12 будет 13. И если мы соединим эти две половинки вместе, чтобы сделать еще один квадрат, всего у нас получилось 14 квадратов. Мы подсчитали количество полных квадраты, и мы складываем половинки квадратов вместе, чтобы получились целые квадраты. Площадь нашей фигуры 14 кв. единицы измерения.
Найдите площадь этой фигуры.
Площадь — это количество пространства в фигуре крышки. Нам нужно найти площадь форму, которую нам дали. Мы можем рассматривать область как количество пространства внутри синих линий. Эта форма была нарисована на квадратная сетка, и мы называем каждый квадрат квадратной единицей. Измеряем площадь в квадрате единицы измерения. Итак, чтобы найти площадь нашей фигуры, нам просто нужно подсчитать количество квадратных единиц, которые он покрывает.
Но это не квадрат. Это треугольник. Вот еще один треугольник. Каждый из этих треугольников стоит половина квадрата. Мы можем сложить две половинки вместе, чтобы сделать целый квадрат. Итак, пока мы насчитали один квадратная единица. Теперь мы можем посчитать все квадраты. Наши две половинки составляют одно целое квадрат, и в верхнем ряду есть еще три, что составляет четыре. У нас есть еще четыре на втором ряд, что дает нам в общей сложности восемь. Еще четыре квадрата в нижнем ряду составляет в общей сложности 12 квадратных единиц. И у нас есть еще один треугольник, который, как мы знаем, стоит половину квадрата. Всего мы насчитали 12 с половиной. квадратных единиц. Площадь этой фигуры равна 12 и половинные квадратные единицы.
Мы посчитали целые квадраты. Складываем половинки квадратов вместе пары, чтобы сделать больше целых квадратов. В целом форма охватывает площадью 12 с половиной квадратных единиц.
Шарлотта нарисовала фигуру с площадью 12 кв. Какие две фигуры имеют площадь, отличается от формы Шарлотты?
Шарлотта нарисовала эту фигуру.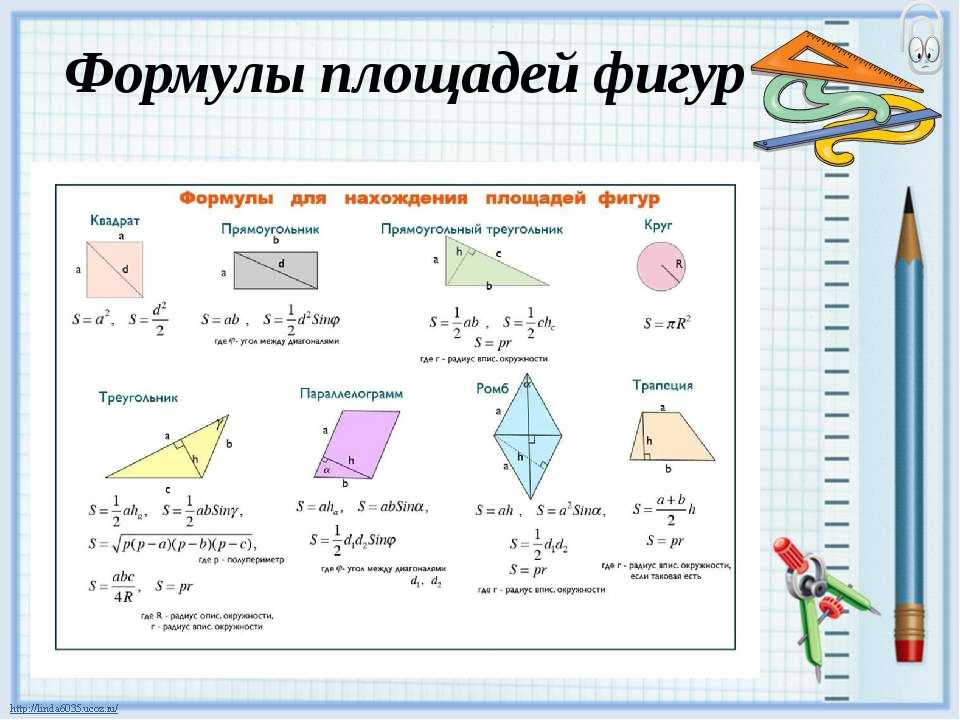 И нам сказали, что ее форма имеет площадью 12 кв. Таким образом, фигура Шарлотты охватывает 12 квадраты на сетке. Вот сколько места в ее форме занимает. Нам показаны еще три фигуры: форма один, форма два и форма три. Мы должны выбрать две формы которые имеют площадь, отличную от формы Шарлотты. Другими словами, нам нужно найти два фигуры, площадь которых не равна 12 кв.
Чтобы найти площадь каждой фигуры, мы просто нужно посчитать количество квадратных единиц, которые он покрывает. Начнем с первой формы. Вот два квадрата и еще один три составляют пять квадратов. Пять и еще два семь, и один больше составляет восемь. Теперь нам нужно посчитать треугольники. Каждый из этих треугольников равен половине квадрат. Итак, если мы сложим две половинки вместе, мы сделаем один целый квадрат. Итак, если мы положим эти две половины вместе у нас будет девять квадратов. Эти две половинки составляют еще одно целое квадрат, что составляет 10. Еще две половинки составляют 11 квадраты. И у нас осталась половина. Таким образом, площадь фигуры один равна 11 и половина квадратных единиц.
Мы знаем, что форма Шарлотты площадью 12 кв. Итак, мы знаем, что форма имеет область, которая отличается от формы Шарлотты. Теперь нам просто нужно найти наш второй форма. Какова площадь фигуры два? Давайте посчитаем количество квадраты. Один плюс три — четыре, пять, шесть семь. На два больше, чем семь, девять. Еще два составляют 11. 12, 13, 14. Таким образом, площадь второй фигуры равна 14. квадратных единиц. Это вторая форма, которая площадь, отличная от формы Шарлотты, потому что площадь формы Шарлотты 12 квадратных единиц. Две фигуры, имеющие площадь Отличаются от формы Шарлотты форма один и форма два.
No related posts.