Плоскость y x: На одной координатной плоскости постройте графики функции: а)y=(x+4)²в)y=(x-5)²c)y=(x-1,5)²

Содержание

Последовательная сборка ЦПГ YX 140 от ПитБайк Клуб

Сборку ЦПГ начинаем с того, что очищаем все плоскости от остатков старых прокладок. Начать можно с плоскости, к которой прилегает цилиндр. Обычно на плоскостях остаются части старых прокладок, их следует удалить или аккуратно канцелярским ножом, или же новой мягкой проволочной щеткой на дрель.

Когда данная плоскость обработана, можно приступить к подготовке поршня, а именно к установке поршневых колец. Как правильно ставить кольца, есть отдельная подробная статья. На помню лишь только, что кольца ставятся метками вверх.

Итак, плоскость картера приготовлена, поршень готов, дошло дело и до самого цилиндра.

С цилиндром, в принципе, все аналогично: чистим плоскости от старых прокладок, очищаем от были и прочей грязи само зеркало цилиндра.

После этого на стенки цилиндра ОБЯЗАТЕЛЬНО наносим небольшое количество масла тонким равномерным слоем.

Делаем это для того, чтобы, во-первых, избежать работы на сухую в момент первого запуска мотора после сборки. Во-вторых, так мы облегчим установку поршня с кольцами в цилиндр. Третье – избежим момента, когда при установке из-за сильного сопротивления или перекоса кольца сломано.

Итак, поршень надет на место. Убеждаемся в том, что он установлен правильной стороной, и замки колец расположены так, как это требуется.

Перед окончательной установкой обезжириваем плоскость цилиндра и картера растворителем, после этого надеваем прокладку.

Не забываем позаботиться о том, чтобы все направляющие и все уплотнительные резинки были на месте.

Также обязательно убедитесь в том, что цепь грм не соскочила с приводной звезды грм на коленвале. Только после этого продеваем цепь сквозь цилиндр.

Ну, а теперь вставляем на место направляющий ролик цепи грм, расположенный внутри полости рубашки цилиндра, и фиксируем его предназначенным для этого болтом.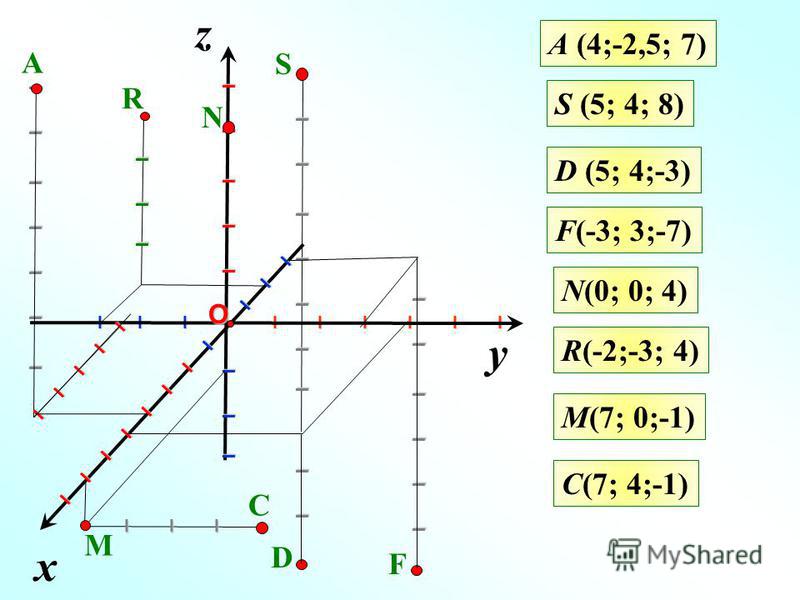

ВНИМАНИЕ! Вставляем и НАЖИВЛЯЕМ крепежный болт цилиндра! Но не затягиваем его! Иначе вы перекосите цилиндр, и получится неизбежный подсос воздуха и течь масла из-под прокладок. Данный болт затягивается только после того, как вы протянули основные четыре шпильки.

Теперь обезжириваем плоскости, головки и цилиндры, устанавливаем прокладку, не забываем обо всех резинках и направляющих втулках.

Надеваем головку, протягивая цепь грм.

Тут точно такой же крепежный боковой болт, который нужно наживить и затягивать только после протяжки основных четырех шпилек.

Остается мелочь: надеваем крышку головки, накручиваем гайки шпилек, не забываем о том, что на нижней правой шпильке должна стоять медная шайба. Ну и, остается все затянуть крест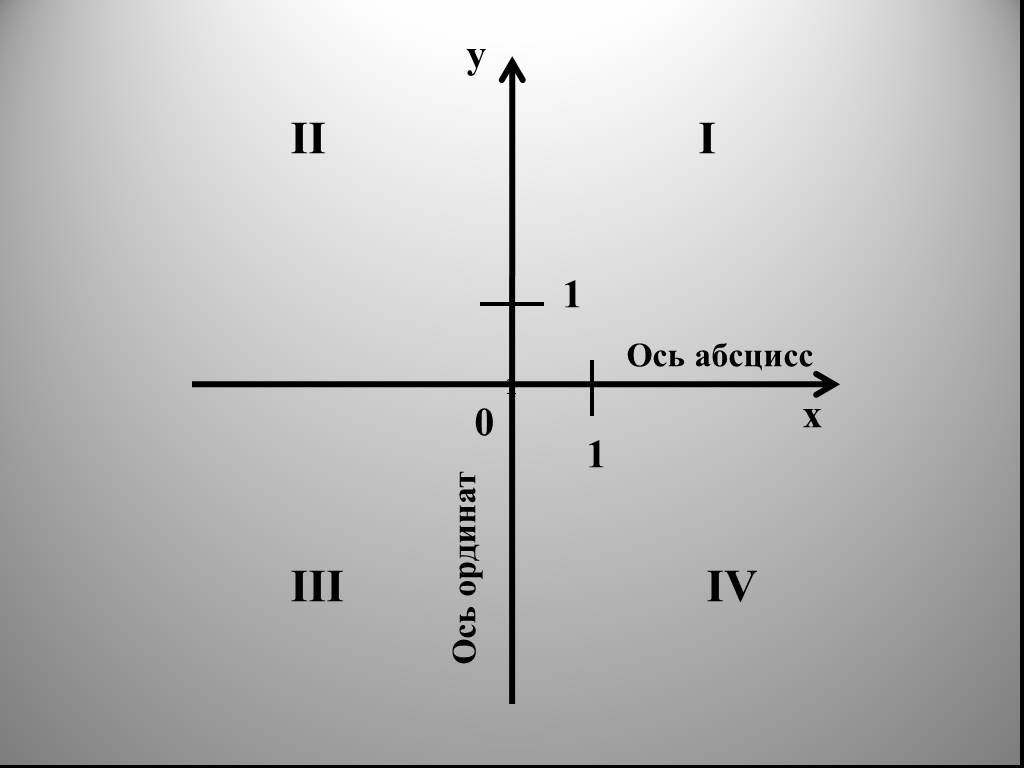 на крест. НЕЛЬЗЯ ЗАТЯГИВАТЬ ПО ОДНОЙ ГАЙКЕ ШПИЛЕК! Нужно равномерно протягивать крест на крест!

Когда шпильки окончательно протянуты, самое время окончательно затянуть те самые боковые крепежные болты.

Остается привернуть приемную трубу и вернуть на место впускной патрубок с карбюратором.

Ну, и конечно, надеваем звезду грм. После этого приступаем к совмещению меток ГРМ и регулировке клапанов.

Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на… Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.

Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.

Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования.

Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1.

Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1.

Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.

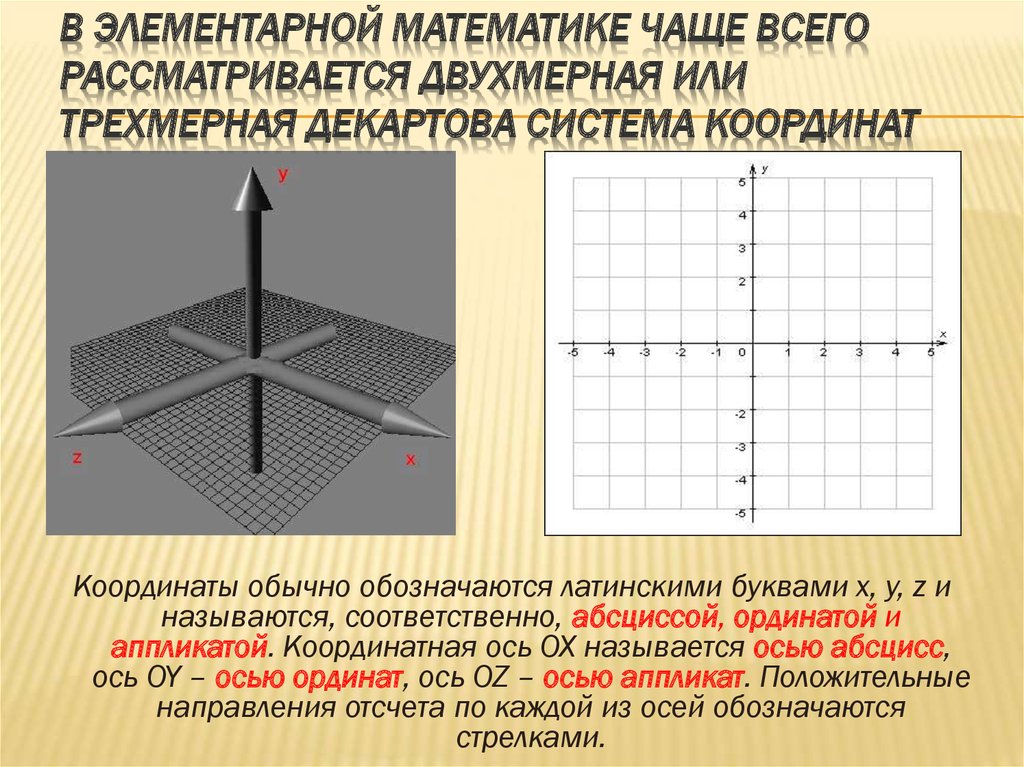
Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности.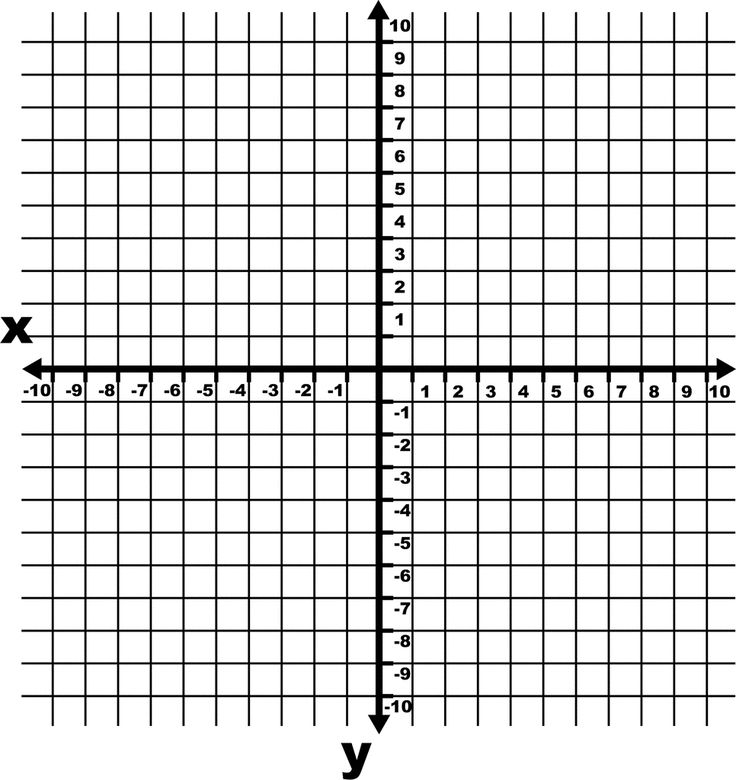

Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика».

Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.

Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

математических слов: плоскость x-y

индекс: нажмите на букву






индекс: предметные области

x-y Плоскость

плоскость, образованная осью x и осью y .

Видеть также

Координата плоскость, y-z плоскость, x-z плоскость

эта страница обновлена 19 июля 17
Математические слова: термины и формулы от алгебры I до исчисления
написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом
Copyright © 2000 Брюс Симмонс
Все права защищены

XZ Самолет | bartleby

Что такое самолет XZ?

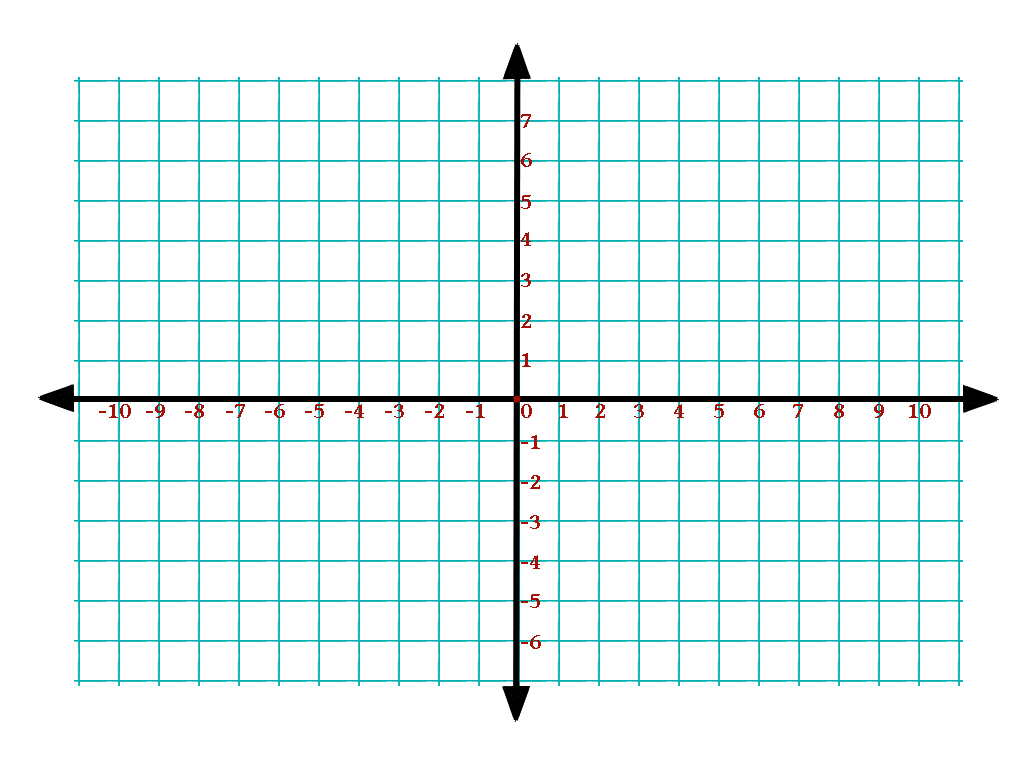
Чтобы понять плоскость XZ, полезно понимать двумерные и трехмерные пространства. Чтобы нанести точку на плоскости, необходимы два числа, и эти два числа на плоскости можно представить в виде упорядоченной пары (a,b), где a и b – действительные числа, a – горизонтальная координата, а b – вертикальная координата. координировать. Этот тип плоскости называется двумерной и содержит две перпендикулярные оси, горизонтальную ось и вертикальную ось.

Теперь мы собираемся расширить это для космоса. В космосе нам нужно три числа для построения графика. Эти три числа можно представить в виде упорядоченной тройки (a, b, c), где a, b и c – действительные числа, а – координата x, b – координата y, а c – координата z. Мы называем это трехмерным пространством, и оно содержит три перпендикулярные оси: ось x, ось y и ось z.

Трехмерное координатное пространство

В трехмерном координатном пространстве посмотрим, что определяют три оси координат. Мы можем нарисовать трехмерное пространство, зафиксировав O как начало координат, а ось x, ось y и ось z, проходящие через O, перпендикулярны друг другу. Обычно мы предполагаем, что оси x и оси y горизонтальны, а ось z вертикальна. Из рисунка ниже видно, что все эти три оси пересекаются в точке O.

Эти три координатные оси определяют три взаимно перпендикулярные плоскости: плоскость XY, плоскость YZ и плоскость XZ, которые иногда называют координатными плоскостями. Из рисунка ниже мы можем сказать, что плоскость XY содержит оси x и ось y, плоскость YZ содержит ось y и ось z, а плоскость XZ содержит ось x и ось z. ось.

Визуализация XZ плоскости

В этом описании мы собираемся визуализировать трехмерное пространство, потому что представить себе трехмерное пространство сложно. Перед визуализацией обсудим, как пространство делится на восемь частей. Из рисунка выше видно, что три координатные плоскости, плоскость XY, плоскость YZ и плоскость XZ, делят все пространство на восемь отсеков, известных как восемь октантов. Знак координат точки зависит от октанта, в котором находится точка.

Нам очень трудно представить фигуру трехмерного пространства.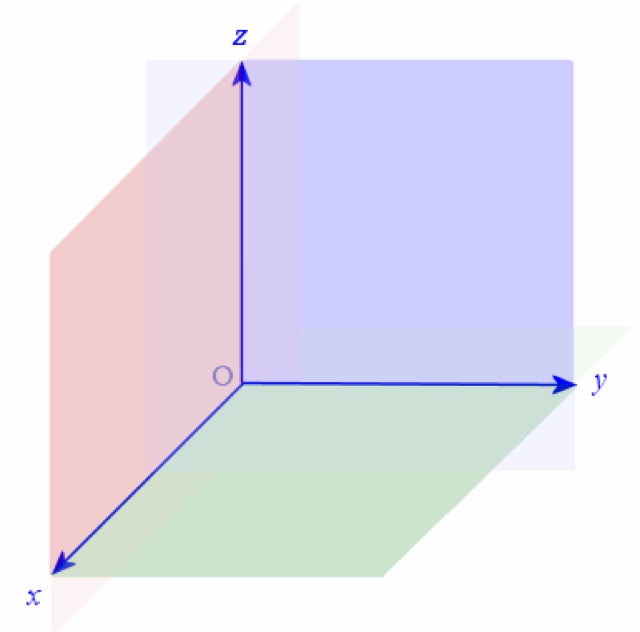 Итак, давайте рассмотрим левую стену как плоскость XZ, правую стену как плоскость YZ, а пол как плоскость XY. Из рисунка ниже можно сказать, что ось x движется вдоль пересечения пола и левой стены, ось y движется вдоль пересечения пола и правой стены, а ось z движется вверх от пола к потолку вдоль пересечения правой и левой стен. Все три оси проходят как в положительном, так и в отрицательном направлениях. Вы можете представить восемь октантов, соединенных одним и тем же углом О. В трехмерном методе плоскость XZ представляет собой ширину и высоту объекта.

Проекция

Пусть P – любая точка пространства, и мы можем обозначить P как (a, b, c), где a, b, c – действительные числа, а – координата x, b – координата y, а c — координата z. Числа a, b, c также называются координатами точки P. Если мы проведем перпендикуляр из точки P к плоскости XZ, мы получим точку Q, координаты которой равны (a, 0, c). Мы называем эту точку Q(a, 0, c) проекцией P на плоскость XZ. Точно так же, если мы проведем перпендикулярную линию из точки P к плоскости YZ и плоскости XY, мы получим R(0, b, c) и S(a, b, 0) – проекции точки P на плоскость YZ и плоскости XZ. самолет.

Уравнение

Для каждой координатной плоскости мы можем написать уравнения , представляющие плоскость. Для плоскости XY уравнение имеет вид z=0, для плоскости XZ уравнение имеет вид y=0, а для плоскости YZ уравнение имеет вид x=0.

Следовательно, плоскость XY может быть определена как x,y,0|x,y∈ℝ, плоскость YZ может быть определена как 0,y,z|y,z∈ℝ, а плоскость XZ может быть определена как х, 0, z | х, z∈ℝ. Иногда учащиеся могут считать, что для этой плоскости XZ y=k для некоторой константы k≠0, но для этого типа плоскость y=k кажется параллельной плоскости XZ. Об этом типе параллельной плоскости мы кратко рассказали ниже. Примем k≠0 за некоторую константу, тогда плоскость x=k параллельна плоскости YZ, плоскость y=k параллельна плоскости XZ, а плоскость y=k параллельна плоскости XZ. плоскость z=k параллельна плоскости XY.

Когда плоскость параллельна плоскости XZ, координата y не изменяется, меняются только координата x и координата z. Точно так же, если плоскость параллельна плоскости XY, то координата z не меняется, меняются только координата x и координата y, а если плоскость параллельна плоскости YZ, то координата x не меняется.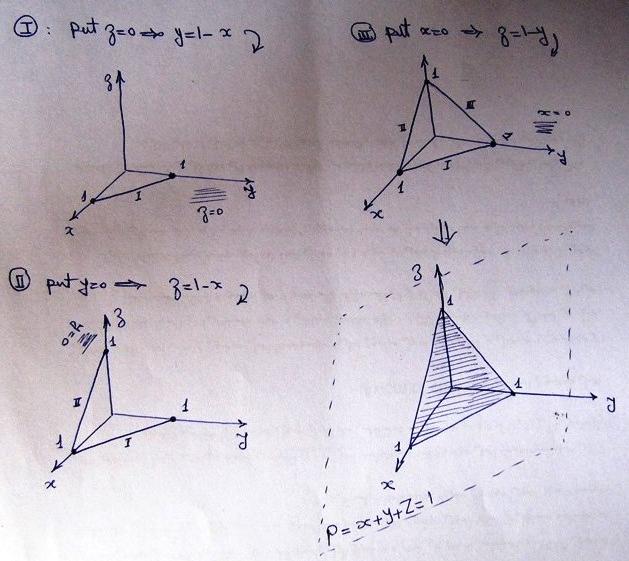 , различаются только координата Y и координата Z.

Например, рассмотрим уравнение y=5, а x, z — любые действительные числа, тогда его можно представить как x,y,z|y=5,x,z∈ℝ.

Тогда y=5 — вертикальная плоскость, параллельная плоскости XZ.

Направление

Положительный и отрицательный символы обозначают, что действительное число является положительным или отрицательным вдоль заданного направления. Координаты, лежащие в первом октанте, являются ненулевыми координатами.

Формула

Расстояние между двумя точками (x ₁, Y ₁, Z ₁) и (x ₂, Y ₂, Z ₂) в космосе дано поставлено с нормом. :

d=x2−x12+y2−y12+z2−z12

Для плоскости XZ расстояние между любыми двумя точками (x ₁ , 0 , z ₁ ) и z ₂ ) равно:

d=x2−x12+z2−z12

Середина отрезка с концами (x ₁ , y ₁ , z 9023x 2 2 _{1 ) и ( , y ₂ , z ₂ ) в пространстве задается формулой:}

M=x1+x22,y1+y22,z1+z22

Для плоскости XZ середина отрезка с концами ( х ₁ , 0, z ₁ ) и (x ₂ , 0, z ₂ ) равно:

M=x1+x22,0,z1+z22