По данным векторам а и б построить векторы: 1. Даны два произвольных вектора а и b. Постройте векторы : а) а+b б) а-b…

Содержание

ЛЕКЦИЯ N3

назад | содержание | вперед

ЛЕКЦИЯ N4.

Векторное пространство. Линейные операции над векторами.

Векторная алгебра.

1.Векторное пространство.

2.Векторная алгебра.

3.Системы координат.

1.Векторное пространство.

Рассмотрим теперь множество К и поле P произвольной природы. Предположим, что для всех элементов из К определены операции сложения и умножения на числа из Р. Будем называть элементы из К векторами, независимо от их конкретной природы.

Множество К называется линейным или векторным пространством над полем P,

если для всех векторов из К определены операции сложения и умножения на числа из P, причем выполнены следующие аксиомы:

А. Каждой паре векторов x, y

отвечает вектор x+y, называемый суммой x и y, причем:
—         сложение коммутативно: x+y=y+x;
—         сложение ассоциативно: x+(y+z)=(x+y)+z;
—         существует единственный нулевой вектор 0 такой, что x+0=x для любого вектора x;
—         для каждого вектора x существует единственный противоположный вектор –x, такой, что x+(-x)=0.
В. Каждой паре a, x, где a — число, а x – вектор, отвечает вектор ax, называемый произведением a и x, причем:
—         умножение на число ассоциативно: a(bx)=(ab)x;
—         1×x=x для любого вектора x.
С. Операция сложения и умножения связаны между собой следующими соотношениями:

—         умножение на число дистрибутивно относительно сложения векторов: a(x+y)=ax+ay;
—         умножение на вектор дистрибутивно относительно сложения чисел: (a+b)x=ax+bx.

В любом линейном пространстве для каждого вектора x имеет место равенство 0×x=0, где в правой части 0 означает нулевой вектор, а в левой – число нуль.
В любом линейном пространстве для любого вектора x справедливо соотношение
–x=(-1)x.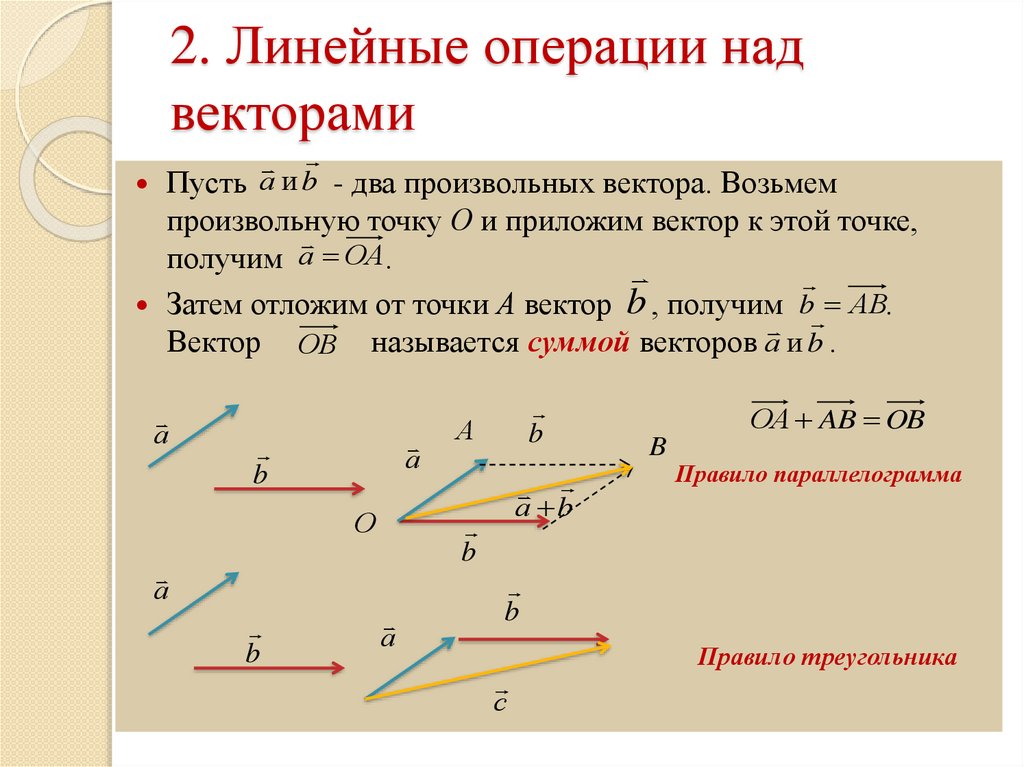
В любом линейном пространстве имеет место равенство a×0=0 для любого a.
С точки зрения операций умножения, сложения и вычитания формально имеют место все правила эквивалентных преобразований алгебраических выражений в любом линейном пространстве. В дальнейшем эти правила мы уже не будем оговаривать особо.

Множество L линейного пространства К называется его линейным подпространством, если при тех же операциях, что и в пространстве К, оно само является линейным пространством.
Множество, состоящее из одного нулевого вектора, является линейным подпространством. Это подпространство называется нулевым.
Наименьшим подпространством является нулевое, наибольшим – само исходное линейное пространство. Эти два пространства называются тривиальными, остальные – нетривиальны.
Каждое линейное пространство в своем описании содержит две существенно различные части. Во-первых, линейное пространство есть совокупность конкретных объектов, называемых векторами.
Во-вторых, над этими конкретными объектами определены операции сложения и умножения на число. Поэтому можно интересоваться либо природой векторов и их свойствами, либо свойствами указанных операций независимо от природы элементов.
Во всех практически интересных случаях построение и исследование линейных пространств осуществляется в два этапа: сначала, учитывая природу векторов, определяют операции сложения и умножения на число, а затем на основе свойств этих операций изучают сами пространства. Поэтому два пространства, устроенные одинаково по отношению к операциям сложения и умножения на число, можно считать обладающими одинаковыми свойствами.
Рассмотрим множество всех линейных пространств, заданных над одним и тем же полем Р. Естественно спросить, чем похожи и чем различаются между собой эти пространства.
Векторы любого класса допускают однозначное представление в виде перемещений (то есть направленных отрезков
) в геометрическом пространстве.
В большинстве приложений векторы появляются как функции точки в геометрическом пространстве.
2.Векторная алгебра.
    Векторы представляют собой направленные отрезки в пространстве, имеющие                        определенную длину. Вектор — отрезок определенной длины, одна из ограничивающих точек которого принята за начало, а другая – за конец.
Длина вектора (модуль) – расстояние между ограничивающими его точками.
К векторам относится и нуль-вектор, у которого начало и конец совпадают.
Определение: Векторы называются коллинеарными, если они располагаются на одной
прямой или на параллельных прямых, то есть если существует прямая, которой они параллельны.
Определение: Векторы называются компланарными, если они лежат в одной
плоскости или если существует плоскость, которой они параллельны. Если компланарные векторы имеют общее начало, то они лежат в одной плоскости.

Определение: Векторы называются равными, если они имеют равные модули,
коллинеарны и направлены в одну сторону. (Если вектора направлены в противоположные стороны при равных модулях и наличии коллинеарности, то они противоположны).
Вектор можно переносить параллельно самому себе, помещая его начало в любую
точку пространства.
Сложение векторов

       Пусть даны два вектора а и b.
1.      Возьмем произвольную точку 0 и построим вектор ОА=a, потом от этой же точки отложим вектор ОВ=b. Построим на этих векторах, как на сторонах, параллелограмм OAСB. Вектор ОС, являющийся диагональю параллелограмма, проведенной из вершины

0, и будет суммой векторов а+b.

2.      От произвольной точки 0 отложим вектор ОА=а , затем от точки А отложим вектор АВ=b. Вектор, соединяющий начало первого слагаемого с концом второго, будет суммой этих векторов ОВ=а+b.



a                    b



Свойства сложения векторов

I.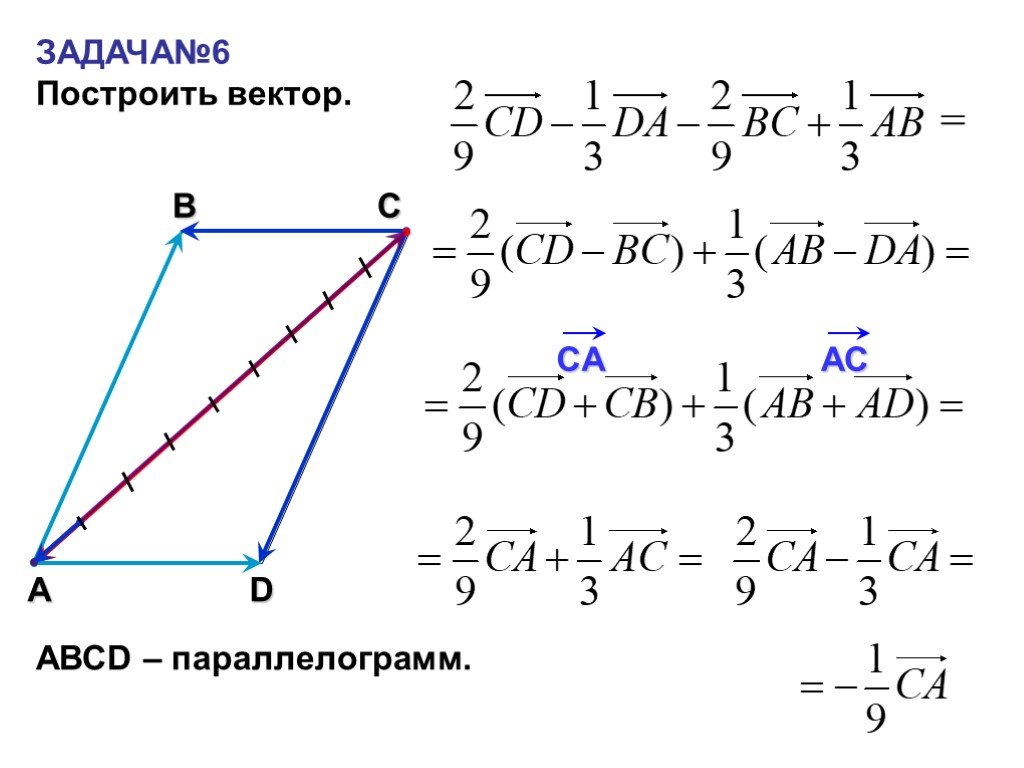                     Сложение векторов коммутативно (переместительное свойство):
а+b=b+а
II.                 Сложение векторов ассоциативно (сочетательное свойство):

а+(b+c)=(а+b)+c
      Сумму любого конечного числа векторов можно построить по следующему правилу: из произвольной точки 0 откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго, к концу второго – начало третьего и т.д. Суммой данных векторов будет вектор, соединяющий начало первого вектора с концом последнего.
      Разность векторов – это третий вектор с=a-b, сумма которого с вычитаемым вектором b дает a.
      Правило построения вектора разности: откладываем векторы OA=a и OB=b из общей точки 0. Вектор, соединяющий концы уменьшаемого вектора a и вычитаемого вектора b, и направленный от вычитаемого к уменьшаемому, и будет разностью векторов a и b.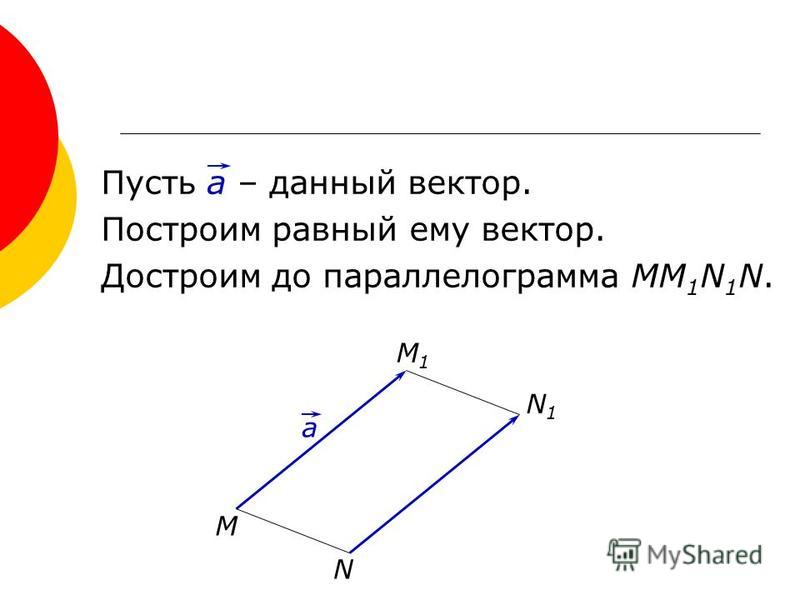

              A

      a


O        b     B

       Если на векторах a и b, отложенных из общей точки, построить параллелограмм, то вектор OC (одна диагональ параллелограмма) равен сумме a+b, а вектор BA (другая диагональ) равен разности a-b.

Для просмотра анимации нажмите.


Умножение вектора на скаляр.

     Пусть даны вектор a и число λ. Произведением вектора a на число λ называется вектор с, коллинеарный вектору а, имеющий длину |с|=|λ|×|а| и то же направление, что и вектор а, если λ>0, и противоположное направление, если λ<0.
     Из определения умножения вектора на число следует, что если b=λa, то векторы b и a коллинеарны. Очевидно, что из коллинеарности векторов следует, что b=λa.
Определение: вектора a и b коллинеарны тогда и только тогда, когда имеет

место равенство b=λa.
1). Для любых чисел λ и γ и любого вектора а справедливо равенство λ(γа)=(λγ)а.
2). Пусть существует вектор а не равный нулю. Для любого коллинеарного ему вектора b существует, и притом только одно λ, удовлетворяющее равенству: b=λa.
     Это число либо λ=|b|/|a|, либо λ=-|b|/|a| в зависимости от того направлены ли вектора a и b одинаково или противоположно.
    Умножение вектора на число обладает распределительным свойством λ(a+b)=λa+λb, (λ₁+λ₂)a=λ₁a+λ₂a.
     Вектор, длина которого равна единице, называется единичным.
     Каждый вектор равен произведению его модуля на единичный вектор того же направления (это следует из определения умножения вектора на число).
Угол между двумя векторами.
     Пусть даны два произвольных вектора a и b. Отложим от произвольной точки векторы OA=a, OB=b.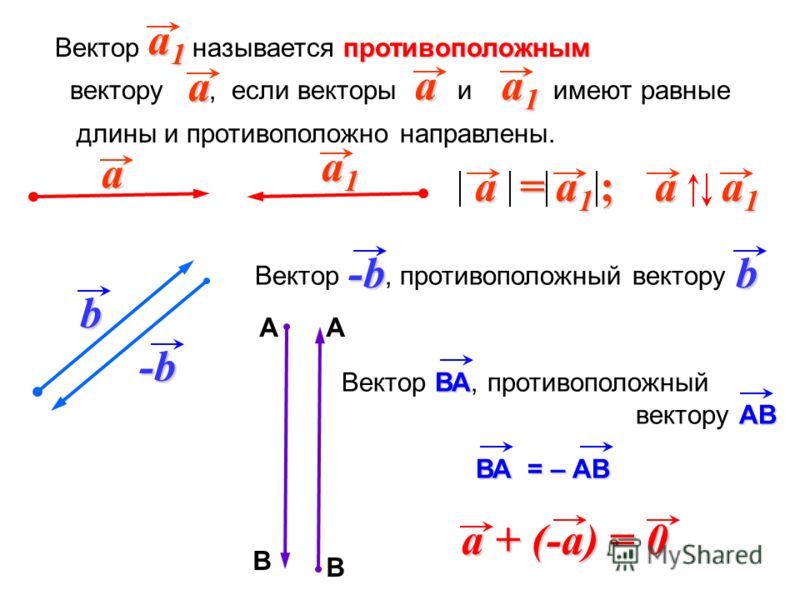 Угол между векторами – это угол, на который надо повернуть один из векторов до его совпадения со вторым.
     Рассмотрим ось l, положительное направление которой совпадает с направлением единичного вектора l^°, расположенного на оси. Тогда, углом между вектором и осью будет угол между векторами а, l^°.
Проекция вектора на ось и составляющая вектора по оси.





Проекцией вектора a на ось l называется длина отрезка A^/B^/, заключенного между основаниями перпендикуляров, опущенных на ось из начала и конца вектора a, которой приписан знак «+», если отрезок A^/B^/ ориентирован в положительную сторону относительно 0l и знак “-“, если наоборот.






Теорема 1: Проекция вектора а на ось l равна модулю вектора а, умноженному на косинус угла между вектором и осью: ПР_Ol(a)=|a|cosφ.
Теорема 2: проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось AC=AB+BC; ПР_OlAC=ПР_Ol(AB)+ПР_Ol(BC)
Теорема 3: если вектор a умножить на число λ, то его проекция на ось также умножится на это число: ПР_Ol(λa)=λ×ПР_Ol(a)
    Определение: вектор, соединяющий проекцию начала вектора а с проекцией его конца, называется составляющей вектора а по оси Ol: сост. Ol=ПР_Ola×l^°=AB.

Линейная зависимость векторов.
     Векторы a₁, a₂,…,_{a_k называются линейно зависимыми, если
существуют числа λ₁, λ₂,…,λ_к, не все
равные нулю, для которых имеет место равенство λ₁а₁+λ₂а₂+…+λ_ка_к=0.}
     Векторы а₁,а₂,…,а_к называются линейно независимыми, если равенство (I) имеет место только при λ₁=λ₂=…=λ_к=0 (то есть в тривиальном случае).
     Полагая, что, например, λ₁≠0 запишем: а₁=-(λ₂а₂)/λ₁-(λ₃а₃)/λ₁-…-(λ_ка_к)/λ₁
     Выражение в правой части – линейная комбинация векторов а₂,а₃,…,а_к.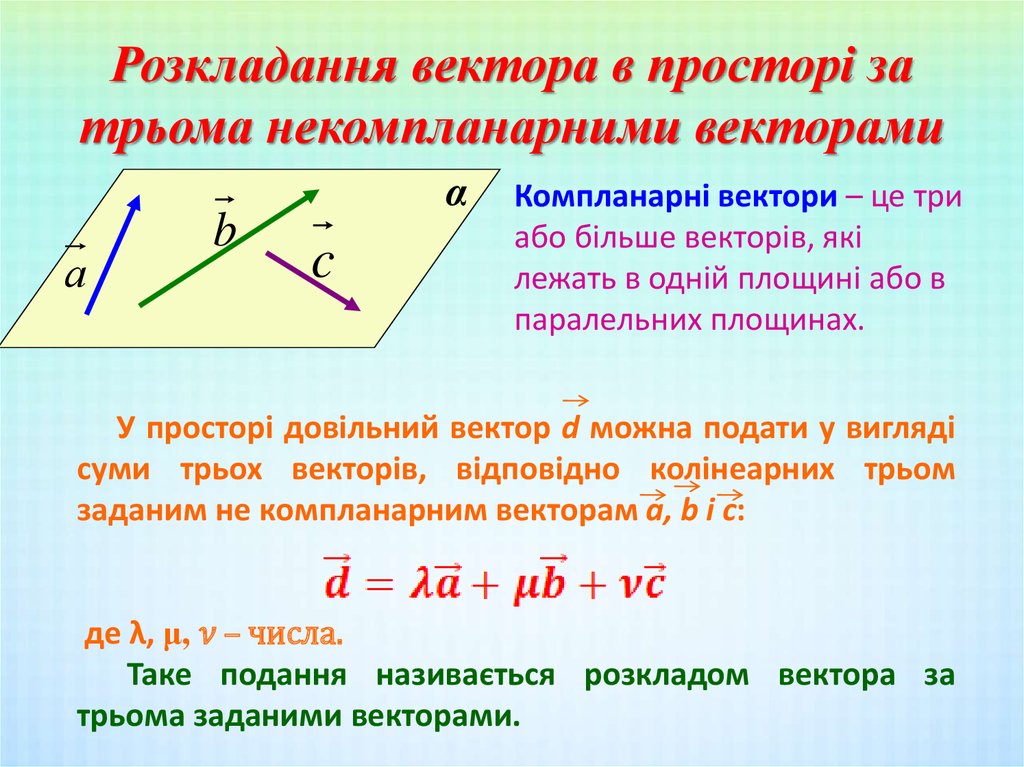
     Если несколько векторов линейно зависимы, то хотя бы один из них всегда можно представить в виде линейной комбинации остальных (верно и обратное).
Линейная зависимость векторов на плоскости.
Теорема 1: всякие три вектора a, b, c на плоскости линейно зависимы.
Доказательство: нужно доказать, что один из векторов является линейной комбинацией остальных.
1)      среди векторов есть пара коллинеарных, пусть a и b, то есть a=λb или a=λb+0×c, то есть a есть линейная комбинация b и c.
2)      Коллинеарных векторов нет.
Перенесем все три вектора в общее начало.
Для просмотра анимации нажмите.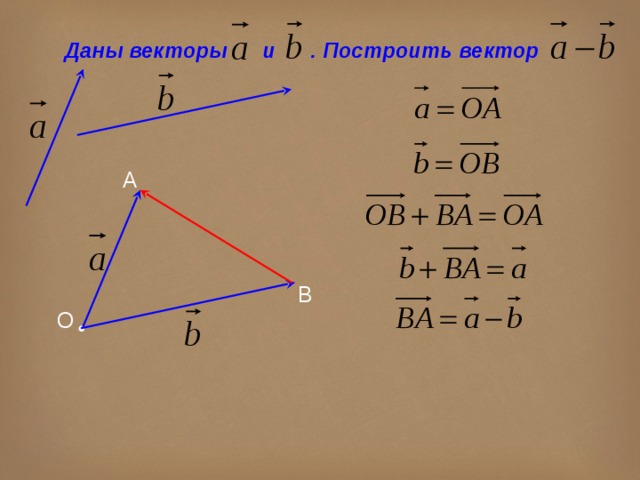

Через конец вектора a проведем прямые, параллельные векторам c и b до пересечения с прямыми, на которых находятся вектора b и c. Тогда, очевидно, что OM=OC+OB, но OC и OB коллинеарны b и c соответственно, то есть OC=λ₁c; OB=λ₂b.
     Поэтому, a=λ₁c+λ₂b, то есть является линейной комбинацией векторов b и c.
    Следствие: Если число данных векторов на плоскости больше трех, то они также линейно зависимы, то есть один из них можно представить в виде линейной комбинации остальных.
Доказательство: пусть даны а₁,а₂,…,а_к; к>3
Из теоремы имеем а₁=μ₂а₂+μ₃а₃
Тогда для k векторов а₁=μ₂а₂+μ₃а₃+…+0×а_k, что и требовалось доказать.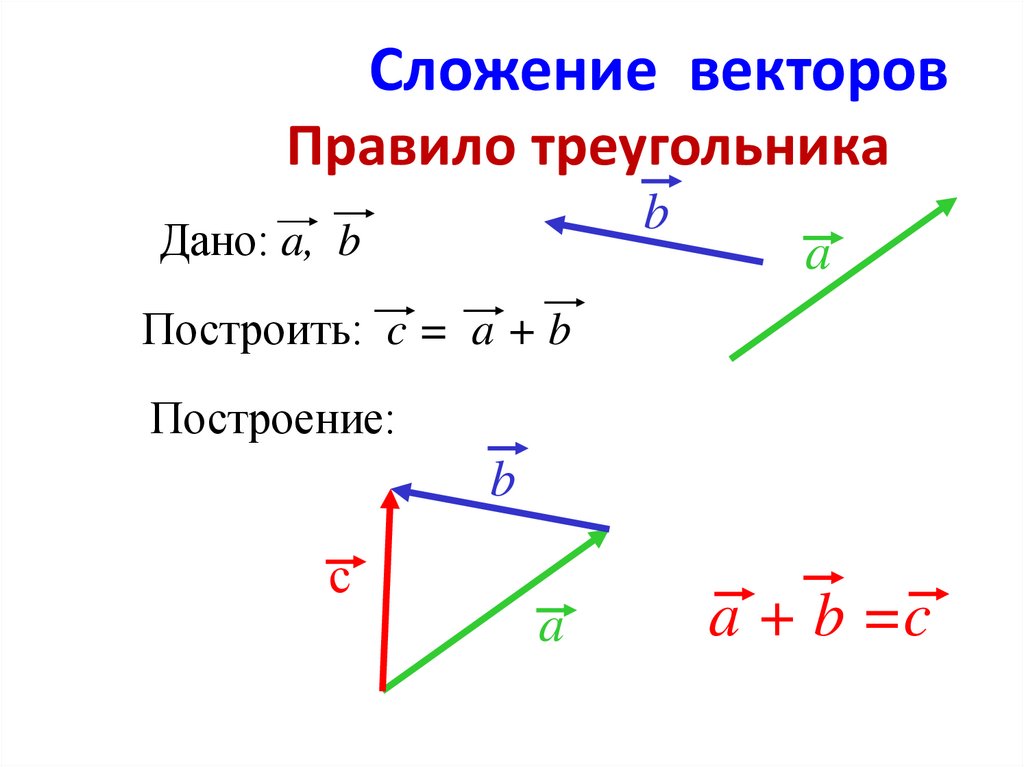
Теорема 2: Для того, чтобы два вектора на плоскости были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны.
     Два коллинеарных вектора линейно зависимы.
     Максимальное число линейно независимых векторов на плоскости равно двум.

Линейная зависимость в пространстве.

Теорема 3: всякие четыре вектора a, b, c, d в пространстве линейно зависимы.

Доказательство: Пусть все векторы имеют общее начало. Покажем, что один из векторов является линейной комбинацией остальных.

1)      Пусть среди них есть тройка компланарных (a, b, c). Так как все компланарные векторы выходят из одной точки, то значит, они лежат в одной
плоскости, а по теореме I они линейно зависимы, то есть один можно записать в виде линейной комбинации остальных: а=μ₂b+μ₃c
И для четырех: a=μ₂b+μ₃c+0×d, то есть a – линейная комбинация b, c, d.
2)      Среди них нет тройки компланарных.
Тогда вектор а можно представить в виде суммы трех векторов, коллинеарных соответственно b,c,d.

Для просмотра анимации нажмите.

Для этого через точку M проведем плоскости параллельные трем
плоскостям, определяемым парами b,c; c,d; d,b, и получим параллелепипед с диагональю а=OM. Очевидно, а=OM=OM₁+M₁P+PM.
Но OM₁=λ₁b, M₁P=OM₂=λ₂c, PM=OM₃=λ₃d.
Следовательно, a=λ₁b+λ₂c+λ₃d, то есть a,b,c,d линейно зависимы.
Следствие: 1) Если число векторов в пространстве больше четырех, то они линейно зависимы.
3)      для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы они были линейно зависимы.
4)      Максимальное число линейно независимых векторов в пространстве равно трем.
Базисом на плоскости называются два любых линейно независимых вектора. Пусть е₁и е₂образуют базис. Любой вектор а на плоскости можно представить в виде: а=λ₁е₁+λ₂е₂(так как три вектора на плоскости линейно зависимы), то есть разложить по базису.
Числа λ₁, λ₂ – аффинные координаты вектора а на плоскости а={λ₁; λ₂}.
Теорема 4: разложение вектора а по базису е₁ и е₂является единственным.
Доказательство: пусть существует разложение одного вектора а по базису е₁,е₂; а=μ₁е₁+μ₂е₂; а=ν₁е₁+ν₂е₂
Вычтем второе уравнение из первого: 0=(μ₁-ν₁)е₁+(μ₂-ν₂)е₂
Но е₁и е₂ линейно независимы, поэтому μ₁-ν₁=0; μ₂-ν₂=0, то есть μ₁=ν₁; μ₂=ν₂ и разложение по базису единственно. Базис в пространстве – это три любых линейно независимых вектора. Всякие три некомпланарных вектора образуют базис.
Любой вектор а однозначно разлагается по векторам базиса: а=λ₁е₁+λ₂е₂+λ₃е₃; где λ₁, l_2, λ₃ – аффинные координаты вектора в пространстве.

3.Системы координат

     Фиксируем в пространстве т.О и рассматриваем произвольную точку М. Радиусом-вектором т. М по отношению к точке О называется вектор ОМ. Если в пространстве кроме точки О выбран некоторый базис, то точке М можно сопоставить упорядоченную тройку чисел – компоненты ее радиус-вектора.
Определение: декартовой системой координат в пространстве называется совокупность точки и базиса.
Точка носит название начала координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат. Первая – ось абсцисс, вторая – ось ординат, третья – ось аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Рассмотрим прямоугольную систему координат в пространстве Oxyz. На каждой из осей выберем единичный вектор, направление которого совпадает с положительным направлением оси: векторы i, j, k, причем |i|=|j|=|k|=1. Эти три взаимно-перпендикулярных вектора называются ортами. Так как эти орты некомпланарны, то они образуют базис,
называемый декартовым ортогональным. Рассмотрим некоторый вектор а в пространстве, переместим его в точку О, то есть построим ОМ=а. Проведя через конец вектора а плоскости, параллельные координатным осям, получим параллелепипед.
а=ОМ₁+М₁Р+РМ, где М₁Р=ОМ₂; МР=ОМ₃
Векторы ОМ₁, ОМ₂, ОМ₃ – составляющие вектора а=ОМ по осям Ox, Oy, Oz ОМ₁=ПР_ОхОМ×i, ОМ₂=ПР_ОуОМ×j, ОМ₃=ПР_ОzOM×k.
Обозначим проекции вектора а=ОМ на оси Ox, Oy, Oz – a_x_,a_y, a_z. Тогда, разложение вектора по ортогональному базису будет таким: а=a_xi+a_yj+a_zk. Это разложение вектора на составляющие по координатным осям. Если проекции вектора а на оси координат равны a_x, a_y, a_z, то можно записать: а={a_x, a_y, a_z}. Это прямоугольные декартовы координаты. Линейные операции над векторами можно заменить арифметическими действиями над их проекциями:
λа=λa_xi+λa_yj+λa_zk
a±b=(a_x±b_x)i+(a_y±b_y)j+(a_z±b_z)k
Направление вектора в пространстве определяется углами α, β, γ, которые вектор составляет с осями координат.
Для просмотра анимации нажмите.

Косинусы этих углов называются направляющими косинусами вектора а:
a_x=|a|×cosa, то есть cosa=;
a_y=|a|×cosb, то есть cosb=;
a_z=|a|×cosg, то есть cosg=.

Вектор a=OM – диагональ параллелепипеда, а зная теорему о диагонали прямоугольного параллелепипеда: |OM|²=|OM₁|²+|OM₂|²+|OM₃|²и |a|=; получим cos²a+cos²b+cos²g=1.

Условия коллинеарности двух векторов.

     Пусть вектор a=a_xi+a_yj+a_zk и b=b_xi+b_yj+b_zk коллинеарны. Тогда, a=λb. Но при умножении вектора на число его проекции на оси также умножаются на это число. Тогда, a_x=λb_x; a_y=λb_y; a_z=λb_z.
Верно и обратное.
Итак, для коллинеарности двух векторов необходимо и достаточно, чтобы их проекции были пропорциональны: a_x/b_x=a_y/b_y=a_z/b_z.
Постройте Самостоятельная работа 33. Вариант 2. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс
Постройте Самостоятельная работа 33. Вариант 2. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс
Интересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
На рисунке 13 изображены два вектора
Постройте вектор  двумя способами.

ответы
Дано:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Психология
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!

Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Использование векторов переноса для преобразования фигур — Криста Кинг Математика
Векторы перевода переводят фигуру из одного места в другое
В этом уроке мы рассмотрим, как использовать векторы перевода для перевода фигуры.
Вектор перемещения — это тип преобразования, который перемещает фигуру на координатной плоскости из одного места в другое. Другими словами, вектор перемещения можно рассматривать как слайд без вращения. Слайд не изменит форму или размер фигуры, а без поворота ориентация тоже не изменится.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Вектор смещения можно нарисовать на координатной сетке или записать как ???\vec{v}=\langle a,b\rangle???. Например, вектор переноса, который перемещает фигуру ???3??? единицы справа и ???2??? единицы вниз могут быть представлены математически как ???\vec{v}=\langle3,-2\rangle???, или графически как
Неважно, где расположен вектор на плоскости.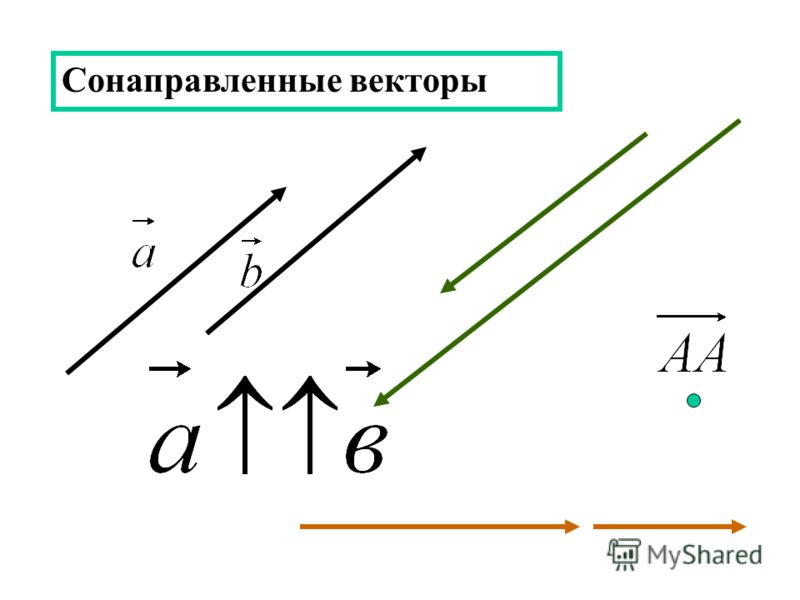 На этом рисунке вектор начинается с ???(1,1)??? и заканчивается на ???(4,-1)???. Но начальная точка и конечная точка вектора не имеют значения. Что имеет значение, так это длина вектора и направление, в котором он указывает, поэтому все, на что вам нужно смотреть, это на сколько единиц перемещается вектор в ???y???-направлении и на сколько единиц вектор перемещается в ???x???-направление.
Использование векторов переноса для преобразования фигур на плоскости
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Как использовать вектор смещения для перемещения треугольника в плоскости xy
Пример
Используйте показанный вектор смещения, чтобы найти координаты треугольника ???A’B’C’???.
Вектор указывает на перевод ???2??? единиц вправо и ???1??? единица вниз.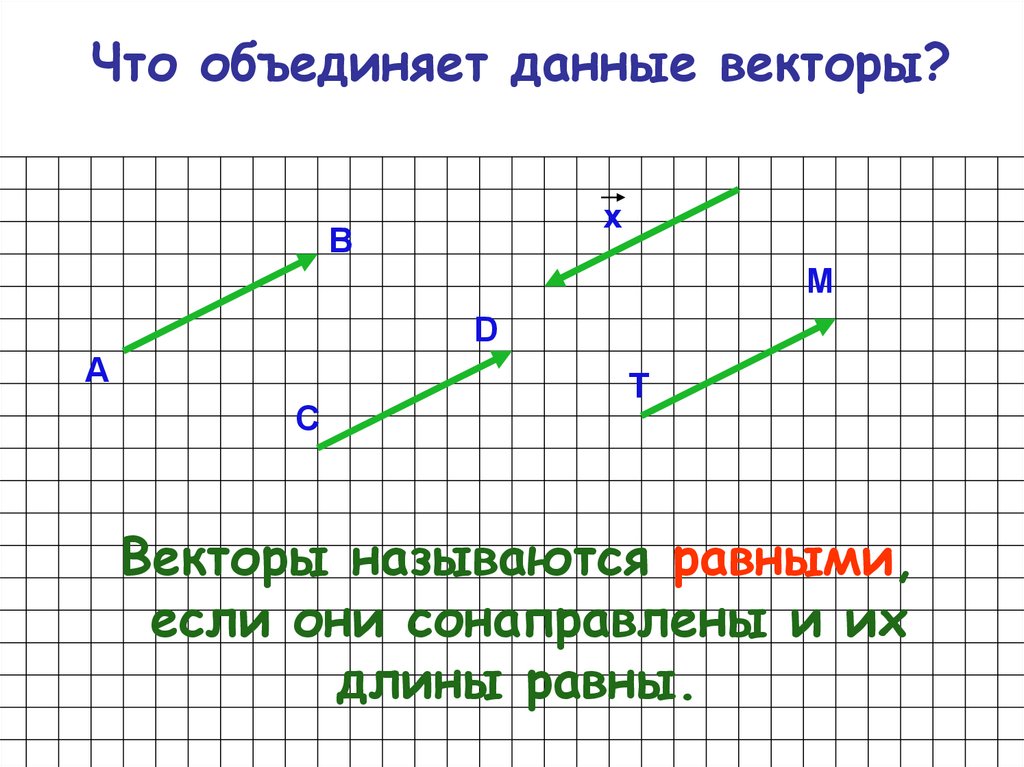 Поэтому мы можем добавить ???2??? ко всем ???x???-значениям и вычесть ???1??? из всех ???y???-значений найти вершины изображения.
Сначала запишем координаты прообраза, треугольника ???ABC???.
???А=(-3,2)???
???В=(-1,0)???
???С=(-2,-1)???
Теперь мы можем произвести вычисления для перемещения каждой вершины.
???A’=(-3+2,2-1)=(-1,1)???
???B’=(-1+2,0-1)=(1,-1)???
???C’=(-2+2,-1-1)=(0,-2)???
Изображение после перевода
начальная и конечная точки вектора перемещения не имеют значения. Важна длина вектора и направление, в котором он указывает.
Нахождение координат изображения по прообразу и вектору переноса
Пример
Треугольник ???ABC??? является прообразом с вершинами в точках ???A=(-5,5)???, ???B=(-2,5)??? и ???C=(-3,0)??? )???. Если треугольник переводится как ???\vec{v}=\langle -5,-6\rangle???, каковы координаты изображения?
Вектор переноса ???\vec{v}=\langle -5,-6\rangle??? означает, что каждая точка перемещается ???5??? единиц влево и ???6??? единиц вниз. Итак, из каждой вершины мы вычтем ???5??? из каждого ???x???-значения и вычесть ???6??? от каждого ???y???-значения.
Тогда вершины изображения
???A’=(-5-5,5-6)=(-10,-1)???
???B’=(-2-5,5-6)=(-7,-1)???
???C’=(-3-5,0-6)=(-8,-6)???
Получить доступ к полному курсу геометрии
Начать
Учиться математикеКриста Кинг 3 апреля 2019 математика, учиться онлайн, онлайн курс, онлайн математика, вектор перевода, перевод цифр, преобразования, геометрия, изображение, прообраз, начальная точка вектора, конечная точка вектора, вектор длина, направление вектора, направление вектора, перевод треугольников
0 лайков
Maths — Vectors — Martin Baker
Как и многие математические понятия, векторы можно понимать и исследовать по-разному.
Существует по крайней мере два способа просмотра векторов:
Алгебраический — Рассматривает вектор как набор скалярных значений как единое целое со сложением, вычитанием и скалярным умножением, которые работают со всем вектором.
Геометрический. Вектор представляет величину как по величине, так и по направлению.
Мы можем абстрагироваться от различий в этих подходах и просто посмотреть, что всегда верно для векторов, когда мы это делаем, мы получаем набор аксиом, обычно в форме уравнений. Примером аксиомы для векторов является «закон дистрибутивности»:
c(v ₁ + v ₂ ) = c v ₁ + c v ₂
, где v ₁ и v ₂ — векторы, а c — скаляр.
Эта аксиома важна, потому что она описывает линейное свойство векторов
Геометрические свойства
Вектор — это величина, имеющая как величину, так и направление, над векторами определены две операции, и обе они имеют очень прямую геометрическую интерпретацию. Мы рисуем вектор как линию со стрелкой, сейчас я буду называть конец без стрелки «началом» вектора, а конец со стрелкой — «концом» вектора.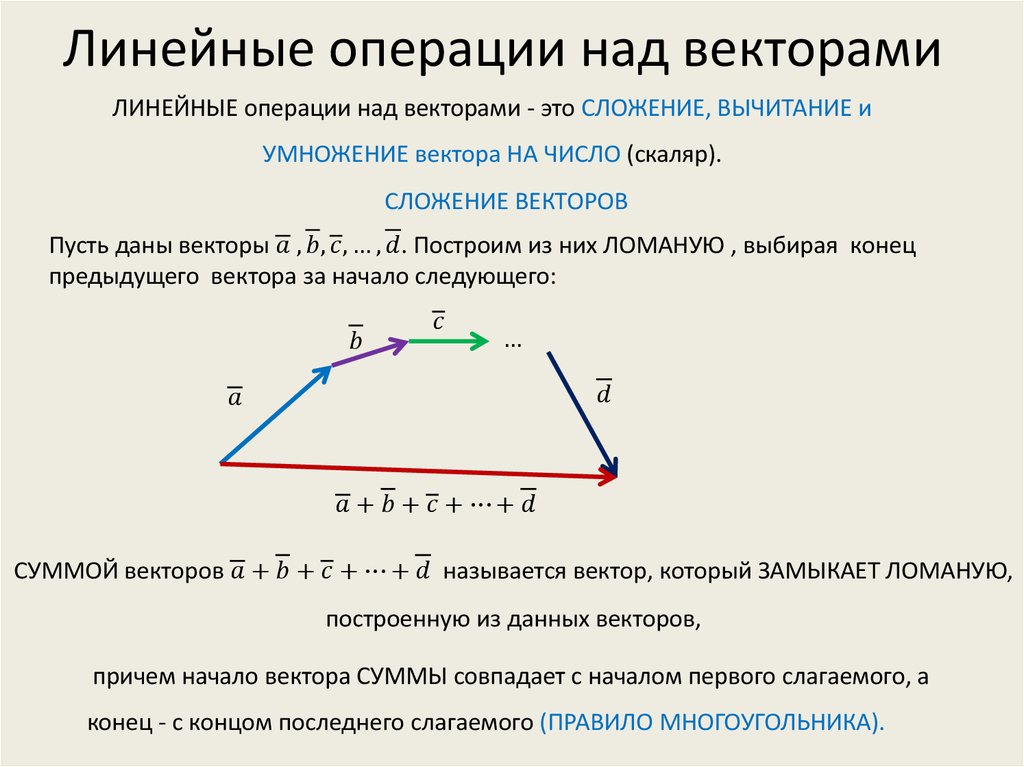
Сложение векторов: чтобы добавить два вектора, мы берем начало второго вектора и перемещаем его в конец первого вектора. Сложение этих двух векторов представляет собой вектор от начала первого вектора до конца второго вектора.
Скалярное умножение изменяет длину вектора без изменения его направления. То есть мы «масштабируем» его на коэффициент умножения. Таким образом, скалярное умножение включает в себя умножение скаляра (одного числа) на вектор, чтобы получить другое число.
Эти две операции: сложение векторов и скалярное умножение можно рассматривать как определение линейного пространства (см. Евклидово пространство).
Так как же нам получить векторы? Мы могли бы принять уже существующую систему координат и определить все наши векторы в этой системе координат, или мы могли бы начать с набора базисных векторов и представить векторы как линейную комбинацию этих базисных векторов, то есть путем скалярного умножения и сложения базисными векторами мы можем создать любой вектор в пространстве при условии, что:
Базисных векторов столько, сколько измерений в пространстве.
Все базисные векторы независимы (не более двух в любой заданной плоскости).
Таким образом, любая точка может быть идентифицирована как:
α V _a + β V _b
где:
α, β = скалярные множители
V _a , V _b = базисные векторы.
Таким образом, два скалярных множителя (α, β) могут представлять положение точки в терминах наших базисных векторов. Это приводит к способу работы с векторами чисто алгебраическим способом.
Алгебраические свойства
Алгебраический подход и его операции объясняются на этой странице, поэтому здесь мы дадим только обзор.
Мы можем думать о векторе как о концепции массива в языке программирования, например,
Векторы имеют размер, равный количеству элементов в массиве.
Все элементы вектора должны быть одного типа.
5,6
9. 3
3,5
7,0
Вектор может отображаться в виде одного столбца
8,4 1,8 5,5 6,2
или как ряд
Однако есть отличие от компьютерного массива, поскольку в случае компьютера элементы массива могут быть любыми допустимыми объектами при условии, что все они одного типа. В случае векторов элементы должны обладать определенными математическими свойствами, в частности, над ними должны быть определены операции сложения и умножения с определенными свойствами. Требуемые свойства элементов вектора заключаются в том, что они должны образовывать математическую структуру, известную как поле (см. рамку справа). В математической терминологии это называется вектором над полем, другими словами, вектором, элементами которого являются поля.
90 102 В(а+б) = В(а) + В(б)
операция обозначение объяснение
дополнение сложение двух векторов выполняется путем сложения соответствующих элементов двух векторов.
скалярное умножение В(с*а) = с * В(а) скалярное произведение вектора получается путем умножения скалярного произведения на каждый из его членов в отдельности.
Эти операции взаимодействуют в соответствии со свойством дистрибутивности:
s*(b+c)=s*b+s*c
Что придает векторам свойство линейности. Теперь мы можем составить набор аксиом для векторов:
аксиома дополнение скалярное умножение
ассоциативность (а+б)+с=а+(б+с) (s1 s2) а = s1 (s2 а)
коммутативность а+б=б+а
распределительность с*(б+с)=с*б+с*к
(с1+с2)*а=с1*а+с2*а
тождество а+0 = а
0+а = а 1 а = а
обратные а+(-а) = 0
(-а)+а = 0
Где:
a,b,c — векторы
0 — тождественный вектор
s,s1,s2 являются скалярами
1 — это скаляр тождества
.
Сравните это с аксиомами для поля (на этой странице)
Векторы также могут иметь дополнительную структуру, определяемую в терминах других определенных для них умножений, таких как точечные и перекрестные произведения, как мы увидим позже. Это необязательно, единственными обязательными операциями являются сложение и скалярное умножение.
Vector Notation
До сих пор мы показывали вектор как набор значений в сетке, поскольку это более удобно на веб-странице html, но обычная запись вектора заключается в заключении значений в квадратные скобки:
Где:
x = компонент в измерении x.
y = компонент в измерении y.
z = компонент в z-измерении.
Иногда, когда мы представляем весь вектор в виде символа, мы можем поместить стрелку над символом (в данном случае v ), чтобы подчеркнуть, что это вектор.
Или в качестве альтернативы мы можем использовать следующие обозначения:
= a ₁ x + a ₂ y + a ₃ z
Где:
x = единичный вектор в размерности.
y = единичный вектор в измерении y.
z = единичный вектор в z-измерении.
Первая форма более удобна при работе с матрицами, тогда как вторая форме легче писать в текстовом виде.
Здесь «x», «y» и «z» — операторы, их часто можно использовать в уравнениях аналогично переменным, но они могут иметь разные законы (например, умножение может не коммутировать). Это может быть удобным способом кодирования законов объединения векторов в обычной алгебре.
Связь с другими математическими величинами
Мы можем расширить концепцию векторов (обычно путем добавления дополнительных типов умножения к встроенным сложению и скалярному умножению), чтобы сформировать более сложные математические структуры, в качестве альтернативы мы могли бы думать о векторах как подмножества этих структур, например:
Как подмножество матрицы или тензора (матрица 1 на n или n на 1). Матрица — это двумерный массив со скалярным произведением.
Как подмножество мультивекторов (алгебра Клиффорда). Например, комплексные числа представляют собой два вектора элементов с добавленным типом умножения.
Чего мы не можем сделать, так это иметь вектор, элементы которого сами являются векторами. Это связано с тем, что элементы вектора должны быть математической структурой, известной как «поле», а вектор сам по себе не является полем, поскольку он не обязательно обладает коммутативным умножением и другими свойствами, необходимыми для поля.
Тем не менее было бы неплохо, если бы мы могли построить матрицу из вектора (нарисованного в виде столбца), элементы которого сами являются векторами (нарисованными в виде строки):
6 1 7 5
8 4 4 2
2 0 6 9
1 3 0 3
Чтобы создать матрицу путем составления векторных структур, нам нужно сделать две вещи с «внутренним вектором»:
Нам нужно транспонировать так, чтобы это была строка, а не столбец.
Нам нужна операция умножения, которая сделает это поле.
Для этого мы создаем «двойник» вектора, это называется ковектором, как описано на этой странице.
Векторы можно умножать на скаляры, даже если они являются отдельными объектами, например, нельзя складывать векторы и скаляры (пока мы не дойдем до алгебры Клиффорда), но мы можем определить тип умножения, называемый скалярным умножением, обычно обозначаемый ‘ *’ или скаляр может быть записан рядом с вектором с подразумеваемым умножением. Этот тип умножения принимает один вектор и один скаляр. Скалярное умножение умножает величину вектора, но не меняет его направление, поэтому:
если есть,
vOut = 2*vIn
где:
vOut и vIn — векторы
тогда vOut будет в два раза больше vIn, но в том же направлении.
Квадратичная структура на линейном пространстве
Однако этих линейных свойств самих по себе недостаточно, чтобы определить свойства евклидова пространства, используя только алгебру. Чтобы определить такие понятия, как расстояние и угол, мы должны определить квадратичную структуру.
For instance pythagoras:
r ² = x ² + y ² + z ²
in algebraic terms,
if a is a three dimensional vector with bases e ₁ , _{e ₂ , _{e ₃}}
a = a ₁ e ₁ + a ₂ e ₂ + a ₃ e ₃
so,
a•a = а ₁ ² + а ₂ ² + a ₃ ²
Другие векторные алгебры
В уже обсуждавшейся векторной алгебре квадрат вектора всегда является положительным числом:
a x a = 0
a • a = положительное скалярное число
Однако мы могли бы определить столь же правильную и непротиворечивую векторную алгебру, которая возводит в квадрат отрицательное число:
a × a = 0
a • a = отрицательное скалярное число
Мы могли бы также определить алгебру, в которой мы смешиваем измерения, некоторые квадратные с положительными, некоторые квадратные с отрицательными. Примером этого является эйнштейновское пространство-время, пространство и время возводятся в квадрат к разным значениям, если пространство возводится в квадрат к положительному, то квадрат времени к отрицательному и наоборот.
Применение векторов
Для 3D-программирования (тема этого сайта) мы в основном заинтересованы с векторами из 2 или 3 чисел.
Вектор размерности 3 может представлять физическую величину, направленную такие как должность, скорость, ускорение, сила, импульс, и т. д.
Например, если вектор представляет точку в пространстве, эти 3 числа представляют положение в координатах x, y и z (см. системы координат). Где x, y и z — взаимно перпендикулярные оси в некоторые согласованные направления и подразделения.
Трехмерный вектор может также представлять смещение в пространстве, например перевод в каком-либо направлении. В случае библиотеки Java Vecmath эти два класса: Point3f и Vector3f, оба производные от Tuple3f. (Обратите внимание на эти использовать числа с плавающей запятой, есть также классы, оканчивающиеся на d, которые содержат двойные значения). Класс Point3f используется для представления абсолютных точек и Класс Vector3f представляет смещение. В большинстве случаев поведение этих классы одинаковые, насколько я знаю разница между этими классами при их преобразовании матрицей Point3f будет преобразован матрицей но Vector3f не будет.
Здесь мы разрабатываем следующие классы для хранения вектора и инкапсуляции операции, описанные здесь,
sfvec2f для 2D-векторов
sfvec3f для 3D-векторов
Можно было бы создать векторный класс, который мог бы содержать вектор любого размерность, но класс переменной размерности был бы менее эффективным. Так как мы при работе с объектами в 3D-пространстве важнее работать с 2D и 3D векторы эффективно.
Другие векторные величины
Нормали
Лучи
Альтернативная интерпретация векторов
До сих пор мы думали о векторе как о положении на 2,3- или n-мерном пространстве.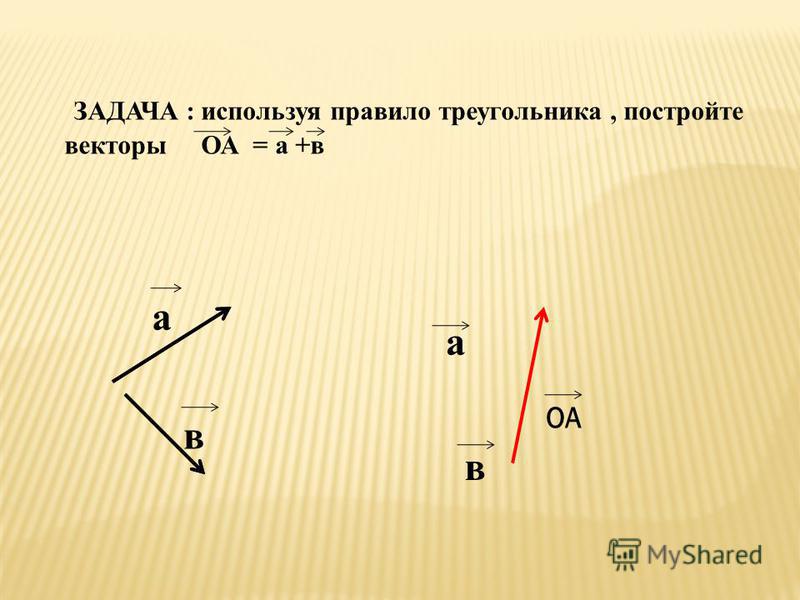 сетка. Однако для некоторых физических ситуаций может не быть готового определенного Декартова система координат. Альтернативой может быть представление вектора как линейная комбинация 3 базисов:
σ ₁
о ₂
σ ₃
Эти основания не обязательно должны быть взаимно перпендикулярны (хотя в большинстве случаев они, вероятно, будут) однако они должны быть независимы друг от друга, другими словами, они не должны быть параллельны друг другу и все 3 не должны находиться в одной плоскости.
Таким образом, трехмерный вектор может быть представлен как [a,b,c], где a,b и c представляют масштабирование по 3 основе сделать вектор следующим:
а о ₁ + б σ ₂ + c σ ₃
Обратите внимание, что если этот вектор представляет положение, то это будет относительное положение, то есть относительно какой-либо другой точки, если мы хотим определить абсолютную точку, мы еще нужно определить происхождение.
Таким образом, проблема остается в том, как определить базис, может быть некоторые естественные их определение в проблемной области. В качестве альтернативы мы могли бы определить базируются как трехмерные векторы с использованием системы координат. Но зачем заморачиваться сделать это, если у нас есть система координат, почему бы просто не представить векторы в эта система координат? Ну, мы можем захотеть изменить систему координат или перевести все векторы каким-то образом (см. здесь). Например, мы можем захотеть представить точки на твердом объекте в некотором локальном системе координат, но сам твердый объект может двигаться относительно некоторой абсолютная система координат.
Дополнительная литература
Векторами можно управлять с помощью матриц, для Пример переведен, повернут, масштабирован, отражен.
Существуют математические объекты, известные как мультивекторы, их можно использовать для выполнения многих задач, которые выполняют векторы, но у них нет некоторые ограничения (например, векторное перекрестное произведение ограничено 3 измерениями и не имеет обратного).
No related posts.