Найти синус угла | Calculators.vip
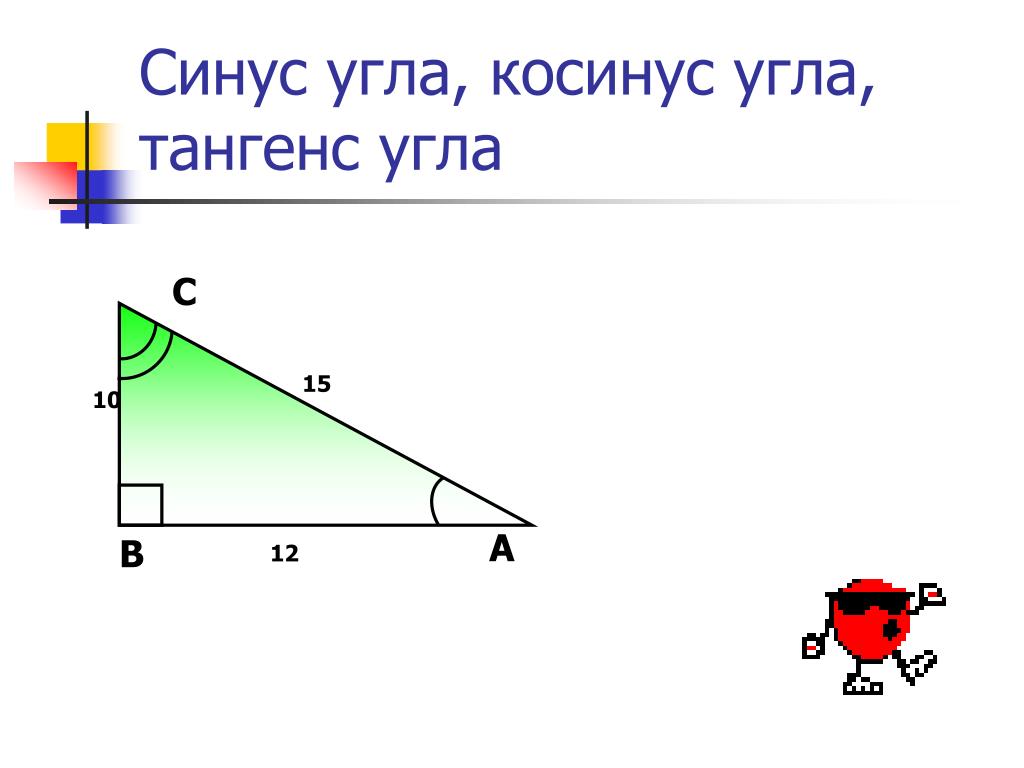
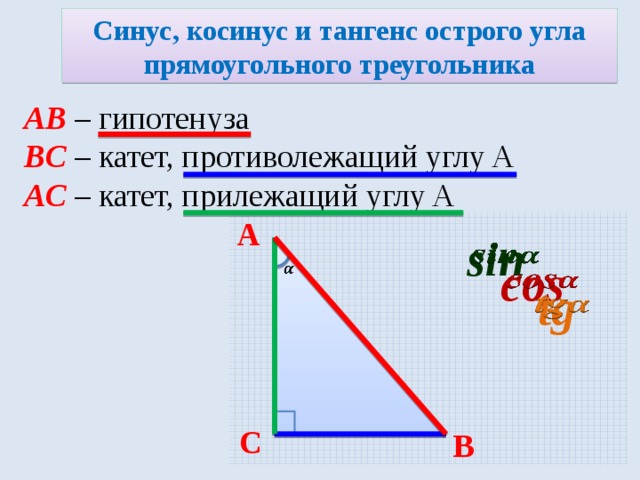
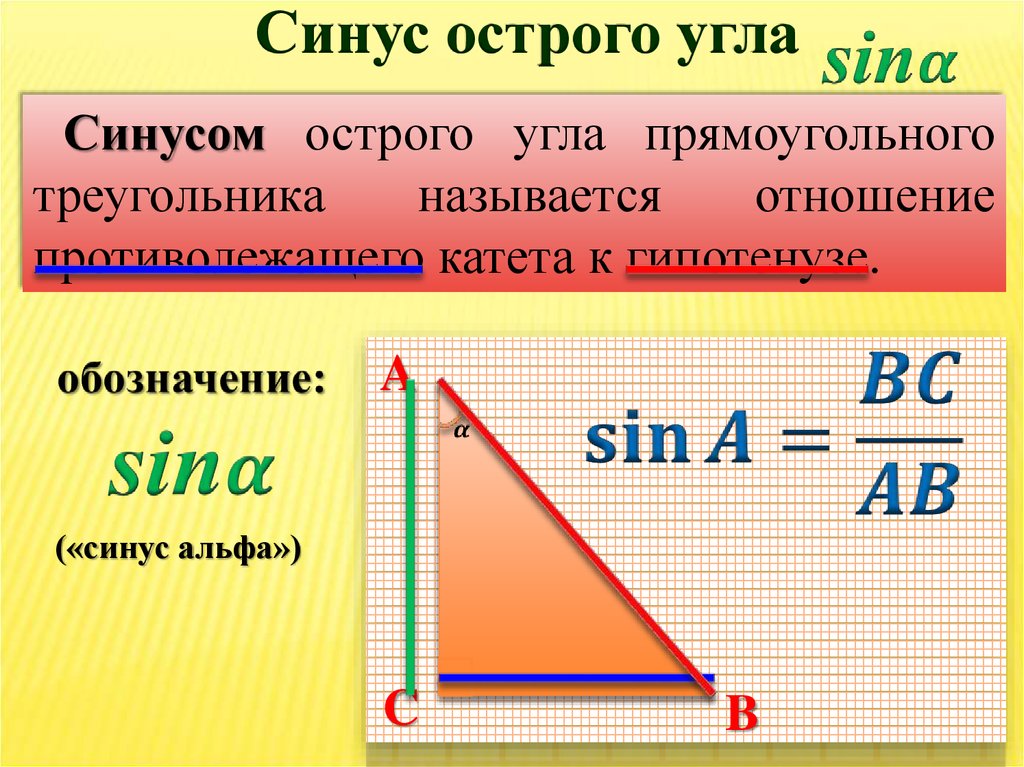
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
.
Поделиться расчетом:
Найти величину
X=SIN(A)X=COS(A)X=TAN(A)X=CTN(A)
A=ARC SIN(X)A=ARC COS(A)A=ARC TAN(X)A=ARC CTN(X)
Первоначальные данные
Градус
Радиан
Вычислить
| 0° до 15° | 16° до 31° | 32° до 45° |
|---|---|---|
| sin(0°) = 0 | sin(16°) = 0.275637 | sin(32°) = 0.529919 |
| sin(1°) = 0.017452 | sin(17°) = 0.292372 | sin(33°) = 0.544639 |
| sin(2°) = 0.034899 | sin(18°) = 0.309017 | sin(34°) = 0.559193 |
| sin(3°) = 0.052336 | sin(19°) = 0.325568 | sin(35°) = 0.573576 |
| sin(4°) = 0.069756 | sin(20°) = 0. 34202 | sin(36°) = 0.587785 |
| sin(5°) = 0.087156 | sin(21°) = 0.358368 | sin(37°) = 0.601815 |
| sin(6°) = 0.104528 | sin(22°) = 0.374607 | sin(38°) = 0.615661 |
| sin(7°) = 0.121869 | sin(23°) = 0.390731 | sin(39°) = 0.62932 |
| sin(8°) = 0.139173 | sin(24°) = 0.406737 | sin(40°) = 0.642788 |
| sin(9°) = 0.156434 | sin(25°) = 0.422618 | sin(41°) = 0.656059 |
| sin(10°) = 0.173648 | sin(26°) = 0.438371 | sin(42°) = 0.669131 |
| sin(11°) = 0.190809 | sin(27°) = 0.45399 | sin(43°) = 0.681998 |
| sin(12°) = 0.207912 | sin(28°) = 0.469472 | sin(44°) = 0.694658 |
| sin(13°) = 0.224951 | sin(29°) = 0.48481 | sin(45°) = 0.707107 |
| sin(14°) = 0.241922 | sin(30°) = 0.5 | |
| sin(15°) = 0.258819 | sin(31°) = 0.515038 |
| 46° до 60° | 61° до 75° | 76° до 90° |
|---|---|---|
sin(46°) = 0.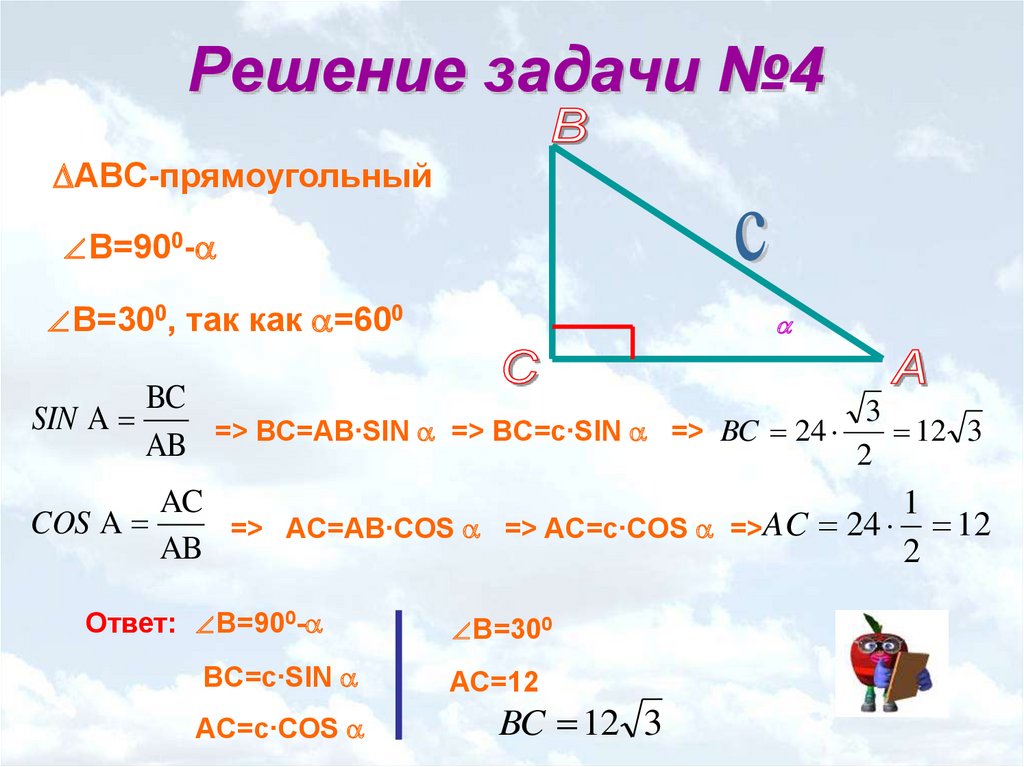 71934 | sin(61°) = 0.87462 | sin(76°) = 0.970296 |
| sin(47°) = 0.731354 | sin(62°) = 0.882948 | sin(77°) = 0.97437 |
| sin(48°) = 0.743145 | sin(63°) = 0.891007 | sin(78°) = 0.978148 |
| sin(49°) = 0.75471 | sin(64°) = 0.898794 | sin(79°) = 0.981627 |
| sin(50°) = 0.766044 | sin(65°) = 0.906308 | sin(80°) = 0.984808 |
| sin(51°) = 0.777146 | sin(66°) = 0.913545 | sin(81°) = 0.987688 |
| sin(52°) = 0.788011 | sin(67°) = 0.920505 | sin(82°) = 0.990268 |
| sin(53°) = 0.798636 | sin(68°) = 0.927184 | sin(83°) = 0.992546 |
| sin(54°) = 0.809017 | sin(69°) = 0.93358 | sin(84°) = 0.994522 |
| sin(55°) = 0.819152 | sin(70°) = 0.939693 | sin(85°) = 0.996195 |
| sin(56°) = 0.829038 | sin(71°) = 0.945519 | sin(86°) = 0.997564 |
sin(57°) = 0.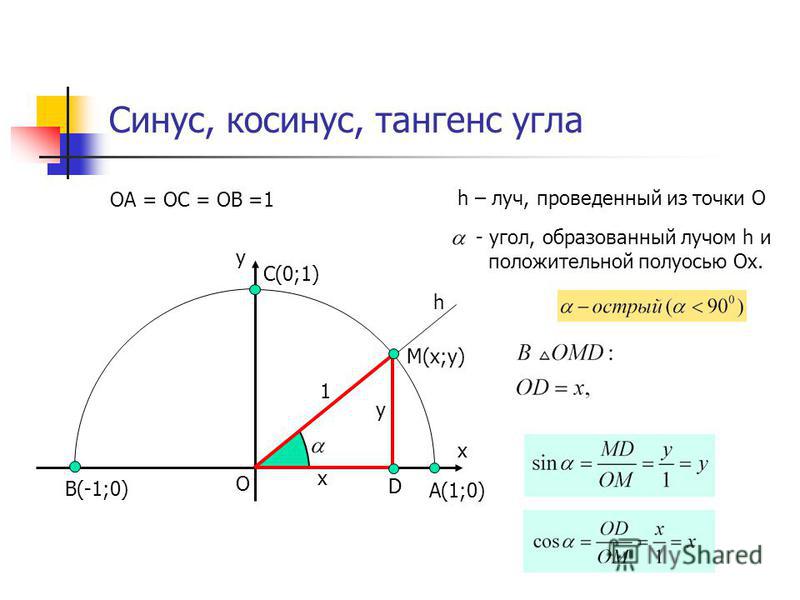 838671 | sin(72°) = 0.951057 | sin(87°) = 0.99863 |
| sin(58°) = 0.848048 | sin(73°) = 0.956305 | sin(88°) = 0.999391 |
| sin(59°) = 0.857167 | sin(74°) = 0.961262 | sin(89°) = 0.999848 |
| sin(60°) = 0.866025 | sin(75°) = 0.965926 | sin(90°) = 1 |
Калькулятор Синусов — Как Найти Синус Угла
Онлайн-калькулятор синусов определит тригнометрические значения синуса для заданного угла в градусах, радианах или π радианах.
Просто найдите время, чтобы узнать, как найти грех, как нарисовать синусоидальный график для представления синусоидальной кривой и многое другое, что поможет вам в решении тригонометрических функций, связанных с синусом.
Что такое грех в математике?В математике функция синуса определяется в виде прямоугольного треугольника. Для выбранного угла это отношение длины стороны, противоположной этому углу, и гипотенузы.
Формула синуса:- Формула синуса: sin (α) = противоположная точка a / гипотенуза c
Однако для решения в калькуляторе синусов нет необходимости вводить формулу, просто введите соответствующие значения.
Кроме того, онлайн-калькулятор CSC позволяет вам найти тригонометрическую функцию косеканса (csc) для введенного угла в градусах, радианах или π радианах.
Как найти синус угла?Синус угла α в прямоугольном треугольнике может быть представлен отношением между противоположной стороной угла и его гипотенузой. Однако вы можете использовать следующую формулу для вычисления греха угла и использовать калькулятор синусов для быстрых и простых вычислений:
Синус (α) = a / c
Пример:
Если длина противоположной стороны угла равна 10, а гипотенуза равна 2, то значение синусоидальной функции можно рассчитать следующим образом:
- грех (α) = 10/6 = 5/2
Синусоидальный график для каждого возможного угла будет иметь повторяющуюся кривую вверх / вниз, известную как синусоида. Синусоидальная кривая начинается с угла 0, затем возрастает до значения 1, а затем уменьшается до значения -1.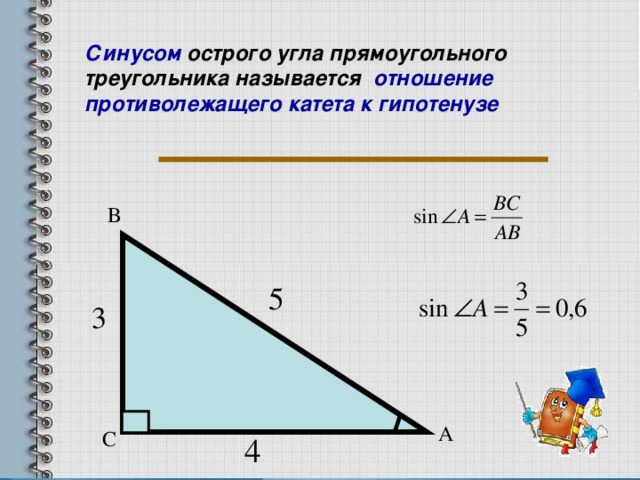
Затем будет продолжаться та же схема, как показано ниже:
Значения синуса для некоторых распространенных углов показаны в следующей таблице:
| Градусы ° | Радианы | синус (х) |
| 0° | 0 | 0 |
| 30° | π/6 | 0.50 |
| 45° | π/4 | 0.707107 |
| 60° | π/3 | 0.866025 |
| 90° | π/2 | 1 |
| 120° | 2π/3 | 0.866025 |
| 135° | 3π/4 | 0.707107 |
| 150° | 5π/6 | 0.50 |
| 180° | π | 0 |
Кроме того, онлайн-калькулятор Arcsin поможет вам вычислить arcsin (x) и отобразить результаты в радианах и градусах.
Как работает калькулятор синусов?Этот калькулятор синусоид функционировал автоматически, следуя уравнению синуса, и выдает значение синуса в мгновение ока для любого угла.
Его рабочий процесс объясняется ниже:
- На первом шаге введите значение ангела
- Выберите градус, радиан или (π) радиан из выпадающего меню в соответствии с вашими требованиями.
- Нажмите кнопку «рассчитать».
Этот калькулятор синусов определит:
- Значение синуса в радианах, градусах или пи (π) радианах в зависимости от требуемого угла.
- Сделайте еще один расчет, нажав на опцию «пересчитать».
Мотив синуса и косинуса состоит в том, чтобы решить треугольник, чтобы определить длину каждой из его сторон и всех его углов. Мы применим синусоидальную функцию, когда есть два угла и одна сторона. С другой стороны, функция косинуса будет применяться, когда даны три стороны или две стороны с включенным углом.
Почему синус называется синусом?Слово «синус» происходит из латинского языка и придумано Робертом Честерским из арабского jiba, что является преобразованием санскритского слова jya-ardha.
Нет, функция синуса не является взаимно однозначной. когда нам нужно определить обратные функции для синуса, области ограничены 0 ≤ x ≤ π.
Синус – нечетная функция?Да, синус – нечетная функция, однако большинство функций в тригонометрии не являются ни нечетными, ни четными, но некоторые функции являются теми или иными. Однако наиболее удобный способ обработки синусоидальной функции – это использование калькулятора синусов.
Заключение:К счастью, этот калькулятор синусов позволит студентам и профессионалам работать со сложными углами и размерами за относительно короткое время. Нет необходимости запоминать тригонометрическое синусоидальное уравнение, просто введите значение, и инструмент произведет точные вычисления.
Использованная литература:Из источника Википедии: Прямоугольный треугольник, Бегущие и стоячие волны, Закон синусов.
Из источника Lumen Learning: графические вариации sin (x), исследование синусоидальных функций, определение амплитуды, вертикальный сдвиг функции.
Из источника Varsity Tutors: функция синуса, графическая функция синуса, амплитуда и период функции Since.
Other Languages: Sine Calculator, kalkulator sinus, Kalkulator Sinus, Sinüs Hesaplama, Sinus Rechner, Sin 計算, Sinus Kalkulačka, Calcular Seno, Calcular Seno, Calcul Sinus, Calcolo Del Seno.
Math Scene — Тригонометрия синуса, косинуса и тангенса
Math Scene — Тригонометрия синуса, косинуса и тангенса — Урок 1 2008 Расмус Эхф | Печать |
Урок 1
ABC — прямоугольный треугольник
Угол А
составляет 30 градусов.
|
Мы пишем это как:а – это символ стороны, противоположной углу A
b — это символ стороны, противоположной углу B
c – это символ стороны, противоположной углу C
Подобные треугольники треугольники, у которых все углы одного треугольника равны углам другого другой треугольник
Эти два треугольника похожи. Отношение двух сторон в одном треугольнике равно отношение соответствующих сторон другого треугольника. |
Использование обозначений в приведенных выше треугольниках получаем следующее:
Коэффициент зависит на величину угла.
Тангенс
Отношение, называемое тангенсом (tan)
острого угла в прямоугольном треугольнике определяется как отношение
между стороной, противоположной углу, и стороной, прилегающей к углу. |
Пример 1 Найти угол А
Первый Тан А = 3 / 4 = 0,75 |
Нам нужно используйте обратную функцию для tan, tan -1 , найти угол. Эта функция находится на той же клавише калькулятора, что и загар. функция (сменный загар).
Мы используем следующая последовательность команд:
сдвиг — желто-коричневый -1 0,75 = 37
Попробуйте следующее на калькуляторе, чтобы увидеть разницу между загаром и загаром -1 :
желто-коричневый 37 = 0,75 tan -1 0,75 = 37
Пример 2 Найти боковая б
тан 37 = 4 / б тан 37 б = 4 0,75 б = 4 б=5,3 |
Старший
Синус (грех)
острый угол прямоугольного треугольника – это отношение
сторона, противоположная углу и гипотенузе треугольника. |
Пример 3 Найдите угол А, дающий ответ с точностью до градуса.
sin A = 3 / 5 = 0,6 дает <А = 37 Сдвиг sin -1 0,6 = 37 |
Пример 4 Найдите сторону а.
грех 37 = a / 5 а = Грех 37 5 а = 3 |
Косинус
Косинус (cos) острый угол в прямоугольном треугольнике — это отношение стороны рядом с углом и гипотенузой треугольника. |
Пример 5 Используйте функцию косинуса, чтобы найти угол A, дающий ответ на ближайший угол.
cos A = 4 / 5 = 0,8 дает Сдвиг cos -1 0,8 = 37 |
Пример 6 Найдите сторону б.
соз 37 = б / 5 б = Кос 37 5 б = 4 |
некоторые значения для sin, cos и tan.
| грех 80 = 0,98 | кос 80 = 0,17 | желтовато-коричневый 80 = 5,67 |
| грех 60 = 0,87 | соз 60 = 0,5 | желтовато-коричневый 60 = 1,73 |
| грех 30 = 0,5 | кос 30 = 0,87 | желтовато-коричневый 30 = 0,58 |
| грех 10 = 0,17 | соз 10 = 0,98 | желтовато-коричневый 10 = 0,18 |
Практикуйте эти методы, а затем
викторина по тригонометрии 1 (грех, косинус и загар).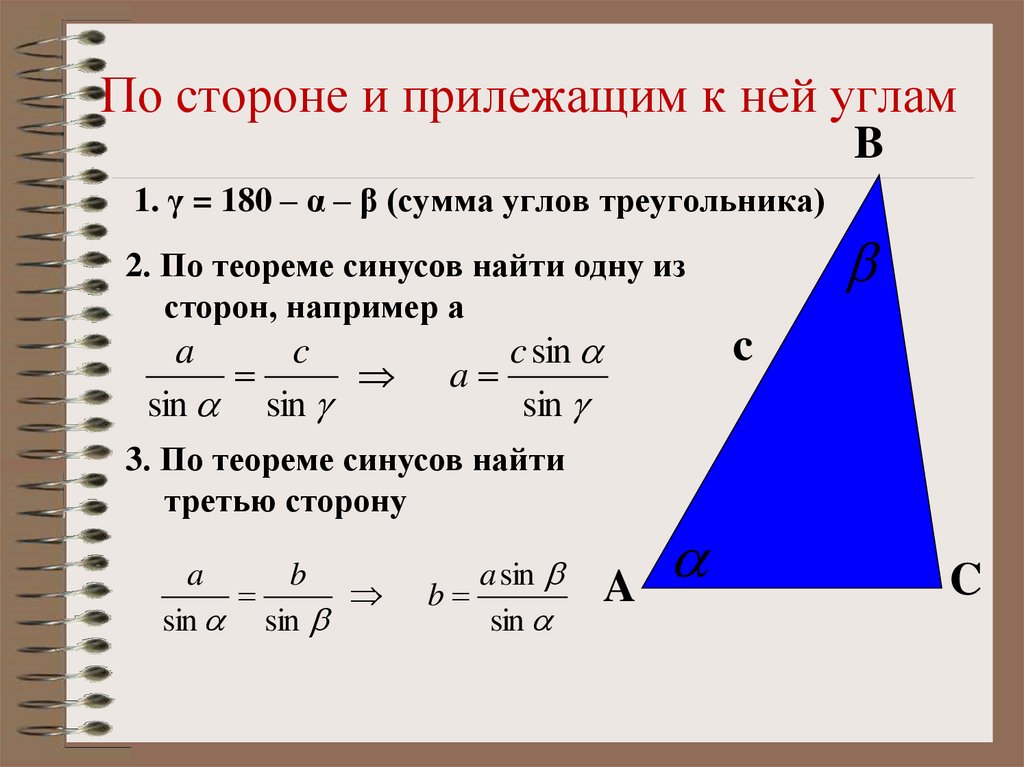
Как найти синус угла
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Справка по математике ACT » Тригонометрия » Синус » Как найти синус угла
Что такое синус?
Возможные ответы:
Правильный ответ:
Синус можно найти с помощью метода SOH CAH TOA. Для синуса делаем.
Сообщить об ошибке
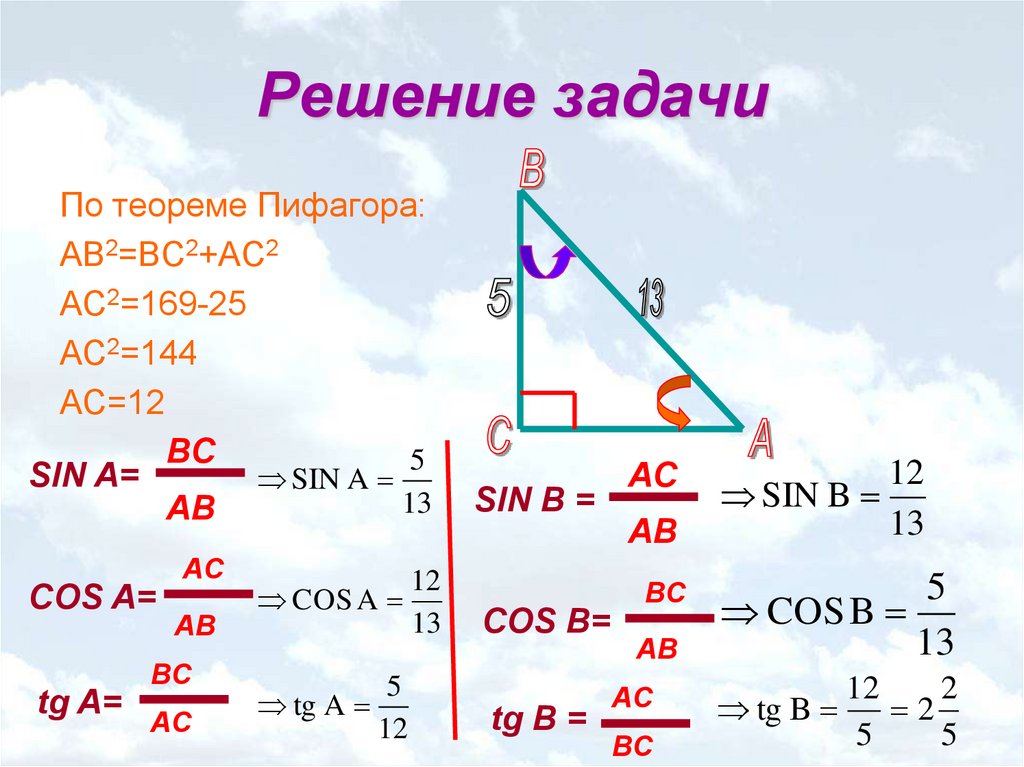
См. прямоугольный треугольник ABC. Чему равен синус угла А, если длина АВ равна 8, а длина ВС равна 6?
Возможные ответы:
0,6
0,8
6
1
10
Объяснение: Синус A = Противоположный / Гипотенуза = BC / AC Чтобы найти AC, используйте Pythagorean Theorum AB 2 + BC 2 = AC 2 64 + 36 = АС 2 100 = AC 2 AC = 10 Синус A = BC / AC = 6 / 10 = 0,6 Возможно Ответы: Q = 3π или не существует 2 Q = π или 3π 2 2 Q = π или 2π Q = π или не существует 2 5 Q = Объяснение: Подставьте x = sinQ и решите новое уравнение x 2 + 3x = –2 с помощью факторизации. Сообщить об ошибке Если , , и , чему равен синус ? Возможные ответы: Правильный ответ: Напомним, что sin = противоположность / гипотенуза. Исходя из показанного рисунка, мы видим, что необходима противоположная сторона и является гипотенузой. Подставьте эти значения для решения. Сообщить об ошибке Показанный треугольник является прямоугольным. Если прямая и прямая, чему равен синус угла при ? Возможные ответы: Правильный ответ: Объяснение: Теперь найдите , используя теорему Пифагора: Сообщите об ошибке 90, если 0 равно 90, угол между и градусами, что из следующего равно ? Возможные ответы: Правильный ответ: Объяснение: Угол между и градусами означает, что угол находится во втором квадранте. Функция тангенса получается путем деления стороны, противоположной углу, на сторону, прилегающую к углу (как показано на рисунке). Следовательно, длина стороны равна единицам длины, а сторона равна единицам высоты. Следовательно, согласно правилам теоремы Пифагора, длина стороны должна быть равна единицам (поскольку ). Функция синуса положительна во втором квадранте. Он также эквивалентен стороне, противоположной углу (), деленной на гипотенузу (). Получается . Сообщить об ошибке Синусоидальная функция имеет период , точку пересечения , амплитуду и не имеет фазового сдвига. Они описывают, какое из этих уравнений? Возможные ответы: Правильный ответ: Объяснение: Глядя на эту форму синуса: Мы можем сделать следующие выводы: Правильный ответ: 9032 6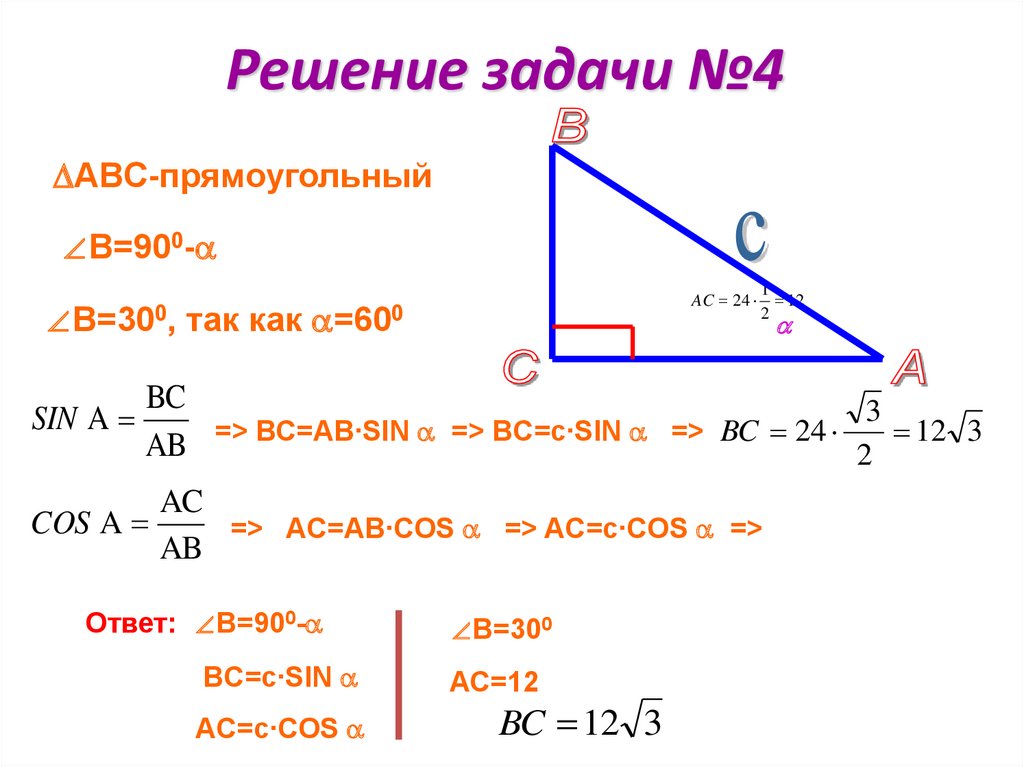 
Обязательно измените переменные обратно на Q. В результате sinQ = –1 или sinQ = –2. Эта функция ограничена между –1 и 1, поэтому sinQ никогда не может быть –2, а sinQ равен –1 только при 3π/2 или 270°.
