Показать что тройка векторов образуют базис: векторная-алгебра / Как доказать, что вектора образуют базис? / Математика

Базис и система координат пространства



Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.

Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.

И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов!

Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)

Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не создают.

Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).

Определение: векторы называются компланарными

, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.

Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы  мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы  не коллинеарны, то третий вектор выражается через них единственным образом:  (почему?).

Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга.

И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.

Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису , где  – координаты вектора  в этом базисе. Также говорят, что вектор  представлен в виде линейной комбинации базисных векторов.

Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно независимых векторов:

Выбранное (где угодно) начало координат , и некомпланарные векторы , взятые в определённом порядке

, задают аффинную систему координаттрёхмерного пространства:

Наиболее привычным и удобным частным случаем аффинной системы координаявляется «школьная» система. Начало координат  и ортонормированный базис  задают декартову прямоугольную систему координат пространства:

Ось абсцисс  изображают под углом в  по отношению к другим осям (к оси ординат  и оси аппликат ). Популярный «тетрадный» масштаб: 1 ед. = 2 клетки по осям  и

1 ед. = диагональ одной клетки – по оси .

И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию:

Для трёх векторов пространства эквиваленты следующие утверждения:

1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.

Противоположные высказывания, думаю, понятны.

Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём орудовать бейсбольной битой линейной алгебры:

Три вектора пространства  компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: .

Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.

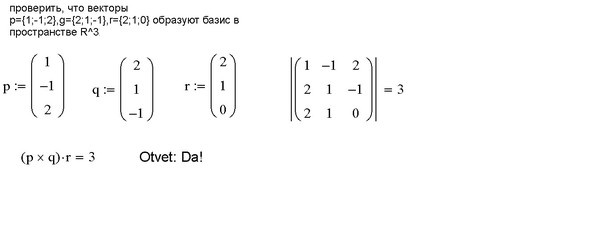
Задача 42

Проверить, образуют ли векторы базис трёхмерного пространства:

а)

б)

Фактически всё решение сводится к вычислению определителей:

а) Вычислим определитель, составленный из координат векторов  

(определитель раскрыт по первой строке):
 
, значит, векторы  линейно независимы (не компланарны) и образуют базис трёхмерного пространства.

Ответ: данные векторы образуют базис.

б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к книге Алгебраический Калькулятор.

Решим творческую задачку:

Задача 43

При каком значении параметра  векторы  будут компланарны?

Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:

По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке:

Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:

Ответ: при

Здесь легко выполнить проверку, для этого нужно подставить полученное значение  в исходный определитель и убедиться, что , раскрыв его заново.

И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и геометрии:

Задача 44

Даны векторы . Показать, что векторы  образуют базис трехмерного пространства и найти координаты вектора  в этом базисе.

Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора  вполне могут образовывать свой базис. И первый этап полностью совпадает с решением Задачи 42 – необходимо проверить, действительно ли векторы  линейно независимы. Для этого нужно вычислить определитель, составленный из координат векторов :

, значит, векторы  линейно независимы и образуют базис трехмерного пространства.

! Важно: координаты векторов  обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.

Теперь вспомним теоретическую часть: если векторы  образуют базис, то любой вектор  можно единственным способом разложить по данному базису: , где  – координаты вектора  в базисе .

Поскольку наши векторы  образуют базис трёхмерного пространства (это уже доказано), то вектор  можно единственным образом разложить по данному базису:
, где  – координаты вектора  в базисе .

И по условию требуется найти координаты .

Для удобства объяснения поменяю части местами: . В целях нахождения  следует расписать данное равенство покоординатно:
 – коэффициенты левой части берём из опр-ля ,
в правую часть записываем координаты вектора .

Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.

Главный определитель системы уже найден:
, значит, система имеет единственное решение.

Дальнейшее дело техники:


и ещё один определитель:

Таким образом:
 – разложение вектора  по базису .

Ответ:

Такая же задача для самостоятельного решения:

Задача 45

Даны векторы . Показать, что векторы  образуют базис и найти координаты вектора  в этом базисе. Систему линейных уравнений решить методом Крамера.

Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.

1.9.1. Векторное произведение векторов. Определение и его смысл

1.8.3. Как определить коллинеарность векторов пространства?

| Оглавление |



Автор: Aлeксaндр Eмeлин

2.2 Базис и координаты на прямой, плоскости и в пространстве

Пусть на плоскости задан ненулевой вектор , тогда для любого вектора , лежащего на этой же прямой, существует единственное вещественное число , такое, что

, (1)

При этом называют базисным вектором, – координатой относительно базиса .

Если на плоскости заданы два ненулевых, неколлинеарных вектора и , то для любого вектора , лежащего в этой же плоскости, существует единственная пара чисел и , таких, что

, (2)

При этом совокупность , называется базисом, – координатами относительно этого базиса. Подчеркнем, что так как и неколлинеарны, то они линейно независимы.

Если в пространстве заданы три ненулевых, некомпланарных (а, следовательно, линейно независимых) вектора , то для любого вектора существует единственная тройка чисел таких, что

, (3)

При этом совокупность называется базисом, – координатами относительно этого базиса.

Линейные комбинации вида (1), (2), (3) называют разложением вектора по базису.

Объединяя три случая, можно дать следующее определение:

Определение. Коэффициенты линейной комбинации, при помощи которой вектор выражается через базис, называются координатами вектора относительно этого базиса.

Теорема 5. Линейные операции над векторами сводятся к таким же операциям над их соответствующими координатами.

Введенные базисы на плоскости и в пространстве называют аффинными. Аффинный базис называется декартовым, если он состоит из единичных взаимно перпендикулярных векторов. Векторы декартова базиса обозначают . Координаты вектора относительно декартова базиса обозначают через .

Определение. Система, состоящая из произвольной точки 0 и векторного аффинного базиса пространства, называется аффинной системой координат этого пространства, точка 0 – начало аффинной системы координат.

Аффинная система координат называется декартовой, если ее векторный базис – декартов.

Определение. Радиус-вектором точки в аффинной или декартовой системе координат называется вектор , где – начало системы координат.

Определение. Координатами точки относительно некоторого базиса называются координаты ее радиус-вектора относительно этого базиса.

Теорема 6. Координаты вектора равны разностям соответствующих координат его конца и начала.

Пример 9. Заданы векторы и . Убедиться, что они коллинеарны и найти разложение по базису .

Решение. У коллинеарных векторов координаты пропорциональны. В нашем случае , следовательно, .

Пример 10. Относительно некоторого базиса даны векторы , и . Убедиться, что векторы и можно взять за базис и найти координаты в этом базисе.

Решение. Координаты и не пропорциональны, следовательно, не параллелен , значит, они линейно независимы и их можно принять за базис. Обозначим искомые координаты через и , тогда . По теореме 5 получим систему из которой находим ; .

Пример 11. В декартовом базисе заданы векторы , , и .

1. Найти координаты вектора в базисе .

2. Убедиться, что векторы образуют базис.

3. Найти координаты вектора в базисе и написать разложение по этому базису.

Решение. 1. Вектор является линейной комбинацией векторов , следовательно, или .

2. Базис состоит из линейно независимых векторов, значит линейная комбинация векторов обратится в только если все коэффициенты этой линейной комбинации равны нулю. Найдем эти коэффициенты из условия , Или . Так как – линейно независимы, то это равенство возможно, если все коэффициенты обратятся в : , следовательно, – линейно независимы и образуют базис.

3. Разложение вектора по базису имеет вид: , где – координаты вектора в этом базисе. По теореме 5 имеем:

Решая эту систему, найдем , т. е. , .

Пример 12. Вектор отложен от точки . Конец его оказался в точке . Найти координаты точки .

Решение. Обозначим координаты точки через . По теореме 6: , , , откуда .

Пример 13. Даны точки , . Найти значения и , при которых точка , лежит на прямой .

Решение. Векторы и коллинеарны, следовательно , откуда , .

Пример 14. Даны три последовательные вершины параллелограмма , , . Найти координаты четвертой вершины .

Решение. Пусть , тогда , . Так как , то их соответствующие координаты равны, поэтому , , . Откуда .

< Предыдущая		Следующая >

Скалярное тройное произведение — Math Insight

Скалярное тройное произведение трех векторов $\vc{a}$, $\vc{b}$ и $\vc{c}$ равно $(\vc{a} \times \vc{b}) \cdot \vc{c}$. Это скаляр продукт, потому что, как и скалярный продукт, он оценивается как одно число. (В этом смысле он отличается от перекрестное произведение, которое является вектором.) скалярное тройное произведение важно, потому что его абсолютное значение $|(\vc{a} \times \vc{b}) \cdot \vc{c}|$ — объем параллелепипед, натянутый на $\vc{a}$, $\vc{b}$ и $\vc{c}$ (т.е. параллелепипед, смежными сторонами которого являются векторы $\vc{a}$, $\vc{b}$ и $\vc{c}$).

Эту формулу объема можно понять из приведенного выше рисунка. Объем параллелепипеда равен площади основания раз больше высоты. Из геометрического определения векторного произведения мы знаем, что его величина, $\|\vc{a} \times \vc{b}\|$, является площадью основания параллелограмма, и что направление вектора $\vc{a} \times \vc{b}$ перпендикулярно основанию. Высота параллелепипеда есть компонента $\vc{c}$ в направлении нормали к основанию, т. е. в направлении $\vc{a} \раз \vc{b}$. Следовательно, высота равна $ \|\vc{c}\| ~ |\cos \phi |$, где $\phi$ — угол между $\vc{c}$ и $\vc{a} \раз \vc{b}$. (Зачем нам нужно абсолютное значение? Если мы поменяли местами $\vc{a}$ и $\vc{b}$ на приведенном выше рисунке, то $\vc{a} \times \vc{b} $ будет указывать вниз, угол $\phi$ будет больше, чем $\pi/2$, а $\cos\phi$ будет быть отрицательным.)

Следовательно, объем параллелепипеда \начать{выравнивать*} \text{Объем} = \|\vc{a} \times \vc{b}\| ~ \|\vc{с}\| ~ |\cos \фи | = |(\vc{a} \times \vc{b}) \cdot \vc{c}|. \конец{выравнивание*} (Вспомните определение скалярного произведения.) Используя формулу векторного произведения в компонентной форме, мы можем записать скаляр тройной продукт в компонентной форме как \начать{выравнивать*} (\vc{a} \times \vc{b}) \cdot \vc{c} «=» \влево| \begin{массив}{cc} а_2 и а_3\\ б_2 и б_3 \конец{массив} \право| с_1 — \влево| \begin{массив}{cc} а_1 и а_3\\ б_1 и б_3 \конец{массив} \право| с_2 + \влево| \begin{массив}{cc} а_1 и а_2\\ б_1 и б_2 \конец{массив} \право| с_3 \\ «=» \влево| \begin{массив}{ccc} c_1 и c_2 и c_3\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \конец{массив} \право|. \конец{выравнивание*}

Приведенный ниже апплет поможет вам понять свойства скалярного тройного произведения $(\vc{a} \times \vc{b}) \cdot \vc{c}$. Он включает контур параллелепипеда, натянутого на эти векторы, объем которого равен $|(\vc{a} \times \vc{b}) \cdot \vc{c}|$, а также вектор, соответствующий перекрестному произведению $\vc{a} \times \vc{b}$. (Извинения дальтоникам за то, что они полагаются на цвета в этом апплете.)

Скалярное тройное произведение может быть положительным, отрицательным или нулевым. (Вот почему нам нужен абсолютный значение объема.) Что определяет знак $(\vc{a} \times \vc{b}) \cdot \vc{c}$? Кроме того, когда $(\vc{a} \times \vc{b}) \cdot \vc{c}=0$, что происходит? (Если вы повернете график после того, как сделал скалярное тройное произведение нулем, вы сразу увидите этот ответ.)

Загрузка апплета

Скалярное тройное произведение. Значение скалярного тройного произведения $(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c} }$ показан вверху, где векторы $\color{blue}{\vc{a}}$ (синим), $\color{green}{\vc{b}}$ (зеленым) и $\color{magenta}{\vc{c}}$ (пурпурного цвета) можно изменить, перетащив их кончики с помощью мыши. Объем составного параллелепипеда (обведен контуром) равен величине $\|(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta} {\vc{с}}\|$. Перекрестное произведение $\color{blue}{\vc{a}} \times \color{green}{\vc{b}}$ показано красным вектором; его величина есть площадь выделенного параллелограмма, являющегося одной гранью параллелепипеда.

Трехмерную перспективу этого графика трудно воспринять, когда график неподвижен. Если вы продолжите вращать фигуру, перетаскивая ее мышью, вы увидите ее намного лучше.

Дополнительная информация об апплете.

Если вам нравится видеть это с цифрами, вот пример расчета объема параллелепипед с помощью скалярного тройного произведения.

Нужны ли нам параллелепипеды?

Скалярное тройное произведение, очевидно, очень полезно, если у вас завалялось много параллелепипедов и вы хотите узнать их объем. Но, если вам вдруг не захотелось узнать объем параллелепипеда, вы можете задаться вопросом, какая польза от скалярного тройного произведения.

Для начала рекомендуем вам сначала освоить векторное произведение. Если у вас достаточно свободных мозговых клеток, чтобы справиться с перекрестным произведением или скалярным тройным произведением, мы рекомендуем сосредоточиться на перекрестном произведении. Его применение более непосредственное, и его использование более широко.

Тем не менее, у скалярного тройного произведения есть свое применение, даже если вы не в восторге от параллелепипедов. В многомерном исчислении оказывается, что за некоторыми важными формулами и теоремами скрываются параллелепипеды. Причина вытекает из определения дифференцируемости функций. В двух словах, дифференцируемость означает, что функция выглядит линейной, если вы увеличиваете масштаб. Исчисление связано с бесконечно малым (т. е. с уменьшением всего), поэтому малая структура, которую вы видите при увеличении, имеет фундаментальное значение. Итог: линейные функции являются фундаментальными в исчислении.

Путь к параллелепипедам лежит через эти линейные функции, которые мы будем называть линейными преобразованиями или линейными картами, чтобы подчеркнуть, как они отображают объекты в другие объекты. Оказывается, трехмерные линейные преобразования всегда переводят параллелепипеды в другие параллелепипеды. Таким образом, свойства линейных карт можно увидеть по тому, как они преобразуют параллелепипеды. Одним из таких свойств является то, как линейные карты расширяют или сжимают объекты. Вот скалярное тройное произведение, поскольку оно измеряет изменяющийся объем. В частности, приведенная выше детерминантная форма скалярного тройного произведения является ключевой, поскольку матрицы сильно связаны с линейными преобразованиями.

Если вы находите это линейное преобразование слишком абстрактным, чтобы помочь вам оценить полезность скалярного тройного произведения, вы также можете подумать о тройных интегралах, определение которых основано на разбиении области на маленькие квадраты. Если вы думаете, что коробка — это тип параллелепипеда, а маленький размер означает, что линейное преобразование уместно, то вам определенно нужно больше выходить и заниматься другими вещами, помимо размышлений о математике. Но именно благодаря этим связям скалярное тройное произведение связывается с тройными интегралами.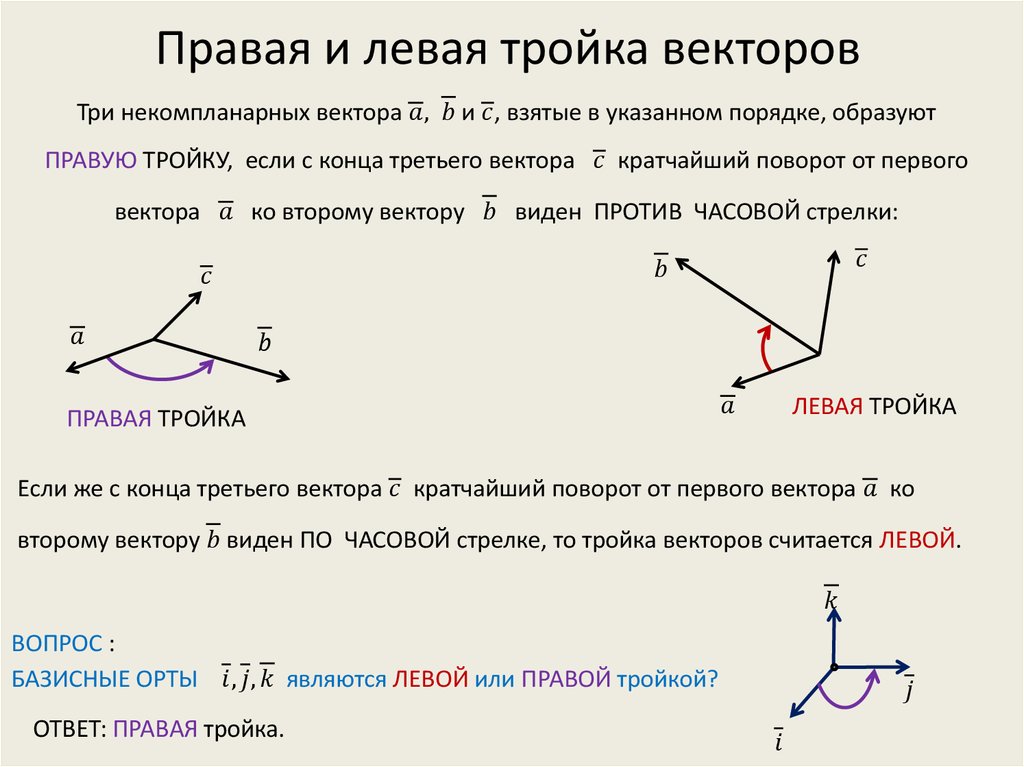 Однако нам не нужно скалярное тройное произведение для обычного тройного интеграла, поскольку мы знаем, как вычислить объем коробки без него. Но когда вы начинаете менять переменные в тройных интегралах, то коробка превращается в параллелепипед, и вычисление объема скалярного тройного произведения становится важным.

4.9: Перекрестное произведение — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

21267

• Кен Каттлер
• Университет Бригама Янга via Lyryx 9{3}.\) Сначала мы обсуждаем геометрический смысл, а затем дается описание в терминах координат, оба из которых важны. Геометрическое описание необходимо для понимания приложений к физике и геометрии, в то время как описание координат необходимо для вычисления векторного произведения.

  Рассмотрим следующее определение.

  Определение \(\PageIndex{1}\): правая система векторов

  Три вектора \(\vec{u},\vec{v},\vec{w}\) образуют правую систему, если когда вы вытягиваете пальцы правой руки вдоль направления вектора \(\vec{u}\) и смыкаете их в направлении \(\vec{v}\), большой палец указывает примерно в направлении \(\ vec{w}\).

  Пример правосторонней системы векторов см. на следующем рисунке.

  Рисунок \(\PageIndex{1}\)

  На этом рисунке вектор \(\vec{w}\) направлен вверх из плоскости, определяемой двумя другими векторами. Укажите пальцами правой руки вдоль \(\vec{u}\) и сомкните их в направлении \(\vec{v}\). Обратите внимание, что если вы вытяните большой палец на правой руке, он указывает в направлении \(\vec{w}\).

  Вам следует подумать, чем правосторонняя система будет отличаться от левосторонней. Попробуйте использовать левую руку, и вы увидите, что вектор \(\vec{w}\) должен указывать в противоположном направлении.

  Обратите внимание, что специальные векторы \(\vec{i},\vec{j},\vec{k}\) всегда образуют правую систему. Если вы вытяните пальцы правой руки вдоль \(\vec{i}\) и сомкнете их в направлении \(\vec{j}\), большой палец укажет в направлении \(\vec{k}\ ).

  Рисунок \(\PageIndex{2}\)

  Ниже приводится геометрическое описание перекрестного произведения. Напомним, что скалярное произведение двух векторов дает скаляр. Напротив, перекрестное произведение приводит к вектору, поскольку произведение дает направление, а также величину. 9{3}.\) Тогда перекрестное произведение , записанное \(\vec{u}\times \vec{v}\), определяется следующими двумя правилами.

  1. Его длина равна \[\| \vec{u}\times \vec{v}\| =\| \vec{и}\| \| \vec{v}\| \sin \theta, \nonumber \], где \(\theta\) — внутренний угол между \(\vec{u}\) и \(\vec{v}\).
  2. Он перпендикулярен как \(\vec{u}\), так и \(\vec{v}\), то есть \[\left( \vec{u}\times \vec{v} \right) \cdot \vec{u}=0, \]\[\left( \vec{u}\times \vec{v} \right) \cdot \vec{v}=0, \nonumber\] и \[\vec{ u},\vec{v},\vec{u}\times \vec{v} \nonumber\] образуют правую систему. T\) можно записать в терминах \(\ vec{i}, \vec{j}, \vec{k}\) как \(\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3 }\vec{k}\).

     Теорема \(\PageIndex{1}\): Координатное описание перекрестного произведения

     Пусть \(\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{ 3}\vec{k}\) и \(\vec{v}=v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\) два вектора. Тогда

     \[\begin{array}{c} \vec{u}\times \vec{v} =\left( u_{2}v_{3}-u_{3}v_{2}\right) \ vec{i}-\left( u_{1}v_{3} — u_{3}v_{1}\right) \vec{j}+ \left( u_{1}v_{2}-u_{2} v_{1}\right) \vec{k} \label{crossprod1} \end{array}\]

     Написание \(\vec{u} \times \vec{v}\) обычным способом, это дано

     \[\vec{u} \times \vec{v} = \left[ \begin{array}{r} u_{2}v_{3}-u_{3}v_{2} \\ -(u_ {1}v_{3}-u_{3}v_{1}) \\ u_{1}v_{2}-u_{2}v_{1} \end{массив} \right]\nonumber \]

     Теперь докажем это предложение.

     Доказательство

     Из приведенной выше таблицы и перечисленных свойств векторного произведения \[\begin{aligned} \vec{u} \times \vec{v} &= \left( u_{1}\vec{i}+u_{ 2}\vec{j}+u_{3}\vec{k}\right) \times\left( v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\ vec{k}\right) \\ &= u_{1}v_{2}\vec{i}\times \vec{j}+u_{1}v_{3}\vec{i}\times \vec{ k}+u_{2}v_{1}\vec{j}\times \vec{i}+ u_{2}v_{3}\vec{j}\times \vec{k}+ +u_{3} v_{1}\vec{k}\times \vec{i}+u_{3}v_{2}\vec{k}\times \vec{j} \\ &=u_{1}v_{2}\ vec{k}-u_{1}v_{3}\vec{j}-u_{2}v_{1}\vec{k}+u_{2}v_{3} \vec{i}+u_{3 }v_{1}\vec{j}-u_{3}v_{2}\vec{i} \\ &=\left( u_{2}v_{3}-u_{3}v_{2}\right ) \vec{i}+\left( u_{3}v_{1}-u_{1}v_{3}\right) \vec{j}+\left( u_{1}v_{2}-u_{ 2}v_{1}\right) \vec{k} \end{aligned}\] \[\label{crossprod2}\] 9{3+1}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{массив} \right\vert\nonumber \] \

     \[=\vec{i}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{массив} \right\vert -\vec{j}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{массив} \right\vert +\vec {k}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{массив} \right\vert\nonumber \]

     Расширение этих определителей приводит к \[\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3}-u_ {3}v_{1}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \nonumber \], что то же, что и \(\eqref{crossprod2}\). 93\) и \(k\) скаляр. Тогда выполняются следующие свойства векторного произведения.

     1. \(\vec{u}\times \vec{v}= -\left( \vec{v}\times \vec{u}\right), \mbox{and} \; \vec{u} \раз \vec{u}=\vec{0}\)
     2. \(\left( k \vec{u}\right)\times \vec{v}= k \left( \vec{u}\times \vec{v}\right) =\vec{u}\times \влево( к \vec{v}\вправо)\)
     3. \(\vec{u}\times \left( \vec{v}+\vec{w}\right) =\vec{u}\times \vec{v}+\vec{u}\times \vec {ж}\)
     4. \(\left( \vec{v}+\vec{w}\right) \times \vec{u}=\vec{v} \times \vec{u}+\vec{w}\times \vec {и}\)

     Доказательство

     Формула \(1.\) следует непосредственно из определения. Векторы \(\vec{u}\times \vec{v}\) и \(\vec{v}\times \vec{u}\) имеют одинаковую величину, \(\left\vert \vec{u }\right\vert \left\vert \vec{v}\right\vert \sin \theta ,\) и применение правила правой руки показывает, что они имеют противоположное направление.

     Формула \(2.\) доказывается следующим образом. Если \(k\) является неотрицательной скалярной величиной, направление \(\left( k \vec{u}\right) \times \vec{v}\) совпадает с направлением \(\vec {u}\times \vec{v}, k \left( \vec{u}\times \vec{v}\right)\) и \(\vec{u}\times \left( k \vec{v }\верно)\). Величина \(k\) умножается на величину \(\vec{u}\times \vec{v}\), которая совпадает с величиной \(k \left( \vec{u}\times \ vec{v}\right)\) и \(\vec{u}\times \left( k \vec{v}\right) .\) Использование этого дает равенство в \(2\). В случае, когда \(k <0,\) все работает так же, за исключением того, что все векторы указывают в противоположном направлении, и вы должны умножать на \(\left\vert k \right\vert\) при сравнении их величин.

     Распределительные законы \(3.\) и \(4.\) установить гораздо труднее. А пока достаточно заметить, что если мы знаем, что \(3.\) истинно, то \(4.\) следует. Таким образом, предполагая \(3.\) и используя \(1.\), \[\begin{aligned} \left( \vec{v}+\vec{w}\right) \times \vec{u} & =-\vec{u}\times \left( \vec{v}+\vec{w}\right) \\ & =-\left( \vec{u}\times \vec{v}+\vec {u}\times \vec{w}\right) \\ & =\vec{v}\times \vec{u}+\vec{w}\times \vec{u}\end{aligned}\]

     Теперь мы рассмотрим пример вычисления перекрестного произведения.

     Пример \(\PageIndex{1}\): найти векторное произведение

     Найти \(\vec{u} \times \vec{v}\) для следующих векторов

     \[\vec{u} = \ влево[ \begin{array}{r} 1 \\ -1 \\ 2 \end{массив} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \ \ 1 \end{array} \right]\nonumber \]

     Решение

     Обратите внимание, что мы можем записать \(\vec{u}, \vec{v}\) в терминах специальных векторов \(\vec{ i}, \vec{j}, \vec{k}\) как

     \[\begin{array}{c} \vec{u} = \vec{i}-\vec{j}+2\vec {k} \\ \vec{v} = 3\vec{i}-2\vec{j}+\vec{k} \end{массив}\nonumber \]

     Мы будем использовать уравнение \(\eqref{crossprod3}\) для вычисления перекрестного произведения.

     \[\vec{u} \times \vec{v} = \left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & -1 & 2 \\ 3 & -2 & 1 \end{array} \right\vert =\left\vert \begin{array}{rr} -1 & 2 \\ -2 & 1 \end{array} \ right\vert \vec{i}-\left\vert \begin{array}{rr} 1 & 2 \\ 3 & 1 \end{array} \right\vert \vec{j}+\left\vert \begin {array}{rr} 1 & -1 \\ 3 & -2 \end{array} \right\vert \vec{k}=3\vec{i}+5\vec{j}+\vec{k} \номер\]

     Мы можем записать этот результат обычным образом, как \[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array } \right]\nonumber \]

     Важным геометрическим применением векторного произведения является следующее. Размер векторного произведения, \(\| \vec{u}\times \vec{v}\|\), представляет собой площадь параллелограмма, определяемую \(\vec{u}\) и \(\vec {v}\), как показано на следующем рисунке.

     Рисунок \(\PageIndex{3}\)

     Мы рассмотрим эту концепцию в следующем примере.

     Пример \(\PageIndex{2}\): площадь параллелограмма

     Найдите площадь параллелограмма, определяемую векторами \(\vec{u}\) и \(\vec{v}\), заданными числом

     \[\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array }{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber \]

     Решение

     Обратите внимание, что эти векторы такие же, как и в примере \(\PageIndex{1}\ ). Напомним из геометрического описания векторного произведения, что площадь параллелограмма — это просто величина \(\vec{u} \times \vec{v}\). Из примера \(\PageIndex{1}\), \(\vec{u} \times \vec{v} = 3\vec{i}+5\vec{j}+\vec{k}\). Мы также можем записать это как

     \[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber \]

     Таким образом площадь параллелограмма

     \[\| \vec{u} \times \vec{v} \| = \sqrt{(3)(3) + (5)(5) + (1)(1)} = \sqrt{9+25+1}=\sqrt{35}\nonumber \]

     Мы также можем используйте это понятие, чтобы найти площадь треугольника. Рассмотрим следующий пример.

     Пример \(\PageIndex{3}\): Площадь треугольника

     Найдите площадь треугольника, определяемую точками \(\left(1, 2, 3 \right) , \left( 0,2,5\ вправо), \влево( 5,1, 2 \вправо)\) 9T.\) Требуемое векторное произведение равно

     \[\left[ \begin{array}{r} -1 \\ 0 \\ 2 \end{array} \right] \times \left[ \begin{ array}{r} 4 \\ -1 \\ -1 \end{array} \right] = \left[ \begin{array}{rrr} 2 & 7 & 1 \end{array} \right]\nonumber \ ]

     Размер этого вектора дает площадь параллелограмма, определяемую как

     \[\sqrt{(2)(2) + (7)(7) + (1)(1)} = \sqrt{ 4+49+1} = \sqrt{54}\nonumber \] Следовательно, площадь треугольника равна \(\frac{1}{2}\sqrt{54}= \frac{3}{2}\sqrt{ 6}.\) 9{3}, P,Q,R\), площадь треугольника определяется выражением \[\frac{1}{2}\| \vec{PQ} \times \vec{PR} \|\номер\]

     Напомним, что \(\vec{PQ}\) — это вектор, идущий из точки \(P\) в точку \(Q\).

     Рисунок \(\PageIndex{4}\)

     В следующем разделе мы рассмотрим другое применение перекрестного произведения.

     Вспомните, что мы можем использовать векторное произведение, чтобы найти площадь параллелограмма. Отсюда следует, что мы можем использовать векторное произведение вместе со скалярным произведением, чтобы найти объем параллелепипеда. Начнем с определения.

     Определение \(\PageIndex{3}\): Параллелепипед

     Параллелепипед , определяемый тремя векторами, \(\vec{u},\vec{v}\) и \(\vec{w} \) состоит из \[\left\{ r\vec{u}+s\vec{v}+t\vec{w}:r,s,t\in \left[ 0,1\right] \right\ }\nonumber \]

     То есть, если вы выберете три числа, \(r,s,\) и \(t\) каждое из \(\left[ 0,1\right]\) и образуете \(r \vec{u}+s\vec{v}+t\vec{w}\), то совокупность всех таких точек составляет параллелепипед, определяемый этими тремя векторами.

     Ниже приведен пример параллелепипеда.

     Рисунок \(\PageIndex{5}\)

     Обратите внимание, что основанием параллелепипеда является параллелограмм, определяемый векторами \(\vec{u}\) и \(\vec{v}\). Следовательно, его площадь равна \(\| \vec{u}\times \vec{v} \|\). Высота параллелепипеда равна \(\| \vec{w}\| \cos \theta\), где \(\theta\) — угол, показанный на рисунке, между \(\vec{w}\) и \( \vec{u}\times \vec{v}\). Объем этого параллелепипеда равен площади основания, умноженной на высоту, которая равна \[\| \vec{u}\times \vec{v}\| \| \vec{ш}\| \cos \theta = \left( \vec{u}\times\vec{v}\right) \cdot \vec{w}\nonumber \] Это выражение известно как произведение коробки и иногда записывается как \(\ left[ \vec{u},\vec{v},\vec{w}\right].\) Вы должны подумать, что произойдет, если вы поменяете местами \(\vec{v}\) с \(\vec{ w}\) или \(\vec{u}\) с \(\vec{w}\). Вы можете видеть геометрически из рисунков, что это просто вводит знак минус. В любом случае коробочное произведение трех векторов всегда равно либо объему параллелепипеда, определяемому тремя векторами, либо \(-1\), умноженному на этот объем. 9n\), определяющие параллелепипед. Тогда объем параллелепипеда является абсолютным значением произведения коробки, заданным \[\left| \left(\vec{u}\times\vec{v}\right) \cdot \vec{w} \right|\nonumber \]

     Рассмотрим пример этой концепции.

     Пример \(\PageIndex{4}\): Объем параллелепипеда

     Найдите объем параллелепипеда, определяемый векторами

     \[\vec{u} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{массив} \right], \vec{v} = \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{массив} \right] , \vec{w} = \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{массив} \right]\nonumber \]

     Решение

     В соответствии с приведенным выше обсуждением выберите любые два из этих векторов, возьмите векторное произведение, а затем возьмите скалярное произведение этого с третьим из этих векторов. Результатом будет либо желаемый объем, либо \(-1\), умноженный на желаемый объем. Следовательно, взяв абсолютное значение результата, мы получим объем.

     Возьмем перекрестное произведение \(\vec{u}\) и \(\vec{v}\). Это дается как

     \[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right] \times \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{массив} \right]\nonumber \] \[=\left\vert \begin{array}{rrr} \vec{i } & \vec{j} & \vec{k} \\ 1 & 2 & -5 \\ 1 & 3 & -6 \end{массив} \right\vert = 3\vec{i}+\vec{j }+\vec{k} = \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{массив} \right]\nonumber \]

     Теперь возьмем скалярное произведение этого вектора на \(\vec{w}\), что даст \[\begin{aligned} (\vec{u} \times \vec{v}) \cdot \vec{w} &= \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{массив} \right] \cdot \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end {массив} \right] \\ &=\left( 3\vec{i}+\vec{j}+\vec{k}\right) \cdot \left( 3\vec{i}+2\vec{ j}+3\vec{k}\right) \\ &=9+2+3 \\ &=14\end{aligned}\]

     Это показывает, что объем этого параллелепипеда составляет 14 кубических единиц.

     Существует фундаментальное наблюдение, вытекающее непосредственно из геометрических определений перекрестного произведения и скалярного произведения.

     Предложение \(\PageIndex{3}\): Порядок продукта

     Пусть \(\vec{u},\vec{v}\) и \(\vec{w}\) — векторы. Тогда \(\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}=\vec{u}\cdot \left( \vec{v}\times \vec{w } \справа).\)

     Доказательство

     Это следует из наблюдения, что либо \(\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}\), либо \(\vec{u}\cdot \left( \ vec{v}\times \vec{w}\right)\) оба дают объем параллелепипеда или оба дают \(-1\), умноженный на объем. 9T .\) Тогда коробочное произведение \(\vec{u}\cdot \left(\vec{v}\times \vec{w}\right)\) определяется следующим образом. \[\begin{align} \vec{u}\cdot \left(\vec{v}\times \vec{w}\right) &= \left[ \begin{array}{r} a \\ b \ \ c \end{массив} \right] \cdot \left| \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ d & e & f \\ g & h & i \end{array} \right| \\ &=а\влево| \begin{array}{rr} e & f \\ h & i \end{array} \right| -b\влево| \begin{array}{rr} d & f \\ g & i \end{array} \right| +с\влево| \begin{array}{rr} d & e \\ g & h \end{array} \right| \\ &= \det \left[ \begin{array}{rrr} a & b & c \\ d & e & f \\ g & h & i \end{array} \right] \end{aligned}\ ]

     Чтобы получить коробочное произведение, вы можете просто взять определитель матрицы, которая получается, если позволить строкам быть компонентами заданных векторов в том порядке, в котором они встречаются в коробочном произведении.

     No related posts.