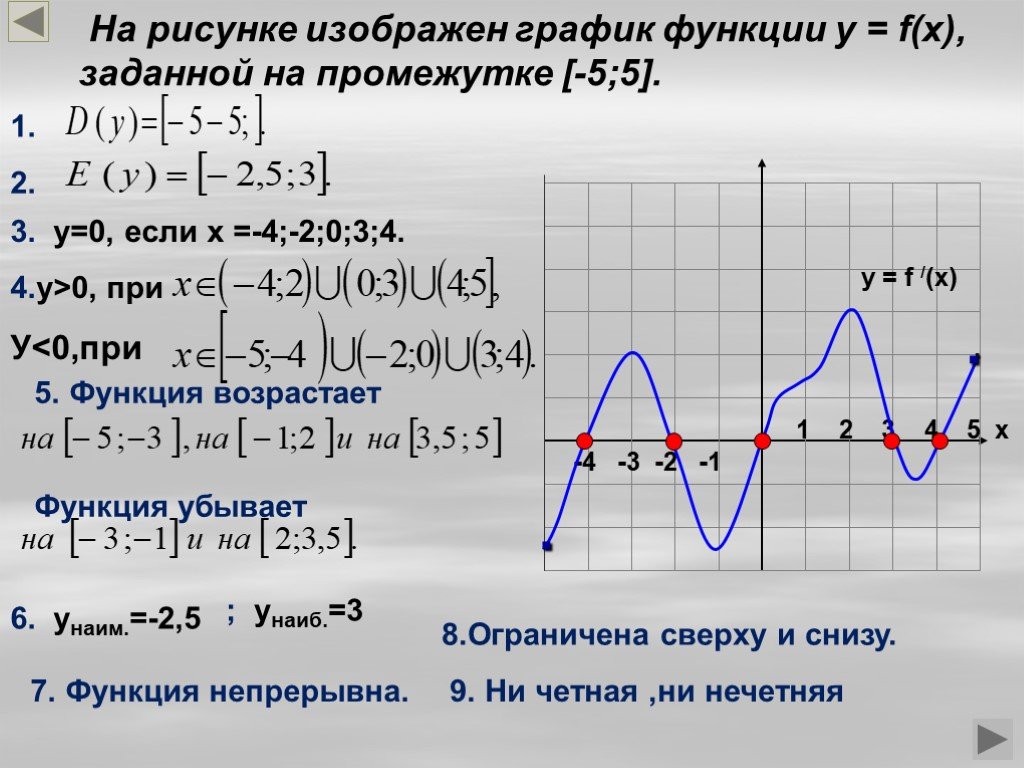
Лабораторная работа № 9.Графики
Цель работы: Научиться строить диаграммы разного уровня сложности.
Задание (в соответствии с индивидуальным вариантом)
Изучить теоретические вопросы по теме лабораторной работы.
Построить графики функций f(x).
Отчет представить в тетради (расчет области допустимых значений (ОДЗ)) и в электронном виде.
Лист книги Excel должен содержать:
написанную в редакторе формул функцию, по которой строится график,
таблицу значений функции,
график функции (название графика, подписи осей).
Диапазон изменений переменной Х и шаг ее изменения подберите самостоятельно.
Теоретическая чать
Пример 1
Построить
график функции (рис. 1).
1).
Решение
При построении графика следует обратить внимание на область определения функции. В данном случае функция не существует при обращении знаменателя в ноль. Решим уравнение: 4x + 8 ≠ 0; 4x ≠ −8; x ≠ −2. Следовательно, при определении значений аргумента следует помнить, что при x = −2 функция не определена. На рис.5.8 видно, что значение аргумента задано в два этапа, не включая (-2) с шагом 0,2.
Рис. 1. График функции
Пример 2
Построить график функции (рис.2).
Решение
ОДЗ: x2−1≥0 x2 ≥1 x=±1 x(−;−1)(1;+). Определение значения аргумента следует провести в два этапа. Например, от -5 до -1, а затем от 1 до 5,с шагом 0,5.
Пример 3
Построить
график функции (рис.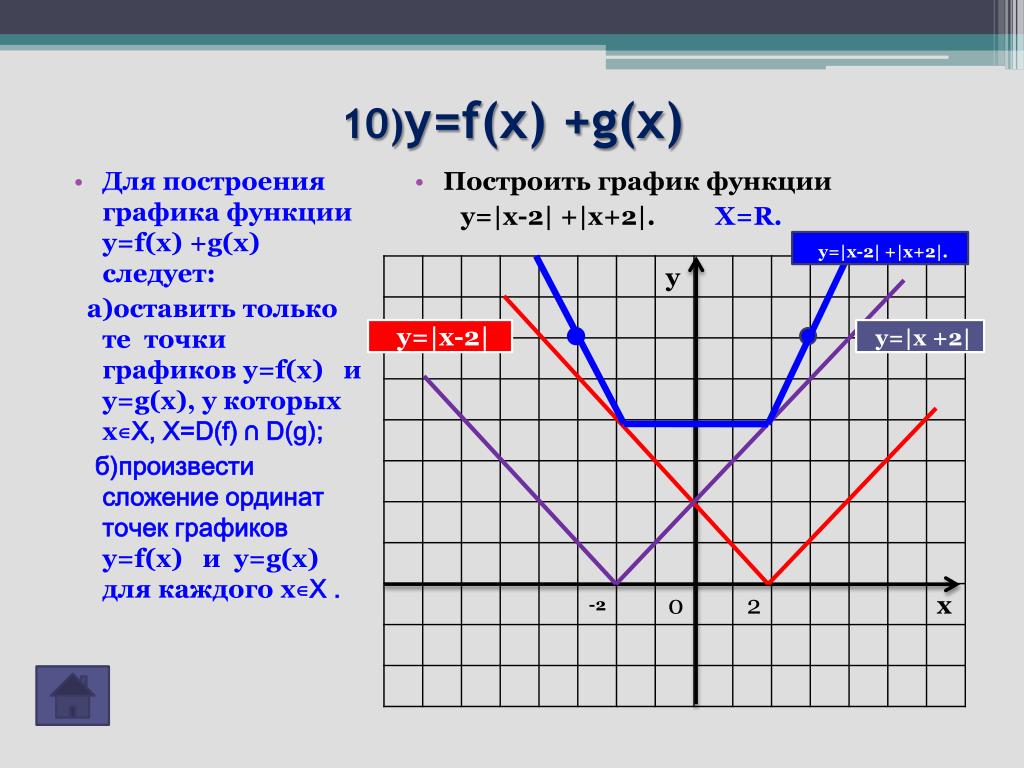 2;EXP(A7))).
2;EXP(A7))).
Рис. 2. График функции
Рис. 3. График функции
Пример 4
Изобразите линию, заданную неявно уравнением: 4y2 +5x2 –20=0.
Решение
Заметим, что заданная уравнением f(x,y)=0 функция описывает кривую линию под названием эллипс. Это можно доказать, если произвести элементарные математические операции:
.
В связи с тем, что линия задана неявно, для ее построения необходимо разрешить заданное уравнение относительно переменной
.
После проведенных преобразований можно увидеть, что линию f(x,y) можно изобразить, построив графики двух функций: и в одной графической области.
Перед
построением определим ОДЗ функций f1(x)
и f2(x).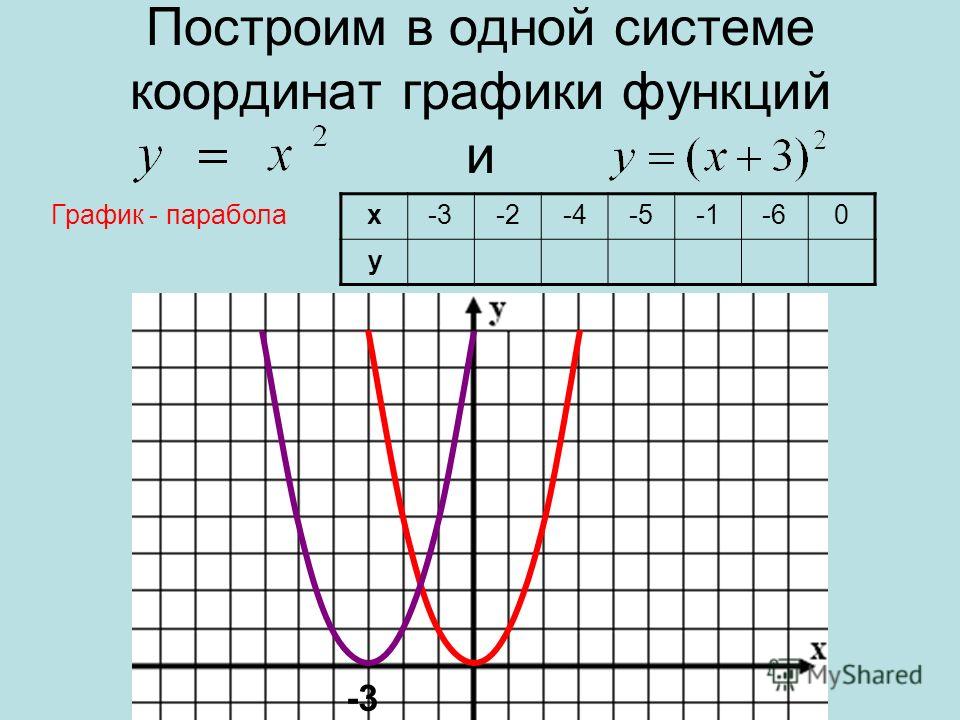 2)/2.
2)/2.
Далее скопируем эти формулы до В42 и С42 соответственно (рис.4). Затем выделим диапазон А2:С42 и, воспользовавшись Мастером диаграмм, построим графики функций f1(x) и f2(x) в одной графической области.
Затем выделим диапазон А2:С42 и, воспользовавшись Мастером диаграмм, построим графики функций f1(x) и f2(x) в одной графической области (рис. 5).
Рис. 4. Создание таблицы в ячейках A2:C42
Рис.5. График функции 4y2 +5×2 –20=0
Пример 5
Изобразите линию, заданную неявно: .
Решение
Уравнение описывает линию под названием гипербола. Разрешим его относительно переменной У:
.
Найдем
ОДЗ функций f1(x)
и f2(x): x2 − 4 ≥ 0 x (− ,
− 2] и [2,+).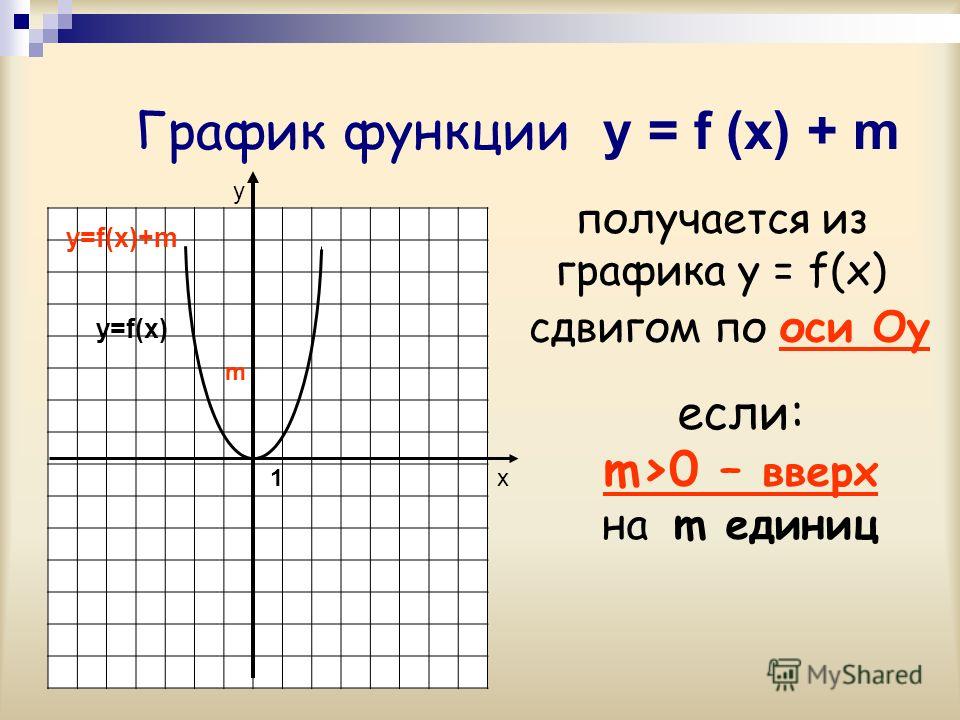
Проведенные исследования показывают, что для построения графика необходимо значения аргумента задавать в два этапа, так как в диапазоне от -2 до 2 функция неопределенна. Задание значений функций f1(x) и f2(x) и построение графика выполняется аналогично ранее рассмотренным примерам. Результаты представлены на рис. 6 и 7.
Рис. 6. Создание таблицы в ячейках А2:С52
Рис. 7. График функции
Варианты заданий
1. Построить график функции f(x).
№ | f(x) | № | f(x) | № | f(x) | |
1 | 11 | 21 | ||||
2 | 12 | 22 | ||||
3 | 13 | 23 | ||||
4 | 14 | 24 | ||||
15 | 25 | |||||
6 | 16 | 26 | ||||
7 | 17 | 27 | ||||
8 | 18 | 28 | ||||
9 | 19 | 29 | ||||
10 | 20 | 30 | ||||
2.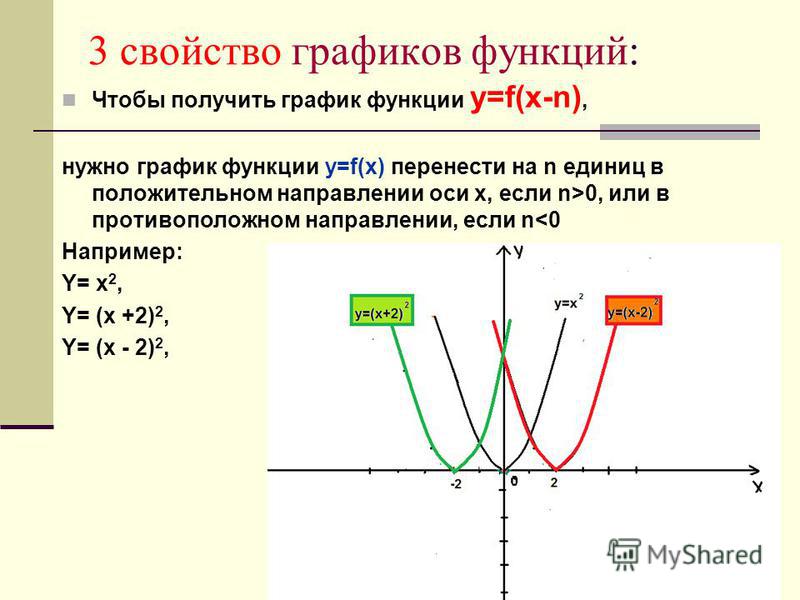 Построить график функции f(x).
Построить график функции f(x).
№ | f(x) | № | f(x) | № | f(x) |
1 | 11 | 21 | |||
2 | 12 | 22 | |||
3 | 13 | 23 | |||
4 | 14 | 24 | |||
5 | 15 | 25 | |||
6 | 16 | 26 | |||
7 | 17 | 27 | |||
8 | 18 | 28 | |||
9 | 19 | 29 | |||
10 | 20 | 30 |
3. Построить график функции
f(x).
Построить график функции
f(x).
f(x) | № | f(x) | № | f(x) | |
1 | 11 | 21 | |||
2 | 12 | 22 | |||
3 | 13 | 23 | |||
4 | 14 | 24 | |||
5 | 15 | 25 | |||
6 | 16 | 26 | |||
7 | 17 | 27 | |||
8 | 18 | 28 | |||
9 | 19 | 29 | |||
10 | 20 | 30 |
4.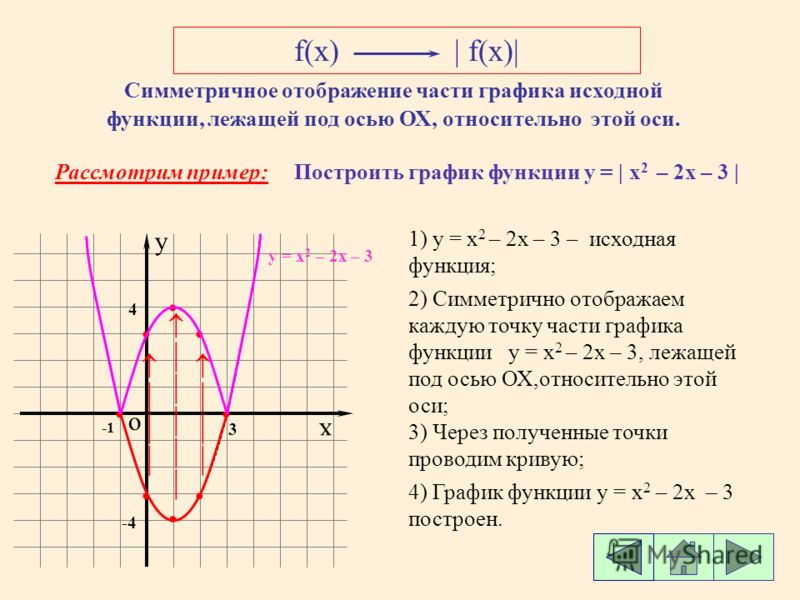 Изобразите линии заданные
неявно уравнением f(x,y)=0
Изобразите линии заданные
неявно уравнением f(x,y)=0
№ | f(x) | № | f(x) | № | f(x) |
1 | 11 | 21 | |||
2 | 12 | 22 | |||
3 | 13 | 23 | |||
4 | 14 | 24 | |||
5 | 15 | 25 | |||
6 | 16 | 26 | |||
7 | 17 | 27 | |||
8 | 18 | 28 | |||
9 | 19 | 29 | |||
10 | 20 | 30 |
Как построить диаграмму в Excel 2003?
Как построить диаграмму в Excel 2007?
Какие типы диаграмм можно построить в Excel?
Как можно вызвать Мастер диаграмм (Excel 2003)?
За сколько шагов можно построить диаграмму с помощью Мастера диаграмм (Excel 2003)?
На каком шаге задается диапазон ячеек для построения диаграммы?
На каком шаге задается название диаграммы?
Что такое легенда в диаграммах?
Как выполнить форматирование диаграммы?
5
Построение графика функции различными методами (самостоятельная работа учащихся) — страница 13
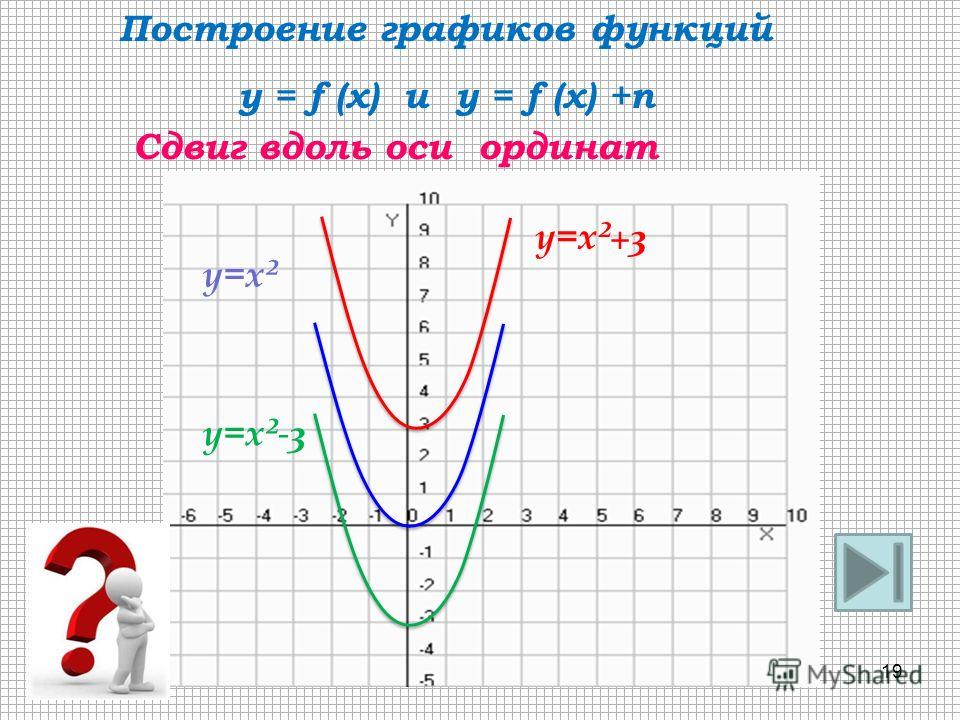
производной к исследованию функции и построению её графика Существенное внимание следует уделить решению разнообразных задач связанных с иследованием функции. “Алгебра и начала анализа, 10 — 11”, авт. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. Тема Основная цель Степенная, покозательная, логарифмическая функции их свойства и графики Познакомить учащихся с графиками этих функций. Познакомить их с многообразием свойств и графиков степенной функции в зависимости от значений оснований и покозателей степени. Особое внимание уделяется иллюстрации свойств функции по графику. Тригонометрические функции и их графики. Научит учащихся строить графики тригонометрических функций. Учащиеся должны научится выполнять эскизы графиков, используя эти свойства, а также устонавливать эти свойства по графику. Применение производной к построению графиков функций При изучении графика функций полезно показать построение графиков функций, которой не являются неприрывной на всей области определения. И особенности построения графиков четной и не четной функции. Программа для школы с углубленным изучением математики. «Алгебра, 8», авт. Н.Я. Виленкин, А.Н. Виленкин, Г.
“Алгебра и начала анализа, 10 — 11”, авт. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. Тема Основная цель Степенная, покозательная, логарифмическая функции их свойства и графики Познакомить учащихся с графиками этих функций. Познакомить их с многообразием свойств и графиков степенной функции в зависимости от значений оснований и покозателей степени. Особое внимание уделяется иллюстрации свойств функции по графику. Тригонометрические функции и их графики. Научит учащихся строить графики тригонометрических функций. Учащиеся должны научится выполнять эскизы графиков, используя эти свойства, а также устонавливать эти свойства по графику. Применение производной к построению графиков функций При изучении графика функций полезно показать построение графиков функций, которой не являются неприрывной на всей области определения. И особенности построения графиков четной и не четной функции. Программа для школы с углубленным изучением математики. «Алгебра, 8», авт. Н.Я. Виленкин, А.Н. Виленкин, Г. С. Сурвилло и др. «Алгебра, 9», авт. Н.Я. Виленкин, Г.С. Сурвилло, А.С. Симонов, А.И. Кудрявцев. Тема График функции. Простейшие преобразования графиков (параллельные переносы вдоль координатных осей). График функции y=k/x. График дробно – линейной функции. График функции вида y=Öx, y=Ö(x-m)+n. Отражение свойств функции на графике. Преобразование графиков функций: симметрия относительно осей координат и относительно прямой y=x. Построение графиков кусочно-заданных функций. Построение графиков функций связанных с модулем. Примеры построения графиков рациональных функций. Графики функций y=[x], y={x}. Графики функций y=xn, y=Öx. «Алгебра, 8», «Алгебра, 9», авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нелеков, С.Б. Суворова, «Учебные пособия, Алгебра. Дополнительные главы к школьному учебнику 8 (9) класса», авт. Ю.Н. Макарычев, Н.Г. Миндюк. Тема Построение преобразование графиков функций. График функции y=k/x. График дробно – линейной функции. График функции вида y=Öx, y=Ö(x-m)+n. График квадратичной функции.
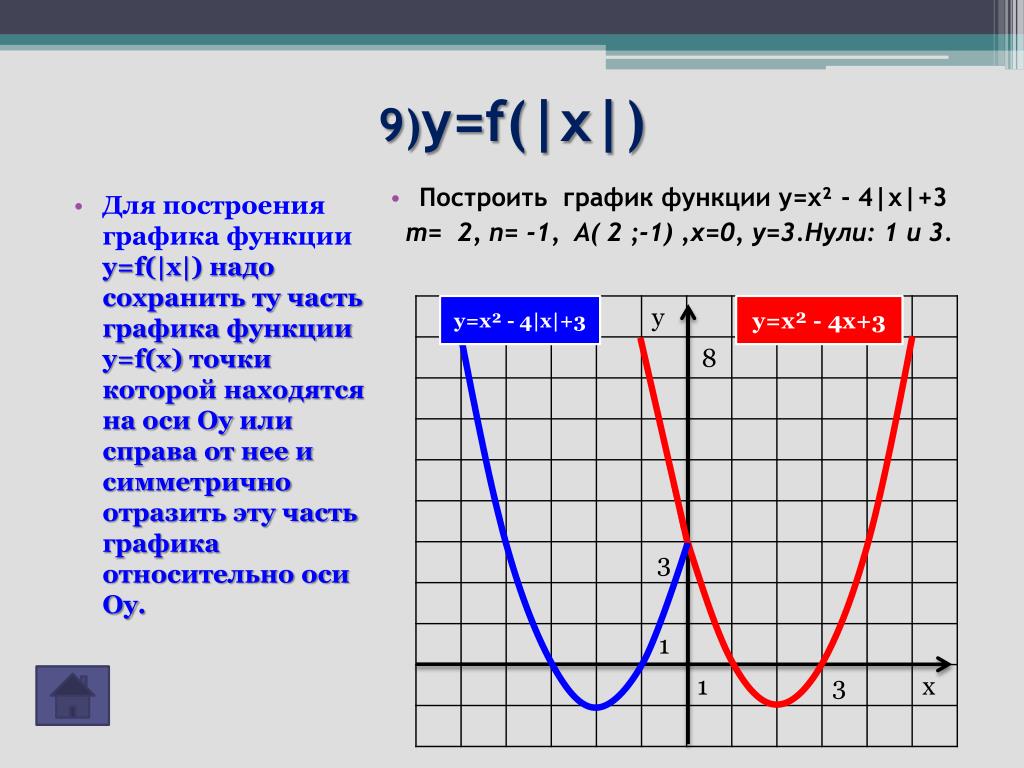
С. Сурвилло и др. «Алгебра, 9», авт. Н.Я. Виленкин, Г.С. Сурвилло, А.С. Симонов, А.И. Кудрявцев. Тема График функции. Простейшие преобразования графиков (параллельные переносы вдоль координатных осей). График функции y=k/x. График дробно – линейной функции. График функции вида y=Öx, y=Ö(x-m)+n. Отражение свойств функции на графике. Преобразование графиков функций: симметрия относительно осей координат и относительно прямой y=x. Построение графиков кусочно-заданных функций. Построение графиков функций связанных с модулем. Примеры построения графиков рациональных функций. Графики функций y=[x], y={x}. Графики функций y=xn, y=Öx. «Алгебра, 8», «Алгебра, 9», авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нелеков, С.Б. Суворова, «Учебные пособия, Алгебра. Дополнительные главы к школьному учебнику 8 (9) класса», авт. Ю.Н. Макарычев, Н.Г. Миндюк. Тема Построение преобразование графиков функций. График функции y=k/x. График дробно – линейной функции. График функции вида y=Öx, y=Ö(x-m)+n. График квадратичной функции.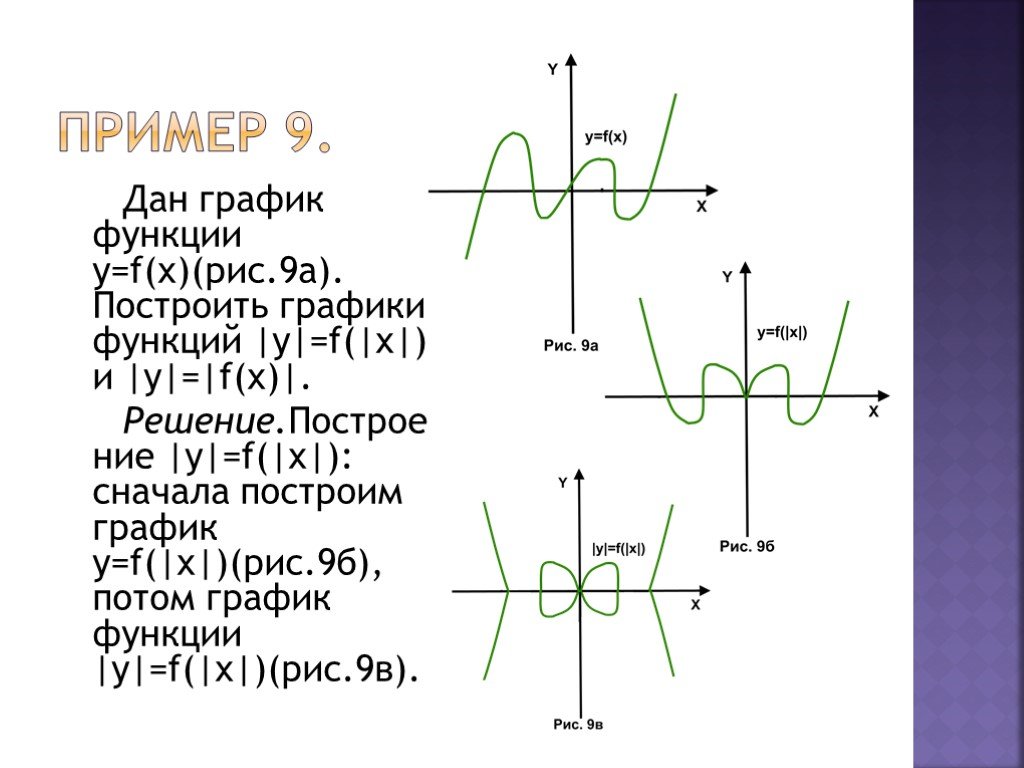 Построение графиков функций. График функций y=-f(x), y=f(-x), y=-f(-x), y=½f(x)½ y=f(½x½). [Графики функций y=½x½ и y={x}.]. «Алгебра и математический анализ, 10», «Алгебра и математический анализ, 11», авт. Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд. Тема Построение графиков функций элементарными методами. Преобразование графиков. Графики дробно – линейных функций. Графики функций, связанных с модулем.
Построение графиков функций. График функций y=-f(x), y=f(-x), y=-f(-x), y=½f(x)½ y=f(½x½). [Графики функций y=½x½ и y={x}.]. «Алгебра и математический анализ, 10», «Алгебра и математический анализ, 11», авт. Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд. Тема Построение графиков функций элементарными методами. Преобразование графиков. Графики дробно – линейных функций. Графики функций, связанных с модулем.
Шпаргалки по специальной педагогике и психологии
Практикум по курсу общая психология. Внимание и память
Деловой этикет
Особенности подросткового возраста
Классификация видов профессиональной деятельности
2 ≤ 1/2 вернуть 1. еще
вернуть 0.
конец
конец
еще
вернуть 0.
конец
конец Если я использую функцию поверхности из Plots.jl , я получаю следующий график
поверхность (-1:0,01:1, -1:0,01:1, f)
Есть ли способ построить функцию без поверхности , автоматически интерполирующей точки разрыва?
Рафаэль Гуэрра
2 92 если г ≤ 1/2 — δ вернуть 1.0 иначе, если r ≥ 1/2 + δ вернуть 0,0 конец вернуть NaN конец δ = 0,01 х = у = -1,0: δ: 1,0 Plots.surface (x, y, (x, y) -> f (x, y, δ)) # Маска контроля качества NaN: тепловая карта (x, y, (x, y) -> f (x, y, δ), ratio=1, lims=(-1,1))
1 Нравится
27 февраля 2023 г. , 18:12
, 18:12
3
Спасибо за ответ!
Да, я думал об этом, но в моем случае трудно вычислить точки разрыва. Они определяются неявным уравнением, которое мне пришлось бы решать с помощью средства поиска корней. Я могу это сделать, но это не так элегантно. 92/4 ≤ 1/2? 1. : 0. х = -1,0:0,01:1,0 у = -2,0:0,01:2,0 г = е. (х, у ‘) е = 0,5 ∇x = vcat(diff(z, dims=1), нули(1, длина(y))) ∇y = hcat(diff(z, dims=2), нули(длина(x))) z[hypot.(∇x, ∇y) .> ϵ] .= NaN поверхность (x, y, z’, xlabel=»x», ylabel=»y», zlabel=»z»)
NB: заменил круглый диск на эллипс для облегчения отладки 3 лайка
jheinen
5
… также должен работать с GR (или графиками с базой данных по умолчанию):
Скриншот 01.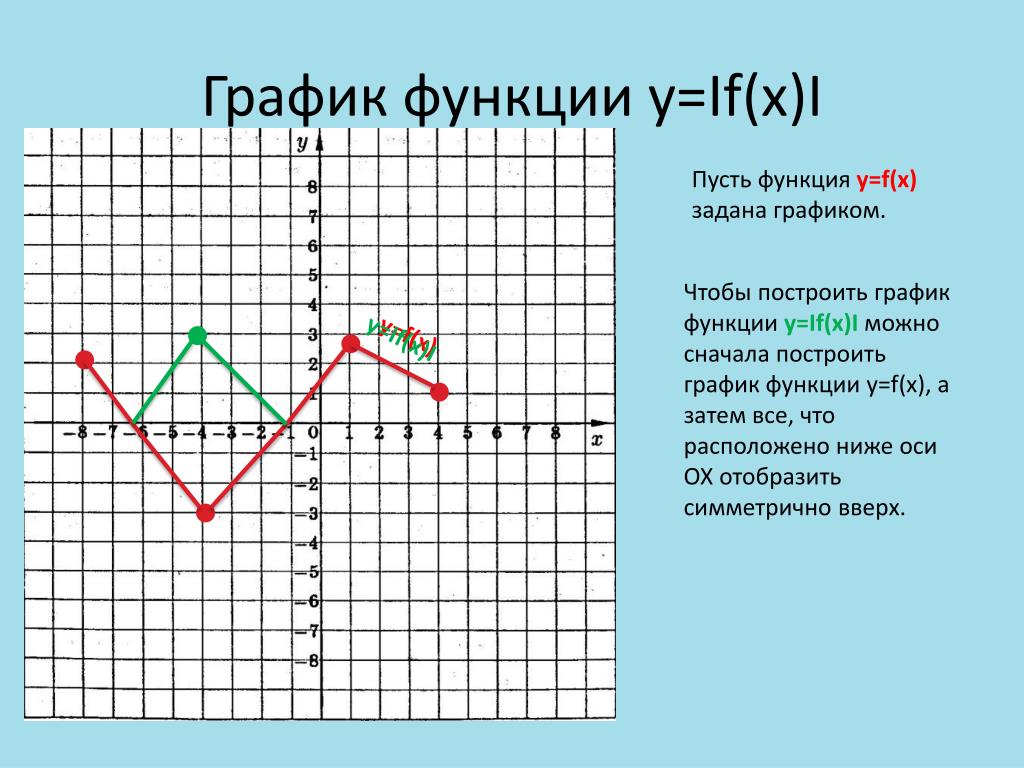 03.2023, 10.47.351430×1176 193 КБ
03.2023, 10.47.351430×1176 193 КБ
rafael.guerra
6
@jheinen, Plots.jl с бэкендом gr() в этом примере, похоже, содержит несколько ошибок.
Ошибка на aspect_ratio=:равно , который не применяется к осям Z:
поверхность (x, y, z', ratio=:equal)
Ошибка в пределах цветовой шкалы, если мы установим zlims , чтобы исправить ошибку aspect_ratio выше:
surface(x, y, z', ratio=:equal, zlims=(-2,2))
1 Нравится
Как построить график z = f(x,y) в двухмерных декартовых координатах?
# 1 Опубликовано в microsoft. |
Как построить график z = f(x,y) в двухмерных декартовых координатах? Фактор Z, который я хочу изобразить, является функцией температуры и давления. z Спасибо Тим Ответить с цитатой |
№ 2 Опубликовано в microsoft.public.excel.charting |
Как построить график z = f(x,y) в двухмерных декартовых координатах? В субботу, 11 августа 2007 г. _Трехмерная поверхностная диаграмма_ даст вам своего рода контурный график, но x и y 9Шкалы 0133 — это шкалы категорий, поэтому вам нужно быть осторожным при выборе значений x В качестве альтернативы вы можете создать _XY (точечную) диаграмму_, используя Что за функция? — Ответить с цитатой |
# 3 Опубликовано в microsoft. |
Как построить график z = f(x,y) в двухмерных декартовых координатах? Спасибо за быстрый ответ, Перед публикацией здесь я пробовал использовать _3D Surface Chart_, но безуспешно. Я попробую второй метод, описанный вами (однако, если у вас есть время, Функция, которую я не могу построить, называется коэффициентом сжимаемости газа. «, можно рассчитать с помощью корреляции Брилла и Беггса или Холла-Ярборо. Тим «Дель Коттер» написал: _Трехмерная поверхностная диаграмма_ даст вам что-то вроде контурного графика, но шкалы x и y В качестве альтернативы вы можете создать _XY (точечную) диаграмму_, используя Что за функция? — Ответить с цитатой |
# 4 Опубликовано в microsoft.public.excel.charting |
Как построить график z = f(x,y) в двухмерных декартовых координатах? В субботу, 11 августа 2007 г. Я имел в виду уравнение и некоторые выборочные коэффициенты. — Ответить с цитатой |
# 5 Опубликовано в microsoft.public.excel.charting |
Как построить график z = f(x,y) в двухмерных декартовых координатах? Корреляции длинные и не укладываются в одну формулу. ВХОДНЫЕ ДАННЫЕ: РАСЧЕТ ЗАВИСИМЫХ ОТ ТЕМПЕРАТУРЫ ТЕРМИНОВ: РАСЧЕТ ПРИВОДНОЙ ПЛОТНОСТИ Y ВЫЧИСЛИТЬ Z-ФАКТОР: Z=A*Ppr/Y «Del Cotter» написал: Это просто несколько линий XY на одной диаграмме XY, каждая с разное Я имел в виду уравнение и некоторые выборочные коэффициенты. — Ответить с цитатой |
# 6 Опубликовано в microsoft. |
Как автоматически рассчитать z-фактор Как автоматически рассчитать коэффициент z с помощью уравнения Холла-Ярборо без изменения (Y) каждый раз, чтобы достичь F = 0? Большое спасибо. Ответить с цитатой |
# 7 Опубликовано в microsoft.public.excel.charting |
Как автоматически рассчитать z-фактор Пожалуйста, не делайте многопостов. |

 public.excel.charting
public.excel.charting , в microsoft.public.excel.charting,
, в microsoft.public.excel.charting, 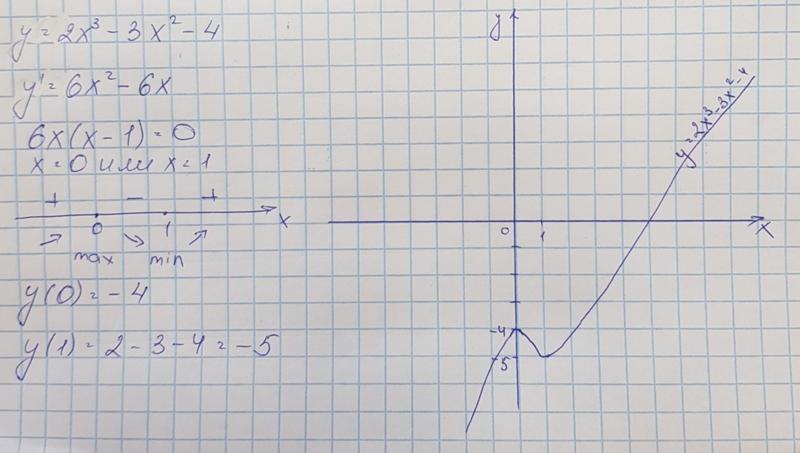 public.excel.charting
public.excel.charting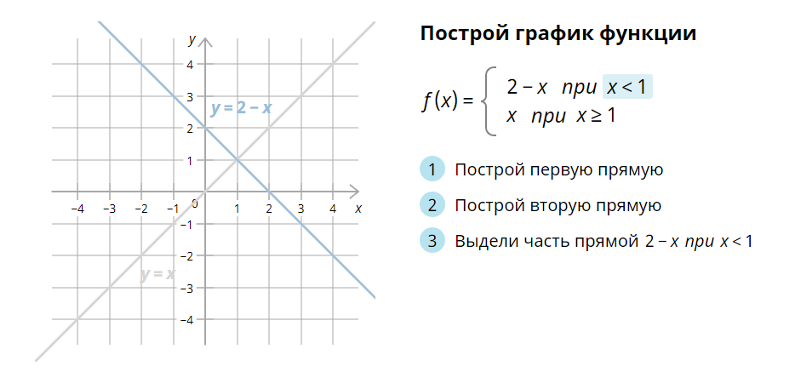 ценности.
ценности.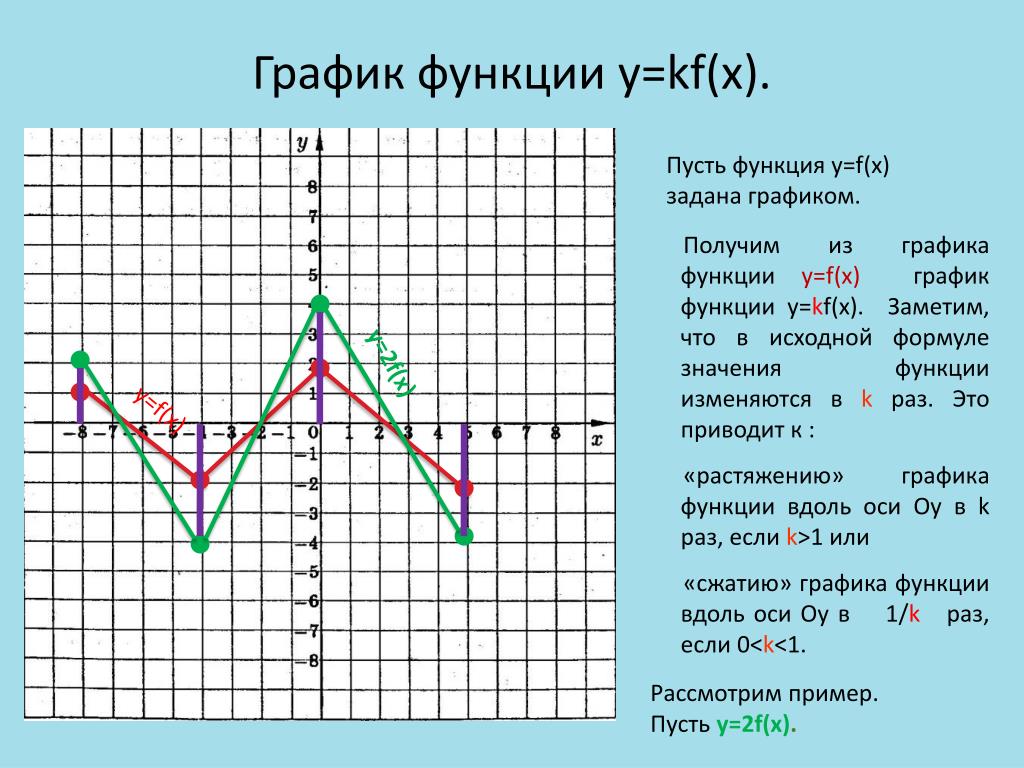 , в microsoft.public.excel.charting,
, в microsoft.public.excel.charting, 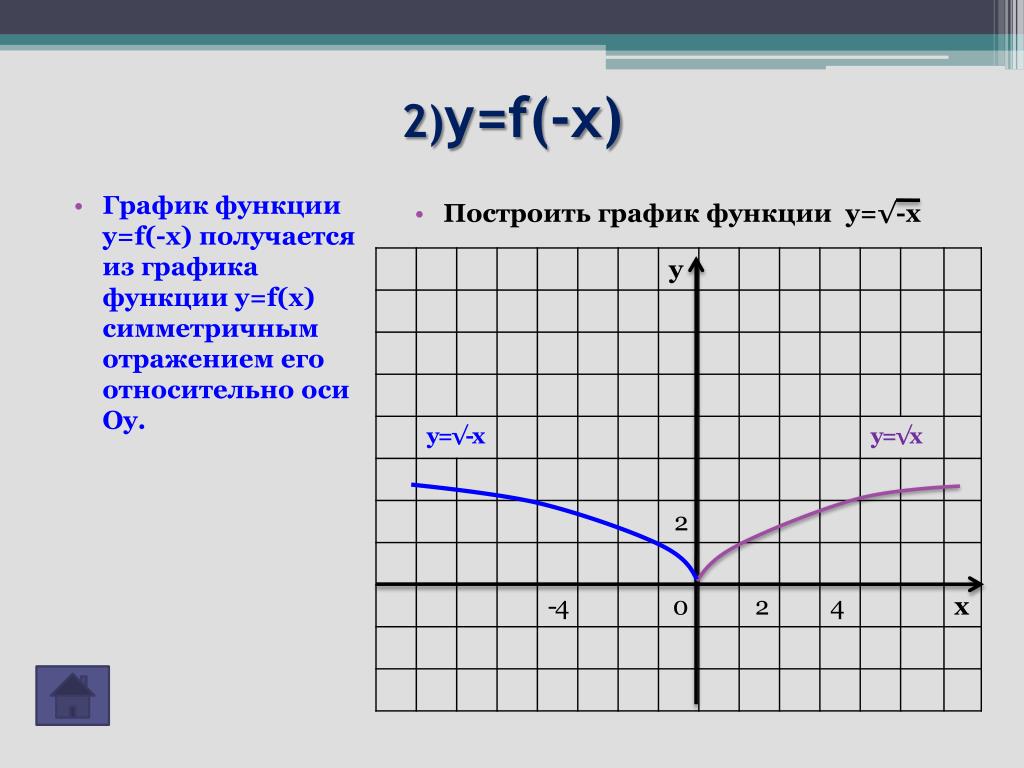
 0+314.0*SGFG Ppc=708.75-57.5*SGFG
0+314.0*SGFG Ppc=708.75-57.5*SGFG 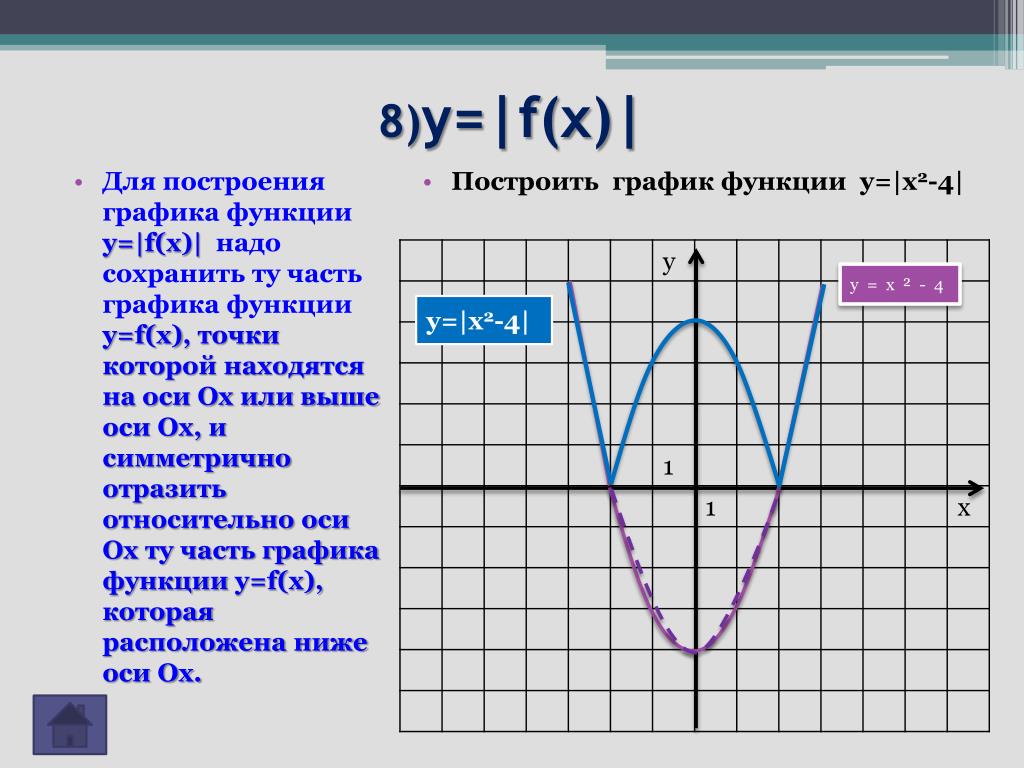 Вы должны увидеть примеры в учебниках по таким предметам, как термодинамика
Вы должны увидеть примеры в учебниках по таким предметам, как термодинамика 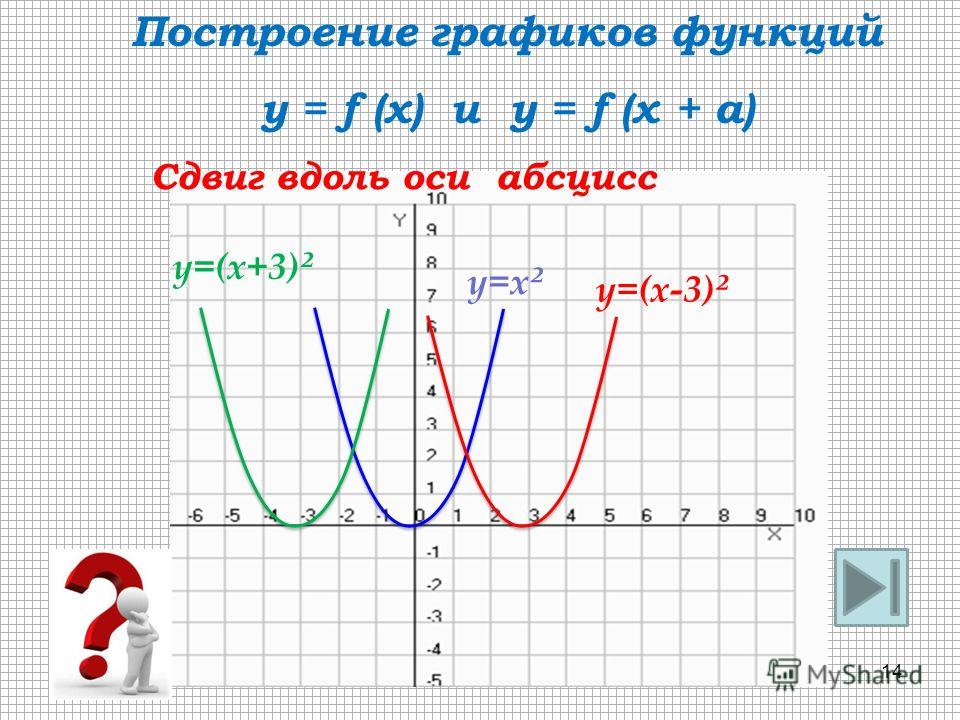 public.excel.charting
public.excel.charting