Дробно-рациональной функцией называется отношение двух многочленов: , коэффициенты при степенях x -действительные числа, причём, будем предполагать, что числитель и знаменатель дроби не имеют общих линейных сомножителей. При построении графика дробно-рациональной функции надо исследовать поведение функции на бесконечности, а также вблизи нулей знаменателя, которые определяют вертикальные асимптоты графика. Рассмотрим поведение функции на . Возможны 4 случая. 1) n<m . Если степень числителя меньше степени знаменателя, то дробно-рациональная функция стремится к нулю при стремлении x к . 2) n=m . В этом случае предел функции на равен отношению старших коэффициентов, это значит, что у функции будет горизонтальная асимптота
. 3) n=m+1 . В этом случае у функции будет наклонная асимптота y=kx+b , которая получается в результате деления числителя дроби на знаменатель: . 4) n≥m+2 . Значения функции стремятся к при стремлении аргумента x к . Знак бесконечности легко определяется по степеням старших членов n,m и коэффициентам an ,bm при старших степенях, а именно, на + ∞ знак определяется знаком произведения an·bm , а на — ∞ — знаком выражения (-1)n-m·an·bm . Теперь рассмотрим поведение дробно-рациональной функции вблизи точек разрыва, т.е. нулей знаменателя. Пусть — корень знаменателя кратности k . Это значит, что при разложении знаменателя на множители
одним из сомножителей будет двучлен . Рассмотрим частный случай дробно-рациональной функции: дробно-линейную функцию , в числителе и знаменателе которой линейные функции. Графиком дробно-линейной функции является гипербола.
Расположение гиперболы определяется вертикальной асимптотой и горизонтальной асимптотой. Вертикальная асимптота — это нуль знаменателя,
то есть прямая , а горизонтальная асимптота-прямая ( случай 2 : n=m). Рассмотрим примеры.
|
Дробно-рациональная функция (задание №23 ОГЭ)
Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная
Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная
Пример1 . Построим график функции , т.е. представим ее в виде : выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
.
Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы вверх на 2 единицы.
При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3.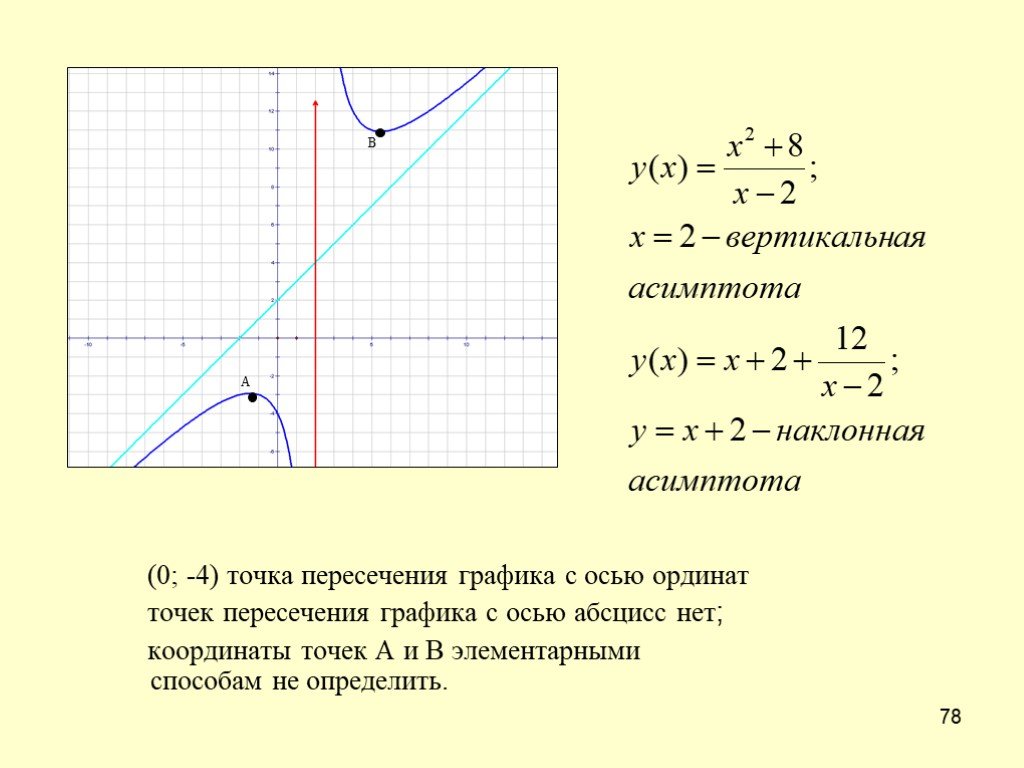 Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):
Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):
x | -7 | -2 | -1 | 0 | 1 | 2 | 2,5 |
y | 1,5 | 1 | 0,75 | 0,33 | -0,5 | -3 | -8 |
x | 3,5 | 4 | 5 | 6 | 7 | 8 | 13 |
y | 12 | 7 | 4,5 | 3,33 | 3,25 | 3 | 2,52 |
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.
Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.
Любую дробь можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
Пример 2.
Построим график функции .
Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.
Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.
Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби относительно малы. Поэтому
.
Стало быть, горизонтальная асимптота – прямая у=3/2.
Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).
Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.
Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.
Найти область определения функции.
Разложить на множители квадратный трехчлен.
Сократить дробь.
Построить график (параболу, гиперболу, кубическую параболу).
Исключить из графика точки, не входящие в область определения («выколотые» точки).
Найти значение функции в «выколотых» точках.
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.

ЗАДАНИЕ
Построить график функции (D(y), на графике – выколотые точки):
Графики рациональных функций
Горячая математикаРациональные функции имеют вид у знак равно ф Икс , куда ф Икс это рациональное выражение .
Некоторые из примеров рациональных функций:
у знак равно 1 Икс , у знак равно Икс Икс 2 − 1 , у знак равно 3 Икс 4 + 2 Икс + 5
Графики рациональных функций нарисовать сложно.
Этапы построения графика рациональных функций:
- Найдите асимптоты рациональной функции, если они есть.
- Нарисуйте асимптоты в виде пунктирных линий.
- Найди Икс -перехват (песок у -перехват рациональной функции, если таковая имеется.
- Найдите значения у для нескольких различных значений Икс .
- Нанесите точки и нарисуйте плавную кривую, чтобы соединить точки. Следите за тем, чтобы график не пересекал вертикальные асимптоты.
Пример:
График рациональной функции
у знак равно 4 Икс + 1 2 Икс + 1
Вертикальная асимптота рациональной функции равна
Икс
-значение, где знаменатель функции равен нулю.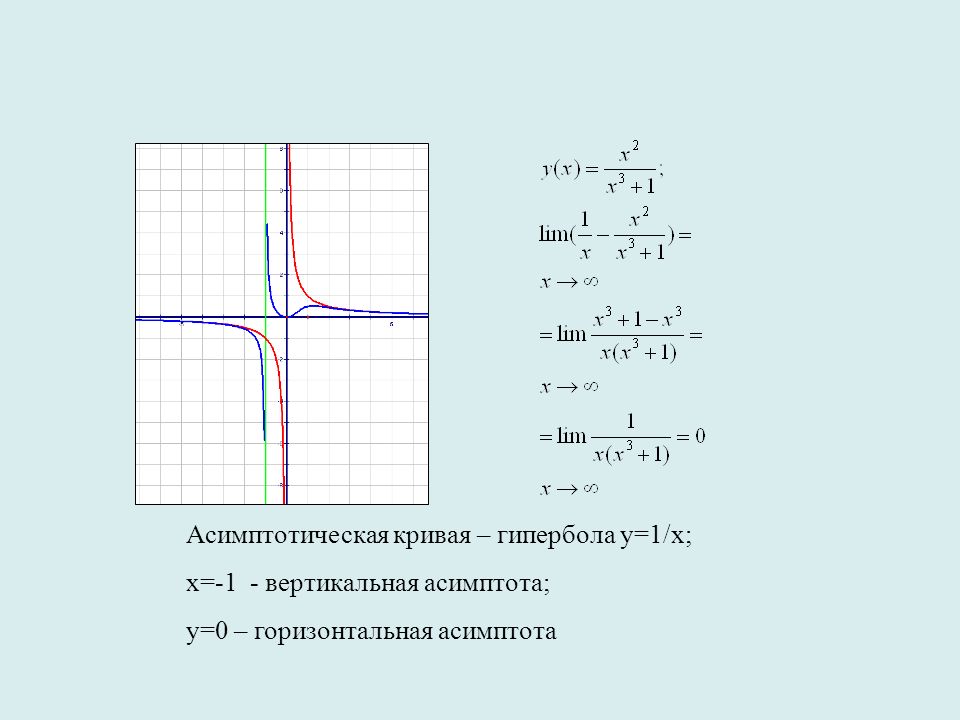 Приравнять знаменатель к нулю и найти значение
Икс
.
Приравнять знаменатель к нулю и найти значение
Икс
.
2 Икс + 1 знак равно 0 Икс знак равно − 1 2
Вертикальная асимптота рациональной функции равна Икс знак равно − 0,5 .
Эта функция имеет Икс -перехват в − 1 4 , 0 а также у -перехват в 0 , 1 . Найдите больше точек на функции и постройте график функции.
Иногда заданную рациональную функцию необходимо упростить, прежде чем строить ее график. В этом случае, если есть какие-либо исключенные значения (где функция не определена), отличные от асимптот, то для построения графика функции требуется дополнительный шаг.
Чтобы представить неопределенную функцию, убедитесь, что функция не является непрерывной гладкой кривой при исключенном значении. Это исключенное значение обычно называют дырой в рациональной функции.
Это исключенное значение обычно называют дырой в рациональной функции.
Например, рациональная функция у знак равно 4 Икс 2 + Икс 2 Икс 2 + Икс имеет отверстие в Икс знак равно 0 .
Обратите внимание, что графики рациональных функций удовлетворяют тест вертикальной линии .
Алгебра — полиномиальные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
В этой главе мы более подробно рассмотрим многочлены. Мы уже решили и изобразили полиномы второй степени ( , то есть квадратных уравнений/функций), и теперь мы хотим распространить это на более общие многочлены. Мы рассмотрим нахождение решений для полиномов более высокой степени и то, как получить грубый набросок для полинома более высокой степени.
В этой главе мы также рассмотрим частичные дроби. На самом деле она не имеет ничего общего с построением графиков полиномов, но ее нужно было куда-то поместить, и эта глава казалась таким же подходящим местом, как и любая другая.
Вот краткий перечень материалов этой главы.
Деление многочленов. В этом разделе мы рассмотрим некоторые основы деления многочленов. Мы определим остаток и делитель, используемые в процессе деления, и введем понятие синтетического деления. Мы также дадим алгоритм деления.
Нули/корни многочленов. В этом разделе мы определим нуль или корень многочлена, а также то, является ли он простым корнем или имеет кратность \(k\). Мы также приведем Фундаментальную теорему алгебры и Факторную теорему, а также пару других полезных фактов.
Графики полиномов. В этом разделе мы опишем процесс, который позволит нам получить грубый набросок графика некоторых полиномов. Мы обсудим, как определить поведение графа на \(x\)-перехватах, и тест старшего коэффициента для определения поведения графа, когда мы допускаем неограниченное возрастание и убывание x.
Нахождение нулей многочленов. Как мы видели в предыдущем разделе, чтобы набросать график многочлена, нам нужно знать, что это за нули. Однако, если мы не можем разложить полином на множители, мы не сможем выполнить этот процесс.


 При приближении аргумента x к числитель дроби представляет некую константу, отличную от нуля, а знаменатель стремится к нулю, а значит,
дробь будет неограниченно возрастать по абсолютной величине, стремясь к . Таким образом, прямая будет вертикальной асимптотой графика функции. Знак бесконечности, к которой стремится функция слева и справа от , можно определить непосредственно подстановкой вместо x в выражение функции числа, близкого к числу с недостатком (слева) или с избытком (справа), но обычно этот знак определяется по методу интервалов,
если нам известны корни числителя и знаменателя.
При приближении аргумента x к числитель дроби представляет некую константу, отличную от нуля, а знаменатель стремится к нулю, а значит,
дробь будет неограниченно возрастать по абсолютной величине, стремясь к . Таким образом, прямая будет вертикальной асимптотой графика функции. Знак бесконечности, к которой стремится функция слева и справа от , можно определить непосредственно подстановкой вместо x в выражение функции числа, близкого к числу с недостатком (слева) или с избытком (справа), но обычно этот знак определяется по методу интервалов,
если нам известны корни числителя и знаменателя.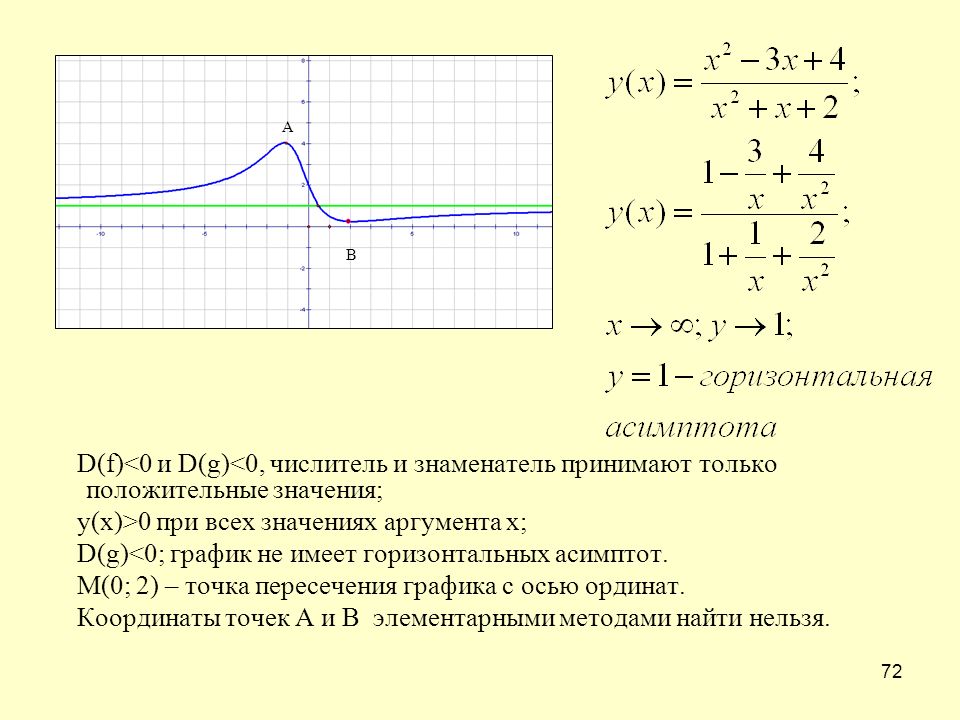 Заметим, что рассматривая дробно-линейную функцию, мы предполагаем, что с ≠ 0 , иначе функция будет линейной, и её графиком будет прямая линия.
Заметим, что рассматривая дробно-линейную функцию, мы предполагаем, что с ≠ 0 , иначе функция будет линейной, и её графиком будет прямая линия.