График функции онлайн с модулем. График функции
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus. ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.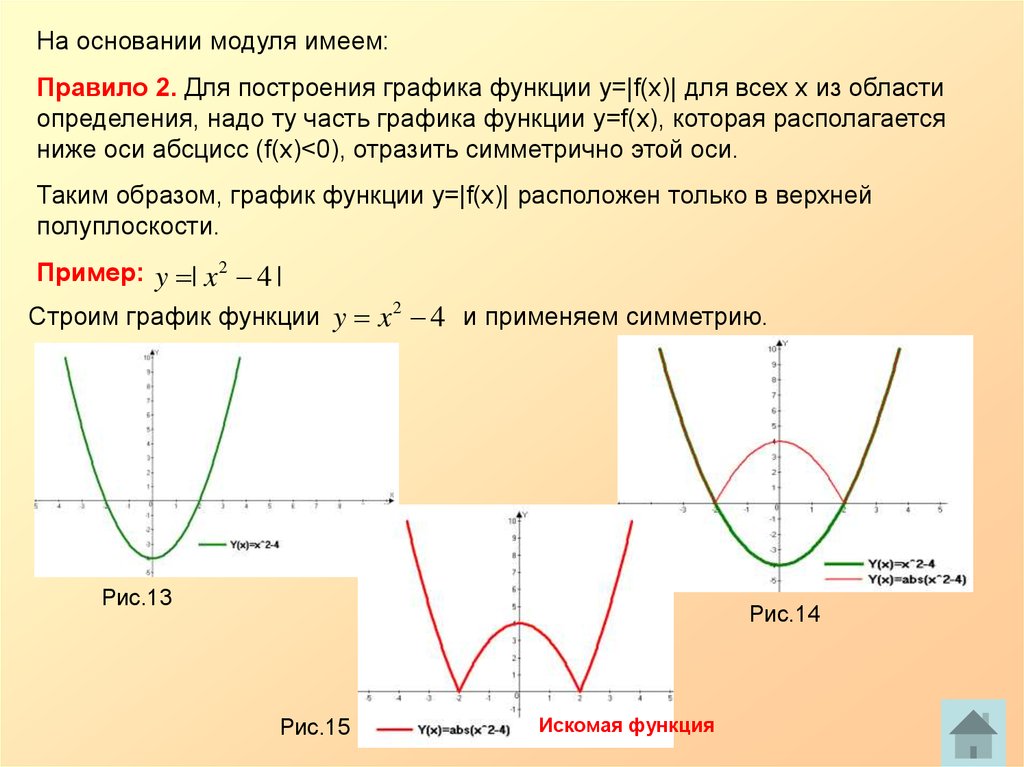
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т.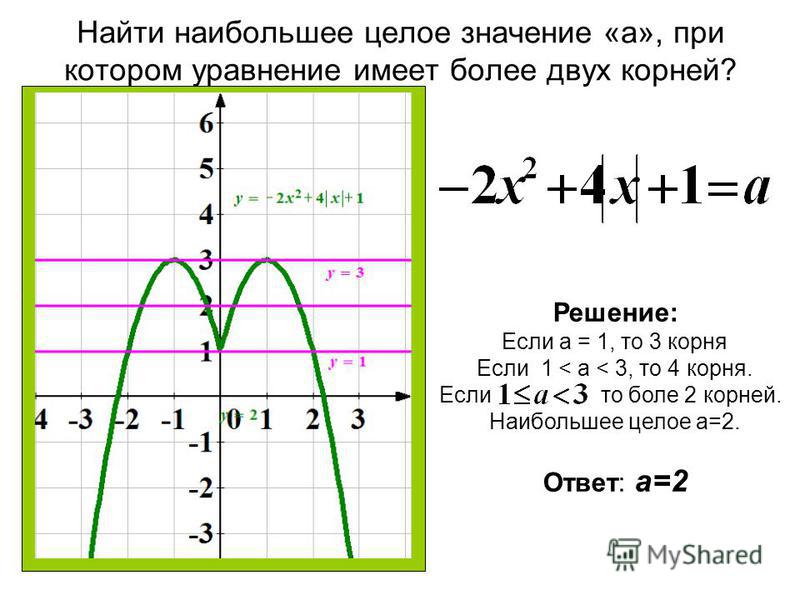 е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью.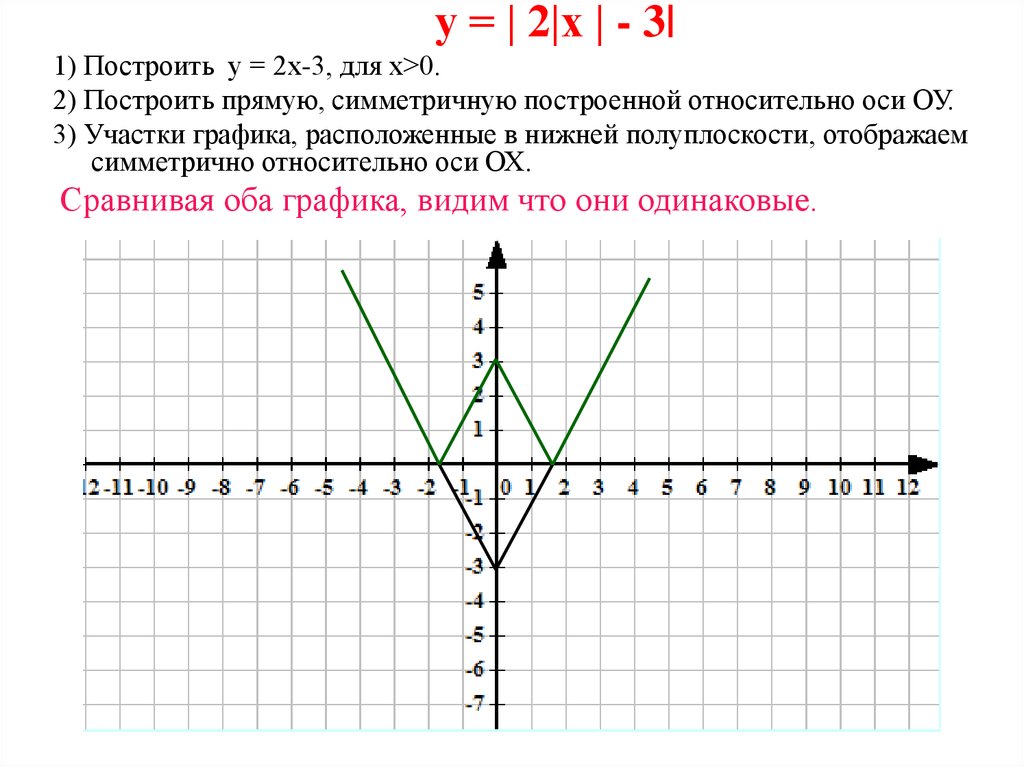 Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис.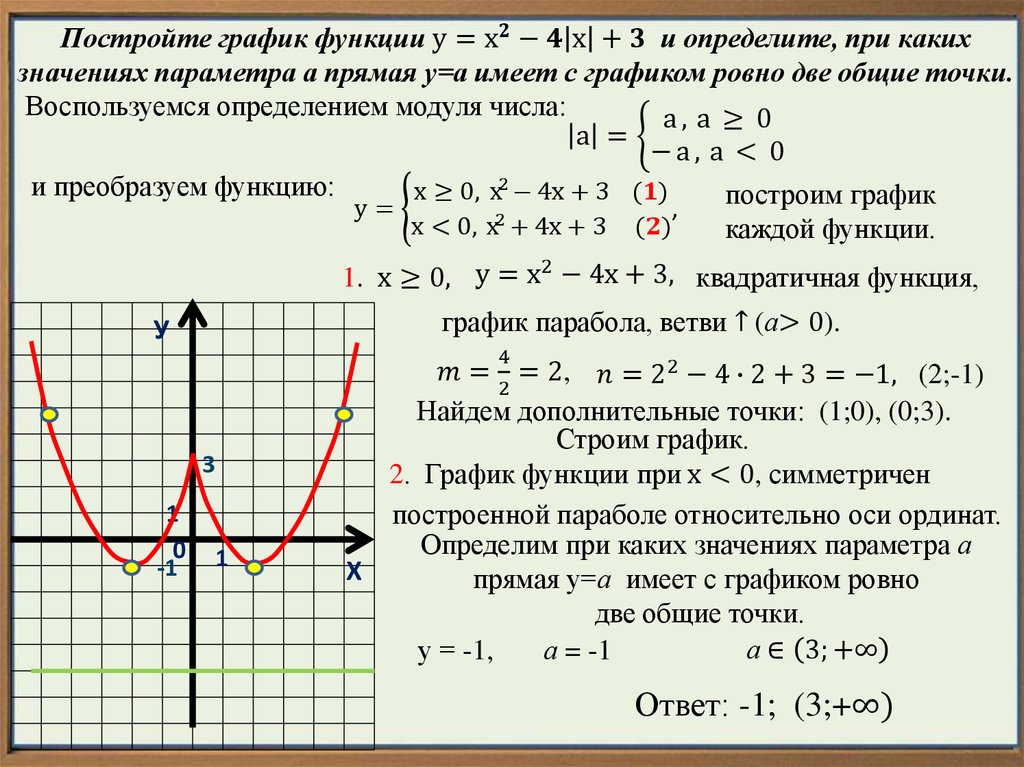
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика.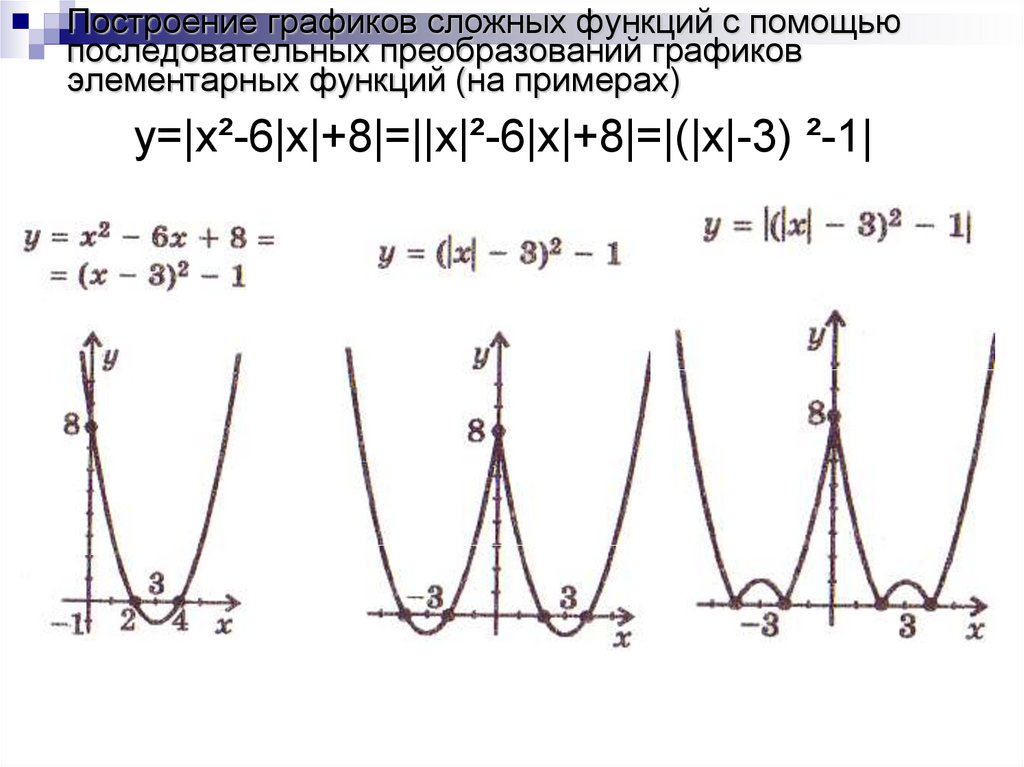
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
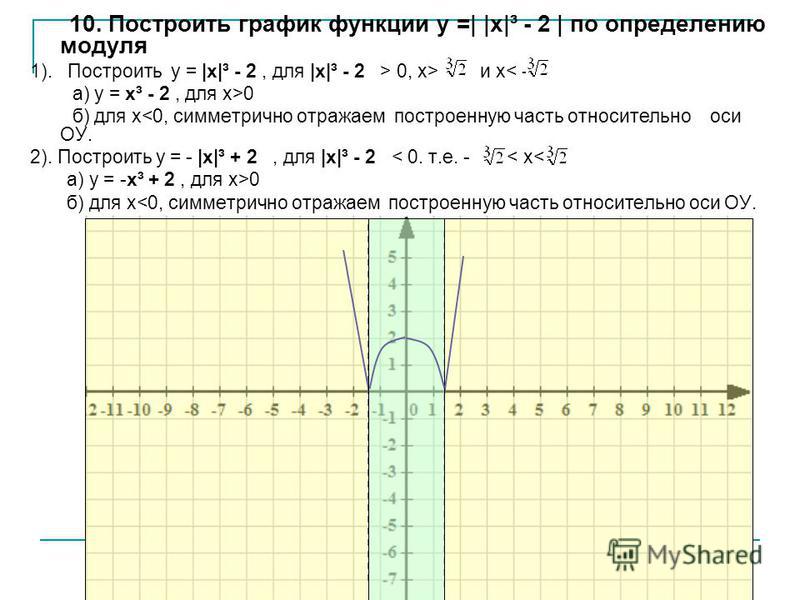
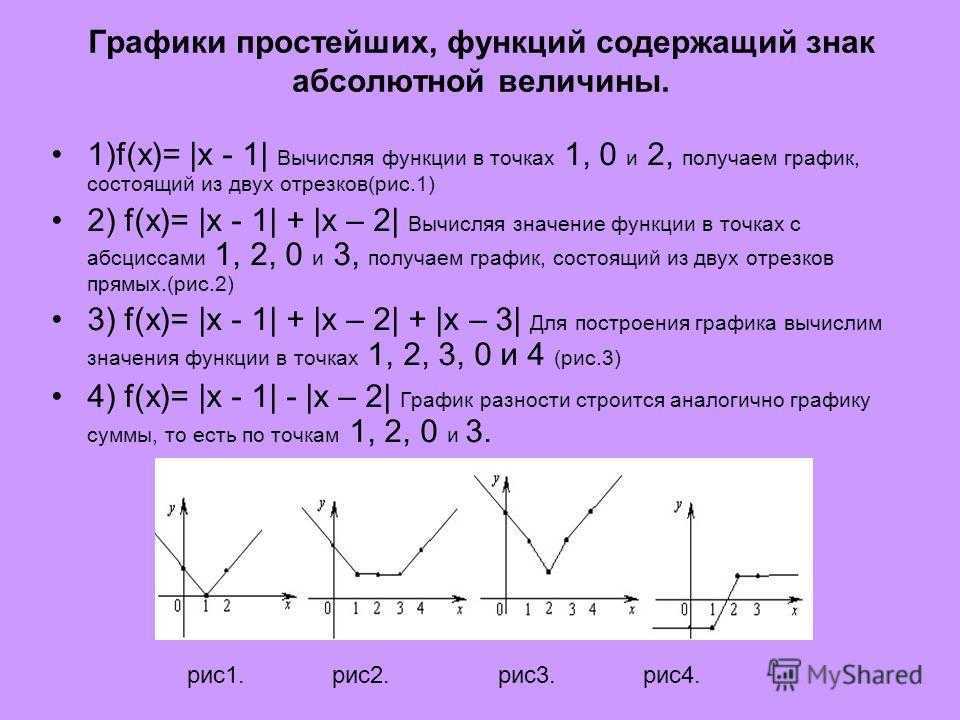
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .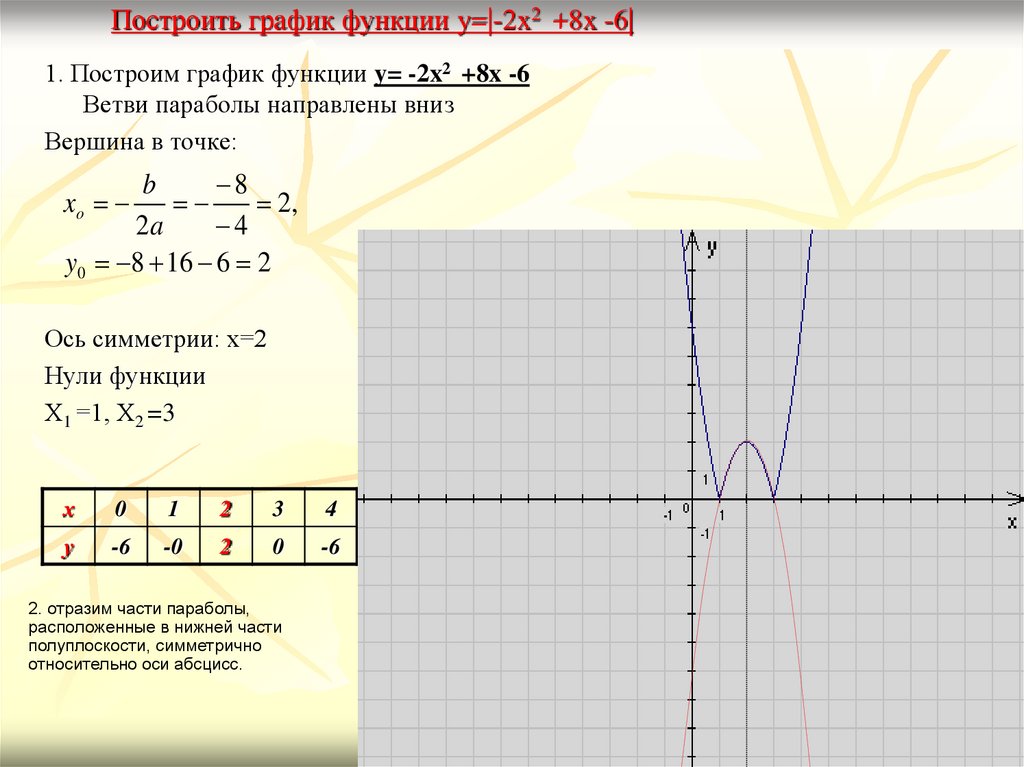
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).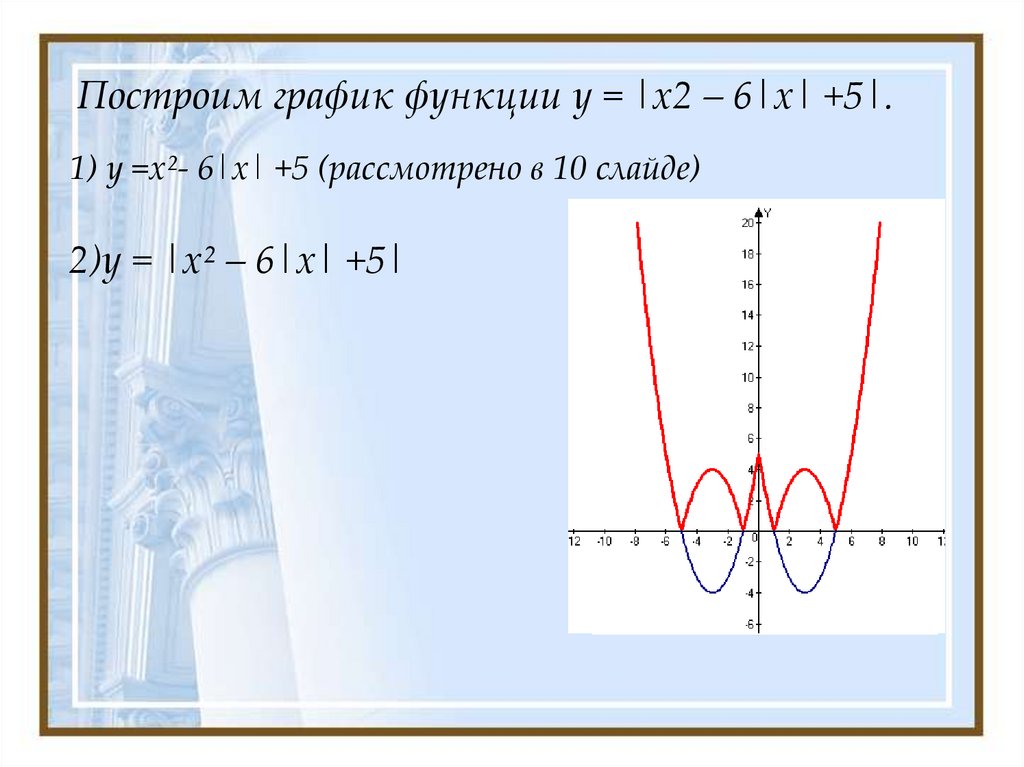
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Построение графиков функций и зависимостей, содержащих знак модуля с использованием информационных технологий
Проблема: повышение уровня математической подготовка учащихся через решение задач повышенной сложности с использованием в учебном процессе современных информационных технологий.
При решении последних заданий в работах, предлагаемых на выпускных экзаменах за курс средней школы, а также при решении задач, предлагаемых на вступительных экзаменах в вузы по математике, могут быть использованы любые известные учащимся математические методы.
Как правило, применение «нестандартных» методов позволяет более эффективно решать многие задачи повышенной сложности. Мой опыт работы в школе показывает, что задания на построение графиков функций и зависимостей, содержащих знак модуля, вызывают у учащихся затруднения.
Цель работы: рассмотреть построение графиков трех видов: y = f(|x|), y = |f(x)|, |y| = f(x) — для дальнейшего применения данного материала на уроках алгебры, на факультативных и дополнительных занятиях.
Построение графиков функций и зависимостей, содержащих знак модуля
В методической литературе этому вопросу уделяется немало внимания; наблюдения показывают, что такие задачи вызывают у учащихся затруднения и они допускают ошибки при построении указанных графиков.
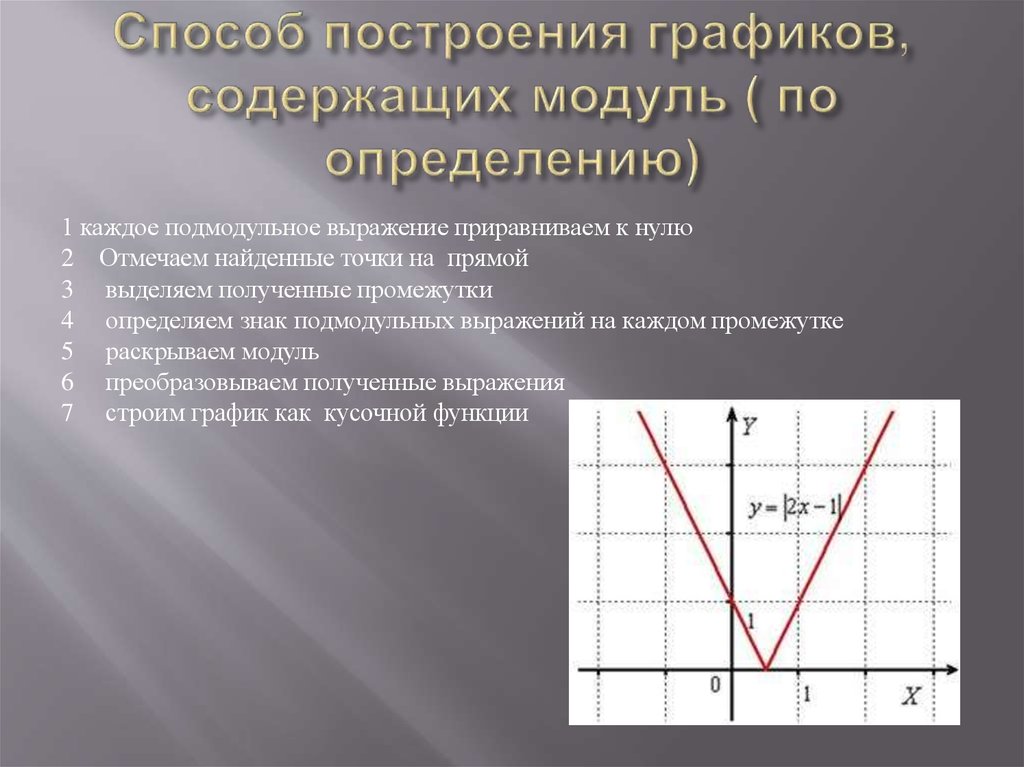
Одна из причин таких ошибок кроется, на мой взгляд, в непонимании учащимися определения модуля числа:
При работе над определением модуля числа учитель должен обратить внимание учащихся на то, что число — x может быть как отрицательное (при x < 0), так и положительное (при х > 0).
В курсе алгебры неполной средней школы на уроках и в период проведения внеклассной работы целесообразно рассмотреть построение графиков трех видов:
y = f(|x|), y = |f(x)|, |y| = f(x).
Для построение всех типов графиков учащимся достаточно хорошо понимать определение модуля и знать виды простейших графиков, изучаемых в школе.
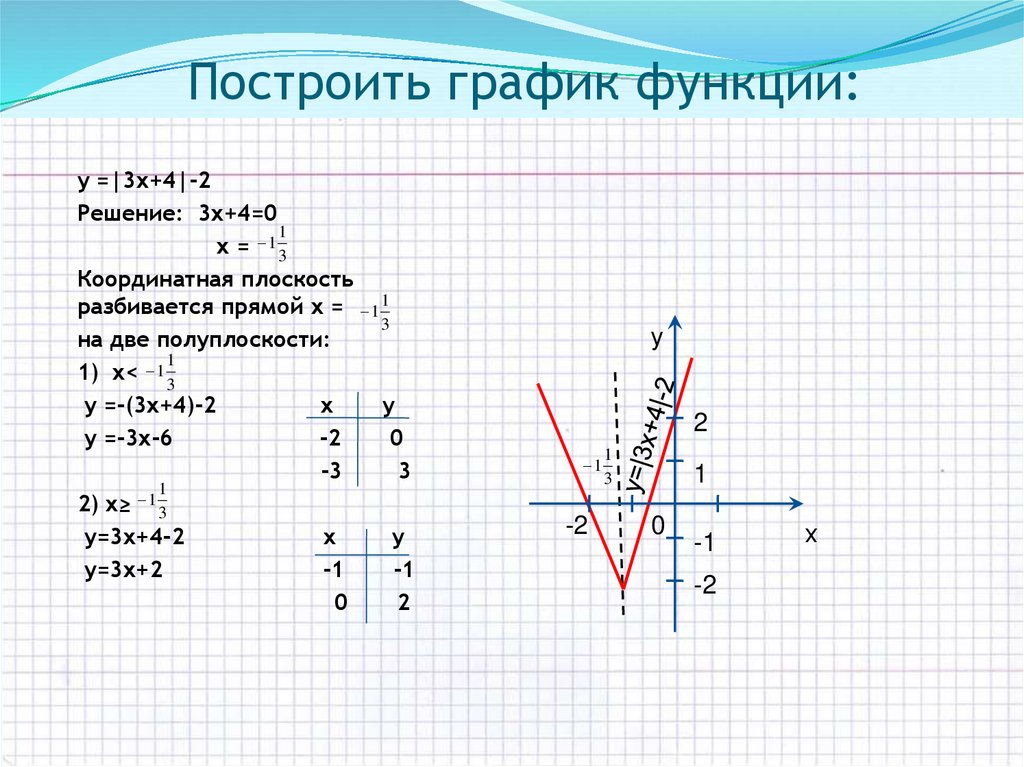
Так, для построения графика функции y = f(|x|) на основании модуля имеем:
Следовательно, график функции y = f(|x|) состоит из двух графиков: y = f(x) — в правой полуплоскости, y = f(-x) — в левой полуплоскости.
Например:
После того, как учащиеся познакомятся с определением четной и нечетной функции, их можно познакомить с правилом 1.
Правило 1: функция y = f(|x|) — четная, поэтому для построения ее графика достаточно построить график функции y = f(x), для всех х ≥ 0 из области определения и отразить полученную часть симметрично оси ординат.
Знание этого правила облегчает построение графиков функций вида y = f(|x|).
Целесообразно предлагать учащимся строить графики двумя способами:
1) на основании определения модуля;
2) на основании правила 1.
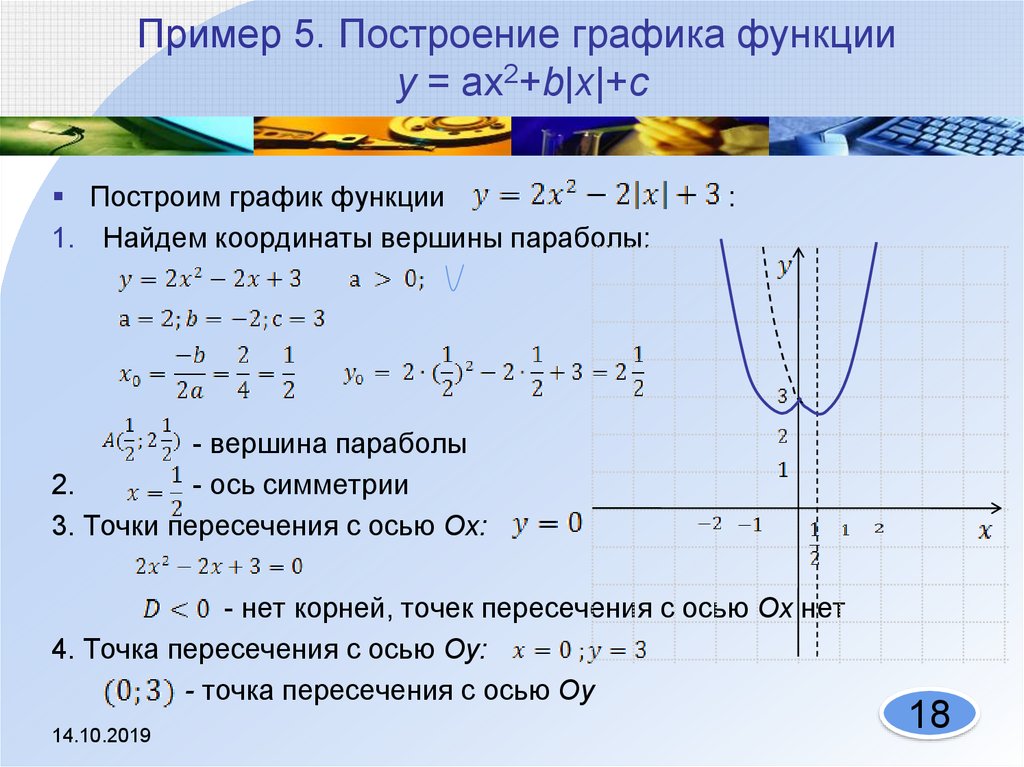
После знакомства с квадратичной функцией весьма интересным и полезным является построение графиков функций:
| Рисунок 1 | Рисунок 2 |
В старших классах после знакомства учащихся с графиками тригонометрических функций полезно построить графики функций y = sin(|x|), y = cos(|x|), y = tg(|x|), обратив внимание учащихся, что график функции y = cos(|x|) совпадает с графиком y = -cos(|x|) (y = cos(|x|) — четная функция).
В современном образовании одним из важных и актуальным вопросом является разработка методики внедрения и использования информационных, компьютерных и мультимедийных продуктов в учебном процессе.
Одной из удобной форм активизации передачи и восприятия информации, на наш взгляд, является компьютерная интерактивная презентация, которую целесообразно использовать учителю в качестве сопровождения при объяснении нового материала.
Пример слайдов компьютерной презентации, иллюстрирующих правило 1:
Знакомство учащихся с построением графиков функций вида y = |f(x)| лучше начинать сразу же, как только они хорошо усвоят определение модуля.
Правило 2: для построения графика функции y = |f(x)| для всех x из области определения, надо ту часть графика функции y = f(x), которая располагается ниже оси абсцисс (f(x)Таким образом, график функции y = |f(x)| расположен только в верхней полуплоскости.
Пример: y = |x2 — 4|.
Строим график функции y = x2 — 4 (рис.
3).
Рисунок 3 Как правило, учащиеся хорошо понимают правило построения графика такой функции. Его можно легко довести до автоматизма. Во избежание формализма в знаниях и умениях учащихся необходимо чередовать построение графиков вида y = f(|x|) и y = |f(x)|.
С построением графиков зависимостей вида |y| = f(x) учащихся можно познакомить на внеклассных занятиях, ибо такие графики вызывают наибольшие затруднения. Учитывая, что в формуле |y| = f(x) f(x) ≥ 0 и на основании определения модуля
,
перепишем формулу |y| = f(x) в виде y = ±f(x), где f(x) ≥ 0.
Исходя из этого, можно сформулировать правило 3.
Правило 3: для построения графиков зависимости (а не функции) достаточно построить график функции y = f(x) для тех x из области определения, при которых f(x) ≥ 0 и отразить полученную часть графика, симметрично оси абсцисс.Таким образом, график зависимости |y| = f(x) состоит из графиков двух функций: y = f(x) и y = —f(x), где f(x) ≥ 0.
Мы убедились, что учитель, проводящий урок с помощью компьютера, имеет возможность интенсифицировать процесс обучения, сделать его более наглядным, динамичным. Такие уроки вызывают большой интерес у учащихся, способствуют повышению качества знаний, расширяют горизонты школьной математики.
В соответствии с этим правилом можно предложить учащимся построить графики (рис. 4):
Рисунок 4 Конечно, нет необходимости требовать от учащихся запоминания правил построения.
Пример экзаменационной работы:
X
1
2
4
½
Y
2
1
½
4
Так как |y| ≥ 0, x ≠ 0, x > 0 y = |f(|x|)|.
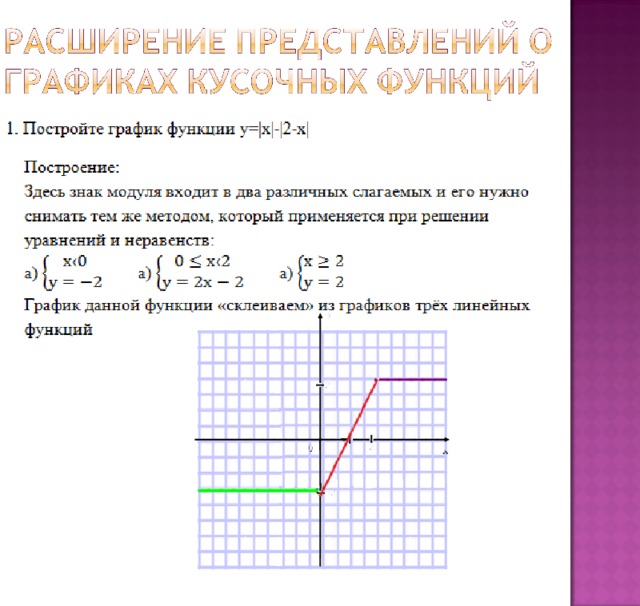
Правило 4: для того, чтобы построить график функции y = |f(|x|)|, надо скачала построить график функции y = f(x) при x > 0, затем при х < 0 построить изображение, симметричное ему относительно оси 0y, а затем на интервалах, где f(|x|) < 0, построить изображение, симметричное графику f(|x|) относительно оси Ох.Рассмотрим еще несколько интересных заданий.
1. Построить график функции ОДЗ: x ≠ -1
2. Построить график функции
3. Построить график функции Упростим:
Получим:
1) 2) 3) Все рассмотренные задания можно использовать на уроках алгебры, факультативных и дополнительных занятиях.
График из текстового файла онлайн с примерами кода
Построить график из текстового файла онлайн с примерами кода
В этой статье решение Построить график из текстового файла онлайн будет продемонстрировано с использованием примеров из языка программирования.
set terminal svg size 400,300 расширенный fname 'arial' fsize 10 butt solid
Как мы видели, задача построения графика из текстового файла онлайн была решена с использованием ряда различных экземпляров.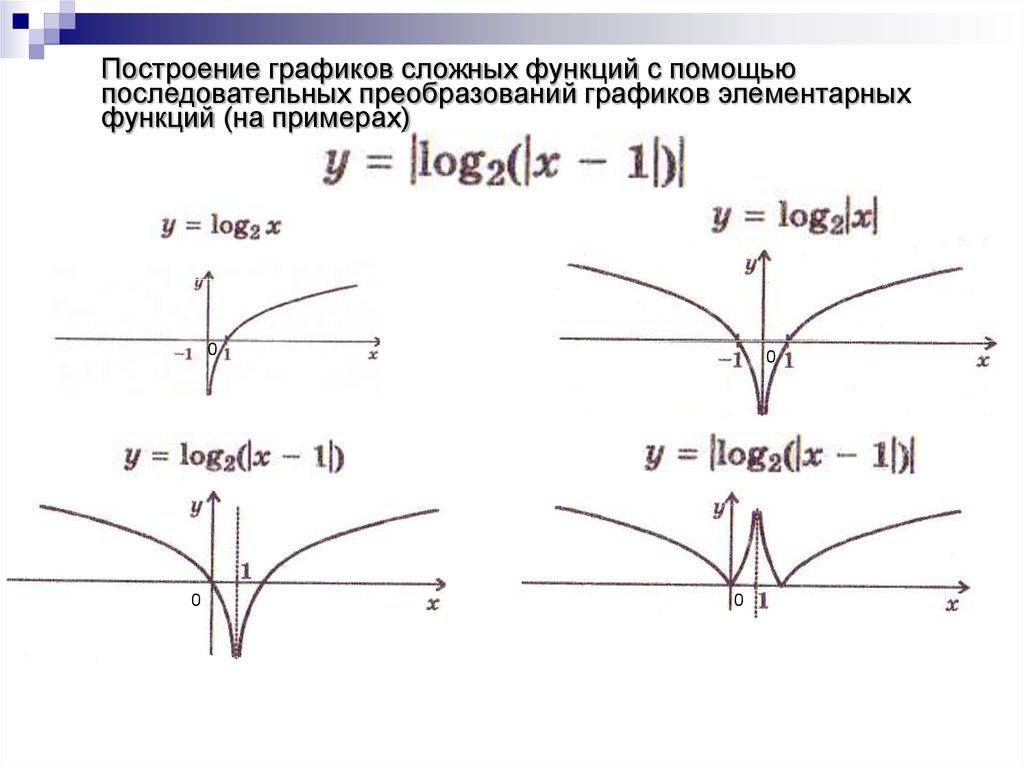
Как построить график онлайн?
Как создать линейный график
- Введите заголовок, метки горизонтальной и вертикальной осей графика.
- Введите имена или значения меток данных или диапазон.
- Установить количество строк.
- Для каждой строки введите значения данных с разделителем-пробелом, меткой и цветом.
- При необходимости проверьте изогнутую линию.
- Нажмите кнопку Draw, чтобы создать линейный график.
Можно ли рисовать графики онлайн?
Canva предлагает ряд бесплатных дизайнерских шаблонов. Все, что вам нужно сделать, это ввести свои данные, чтобы получить мгновенные результаты. Переключайтесь между различными типами диаграмм, такими как гистограммы, линейные графики и круговые диаграммы, без потери данных.
Как построить график в текстовом файле?
Программный подход:
- Импорт matplotlib. модуль pyplot для визуализации.
- Открытый образец. txt в режиме чтения ‘r’ с помощью функции file open().

- Перебрать каждую строку в файле, используя цикл for.
- Добавьте каждую строку файла в список, необходимый для нашей визуализации.
- Использование плт.
Как построить график в текстовом файле в Matlab?
Как построить график из данных?
Как построить график в Excel
- Введите данные в Excel.
- Выберите один из девяти вариантов графиков и диаграмм.
- Выделите свои данные и нажмите «Вставить» нужный график.
- При необходимости переключите данные на каждой оси.
- Настройте макет и цвета ваших данных.
- Измените размер условных обозначений диаграммы и меток осей.
Как сделать график с помощью Word?
Как? На вкладке «Вставка» в группе «Иллюстрации» нажмите «Диаграмма». В диалоговом окне «Вставить диаграмму» нажимайте стрелки для прокрутки типов диаграмм. Выберите нужный тип диаграммы и нажмите кнопку ОК.
Десмос бесплатен?
Desmos — это бесплатный инструмент для построения графиков и обучения математике, доступный в Интернете, а также для iOS и Android.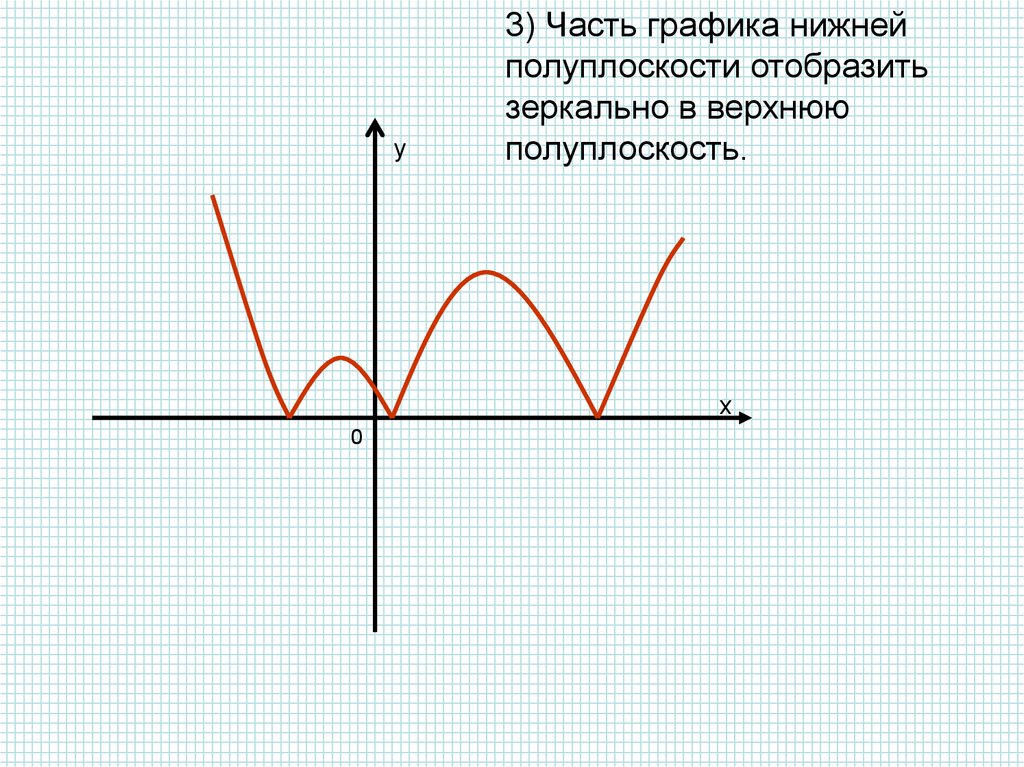 В дополнение к построению уравнений в классе доступны занятия, которые помогут учащимся узнать о различных математических концепциях.
В дополнение к построению уравнений в классе доступны занятия, которые помогут учащимся узнать о различных математических концепциях.
Является ли Plotly chart Studio бесплатным?
Plotly — бесплатная графическая библиотека с открытым исходным кодом для Python. Мы рекомендуем вам прочитать наше руководство по началу работы, чтобы получить последние инструкции по установке или обновлению, а затем перейти к нашим учебным пособиям по основам Plotly или погрузиться прямо в некоторые учебные пособия по базовым диаграммам.
Как сделать график в Документах Google?
Как вывести данные из Блокнота в Excel?
Перейдите в Excel и выберите «Файл»> «Открыть» и выберите текстовый файл. Excel автоматически распознает его как текстовый файл и запустит мастер импорта: Параметр «С разделителями» указывает, что для разделения полей данных используется символ, например запятая или табуляция.
Категории Без категорийCopyright © Все права защищены. Тех
МодульDivi Bar Chart — Elegant Themes
Модуль Divi Bar Chart — Elegant Themes Гистограмма отлично подходит для динамического отображения данных в визуальной диаграмме на вашем веб-сайте. Модуль гистограммы для Divi позволяет создавать и стилизовать гистограмму прямо в Divi Builder. Вы можете добавлять данные для построения новой диаграммы вручную или динамически извлекать данные из внешнего источника (например, Google Sheets). После того, как все данные будут получены, вы можете настроить стиль диаграммы, используя параметры Divi Builder.
Модуль гистограммы для Divi позволяет создавать и стилизовать гистограмму прямо в Divi Builder. Вы можете добавлять данные для построения новой диаграммы вручную или динамически извлекать данные из внешнего источника (например, Google Sheets). После того, как все данные будут получены, вы можете настроить стиль диаграммы, используя параметры Divi Builder.
Просмотр демонстрации модуля Приобрести этот модуль
Документация модуля
Как использовать модуль гистограммы
Это премиальный модуль, созданный Iqonic Design. Он доступен для покупки в Divi Marketplace. Divi имеет процветающую экосистему сторонних модулей, которые значительно расширяют потенциал Divi. Это одна из сильных сторон Divi! После установки плагина модуль гистограммы станет доступен на вашем сайте. Затем вы можете настроить его, используя широкий спектр настроек дизайна Divi.
Просмотр документации модуля
Часто задаваемые вопросы
Что такое модуль Divi?
Модули Divi — это элементы контента, которые можно использовать для создания страниц в Divi.
Развернуть менюСвернуть меню Каждый модуль имеет уникальный набор функций, элементов и настроек дизайна, которые помогут вам создать что-то уникальное. Разные модули служат разным целям. Используя огромный набор модулей Divi, вы можете создать сайт практически любого типа.
Каждый модуль имеет уникальный набор функций, элементов и настроек дизайна, которые помогут вам создать что-то уникальное. Разные модули служат разным целям. Используя огромный набор модулей Divi, вы можете создать сайт практически любого типа.Включен ли этот модуль бесплатно в мое членство в Divi?
Это коммерческий модуль стороннего производителя, созданный и проданный Iqonic Design. Его можно купить на Divi Marketplace. Каждый модуль, разработанный Elegant Themes, доступен бесплатно с вашим членством в Divi, а сторонние модули доступны для покупки в Divi Marketplace. Divi Marketplace полон сотен замечательных бесплатных и коммерческих продуктов, расширяющих функциональность Divi. Эта процветающая экосистема является одним из величайших активов Divi!
Развернуть менюСвернуть менюГде я могу найти дополнительные модули Divi?
Благодаря процветающему сообществу разработчиков Divi существует множество сторонних модулей Divi, доступных бесплатно и для покупки.


 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.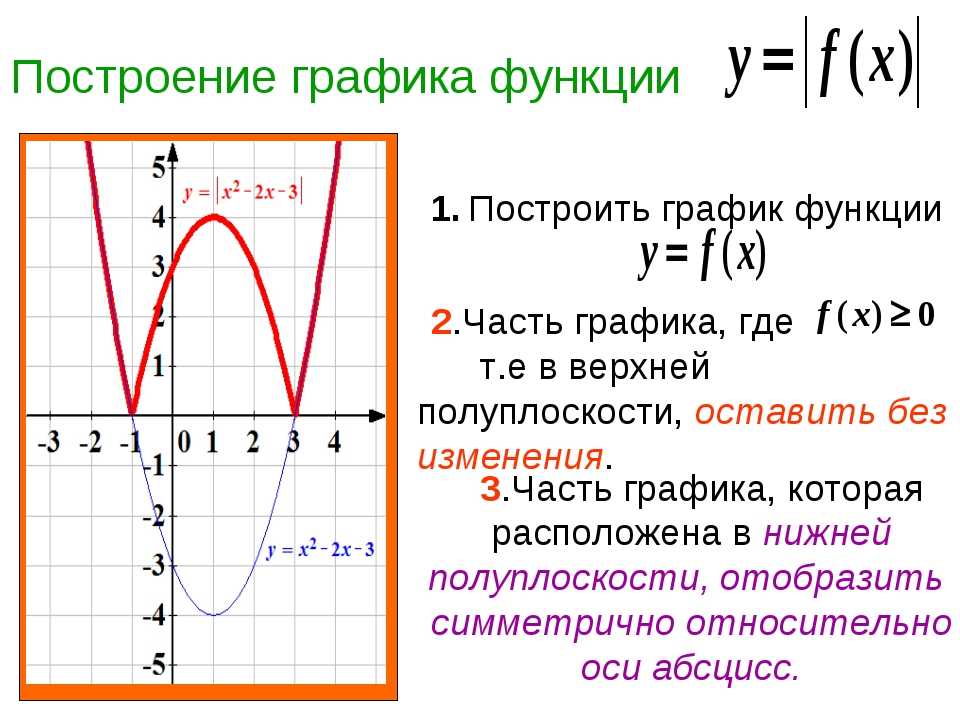
 3).
3).
 Каждый модуль имеет уникальный набор функций, элементов и настроек дизайна, которые помогут вам создать что-то уникальное. Разные модули служат разным целям. Используя огромный набор модулей Divi, вы можете создать сайт практически любого типа.
Каждый модуль имеет уникальный набор функций, элементов и настроек дизайна, которые помогут вам создать что-то уникальное. Разные модули служат разным целям. Используя огромный набор модулей Divi, вы можете создать сайт практически любого типа.