Построить график x 2 1: Mathway | Популярные задачи

2

Аналитическая геометрия в пространстве

Аналитическая геометрия в пространстве

Лабораторная работа №10

Аналитическая геометрия в пространстве

Цель:

• Построение поверхностей второго порядка с помощью системы Mathematica.

Для построения трехмерных поверхностей используется функция:
Plot3D [ f, { x ,x_min, x_max} , {y , y_min, y_max} ]

Чтобы построить график поверхности второго порядка, нужно сначала выразить переменную z из канонического уравнения, например, с помощью функции Solve, которая используется для решения уравнений, указав в качестве переменной только переменную z.
Например, выразим из уравнения эллипсоида x²+y²+z²=1 переменную z:
Solve [ x² + y² + z² = 1, z ]
Получим: { z -> -√(-1-x²-y²), z -> √(-1-x

2-y²) }
Это значит, что построение эллипсоида сводится к построению двух поверхностей в одной системе координат:
z = -√(-1-x²-y²) и z = √(-1-x²-y²).

Так как графики нужно построить в одной системе координат, то воспользуемся функцией Show [ z₁, z₂ ]. При построении графиков с целью улучшения качества графиков используем опцию PlotPoints -> n, которая указывает, сколько точек должно участвовать в построении ( n — натуральное число ). Опция Mesh -> False удаляет линии каркаса поверхности, что способствует большей наглядности в её отображении.

1. Эллипсоид
Каноническое уравнение: x² / a² + y² / b² + z² / c² = 1.
На рисунке 1 показано построение эллипсоида, заданного уравнением x² + y² + z² = 1.

Задание: Измениет параметры a, b, c и установите, как их увеличение или уменьшение влияет на изображение поверхности.

pис. 1

2. Однополостный гиперболоид
Каноническое уравнение: x² / a² + y² / b² — z² / c² = 1.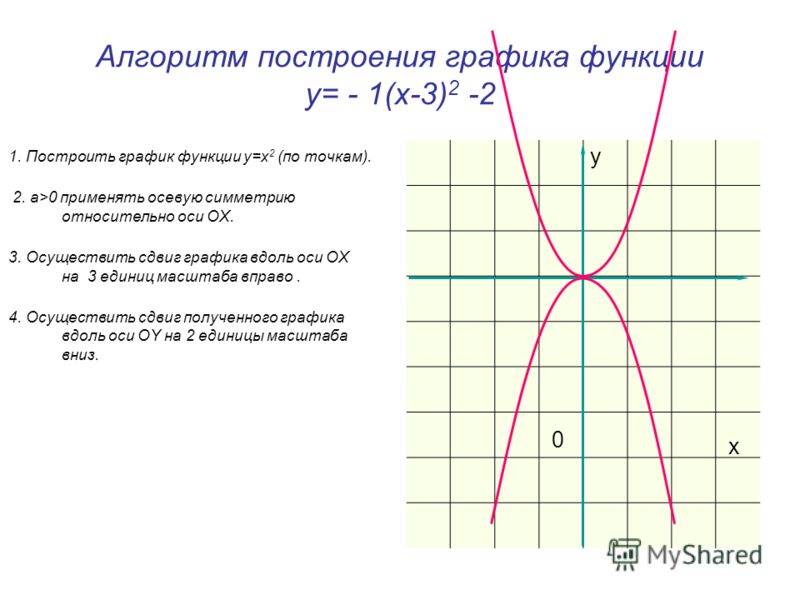
На рисунке 2 показано построение однополостного гиперболоида, заданного уравнением x² / 4 + y² / 1 — z² / 4 = 1.

pис. 2

3. Двуполостный гиперболоид
Каноническое уравнение: x² / a² — y² / b² — z² / c² = 1.
На рисунке 3 показано построение двуполостного гиперболоида, заданного уравнением x² / 4 — y² / 9 — z² / 1 = 1.

pис. 3

4. Гиперболический параболоид
Каноническое уравнение: z = x² / a² — y² / b².
На рисунке 4 показано построение гиперболического параболоида, заданного уравнением z = x² — y².

pис. 4

Задание: Постройте эллиптический параболоид. Каноническое уравнение z = x² / a² + y² / b².

Быстрая навигация:

Лабораторные работы по Mathematica Построение графиков ф-й ч.I Построение графиков ф-й ч.II Решение уравнений Суммы и произведения Пределы Производные Определенные интегралы Трехмерные поверхности Кратные интегралы Разложение функции в ряд Матрицы и операции с ними Дифференциальные уравнения Правильные многогранники Полуправильные многогранники Звездчатые многогранники

набросок-график-функции-которая-удовлетворяет-всем-следующим-условиям — Googlesuche из следующих …

cf.linnbenton.edu › mathsci › math › maurerv › upload

Нарисуйте график одной функции, которая удовлетворяет ВСЕМ следующим условиям. (Возможно много правильных ответов.).

Нарисуйте график, удовлетворяющий предельным условиям — YouTube

www. youtube.com › смотреть

02.09.2018 · Графики кусочных функций, домен и диапазон — пределы, непрерывность и абсолютное значение … график примера функции, удовлетворяющей… — YouTube

www.youtube.com › смотреть

09.08.2020 · Нарисовать график примера функции, удовлетворяющей всем заданным условиям.lim x …
Дата: 1:31
Прислан: 09.08.2020

Набросок графика функции, удовлетворяющей заданным условиям

www.youtube.com › смотреть

15.01.2017 · Ваш браузер не может воспроизвести это видео. Узнать больше. Переключить камеру.
Dauer: 5:02
Прислано: 15.01.2017

Нарисуйте график, удовлетворяющий следующим условиям условия, кроме № 3, который находится в (0, −1), что является изолированной точкой. Но ваш график имеет несколько значений y …

нарисуйте график функции, удовлетворяющей всем заданным условиям

www.wyzant.com › Ресурсы › Спросите эксперта

Наклон функции f(x) при x=0, 2 и 5 равен 0. То есть наклон горизонтальный. То есть в этих точках есть максимум или минимум.

Ähnliche Fragen

При каких условиях график представляет функцию?

Как определить, является ли каждый график графиком функции?

нарисуйте график функции, удовлетворяющей всем следующим условиям.

www.wyzant.com › Ресурсы › Спросите эксперта

1. limx—> -1 f (x)=3 2. f разрывна в точке -1 3. область определения f равна (- бесконечности, + бесконечность) 4. limx—>- бесконечность f (x) = 5

[решено] Нарисуйте график функции, удовлетворяющей всем заданным

www.studocu.com › en-us › сообщения › вопрос › s…

Условие «f »(x) < 0, если x < 1 или x > 3» говорит о том, что функция вогнута вниз на интервалах (-∞,1) и (3, ∞). Сочетая вышеуказанные условия, …

Решено Нарисуйте график функции, удовлетворяющей всем условиям | Chegg.com

www.chegg.com › вопросы и ответы › sketch-g…

Вопрос: Нарисуйте график функции, удовлетворяющей всем заданным условиям. f'(0) = f'(2) = f'(4) = 0, f'(x)> 0, если x < 0 или 2 < x < 4, f'(x) < 0, если 0 < ..

Нарисуйте график функции, удовлетворяющей всем заданным условиям.

homework.study.com › … › Точка перегиба 92/x * I(x<0. На рис. 1 приведен график кусочно-непрерывной ...

Ähnlichesuchanfragen

Нарисуйте график функции, удовлетворяющей всем заданным условиям. Ограничения

Нарисуйте график функции Калькулятор пределов, удовлетворяющий заданным условиям

Нарисуйте график функции f, удовлетворяющей всем следующим условиям

Нарисуйте график, удовлетворяющий следующим условиям.0003

Нарисуйте график непрерывной функции, удовлетворяющей следующим условиям

Нарисуйте график с использованием пределов pdf

Нарисуйте график, удовлетворяющий следующим условиям производных

График по точкам

3.2 График по точкам

Цели обучения

1. Проверка решений линейных уравнений с двумя переменными.
2. Линии графика по точкам.
3. Определите и начертите горизонтальные и вертикальные линии.

Решения уравнений с двумя переменными

Линейное уравнение с двумя переменнымиУравнение с двумя переменными, которое можно записать в стандартной форме ax+by=c, где действительные числа a и b не равны нулю. имеет стандартную форму ax+by=c, где a , b и c — действительные числа, а a и b не оба равны 0. Решениями уравнений этой формы являются упорядоченные пары ( x ,  y ), где координаты при подстановке в уравнение дают верное утверждение.

 

Пример 1: Определите, являются ли (1, −2) и (−4, 1) решениями уравнения 6x−3y=12.

Решение: Подставьте значения x — и y в уравнение, чтобы определить, дает ли упорядоченная пара истинное утверждение.

Ответ: (1, −2) — решение, а (−4, 1) — нет.

 

Часто линейное уравнение задается в форме, где одна из переменных, обычно у , изолирован. Если это так, то мы можем проверить, что упорядоченная пара является решением, подставив значение одной из координат и упростив, чтобы увидеть, получим ли мы другое.

 

Пример 2: Являются ли ( 12, −3) и (−5, 14) решениями уравнения y=2x−4?

Решение: Подставьте значения x и упростите, чтобы увидеть, получаются ли соответствующие значения y .

Ответ: ( 12, −3) — решение, а (−5, 14) — нет.

 

Попробуйте! Является ли (6, −1) решением уравнения y=−23x+3?

Ответ: Да

Решение для видео

(нажмите, чтобы посмотреть видео)

Когда заданы линейные уравнения с двумя переменными, мы можем решить для одной из переменных, обычно y , и получить эквивалентное уравнение следующим образом:

Записав эту форму, мы увидим, что

y зависит от x . Здесь x — это независимая переменная. Переменная, которая определяет значения других переменных. Обычно мы думаем о x — значение как независимая переменная. а y — зависимая переменная. Переменная, значение которой определяется значением независимой переменной. Обычно мы рассматриваем значение y как зависимую переменную.

Линейное уравнение y=2x−4 можно использовать для поиска упорядоченных парных решений. Если мы заменим x любым вещественным числом, то сможем упростить поиск соответствующего значения y . Например, если x=3, то y=2(3)−4=6−4=2, и мы можем сформировать упорядоченное парное решение (3, 2). Так как есть бесконечно много действительных чисел, которые можно выбрать для x линейное уравнение имеет бесконечно много упорядоченных парных решений ( x ,

y ).

 

Пример 3: Найдите упорядоченные парные решения уравнения 5x−y=14 с заданными x -значениями {−2, −1, 0, 4, 6}.

Решение: Сначала найдите y .

Затем подставьте значения x в уравнение y=5x−14, чтобы найти соответствующие значения y .

Ответ: {(−2, −24), (−1, −19), (0, −14), (4, 6), (6, 16)}

 

В предыдущем примере даны определенные x -значения, но это не всегда так. Рассматривая x как независимую переменную, мы можем выбрать любые значения для x , а затем подставить их в уравнение, чтобы найти соответствующие значения y . Этот метод дает столько упорядоченных парных решений, сколько нам нужно.

 

Пример 4: Найдите пять упорядоченных парных решений уравнения 6x+2y=10.

Решение: Сначала найдите y .

Затем выберите любой набор значений x . Обычно мы выбираем некоторые отрицательные значения и некоторые положительные значения. В этом случае мы найдем соответствующие y -значения, когда x равно {−2, −1, 0, 1, 2}. Сделайте замены, необходимые для заполнения следующей таблицы (часто называемой t-диаграммой):

Ответ: {(−2, 11), (−1, 8), (0, 5), (1, 2 ), (2, −1)}. Поскольку существует бесконечно много упорядоченных парных решений, ответы могут различаться в зависимости от выбора значений независимой переменной.

 

Попробуйте! Найдите пять упорядоченных парных решений уравнения 10x−2y=2.

Ответ: {(−2, −11), (−1, −6), (0, −1), (1, 4), (2, 9)} ( ответы могут отличаться )

Видеорешение

(нажмите, чтобы посмотреть видео)

График по точкам

Поскольку решения линейных уравнений представляют собой упорядоченные пары, их можно изобразить в прямоугольной системе координат. Множество всех решений линейного уравнения можно представить на прямоугольной координатной плоскости с помощью прямой линии, соединяющей не менее двух точек; эта линия называется ее графиком. Точка на числовой прямой, связанная с координатой. Чтобы проиллюстрировать это, постройте пять упорядоченных парных решений, {(−2, 11), (−1, 8), (0, 5), (1 , 2), (2, −1)}, к линейному уравнению 6x+2y=10.

Обратите внимание, что точки лежат на одной прямой; это будет иметь место для любого линейного уравнения. Проведите линию через точки с помощью линейки и добавьте стрелки на обоих концах, чтобы указать, что график продолжается бесконечно.

Полученная линия представляет все решения уравнения 6x+2y=10, которых бесконечно много. Шаги для построения линий с помощью точек показаны в следующем примере.

 

Пример 5: Найдите пять упорядоченных парных решений и постройте график: 10x−5y=10.

Решение:

Шаг 1: Найдите y .

Шаг 2 : Выберите не менее двух значений x и найдите соответствующие значения y . В этом разделе мы выберем пять действительных чисел для использования в качестве значений x . Рекомендуется выбирать 0 и некоторые отрицательные числа, а также некоторые положительные числа.

Пять упорядоченных парных решений: {(−2, −6), (−1, −4), (0, −2), (1, 0), (2, 2)}

Шаг 3: Выберите подходящий масштаб, нанесите точки и проведите через них линию с помощью линейки. В этом случае выберите шкалу, в которой каждая галочка на оси y представляет 2 единицы, поскольку все значения y кратны 2.

Ответ:

Не всегда будет так, что y можно решить в терминах x с целыми коэффициентами. На самом деле коэффициенты часто оказываются дробями.

 

Пример 6: Найдите решения для пяти упорядоченных пар и постройте график: −5x+2y=10.

Решение:

Помните, что вы можете выбрать любое действительное число для независимой переменной x , так что выбирайте здесь с умом. Поскольку знаменатель коэффициента переменной x равен 2, вы можете избежать дробей, выбрав кратные 2 для значений x . В этом случае выберите набор из x -значений {−6, −4, −2, 0, 2} и найдите соответствующие г -значения.

Пять решений: {(−6, −10), (−4, −5), (−2, 0), (0, 5), (2, 10)}. Здесь мы выбираем масштабирование по оси x с числом, кратным 2, и по оси y с числом, кратным 5.

Ответ:

 

Попробуйте! Найдите пять упорядоченных парных решений и постройте график: x+2y=6.

Ответ: {(−2, 4), (0, 3), (2, 2), (4, 1), (6, 0)}

Решение для видео

(нажмите, чтобы посмотреть видео)

Горизонтальные и вертикальные линии

Нам необходимо распознать путем проверки линейные уравнения, которые представляют собой вертикальную или горизонтальную линию.

 

Пример 7: График с пятью точками: y=−2.

Решение: Поскольку в данном уравнении нет переменной x , мы можем переписать его с коэффициентом 0 для x .

Выберите любые пять значений для x и убедитесь, что соответствующее значение y всегда равно −2.

Теперь у нас есть пять упорядоченных парных решений для построения графика {(−2, −2), (−1, −2), (0, −2), (1, −2), (2, −2)}.

Ответ:

Когда коэффициент для переменной x равен 0, график представляет собой горизонтальную линию. В общем, уравнение для горизонтальной линии Любая линия, уравнение которой можно записать в виде y = k , где k — действительное число. можно записать в виде y=k, где k представляет собой любое действительное число.

 

Пример 8: График с пятью точками: x = 3.

Решение: Поскольку в данном уравнении нет переменной y , перепишем его с коэффициентом 0 для y .

Выберите любые пять значений для y и убедитесь, что соответствующее x -значение всегда равно 3.

Теперь у нас есть пять упорядоченных парных решений для построения: {(3, −2), (3, −1) , (3, 0), (3, 1), (3, 2)}.

Ответ:

Когда коэффициент при переменной y равен 0, график представляет собой вертикальную линию. В общем случае уравнение вертикальной линии Любая линия, уравнение которой можно записать в виде x = k , где k — действительное число. можно записать как x=k, где k представляет собой любое действительное число.

Подводя итог, если k действительное число,

 

Попробуйте! Отобразите y=5 и x=−2 на одном наборе осей и определите, где они пересекаются.

Ответ: (−2, 5)

Решение для видео

(нажмите, чтобы посмотреть видео)

Ключевые выводы

• Решения линейных уравнений с двумя переменными ax+by=c представляют собой упорядоченные пары ( x , y ), где координаты при подстановке в уравнение дают верное утверждение.
• Линейные уравнения с двумя переменными имеют бесконечно много упорядоченных парных решений. Когда решения изображены на графике, они коллинеарны.
• Чтобы найти упорядоченные парные решения, выберите значения для независимой переменной, обычно x , и подставьте их в уравнение, чтобы найти соответствующие y -значения.
• Чтобы построить график линейных уравнений, определите как минимум два упорядоченных парных решения и проведите через них линию с помощью линейки.
• Горизонтальные линии описываются как y = k , где k — любое действительное число.
• Вертикальные линии описываются как x = k , где k — любое действительное число.

Тематические упражнения

Часть A: Решения для линейных систем

Определить, является ли заданная точка решением.

1. 5x−2y=4; (−1, 1)

2. 3x−4y=10; (2, −1)

3. −3x+y=−6; (4, 6)

4. −8x−y=24; (−2, −3)

5. −x+y=−7; (5, −2)

6. 9x−3y=6; (0, -2)

7. 12x+13y=-16; (1, −2)

8. 34x−12y=−1; (2, 1)

9. 4x−3y=1; (12, 13)

10. −10x+2y=−95; (15, 110)

11. у=13х+3; (6, 3)

12. y=−4x+1; (−2, 9)

13. y=23x−3; (0, −3)

14. у=-58х+1; (8, -5)

15. у=-12х+34; (−12, 1)

16. y=−13x−12; (12, −23)

17. у=2; (−3, 2)

18. у=4; (4, −4)

19. х=3; (3, −3)

20. х=0; (1, 0)

Найдите упорядоченные парные решения по набору x -значений.

21. у=-2х+4; {−2, 0, 2}

22. y=12x−3; {−4, 0, 4}

23. y=−34x+12; {−2, 0, 2}

24. y=−3x+1; {−1/2, 0, 1/2}

25. у=-4; {−3, 0, 3}

26. у=12х+34; {−1/4, 0, 1/4}

27. 2x−3y=1; {0, 1, 2}

28. 3x−5y=−15; {−5, 0, 5}

29. –x+y=3; {−5, −1, 0}

30. 12x−13y=−4; {−4, −2, 0}

31. 35x+110y=2; {−15, −10, −5}

32. x−y=0; {10, 20, 30}

Найдите упорядоченные парные решения, учитывая набор значений y .

33. у=12х-1; {−5, 0, 5}

34. y=−34x+2; {0, 2, 4}

35. 3x−2y=6; {−3, −1, 0}

36. −x+3y=4; {−4, −2, 0}

37. 13x−12y=−4; {−1, 0, 1}

38. 35x+110y=2; {−20, −10, −5}

Часть B: Линии графика

Учитывая набор x -значений {−2, −1, 0, 1, 2}, найдите соответствующее y — значения и график их.

39. y=x+1

40. y=−x+1

41. y=2x−1

42. y=−3x+2

43. y=5x−10

44. 5x+y=15

45. 3x−y=9

46. 6x−3y=9

47. y=−5

48. y=3

Найдите не менее пяти упорядоченных парных решений и граф.

49. y=2x−1

50. y=−5x+3

51. y=−4x+2

52. y=10x−20

53. y=−900×32

54. y=13x−1

55. y=23x−6

56. y=−23x+2

57. y=x

58. y=−x

55. −2x+55y =−15

60. x+5y=5

61. 6x−y=2

62. 4x+y=12

63. −x+5y=0

64. x+2y=0

65. 110x−y=3

66. 32x+5y=30

Часть C: Горизонтальные и вертикальные линии

at 9013 Найти не менее пяти упорядоченных парных решений и изобразите их графически.

67. y=4

68. y=-10

69. x=4

70. x=-1

71. y=0

3

90.0 x=0 =34

74. x=−54

75. Нарисуйте линии y=−4 и x=2 на одном и том же наборе осей. Где они пересекаются?

76. Нарисуйте линии y=5 и x=-5 на одном наборе осей. Где они пересекаются?

77. Какое уравнение описывает ось x ?

78. Какое уравнение описывает ось y ?

Часть D: Смешанная практика

График по точкам.

79. y=-35x+6

80. y=35x-3

81. y=-3

82. x=-5

83. 3x-2y=6

3

3 2x+3y=−12

Часть E: Темы на доске обсуждений

85.