Построить параболу: Парабола, квадратичная функция. Как решаются квадратные уравнения?

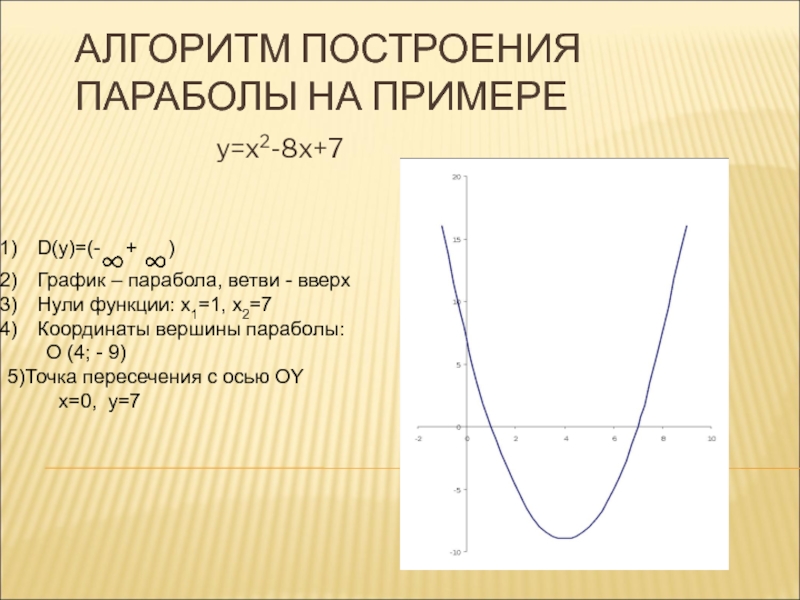
Парабола, её каноническое уравнение, вершина, форма и характеристики параболы

О чем статья

Парабола

Парабола – это множество точек плоскости, которые равноотделённые  от заданной точки, что называется фокусом и заданной прямой под названием директриса.

Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус  на оси  так, чтобы начало координат  помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через  расстояние от фокуса к директрисе, тогда у фокуса будут координаты , .

Для произвольной точки параболы расстояний , а расстояние к директрисе . По определению из рис. 1 видим, что , а и поэтому:

Рис. 1

(1)

– каноническое уравнение параболы.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Что такое вершина параболы

Вершина параболы – это парабола, которая проходит через точки . Если точка принадлежит параболе, то и тоже принадлежит параболе, так как из:

.

Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:

Чтобы найти вершину параболы, необходимо знать формулу: .

Давайте посмотрим, как данная формула действует, допустим дано уравнение:

Тогда:

, , .  Чтобы найти величины , и , в квадратном уравнении коэффициент при , при , постоянная (коэффициент без переменной) = . Если взять тот же пример, , получается, что:

, , .

Форма и характеристики параболы

Исследуем за каноническим уравнением форму и расположение параболы:

1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси .  Ось – это ось, которая симметрична параболе.

2. Так как , тогда , откуда получается, что парабола расположена справа от оси .

3. При мы имеем , то есть парабола проходит через начало координат. Точка – это вершина параболы.

4. При увеличении значений переменной модуль тоже возрастает. Изобразим параболу на рисунке:

Рис. 2

5. В полярной системе координат, у канонического уравнения параболы такой вид:

6. Уравнение , , , тоже описывают параболы:

Рис. 3

Оптическое свойство параболы

У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.

При положительном уравнении:

описывают параболу симметричную относительно с вершиной в точке , ветви которой направлены влево (рис. 3 (а)).

Аналогично изложенному, уравнение и описывают параболы с вершиной в точке симметрично относительно , ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение решить относительно

 и обозначить , тогда получим известное со школьного курса уравнение параболы . Теперь её фокусное расстояние .

Примеры решения

Пример 1

Задача

Найти координаты фокуса и составить уравнение директрисы параболы .

Решение

Сравнивая каноническое уравнение и данное , получим , , тогда. Так как уравнение директрисы , тогда в данном случае .

Ответ

координаты фокуса: , а уравнение директрисы параболы: .

Пример 2

Задача

Составить каноническое уравнение параболы:

а) с фокусом в точке ;

б) с фокусом в точке .

Решение

а). Так как фокус  на положительной полуоси , тогда парабола симметрична относительно с вершиной в точке и , поэтому и согласно формуле (1) .

б). Фокус  лежит на отрицательной полуоси с вершиной в точке , ветви направлены вниз, каноническое уравнение следует искать в виде . Фокусное расстояние параболы и уравнение запишется .

Ответ

а) каноническое уравнение параболы с фокусом в точке :  ;

б) каноническое уравнение с фокусом в точке : .

Пример 3

Задача

Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.

Решение

Выделим относительно переменной полный квадрат

= = = = = = .

Обозначим , .  Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку , получим каноническое уравнение параболы .

Ветви этой параболы направлены вниз симметрично относительно оси , , – фокусное расстояние. В новой системе координат фокус находится в точке , уравнение директрисы в новой системе .

Повернёмся к старым координатам при помощи замены , . Уравнение оси в новой системе , а в старой – уравнение оси параболы.

Уравнение директрисы в новой системе координат , а в старой .

В новой системе для фокуса , , а в старой системе , , то есть .

Ответ

Каноническое уравнение параболы – ;

вершина – ветви параболы направлены вниз;

, , – фокусное расстояние, а фокус находится в точке ;

уравнение оси ;

уравнение директрисы .

Парабола

Параболой называется множество всех точек, расстояния от которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны (рис.2).

Уравнение параболы получается из уравнения кривой второго порядка (1). Если коэффициент В = О, а также один из коэффициентов А или С равен нулю, для определенности пусть А = О, С  0, то есть:

Су² + Dx + Ey + F = 0. (3)

Это уравнение параболы с осью симметрии, перпендикулярно оси ординат.

При А≠0, С=0 получим:

Ax²+Dx + Ey + F = 0.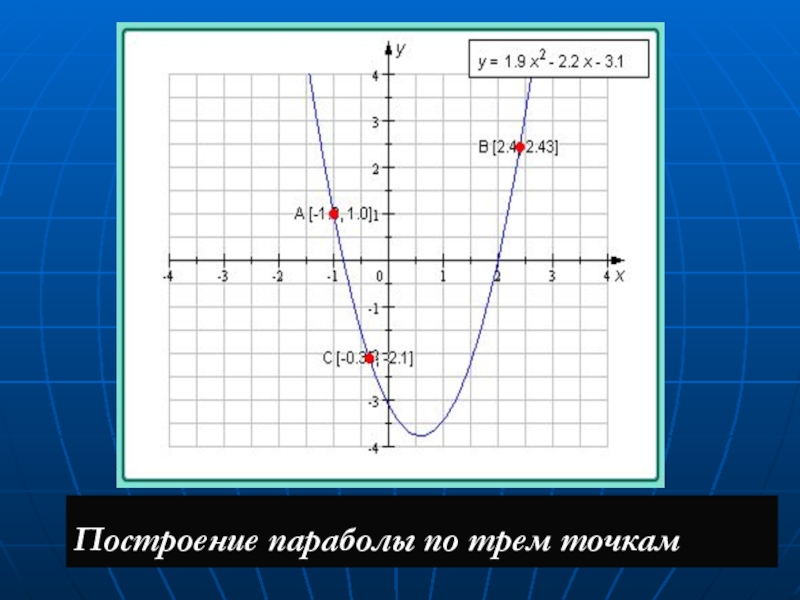 (4)

В данном случае это — уравнение параболы с осью симметрии, перпендикулярной оси абсцисс.

Уравнения (3) и (4) представляют собой общие уравнения параболы. Каноническими уравнениями параболы являются:

у² = 2рх, где р — параметр параболы, расстояние от фокуса до директрисы, для кривой с горизонтально расположенной осью;

х² = 2ру — для параболы с вертикально расположенной осью. Схематичное изображение параболы представлено на рис.2.

Рис. 2. Схематическое изображение параболы

Для построения параболы в MS Excel уравнение параболы должно быть приведено к виду y=f(x) (разрешено относительно переменной y). Построение диаграммы параболы осуществляется по тем же шагам, что и построение окружности.

Задание 1. Построить параболу x²

=12y в диапазоне x  [-4; 4] с шагом h = 0.5

Задание 2. Построить параболу y²=8x в диапазоне x  [-4; 4] с шагом h = 0.5

Кривая второго порядка (1) называется гиперболой, если коэффициенты A и С имеют противоположные знаки, то есть АС < 0.

Характеристическое свойство гиперболы выражается в том, что она является множеством точек, разность расстояний от которых до двух данных точек (F₁, F₂), называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами (рис.3).

Каноническое уравнение гиперболы имеет вид:

Здесь с — расстояние от начала координат до фокусов,

а — расстояние от начала координат до вершин гиперболы.

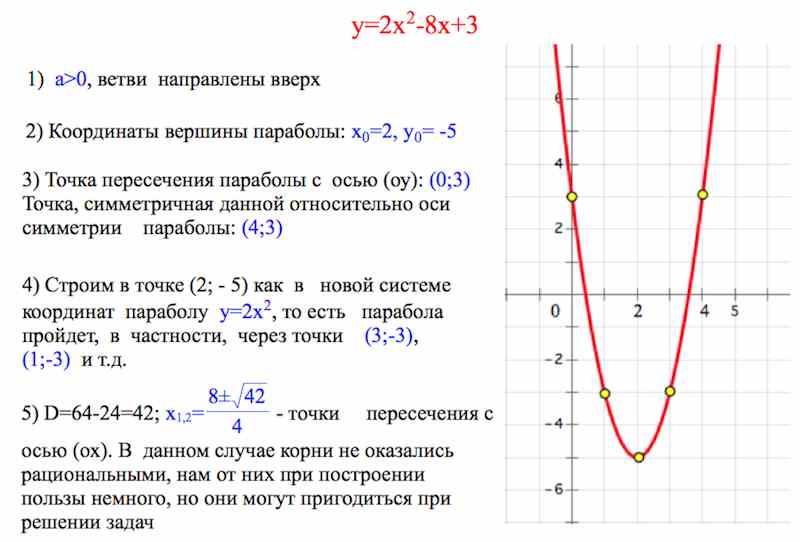
— эксцентриситет,

— асимптоты гиперболы.

Рис. 3. Схематическое изображение гиперболы

В простейшем случае уравнение гиперболы имеет вид .

Задание 3. Построить гиперболу для x  [-10; 10]. Шаг рассчитать самостоятельно, количество точек разбиения отрезка n=20. (, x_i = a + i*h или x_i+1=x_i+h)

Задание 4. Построить гиперболу для x  [0,1; 

5,05] при n=20.

Эллипс

Кривая второго порядка (1) называется эллипсом, если коэффициенты A и С имеют одинаковые знаки, то есть АС > 0. Если коэффициент В также равен нулю, то это эллипс с осями, параллельными координатным осям. Если, кроме того, коэффициенты D = Е = 0, то центр эллипса находится в начале координат.

Обычно в качестве определения эллипса используют его характеристическое свойство: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.

Каноническое уравнение эллипса может быть получено из его определения.

Обозначим постоянную сумму расстояний от фокусов до точек эллипса

2а, а расстояние между фокусами — 2с.

Систему координат введем следующим образом: ось х проходит через фокусы, ось у — через середину отрезка F₁F₂ (рис. 4).

Рис. 4. Расположение фокусов и точки на эллипсе (a>c)

Каноническое уравнение эллипса .

Эксцентриситетом эллипса называется величина .

Так как а>с, то , то есть для эллипса, если коэффициент В=0. эксцентриситет <1. Схематичное изображение эллипса представлено на рис.5.

Рис. 5. Схематичное изображение эллипса

Построение эллипса в MS Excel аналогично построению окружности.

Задание 5. Построить эллипс диапазон и шаг выбрать самостоятельно.

Калькулятор параболы

Авторы: Богна Шик и Войцех Сас, доктор философии

Отзыв Стивена Вудинга и Джека Боуотера

Последнее обновление: 10 февраля 2023 г.

Содержание:

• Что такое парабола?
• Уравнение параболы в вершинной форме
• Фокус параболы и директриса
• Как использовать калькулятор уравнения параболы: пример калькулятор параболы, чтобы быть идеальным инструментом для вас. Он не только предоставит вам уравнение параболы как в стандартной форме , так и в форме вершины , но также вычислить для вас вершину параболы, фокус и директрису.

  Что такое парабола?

  источник: Wikimedia

  Парабола — это U-образная симметричная кривая . Его основное свойство состоит в том, что каждая точка, лежащая на параболе, равноудалена как от некоторой точки, называемой фокусом параболы, так и от прямой, называемой ее директрисой. Это также кривая, соответствующая квадратным уравнениям.

  Ось симметрии параболы всегда перпендикулярна директрисе и проходит через точку фокусировки. Вершина параболы — это точка, в которой парабола делает самый крутой поворот; он находится на полпути между фокусом и директрисой.

  Реальным примером параболы является траектория, прочерченная объектом, движущимся снарядом.

  Уравнение параболы в форме вершины

  Стандартная форма квадратного уравнения: y = ax² + bx + c . Вы можете использовать этот калькулятор вершин, чтобы преобразовать это уравнение в вершинную форму, которая позволит вам найти важные точки параболы — ее вершину и фокус.

  Уравнение параболы в его вершинной форме имеет вид y = a(x - h)² + k , где:

  • a — То же, что и коэффициент a в стандартной форме;
  • h — x-координата вершины параболы; и
  • k — координата y вершины параболы.

  Вы можете рассчитать значения

  h и k из следующих уравнений:

  h = - b/(2a)

  k = c - b²/(4a)

  Фокус и директриса параболы

  Калькулятор формы вершины параболы также находит фокус и директрису параболы. Все, что вам нужно сделать, это использовать следующие уравнения:

  • Координата x фокуса: x₀ = — b/(2a) ;
  • Координата Y фокуса: y₀ = c — (b² — 1)/(4a) ; и
  • Уравнение директрисы: y = c — (b² + 1)/(4a) .

  Как пользоваться калькулятором уравнения параболы: пример

  1. Введите коэффициенты a, b и c стандартной формы вашего квадратного уравнения. Предположим, что уравнение y = 2x² + 3x — 4 , что означает, что a = 2, b = 3 и c = -4.

  2. Рассчитайте координаты вершины, используя приведенные выше формулы:

     ч = — б/(2а) = -3/4 = -0,75

     k = c — b²/(4a) = -4 — 9/8 = -5,125

  3. Найдите координаты фокуса параболы. Координата x фокуса такая же, как у вершины (x₀ = -0,75), а координата y:

     y₀ = c — (b² — 1)/(4a) = -4 — (9-1)/8 = -5

  4. Найдите директрису параболы. Вы можете использовать калькулятор параболы, чтобы сделать это за вас, или вы можете использовать уравнение:

     y = c — (b² + 1)/(4a) = -4 — (9+1)/8 = -5,25

  Если вы хотите узнать больше о понятиях координатной геометрии, мы рекомендуем проверить калькулятор средней скорости изменения и калькулятор прямой кишки.

  Часто задаваемые вопросы

  Что такое парабола?

  Парабола представляет собой симметричную U-образную кривую, каждая точка которой равноудалена от директрисы и фокуса.

  Как определить параболу?

  Парабола определяется уравнением, которому удовлетворяет каждая точка кривой. Математически y = ax² + bx + c .

  Как вычислить вершину параболы?

  Для вычисления вершины параболы, заданной координатами (x, y):

  1. Найдите координату x, используя формулу оси симметрии:

     х₀ = — б/(2а)

  2. Найдите координату y, используя уравнение параболы:

     y₀ = c — (b² — 1)/(4a)

  Как рассчитать фокус параболы?

  Чтобы вычислить фокус параболы, заданной координатами (x, y):

  1. Найдите координату y по формуле y = c - (b² + 1)/(4a) .
  2. Найдите координату x, используя уравнение параболы.

     No related posts.