Аналитическая геометрия
Глава 2 Глава 4
3.7 Парабола 3.9 Касательные
 
Для кривых второго порядка — эллипса, гиперболы и параболы — можно получить простое описание в полярных координатах. Для этого надо поместить начало координат в фокусе (мы выбираем правый фокус) и полярную ось совместить с положительным направлением оси $x$.
 
Рис 8: Эллипс в полярной системе координат.
 
1. Эллипс.
Описанная система координат изображена на рис. 8. При обсуждении эллипса была получена формула для фокального радиуса: $\rho = a-\varepsilon x$. Из рисунка следует: $x=c+\rho \cos \varphi$. Подставляя, получаем:
\[
\rho = a-\varepsilon c-\varepsilon \rho \cos \varphi.
\]
Собирая слагаемые с $\rho $, приходим к уравнению
\[
\rho=\frac{p}{1+\varepsilon \cos \varphi}, \quad p=a-\varepsilon c.
 
Рис 9: Гипербола в полярной системе координат.
 
Для гиперболы имеем, согласно проведенным выше вычислениям, $\rho = \varepsilon x-a$. Из картинки 9 следует, что $x=c+\rho \cos \varphi$. Подставляя это значение и собирая слагаемые с $\rho $, получаем:
\[
\rho =\frac{p}{1+\varepsilon \cos \varphi}, \quad p=a-\varepsilon c,
\]
уравнение гиперболы в полярной системе координат. Формально это уравнение совпадает с уравнением эллипса, однако имеется важное отличие: $\varepsilon >1$. Это означает, что есть углы, для которых знаменатель отрицателен — при этих значениях угла гипербола не имеет точек. Для двух значений угла знаменатель обращается в 0, так что при этих углах $\rho$ обращается в бесконечность.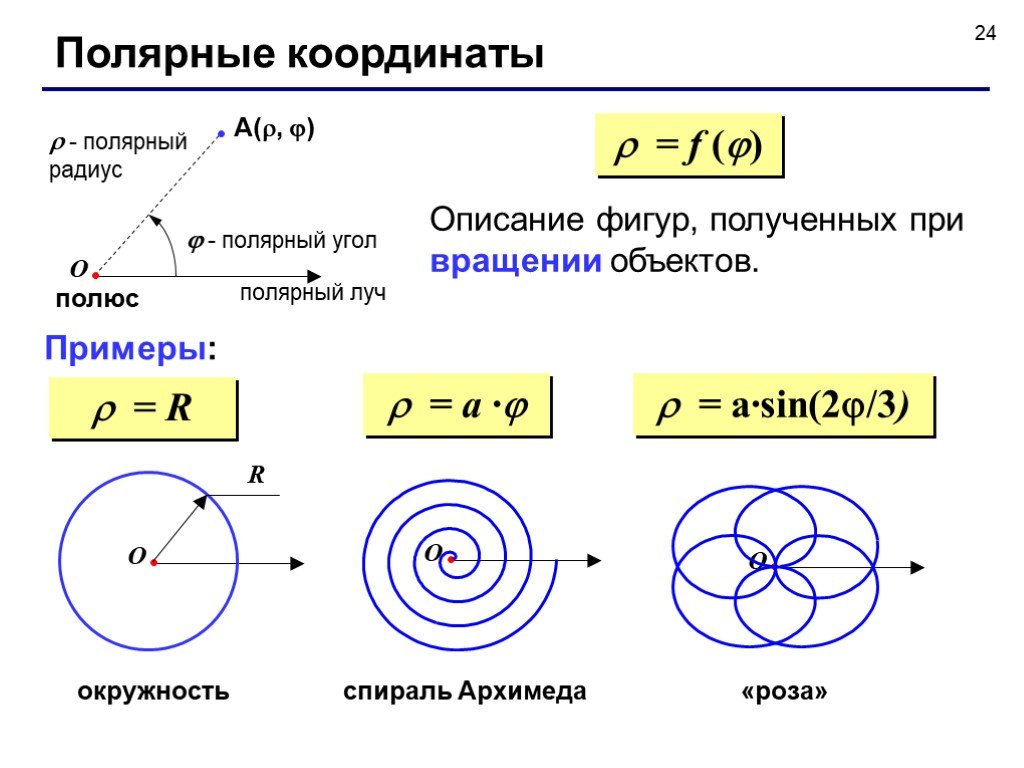
3. Парабола.
 
Рис 10: Парабола в полярной системе координат.
 
Пусть точка $M=(x,y)$ лежит на параболе. Согласно приведенным выше вычислениям, $\rho = x+p/2$, а согласно картинке 10 имеем: $x=p/2 +\rho \cos \varphi $. Подставляя в первое соотношение и собирая слагаемые с $\rho$, получаем:
\[
\rho =\frac{p}{1-\cos \varphi}.
\]
Это и есть уравнение параболы в полярной системе координат. Отметим, что только при $\varphi = 0 $ знаменатель обращается в ноль, что соответствует обращению в $\infty$ величины $\rho$. Таким образом, парабола также содержит бесконечно удаленные точки.
Отметим, что уравнения всех трех кривых в полярной системе координат по существу совпадают — отличается только один коэффициент в знаменателе, точнее, допустимые значения этого параметра.
 
3.7 Парабола 3.9 Касательные
 
Уравнение эллипса, гиперболы, параболы в полярной системе координат.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пример.
Пусть $\Gamma -$ эллипс, ветвь гиперболы или парабола, $F -$ фокус этой кривой, $D -$ соответствующая директриса. Вывести уравнение кривой $\Gamma$ в полярной системе координат, полюс которой совпадает с фокусом а полярная ось сонаправлена с осью кривой (см рисунок 1).
Решение.
Общее свойство эллипса, гиперболы и параболы состоит в следующем $$M\in\Gamma\Leftrightarrow\frac{\rho(M, F)}{\rho(M, D)}=const=e,\qquad\qquad (1)$$где $e -$ эксцентриситет кривой ( $e<1$ для эллипса, $e>1$ для гиперболы и $e=1$ для параболы)
Обозначим расстояние от фокусы до директрисы через $\frac{p}{e}$( $p-$ параметр кривой, называемый полуфокальным параметром).
2}=\sqrt{25-16}=3.$
$e=\frac{c}{a}=\frac{3}{5}.$
Расстояние от фокуса до директрисы $\frac{p}{e}=\frac{a}{e}-c\Rightarrow p=e\left(\frac{a}{e}-c\right)\Rightarrow p=\frac{3}{5}\left(\frac{5}{\frac{3}{5}-3}\right)=\frac{3}{5}\cdot\frac{25-9}{3}=\frac{16}{5}.$
Далее, подставляя найденные параметры в полярное уравнение (2), найденное в предыдущей задаче, найдем уравнение данного эллипса:
$$r=\frac{\frac{16}{5}}{1-\frac{3}{5}\cos\varphi}=\frac{16}{5-3\cos\varphi}.$$
Ответ: $r=\frac{16}{5-3\cos\varphi}.$
{jumi[*4]}
2.324(а).
Написать каноническое уравнение кривой второго порядка $r=\frac{9}{5-4\cos\varphi}.$
Решение.
Приведем заданное уравнение, к уравнению вида $r=\frac{p}{1-e\cos\varphi}:$
$$r=\frac{9}{5-4\cos\varphi}=\frac{9}{5(1-\frac{4}{5}\cos\varphi)}=\frac{\frac{9}{5}}{1-\frac{4}{5}\cos\varphi}.$$
Отсюда имеем: $e=\frac{4}{5},$ $p=\frac{9}{5}.$ Поскольку $e<1,$ то данная кривая — эллипс.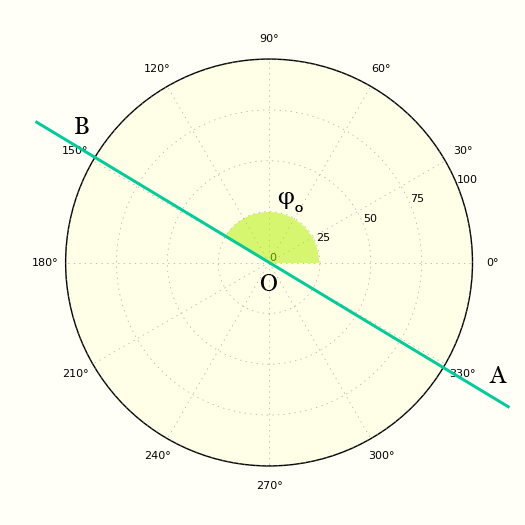
2\varphi}.$
Исчисление II — Параметрические уравнения и полярные координаты
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
В этом разделе мы рассмотрим параметрические уравнения и полярные координаты.
Хотя на первый взгляд кажется, что у этих двух предметов не так уж много общего, мы увидим, что некоторые темы в полярных координатах можно решить с помощью параметрических уравнений, и поэтому в этом смысле они хорошо подходят друг другу в этой главе 9.0003
Мы также рассмотрим, как решать многие стандартные задачи исчисления, такие как касательные и площадь, в терминах параметрических уравнений и полярных координат.
Вот список тем, которые мы рассмотрим в этой главе.
Параметрические уравнения и кривые. В этом разделе мы познакомимся с параметрическими уравнениями и параметрическими кривыми (т. е. графиками параметрических уравнений). Мы изобразим несколько наборов параметрических уравнений и обсудим, как исключить параметр, чтобы получить алгебраическое уравнение, которое часто помогает в процессе построения графика. 9{2}}\) для параметрических кривых. Мы также обсудим использование этих производных формул для нахождения касательной для параметрических кривых, а также определение того, где параметрическая кривая возрастает/убывает и вогнута вверх/вогнута вниз.
Площадь с помощью параметрических уравнений. В этом разделе мы обсудим, как найти площадь между параметрической кривой и осью \(x\), используя только параметрические уравнения (вместо исключения параметра и использования стандартных методов исчисления I на полученное алгебраическое уравнение).
Длина дуги с помощью параметрических уравнений. В этом разделе мы обсудим, как найти длину дуги параметрической кривой, используя только параметрические уравнения (вместо исключения параметра и использования стандартных методов исчисления для полученного алгебраического уравнения).
Площадь поверхности с помощью параметрических уравнений. В этом разделе мы обсудим, как найти площадь поверхности твердого тела, полученную путем вращения параметрической кривой вокруг оси \(x\) или \(y\), используя только параметрические уравнения ( вместо того, чтобы исключить параметр и использовать стандартные методы исчисления для полученного алгебраического уравнения).
Полярные координаты.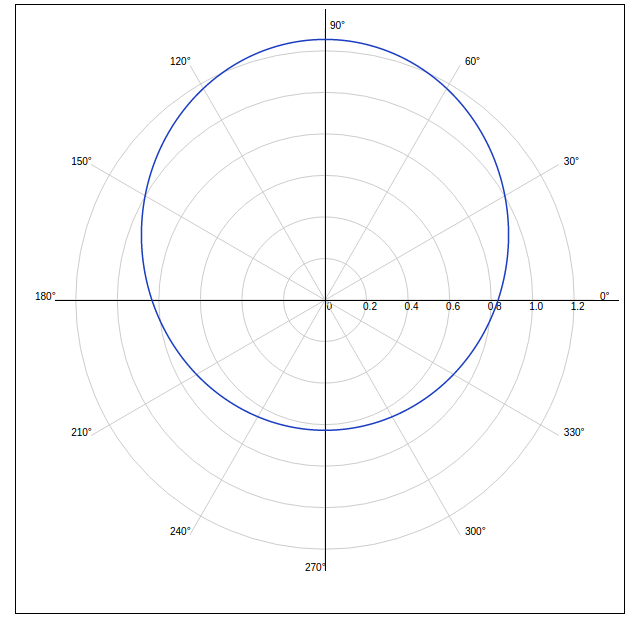
Касательные с полярными координатами. В этом разделе мы обсудим, как найти производную \(\frac{dy}{dx}\) для полярных кривых. Мы также обсудим использование этой формулы производной для нахождения касательной к полярным кривым, используя только полярные координаты (вместо преобразования в декартовы координаты и использования стандартных методов исчисления).
Область с полярными координатами. В этом разделе мы обсудим, как определить область, ограниченную полярной кривой. Области, которые мы рассматриваем в этом разделе, имеют тенденцию (хотя и не всегда) иметь смутную форму, напоминающую кусок пирога или пиццы, и мы ищем площадь области от внешней границы (определяемой полярным уравнением) и начала координат.
Длина дуги с полярными координатами. В этом разделе мы обсудим, как найти длину дуги полярной кривой, используя только полярные координаты (вместо преобразования в декартовы координаты и использования стандартных методов исчисления).
Площадь поверхности с полярными координатами. В этом разделе мы обсудим, как найти площадь поверхности твердого тела, полученную путем вращения полярной кривой вокруг оси \(x\) или \(y\), используя только полярные координаты (а не чем преобразование в декартовы координаты и использование стандартных методов исчисления).
Новый взгляд на длину дуги и площадь поверхности. В этом разделе мы обобщим все формулы длины дуги и площади поверхности, которые мы разработали в течение последних двух глав.
4 лучших способа привлечь внимание с помощью TI-84 Plus
Опубликовано 05.02.2018 автором Kimberly Gonzales
Студенты и преподаватели часто задают нам этот вопрос: как рисовать такие предметы, как сердечки и цветы, на графическом калькуляторе TI? В честь Дня святого Валентина мы здесь, чтобы поделиться любовью и научить вас, как превратить калькулятор TI в любовную записку.
Ваши одноклассники будут падать в обморок от этих красочных творений.
Для начала вам необходимо перевести графический калькулятор TI-84 Plus в полярный режим. Нажмите режим ключ, затем нажимайте кнопку со стрелкой вниз, пока не дойдете до ФУНКЦИИ, затем переместитесь на 2 пробела вправо до ПОЛЯР и нажмите введите . Теперь вы в правильном настроении режиме 😊.
1: Загипнотизируйте свою любимую
Используйте свой калькулятор, чтобы построить спираль, которая обязательно привлечет внимание этого особенного человека.
Нажмите клавишу y= . В r1 введите θ, нажав « X,T,θ,n «. Затем нажмите клавишу окна . Затем в θmax попробуйте ввести 5π. Затем нажмите клавишу масштабирования . Используйте стрелку вниз, чтобы перейти к ZoomFIT. Работает в любом случае.
Хотите спираль побольше? Попробуйте изменить θmax на большее число.
2: Обнимите этих бабочек
Влюбленность обычно приходит вместе с бабочками? Так почему бы не научиться как построить кривую бабочки:
Для этого нажмите клавишу y= . Затем в r1 введите уравнение для кривой бабочки выше. Затем нажмите клавишу масштабирования . Снова нажмите 0 или стрелку вниз до ZoomFIT. Теперь вы должны чувствовать себя нечетко внутри.
3: Не покупайте цветы, граф первый!
Пошлите своей валентинке цветок, нарисовав один из них на калькуляторе TI.
Нажмите кнопку y= ключ. В r1 введите cos(2θ) . Затем в r2 введите sin(2θ) . Затем нажмите клавишу масштабирования . Затем вам нужно будет ввести 0 или ZoomFIT, чтобы завершить свой шедевр.